Detecting Heavy Higgs Bosons from Natural SUSY
at a 100 TeV Hadron Collider

With the discovery of the 125 GeV Standard Model-like Higgs boson at LHC higgs , all the particle states required by the Standard Model (SM) have been confirmed. And yet, many mysteries of nature still remain unsolved. Supersymmetric extensions of the SM are highly motivated in that they offer a solution to the gauge hierarchy problem (GHP) ghp which arises from the quadratic sensitivity of the Higgs boson mass to high scale physics. SUSY models are also supported indirectly by various precision measurements within the SM: 1. the weak scale gauge couplings nearly unify under renormalization group evolution at energy scale $m_{GUT}\simeq 2\times 10^{16}$ GeV in the MSSM, but not the SM gcu , 2. the measured value of top quark mass falls within the range needed to initiate a radiative breakdown of electroweak symmetry in the MSSM top , 3. the measured value of the Higgs boson mass $m_{h}\simeq 125$ GeV falls within the narrow range of MSSM predicted values mhiggs , and 4. precision electroweak measurements actually favor heavy SUSY over the SM sven .

Recent LHC searches with $\sqrt{s}=$ 13 TeV and integrated luminosity $L=139\;{\rm fb}^{-1}$ have put lower bounds on the mass of the gluino of about 2.2 TeV atlasg ; cmsg and on the mass of top squark of about 1.1 TeV atlast ; cmst . These limits, which have been obtained using simplified model analyses assuming that the sparticle spectrum is not compressed, fall well above upper bounds derived from early naturalness considerations bg ; dg ; ac ; unn1 ; unn . However, the naturalness estimates from the log-derivative measure are highly dependent on what one regards as independent parameters of the theory dew .¹¹1The various soft SUSY breaking terms which are adopted for the log-derivative measure are introduced to parameterize one’s ignorance of how soft terms arise. In more UV-complete models such as string theory, then the various soft terms are all calculable and not independent. Ignoring this could result in an over-estimate of the UV sensitivity of the theory by orders of magnitude. We adopt the more conservative quantity $\Delta_{EW}$, that allows for the possibility of correlations among model parameters, as a measure of naturalness rns . $\Delta_{EW}$ can be extracted from Eq. (1),

which relates the mass of Standard Model $Z$ boson to SUSY Lagrangian parameters at the weak scale and is obtained from the minimization conditions of the MSSM scalar potential baerbook . The electroweak fine-tuning parameter $\Delta_{EW}$ is defined by,

The condition for naturalness is that the maximal contribution to the $Z$ mass should be within a factor of several of its measured value. We consider spectra that yield $\Delta_{EW}>\Delta_{EW}(\rm max)=30$ as fine-tuned upper .

This condition then requires :

• •

  the SUSY-conserving $\mu$ parameter $\approx$ 110-350 GeV;

• •

  the up-Higgs soft mass term $m_{H_{u}}^{2}$ may be large at high scales but can be radiatively-driven to (negative) natural values $\sim-m_{weak}^{2}$ at the weak scale;

• •

  The finite radiative correction $\Sigma_{u}^{u}(\tilde{t}_{1,2})$ has an upper bound of $(350$ GeV)² which is possible even for $m_{\tilde{t}}$ up to 3 TeV and $m_{\tilde{g}}$ $\approx$ 6 TeV bounds , compatible with LHC constraints;

• •

  the heavy Higgs masses $m_{A,H,H^{\pm}}\sim|m_{H_{d}}|$, with $|m_{H_{d}}|/\tan\beta\sim{m_{Z}\over\sqrt{2}}\sqrt{\Delta_{EW}}$.

We thus see that naturalness requires bbbms

and further, that for $\tan\beta\sim 5-50$, the heavy Higgs boson masses may be expected to lie in the (multi)-TeV range for an electroweak fine-tuning of up to a part in thirty.

The conditions mentioned above are satisfied in radiatively-driven natural supersymmetric (RNS) models. One of the features of RNS models is that the heavier Higgs bosons may lie in the multi-TeV range while at least some of the electroweakinos (EWinos) are below a few hundred GeV. This means that generically we expect that in natural SUSY models the supersymmetric decay modes of the heavy Higgs bosons should be kinematically accessible, and often with branching fractions comparable to SM decay modes. If SUSY decay modes of the heavy Higgs bosons are allowed, then 1. SM search modes will be suppressed due to the presence of the SUSY decay modes and 2. potentially new avenues for heavy Higgs discovery may open up. This situation was investigated long ago under the supposition that the lightest EWinos were predominantly gaugino-like bbdkt . In Ref. bbkt , a lucrative $A,H\rightarrow\tilde{\chi}_{2}^{0}\tilde{\chi}^{0}_{2}\rightarrow 4\ell+\not{E}_{T}$ search mode was identified for LHC. However, in RNS models, we expect instead that the lightest EWinos to be dominantly higgsino-like.

Thus, we explore here a new possible heavy Higgs discovery channel for SUSY models with light higgsinos. We identify the dominant new SUSY decay mode for heavy neutral Higgs in natural SUSY models as $H,\ A\rightarrow\tilde{\chi}_{1}^{\pm}\tilde{\chi}_{2}^{\mp}$ that proceeds with full gauge strength²²2By full gauge strength, we only mean that the Higgs scalar-higgsino-gaugino vertex is unsuppressed. We recognize, of course, that the overall coupling of the heavy Higgs sector to the gauge boson sector is suppressed by mixing angles in the scalar Higgs sector. (provided that the decay is kinematically allowed). Allowing for chargino cascade decays, then an analogous clean $4\ell+\not{E}_{T}$ signature can be found. It includes leptons from the lighter chargino decay $\tilde{\chi}_{1}^{-}\rightarrow\ell^{-}\bar{\nu}_{\ell}\tilde{\chi}_{1}^{0}$ where the final state leptons are expected to be quite soft in the chargino rest frame due to the expected small mass gap $m_{\tilde{\chi}_{1}^{-}}-m_{\tilde{\chi}_{1}^{0}}$. However, due to $m_{H,A}$ lying in the TeV-range, these final state leptons may be strongly boosted and thus can potentially contribute to the signal. In this paper, we examine the particular reaction $pp\rightarrow H,\ A\rightarrow\tilde{\chi}_{1}^{\pm}\tilde{\chi}_{2}^{\mp}\rightarrow 4\ell+\not{E}_{T}$ where due to the heavy Higgs resonance, we expect $M_{T}(4\ell,\not{E}_{T})$ to be kinematically bounded by $m_{H,A}$ (see Fig. 1). While this reaction will prove difficult to extract at HL-LHC – due in part to the several leptonic branching fractions which are required – we find that discovery in this channel should be possible at the FCC-hhBordry:2018gri or SPPCCEPC-SPPCStudyGroup:2015csa $pp$ collider with $\sqrt{s}\sim 100$ TeV and 15 ab^-1 of integrated luminosity. The FCC-hh or SPPC collider has emerged as the next target hadron collider for CERN after HL-LHC in the updated European strategy report euro .

To be specific, we will adopt a RNS benchmark (BM) point as listed in Table 1, as generated using Isajet 7.88 isajet . This BM comes from the two-extra-parameter non-universal Higgs model NUHM2 nuhm2 . The NUHM2 model parameter space is given by $m_{0},m_{1/2},A_{0},\tan\beta$ along with non-universal Higgs mass soft terms $m_{H_{u}}\neq m_{H_{d}}\neq m_{0}$. Using the EW minimization conditions, it is convenient to trade the high scale soft terms $m_{H_{u}},\ m_{H_{d}}$ for the weak scale parameters $\mu$ and $m_{A}$. This BM point yields $m_{\tilde{g}}\simeq 2.4$ TeV, somewhat beyond the LHC lower limit of 2.2 TeV obtained from a simplified model analysis. The heavy neutral Higgs scalars have mass $m_{H,A}\sim 1.2$ TeV which is somewhat beyond the recent ATLAS limitATLAS-H that requires $m_{H,A}~{}\mbox{\raisebox{-2.58334pt}{$\stackrel{{\scriptstyle>}}{{\sim}}$}}~{}1$ TeV for $\tan\beta=10$ via an $H,\ A\rightarrow\tau^{+}\tau^{-}$ search at $\sqrt{s}=13$ TeV and 139 fb^-1 of integrated luminosity (while assuming no SUSY decay modes of the heavy Higgs bosons). Also, the SUSY $\mu$ parameter is taken to be $\mu=200$ GeV so that the BM point lies just beyond the recent analyses of the soft dilepton plus monojet higgsino signallhcsoftdilep . For the listed BM point, the lighter EWinos $\tilde{\chi}_{1,2}^{0}$ and $\tilde{\chi}_{1}^{\pm}$ are higgsino-like while $\tilde{\chi}_{3}^{0}$ is bino-like and $\tilde{\chi}_{4}^{0}$ and $\tilde{\chi}_{2}^{\pm}$ are wino-like.

Here, we will focus on the $s$-channel heavy neutral Higgs boson production reactions $pp\rightarrow H,\ A$ which occurs via the gluon-gluon and $b\bar{b}$ fusion subprocesses. Other reactions such as $pp\rightarrow qqH$ (VV fusion reactions) $WH$, $ZH$ and $t\bar{t}H$ all occur at lower rates higgspro and also lead to different final state topologies. Hence, we will not include these in our analysis.

In Fig. 2, we show the heavy neutral Higgs production cross sections at next-to-next-to-leading order (NNLO) in QCD. We adopt the SusHi program Harlander:2012pb ; Harlander:2016hcx ; Harlander:2002wh ; Harlander:2003ai ; Aglietti:2004nj ; Bonciani:2010ms ; Degrassi:2010eu ; Degrassi:2011vq ; Degrassi:2012vt ; Harlander:2005rq ; Chetyrkin:2000yt to generate these results, which include QCD corrections and effects from top and bottom squark loops. Higher order QCD corrections typically boost these cross sections above their leading order estimates. Frame (a) shows results for $\sqrt{s}=14$ TeV while frame (b) shows results for $\sqrt{s}=100$ TeV. We see that even for $\tan\beta=10$, heavy Higgs boson production via $b\bar{b}$ fusion dominates that from gluon fusion. From frame (a), we see that for $m_{A}\sim 800$ GeV, the total production cross sections occur for both $H$ and $A$ production at the $\sim 40$ fb level. As $m_{A}$ increases, the rates fall and are already below the 0.2 fb level for $m_{A}~{}\mbox{\raisebox{-2.58334pt}{$\stackrel{{\scriptstyle>}}{{\sim}}$}}~{}2$ TeV. We can anticipate that once we fold in various leptonic branching fractions and include detector acceptances, we will not expect very high rates for multi-lepton signals from heavy neutral SUSY Higgs bosons at LHC14. In frame (b), we show the results for $\sqrt{s}=100$ TeV. Here, the cross sections are increased by factors of 70-500 as $m_{A}$ varies from 800-2000 GeV.

In this Section, we present some updated heavy neutral and charged Higgs branching fractions which we extract from the Isajet 7.88 code isajet . We adopt the benchmark point from Table 1 except now we allow the heavy Higgs mass $m_{A}$ to vary. In frame (a), we show branching fractions for the heavy neutral scalar $H$. At low $m_{H}$, the SM modes $H\rightarrow b\bar{b}$, $\tau\bar{\tau}$ and $t\bar{t}$ are dominant, with their exact values depending on $\tan\beta$ (large $\tan\beta$ enhances the $b\bar{b}$ and $\tau\bar{\tau}$ modes). For $m_{H}\sim 400-650$ GeV, the SM modes are still dominant even though the light electroweakino modes are open. We can understand this by examining the Higgs sector Lagrangian in the notation of Ref. baerbook , Sec. 8.4:

where ${\cal S}_{i}$ labels various matter and Higgs scalars (labeled by $i$), $\psi_{i}$ is the fermionic superpartner of ${\cal S}_{i}$, and $\lambda_{A}$ is the gaugino with gauge index $A$. Also, $g$ is the gauge coupling for the gauge group and $t_{A}$ are the corresponding gauge group generator matrices. Letting ${\cal S}_{i}$ be the Higgs scalar fields, then we see that the Higgs-EWino coupling is maximal when there is little mixing in that the Higgs fields couple directly to gaugino plus higgsino. Back in Fig. 3(a), for $m_{H}$ small, then the only open decay modes are $H$ to higgsino plus higgsino, and so the coupling must be dynamically suppressed because the gaugino component of the lightest EWinos is very small. Thus the SM modes are still dominant. As $m_{H}$ increases, then the decay to gaugino plus higgsino turns on and the above coupling is unsuppressed (as has also been noted in footnote 2, above). For our choice of SUSY parameters, this happens around $m_{H}\sim 650$ GeV for $H$ decay to higgsino plus bino and around $m_{H}\sim 1050$ GeV for $H$ decay to wino plus higgsino. Since the latter coupling involves the larger $SU(2)_{L}$ gauge coupling, the decay $H\rightarrow$ wino plus higgsino ultimately dominates the branching fraction once it is kinematically allowed. Thus, for $m_{H}~{}\mbox{\raisebox{-2.58334pt}{$\stackrel{{\scriptstyle>}}{{\sim}}$}}~{}1250$ GeV, $H\rightarrow\tilde{\chi}_{1}^{\pm}\tilde{\chi}_{2}^{\mp}$ dominates the branching fraction (blue curve), while decays of $H$ to the lighter neutral higgsino-like neutralino plus the heavier neutral wino or bino-like neutralino (green curve) have a branching fraction about half as large. In this range of $m_{H}$, the SM $H$ decay modes are severely depressed from their two-Higgs doublet (non-SUSY) expectation. This will make heavy Higgs detection via $t\bar{t}$, $b\bar{b}$ and $\tau\bar{\tau}$ much more difficult. On the other hand, it opens up new discovery channels by searching for the dominant $H\rightarrow$ EWino modes.

In Fig. 3(b), we show the same branching fractions except now for the pseudoscalar $A$. The branching fractions look qualitatively similar to those in frame (a) since the same reasoning applies. Thus, the $A$ will decay mainly to SM modes for smaller values of $m_{A}$ even though decays to higgsino-like pairs are available. It is only when decays to gaugino plus higgsino open up that the branching fractions to SUSY modes begin to dominate.

For completeness, we also show in Fig. 3(c) the branching fractions for charged Higgs decays $H^{+}$. As in the previous cases, $H^{+}$ decay to SM modes $t\bar{b}$ and $\tau^{+}\nu_{\tau}$ dominate at low values of $m_{H^{+}}$ even though decay to $\tilde{\chi}_{1}^{+}\tilde{\chi}^{0}_{1,2}$ modes are kinematically allowed. As $m_{H^{+}}$ increases, then decays to $\tilde{\chi}_{1}^{+}\tilde{\chi}^{0}_{3}$ (higgsino-bino) followed by $\tilde{\chi}_{2}^{+}\tilde{\chi}^{0}_{1,2}$ and $\tilde{\chi}^{0}_{4}\tilde{\chi}_{1}^{+}$ (higgsino-wino) turn on and rapidly dominate the decays.

Some dominant heavy neutral Higgs decay branching fractions are shown in Table 2 for the benchmark point shown in Table 1. We see again that for the benchmark point the $H,\ A$ decays to SM modes are suppressed compared to decay rates into gaugino plus higgsino.

In Fig. 4, we combine the $H,\ A$ production rates from Fig. 2 with the Higgs boson and sparticle branching fractions to the $4\ell+\not{E}_{T}$ final state depicted in Fig. 1. We see from Fig. 4(a) that, for $\tan\beta=10$, even without cuts we expect at most $\sim 7$ signal events at HL-LHC, assuming an integrated luminosity of 3000 fb^-1. Moreover, we expect that this will be reduced considerably once detector efficiency and analysis cuts are folded in. However, as we can see from frame (b), the raw signal cross section is larger at the higher energy FCC-hh or SPPC by a factor 150-500 (compared to LHC14), so that with the projected 15 ab^-1 of integrated luminosity, we may hope to be able to extract an observable signal even after cuts. We will, therefore, mostly focus our attention on a 100 TeV $pp$ collider in the remainder of this paper.

The reader may be concerned that our dismissal of the possibility of a signal in the $4\ell+\not{E}_{T}$ channel at LHC14 was based on the event rate for $\tan\beta=10$ when it is well-known that the couplings of the $A$ and $H$ both increase with $\tan\beta$, resulting in an increased rate for $H/A$ production from bottom quark fusion. It should, however, be remembered that the range of $m_{A}$ excluded by the current upper limit on the cross section times branching ratio for the decay $\phi\rightarrow\tau\bar{\tau}$ ($\phi=A,H$) also increases with $\tan\beta$ for this same reason. This is illustrated in Fig. 5 where we show the expectations for the resonant production of tau pairs from the decay of $H/A\rightarrow\tau\bar{\tau}$ versus $m_{A}$ for several values of $tan\beta$. Other parameters are taken to be the same as for the model-line introduced earlier. The horizontal black line is the current ATLAS upper bound on this rate ATLAS-H . We see that while $m_{A}>1.1$ TeV for $\tan\beta=10$, for $\tan\beta=50$, $m_{A}>2$ TeV. Scaling the cross section in the left frame of Fig. 4 by the ratio of the corresponding values of $\tan^{2}\beta$ still leaves us with just a handful of events before cuts at the HL-LHC for currently allowed values of $m_{A}$.

Our signal $pp\rightarrow H,A\rightarrow\chi_{1}^{\pm}\chi_{2}^{\mp}\rightarrow 4\ell+\not{E}_{T}$ contains 4 leptons and missing energy in the final states, where one pair of leptons comes from the decay of a $Z$-boson. Since, as just mentioned, the signal rate is too small at the HL-LHC, we will from now on mostly focus our attention on a 100 TeV $pp$ collider.

Our simplified study has been carried out at parton level. The dominant SM background to the $4\ell+\not{E}_{T}$ events comes from $W^{\pm}W^{\mp}V$, $t\bar{t}V$, $Zh$ and $ZZV$ ($V=W^{\pm},Z,\gamma$). Notice that the partonic final states from the signal, as well as from all the backgrounds other than $t\bar{t}V$ production, are free of any hadronic activity. We use tree-level matrix elements from the HELAS library in Madgraph to evaluate the backgrounds, and then scale our cross section to NLO with $K$-Factors calculated using MCFM  mcfm .⁴⁴4The $K$-factors that we use are, $K_{WWV}=1.36$, $K_{t\bar{t}V}=1.30$, $K_{Zh}=1.40$ and $K_{ZZV}=1.40$. For the $t\bar{t}V$ background we veto events which contain any $b$-jets (i.e. $b$-quarks) with $p_{T}>20$ GeV and $|\eta(b)|<2.5$. This serves as a powerful cut in reducing this background. However, with PDF enhancements, we find that this background becomes the second most dominant background at $\sqrt{s}=$ 100 TeV. $W^{\pm}W^{\mp}V$ proves to be the most dominant background at all energies.

To select events, we identify the isolated leptons if they satisfy

• •

  $p_{T}$ ($\ell_{1}$, $\ell_{2}$, $\ell_{3}$, $\ell_{4}$) $>$ 20 GeV, 10 GeV, 10 GeV, 10 GeV;

• •

  $|\eta|$ ($\ell_{1}$, $\ell_{2}$, $\ell_{3}$, $\ell_{4}$) $<$ 2.5.

We model experimental errors in the measurement of lepton energies by Gaussian smearing electron and muon energies using ATLAS:2013-004 ,

where $\oplus$ denotes addition in quadrature.

Since the signal of interest has a final state of $4\ell+\not{E}_{T}$, we started with a set of minimal cuts, labeled as Cuts A, which include :

• •

  Veto events with $b$-jets $p_{T}$ (jet) $>$ 20 GeV and $|\eta|$ (jet) $<$ 2.5 as already mentioned;

• •

  $\Delta_{R}(j,\ell)>$ 0.4, where $j$ denotes a $b$-quark with $p_{T}<20$ GeV or with $|\eta_{b}|>0.4$, to mimic lepton isolation;

• •

  Invariant mass for two opposite sign same flavor leptons $M_{\ell^{+}\ell^{-}}$ $>$ 10 GeV, to reduce the background from $\gamma^{*}\rightarrow\ell\bar{\ell}$;

• •

  $\not{E}_{T}>125$ GeV.

After applying cut A, the mass distributions and $\not{E}_{T}$ distribution obtained (upon summing $b\bar{b}$ and $gg$ initiated processes) are shown in Fig 6 and 7, respectively.

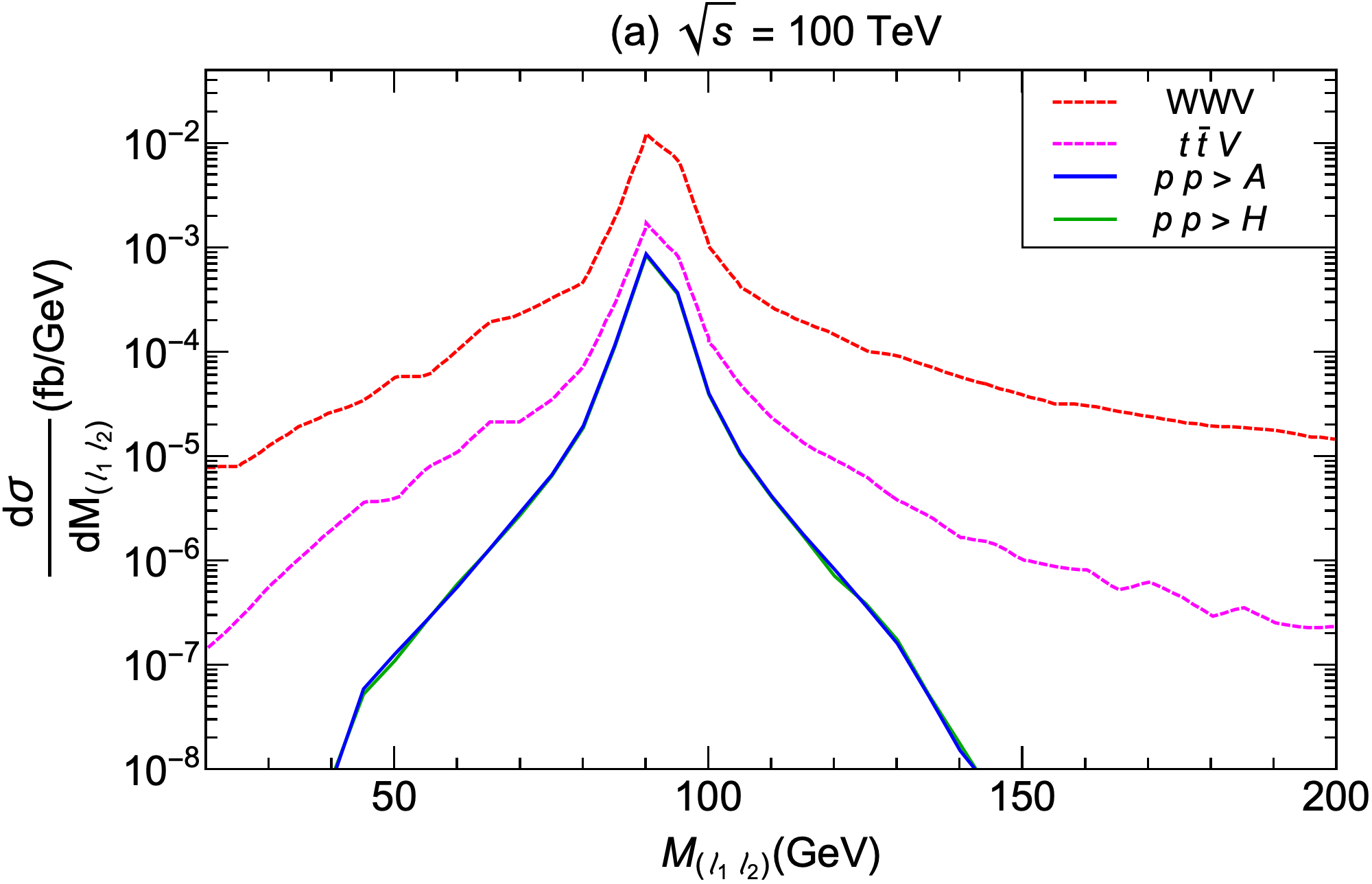
Since neutralinos and neutrinos escape detection (and so serve as sources of missing energy) it is not possible to reconstruct the invariant mass of $H$ or $A$ as a bump in the invariant mass of the final state. We can, however, sharpen the signal by additional cuts. Motivated by Aaboud:2018xdl , we apply $\not{E}_{T}\geq 275$ GeV cut, since we have two neutralinos of mass $\sim$ 100 GeV in the final state. As can be seen from Figs 6 and 7, the following mass cuts and $\not{E}_{T}$ cuts can reduce the SM background very efficiently. Further cuts applied are :

• •

  We define $\ell_{1}$ and $\ell_{2}$ as the two leptons whose invariant mass is closest to $m_{Z}$ and require $|M(\ell_{1},\ell_{2})-m_{Z}|<10$ GeV since the signal includes one $Z$ boson;⁵⁵5Although we do not explicitly require it, for the most part, $\ell_{1}$ and $\ell_{2}$ have opposite sign and same flavour.

• •

  $10<M(\ell_{3},\ell_{4})<75$ GeV, where $\ell_{3}$ and $\ell_{4}$ denotes the remaining leptons.

• •

  $0.14\ m_{A}<M(4\ell)<0.34\ m_{A}$

• •

  $\not{E}_{T}>275$ GeV.

Of course, since $m_{A}$ is not a priori known, the cut on $M(4\ell)$ needs further explanation. Unless $m_{A}$ has already been measured from studies of $A$ or $H$ decays via SM channels, operationally, $m_{A}$ here refers to the upper end point of the signal $M_{T}(4\ell,\not{E}_{T})$ distribution shown in frame (d) of Fig. 6, assuming that it can be experimentally extracted.⁶⁶6We appreciate that the extraction of this end point may be very difficult. Since this is a first exploration of the $4\ell+\not{E}_{T}$ signal from the decay of heavy Higgs bosons in natural SUSY models, we do not attempt to explore the details of the end point determination, but simply assume that it can be extracted from the data. We note that the optimal choice of the $M(4\ell)$ cut would only be weakly sensitive to the lightest neutralino mass for $m_{A,H}\gg m_{\tilde{\chi}^{0}_{1}}$. The cut set A, augmented by the cuts listed above, is labeled as cut set B.

In Fig. 8, we show the signal cross section versus $m_{A}$ after cuts B at (a) the HL-LHC, and (b) a 100 TeV $pp$ collider. We indeed see from frame (a) that for all values of $m_{A}$ the signal lies well below the one event level. Although perhaps only of academic interest, it is worth noting that a comparison of this figure with Fig. 4(a) shows that the signal efficiency is $\sim$ 5-10% despite the requirement all four leptons are required to have a $p_{T}$ of at least 10 GeV. This is a reflection of the boost the electroweakinos, and concomitantly the leptons, gain when they originate in the decays of the heavy Higgs bosons. From Fig. 8(b), we project that at the FCC or at the SPPC with an integrated luminosity of 15 ab^-1, several tens of signal events may be expected after cuts B over most of the range of $m_{A}$ in the figure.

In this section, we study the discovery potential of the $4\ell+\not{E}_{T}$ signal for heavy Higgs bosons at a 100 TeV $pp$ collider using a traditional cut-and-count analysis. To this end, we show in Table 3 our results for the signal after the cut set B for three benchmark points (BPs) with varying $m_{A}$ (with other parameters fixed to their values in Table 1), along with the main sources of SM backgrounds. The subdominant background listed in the fourth-last row is the combined background resulting from SM $Zh$ and from $ZZV$ production.

In Fig. 9, we present our estimates of statistical significance stat ,

for 1100 GeV $\leq m_{A}\leq 2000$ GeV. Our selection cuts work well in removing a large part of the background. We see that with a center of mass energy of 100 TeV and integrated luminosity of $\mathcal{L}$ = 15 $\rm ab^{-1}$, we have enough events to claim a $5\sigma$ discovery for $m_{A}\sim 1.1-1.65$ TeV. We also obtain a 95% CL exclusion limit for the $H,\ A\rightarrow 4\ell+\not{E}_{T}$ signal for values of $m_{A}$ extending out as far as 2 TeV.

We now turn to an examination of whether we can use machine learning techniques to suppress the background further and concomitantly increase the reach. In the next section, we study the use of boosted decision trees to further enhance the signal.

We have just seen that the cut-based signal from heavy Higgs boson decays via the $4\ell+\not{E}_{T}$ channel yields a statistically significant discovery level over a limited range of $m_{A}$ values even at a 100 TeV $pp$ collider. Of course, it is possible that this signal may be combined with a signal from other channels to claim discovery over a wider range. The point of this study, however, is to examine how much improvement may be possible without combining other channels if we go beyond the traditional cut-based analysis which as we saw yields a discovery significance of $N_{ss}>5$ for $m_{A}\sim 1.1-1.65$ TeV for $\sqrt{s}$ = 100 TeV and 15 ab^-1 of integrated luminosity.

It has been found that ML techniques can greatly improve the signal-to-background discrimination and they are widely used by experimental analyses. In this section we use boosted decision trees (BDT) for which algorithms are included in the ToolKit for MultiVariate Analysis (TMVA) TMVA , a multivariate analysis package included with ROOT. For this study, we have used the following variables for training and testing,

• •

  The invariant mass $M(4\ell)$.

• •

  The invariant masses $M(\ell_{1},\ell_{2})$ and $M(\ell_{3},\ell_{4})$

• •

  $\not{E}_{T}$, missing transverse energy.

We have generated signal files for each value of $m_{A}$ along with the backgrounds at 100 TeV after applying the cut set B, except that we have now relaxed the cut on $\not{E}_{T}$ to be $\not{E}_{T}>200$ GeV before passing the samples for training and testing. We train 400,000 signal events and 400,000 background events for each channel. We used the same number of events for testing. Figure 10 shows the BDT response for three BPs with different $m_{A}$ values.

In Table 4, we present our estimate of $N_{ss}$ from the BDT analysis for the same BP points as in Table 3. We see that there is, indeed, a significant improvement over the previous cut-based analysis.

Fig. 11 shows the individual contributions from each of $H$ and $A$ for the BDT analysis along with the significance from the combined $H$ and $A$ signal. This may be compared to the significance shown in Fig. 9 for the traditional cut-and-count analysis. We see that, by using the BDT analysis, we would be able to discover $H$ and $A$ at the $5\sigma$ level via $H,\ A\rightarrow 4\ell+\not{E}_{T}$ channel for $m_{A}\sim 1-2$ TeV – a considerable improvement in range of $m_{A}$ over the usual cut-based method!

In this paper, we have examined heavy neutral Higgs boson discovery as motivated by natural SUSY models with light higgsinos. In such models, the heavy Higgs $H,\ A$ decays to electroweakinos are almost always open since the lightest higgsinos are expected to have masses below $\sim 350$ GeV range whilst the $H$ and $A$ bosons can have TeV-scale masses. Since decays to pairs of higgsino-like states are dynamically suppressed, our channel of primary interest is $H,\ A\rightarrow\tilde{\chi}_{1}^{\pm}\tilde{\chi}_{2}^{\mp}$ decay, followed by $\tilde{\chi}_{2}^{\pm}\rightarrow Z\tilde{\chi}_{1}^{\pm}$ followed by $Z\rightarrow\ell^{+}\ell^{-}$ and then each $\tilde{\chi}_{1}^{\pm}\rightarrow\ell^{\pm}\nu_{\ell}\tilde{\chi}_{1}^{0}$. Combining all flavours of decays to $e$ and $\mu$ leads to a distinctive $H,\ A\rightarrow 4\ell+\not{E}_{T}$ signature for heavy Higgs boson decay to SUSY particles. The leptons from $\tilde{\chi}_{1}^{\pm}$ decay are soft in the $\tilde{\chi}_{1}^{\pm}$ rest frame but are boosted to higher energies due to the large $m_{H,A}$ masses. Thus, we evaluated this signal channel against dominant SM backgrounds for both HL-LHC and for FCC-hh or SPPC with $\sqrt{s}=100$ TeV, applying judicious cuts on various combinations of invariant masses of the leptons, and also requiring $\not{E}_{T}>275$ GeV. Our selection requirements retain much of the signal while removing the physics background efficiently.

In our analysis we have focused on production of the heavy Higgs bosons with a mass ($m_{H}\simeq m_{A}$) between 1 TeV and 2 TeV. While a signal (in the $4\ell+\not{E}_{T}$ channel) is not likely to be observable at HL-LHC, prospects are much better at FCC-hh or SPPC. The best case for discovery is near $m_{A}\simeq 1.2-1.3$ TeV that has a balance between kinematics of leptons in the final state and production cross sections. We note the following:

• •

  A 100 TeV hadron collider offers promise to discover a heavy neutral Higgs boson via one of its dominant SUSY decay modes in natural SUSY models with a mass $\sim 1-2$ TeV. With a conventional cut-based analysis, we are able to obtain a $N_{ss}>5$ statistical significance over a range $m_{A}\sim 1.1-1.65$ TeV. We find though that a BDT analysis of the same signal can potentially improve the significance greatly giving $N_{ss}$ as high as 16 for $m_{A}\simeq~{}1.3$ TeV, and $N_{ss}>5$ over a range $m_{A}\sim 1-2$ TeV even via our proposed very difficult discovery channel.

• •

  For somewhat smaller values of heavy Higgs boson masses characterized by $m_{A}~{}\mbox{\raisebox{-2.58334pt}{$\stackrel{{\scriptstyle<}}{{\sim}}$}}~{}1$ TeV, the signal cross section is suppressed both by smaller branching ratio into the SUSY mode, and also by a smaller boost of the daughter EWinos which, in turn, reduces the efficiency with which the softer leptons pass the cuts. Nonetheless, the heavy neutral SUSY Higgs bosons should be detectable in this range via SM decay modes such as $H,\ A\rightarrow\tau\bar{\tau}$.

• •

  For increasing $m_{A}$ values beyond $\sim 1.3$ TeV, the Higgs production cross section becomes much smaller since the $gg$ and $b\bar{b}$ fusion production cross sections are increasingly suppressed.

• •

  We stress that we have focused only on the signal from a difficult SUSY decay mode of the heavy Higgs boson with an eye to assessing how ML techniques could serve to enhance difficult-to-see signals. Hence we have not examined the possibility of combining SUSY modes or whether the discovery of a heavy Higgs boson might be possible from a study of its SM decays.

For $m_{A}\simeq m_{H}$ significantly beyond 1 TeV and $\tan\beta\sim 10-50$, it may become increasingly challenging to search for heavy Higgs bosons via their decays into SM particles due to the diminished branching fractions to $b\bar{b}$ and $\tau\bar{\tau}$, once the dominant SUSY decay channels become allowed. The chargino and neutralino discovery channel for heavy Higgs bosons at high energy hadron colliders offers an important opportunity to discover the heavy neutral Higgs bosons via their decay into EWinos. An upgrade to a 100 TeV hadron collider seems essential for heavy Higgs $H$ and $A$ discovery via the natural SUSY $4\ell+\not{E}_{T}$ channel.

We thank an anonymous referee for useful suggestions. This work was supported in part by the US Department of Energy, Office of High Energy Physics Grant No. DE-SC-0009956 and DE-SC-0017647. The work of DS was supported in part by the Ministry of Science and Technology (MOST) of Taiwan under Grant No. 110-2811-M-002-574, and work of RJ is supported by MOST 110-2639-M-002-002-ASP.