Detecting Bulk Topology of Quadrupolar Phase from Quench Dynamics
Abstract
Direct measurement of a bulk topological observable in topological phase of matter has been a long-standing issue. Recently, detection of bulk topology through quench dynamics has attracted growing interests. Here, we propose that topological characters of a quantum quadrupole insulator can be read out by quench dynamics. Specifically, we introduce a quantity, a quadrupole moment weighted by the eigenvalues of the chiral operator, which takes zero for the trivial phase and finite for the quadrupolar topological phase. By utilizing an efficient numerical method to track the unitary time evolution, we elucidate that the quantity we propose indeed serves as an indicator of topological character for both noninteracting and interacting cases. The robustness against disorders is also demonstrated.
Introduction.— Understanding topological aspects of quantum matters has been one of the central issues in modern condensed matter physics [1, 2]. Discovery of topological insulators (TIs) [3, 4, 5, 6, 7] is highlighted as one of the most prominent steps that makes the roles of topology manifest. Specifically, it was found that topological natures of Bloch electrons characterized by topological invariants result in boundary modes robust against perturbations [8]. This relation between bulk topology and boundary modes is called bulk-boundary correspondence (BBC), and it has served as a central notion in studies on topological materials [9, 10].
BBC also ties topologically protected boundary modes with quantized responses to external fields, which is another characteristic of TIs. A representative example is the quantum Hall effect where the number of edge modes corresponds to the Hall conductance [8, 9, 10]. Another example is the quantization of an electric dipole moment attributed to the quantized Berry’s phase of Bloch electrons in one dimension [11, 12, 13, 14, 15, 16, 17, 18, 19, 20]. From the viewpoint of BBC, this is attributed to the boundary states localized at the ends of one-dimensional systems. Recently, this topological viewpoint of an electric dipole is further extended [21, 22] to higher-rank multipole moments [23, 24, 25, 26, 27, 28] (e.g., quadrupole and octapole) in two or higher dimensions, that are attributed to the boundary states localized at the corners. Such a topological phase of matter hosting boundary modes with codimension greater than one is nowadays established as a higher-order topological phase, and large amount of theoretical [29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47] and experimental [48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61] efforts have been devoted to understanding and realizing this phase.
It had been a common belief that topological invariants themselves are not observed from featureless gapped ground states, but characteristic boundary modes enable us to observe them. However, recently, an approach to directly access bulk topological natures was proposed, that is, dynamical aspects of topological phases [62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81]. Such attempts are essential because they are beyond the aforementioned common belief on topological phases. In the literature, the semiclassical approach of wave-packet dynamics has successfully illustrated the role of Berry curvature in transport phenomena [62, 63]. Another direction, on which we focus in this Letter, is considering quench dynamics from completely localized initial states. At single-particle level, i.e., without the Fermi sea of the filled bands, the information of Bloch bands in an entire Brillouin zone can be embedded by setting a spatially localized initial state; this is attributed to the fact that the localized states can be expressed as a linear combination of all the states in the Fourier space. As such, topological invariants can be extracted from the time-dependent quantities. For instance, for chiral-symmetric one-dimensional systems, the quantity called the mean chiral displacement (MCD), which is the polarization weighted by the eigenvalue of the chiral operator, successfully extracts the topological winding number of the system, and thus distinguishes the topological states from the trivial states [68, 69, 70, 80]. Moreover, measurements of such quantities are experimentally feasible in various setups, e.g., discrete quantum walk in a photonic system based on the orbital angular momentum of a light beam [68].
Considering the findings listed above, one is naturally tempted to ask the following questions: (i) Can we apply the measurement of topological invariants through dynamics to higher-order topological (or quadrupolar) phases? (ii) If so, can it be also applicable to interacting systems and/or disordered ones? In this Letter, to address these issues, we investigate two-particle dynamics of the interacting Benalcazar-Bernevig-Hughes (BBH) model [23, 24]. We heuristically find a quantity whose long time average can characterize the topology. This quantity is a modified bulk quadrupole moment, which is reminiscent of the MCD in one-dimensional systems. Therefore, this quantity is also experimentally measurable. By using a numerically efficient algorithm of tracing the unitary time evolution of the two-particle wave function (one may increase the number of particles in principle), we elucidate that the quantity introduced here characterizes the topological nature of the BBH model, for both noninteracting and interacting cases. Furthermore, the characteristic behavior of this quantity is robust against moderate strength of disorders, indicating the feasibility of experimental measurements in realistic setups that are not completely clean.
Hereafter, we set .
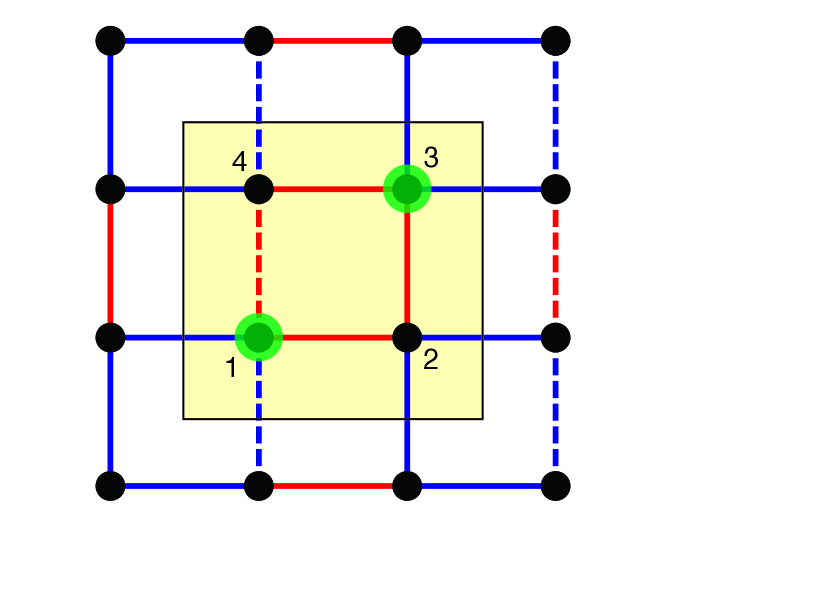
Model and method.— We consider the model proposed in Refs. [23, 24], incorporating an interaction and a disorder. The Hamiltonian reads , where , , and . Here and denote, respectively, the annihilation and creation operators of spinless fermions, and denotes the sites on a square lattice specified by a pair of indices and , where is the position of the unit cell, and labels the sublattice (Fig. 1). is the density operator. The symbol represents the nearest-neighbor pairs of sites. The transfer integral is indicated in Fig. 1; there are two parameters, and . We note that preserves the chiral symmetry, such that with . In addition to , we consider two terms and . Here, denotes the strength of the intersite interaction and is the strength of the disorder potential, chosen randomly in .
The topological properties of the hopping term has been well investigated in the literature. For , the system is gapped at the half-filling. The half-filled ground state is topologically trivial (nontrivial) when (). The topological nature can be captured by topological invariants such as the nested Wilson loop [23, 24], the quadrupole moment [25, 26, 27], the entanglement-related quantities [36, 82, 47], and the Berry phase [45]. Furthermore, nontrivial topology results in the emergence of the corner states, which is characteristics of the higher-order topological phases. The aim of this study is to extract the topological nature without relying on the corner states.
The quench dynamics of the system can be dictated by the unitary time evolution of the many-body wave function, . To obtain numerically, we approximate as follows. First, we discretize the time as , with being small time step (compared with the hopping parameters); we set in the present work. Then, we have . The remaining task is to approximate . To this end, we employ the fourth-order Suzuki-Trotter decomposition [83, 84], namely, , where and Note that, in defining , we divide the Hamiltonian into pieces, , which do not necessarily commute each other. Here, we set , and we show the explicit forms of - in Supplemental Material [85]. The Suzuki-Trotter decomposition of largely reduces computational costs. Hence, we can access long time dynamics with relatively large system size in short computational time, compared with other methods such as exact diagonalization.

Mean chiral quadrupole moment.— The main proposal of this Letter is the introduction of a quantity characterizing the topological nature of the quadrupolar phase, which may be termed the mean chiral quadrupole moment (MCQM):
| (1) |
where
| (2) |
Here is the eigenvalue of the chiral operator; it takes for and for . Note that, to make the MCQM well defined, we have to fix the labeling of the unit cells and sublattices in the beginning, since this quantity depends on the choice of the frame. Except for , follows the conventional definition of the quadrupole operator under the open boundary condition [23, 24, 25, 26, 27, 28]. This quantity can be regarded as an extension of the MCD which dictates the winding number of one-dimensional TIs in classes AIII and BDI in the topological classification, having even number of bands [68, 69, 70, 80]. Note that, in actual experiments, all we need to measure is the site-resolved particle density. This guarantees accessibility of this quantity if spatial resolution of experimental setup is sufficiently fine. It is also noteworthy that this quantity is sensitive to the choice of the initial state. In the present study, we choose the initial state such that two particles are localized at two diagonal sites on the inter-unit-cell plaquette located at the middle of the system, as schematically depicted as green circles in Fig. 1. In Supplemental Material, we show the numerical data for a different choice of initial state, namely, two particles are localized at two diagonal sites on the intra-unit-cell plaquette, where we see that the failure of the distinction between topological and trivial cases.
How does the MCQM extract the topological nature of the quadrupole insulators? To see this, we present an intuitive understanding of the implication of the MCQM, namely, the argument of the decoupled four-site cluster limit. In the prior works [86, 87, 21, 45, 43, 88], it was found that this argument is essential for understanding the ground-state properties of the insulating state, since the ground state is adiabatically connected to this limit and topological properties of gapped ground states are unchanged under the change of model parameters unless the excitation gap is closed. Regarding the dynamical properties, for which the information of all the eigenstates matters, the notion of adiabatic connection does not hold straightforwardly, but it still gives a useful insight. In fact, such an argument works in one-dimensional systems as well [85].
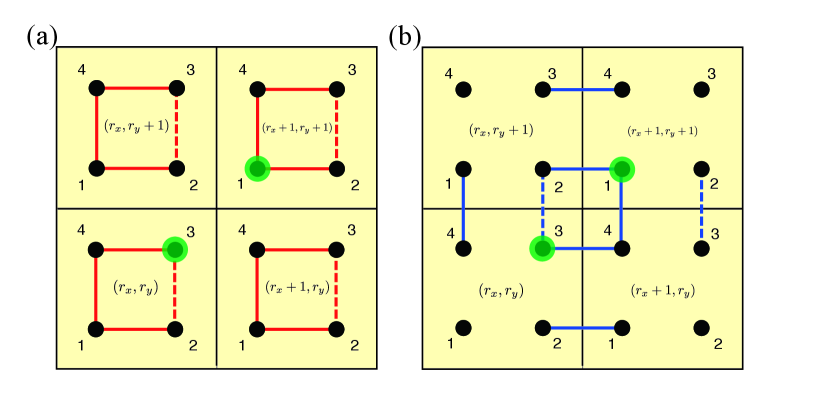
For the decoupled limits, the particles are confined in the plaquette on which the particle is initially located, thus unitary time evolution can exactly be tracked by solving the four-site problem. Thus, in these limits, the exact form of is accessible. For the details of the calculations, see Supplemental Material [85]. For the present choice of the initial state, we find that, for the trivial limit, i.e., [Fig. 2(a)], one has
| (3) |
where stands for the long time average of . Meanwhile, for the nontrivial limit i.e., [Fig. 2(b)], one has
| (4) |
Equation (4) indicates that nonvanishing value of under the proper choice of the initial state reflects the presence of the nontrivial topology in the bulk. It should be noted that the difference between the trivial limit and the the nontrivial limit is whether the plaquettes with finite hoppings are intra-unit-cell ones or an inter-unit-cell ones. In fact, even away from the limiting cases, assigning larger hoppings on inter-unit-cell plaquettes than the intra-unit-cell ones is essential to obtain the finite value of , as we will show later.
We briefly remark the role of . In fact, the similar factor is included in the MCD for one-dimensional systems [69, 70]. In that case, its role is to make the contributions from the negative-energy bands and those from the positive-energy bands additive; otherwise they cancel each other. This fact also implies that the MCD is adaptable to chiral symmetric systems with an even number of topological bands. In fact, in the MCQM is incorporated in the same spirit, but in a rather heuristic manner. Nevertheless, it is indeed essential so that the MCQM serves as a topological marker, as clarified in the decoupled cluster argument [85]. Moreover, the topological characterization is valid even in the presence of the chiral-symmetry-breaking term, , as we will show later.
Numerical demonstration.— We now demonstrate the validity of the MCQM for topological characterization. In Figs. 3(a) and 3(b), we plot to for topological and trivial cases respectively, for the clean systems (i.e., ). Here the numerical computations are carried out for -site (i.e., -unit cell) systems under the open boundary condition. At the initial state, two particles are localized at the sublattice 1 at the unit cell and the sublattice 3 at the unit cell . We see in these figures that, for the topological case with weak interaction (), oscillates around as expected, whereas it oscillates around for the trivial case. Therefore, the long time average of indeed can be used to extract the topological character of this model.
We also remark the boundary effects. In fact, the particles are initially located near the center of the system, and they reach the boundary at . Although the amplitude of the oscillation of the MCQM increases after reaching the boundary, the center of the oscillation is still unchanged, manifesting the robustness of against the boundary effects. Also, the fact that the finite value of MCQM in the topological case is obtained before reaching the boundary indicates that the finite MCQM is not attributed to the corner states, and thus this is indeed the bulk property.
It can also be found in Fig. 3(a) that the role of the interaction becomes manifest even for moderate strength of the interaction (). In the topological case, the MCQM deviates from the noninteracting case, namely, the MCQM exhibits gradual increase (decrease) to (). This value of is smaller than the band gap at the half-filling. This result indicates the essential difference between the dynamical properties and the ground-state properties at the half-filling, because the latter is stable against interactions as far as the excitation gap is not closed [45]. We also note that, in the trivial case, the MCQM seems to be rather insensitive to the interaction strength.
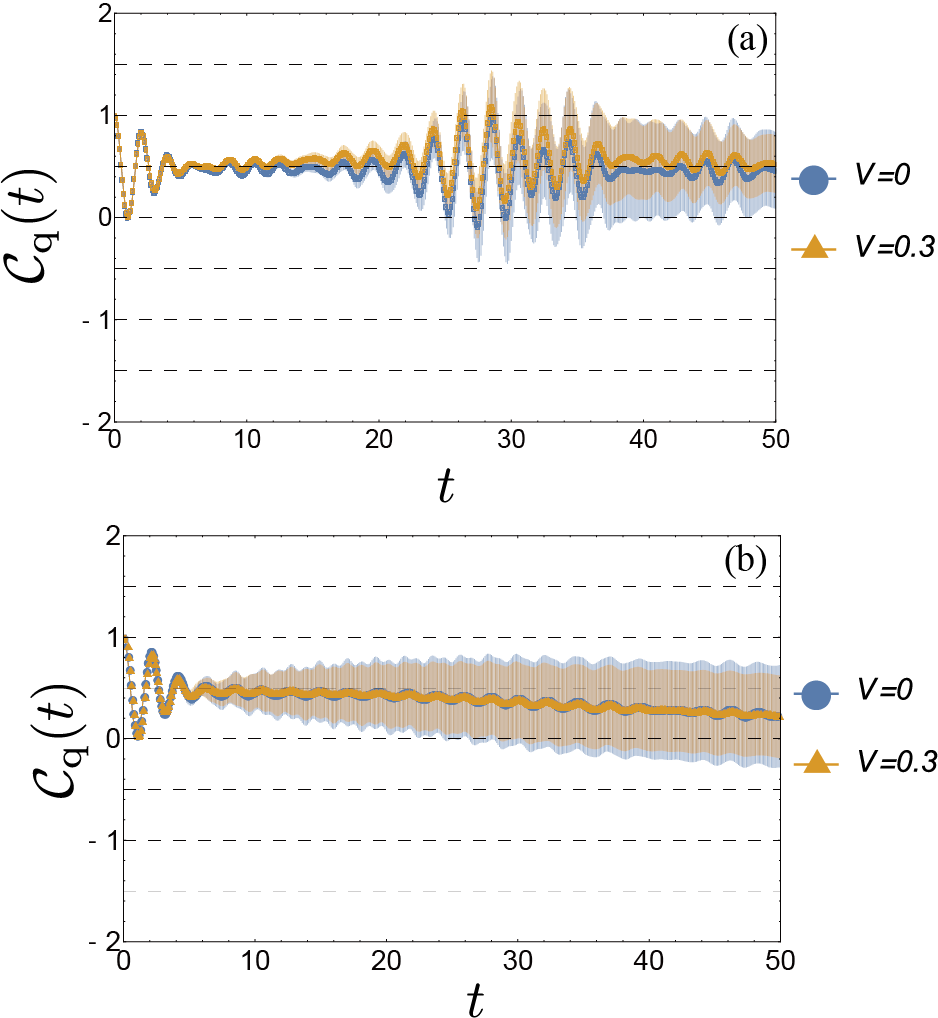
It should also be noted that the “topological transition” of the dynamical properties is not as sharp as that for the ground state. To show this, we plot as a function of in Fig. 3(c). We see that the dependence on of is smooth, rather than a steep jump; this is another indication of the difference between the dynamical properties and the ground-state properties, as the latter is characterized by the jump of the quantized topological number. Note that, at the critical point (), the behavior of is qualitatively different from that deep inside the topological or trivial cases, namely, does not oscillate around a certain value; see Supplemental Material [85]. This behavior will serve as a useful hallmark indicating that the system is near the critical point.
Robustness against disorders.— We further study the effects of disorder potentials, to test the robustness of the MCQM. In Fig. 4, we plot for the topological case with weak () and moderate () disorders. Here the average is taken over 432 configurations of the random disorder potential. We see that remains to oscillate around for a weak disorder case. In particular, for where the particles do not reach the boundary, the error bars due to the disorder average are very small. Even for the moderate disorder case, the short-time behavior (i.e., ) is almost unaffected by the disorders. However, after the long time (), the starts to decrease gradually and deviates from . These results manifest the robustness of the MCQM against disorders, which indicates that this is a measurable quantity in experiments for moderately clean samples.
Summary.— We have proposed how to extract the topological character of the quadrupolar phase by the quench dynamics. Specifically, we introduce the MCQM as a marker of a topological character. Although the initial state in the present setup is localized, the system is translationally invariant without any boundaries. The numerical results on the two-particle BBH model indicate that the MCQM indeed captures the topological nature for weakly interacting and moderately clean systems. It has also been clarified that there are essential differences between the ground-state topological properties at the half-filling and the MCQM, with respect to the stability against the interactions and the sharpness of the topological transition. This is attributed to the fact that the former is protected by the finite excitation gap, whereas the latter is affected by the information of all the eigenvalues and eigenvectors.
It is worth pointing out that our method of tracking two-particle dynamics is also applicable to bosonic systems. We find that the results are qualitatively the same as those for fermions [85]. This may indicate that each particle contributes to the MCQM additively as far as the few-body systems are concerned and it holds regardless of whether the system is bosonic or fermionic. Considering this fact, the present method can cover a wide range of experimental setups, including fermionic and bosonic ultracold atoms under the optical lattice, photonic crystals, and discrete quantum walks. Meanwhile, insensitivity for the particle statistics may not hold for the many-bony systems and studying such cases is an interesting future problem [80]. We hope our proposal opens up a way to understanding novel aspects of the quadrupolar phase.
Acknowledgements.
This work is supported by the JSPS KAKENHI, Grants No. JP17H06138, NO. JP20K14371 (T. M.), Japan, and JST CREST, Grant No. JPMJCR19T1, Japan. Parts of numerical calculations were carried out on the Supercomputer Center at Institute for Solid State Physics, University of Tokyo.References
- Thouless et al. [1982] D. J. Thouless, M. Kohmoto, M. P. Nightingale, and M. den Nijs, Phys. Rev. Lett. 49, 405 (1982).
- Haldane [1988] F. D. M. Haldane, Phys. Rev. Lett. 61, 2015 (1988).
- Kane and Mele [2005a] C. L. Kane and E. J. Mele, Phys. Rev. Lett. 95, 146802 (2005a).
- Kane and Mele [2005b] C. L. Kane and E. J. Mele, Phys. Rev. Lett. 95, 226801 (2005b).
- Bernevig et al. [2006] B. A. Bernevig, T. L. Hughes, and S.-C. Zhang, Science 314, 1757 (2006).
- Hasan and Kane [2010] M. Z. Hasan and C. L. Kane, Rev. Mod. Phys. 82, 3045 (2010).
- Qi and Zhang [2011] X.-L. Qi and S.-C. Zhang, Rev. Mod. Phys. 83, 1057 (2011).
- Halperin [1982] B. I. Halperin, Phys. Rev. B 25, 2185 (1982).
- Hatsugai [1993a] Y. Hatsugai, Phys. Rev. Lett. 71, 3697 (1993a).
- Hatsugai [1993b] Y. Hatsugai, Phys. Rev. B 48, 11851 (1993b).
- Zak [1989] J. Zak, Phys. Rev. Lett. 62, 2747 (1989).
- King-Smith and Vanderbilt [1993] R. D. King-Smith and D. Vanderbilt, Phys. Rev. B 47, 1651 (1993).
- Vanderbilt and King-Smith [1993] D. Vanderbilt and R. D. King-Smith, Phys. Rev. B 48, 4442 (1993).
- Resta [1994] R. Resta, Rev. Mod. Phys. 66, 899 (1994).
- Ryu and Hatsugai [2002] S. Ryu and Y. Hatsugai, Phys. Rev. Lett. 89, 077002 (2002).
- Souza et al. [2004] I. Souza, J. Íñiguez, and D. Vanderbilt, Phys. Rev. B 69, 085106 (2004).
- Qi et al. [2008] X.-L. Qi, T. L. Hughes, and S.-C. Zhang, Phys. Rev. B 78, 195424 (2008).
- Hatsugai [2009] Y. Hatsugai, Solid State Communications 149, 1061 (2009), recent Progress in Graphene Studies.
- Fang et al. [2012] C. Fang, M. J. Gilbert, and B. A. Bernevig, Phys. Rev. B 86, 115112 (2012).
- Watanabe and Oshikawa [2018] H. Watanabe and M. Oshikawa, Phys. Rev. X 8, 021065 (2018).
- Hatsugai and Maruyama [2011] Y. Hatsugai and I. Maruyama, Europhys. Lett. 95, 20003 (2011).
- Kariyado and Hatsugai [2014] T. Kariyado and Y. Hatsugai, Phys. Rev. B 90, 085132 (2014).
- Benalcazar et al. [2017a] W. A. Benalcazar, B. A. Bernevig, and T. L. Hughes, Phys. Rev. B 96, 245115 (2017a).
- Benalcazar et al. [2017b] W. A. Benalcazar, B. A. Bernevig, and T. L. Hughes, Science 357, 61 (2017b).
- Ono et al. [2019] S. Ono, L. Trifunovic, and H. Watanabe, Phys. Rev. B 100, 245133 (2019).
- Kang et al. [2019] B. Kang, K. Shiozaki, and G. Y. Cho, Phys. Rev. B 100, 245134 (2019).
- Wheeler et al. [2019] W. A. Wheeler, L. K. Wagner, and T. L. Hughes, Phys. Rev. B 100, 245135 (2019).
- Watanabe and Ono [2020] H. Watanabe and S. Ono, Phys. Rev. B 102, 165120 (2020).
- Hashimoto et al. [2017] K. Hashimoto, X. Wu, and T. Kimura, Phys. Rev. B 95, 165443 (2017).
- Hayashi [2018] S. Hayashi, Communications in Mathematical Physics 364, 343 (2018).
- [31] Y. Xu, R. Xue, and S. Wan, arXiv:1711.09202 [cond-mat.str-el] .
- Schindler et al. [2018a] F. Schindler, A. M. Cook, M. G. Vergniory, Z. Wang, S. S. P. Parkin, B. A. Bernevig, and T. Neupert, Science Advances 4, 10.1126/sciadv.aat0346 (2018a).
- Ezawa [2018] M. Ezawa, Phys. Rev. Lett. 120, 026801 (2018).
- Khalaf [2018] E. Khalaf, Phys. Rev. B 97, 205136 (2018).
- Kunst et al. [2018] F. K. Kunst, G. van Miert, and E. J. Bergholtz, Phys. Rev. B 97, 241405 (2018).
- Fukui and Hatsugai [2018] T. Fukui and Y. Hatsugai, Phys. Rev. B 98, 035147 (2018).
- You et al. [2018] Y. You, T. Devakul, F. J. Burnell, and T. Neupert, Phys. Rev. B 98, 235102 (2018).
- Călugăru et al. [2019] D. Călugăru, V. Juričić, and B. Roy, Phys. Rev. B 99, 041301 (2019).
- Okuma et al. [2019] N. Okuma, M. Sato, and K. Shiozaki, Phys. Rev. B 99, 085127 (2019).
- Araki et al. [2019] H. Araki, T. Mizoguchi, and Y. Hatsugai, Phys. Rev. B 99, 085406 (2019).
- Dubinkin and Hughes [2019] O. Dubinkin and T. L. Hughes, Phys. Rev. B 99, 235132 (2019).
- Benalcazar et al. [2019] W. A. Benalcazar, T. Li, and T. L. Hughes, Phys. Rev. B 99, 245151 (2019).
- Kudo et al. [2019] K. Kudo, T. Yoshida, and Y. Hatsugai, Phys. Rev. Lett. 123, 196402 (2019).
- Okugawa et al. [2019] R. Okugawa, S. Hayashi, and T. Nakanishi, Phys. Rev. B 100, 235302 (2019).
- Araki et al. [2020] H. Araki, T. Mizoguchi, and Y. Hatsugai, Phys. Rev. Research 2, 012009 (2020).
- Rasmussen and Lu [2020] A. Rasmussen and Y.-M. Lu, Phys. Rev. B 101, 085137 (2020).
- Zhu et al. [2020] P. Zhu, K. Loehr, and T. L. Hughes, Phys. Rev. B 101, 115140 (2020).
- Schindler et al. [2018b] F. Schindler, Z. Wang, M. G. Vergniory, A. M. Cook, A. Murani, S. Sengupta, A. Y. Kasumov, R. Deblock, S. Jeon, I. Drozdov, H. Bouchiat, S. Guéron, A. Yazdani, B. A. Bernevig, and T. Neupert, Nature Physics 14, 918 (2018b).
- Serra-Garcia et al. [2018] M. Serra-Garcia, V. Peri, R. Süsstrunk, O. R. Bilal, T. Larsen, L. G. Villanueva, and S. D. Huber, Nature 555, 342 EP (2018).
- Imhof et al. [2018] S. Imhof, C. Berger, F. Bayer, J. Brehm, L. W. Molenkamp, T. Kiessling, F. Schindler, C. H. Lee, M. Greiter, T. Neupert, and R. Thomale, Nature Physics 14, 925 (2018).
- Xie et al. [2018] B.-Y. Xie, H.-F. Wang, H.-X. Wang, X.-Y. Zhu, J.-H. Jiang, M.-H. Lu, and Y.-F. Chen, Phys. Rev. B 98, 205147 (2018).
- Peterson et al. [2018] C. W. Peterson, W. A. Benalcazar, T. L. Hughes, and G. Bahl, Nature 555, 346 (2018).
- Noh et al. [2018] J. Noh, W. A. Benalcazar, S. Huang, M. J. Collins, K. P. Chen, T. L. Hughes, and M. C. Rechtsman, Nature Photonics 12, 408 (2018).
- Mittal et al. [2019] S. Mittal, V. V. Orre, G. Zhu, M. A. Gorlach, A. Poddubny, and M. Hafezi, Nature Photonics 13, 692 (2019).
- Ota et al. [2019] Y. Ota, F. Liu, R. Katsumi, K. Watanabe, K. Wakabayashi, Y. Arakawa, and S. Iwamoto, Optica 6, 786 (2019).
- El Hassan et al. [2019] A. El Hassan, F. K. Kunst, A. Moritz, G. Andler, E. J. Bergholtz, and M. Bourennane, Nature Photonics 13, 697 (2019).
- Xue et al. [2019] H. Xue, Y. Yang, F. Gao, Y. Chong, and B. Zhang, Nature Materials 18, 108 (2019).
- Ni et al. [2019] X. Ni, M. Weiner, A. Alù, and A. B. Khanikaev, Nature Materials 18, 113 (2019).
- Zhang et al. [2019a] X. Zhang, B.-Y. Xie, H.-F. Wang, X. Xu, Y. Tian, J.-H. Jiang, M.-H. Lu, and Y.-F. Chen, Nature Communications 10, 5331 (2019a).
- Zhang et al. [2019b] X. Zhang, H.-X. Wang, Z.-K. Lin, Y. Tian, B. Xie, M.-H. Lu, Y.-F. Chen, and J.-H. Jiang, Nature Physics 15, 582 (2019b).
- Kempkes et al. [2019] S. N. Kempkes, M. R. Slot, J. J. van den Broeke, P. Capiod, W. A. Benalcazar, D. Vanmaekelbergh, D. Bercioux, I. Swart, and C. Morais Smith, Nature Materials 18, 1292 (2019).
- Chang and Niu [1996] M.-C. Chang and Q. Niu, Phys. Rev. B 53, 7010 (1996).
- Xiao et al. [2010] D. Xiao, M.-C. Chang, and Q. Niu, Rev. Mod. Phys. 82, 1959 (2010).
- Atala et al. [2013] M. Atala, M. Aidelsburger, J. T. Barreiro, D. Abanin, T. Kitagawa, E. Demler, and I. Bloch, Nature Physics 9, 795 (2013).
- Mazza et al. [2015] L. Mazza, M. Aidelsburger, H.-H. Tu, N. Goldman, and M. Burrello, New Journal of Physics 17, 105001 (2015).
- Meier et al. [2016] E. J. Meier, F. A. An, and B. Gadway, Nature Communications 7, 13986 (2016).
- Wang et al. [2017] C. Wang, P. Zhang, X. Chen, J. Yu, and H. Zhai, Phys. Rev. Lett. 118, 185701 (2017).
- Cardano et al. [2017] F. Cardano, A. D’Errico, A. Dauphin, M. Maffei, B. Piccirillo, C. de Lisio, G. De Filippis, V. Cataudella, E. Santamato, L. Marrucci, M. Lewenstein, and P. Massignan, Nature Communications 8, 15516 (2017).
- Meier et al. [2018] E. J. Meier, F. A. An, A. Dauphin, M. Maffei, P. Massignan, T. L. Hughes, and B. Gadway 10.1126/science.aat3406 (2018).
- Maffei et al. [2018] M. Maffei, A. Dauphin, F. Cardano, M. Lewenstein, and P. Massignan, New Journal of Physics 20, 013023 (2018).
- Yang et al. [2018] C. Yang, L. Li, and S. Chen, Phys. Rev. B 97, 060304 (2018).
- Gong and Ueda [2018] Z. Gong and M. Ueda, Phys. Rev. Lett. 121, 250601 (2018).
- Zhang et al. [2018] L. Zhang, L. Zhang, S. Niu, and X.-J. Liu, Science Bulletin 63, 1385 (2018).
- Zhang et al. [2019c] L. Zhang, L. Zhang, and X.-J. Liu, Phys. Rev. A 99, 053606 (2019c).
- Hu and Zhao [2020] H. Hu and E. Zhao, Phys. Rev. Lett. 124, 160402 (2020).
- Longhi [2019] S. Longhi, Opt. Lett. 44, 2530 (2019).
- Qiu et al. [2019] X. Qiu, T.-S. Deng, Y. Hu, P. Xue, and W. Yi, iScience 20, 392 (2019).
- Wang et al. [2019a] K. Wang, X. Qiu, L. Xiao, X. Zhan, Z. Bian, W. Yi, and P. Xue, Phys. Rev. Lett. 122, 020501 (2019a).
- Wang et al. [2019b] K. Wang, X. Qiu, L. Xiao, X. Zhan, Z. Bian, B. C. Sanders, W. Yi, and P. Xue, Nature Communications 10, 2293 (2019b).
- Haller et al. [2020] A. Haller, P. Massignan, and M. Rizzi, Phys. Rev. Research 2, 033200 (2020).
- Ji et al. [2020] W. Ji, L. Zhang, M. Wang, L. Zhang, Y. Guo, Z. Chai, X. Rong, F. Shi, X.-J. Liu, Y. Wang, and J. Du, Phys. Rev. Lett. 125, 020504 (2020).
- Wang et al. [2018] Q. Wang, D. Wang, and Q.-H. Wang, EPL (Europhysics Letters) 124, 50005 (2018).
- Hatsugai and Sugi [2001] Y. Hatsugai and A. Sugi, International Journal of Modern Physics B 15, 2045 (2001).
- Suzuki [1990] M. Suzuki, Physics Letters A 146, 319 (1990).
- [85] See Supplemental Material for a technical detail of our numerical calculation, the decoupled cluster argument, the MCQM for the different choice of the initial state, the MCQM near the critical point, and the results for the bosonic systems, which includes Ref Su1979.
- Hatsugai [2006] Y. Hatsugai, Journal of the Physical Society of Japan 75, 123601 (2006).
- Hatsugai [2007] Y. Hatsugai, Journal of Physics: Condensed Matter 19, 145209 (2007).
- Mizoguchi et al. [2019] T. Mizoguchi, H. Araki, and Y. Hatsugai, Journal of the Physical Society of Japan 88, 104703 (2019).