Detecting Adversarial Examples from Sensitivity Inconsistency of Spatial-Transform Domain

For the primal classifier $\mathcal{F}$ trained on the dataset $\mathbf{X}$, let $\mathcal{B}_{i,j}$ be the decision boundary between class $i$ and class $j$. Let also $\tilde{\mathcal{B}}_{i,j}$ be a transformed version of $\mathcal{B}_{i,j}$ corresponding to the dual classifier $\mathcal{G}$. We expect that $\mathcal{B}_{i,j}$ is similar to $\tilde{\mathcal{B}}_{i,j}$ except for those highly-curved parts. Apparently, the shape of $\mathcal{B}_{i,j}$ highly correlates with the prediction confidence of $\mathcal{F}$ on the training samples. Therefore, the problem of ensuring $\tilde{\mathcal{B}}_{i,j}$ and $\mathcal{B}_{i,j}$ to be similar except for highly-curved parts reduces to make $\mathcal{F}$ and $\mathcal{G}$ generate similar prediction confidences on NEs, but vastly different ones on AEs. Considering all the boundaries $\mathcal{B}_{i,j}$’s, we formulate the following optimization problem to search for $\mathcal{G}$:

where the cost function is designed to minimize the worst-case deviation of $\mathcal{G}$ from $\mathcal{F}$ on NEs, and the constraint guarantees their prediction confidences on AEs to be significant enough.

A straightforward way for solving this problem is to train the classifier $\mathcal{G}$ by integrating the constraint into the loss term. However, such naive solution easily causes overfitting (Raghunathan et al. 2019; Cai et al. 2018). In this work, we resort to a transform-domain technique for getting an approximated solution of (2). An intuition why we search for $\mathcal{G}$ in the transform domain is because DNN classifiers trained in the same domain tend to produce similar decision boundaries including the highly-curved parts (Charles, Rosenberg, and Papailiopoulos 2019; Fawzi, Fawzi, and Fawzi 2018; Tramèr et al. 2018). A crucial problem now is how to appropriately choose the domain transform. Fawzi et. al found that the decision boundary near NEs is flat along most directions, with merely few directions being highly-curved (Fawzi et al. 2018). To maintain these flat parts, so as to preserve the results on NEs, we firstly could use linear transforms. Secondly, we should simultaneously flatten the highly-curved parts, which could be achieved by introducing distortions. The theory of manifold learning indicates that the distortion of the geometrical structure is caused by the dimensionality difference between the ambient and intrinsic spaces (Erba, Gherardi, and Rotondo 2019; Tian et al. 2017). Owing to these two reasons, we propose to design a linear, dimension-reducing transform, based on which we search for the desired $\mathcal{G}$. To this end, we define the transformation WAWT below. Let $\mathbf{x}\in\mathbf{X}$, and its WAWT transformed version $\tilde{\mathbf{x}}$ can be expressed as:

where $\mathbf{x}_{ll}$, $\mathbf{x}_{lh}$,$\mathbf{x}_{hl}$, and $\mathbf{x}_{hh}$ represent the four sub-bands of a wavelet transform. Here, $w_{i}$’s are used to balance the importance of different sub-bands. Clearly, due to the lower dimension of each sub-band, $\mathbf{H}$ is a linear, dimension-reducing transform, as we expect. More details on WAWT can be found in the supplementary material.

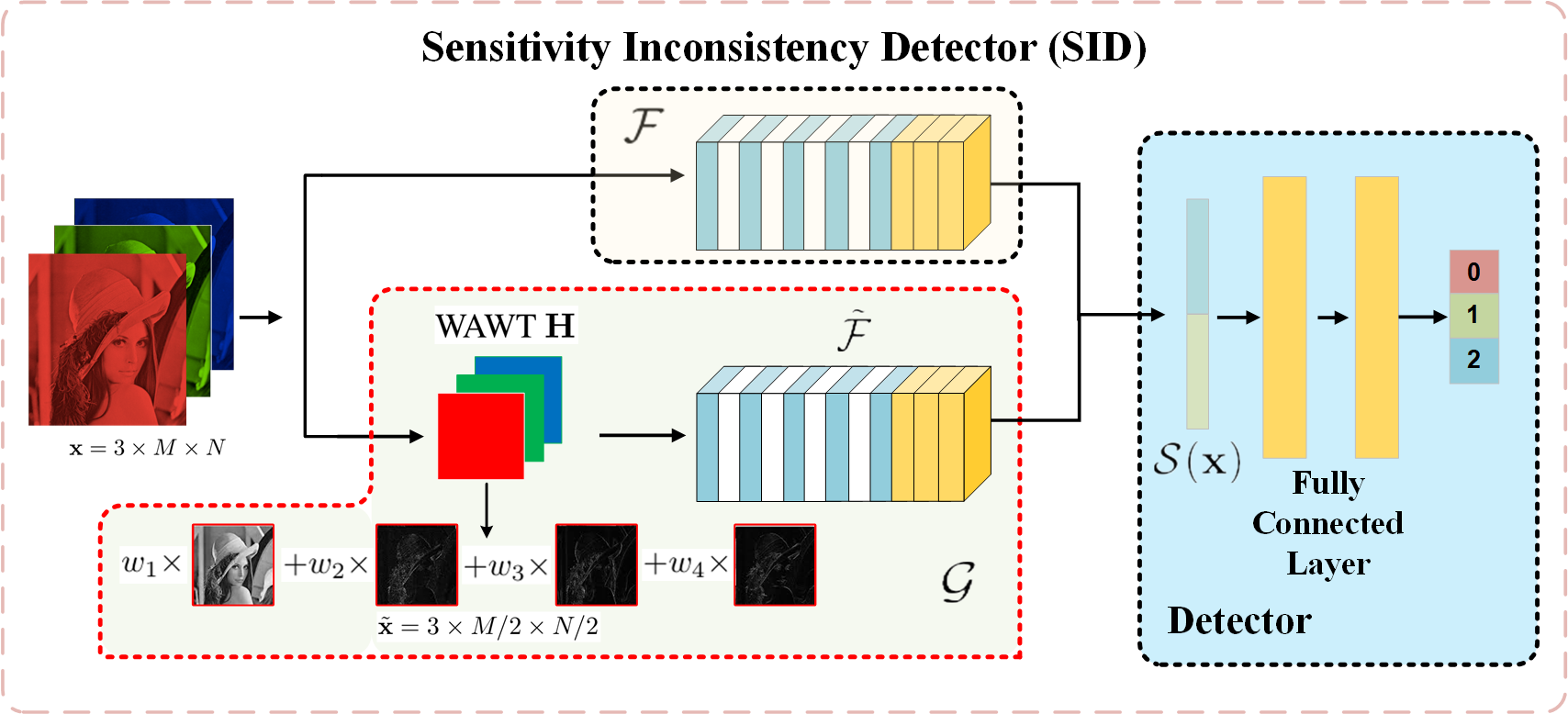
Now, we can construct a classifier $\tilde{\mathcal{F}}(\tilde{\mathbf{x}})$ in the WAWT domain, and then the dual classifier can be naturally designed as $\mathcal{G}(\mathbf{x})=\tilde{\mathcal{F}}(\mathbf{H}\mathbf{x})$. Training the dual classifier $\mathcal{G}$ is rather straightforward, by noticing that $\mathcal{G}$ is the composition of $\mathbf{H}$ with $\tilde{\mathcal{F}}$. As shown in Fig. 2 (the part enclosed by the red dashed line), $\mathcal{G}$ could be readily implemented by a DNN composed of the concatenation of $\tilde{\mathcal{F}}$ and WAWT layers with four trainable $w_{i}$’s. To guarantee that $\mathcal{G}$ and $\mathcal{F}$ have similar classification performance on NEs, the network structure of $\tilde{\mathcal{F}}$ is exactly the same as $\mathcal{F}$, except the input dimension. Note that the primal and the dual classifiers are trained separately.

Before diving into the design of the AE detector, let us first provide some theoretical analyses on the constructed dual classifier.

We aim to demonstrate: if the predication confidence of the dual classifier $\mathcal{G}$ constructed based on the WAWT $\mathbf{H}$ is consistent with that of the primal classifier $\mathcal{F}$ on NEs, then $\mathcal{G}$ can approximate the optimal solution of the problem (2) with a given $\xi$. We first restrict our theoretical analysis to affine and quadratic classifiers, as most of existing theoretical works assumed (Fawzi, Moosavi-Dezfooli, and Frossard 2016; Fawzi et al. 2018). We then offer empirical justifications for the general DNN classifiers. To make the analysis tractable, we assume that the dataset $\mathbf{X}$ is composed by $K$ different classes of samples $\mathbf{X}_{k}$ $(k=1,...,K)$, each of which is drawn from a $p$-dimensional Gaussian distribution $\mathcal{N}(\bm{\mu}_{k},\bm{\Sigma}_{k})$.

For the affine classifier, we have the following theorem.

Theorem 1 implies that, if the prediction confidence difference of the affine $\mathcal{F}$ and $\mathcal{G}$ is bounded by $\delta$, then the approximation precision of $\mathcal{G}$ to the optimal solution of problem (2) is determined by the probability in (5). To further illustrate the approximation precision, we randomly generate $10$-class mixture of Gaussian data $\mathbf{X}$, and set $\eta=0.5$. Each class contains 100 examples of dimension 256. Fig. 3 shows how the lower bound in (5) decays with respect to the increasing $t$. As can be observed, even when $t$ increases to $60\%\delta$, this probability bound is still larger than 0.95, implying that the constructed $\mathcal{G}$ is a precisely approximated solution of problem (2) with $\xi=1.6\delta$. In fact, Theorem 1 also reflects the necessity of constructing $\mathcal{G}$ in the linear, dimension-reducing transform domain determined by $\mathbf{H}$. If otherwise $\mathbf{H}$ is a dimension-preserving mapping, then $\mathbf{H}$ is an invertible matrix. In this case, $\mathbf{H}^{T}(\mathbf{H}\bm{\Sigma}\mathbf{H}^{T})^{-1}\mathbf{H}=\bm{\Sigma}^{-1}$, making $\mathbf{C}_{k}=\bm{0},\forall k$. Hence, $\sqrt{(t+\delta)/\mathbf{C}_{k}\bm{\Sigma}_{k}\mathbf{C}^{T}_{k}}\rightarrow\infty$. Following the property of the Macrcum-Q function (Kapinas, Mihos, and Karagiannidis 2009), the lower bound in (5) vanishes as the second term goes to infinity, regardless $t$ and $\sigma$. Besides, the Macrcum-Q function $Q_{1/2}(\cdot)$ in (5) increases as $|\mathbf{C}_{k}(\frac{1}{2}\mathbf{I}-\eta\bm{\Sigma}^{-1})\bm{\mu}_{k}|$ does, which means that a large $\eta$ would result in a large lower bound in (5) and thus the designed dual classifier $\mathcal{G}$ is more precise.

For the case of quadratic classifier, we can similarly have Theorem 2.

A similar curve on the lower bound in (6) can be found in Fig.3, as in the affine case. From Theorem 2, we can also see that if $\mathbf{H}$ is invertible as a dimension preserving mapping, then the matrix (7) becomes a zero matrix with $\bm{\lambda}_{k}=\bm{0}$, $\forall k$. Consequently, $1-P(\sqrt{\delta+t};\bm{0})+P(-\sqrt{\delta+t};\bm{0})=0$ for any $\delta,t>0$, resulting in a trivial bound in (6). This again validates the usage of the linear, dimension-reducing $\mathbf{H}$. Moreover, the lower bound increases as the increase of $\eta$. It becomes even clearer when each $\mathbf{X}_{k}$ is sampled from an independent multivariate Gaussian. In this case, the lower bound in (6) reduces to $1-\mathcal{T}({3p}/{8},\sqrt{(t+\delta)/{4(1+\eta)^{4}}})$, where the regularized gamma function $\mathcal{T}(\cdot)$ is decreasing as the increase of $\eta$ (see the Corollary 2 in the supplementary materials). The proofs of Theorems 1 and 2 are also given in the supplementary materials.

In addition to these theoretical proofs, we give the empirical justifications on the effectiveness of the constructed $\mathcal{G}$, for general DNN classifier with complex decision boundaries. As an example, we choose the VGG classifier on CIFAR10 as the primal classifier $\mathcal{F}$, and then separately train the dual classifier $\mathcal{G}$. During the training process of $\mathcal{G}$, we calculate the values of the objective function in problem (2) on 500 test images, and the values of the constraint on their AEs produced by DeepFool (Moosavi-Dezfooli, Fawzi, and Frossard 2016). Fig. 3 shows how the objective function and the constraint vary with the number of iterations of mini-batches. As can be observed, $\mathcal{G}$ tends to approximate the optimal solution of the problem (2) with $\xi=7.11$, in which case the objective function is minimized to 5.95.

For a given unknown example $\mathbf{x}_{0}$, a natural measure to evaluate its sensitivity against the decision boundary transformation can be defined as:

where $f_{i}(\mathbf{x}_{0})$ and $g_{i}(\mathbf{x}_{0})$ are the associated prediction conferences under $\mathcal{F}$ and $\mathcal{G}$, respectively. The vectorized $\mathcal{S}(\mathbf{x}_{0})$ is then called the feature of sensitivity inconsistency of $\mathbf{x}_{0}$. The design process of $\mathcal{G}$ naturally endows the sensitivity inconsistency with the power to discriminate NEs and AEs. More precisely, $\forall\mathbf{x}\in\mathbf{X},\hat{\mathbf{x}}\in\hat{\mathbf{X}}$, if $\mathcal{G}$ is the solution of problem (2), then there exists a gap between $\left\|\mathcal{F}(\hat{\mathbf{x}})-\mathcal{G}(\hat{\mathbf{x}})\right\|_{2}$ and $\left\|\mathcal{F}(\mathbf{x})-\mathcal{G}(\mathbf{x})\right\|_{2}$. In other words, the inequality $\|\mathcal{S}(\hat{\mathbf{x}})\|^{2}_{2}-\|\mathcal{S}(\mathbf{x})\|^{2}_{2}\geq\epsilon$ always holds for a certain $\epsilon$. In this case, there would exist a sphere such that $\mathcal{S}(\mathbf{x})$ is located at the inside of it, while $\mathcal{S}(\hat{\mathbf{x}})$ is distributed on the outside. Therefore, $\mathbf{x}$ and $\hat{\mathbf{x}}$ can be well separated.

To further show the separability of NEs and AEs based on the feature of sensitivity inconsistency, we give an example in Fig. 3, where the considered $\mathcal{F}$ and $\mathcal{G}$ are VGG trained on CIFAR10 and its dual version. We randomly select 300 correctly classified examples from the test set and generate their adversarial counterparts using DeepFool. Then, we use the algorithm T-SNE (Maaten and Hinton 2008) to visualize the feature of sensitivity inconsistency of selected AEs and NEs. As can be observed, the feature vectors corresponding to them are largely separable. This example further motivates us to use the feature of sensitivity inconsistency for distinguishing AEs from NEs.

We now give the details of SID, by virtue of the developed feature of sensitivity inconsistency. The schematic diagram of SID is depicted in Fig. 2, which consists of three parts: the pre-trained primal classifier $\mathcal{F}$, the dual classifier $\mathcal{G}$, and a detector trained on features of sensitivity inconsistency. For a given $\mathcal{F}$, the dual classifier $\mathcal{G}$ is the composition of a WAWT layer and a DNN classifier with the same structure as $\mathcal{F}$. The output prediction confidence of $\mathcal{F}$ and $\mathcal{G}$ is then passed into the detector which is composed of two fully connected layers. To improve the discrimination capability of SID, we design the detector as a three-class classifier; in addition to AEs (label 0) and NEs (label 1), those examples which are inconsistently classified by $\mathcal{F}$ and $\mathcal{G}$ are categorized into the third class (label 2).

The details of training the SID is given in Algorithm 1, which starts with the generation of adversarial and noisy counterparts to NEs. Similar to prior studies (Ma et al. 2018; Lee et al. 2018), these NEs ($\mathbf{X}_{c}$) are assumed to be correctly classified by $\mathcal{F}$. For one mini-batch of NEs ($\mathbf{B}_{c}$), the corresponding AE mini-batch ($\mathbf{B}_{a}$) is generated using an attack strategy $\mathcal{A}$ (line 3). The noisy mini-batch ($\mathbf{B}_{n}$) can be readily produced by adding random noises with the same noise magnitude as the adversarial perturbation added on $\mathbf{B}_{a}$ (line 4). Examples in $\mathbf{B}_{c}$ and $\mathbf{B}_{n}$ are further split into $\mathbf{D}_{1}$ which contains the examples consistently classified by $\mathcal{F}$ and $\mathcal{G}$, and $\mathbf{D}_{2}$, which corresponds to the inconsistently classified ones (line 5-6). We now have prepared a batch of examples $\mathbf{D}$ composed by three classes of examples, $\mathbf{B}_{a}$, $\mathbf{D}_{1}$, and $\mathbf{D}_{2}$ whose labels are $0$, $1$, and $2$ respectively (line 7). Upon having $\mathbf{D}$, we can calculate the sensitivity inconsistency $\mathcal{S}(\mathbf{x})$ of each $\mathbf{x}\in\mathbf{D}$ via (8), and minimize the average cross entropy of SID on $\mathbf{D}$ (line 8). After exhausting all mini-batches in $\mathbf{X}_{c}$, and repeating the above process for $E$ times, we finally obtain the trained SID.

At the testing stage, classes 1 and 2 are merged. That is, a given example $\mathbf{x}_{0}$ is identified as an AE if the predicted label from SID is $0$; otherwise, it is treated as a NE.

We first show the performance comparison when AEs for training and testing are all generated by the same attack. In Table 1, we compare the AUC scores of different detectors, where the attack methods DeepFool (Moosavi-Dezfooli, Fawzi, and Frossard 2016), FGSM (Goodfellow, Shlens, and Szegedy 2015), BIM (Kurakin, Goodfellow, and Bengio 2017), and C&W (Carlini and Wagner 2017) are considered. The perturbation magnitudes $\eta$ of all the AEs can be found in the supplementary file. Compared with LID, MD, and FS, our proposed SID outperforms them in most cases, especially when the attack methods are more sophisticated, e.g., BIM, DeepFool, and C&W.

To more thoroughly show the advantages of SID, we give the AUC scores of different detectors on AEs generated by FGSM, BIM and DeepFool, with respect to the varying $\eta$. As can be seen from Fig. 4, SID achieves better AUC performance than all the competing detectors on AEs generated by BIM and DeepFool, for all $\eta$’s. In the cases of AEs produced by FGSM, our SID is still the best when $\eta\leq 0.41$, and gradually becomes inferior to LID and MD when $\eta$ further increases. Arguably, when $\eta$ is large, FGSM could be deemed as unsuccessful, as the incurred distortions would be too large. In fact, when $\eta$ is significant enough (e.g., $\eta>3.68$), the AUC performance of all detectors is almost perfect in the case of FGSM. This observation, in turn, reflects that the detection challenges mainly lie in the regime of small $\eta$, in which SID is the best detector in all the tested cases.

We also compare the generalizability of different detectors in Table 2. Note that here FS is not considered, as the training of FS merely relies on NEs. It can be found that the generalizability of SID is much improved in most cases, compared with MD and LID. Such desirable generalizability is attributed to the fact that AEs in the same curved regions would have similar sensitivity to the boundary transformation. For those sophisticatedly designed attacks such as DeepFool, BIM, and C&W, the generated AEs can be regarded as good approximations to the optimal ones (in the sense of (1)). This implies that these AEs from different sources would be concentrated in the same curved regions as the underlying optimal ones, and hence, would exhibit similar sensitivity inconsistency. Hence, naturally, SID trained on one source is very likely to be able to detect AEs from other sources.

We now evaluate the robustness of SID under the white box attack. In this scenario, an attacker knows everything including model parameters, training dataset, details on SID, etc. The purpose is to generate AEs to mislead the target classifier and simultaneously fool SID. A widely-adopted white box attack strategy is to maximize the cost function $\mathcal{L}$ of the classification model and loss $l$ of the detector at the same time (Lee et al. 2018; Ma et al. 2018). Namely,

where $y_{c}$ is the ground-truth label of the NE $\mathbf{x}$, $y_{d}=0$ indicates that $\hat{\mathbf{x}}=\mathbf{x}+\mathbf{r}$ is an AE, $\eta$ is the maximal allowable adversarial perturbation magnitude, and $\alpha$ is a tradeoff parameter.

To evaluate the robustness of SID, we randomly select 1000 NEs, which are correctly classified by ResNet, from CIFAR10 and SVHN respectively. We then generate their adversarial counterparts according to the white box attack strategy (LABEL:WhiteBoxAttack). The performance degradation of SID to the white box attack is examined in Table 3. The first 2 rows give the results for SID trained on AEs produced by BIM with two different settings of $\eta$ (BIM-L and BIM-S for large and small $\eta$’s). The remaining two rows report the results for the cases of FGSM (FGSM-L and FGSM-S for large and small $\eta$’s). Detailed settings of $\eta$ can be found in the supplementary file. Here, $A_{O}$ and $A_{W}$ represent the AUC scores of detecting the original AEs and the ones generated by the white box attack. For instance, the SID trained on BIM-L source achieves $99.81\%$ AUC score on detecting original AEs targeted on ResNet-CIFAR10, while still obtaining $98.31\%$ on detecting AEs produced by the white box attack. As the AUC scores for detecting original AEs and the ones from (LABEL:WhiteBoxAttack) are close, we claim that SID shows promising robustness against the white box attack.