Deriving Activation Functions via Integration
Abstract
Activation functions play a crucial role in introducing non-linearities to deep neural networks. We propose a novel approach to designing activation functions by focusing on their gradients and deriving the corresponding functions through integration. Our work introduces the Expanded Integral of the Exponential Linear Unit (xIELU), a trainable piecewise activation function derived by integrating trainable affine transformations applied on the ELU activation function. xIELU combines two key gradient properties: a trainable and linearly increasing gradient for positive inputs, similar to ReLU2, and a trainable negative gradient flow for negative inputs, akin to xSiLU. Conceptually, xIELU can be viewed as extending ReLU2 to effectively handle negative inputs. In experiments with 1.1B parameter Llama models trained on 126B tokens of FineWeb Edu, xIELU achieves lower perplexity compared to both ReLU2 and SwiGLU when matched for the same compute cost and parameter count.
1 Introduction
The choice of activation function significantly impacts a model’s performance, training dynamics, and generalization capabilities. Activation functions have progressed from the simple step function (McCulloch and Pitts, 1943) to more complex variants like ReLU (Nair and Hinton, 2010), ELU (Clevert et al., 2015), GELU (Hendrycks and Gimpel, 2016), and SiLU (Hendrycks and Gimpel, 2016; Ramachandran et al., 2017; Elfwing et al., 2017). Higher-order activation functions such as ReLU2 (So et al., 2021) and SwiGLU (Shazeer, 2020) have since demonstrated improved effectiveness and gained widespread adoption in Large Language Models (LLMs).
GELU and SiLU have emerged as effective alternatives to ReLU in many deep learning applications, due to their more favorable gradient properties. Unlike ReLU, which entirely suppresses negative inputs, GELU and SiLU provide non-zero gradients for negative inputs, thereby mitigating the "dying ReLU" problem (Maas et al., 2013). Studies have shown that ReLU2 outperforms both GELU and SiLU in LLMs (So et al., 2021; Zhang et al., 2024). However, ReLU2 also suppresses negative inputs and should inherit the same limitations as ReLU. An intuitive approach to improving ReLU2 is to incorporate non-zero gradients for negative inputs, paralleling the approach taken by GELU and SiLU to improve upon ReLU.
Trainable activation functions introduce learnable parameters that allow non-linearities to adapt to specific tasks or datasets, with examples including Swish (Ramachandran et al., 2017), PReLU (He et al., 2015b), and SELU (Klambauer et al., 2017). However, these approaches have seen limited adoption in LLMs, as they have not consistently outperformed simpler non-trainable alternatives, despite theoretically enhancing model expressivity. The xSiLU activation function (Huang, 2024) proposes incorporating trainable parameters to control affine transformations on the gradient. In contrast to earlier approaches, the use of trainable parameters in xSiLU leads to better results due to its control over the negative gradient flow.
We propose a novel approach to activation function design that focuses on gradient properties. Rather than designing the activation function directly, we derive it through integration of desired gradient behaviors, leading to our proposed Expanded Integral of the Exponential Linear Unit (xIELU). xIELU combines the beneficial properties of existing activation functions: the linearly increasing gradient of ReLU2 for positive inputs and a trainable negative gradient flow for negative inputs similar to xSiLU. Our empirical results demonstrate that this combination of gradient properties leads to improved performance over existing activation functions in LLMs.
Our contributions are summarized as follows:
-
•
We introduce a novel approach to designing activation functions by focusing on gradient properties and deriving the functions through integration.
-
•
We introduce xIELU, a novel activation function that outperforms ReLU2 and SwiGLU when matched for the same compute cost and parameter count.
-
•
We demonstrate the effectiveness of trainable activation functions. Our analysis shows that xIELU adaptively reduces its non-linearity for higher-level representations deeper in the network.
2 Background
This section provides an overview of the activation functions related to xIELU, which is based on the integral of ELU. The positive component of xIELU behaves similarly to ReLU2, while its negative component incorporates a trainable gradient flow similar to xSiLU. Figure 1 provides visualizations of these activation functions and their gradients.
2.1 Exponential Linear Unit
The Exponential Linear Unit (ELU) (Clevert et al., 2015) is a piecewise activation function that is continuous and monotonically increasing. It is bounded below for negative inputs and increasing linearly for positive inputs. Mathematically, ELU is defined as:
| (1) |
where is a non-trainable hyperparameter controlling the negative saturation level, typically set to 1.
For negative inputs, the gradient is bounded within (0, ]. Notably, ELU does not allow the gradient to take on negative values, which has been identified as a favorable property (Huang, 2024). We base the gradient of xIELU on the ELU function due to its simple integral expression and empirical effectiveness. We explore alternative functions for the positive and negative components in Section 4.2.
2.2 ReLU Squared
ReLU Squared (ReLU2) (So et al., 2021) squares positive inputs while maintaining zero output for non-positive inputs. Its computational efficiency and strong performance in standard MLP blocks have led to widespread adoption in LLMs, alongside SwiGLU in gated MLP blocks. Mathematically, ReLU2 is defined as:
| (2) |
The effectiveness of ReLU2 is commonly attributed to its similarity to GLUs, as it is equivalent to ReGLU when the U and V weight matrices are identical. However, the theoretical understanding of GLU variants remains limited (Shazeer, 2020). We offer an alternative interpretation: the effectiveness of ReLU2 can be attributed to its linearly increasing gradient for positive inputs. This linear growth in gradient flow allows the network to learn from large activation values more effectively than GELU and SiLU, where gradients are bounded above. Our experiments show that piecewise activation functions with linearly increasing gradients for positive inputs consistently achieve better performance than gradients that are bounded above. ReLU2 has the following gradient:
| (3) |
ReLU2 inherits ReLU’s limitation of suppressing negative inputs, which can lead to "dead" neurons that become permanently inactive during training. We extend ReLU2 to address this limitation by allowing non-zero gradient for negative inputs
2.3 Expanded Gating Ranges
Expanded SiLU (xSiLU) (Huang, 2024) proposes introducing trainable parameters to expand the gradient limits of SiLU from to . This transformation corresponds to expanding the range of sigmoid, the gating function of SiLU, from to . This modification can improve self-gated activation functions like GELU and SiLU, while also enabling the use of unconventional gating functions like arctangent. The improvement in performance is mainly attributed to the introduction of trainable parameters that control the negative gradient flow. The xSiLU function is derived as follows:
| (4) |
where is a trainable scalar parameter that controls the negative gradient flow by expanding the gradient limits from to .
More generally, this approach involves selecting a base function for the gradient and deriving a new activation function by computing the integral of an affine transformation applied to .
| (5) |
where controls the gradient flow, shifts the gradient by a constant value and determines the y-intercept of the gradient, and , the constant of integration, shifts the activation function by a constant value and determines the y-intercept of the activation function, with all parameters chosen as scalars.


3 Methodology
We derive xIELU by integrating trainable affine transformations applied to a modified version of the ELU activation function. We multiply the positive gradient of xIELU by 2 to simplify the derived integral expression. Since ELU is defined piecewise, we derive xIELU’s positive and negative components separately by integrating the following gradients:
| (6) |
where and are trainable parameters controlling the gradient flows for positive and negative inputs respectively, and and are trainable parameters determining the y-intercepts of the gradient for positive and negative inputs respectively.
3.1 Derivation
For positive inputs, integrating the linear gradient yields a quadratic function:
| (7) |
where is a trainable scalar parameter controlling the positive gradient flow. We set to match the gradient y-intercept of xIELU with established activation functions like GELU and SiLU. Setting ensures the function passes through the origin, maintaining consistency with other activation functions.
For negative inputs, integrating the exponential gradient gives:
| (8) |
where is a trainable scalar parameter controlling the negative gradient flow. We set to ensure gradient continuity, and to ensure function continuity. This yields the complete expression for xIELU:
| (9) |
3.2 Numerical Stability
Both xIELU and its gradient compute for , which can suffer from catastrophic cancellation when approaches zero from below. To ensure numerical stability during training, specialized functions like torch.expm1() need to be applied for both xIELU and its gradient. Alternatively, imposing an upper bound on negative values (e.g. -1e-6) before computing the exponential can also prevent catastrophic cancellation.
We also constrain the values of and to improve training stability, introducing a small training overhead that can be precomputed and removed during inference:
-
•
: Implemented by taking the softplus of , ensuring only positive gradients for positive inputs.
-
•
: Implemented by adding to the softplus of , ensuring the presence of negative valued gradients for negative inputs.
A basic implementation of xIELU is provided in Appendix A.3.



3.3 Computational Analysis
xIELU’s computational requirements can be broken down into the following operations:
-
•
One multiplication for the shared term
-
•
Two multiplications and one addition for the positive component
-
•
One exponential operation, one multiplication, and three additions for the negative component
-
•
One conditional branch to select between positive and negative components
For comparison, GELU and SiLU have the following computational requirements:
-
•
GELU with tanh approximation requires two exponentiations, six multiplications, four additions, and one division
-
•
SiLU requires one exponentiation, two multiplications, one addition, and one division
Exponentiation is a more computationally expensive operation than addition, multiplication or division. xIELU requires one exponentiation, making its theoretical computational cost similar to SiLU (one exponentiation) and more efficient than GELU (two exponentiations). However, since GELU and SiLU are well-established functions with highly optimized CUDA implementations, our current basic implementation of xIELU is comparatively slower. A kernel-fused implementation of xIELU should improve its computational efficiency to match the optimized implementations of GELU and SiLU.
4 Experiments and Discussion
4.1 Main Results
We conducted our experiments using Llama models (Touvron et al., 2023a, b), which are transformer-based architectures (Vaswani et al., 2017) that incorporate RMSNorm (Zhang and Sennrich, 2019) and Rotary Position Embeddings (Su et al., 2023). For our comparative analysis, we evaluated SwiGLU (the original Llama activation), ReLU2, and xIELU in the MLP blocks. For SwiGLU, we used gated MLP blocks with a hidden dimension of 6,144. For xIELU and ReLU2, we used standard MLP blocks with a hidden dimension of 9,216. This configuration ensures equivalent compute cost and parameter count across all variants. We initialized xIELU with and disabled weight decay for both parameters.
Following the DeepSeek scaling laws (DeepSeek-AI et al., 2024), we trained 1.1B parameter models from scratch with an approximately optimal batch size of 1.8M tokens and sequence length of 4096 on 126B tokens from the FineWeb Edu dataset (Penedo et al., 2024), processed using the Mistral NeMo tokenizer (Mistral AI, 2024). We implemented a warmup-stable-decay (WSD) learning rate schedule (Hägele et al., 2024; Zhai et al., 2022; Hu et al., 2024): a linear warmup phase and a constant learning rate of 8e-4 for 100B tokens, followed by a 20% cooldown phase using 1-sqrt decay over 26B tokens. Detailed hyperparameter settings are available in Appendix A.1.
Table 1 presents performance metrics comparing xIELU, SwiGLU, and ReLU2 activation functions across two training phases: the initial 100B tokens with constant learning rate and the subsequent 26B token cooldown phase. Figure 3(a) visualizes the loss curves for different activation functions during the cooldown phase. xIELU outperforms both SwiGLU and ReLU2, two widely adopted activation functions in LLMs.
| Activation | 100B Loss | 100B Perplexity | 126B Loss | 126B Perplexity |
|---|---|---|---|---|
| SwiGLU | 2.485 0.008 | 12.008 | 2.353 0.004 | 10.517 |
| ReLU2 | 2.473 0.007 | 11.858 | 2.337 0.004 | 10.352 |
| xIELU | 2.461 0.008 | 11.718 | 2.323 0.004 | 10.207 |
Table 2 benchmarks activation function speeds on a single node with 4 H100 GPUs. While xIELU currently exhibits marginally slower performance compared to SwiGLU and ReLU2, this comparison uses only a basic implementation of xIELU relying on torch.compile() for optimization. In contrast, SwiGLU, GELU, SiLU, and ReLU2 leverage highly optimized implementations alongside torch.compile(). We expect performance improvements for xIELU through CUDA kernel fusion and similar optimization techniques.
| Activation | Sequence Length | Batch Size | Time/Iteration (ms) |
|---|---|---|---|
| xIELU | 4096 | 5 | 560 |
| SwiGLU | 4096 | 5 | 549 |
| GELU | 4096 | 5 | 544 |
| SiLU | 4096 | 5 | 540 |
| ReLU2 | 4096 | 5 | 534 |


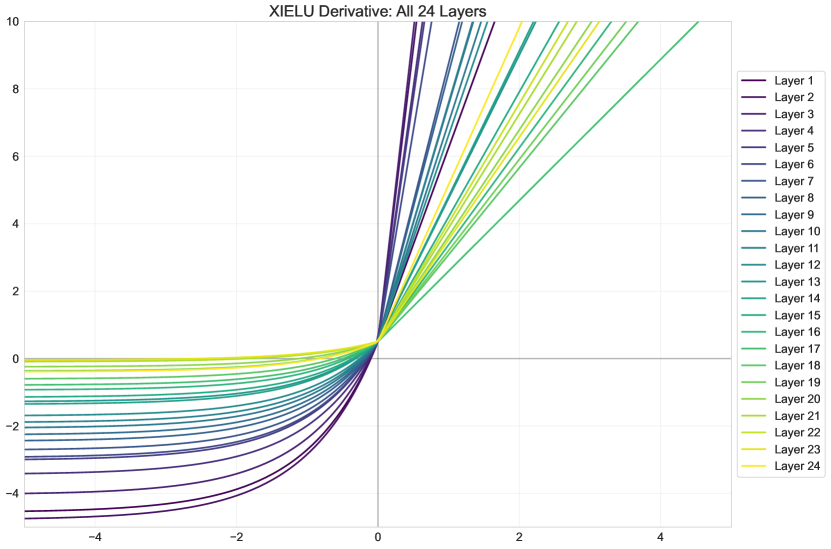
Figure 3(b) shows how xIELU’s trainable parameters and vary across network depth, with detailed visualizations of the function and its derivatives provided in Appendix Figure 4. Both parameters demonstrate a decreasing trend in deeper layers, indicating that xIELU adaptively reduces its non-linearity when handling higher-level representations. This progression towards simpler transformations for higher-level representations parallels design choices in hierarchical vision architectures (Szegedy et al., 2014; Simonyan and Zisserman, 2015; He et al., 2015a), where such behavior is typically enforced through architectural constraints such as dimensionality reduction. Notably, xIELU learns this pattern naturally during training without relying on inductive biases.
xIELU learns large values for , resulting in large negative gradients for negative inputs, particularly in earlier layers of the network. This produces positive activation outputs for negative inputs, which may enhance signal propagation through deeper layers. In contrast, standard activation functions handle negative inputs differently: ReLU outputs zero, GELU and SiLU converge to zero, and ELU converges to a fixed negative value. The generation of positive outputs from negative inputs has precedent in gated architectures, as seen in GEGLU and SwiGLU when both gate and input are negative.
We conducted experiments using a simple initialization of across all layers for xIELU. As shown in Figure 3(b), the learned values of and deviate significantly from these initial values. This initialization scheme was chosen based on smaller-scale experiments, where and showed smaller changes from their initial values. Further improvements might be achieved by using larger initialization values or varying the initialization across network depth.
4.2 Ablation
| Base | Modification | Perplexity |
|---|---|---|
| xIELU | - | 17.518 |
| SwiGLU | - | 17.583 |
| xIELU | Positive component x3 | 17.747 |
| xIELU | Negative component xSiLU | 17.837 |
| xIELU | Trainable | 17.880 |
| xSiLU | - | 17.914 |
| ReLU2 | - | 18.115 |
| xIELU | Fixed set to 1.0 | 18.146 |
| xIELU | Negative component SiLU | 18.176 |
| xIELU | Negative component set to 0 | 18.399 |
| SiLU | - | 18.576 |
To better understand xIELU’s design choices and validate our approach, we conducted ablation experiments using Llama models trained from scratch on 4B tokens from the FineWeb Edu dataset processed with the Meta Llama 3 tokenizer (Dubey et al., 2024). For our ablation analysis, we used 1.1B parameter models with sequence length 1024 and batch size of 82K tokens. The learning rate follows a combined schedule of linear warmup and cosine decay from 6e-4 to 6e-5. Detailed hyperparameter settings are provided in Appendix A.1. Ablation results are presented in Table 3.
For the positive component, a linearly increasing gradient achieves the best performance. Activation functions with gradients bounded above, such as SiLU and xSiLU, underperform, likely due to their limited capacity to propagate gradient information across layers. Conversely, higher-order functions like x3, with quadratically increasing gradients, also exhibit inferior performance. We hypothesize that these excessively steep gradients can destabilize training and hinder convergence.
For the negative component, a trainable negative gradient flow based on the exponential function achieves the best performance. Attempts to extend ReLU2 with the negative component of SiLU worsens performance compared to ReLU2 alone. In contrast, extending ReLU2 with the negative component of xSiLU leads to improved performance. Switching from an xSiLU-based to an exponential-based trainable negative gradient flow further improves performance. We hypothesize that this improvement arises from the monotonically increasing nature of the gradient of the exponential function.
4.3 Limitations
While xIELU demonstrates promising results, there are several important limitations to consider. First, our current implementation is slower than highly optimized implementations of established activation functions, though we expect this gap can be reduced through CUDA kernel fusion and optimization techniques. Second, while our experiments with 1.1B parameter models provide evidence for xIELU’s effectiveness, we have yet to validate these results at larger scales. Testing with larger models across different architectures and tasks would help establish how xIELU’s benefits generalize. Third, without true zeros in its outputs, xIELU lacks activation sparsity (Mirzadeh et al., 2023; Song et al., 2024) and its associated computational benefits.
5 Conclusion
In this work, we introduced a novel approach to activation function design by explicitly focusing on gradient properties and deriving functions through integration. This methodology led to the development of xIELU, which combines the beneficial gradient characteristics of existing activation functions: the linearly increasing gradient of ReLU² for positive inputs and trainable negative gradient flow inspired by xSiLU for negative inputs. Our empirical results with 1.1B parameter Llama models demonstrate that xIELU achieves superior performance compared to both ReLU² and SwiGLU while maintaining comparable computational efficiency. The effectiveness of xIELU suggest that focusing on gradient properties is a promising direction for developing new activation functions.
6 Acknowledgments
This work was supported as part of the Swiss AI Initiative by a grant from the Swiss National Supercomputing Centre (CSCS) under project ID a06 (Horizontal: LLMs) on Alps.
References
- Clevert et al. [2015] Djork-Arn’e Clevert, Thomas Unterthiner, and Sepp Hochreiter. Fast and accurate deep network learning by exponential linear units (elus), 2015.
- DeepSeek-AI et al. [2024] DeepSeek-AI, :, Xiao Bi, Deli Chen, Guanting Chen, Shanhuang Chen, Damai Dai, Chengqi Deng, Honghui Ding, Kai Dong, Qiushi Du, Zhe Fu, Huazuo Gao, Kaige Gao, Wenjun Gao, Ruiqi Ge, Kang Guan, Daya Guo, Jianzhong Guo, Guangbo Hao, Zhewen Hao, Ying He, Wenjie Hu, Panpan Huang, Erhang Li, Guowei Li, Jiashi Li, Yao Li, Y. K. Li, Wenfeng Liang, Fangyun Lin, A. X. Liu, Bo Liu, Wen Liu, Xiaodong Liu, Xin Liu, Yiyuan Liu, Haoyu Lu, Shanghao Lu, Fuli Luo, Shirong Ma, Xiaotao Nie, Tian Pei, Yishi Piao, Junjie Qiu, Hui Qu, Tongzheng Ren, Zehui Ren, Chong Ruan, Zhangli Sha, Zhihong Shao, Junxiao Song, Xuecheng Su, Jingxiang Sun, Yaofeng Sun, Minghui Tang, Bingxuan Wang, Peiyi Wang, Shiyu Wang, Yaohui Wang, Yongji Wang, Tong Wu, Y. Wu, Xin Xie, Zhenda Xie, Ziwei Xie, Yiliang Xiong, Hanwei Xu, R. X. Xu, Yanhong Xu, Dejian Yang, Yuxiang You, Shuiping Yu, Xingkai Yu, B. Zhang, Haowei Zhang, Lecong Zhang, Liyue Zhang, Mingchuan Zhang, Minghua Zhang, Wentao Zhang, Yichao Zhang, Chenggang Zhao, Yao Zhao, Shangyan Zhou, Shunfeng Zhou, Qihao Zhu, and Yuheng Zou. Deepseek llm: Scaling open-source language models with longtermism, 2024.
- Dubey et al. [2024] Abhimanyu Dubey, Abhinav Jauhri, Abhinav Pandey, Abhishek Kadian, Ahmad Al-Dahle, Aiesha Letman, Akhil Mathur, Alan Schelten, Amy Yang, Angela Fan, Anirudh Goyal, Anthony Hartshorn, Aobo Yang, Archi Mitra, Archie Sravankumar, Artem Korenev, Arthur Hinsvark, Arun Rao, Aston Zhang, Aurelien Rodriguez, Austen Gregerson, Ava Spataru, Baptiste Roziere, Bethany Biron, Binh Tang, Bobbie Chern, Charlotte Caucheteux, Chaya Nayak, Chloe Bi, Chris Marra, Chris McConnell, Christian Keller, Christophe Touret, Chunyang Wu, Corinne Wong, Cristian Canton Ferrer, Cyrus Nikolaidis, Damien Allonsius, Daniel Song, Danielle Pintz, Danny Livshits, David Esiobu, Dhruv Choudhary, Dhruv Mahajan, Diego Garcia-Olano, Diego Perino, Dieuwke Hupkes, Egor Lakomkin, Ehab AlBadawy, Elina Lobanova, Emily Dinan, Eric Michael Smith, Filip Radenovic, Frank Zhang, Gabriel Synnaeve, Gabrielle Lee, Georgia Lewis Anderson, Graeme Nail, Gregoire Mialon, Guan Pang, Guillem Cucurell, Hailey Nguyen, Hannah Korevaar, Hu Xu, Hugo Touvron, Iliyan Zarov, Imanol Arrieta Ibarra, Isabel Kloumann, Ishan Misra, Ivan Evtimov, Jade Copet, Jaewon Lee, Jan Geffert, Jana Vranes, Jason Park, Jay Mahadeokar, Jeet Shah, Jelmer van der Linde, Jennifer Billock, Jenny Hong, Jenya Lee, Jeremy Fu, Jianfeng Chi, Jianyu Huang, Jiawen Liu, Jie Wang, Jiecao Yu, Joanna Bitton, Joe Spisak, Jongsoo Park, Joseph Rocca, Joshua Johnstun, Joshua Saxe, Junteng Jia, Kalyan Vasuden Alwala, Kartikeya Upasani, Kate Plawiak, Ke Li, Kenneth Heafield, Kevin Stone, Khalid El-Arini, Krithika Iyer, Kshitiz Malik, Kuenley Chiu, Kunal Bhalla, Lauren Rantala-Yeary, Laurens van der Maaten, Lawrence Chen, Liang Tan, Liz Jenkins, Louis Martin, Lovish Madaan, Lubo Malo, Lukas Blecher, Lukas Landzaat, Luke de Oliveira, Madeline Muzzi, Mahesh Pasupuleti, Mannat Singh, Manohar Paluri, Marcin Kardas, Mathew Oldham, Mathieu Rita, Maya Pavlova, Melanie Kambadur, Mike Lewis, Min Si, Mitesh Kumar Singh, Mona Hassan, Naman Goyal, Narjes Torabi, Nikolay Bashlykov, Nikolay Bogoychev, Niladri Chatterji, Olivier Duchenne, Onur Çelebi, Patrick Alrassy, Pengchuan Zhang, Pengwei Li, Petar Vasic, Peter Weng, Prajjwal Bhargava, Pratik Dubal, Praveen Krishnan, Punit Singh Koura, Puxin Xu, Qing He, Qingxiao Dong, Ragavan Srinivasan, Raj Ganapathy, Ramon Calderer, Ricardo Silveira Cabral, Robert Stojnic, Roberta Raileanu, Rohit Girdhar, Rohit Patel, Romain Sauvestre, Ronnie Polidoro, Roshan Sumbaly, Ross Taylor, Ruan Silva, Rui Hou, Rui Wang, Saghar Hosseini, Sahana Chennabasappa, Sanjay Singh, Sean Bell, Seohyun Sonia Kim, Sergey Edunov, Shaoliang Nie, Sharan Narang, Sharath Raparthy, Sheng Shen, Shengye Wan, Shruti Bhosale, Shun Zhang, Simon Vandenhende, Soumya Batra, Spencer Whitman, Sten Sootla, Stephane Collot, Suchin Gururangan, Sydney Borodinsky, Tamar Herman, Tara Fowler, Tarek Sheasha, Thomas Georgiou, Thomas Scialom, Tobias Speckbacher, Todor Mihaylov, Tong Xiao, Ujjwal Karn, Vedanuj Goswami, Vibhor Gupta, Vignesh Ramanathan, Viktor Kerkez, Vincent Gonguet, Virginie Do, Vish Vogeti, Vladan Petrovic, Weiwei Chu, Wenhan Xiong, Wenyin Fu, Whitney Meers, Xavier Martinet, Xiaodong Wang, Xiaoqing Ellen Tan, Xinfeng Xie, Xuchao Jia, Xuewei Wang, Yaelle Goldschlag, Yashesh Gaur, Yasmine Babaei, Yi Wen, Yiwen Song, Yuchen Zhang, Yue Li, Yuning Mao, Zacharie Delpierre Coudert, Zheng Yan, Zhengxing Chen, Zoe Papakipos, Aaditya Singh, Aaron Grattafiori, Abha Jain, Adam Kelsey, Adam Shajnfeld, Adithya Gangidi, Adolfo Victoria, Ahuva Goldstand, Ajay Menon, Ajay Sharma, Alex Boesenberg, Alex Vaughan, Alexei Baevski, Allie Feinstein, Amanda Kallet, Amit Sangani, Anam Yunus, Andrei Lupu, Andres Alvarado, Andrew Caples, Andrew Gu, Andrew Ho, Andrew Poulton, Andrew Ryan, Ankit Ramchandani, Annie Franco, Aparajita Saraf, Arkabandhu Chowdhury, Ashley Gabriel, Ashwin Bharambe, Assaf Eisenman, Azadeh Yazdan, Beau James, Ben Maurer, Benjamin Leonhardi, Bernie Huang, Beth Loyd, Beto De Paola, Bhargavi Paranjape, Bing Liu, Bo Wu, Boyu Ni, Braden Hancock, Bram Wasti, Brandon Spence, Brani Stojkovic, Brian Gamido, Britt Montalvo, Carl Parker, Carly Burton, Catalina Mejia, Changhan Wang, Changkyu Kim, Chao Zhou, Chester Hu, Ching-Hsiang Chu, Chris Cai, Chris Tindal, Christoph Feichtenhofer, Damon Civin, Dana Beaty, Daniel Kreymer, Daniel Li, Danny Wyatt, David Adkins, David Xu, Davide Testuggine, Delia David, Devi Parikh, Diana Liskovich, Didem Foss, Dingkang Wang, Duc Le, Dustin Holland, Edward Dowling, Eissa Jamil, Elaine Montgomery, Eleonora Presani, Emily Hahn, Emily Wood, Erik Brinkman, Esteban Arcaute, Evan Dunbar, Evan Smothers, Fei Sun, Felix Kreuk, Feng Tian, Firat Ozgenel, Francesco Caggioni, Francisco Guzmán, Frank Kanayet, Frank Seide, Gabriela Medina Florez, Gabriella Schwarz, Gada Badeer, Georgia Swee, Gil Halpern, Govind Thattai, Grant Herman, Grigory Sizov, Guangyi, Zhang, Guna Lakshminarayanan, Hamid Shojanazeri, Han Zou, Hannah Wang, Hanwen Zha, Haroun Habeeb, Harrison Rudolph, Helen Suk, Henry Aspegren, Hunter Goldman, Ibrahim Damlaj, Igor Molybog, Igor Tufanov, Irina-Elena Veliche, Itai Gat, Jake Weissman, James Geboski, James Kohli, Japhet Asher, Jean-Baptiste Gaya, Jeff Marcus, Jeff Tang, Jennifer Chan, Jenny Zhen, Jeremy Reizenstein, Jeremy Teboul, Jessica Zhong, Jian Jin, Jingyi Yang, Joe Cummings, Jon Carvill, Jon Shepard, Jonathan McPhie, Jonathan Torres, Josh Ginsburg, Junjie Wang, Kai Wu, Kam Hou U, Karan Saxena, Karthik Prasad, Kartikay Khandelwal, Katayoun Zand, Kathy Matosich, Kaushik Veeraraghavan, Kelly Michelena, Keqian Li, Kun Huang, Kunal Chawla, Kushal Lakhotia, Kyle Huang, Lailin Chen, Lakshya Garg, Lavender A, Leandro Silva, Lee Bell, Lei Zhang, Liangpeng Guo, Licheng Yu, Liron Moshkovich, Luca Wehrstedt, Madian Khabsa, Manav Avalani, Manish Bhatt, Maria Tsimpoukelli, Martynas Mankus, Matan Hasson, Matthew Lennie, Matthias Reso, Maxim Groshev, Maxim Naumov, Maya Lathi, Meghan Keneally, Michael L. Seltzer, Michal Valko, Michelle Restrepo, Mihir Patel, Mik Vyatskov, Mikayel Samvelyan, Mike Clark, Mike Macey, Mike Wang, Miquel Jubert Hermoso, Mo Metanat, Mohammad Rastegari, Munish Bansal, Nandhini Santhanam, Natascha Parks, Natasha White, Navyata Bawa, Nayan Singhal, Nick Egebo, Nicolas Usunier, Nikolay Pavlovich Laptev, Ning Dong, Ning Zhang, Norman Cheng, Oleg Chernoguz, Olivia Hart, Omkar Salpekar, Ozlem Kalinli, Parkin Kent, Parth Parekh, Paul Saab, Pavan Balaji, Pedro Rittner, Philip Bontrager, Pierre Roux, Piotr Dollar, Polina Zvyagina, Prashant Ratanchandani, Pritish Yuvraj, Qian Liang, Rachad Alao, Rachel Rodriguez, Rafi Ayub, Raghotham Murthy, Raghu Nayani, Rahul Mitra, Raymond Li, Rebekkah Hogan, Robin Battey, Rocky Wang, Rohan Maheswari, Russ Howes, Ruty Rinott, Sai Jayesh Bondu, Samyak Datta, Sara Chugh, Sara Hunt, Sargun Dhillon, Sasha Sidorov, Satadru Pan, Saurabh Verma, Seiji Yamamoto, Sharadh Ramaswamy, Shaun Lindsay, Shaun Lindsay, Sheng Feng, Shenghao Lin, Shengxin Cindy Zha, Shiva Shankar, Shuqiang Zhang, Shuqiang Zhang, Sinong Wang, Sneha Agarwal, Soji Sajuyigbe, Soumith Chintala, Stephanie Max, Stephen Chen, Steve Kehoe, Steve Satterfield, Sudarshan Govindaprasad, Sumit Gupta, Sungmin Cho, Sunny Virk, Suraj Subramanian, Sy Choudhury, Sydney Goldman, Tal Remez, Tamar Glaser, Tamara Best, Thilo Kohler, Thomas Robinson, Tianhe Li, Tianjun Zhang, Tim Matthews, Timothy Chou, Tzook Shaked, Varun Vontimitta, Victoria Ajayi, Victoria Montanez, Vijai Mohan, Vinay Satish Kumar, Vishal Mangla, Vítor Albiero, Vlad Ionescu, Vlad Poenaru, Vlad Tiberiu Mihailescu, Vladimir Ivanov, Wei Li, Wenchen Wang, Wenwen Jiang, Wes Bouaziz, Will Constable, Xiaocheng Tang, Xiaofang Wang, Xiaojian Wu, Xiaolan Wang, Xide Xia, Xilun Wu, Xinbo Gao, Yanjun Chen, Ye Hu, Ye Jia, Ye Qi, Yenda Li, Yilin Zhang, Ying Zhang, Yossi Adi, Youngjin Nam, Yu, Wang, Yuchen Hao, Yundi Qian, Yuzi He, Zach Rait, Zachary DeVito, Zef Rosnbrick, Zhaoduo Wen, Zhenyu Yang, and Zhiwei Zhao. The llama 3 herd of models, 2024.
- Elfwing et al. [2017] Stefan Elfwing, Eiji Uchibe, and Kenji Doya. Sigmoid-weighted linear units for neural network function approximation in reinforcement learning, 2017.
- He et al. [2015a] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Deep residual learning for image recognition, 2015a.
- He et al. [2015b] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification, 2015b.
- Hendrycks and Gimpel [2016] Dan Hendrycks and Kevin Gimpel. Gaussian error linear units (gelus), 2016.
- Hu et al. [2024] Shengding Hu, Yuge Tu, Xu Han, Chaoqun He, Ganqu Cui, Xiang Long, Zhi Zheng, Yewei Fang, Yuxiang Huang, Weilin Zhao, Xinrong Zhang, Zheng Leng Thai, Kaihuo Zhang, Chongyi Wang, Yuan Yao, Chenyang Zhao, Jie Zhou, Jie Cai, Zhongwu Zhai, Ning Ding, Chao Jia, Guoyang Zeng, Dahai Li, Zhiyuan Liu, and Maosong Sun. Minicpm: Unveiling the potential of small language models with scalable training strategies, 2024.
- Huang [2024] Allen Hao Huang. Expanded gating ranges improve activation functions, 2024.
- Hägele et al. [2024] Alexander Hägele, Elie Bakouch, Atli Kosson, Loubna Ben Allal, Leandro Von Werra, and Martin Jaggi. Scaling laws and compute-optimal training beyond fixed training durations, 2024.
- Klambauer et al. [2017] Gunter Klambauer, Thomas Unterthiner, Andreas Mayr, and Sepp Hochreiter. Self-normalizing neural networks, 2017.
- Maas et al. [2013] Andrew L Maas, Awni Y Hannun, and Andrew Y Ng. Rectifier nonlinearities improve neural network acoustic models, 2013.
- McCulloch and Pitts [1943] Warren S. McCulloch and Walter Pitts. A logical calculus of the ideas immanent in nervous activity, 1943.
- Mirzadeh et al. [2023] Iman Mirzadeh, Keivan Alizadeh, Sachin Mehta, Carlo C Del Mundo, Oncel Tuzel, Golnoosh Samei, Mohammad Rastegari, and Mehrdad Farajtabar. Relu strikes back: Exploiting activation sparsity in large language models, 2023.
- Mistral AI [2024] Mistral AI. Mistral NeMo: Frontier AI in your hands, 2024. URL https://mistral.ai/news/mistral-nemo/.
- Nair and Hinton [2010] Vinod Nair and Geoffrey E Hinton. Rectified linear units improve restricted boltzmann machines, 2010.
- Penedo et al. [2024] Guilherme Penedo, Hynek Kydlíček, Loubna Ben allal, Anton Lozhkov, Margaret Mitchell, Colin Raffel, Leandro Von Werra, and Thomas Wolf. The fineweb datasets: Decanting the web for the finest text data at scale, 2024.
- Ramachandran et al. [2017] Prajit Ramachandran, Barret Zoph, and Quoc V Le. Searching for activation functions, 2017.
- Shazeer [2020] Noam Shazeer. Glu variants improve transformer, 2020.
- Simonyan and Zisserman [2015] Karen Simonyan and Andrew Zisserman. Very deep convolutional networks for large-scale image recognition, 2015.
- So et al. [2021] David R So, Wojciech Mani, Yinhan Liu, Zihang Dai, Sam Shleifer, Naman C Landolfi, Alan He, and Quoc V Le. Primer: Searching for efficient transformers for language modeling, 2021.
- Song et al. [2024] Chenyang Song, Xu Han, Zhengyan Zhang, Shengding Hu, Xiyu Shi, Kuai Li, Chen Chen, Zhiyuan Liu, Guangli Li, Tao Yang, and Maosong Sun. Prosparse: Introducing and enhancing intrinsic activation sparsity within large language models, 2024.
- Su et al. [2023] Jianlin Su, Yu Lu, Shengfeng Pan, Ahmed Murtadha, Bo Wen, and Yunfeng Liu. Roformer: Enhanced transformer with rotary position embedding, 2023.
- Szegedy et al. [2014] Christian Szegedy, Wei Liu, Yangqing Jia, Pierre Sermanet, Scott Reed, Dragomir Anguelov, Dumitru Erhan, Vincent Vanhoucke, and Andrew Rabinovich. Going deeper with convolutions, 2014.
- Touvron et al. [2023a] Hugo Touvron, Thibaut Lavril, Gautier Izacard, Xavier Martinet, Marie-Anne Lachaux, Timothée Lacroix, Baptiste Rozière, Naman Goyal, Eric Hambro, Faisal Azhar, Aurelien Rodriguez, Armand Joulin, Edouard Grave, and Guillaume Lample. Llama: Open and efficient foundation language models, 2023a.
- Touvron et al. [2023b] Hugo Touvron, Louis Martin, Kevin Stone, Peter Albert, Amjad Almahairi, Yasmine Babaei, Nikolay Bashlykov, Soumya Batra, Prajjwal Bhargava, Shruti Bhosale, Dan Bikel, Lukas Blecher, Cristian Canton Ferrer, Moya Chen, Guillem Cucurull, David Esiobu, Jude Fernandes, Jeremy Fu, Wenyin Fu, Brian Fuller, Cynthia Gao, Vedanuj Goswami, Naman Goyal, Anthony Hartshorn, Saghar Hosseini, Rui Hou, Hakan Inan, Marcin Kardas, Viktor Kerkez, Madian Khabsa, Isabel Kloumann, Artem Korenev, Punit Singh Koura, Marie-Anne Lachaux, Thibaut Lavril, Jenya Lee, Diana Liskovich, Yinghai Lu, Yuning Mao, Xavier Martinet, Todor Mihaylov, Pushkar Mishra, Igor Molybog, Yixin Nie, Andrew Poulton, Jeremy Reizenstein, Rashi Rungta, Kalyan Saladi, Alan Schelten, Ruan Silva, Eric Michael Smith, Ranjan Subramanian, Xiaoqing Ellen Tan, Binh Tang, Ross Taylor, Adina Williams, Jian Xiang Kuan, Puxin Xu, Zheng Yan, Iliyan Zarov, Yuchen Zhang, Angela Fan, Melanie Kambadur, Sharan Narang, Aurelien Rodriguez, Robert Stojnic, Sergey Edunov, and Thomas Scialom. Llama 2: Open foundation and fine-tuned chat models, 2023b.
- Vaswani et al. [2017] Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N. Gomez, Lukasz Kaiser, and Illia Polosukhin. Attention is all you need, 2017.
- Zhai et al. [2022] Xiaohua Zhai, Alexander Kolesnikov, Neil Houlsby, and Lucas Beyer. Scaling vision transformers, 2022.
- Zhang and Sennrich [2019] Biao Zhang and Rico Sennrich. Root mean square layer normalization, 2019.
- Zhang et al. [2024] Zhengyan Zhang, Yixin Song, Guanghui Yu, Xu Han, Yankai Lin, Chaojun Xiao, Chenyang Song, Zhiyuan Liu, Zeyu Mi, and Maosong Sun. Relu2 wins: Discovering efficient activation functions for sparse llms, 2024.
Appendix A Appendix
A.1 Base Experiment Setup
| Hyperparameter | Value |
|---|---|
| Sequence Length | 4096 |
| Batch Size | 440 |
| Vocab Size | 147456 |
| Hidden Size | 1536 |
| Intermediate Size | 6144 or 9216 |
| Num Hidden Layers | 24 |
| Num Attention Heads | 16 |
| Weight Decay | 0.1 |
| Grad Clip | 1.0 |
| Optimizer | AdamW |
| Adam Beta1 | 0.9 |
| Adam Beta2 | 0.95 |
| Adam Epsilon | 1e-8 |
| Rope Theta | 500000 |
| Max Learning Rate | 8e-4 |
| Min Learning Rate | 0.0 |
| LR Warmup Steps | 2000 |
| LR Warmup Style | Linear |
| LR Constant Steps | 53500 |
| LR Cooldown Steps | 14500 |
| LR Cooldown Style | 1-sqrt |
A.2 Ablation Experiment Setup
| Hyperparameter | Value |
|---|---|
| Sequence Length | 1024 |
| Batch Size | 80 |
| Vocab Size | 128256 |
| Hidden Size | 1536 |
| Intermediate Size | 6144 or 9216 |
| Num Hidden Layers | 24 |
| Num Attention Heads | 16 |
| Weight Decay | 0.01 |
| Grad Clip | 1.0 |
| Optimizer | AdamW |
| Adam Beta1 | 0.9 |
| Adam Beta2 | 0.95 |
| Adam Epsilon | 1e-8 |
| Rope Theta | 500000 |
| Max Learning Rate | 6e-4 |
| Min Learning Rate | 6e-5 |
| LR Warmup Steps | 200 |
| LR Warmup Style | Linear |
| LR Cooldown Steps | 49800 |
| LR Cooldown Style | Cosine |
A.3 xIELU Implementation
Basic implementation of xIELU using PyTorch. Relies on torch.compile() for optimization.
import torch
import torch.nn as nn
import torch.nn.functional as F
class XIELU(nn.Module):
def __init__(self, alpha_p_init=0.8, alpha_n_init=0.8, beta=0.5, eps=-1e-6):
super(XIELU, self).__init__()
self.beta = beta
self.alpha_p = nn.Parameter(torch.log(torch.tensor(alpha_p_init)) - 1)
self.alpha_n = nn.Parameter(torch.log(torch.tensor(alpha_n_init - self.beta)) - 1)
self.eps = torch.tensor(eps)
def forward(self, x):
alpha_p = F.softplus(self.alpha_p)
alpha_n = self.beta + F.softplus(self.alpha_n)
return torch.where(x > 0,
alpha_p * x * x + self.beta * x,
alpha_n * torch.expm1(torch.min(x, self.eps)) - alpha_n * x + self.beta * x)