Density-corrected DFT explained: Questions and answers
I. Introduction
In any practical Kohn-Sham density functional theory (KS-DFT) calculation, of which there are tens of thousands reported each year, the exchange-correlation (XC) is approximated, and there are literally hundreds of approximations in common use today.[1] In every single case, one can consider the error in the calculation as arising from two different sources: the error in the self-consistent (SC) density and the error in the final evaluation of the total energy.[2] Density-corrected DFT (DC-DFT) is a formal framework for distinguishing these two types of error.[3, 4]
To be clear, in the vast majority of DFT calculations reported, the SC density is an excellent approximation to the exact density, so that the error in the energy is almost entirely due to the functional approximation to the energy. However, in a significant subset of calculations where standard approximations show surprisingly large errors, these errors can be traced to the error in the SC density.[5, 6] In such cases, use of a more accurate density usually reduces the error significantly (typically by a factor of 2 or more). This has been demonstrated for specific classes of problems, such as electron affinities[7], dissociation energy curve of diatomic molecules[5, 8], radical ions in solution[4], -hole interaction energies of halogen bonds[6], and spin gaps of transition metal complexes[9].
This observation would be useless if one always needed highly accurate densities to generate these improvements in energies, as such densities would cost at least as much as generating highly accurate energies via, e.g., CCSD(T).[8] However, in practice, when standard semilocal density functionals fail due to density-driven errors, the Hartree-Fock (HF) density is usually sufficient to generate energetic improvements that are comparable to those of the exact density. In various calculations going back to the early 1990’s and the rise of DFT for computation in chemistry, there have been applications of this approach, dubbed HF-DFT, mostly for convenience, but no general understanding of when it should be applied.[10, 11, 12, 13, 14, 15, 16] Once codes were reworked to automatically perform self-consistent DFT calculations, which has both formal and practical advantages, it became largely obsolete.
DC-DFT is the theory that explains when HF-DFT should be applied and when it should work. The significance of DC-DFT is that it helps the systematic development of density functional approximation by providing a principle for determining the true error. The exact functional is free of density errors, since both its energy and its functional derivative (which determines the density) are exact. For any approximation, the error in the energy has contributions from both the functional and the density. Typical DFT error analysis is based on the total energy error and does not distinguish the source of the error nor determine the accuracy of the functional. According to the principles of DC-DFT, researchers should use just functional errors (or use them together with density-driven errors) to formulate strategies and guidelines for functional correction and development. In the early days of DFT in quantum chemistry, these principles were largely irrelevant, as functionals were rather crude and most calculations had relatively negligible density-driven errors (hence the use of HF-DFT when convenient). With the rise in applications of DFT to many different systems throughout chemistry[17, 18, 19], the characterization of errors for specific properties or systems, and the ever increasing accuracy of modern functionals[1, 20], the importance of the principles of DC-DFT has grown enormously.

DC-DFT is a rigorous theory, separating errors using the exact density. It identifies approximate DFT calculations as abnormal when the density-driven error is signficant. In practice, it is most often applied using the HF density in place of the exact one, and using a simple heuristic like density sensitivity in place of abnormality to decide if the HF density should be used in place of the self-consistent density. We have called that procedure DC(HF)-DFT, meaning density-corrected DFT, using the HF density but only when it is appropriate.
The most immediate application of DC(HF)-DFT is to understand HF-DFT, by producing a recipe stating when it should improve over SC-DFT. Thus, DC(HF)-DFT includes two criteria for when a HF density should be used instead of a SC density. The most important is that the calculation under consideration should be contaminated by a density-driven error. Simple measures that are suitable for many circumstances have evolved.[21] The current criteria is if the energy calculation shows pronounced density sensitivity, i.e., the result changes appreciably when evaluated on two distinct densities. Second, because the HF density is a proxy for the exact density, we avoid its use when it is spin contaminated (note that spin contamination is typically less of a problem for SC-DFT).[22] These criteria are both common sense and understandable in terms of the general theory of DC-DFT.
This paper explains the current state of the art of DC(HF)-DFT, and its relation to HF-DFT (meaning always using HF densities instead of self-consistent ones). In the background section, we give both the general theory of DC-DFT and the history of HF-DFT. The recent work of Jan Martin and co-workers in Ref. [23] was possibly the most comprehensive study of HF-DFT to date (although, as we detailed below, it contained several conceptual confusions and other difficulties). But it did not apply DC(HF)-DFT methodology in its current form. We illustrate with many examples from Ref. [23] data the detailed performance of DC(HF)-DFT.
II. Background
i. DC-DFT
The core idea of DC-DFT is to separate the energetic error of any SC-DFT calculation into a functional contribution and a density-driven error, where the latter vanishes if an approximate functional is evaluated on the exact density. Writing the total SC-DFT energy error as: , where and are the exact energy functional and density, and and are their approximate counterparts, is decomposed as:[3, 8, 21]:
| (1) |
where is the functional error and is the density-driven error. Almost all present DFT calculations use the KS scheme[24], in which the functional error is simply the error in the XC approximation, evaluated on the exact density. Moreover, almost all such calculations are for energy differences, so one applies Eq. 1 to each calculation separately, and subtracts.
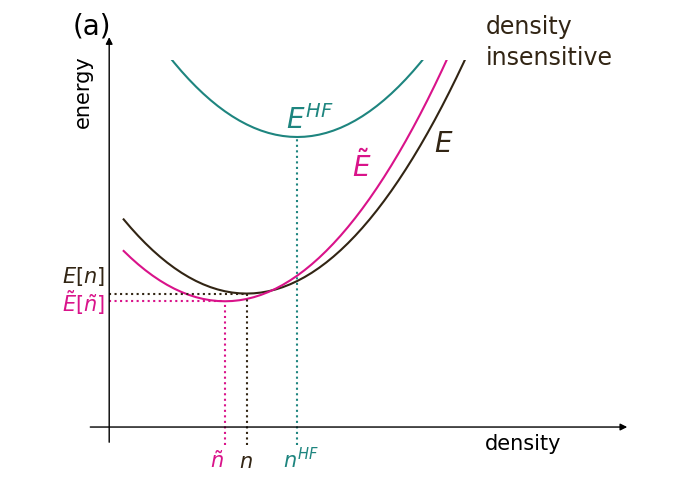
Most standard XC approximations begin with a semi-local form, including a generalized gradient approximation (GGA). For many molecules and properties of chemical interest, such as dissociations energies, the magnitude of with such functionals is much smaller than that of , and can be neglected. On the other hand, in density-sensitive calculations, represents a significant fraction of the total error (see the cartoons in Fig. 1 comparing density-sensitive and insensitive calculations). The density-sensitivity of a DFT calculation depends on the system under study, the property being extracted, and the approximate functional.
Generically (but not always), removal of the density-driven error in density-sensitive calculations improves the result substantially. Rigorously, a precise calculation of by Eq. 1 requires highly accurate densities from, e.g., correlated wavefunction calculations. This can only be done for smaller systems. Moreover, the well-known difficulties of performing KS inversions within atom-centered bases limit the precision of such calculations[25, 26], which must be accurate enough to measure the difference in density-driven error between the SC-DFT density and the more accurate one.[8]
By definition, the theory of DC-DFT tells us that, for the vast majority of modern KS-DFT calculations, the SC density is a very good approximation to the exact density. It even provides an extremely meaningful metric of the quality of a density, namely how much of the energy error is due to the density error.[21] Given the formal and practical advantages of SC densities, we should only consider using a different density when the density-driven error is significant.
Finally, we mention that there is extensive theory behind Eq. 1. Ref. [27] shows the functional analysis that can be applied, and derives 79 more equations from Eq. 1. An almost identical analysis applied to geometries in computational chemistry (ranging from force fields to ab initio quantum chemical methods), produces a cornucopia of results.[28] The performance of such methods for molecular geometries typically differs drastically from their energetic performance.
ii. HF-DFT as a DC-DFT procedure
We define HF-DFT as the practice of evaluating an XC approximation on the HF density and orbitals in all cases.[29] For many standard XC approximations, molecules, and properties, when the calculation is density sensitive, HF-DFT yields more accurate results than SC-DFT. For insensitive calculations, this may or may not be true, but it is irrelevant, as the density-driven errors are negligible. Thus the theory of DC-DFT provides criteria for when HF-DFT should yield a better result. The first is that the calculation should be density sensitive. The second is that the HF density should be a good proxy for the exact density, and hence not be, e.g., spin-contaminated or flawed in some other way.
Thus HF-DFT is a procedure, whereas DC-DFT is a theoretical framework, and the two terms should not be used interchangeably. We use the acronym DC(HF)-DFT to denote the use of HF-DFT only when a calculation is density-sensitive and its HF wavefunction is not spin-contaminated. Unfortunately, this distinction has not always been emphasized in the past. In their paper, Ref. [23] applied the HF-DFT procedure to every calculation in the GMTKN55 database[19], which goes against the basic principles of DC-DFT, and provides little or no information about the performance of DC(HF)-DFT.
By the use of the exact , is completely eliminated (Eq. 1), but is prohibitively expensive in practice. HF densities offer a viable alternative for reducing large density-driven errors. In this way, only for density-sensitive calculations, the approximation is made. Using in place of SC to reduce density-driven errors makes sense when:
| (2) |
This condition is sufficient, but is not always neccessary. When HF overlocalizes, HF-DFT can outperform SC-DFT for functionals that delocalize, even if Eq. 2 is not satisfied. From the KS inversion that gives us access to highly accurate densities and KS orbitals for small systems, it has been found that Eq. 2 holds for typical cases when is large.[8] This, in turn, justifies the choice of using in place of in those calculations. It was also found that, for orbital-dependent XC approximations, the replacement of the KS kinetic energy with the HF kinetic energy also introduces errors that are far smaller than .[8]
Since measuring by Eq. 1 requires exact densities, the more practical density sensitivity measure has been introduced:[21, 6, 8]
| (3) |
where tilde indicates a given functional approximation. This measure requires two non-emprirical densities: HF densities which are typically overlocalized and LDA densities which are typically delocalized. Neither density is too expensive in routine molecular calculations. In this way, serves as a practical indicator of the density sensitivity of a given reaction and approximate functional. For small molecules, 2 kcal/mol implies density sensitivity, that the calculation may suffer from a large , and for semilocal approximations, HF-DFT will likely improve a functional’s performance.[21] Therefore, SC densities should be replaced by HF ones only in density-sensitive calculations. Even in those cases, one has to keep an eye on whether is severely flawed by spin-contamination, as then the use of HF densities (at least those from the spin unrestricted formalism) is not recommended either. There is a need to develop a clever way to deal with the spin contamination issue, but for now, we are converting HF density to SC density for practical reasons. The cutoff of 2 kcal/mol is taken as typical for covalent bonds in small molecules. As molecules grow, the cutoff must grow.[30] For reactions where small energy changes matters like non-covalent interactions, a smaller cutoff is appropriate.
iii. History: HF-DFT before and after DC-DFT
The use of the HF-DFT procedure long predates the analysis of DC-DFT [12, 14, 31]. As far back as the 1970’s, Colle and Salvetti developed approximate correlation functionals that were trained and applied to HF densities[32], and led to the LYP functional[33]. Other functionals, such as those of Gordon and Kim[34], and Wilson and Levy[35] were developed in a similar fashion, and these functionals were at the time highly competitive for weak interactions[34, 36] Even the B88 GGA[37] was developed on HF atomic densities. Gill et al. used HF-DFT for practical reasons to test the accuracy of GGAs and hybrids without a need to obtain SC densities and orbitals for each of the functionals.[11, 12] Another reason why HF-DFT can be considered more practical than SC-DFT is that the former requires no grids for the XC potential at each self-consistent field (SCF) iteration.[38] In all these cases, we would now say that the authors were assuming (correctly) that the calculations were density-insensitive, and the error was dominated by the error in the XC approximation, regardless of HF versus SC density.
However, some pioneering efforts did notice that, for some problems where SC-DFT was underperforming, HF-DFT gave systematic improvements. This was most often observed for barrier height calculations, as demonstrated by different authors.[39, 31, 38, 21] We now understand that this entire class of calculation is typically density-sensitive (see below) and DC-DFT tells us why HF-DFT works better here but not, say, for main-group reaction energies. Some of our own earlier works on electron affinities[7, 40, 41] are couched in terms of self-interaction error and were not understood in terms of the general principles of DC-DFT until later.[2, 3] On the other hand, DC-DFT has reignited interest in functionals of the HF density.[42] For example, it has been shown that the large-coupling strength expansion of the Møller-Plesset adiabatic connection is a functional of the HF density.[43, 44, 45] This finding motivated the development of a new class of functionals applied to HF densities, which have been found to be highly accurate for weak interactions.[45]
After DC-DFT was developed[3],
explaining the success and validity of HF-DFT results,
Sim and co-workers could then identify specific classes of calculations that
are prone to density-driven errors, where HF-DFT should (and does) give improved results over SC-DFT.
In addition to barrier heights, these include: dissociation of stretched molecules[5], some radical reaction energies[4],
electron affinities[41, 40, 7], specific torsional barriers[46],
some weak interactions[6], spin gaps of Fe(II) complexes[9],
interaction of water clusters[47],
etc.
The work of Ref. [23] is perhaps the most systematic benchmark of the HF-DFT procedure, but uses nothing from DC-DFT.
In the rest of this paper,
we shall analyze their results within DC-DFT, the modern theory behind HF-DFT.




III. Specific examples
i. When should HF-DFT give improved results, and when should it not? HF-DFT works only for density sensitive cases.
The theory behind DC-DFT shows that correcting the density is relevant only when the self-consistent density is unusually inaccurate. We use density sensitivity as a proxy for this criterion and use a typical number (2 kcal/mol) as a heuristic for small molecules with chemical bonds.
It is not possible to see improvements by simply reporting HF-DFT numbers from large databases. In many classes of calculations, the insensitive cases heavily outnumber the sensitive cases. The gains from using HF densities in sensitive cases can be easily hidden by the many insensitive cases, where it often worsens energetics relative to self-consistency.
We illustrate these points with PBE calculations on four specific databases in Fig. 2. The first is the BH76 database of barrier heights. Clearly, HF densities yield better energies when is above 2 kcal/mol, which is the vast majority of cases in this database. But for the few insensitive cases, we see HF-DFT usually yields worse results. The same pattern is repeated for B30, a database of halogen and other bonding energies. On the other hand, for AL2X6, most are not density-sensitive and HF-DFT worsens the energetics. (The one larger than 2 kcal/mol is still better self-consistently, suggesting a higher threshold is needed here.) Finally, in the DARC data set, no case has a sensitivity greater than 2 kcal/mol and self-consistent calculations are better in almost every case. For this data set, HF-DFT worsens the MAE of SC-DFT by about 1 kcal/mol, but DC(HF)-DFT does not.
These observations illustrate the importance of measuring density errors using energies. The errors of semilocal functionals for both Diels-Alder reactions and barrier heights are both due to delocalization error.[49, 50] The density errors are energetically very relevant to barrier height energetics, but irrelevant to Diels-Alder reactions. DC-DFT accounts for this distinction, whereas HF-DFT does not.
ii. Is it easy to spot density-sensitivity? Not always.
| SC | HF | SC-D4 | HF-D4 | DC(HF) | DC(HF)-D4 | |||
|---|---|---|---|---|---|---|---|---|
| BH76 | all | 8.0 | 8.8 | 3.9 | 9.3 | 4.0 | 4.4 | 4.7 |
| w/o 12 spinc | 6.6 | 8.5 | 3.3 | 8.9 | 3.6 | 3.3 | 3.5 | |
| RC21 | all | 9.2 | 5.4 | 4.6 | 6.9 | 4.0 | 4.3 | 4.1 |
| w/o 9 spinc | 11.3 | 6.8 | 4.8 | 8.5 | 3.8 | 4.8 | 3.8 | |
| RSE43 | all | 3.7 | 3.1 | 2.0 | 3.0 | 2.0 | 2.0 | 1.9 |
| w/o 8 spinc | 2.0 | 2.9 | 1.0 | 2.8 | 0.9 | 1.5 | 1.5 |
In Table 1, we show PBE mean absolute errors, in its HF-, DC(HF)-, and SC- versions with and without the D4 dispersion enhancement[52], for three density-sensitive data sets, including and excluding cases where unrestricted HF (UHF) densities are spin-contaminated. For all three datasets, HF-PBE improves over SC-PBE, often substantially. On the other hand, addition of D4 to self-consistent results often worsens them, because the D4 corrections cannot account for poor densities. But D4 corrections on HF densities generally do not worsen them. Situations where Grimme’s dispersion enhancement worsens self-consistent results due to large density-driven errors have been already described.[53, 54]
Next, we consider the effect of spin contamination in the UHF calculations. For spin-contaminated cases, DC(HF)-PBE reverts to SC-PBE, simply because we no longer believe the HF density is a better approximation to the exact density. When HF spin-contaminated cases are excluded, the accuracy of DC(HF)-PBE for BH76 is about the same as that of HF-PBE. This indicates that for BH76 even spin-contaminated HF densities lower large PBE density-driven errors. But, for RC21, DC(HF)-PBE improves over HF-PBE and there we can see the benefit of reverting DC(HF)-PBE to SC-PBE when HF is spin-contaminated. In the case of RSE43, the MAE of DC(HF)-PBE is about the same as that of HF-PBE. But when HF spin-contaminated cases are excluded, DC(HF)-PBE worsens HF-PBE. Why is that? It appears that our generic cut-off of 2 kcal/mol for density-sensitive calculations is too large for RSE43, whose averaged absolute energies are several times smaller than those of RC21 and BH76 [19]. When this cut-off is lowered to 1 kcal/mol, the MAE of DC(HF)-PBE for RSE43 (HF spin-contaminated cases excluded) is lowered by 0.5 kcal/mol (see the right panel of Fig. S1). This demonstrates the cutoff of 2 kcal/mol is simply a heuristic aimed at covalent bonds in small molecules, and should be sensibly adjusted in different situations.

iii. Do range-separated hybrids have smaller density-driven errors than their global counterparts? Yes.
Ref. [23] found that "range-separated hybrids do not benefit much from HF-DFT as so much HF exchange is already present at a long range." In fact, in an earlier study, we showed that indeed range-separated hybrids (RSHs) suffer much less from density-driven errors than their global counterparts.[53] For example, semilocal DFT caclulations of the WATER27 clusters are prone to large density-driven errors as suggested by their large density sensitivities, which in the case of PBE approaches 30 kcal/mol. Unless this density-driven error is corrected (by, e.g., HF-DFT), dispersion corrections can even worsen the results.[53, 54] In contrast to standard semilocal calculations of the WATER27 clusters, a state-of-the-art RSH developed by Mardirossian and Head-Gordon[20], B97M-V, suffers far less from density-driven errors, and its density-sensitivities for WATER27 cluster are about 10 times smaller than those of PBE and 3 times smaller those of B3LYP[53]. Thus DC-DFT explains why such functionals have small density-driven errors.

To further understand density-driven errors in RSHs, consider NaCl. Standard semilocal functionals fail beyond about 5.8 Å, due to incorrect charge transfer, a specific type of delocalization error[56]. We perform calculations for NaCl at 6.4 Å using LC-BLYP, which employs B88 exchange at short distances and HF exchange at long distances. We calculate for the atomization energy of this system as a function of the range-separation parameter, , by using accurate density from CCSD as done in Ref. [8]. The results are shown in Fig. 3. The inset shows the intrinsic atomic orbital (IAO)[55] population of the Na atom as a function of and the dotted horizontal lines represents accurate IAO from CCSD (calculated via inverted KS orbitals[8]). The CCSD and HF’s IAOs are virtually indistinguishable. If for example, the turnover distance to full exchange is sufficiently large that significant density-driven errors would occur, just as in global hybrids. But already at , the default value used in LC-BLYP [57], and the deviation of the IAO charge from the reference are small.
iv. Can one see that the HF density is more accurate than the self-consistent density by studying density plots? Typically, it is hopeless.
There is a long history of studying density differences and density error plots in DFT, in both physics and chemistry, with the aim of improving approximations. Comparison is not only related to the difference between HF and self-consistent DFT approximations, but also for the density of other methods such as MP and CASSCF.[58] Very little insight can be gained for improving functionals from such plots, due to the complexities of the relation between densities and potentials, as well as that between potentials and energy functionals. Because most good XC energy approximations yield good densities in most calculations, despite their very poor approximate potentials, it is very difficult to trace the effects of a good energy approximation in the (often) tiny differences in densities. Even in cases where we know a better density is yielding better energetics, it is often not possible to say which aspects are relevant. (See Fig. 4 of Ref. [9].)
The clearest case is that of small anions. For atomic anions, the true self-consistent density with semilocal functionals is typically one with about 0.3 electrons escaping to infinity, and electrons bound to the nucleus. In that case, the error in the density is glaringly obvious, even to the eye (see Fig. 2 of Ref. [3]). But for a complicated molecular reaction in which a small energy difference is being calculated (such as a barrier height of the type we have already studied), the difference in such differences is typically both small and subtle and tremendously difficult to interpret.
In Fig. 4, we illustrate this with two density difference plots, being differences between HF and PBE densities. These differences tend to be invisible on the scale of the densities themselves (without labels, could one guess which density is HF and which is PBE?) and the differences display many changes of sign. The upper panel (c) is for the reactants, the lower for the transition state geometry. How can one tell that one case is density sensitive, and the other not? But the extreme right-hand panel tells us that there is a significant energetic difference between the two different densities when calculating the reaction barrier, and indeed the density sensitivity of the PBE barrier is higher than 2 kcal/mol (4.9 kcal/mol and 9.1 kcal/mol for forward and backward each). Moreover, PBE evaluated on the SC density predicts that the forward reactions has no barrier, whereas the PBE barrier calculated from the HF density is highly accurate. Again, this is something that one would not be able to deduce by comparing the (d) and (e) density plots.
Ref. [23] comments: "What is the effect of the HF density here really? We attempted to create a difference density plot between HF-PBE and PBE for the water dimer, but nothing of note is easily visible." This is typically the case, but only emphasizes the importance of the DC(HF)-DFT energtic criteria for the accuracy of densities. In Ref. [21], handmade measures of errors in the density are too arbitrary to be of universal use.
DC-DFT builds an energetic criterion for measuring errors in approximate densities:
| (4) |
which is always a single nonegative energy and provides an unambiguous measure for all systems and approximate densities. In general, obtaining is expensive as computing requires the inversion of a many-body problem and becomes more difficult than computing itself. is typically very close to [27], which although still expensive can be computed for more systems to gain insights into the density errors. For larger systems, where computing becomes intractable, the sensitivity quantity of Eq. 3 designed to signal large density-driven errors can be used instead.
v. Can double hybrids benefit from HF-DFT? Yes, if DC-DFT is applied very carefully.

By generalizing their findings for standard hybrids, Ref. [23] concluded that HF-DFT is not beneficial for double hybrids (DHs) as these use large percentages of the HF exchange (typically ). We agree with Ref. [23] that it is reasonable to expect that the higher the exact percentage in a global hybrid is, the smaller DC-DFT correction is made by the use of HF densities. However, one has to be careful with the generalization of this statement to DHs given that the MP2-like energy expression evaluated on the KS orbitals is often very different from the same energy expression evaluated on the HF orbitals.[59] For that reason, the accuracy of standard DHs deteriorates when HF orbitals are used and so does the accuracy of HF-DHs when applied to the DFT orbitals (this is illustrated in Fig. S4 of Ref. [53]). At a more formal level, the adiabatic connection formalism that underpins the construction of the recently proposed HF-DHs[43, 45, 60] is different from the usual DFT adiabatic connection used to rationalize and build standard DHs[61, 62].
Finally, we have recently developed ’BL1p’, a single-parameter HF-DH trained and applied to HF densities. Using principles of DC-DFT in its design, BL1p fixes the problems of conventional DHs when applied to prototypical calculations suffering from large density-driven errors.[53] In Fig. 5, we show the NaCl dissociation as a prototypical case where density-driven errors are large, where the standard DHs fail at large distances, despite containing large amounts of the exact exchange but BL1p does not. Despite the claims of Ref. [23], DC-DFT had already provided improvements in DHs[53].
vi. Does HF-DFT work better than self-consistent DFT for electron affinities? Yes, because standard calculations are unconverged, as demonstrated by their positive HOMO energies.

| Electron Affinity (kcal/mol) | (kcal/mol) | |||||||
| PBE | B3LYP | |||||||
| name | SC | DC | SC | DC | PBE | B3LYP | HF | exact |
| CH | 3.9 | 3.1 | -1.2 | -2.3 | 56.1 | 37.5 | -47.4 | -27.9 |
| CH2 | 0.5 | -0.5 | -0.8 | -1.3 | 55.2 | 37.3 | -31.7 | -13.4 |
| CH3 | -2.4 | -3.4 | -5.1 | -5.7 | 63.6 | 45.2 | -18.8 | -1.2 |
| NH | -0.3 | -1.8 | -3.0 | -4.1 | 79.3 | 57.8 | -9.3 | -8.3 |
| NH2 | -0.8 | -2.0 | -4.2 | -5.1 | 68.0 | 46.4 | -29.2 | -16.8 |
| OH | 4.1 | 0.8 | -1.0 | -3.0 | 46.7 | 22.3 | -68.7 | -41.7 |
| SiH | 0.5 | 0.2 | -4.0 | -4.8 | 36.6 | 25.6 | -34.0 | -29.3 |
| SiH2 | 2.4 | 1.8 | -1.6 | -2.6 | 37.9 | 27.0 | -30.4 | -25.1 |
| SiH3 | -0.7 | -0.6 | -2.4 | -2.1 | 23.1 | 8.3 | -43.5 | -31.4 |
| PH | -3.1 | -3.2 | -3.9 | -3.8 | 50.6 | 35.1 | -18.5 | -23.5 |
| PH2 | -3.7 | -3.3 | -5.2 | -4.8 | 46.1 | 30.8 | -24.7 | -28.8 |
| HS | -0.5 | -0.7 | -2.5 | -2.5 | 21.3 | 3.9 | -59.7 | -54.2 |
| O2 | -0.1 | -2.4 | 0.2 | -1.1 | 76.4 | 47.7 | -56.9 | -9.5 |
| NO | 3.0 | 0.3 | 3.6 | 1.6 | 87.8 | 57.1 | -59.8 | 0.2 |
| PO | 1.3 | 0.8 | 0.0 | -0.8 | 46.7 | 28.7 | -47.8 | -24.9 |
| S2 | -2.4 | -2.0 | -2.0 | -1.6 | 28.2 | 10.4 | -52.9 | -38.0 |
| Cl2 | 4.6 | 4.5 | 7.6 | 7.1 | -22.4 | -45.9 | -106.8 | -54.7 |
| MAE | 2.0 (1.5) | 1.9 (1.3) | 2.8 (2.0) | 3.2 (1.8) | ||||
| MAE∗ | 2.9 (2.2) | 1.8 (1.6) | 2.1 (2.0) | 2.0 (1.7) | ||||
It has long been known[34] that semilocal functionals fail to bind an additional electron to neutral atoms when a fully converged self-consistent solution is found. This is because the approximate KS potential (evaluated on the exact density) is far too shallow and becomes positive not far from the nucleus and stays that way until extremely far away (about 15 Å). This feature that makes it possible to extract accurate anion energies with reasonable standard atom-centered basis, because such basis cannot represent the regions distant from the nucleus. Thus such calculations yield a useful representation of the density, but at the price of having a positive HOMO, a definitive sign of an unconverged result. Such calculations are formally unjustified, as pointed out by Rösch and Trickey.[63] In a fully numerical calculation, one finds that the minimizing density loses about 0.3 electron to the continuum, and only binds about 1.7 electrons (for H-). Thus the truly converged self-consistent solution[64] is extremely density sensitive (perhaps the most visible example we know of) and properly converged calculations have large density-driven errors.
Nonetheless, the trick of using a reasonable atomic basis does yield a reasonable density, despite formally being a meta-stable state, and thus accurate energetics. In fact, many electron affinities (EA) calculated in this way are more accurate than the corresponding ionization potentials. Ref. [23] finds that HF-DFT "appears to do more harm than good" when electron-affinities are calculated, and indeed the numbers are comparable. But DC-DFT provides formally more solid ground for calculating electron affinities than the standard DFT approximations with limited basis sets.[7, 40]
Consider what happens when we try to add an extra electron to the hydrogen atom within the PBE functional. First, we do the calculation in a large atomic basis. For the electron affinity of the hydrogen atom, PBE/aug-cc-pV6Z yields an error that is less than 1 kcal/mol (see Table S1 for numerical details). Moreover, the density sensitivity of this calculation is about 1 kcal/mol, which is less than our sensitivity threshold. This consideration would naively indicate that there is no need to invoke HF-DFT. But the positive HOMO of PBE reminds us that H- is artificially bound by a finite atom-centered basis set despite its large size (aug-cc-pV6Z). The results for both electron affinity and are unconverged. If, instead, we converge the PBE calculation of H- by enabling fractional occupations until the HOMO energy hits zero (as done in Ref. [21]), things change dramatically. About 0.37 of an electron is lost confirming that the converged PBE calculation does not even bind H-. Moreover, the converged becomes 8 kcal/mol, showing that the calculation is in fact extremely density-sensitive.
We now repeat this test for the G21EA dataset and compare converged (a fraction of charge enabled until the HOMO hits zero) vs. unconverged (anions bound only by a finite basis) of PBE. These are shown in Figure 6 as a function of the HOMO energies of the anions (these are mostly positive as calculated from a finite basis set). First we note that the two sensitivities are identical in only one case (Cl2), where self-consistent PBE gives a negative HOMO energy and therefore a bound anion. In all other cases, the unconverged calculations severely underestimate . Furthermore, Fig. 6 also shows a clear correlation between the HOMO energy of the anion and of EA. In nearly all cases, the converged is above our 2 kcal/mol threshold. Thus DC-DFT invokes HF-DFT for calculations of the affinities given that HF HOMOs of the anions are bound and properly converged PBE calculations in nearly all cases give unbound anions.
What about the numbers? Basis-set bound DFT calculations give reasonable accuracies for the electron affinities. Table 2 shows electron affinity errors of PBE and B3LYP and their HF-DFT counterparts, and the corresponding anion HOMO energies. The MAEs of DC-DFT and basis-set bound (unconverged) DFT are comparable. But note that the RMSD values are noticeably smaller for DC-DFT, showing a smaller variance and less outliers. Moreover, if the smaller aug-cc-pVQZ basis set is used instead, as it often is in practice, many results shift by amounts comparable to these errors (see Table S3). Finally, we note that these molecules form the G21EA data set, with CN excluded as its HF wavefunction is heavily spin contaminated, so DC-DFT simply reverts to SC-DFT for that case. If, however, restricted open-shell HF (ROHF) is used instead of UHF for the CN molecule, the error of HF-PBE is greatly reduced. We currently use UHF as a default in our HF-DFT calculations of open-shell systems and we will further investigate the usability of ROHF-DFT[65] in the future.
vii. Is slow grid convergence as much a problem for HF-SCAN as it is for SCAN? Yes, it can be.
Ref. [23] have shown the HF-SCAN displays an excellent performance for the GMTKN55 database and gets beaten only by few modern and highly parameterized functionals. The painfully slow convergence of SC-SCAN calculations is well known, and even for simple atomization energies SCAN is difficult to converge within the available grid sizes in many standard quantum-chemical codes.[66] In the case of HF-SCAN, the orbitals are taken from a HF calculation so grids are only needed for the final energy evaluation and not for the whole SCF procedure. For that reason, one would assume that the grid convergence is less of a problem for HF-SCAN. Nevertheless, as shown in Fig. S4 for the G21IP dataset, HF-SCAN is also not converging within the grid sizes available in the quantum-chemical package ORCA. The r2SCAN functional is designed to fix the grid convergence issues of SCAN, and as shown in Fig. S4, the HF-r2SCAN results converge even within smaller ORCA grids. At the same time, the accuracy of HF-SCAN is comparable to HF-r2SCAN (see, e.g., Fig. S4 illustrating this for the G21IP dataset). These difficulties are overcome by using extremely large grids in Qchem, showing that HF-SCAN can yield highly accurate MB-pol potentials for water simulations.[67]
viii. What are the current limitations of DC-DFT and where else can it be applied?
Homonuclear dimers: As a form of DC-DFT, HF-DFT is meant to reduce only density-driven errors and not functional errors. In cases where DFT errors are large even when an approximate functional is evaluated on the exact density, HF-DFT cannot help. While HF-DFT substantially reduces the errors of DFT in stretched heterodimers, this is not the case for homodimers. For example, upon stretching H or He, the standard DFT methods have large self-interaction errors, only a tiny fraction of which is density-driven.[53] HF-DFT also cannot help stretching H2[3], the case where standard DFT methods have large static correlation error[59].
Transition metals: DC(HF)-DFT has been mostly applied to main-group chemistry, but it also can be greatly useful in the transition-metal chemistry (see, e.g., Ref. [9] for the calculations of spin gaps of Fe(II) complexes). Further study on the usefulness of HF-DFT for the transition-metal chemsitry is warranted.[30]
Materials and surface science calculations: Different forms of DC-DFT have been also used to analyse the errors of DFT for surface science applications. The cases where more accurate densities improves the results of semilocal functionals drastically improves the adsorption description of CO on metallic surfaces have been identified.[68] In other cases, such as the challenging barrier height for attaching O2 to the Al(111) surface, GGAs benefit little from more accurate densities.[69] This implies that the accuracy of their density is satisfactory at the GGA level and evaluating a hybrid functional on those GGA densities gives results similar to fully SC-hybrid calculations, but at a fraction of the cost.[69] Similar cost reduction strategies have been applied to semiconductor calculations.[70] In future years, where and how DC-DFT can be useful in surface and material science needs to be further explored.
Forces: Despite being a non-SCF scheme, the calculation of the analytical gradients for HF-DFT is just slightly more involved than those of SC-DFT. This has been demonstrated by Bartlett and co-workers[38, 71]. The more recent Pyxdh code[72] is written based on the PYSCF package[73] and with little modifications can be used for HF-DFT geometry optmizations. Besides earlier calculations of barrier heights by using HF-DFT optmized transition states[38] and exploration of radical potential energy surfaces[4], the performance of HF-DFT for molecular structures relative to their SC-DFT counterparts is yet to be systematically explored. This is another topic that we will cover in the future, and recently developed unambigious measures for assessing the quality of approximate molecular structures should prove useful.[28]
IV. Conclusions
We hope this short work explains and clarifies many of the basic issues behind density-corrected DFT. Most important among these are (a) that there exist many situations where the energy error in a DFT calculation has a significant density-driven contribution, (b) that blind application of HF-DFT (using DFT approximations on HF densities) is not DC-DFT and most (if not all) of the benefits of DC-DFT are lost in the details of large databases, but (c) careful application of the principles of DC-DFT shows that DC-(HF)-DFT, as a practical scheme, almost always works for density-sensitive cases.
SS and ES are grateful for support from the National Research Foundation of Korea (NRF-2020R1A2C2007468 and NRF-2020R1A4A1017737). KB acknowledges funding from NSF (CHEM 1856165). SV acknowledges funding from the Marie Skłodowska-Curie grant 101033630 (EU’s Horizon 2020 programme). We thanks G.Santra and J.M.L. Martin for helpful discussions and providing the data on which Ref. [23] was based.
References
- [1] Narbe Mardirossian and Martin Head-Gordon. Thirty years of density functional theory in computational chemistry: an overview and extensive assessment of 200 density functionals. Molecular Physics, 115(19):2315–2372, 2017.
- [2] Adam Wasserman, Jonathan Nafziger, Kaili Jiang, Min-Cheol Kim, Eunji Sim, and Kieron Burke. The importance of being self-consistent. Annual Review of Physical Chemistry, 68(1):555–581, 2017.
- [3] Min-Cheol Kim, Eunji Sim, and Kieron Burke. Understanding and reducing errors in density functional calculations. Physical Review Letters, 111(7):073003, 2013.
- [4] Min-Cheol Kim, Eunji Sim, and Kieron Burke. Ions in solution: Density corrected density functional theory (dc-dft). The Journal of Chemical Physics, 140(18):18A528, 2014.
- [5] Min-Cheol Kim, Hansol Park, Suyeon Son, Eunji Sim, and Kieron Burke. Improved dft potential energy surfaces via improved densities. The Journal of Physical Chemistry Letters, 6(19):3802–3807, 2015.
- [6] Yeil Kim, Suhwan Song, Eunji Sim, and Kieron Burke. Halogen and chalcogen binding dominated by density-driven errors. The Journal of Physical Chemistry Letters, 10(2):295–301, 2018.
- [7] Min-Cheol Kim, Eunji Sim, and Kieron Burke. Communication: Avoiding unbound anions in density functional calculations. The Journal of Chemical Physics, 134(17):171103, 2011.
- [8] Seungsoo Nam, Suhwan Song, Eunji Sim, and Kieron Burke. Measuring density-driven errors using kohn–sham inversion. Journal of Chemical Theory and Computation, 16(8):5014–5023, July 2020.
- [9] Suhwan Song, Min-Cheol Kim, Eunji Sim, Anouar Benali, Olle Heinonen, and Kieron Burke. Benchmarks and reliable dft results for spin gaps of small ligand fe (ii) complexes. Journal of Chemical Theory and Computation, 14(5):2304–2311, 2018.
- [10] Enrico Clementi and Subhas J Chakravorty. A comparative study of density functional models to estimate molecular atomization energies. The Journal of Chemical Physics, 93(4):2591–2602, 1990.
- [11] Peter MW Gill, Benny G Johnson, John A Pople, and Michael J Frisch. An investigation of the performance of a hybrid of hartree-fock and density functional theory. International Journal of Quantum Chemistry, 44(S26):319–331, 1992.
- [12] Peter MW Gill, Benny G Johnson, John A Pople, and Michael J Frisch. The performance of the Becke—Lee—Yang—Parr (B—LYP) density functional theory with various basis sets. Chemical Physics Letters, 197(4-5):499–505, 1992.
- [13] Nicholas C Handy, Paul E Maslen, Roger D Amos, Jamie S Andrews, Christopher W Murray, and Gregory J Laming. The harmonic frequencies of benzene. Chemical physics letters, 197(4-5):506–515, 1992.
- [14] Gustavo E Scuseria. Comparison of coupled-cluster results with a hybrid of hartree–fock and density functional theory. The Journal of chemical physics, 97(10):7528–7530, 1992.
- [15] Benny G Johnson, Peter MW Gill, and John A Pople. Preliminary results on the performance of a family of density functional methods. The Journal of chemical physics, 97(10):7846–7848, 1992.
- [16] Nevin Oliphant and Rodney J Bartlett. A systematic comparison of molecular properties obtained using hartree–fock, a hybrid hartree–fock density-functional-theory, and coupled-cluster methods. The Journal of Chemical Physics, 100(9):6550–6561, 1994.
- [17] R. O. Jones. Density functional theory: Its origins, rise to prominence, and future. Rev. Mod. Phys., 87:897–923, Aug 2015.
- [18] Jan Rezac and Pavel Hobza. Benchmark calculations of interaction energies in noncovalent complexes and their applications. Chemical reviews, 116(9):5038–5071, 2016.
- [19] Lars Goerigk, Andreas Hansen, Christoph Bauer, Stephan Ehrlich, Asim Najibi, and Stefan Grimme. A look at the density functional theory zoo with the advanced gmtkn55 database for general main group thermochemistry, kinetics and noncovalent interactions. Physical Chemistry Chemical Physics, 19(48):32184–32215, 2017.
- [20] Narbe Mardirossian and Martin Head-Gordon. b97m-v: A combinatorially optimized, range-separated hybrid, meta-gga density functional with vv10 nonlocal correlation. The Journal of chemical physics, 144(21):214110, 2016.
- [21] Eunji Sim, Suhwan Song, and Kieron Burke. Quantifying density errors in dft. The Journal of Physical Chemistry Letters, 9(22):6385–6392, 2018.
- [22] John P. Perdew, Adrienn Ruzsinszky, Lucian A. Constantin, Jianwei Sun, and Gábor I. Csonka. Some fundamental issues in ground-state density functional theory: A guide for the perplexed. Journal of Chemical Theory and Computation, 5(4):902–908, 2009. PMID: 26609599.
- [23] Golokesh Santra and Jan ML Martin. What types of chemical problems benefit from density-corrected dft? a probe using an extensive and chemically diverse test suite. Journal of chemical theory and computation, 17(3):1368–1379, 2021.
- [24] Walter Kohn and Lu Jeu Sham. Self-consistent equations including exchange and correlation effects. Physical Review, 140(4A):A1133, 1965.
- [25] Qingsheng Zhao, Robert C Morrison, and Robert G Parr. From electron densities to kohn-sham kinetic energies, orbital energies, exchange-correlation potentials, and exchange-correlation energies. Physical Review A, 50(3):2138, 1994.
- [26] Qin Wu and Weitao Yang. A direct optimization method for calculating density functionals and exchange–correlation potentials from electron densities. The Journal of Chemical Physics, 118(6):2498–2509, 2003.
- [27] Stefan Vuckovic, Suhwan Song, John Kozlowski, Eunji Sim, and Kieron Burke. Density functional analysis: The theory of density-corrected dft. Journal of Chemical Theory and Computation, 15(12):6636–6646, 2019.
- [28] Stefan Vuckovic and Kieron Burke. Quantifying and understanding errors in molecular geometries. The Journal of Physical Chemistry Letters, 11(22):9957–9964, November 2020.
- [29] Yonsei University Theoretical and Computational Chemistry Laboratory. Density corrected-density functional theory. http://tccl.yonsei.ac.kr/mediawiki/index.php/DC-DFT.
- [30] Carlos Martín-Fernández and Jeremy N Harvey. On the use of normalized metrics for density sensitivity analysis in dft. The Journal of Physical Chemistry A, 2021.
- [31] Benjamin G Janesko and Gustavo E Scuseria. Hartree–fock orbitals significantly improve the reaction barrier heights predicted by semilocal density functionals. The Journal of Chemical Physics, 128(24):244112, 2008.
- [32] Renato Colle and Oriano Salvetti. Approximate calculation of the correlation energy for the closed shells. Theoretica Chimica Acta, 37(4):329–334, 1975.
- [33] Chengteh Lee, Weitao Yang, and Robert G Parr. Development of the colle-salvetti correlation-energy formula into a functional of the electron density. Physical Review B, 37(2):785–789, 1988.
- [34] Roy G Gordon and Yung Sik Kim. Theory for the forces between closed-shell atoms and molecules. The Journal of Chemical Physics, 56(6):3122–3133, 1972.
- [35] Leslie C Wilson and Mel Levy. Nonlocal wigner-like correlation-energy density functional through coordinate scaling. Physical Review B, 41(18):12930, 1990.
- [36] Tiffany R Walsh. Exact exchange and wilson–levy correlation: a pragmatic device for studying complex weakly-bonded systems. Physical Chemistry Chemical Physics, 7(3):443–451, 2005.
- [37] Axel D Becke. Density-functional exchange-energy approximation with correct asymptotic behavior. Physical Review A, 38(6):3098–3100, 1988.
- [38] Prakash Verma, Ajith Perera, and Rodney J. Bartlett. Increasing the applicability of dft i: Non-variational correlation corrections from hartree-fock dft for predicting transition states. Chemical Physics Letters, 524:10 – 15, 2012.
- [39] Jorge M Seminario. Energetics using dft: comparions to precise ab initio and experiment. Chemical physics letters, 206(5-6):547–554, 1993.
- [40] Donghyung Lee, Filipp Furche, and Kieron Burke. Accuracy of electron affinities of atoms in approximate density functional theory. The Journal of Physical Chemistry Letters, 1(14):2124–2129, 2010.
- [41] Donghyung Lee and Kieron Burke. Finding electron affinities with approximate density functionals. Molecular Physics, 108(19-20):2687–2701, 2010.
- [42] Andreas Görling and Mel Levy. Exact kohn-sham scheme based on perturbation theory. Physical Review A, 50(1):196, 1994.
- [43] Timothy J Daas, Juri Grossi, Stefan Vuckovic, Ziad H Musslimani, Derk P Kooi, Michael Seidl, Klaas JH Giesbertz, and Paola Gori-Giorgi. Large coupling-strength expansion of the møller–plesset adiabatic connection: From paradigmatic cases to variational expressions for the leading terms. The Journal of Chemical Physics, 153(21):214112, 2020.
- [44] Michael Seidl, Sara Giarrusso, Stefan Vuckovic, Eduardo Fabiano, and Paola Gori-Giorgi. Communication: Strong-interaction limit of an adiabatic connection in hartree-fock theory. The Journal of chemical physics, 149(24):241101, 2018.
- [45] Timothy J Daas, Eduardo Fabiano, Fabio Della Sala, Paola Gori-Giorgi, and Stefan Vuckovic. Noncovalent interactions from models for the møller–plesset adiabatic connection. The journal of physical chemistry letters, 12:4867–4875, 2021.
- [46] Seungsoo Nam, Eunbyol Cho, Eunji Sim, and Kieron Burke. Explaining and fixing dft failures for torsional barriers. The journal of physical chemistry letters, 12(11):2796–2804, 2021.
- [47] Eleftherios Lambros, Saswata Dasgupta, Etienne Palos, Steven Swee, Jie Hu, and Francesco Paesani. General many-body framework for data-driven potentials with arbitrary quantum mechanical accuracy: Water as a case study. Journal of Chemical Theory and Computation, 17(9):5635–5650, 2021.
- [48] Antonio Bauza, Ibon Alkorta, Antonio Frontera, and Jose Elguero. On the reliability of pure and hybrid dft methods for the evaluation of halogen, chalcogen, and pnicogen bonds involving anionic and neutral electron donors. Journal of Chemical Theory and Computation, 9(11):5201–5210, 2013.
- [49] Erin R Johnson, Paula Mori-Sánchez, Aron J Cohen, and Weitao Yang. Delocalization errors in density functionals and implications for main-group thermochemistry. The Journal of Chemical Physics, 129(20):204112, 2008.
- [50] Diptarka Hait and Martin Head-Gordon. Delocalization errors in density functional theory are essentially quadratic in fractional occupation number. The journal of physical chemistry letters, 9(21):6280–6288, 2018.
- [51] Adam Rettig, Diptarka Hait, Luke W Bertels, and Martin Head-Gordon. Third-order møller–plesset theory made more useful? the role of density functional theory orbitals. Journal of Chemical Theory and Computation, 16(12):7473–7489, 2020.
- [52] Eike Caldeweyher, Sebastian Ehlert, Andreas Hansen, Hagen Neugebauer, Sebastian Spicher, Christoph Bannwarth, and Stefan Grimme. A generally applicable atomic-charge dependent london dispersion correction. The Journal of Chemical Physics, 150(15):154122, 2019.
- [53] Suhwan Song, Stefan Vuckovic, Eunji Sim, and Kieron Burke. Density sensitivity of empirical functionals. The journal of physical chemistry letters, 12(2):800–807, 2021.
- [54] Nisha Mehta, Thomas Fellowes, Jonathan M White, and Lars Goerigk. Chal336 benchmark set: How well do quantum-chemical methods describe chalcogen-bonding interactions? Journal of Chemical Theory and Computation, 17(5):2783–2806, 2021.
- [55] Gerald Knizia. Intrinsic atomic orbitals: An unbiased bridge between quantum theory and chemical concepts. Journal of chemical theory and computation, 9(11):4834–4843, 2013.
- [56] Adrienn Ruzsinszky, John P Perdew, Gábor I Csonka, Oleg A Vydrov, and Gustavo E Scuseria. Spurious fractional charge on dissociated atoms: Pervasive and resilient self-interaction error of common density functionals. The Journal of Chemical Physics, 125(19):194112, 2006.
- [57] O. A. Vydrov and G. E. Scuseria. Assessment of a long-range corrected hybrid functional. J. Chem. Phys., 125:234109, 2006.
- [58] Dieter Cremer. Density functional theory: coverage of dynamic and non-dynamic electron correlation effects. Molecular Physics, 99(23):1899–1940, 2001.
- [59] Aron J Cohen, Paula Mori-Sánchez, and Weitao Yang. Challenges for density functional theory. Chemical Reviews, 112(1):289–320, 2011.
- [60] Stefan Vuckovic, Eduardo Fabiano, Paola Gori-Giorgi, and Kieron Burke. Map: An mp2 accuracy predictor for weak interactions from adiabatic connection theory. Journal of Chemical Theory and Computation, 16(7):4141–4149, May 2020. PMID: 32379454.
- [61] David C Langreth and John P Perdew. The exchange-correlation energy of a metallic surface. Solid State Communications, 17(11):1425–1429, 1975.
- [62] Kamal Sharkas, Julien Toulouse, and Andreas Savin. Double-hybrid density-functional theory made rigorous. The Journal of Chemical Physics, 134(6):064113, 2011.
- [63] Notker Rösch and SB Trickey. Comment on “Concerning the applicability of density functional methods to atomic and molecular negative ions”[J. Chem. Phys. 105, 862 (1996)]. The Journal of Chemical Physics, 106(21):8940–8941, 1997.
- [64] Andrzej A Jaręcki and Ernest R Davidson. Density functional theory calculations for f-. Chemical Physics Letters, 300(1-2):44–52, 1999.
- [65] Robert CR Pennifold, Simon J Bennie, Thomas F Miller III, and Frederick R Manby. Correcting density-driven errors in projection-based embedding. The Journal of chemical physics, 146(8):084113, 2017.
- [66] James W Furness, Aaron D Kaplan, Jinliang Ning, John P Perdew, and Jianwei Sun. Accurate and numerically efficient r2scan meta-generalized gradient approximation. The journal of physical chemistry letters, 11(19):8208–8215, 2020.
- [67] Saswata Dasgupta, Eleftherios Lambros, John Perdew, and Francesco Paesani. Elevating density functional theory to chemical accuracy for water simulations through a density-corrected many-body formalism. ChemRxiv doi:10.33774/chemrxiv-2021-hstgf-v3, 2021.
- [68] Abhirup Patra, Haowei Peng, Jianwei Sun, and John P. Perdew. Rethinking CO adsorption on transition-metal surfaces: Effect of density-driven self-interaction errors. Physical Review B, 100(3), July 2019.
- [69] Nick Gerrits, Egidius W. F. Smeets, Stefan Vuckovic, Andrew D. Powell, Katharina Doblhoff-Dier, and Geert-Jan Kroes. Density functional theory for molecule–metal surface reactions: When does the generalized gradient approximation get it right, and what to do if it does not. The Journal of Physical Chemistry Letters, 11(24):10552–10560, December 2020.
- [70] Jonathan M. Skelton, David S. D. Gunn, Sebastian Metz, and Stephen C. Parker. Accuracy of hybrid functionals with non-self-consistent kohn–sham orbitals for predicting the properties of semiconductors. Journal of Chemical Theory and Computation, 16(6):3543–3557, May 2020.
- [71] Hideo Sekino, Nevin Oliphant, and Rodney J Bartlett. Property evaluation using the hartree–fock-density-functional-theory method: An efficient formalism for first-and second-order properties. The Journal of chemical physics, 101(9):7788–7794, 1994.
- [72] Python xdh project, available from https://github.com/ajz34/py_xdh.
- [73] Qiming Sun, Timothy C. Berkelbach, Nick S. Blunt, George H. Booth, Sheng Guo, Zhendong Li, Junzi Liu, James D. McClain, Elvira R. Sayfutyarova, Sandeep Sharma, Sebastian Wouters, and Garnet Kin-Lic Chan. PySCF: the Python-based simulations of chemistry framework, 2017.
V. Supporting Information
| CCSD | 17.3 | |
| HF-PBE | 15.6 | |
| PBE (un-conv.) | 16.6 | |
| PBE (conv.) | 23.9 | |
| (un-conv.) | 1.1 | |
| (conv.) | 8.4 |
| SC | HF | DC(HF) | SC-D4 | HF-D4 | DC(HF)-D4 | |||
|---|---|---|---|---|---|---|---|---|
| BH76 | 12 spinc | 8.0 | 8.8 (5.0) | 3.9 (3.7) | 4.4 (5.0) | 9.3 (5.1) | 4.0 (3.7) | 4.7 (5.1) |
| w/o spinc | 6.6 | 8.5 (3.8) | 3.3 (2.6) | 3.3 (2.4) | 8.9 (3.9) | 3.6 (2.7) | 3.5 (2.6) | |
| RC21 | 9 spinc | 9.2 | 5.4 (3.2) | 4.6 (3.5) | 4.3 (3.1) | 6.9 (3.7) | 4.0 (2.7) | 4.1 (2.9) |
| w/o spinc | 11.3 | 6.8 (2.8) | 4.8 (3.2) | 4.8 (3.2) | 8.5 (2.9) | 3.8 (2.4) | 3.8 (2.4) | |
| RSE43 | 8 spinc | 3.7 | 3.1 (1.4) | 2.0 (3.3) | 2.0 (1.7) | 3.0 (1.4) | 2.0 (3.4) | 1.9 (1.6) |
| w/o spinc | 2.0 | 2.9 (1.2) | 1.0 (0.8) | 1.5 (1.1) | 2.8 (1.2) | 0.9 (0.7) | 1.5 (1.0) |



| Electron Affinity (kcal/mol) | (kcal/mol) | |||||||
|---|---|---|---|---|---|---|---|---|
| PBE | B3LYP | |||||||
| name | SC | DC | SC | DC | PBE | B3LYP | HF | exact |
| CCH | 7.5 | 5.5 | 1.5 | -0.2 | 44.0 | 28.4 | -49.3 | -27.9 |
| CH2 | 3.6 | 1.8 | 1.8 | 0.8 | 44.5 | 29.5 | -33.5 | -13.4 |
| CH3 | 1.6 | -0.2 | -1.8 | -2.8 | 48.7 | 34.0 | -22.1 | -1.2 |
| NH | 4.7 | 1.4 | 1.2 | -1.2 | 64.3 | 46.7 | 1.0 | -8.3 |
| NH2 | 2.6 | 0.7 | -1.5 | -2.6 | 57.0 | 38.2 | -31.3 | -16.8 |
| OH | 3.6 | 0.8 | -1.2 | -3.0 | 49.1 | 23.7 | -68.6 | -41.7 |
| SiH | 2.8 | 2.2 | -1.9 | -2.9 | 28.7 | 18.9 | -35.7 | -29.3 |
| SiH2 | 4.0 | 3.2 | -0.2 | -1.3 | 32.1 | 22.4 | -30.4 | -25.1 |
| SiH3 | -0.2 | -0.1 | -1.9 | -1.6 | 20.4 | 6.3 | -44.2 | -31.4 |
| PH | 1.0 | 0.6 | -0.1 | -0.3 | 38.0 | 24.4 | -21.3 | -23.5 |
| PH2 | -0.2 | 0.0 | -2.0 | -1.8 | 35.1 | 21.4 | -28.7 | -28.8 |
| HS | -0.6 | -0.7 | -2.5 | -2.4 | 22.0 | 4.3 | -59.7 | -54.2 |
| O2 | -0.2 | -2.3 | 0.2 | -1.0 | 77.7 | 48.1 | -57.0 | -9.5 |
| NO | 6.2 | 1.4 | 5.5 | 2.6 | 75.9 | 50.7 | -60.2 | 0.2 |
| CN | -2.8 | 17.3 | 1.6 | 19.1 | 0.0 | -27.1 | -120.9 | -89.5 |
| PO | 3.8 | 2.6 | 1.9 | 0.8 | 39.2 | 23.5 | -48.7 | -24.9 |
| S2 | -2.0 | -1.5 | -1.5 | -1.1 | 28.5 | 10.4 | -53.0 | -38.0 |
| Cl2 | 5.4 | 5.2 | 8.4 | 7.9 | -22.5 | -46.0 | -106.8 | -54.7 |
| MAE | 2.9 (2.1) | 2.6 (3.9) | 2.0 (1.9) | 3.0 (4.2) | ||||
| MAE* | 2.9 (2.2) | 1.8 (1.6) | 2.1 (2.0) | 2.0 (1.7) | ||||
