hhmmsstime
Dense real Rel flow orbits and absolute period leaves
Abstract.
We show the existence of a dense orbit for real Rel flows on the area- locus of every connected component of every stratum of holomorphic -forms with at least distinct zeros. For this purpose, we establish a general density criterion for -orbit closures, based on finding an orbit of a real Rel flow whose closure contains a horocycle. This criterion can be verified using explicit constructions of holomorphic -forms with a periodic horizontal foliation. Our constructions also provide explicit examples of dense leaves of the absolute period foliation and many subfoliations of these loci.
1. Introduction
This paper contributes to the study of the dynamics of flows and foliations on spaces of holomorphic -forms. Fix and a partition of . The stratum is the moduli space of nonzero holomorphic -forms on closed Riemann surfaces of genus with zero orders given by . We denote elements of by pairs . The holomorphic -form provides geometric structures on , including a flat metric and a foliation by horizontal lines, with singularities along the zero set .
When , it is possible to deform by moving the zeros of relative to each other without changing the integrals of along closed loops in . Let be the vector space of functions modulo constants. A nonzero determines a family of holomorphic -forms such that for any and zeros of , we have
The holomorphic -forms are obtained from by slitting and regluing along certain segments emanating from the zeros of . After passing to a finite cover obtained by labelling the zeros , these deformations determine a partially defined flow. Define
When , this flow is called a real Rel flow. Orbits of real Rel flows are not always well-defined for all time, since distinct zeros may collide in finite time, but it is known that this is the only obstruction [BSW], [MW2]. We denote the flow orbit through by when it is well-defined for all time.
Main results.
Our two main results address the topological dynamics of real Rel flows and the foliations obtained by “complexifying” these flows. We state these results in Theorems 1.1 and 1.5 below, and we outline our methods of proof.
Since the area of a holomorphic -form is constant along a real Rel flow orbit, let be the area- locus in . A basic question in topological dynamics is the existence of a dense orbit. Our first main result completely answers this question for real Rel flows on strata.
Theorem 1.1.
Suppose , fix a nonzero , and let be a connected component of . There exists such that is dense in .
Previously, Theorem 1.1 was unknown even in the case .
When , the stratum also admits a holomorphic foliation called the absolute period foliation. Two holomorphic -forms lie on the same leaf of if and only if there is a path between them along which the integrals along closed loops are constant. Leaves of have a natural locally Euclidean metric, recorded by integrals along paths between distinct zeros. Orbits of real Rel flows project to geodesics on leaves of , so our density result has consequences for the absolute period foliation.
Corollary 1.2.
Suppose , and let be a connected component of . There exists a leaf of that is dense in .
In [Win], a stronger density result is proven for leaves of in the case where and is connected. The above results are not explicit. However, our proofs will involve explicit constructions and will provide explicit examples of dense leaves of and of many foliations whose leaves are contained in leaves of . Our second main result will provide a stronger and explicit version of Corollary 1.2.
Real Rel and horocycles.
Our study of real Rel flows is based on a study of their centralizers and normalizers. In our setting, we are most interested in the action of and its subgroups on . The horocycle flow and the geodesic flow are defined by the actions of
respectively. Real Rel flows commute with the horocycle flow, and both are normalized by the geodesic flow.
One of the novelties in our approach to Theorem 1.1 is an application of a recent result in [For] to the study of real Rel flows. Suppose that the closure of contains the horocycle through . Since the geodesic flow normalizes both real Rel flows and the horocycle flow, this property is invariant under the geodesic flow. By Corollary 1.3 in [For], pushforwards of horocycle arcs under the geodesic flow equidistribute in the associated -orbit closure, outside a sequence of times of zero upper density. By applying for an appropriate sequence of times , we obtain real Rel flow orbits that become more and more dense in an -orbit closure. A short argument using the Baire category theorem then yields the existence of a real Rel flow orbit whose closure contains an -orbit closure. Thus, we obtain a simple and general criterion for the existence of a dense real Rel flow orbit in an -orbit closure. We present this argument in Section 3.
Theorem 1.3.
Suppose , and fix a nonzero . Fix , and let be the -orbit closure of . If is contained in and the closure of contains the horocycle through , then there exists such that is dense in .
Our second observation is that holomorphic -forms with a periodic horizontal foliation can provide explicit examples for which the closure of contains the horocycle through . In this case, is covered by finitely many cylinders of horizontal closed geodesics along with finitely many horizontal geodesic segments between zeros. The horocycle through is given by twisting each horizontal cylinder. The heights and circumferences of the horizontal cylinders, and the lengths of horizontal geodesic segments, are constant along the horocycle. The heights and circumferences of horizontal cylinders are also constant along a real Rel flow orbit, but the lengths of certain horizontal geodesic segments between zeros may change. However, if whenever and are the endpoints of a horizontal geodesic segment, then can also be described by twisting the horizontal cylinders. In this setting, both the horocycle flow and the real Rel flow can essentially be thought of as linear flows on a compact torus parametrized by twist parameters for the horizontal cylinders. This was previously described in [HW] in the case of holomorphic -forms with exactly two zeros. In Section 4, we show that if every horizontal cylinder is twisted along , and if distinct horizontal cylinders do not contain homologous closed geodesics, then it is possible to perturb the horizontal cylinder circumferences so that is dense in this twist torus and so that the -orbit of is dense in the area- locus of its stratum component. For the latter density property, we rely on the explicit density criterion for -orbits in strata from [Wri1]. Theorem 1.1 is thus reduced to the following construction which is carried out in Section 5.
Theorem 1.4.
Suppose , fix a nonzero , and let be a connected component of . There exists with a periodic horizontal foliation satisfying the following properties.
-
(1)
If and are the endpoints of a horizontal geodesic segment, then .
-
(2)
If and are zeros in the top and bottom boundaries, respectively, of the same horizontal cylinder, then .
-
(3)
Distinct horizontal cylinders do not contain homologous closed geodesics.
The constructions in the proof of Theorem 1.4 are rather involved and occupy the bulk of this paper. Briefly, we first use an intricate connected sum of tori to establish the case where every satisfies and the components of are distinct, and we then deal with the remaining cases using well-known surgeries.
Our second main result is an explicit density result for “complexified” real Rel flow orbits. A real vector subspace of determines a foliation of whose leaves project into leaves of . Our second main result provides explicit dense leaves of many subfoliations of with complex -dimensional leaves in all stratum components with multiple zeros.
Theorem 1.5.
Suppose , fix a nonzero with distinct components, and let . Let be a connected component of . There is an explicit with periodic horizontal and vertical foliations, such that the leaf of through is dense in .
A novelty in our approach to Theorem 1.5 is that it is based on analyzing periodic foliations in multiple directions simultaneously. Much of the proof of Theorem 1.5 is contained in the proof of Theorem 1.4. In most cases, the holomorphic -forms we construct here have a periodic vertical foliation with exactly analogous properties. In particular, we end up constructing explicit holomorphic -forms such that the closure of contains the horocycle through , and such that the closure of contains the opposite horocycle through .
We expect that the hypothesis that has distinct components can be removed. However, with our approach, it seems that doing so would greatly increase the length of this paper, and we decided not to pursue this. Part of our motivation for proving Theorem 1.5 is as a complement to Theorem 1.2 in [Win], which produces explicit full measure sets of dense leaves of in . The holomorphic -forms in these dense leaves of are in some sense as far as possible from having a periodic foliation in any direction. We hope that the methods in these two papers can be combined to make progress toward classifying the closures of leaves of and . Lastly, we remark that the criterion in Theorem 1.3 can be readily verified for other -orbit closures, and we briefly discuss this in Section 5 as well.
Notes and references.
In [BSW] and [MW2], it is shown that the only obstruction to a real Rel flow orbit being well-defined for all time comes from horizontal saddle connections. Related completeness results for leaves of are proven in [McM2] and [McM3]. In the terminology of [McM2], Theorem 1.1 implies the existence of dense relative period geodesics in the area- locus of every connected component of when .
The study of real Rel flows and the horocycle flow on strata are often intertwined. In [BSW], real Rel flows play an important role in the classification of orbit closures and invariant measures for the horocycle flow on the eigenform loci in . It would be interesting to see if closures of real Rel flow orbits in these eigenform loci can also be classified. In [MW1], it is shown that horocycles in strata do not diverge, and that almost every holomorphic -form in a horocycle has a uniquely ergodic vertical foliation. Similar results for families of interval exchange transformations arising from horocycles are proven in [MW2]. In contrast, [HW] gives an example of a real Rel flow orbit that is well-defined for all time but diverges in its stratum. Moreover, in [HW], it is shown that the Arnoux-Yoccoz surface in genus gives an example for which there is a unique holomorphic -form in a real Rel flow orbit with a uniquely ergodic vertical foliation, while all others have a periodic vertical foliation. Other exotic behaviors of vertical foliations along relative period geodesics are exhibited in [McM3] and [McM4]. In [CSW], it is shown that closures of horocycles in can have non-integer Hausdorff dimension. In light of [CSW], it would be interesting to see if closures of real Rel flow orbits in can also have non-integer Hausdorff dimension.
In [Ygo], a related criterion to our Theorem 1.3 is given for the density of leaves of the absolute period foliation in the special case of affine invariant manifolds of rank (defined in [Wri2]). The criterion in [Ygo] is based on finding horizontally periodic surfaces where the horizontal cylinders can be twisted while staying in the absolute period leaf and accumulating on a horocycle. Horocycle invariance of the leaf closure is promoted to -invariance, and thus density due to the rank condition, using the existence of holomorphic -forms with a hyperbolic Veech group element in every absolute period leaf in rank . A key difference in our criterion is the use of Corollary 1.3 in [For], which is needed to obtain a density result for real Rel flow orbits (as opposed to the full absolute period foliation) as well as to obtain a general result for -orbit closures. Additionally, hyperbolic Veech group elements do not play a role in our arguments. Jon Chaika and Barak Weiss have informed us of work in progress in which they prove that real Rel flows are ergodic on connected components of when , conditional on an extension of the results of [EM] to products of strata. We remark that their ergodicity result does not imply Theorem 1.5, since holomorphic -forms in a stratum with a periodic foliation form a measure zero subset.
The dynamics of on have been more extensively studied, for instance, in [CDF], [Ham], [HW], [McM3], [Win], [Ygo]. Ergodicity of on is proven in [McM3] for , and for all in [CDF], [Ham]. Moreover, a classification of closures of leaves of is given in [CDF]. In [HW] and [Ygo], examples of dense leaves are given in a certain connected component of and in . In [Win], ergodicity of on the area- locus of connected strata with and the non-hyperelliptic connected component of for even is proven. Moreover, in [Win], explicit full measure sets of dense leaves are given in these loci.
Acknowledgements.
The author thanks Curt McMullen for encouragement and comments on earlier versions of this work. This material is based upon work supported by the National Science Foundation Graduate Research Fellowship Program under grant DGE-1144152.
2. Background
We review the flat geometry of holomorphic -forms, strata of holomorphic -forms, the -action on strata, and the absolute period foliation of a stratum. We refer to [BSW], [McM2], and [Zor] for further background.
Flat geometry.
Let be a closed Riemann surface of genus , and let be a nonzero holomorphic -form on . The zero set is finite, and the orders of the zeros form a partition of . For each , there is a simply connected open neighborhood of and an injective holomorphic map given by and satisfying . These maps provide an atlas of charts on whose transition maps are translations. Translation-invariant structures on can be pulled back to structures on with singularities at the zeros of . In particular, associated to the pair is a flat metric with a cone point of angle at a zero of order . Additionally, the foliations of by horizontal and vertical lines determine a horizontal foliation and a vertical foliation of each with singular leaves meeting at a zero of order .
A saddle connection on is an oriented geodesic segment with endpoints in and otherwise disjoint from . Any closed geodesic in is contained in a maximal open cylinder given by a union of freely homotopic parallel closed geodesics. The boundary of a cylinder is a finite union of parallel saddle connections. Any cylinder is isometric to a unique Euclidean cylinder of the form with , and and are the height and circumference of , respectively. A horizontal cylinder is a cylinder containing a closed geodesic such that . The orientation of determines a top boundary of and a bottom boundary of , which are not necessarily disjoint. Given a saddle connection which crosses a horizontal cylinder from bottom to top, the twist parameter of with respect to is defined by . We similarly define a vertical cylinder with in place of , as well as the left boundary, the right boundary, and the twist parameter of a vertical cylinder with respect to a saddle connection crossing the cylinder from right to left. Two cylinders are homologous if they contain closed geodesics that represent the same element of . The horizontal foliation of is periodic if every leaf is compact. In this case, is a union of finitely many disjoint horizontal cylinders and finitely many horizontal saddle connections. Similarly for the vertical foliation of .
Strata.
The moduli space of holomorphic -forms classifies pairs as above. The space is a union of strata indexed by partitions of . A holomorphic -form is in if and only if it has exactly distinct zeros of orders . The bundle of relative homology groups is locally trivial over . Given , we can define period coordinates on a small neighborhood of by . By choosing a basis for , we obtain a map
and the components are called the period coordinates of . Period coordinates give the structure of a complex orbifold of dimension . The area of is given by , and the area- locus of is denoted by .
We recall the classification of connected components of strata from [KZ]. Suppose are even. Let be a smooth oriented closed loop. Using the translation structure on , the index is defined as times the total change in angle along the loop . In other words, is the degree of the Gauss map . Let be a collection of smooth oriented closed loops in that represents a symplectic basis for with respect to the algebraic intersection form. The parity of the spin structure is defined by
| (1) |
and is independent of the choice of symplectic basis of and the choice of representative loops. Moreover, is an invariant of the connected component of in . A connected component is even or odd if it consists of holomorphic -forms with or , respectively. A connected component is hyperelliptic if it consists of holomorphic -forms on hyperelliptic Riemann surfaces with a unique zero, or if it consists of holomorphic -forms on hyperelliptic Riemann surfaces with exactly two zeros that have equal order and are exchanged by the hyperelliptic involution. A connected component that is not hyperelliptic is nonhyperelliptic.
Theorem 2.1.
([KZ], Theorems 1-2, Corollary 5) For , the connected components of are given as follows.
-
(1)
If or , then has a unique hyperelliptic component.
-
(2)
If all are even, then has exactly two nonhyperelliptic components: one even component and one odd component.
-
(3)
If some is odd, then has a unique nonhyperelliptic component.
If and some is odd, then is connected. If and all are even, then has exactly two components: one odd component, and one hyperelliptic component which is also an even component. If , then is connected.
The -action.
Let be the group of automorphisms of the vector space with positive determinant. The standard -linear action of on induces an action on , and this action preserves each stratum. The action of the subgroup also preserves the area- locus. For , define
The action of the diagonal subgroup is the geodesic flow, and the action of the unipotent subgroup is the horocycle flow. The subgroups and generate .
In [EMM], rigidity theorems are proven for -orbit closures in strata. In particular, orbit closures are properly immersed suborbifolds locally defined by homogeneous -linear equations in period coordinates. Building off of this work, explicit full measure subsets of dense -orbits in connected components of strata are given in [Wri1]. Let be the algebraic closure of .
Theorem 2.2.
([Wri1], Corollary 1.3) If the period coordinates of are linearly independent over , then the -orbit of is dense in its connected component in .
See [Wri1] for a more general result. We only stated the special case that we will use.
The absolute period foliation.
Given , the projection from relative to absolute cohomology
defines a holomorphic submersion on a neighborhood of in . The fibers have complex dimension and form the leaves of a holomorphic foliation called the absolute period foliation of . Holomorphic -forms on the same leaf of have the same area. The action of sends leaves of to leaves of .
Consider the finite cover
obtained by labelling the zeros of holomorphic -forms in . The foliation lifts to a foliation of , which we call the absolute period foliation of . Consider the quotient vector spaces
where is the constant vector. The labelling of zeros provides a canonical identification of the kernel of with . Note that for , the difference between two components is well-defined. The corresponding element of the kernel of evaluates to on any path from to . Associated to a real vector subspace is then a foliation of whose leaves are contained in leaves of the absolute period foliation of . In the case where and , the action of sends leaves of to leaves of .
Let be the leaf of the absolute period foliation of through . Given and paths from to , the relative period map
provides local coordinates on a neighborhood of in . The map does not depend on the choice of , but different choices of paths may translate the components of by absolute periods, which are constant on . These local coordinates give a translation structure modelled on , and in particular a straight-line flow associated to each nonzero . This straight-line flow gives rise to a partially defined flow on called a Rel flow. When , this partially defined flow is called a real Rel flow. Orbits of Rel flows are not always well-defined for all time, since distinct zeros may collide in finite time. Rel flows will be denoted by with when well-defined. The map
is well-defined and continuous on an open subset of . We denote by
the maximal domain of definition of the map . For real Rel flows, the only obstructions to having come from horizontal saddle connections with distinct endpoints.
Theorem 2.3.
([BSW], Corollary 6.2) Fix a nonzero . We have if and only if for all , does not have a saddle connection from to such that for some .
See also [MW2] and [McM2]. In particular, if does not have a horizontal saddle connection with distinct endpoints, then is well-defined.
The horocycle flow commutes with real Rel flows, and the geodesic flow normalizes real Rel flows. For nonzero, , and , we have
where in each case the left-hand side is well-defined if and only if the right-hand side is.
The slit construction.
We describe a local surgery for changing the zero orders of a holomorphic -form, or a collection of holomorphic -forms on disjoint surfaces, without changing any absolute periods. See Sections 8-9 in [EMZ], Section 5 in [CDF], and Section 3 in [McM2] for related discussions.
Let , , be a collection of holomorphic -forms. Choose a nonzero , choose points , and choose , where is the order of at . Suppose there are oriented geodesic segments in with , starting at and disjoint from except possibly at , and such that the counterclockwise angle around from to is . We view the segments
as being cyclically ordered. For notational simplicity, we rename the segments
respectively. We refer to the following surgery as applying the slit construction to the segments . For , slit to obtain a pair of oriented segments , corresponding to the left and right sides of , respectively. Glue to isometrically and respecting the orientations, where indices are taken modulo . The result is a connected topological surface, and the complex structure and the given holomorphic -forms extend over the slits to give a holomorphic -form .
The starting points of the segments yield a zero of of order , and the ending points of the segments yield a zero of order . In the special case where and , the zero of order is split into two zeros of orders and . In the special case where for all , the starting points of the segments yield a zero of of order , and the ending points of the segments yield another zero of of order .
3. Dense real Rel flow orbits
In this section, we give a criterion for the existence of dense real Rel flow orbits in -orbit closures in strata of holomorphic -forms with labelled zeros. We rely on an equidistribution result in [For] for geodesic pushforwards of horocycle arcs, which builds off of the equidistribution results in [EM] and [EMM] for the action of the upper-triangular subgroup
Throughout this section, is fixed and is a fixed partition of .
Theorem 3.1.
(Corollary 1.3, [For]) Let be the length measure on a horocycle arc , normalized to have total mass , and let be the -invariant affine probability measure supported on the -orbit closure of . There exists a subset of zero upper density such that
in the weak-* topology.
This result is useful in the study of real Rel flows, since real Rel flows commute with the horocycle flow and both flows are normalized by the geodesic flow. Our density criterion for real Rel flow orbits is the following.
Theorem 3.2.
Suppose , and fix a nonzero . Fix , and let be the -orbit closure of . If is contained in and the closure of contains the horocycle through , then there exists such that is dense in .
Proof.
Fix , and let be the length measure on the horocycle arc , normalized to have total mass . Let be the -invariant affine probability measure supported on . By Theorem 3.1, there is a sequence such that in the weak-* topology. The relation
implies that the support of is given by
By Theorem 2.1 in [EMM], the -orbit of is dense in . For , there are sequences such that . Since the map is well-defined and continuous on an open subset of , for we have that
Then since , and since is -invariant and closed, we have .
For each nonempty open subset , define
For each , the map is well-defined and continuous on an open subset of , so is open. Since the support of is , we have , and since , for sufficiently large the support of intersects , which means there exists such that . Clearly , and so
By hypothesis, the closure of contains the horocycle through . For , there is a sequence such that . We then have
or equivalently,
Since is arbitrary, the closure of contains the horocycle through , and in particular contains the support of . Since , by definition
so the closure of is contained in the closure of . Then there is such that is contained in the closure of . Since , the union is dense in , thus is dense in .
Now choose a countable basis for the topology on . For each , we have that is open and dense in . It follows from Theorem 2.3 that for any , the set of such that is a dense open subset of . Then the set of
such that is a countable intersection of dense open subsets of , so by the Baire category theorem it is dense and in particular nonempty. For any such , we have that intersects for all , and is therefore dense in . ∎
In Section 5, we will construct explicit holomorphic -forms satisfying the hypotheses of Theorem 3.2. However, we emphasize that the dense real Rel flow orbits provided by Theorem 3.2 are not explicit. For instance, a holomorphic -form satisfying the hypotheses of Theorem 3.2 may have a periodic horizontal foliation, but in that case, the closure of does not contain the -orbit of .
4. Twist parameters for the horocycle flow and real Rel flows
In this section, we study the horocycle flow and real Rel flows in the special case of holomorphic -forms with a periodic horizontal foliation. See Section 6 in [HW] for a more detailed discussion in the case of holomorphic -forms with exactly zeros. Using the density criterion for real Rel flow orbits in Section 3, and the density criterion for -orbits in Section 2, we reduce Theorem 1.1 to a problem of constructing certain holomorphic -forms with a periodic horizontal foliation. Throughout this section, is fixed and is a fixed partition of with .
Horizontal twist maps.
Suppose has a periodic horizontal foliation, and let be the horizontal cylinders on . Let and be the height and circumference of , respectively. Choose a saddle connection crossing from bottom to top, and let be the twist parameter of with respect to . Let be a closed geodesic with . Cutting along , twisting to the left by , and regluing, changes the twist parameter of from to . The lengths of the horizontal saddle connections and the heights and circumferences of the horizontal cylinders on are unchanged in the process. In this way, we obtain a continuous map . For convenience, we rescale the inputs to obtain a horizontal twist map
such that
Horocycle and real Rel flows.
The horocycle flow preserves the lengths of horizontal saddle connections and the heights and circumferences of horizontal cylinders. The horocycle through is obtained by twisting each horizontal cylinder at a rate proportional to its height. For , we have
We will only need to know that is in the image of .
Next, fix a nonzero . The real Rel flow associated to also preserves the heights and circumferences of horizontal cylinders. However, if , then the length of a horizontal saddle connection from to is not preserved. Suppose additionally that whenever and are the endpoints of a horizontal saddle connection on . Then by Theorem 2.3, is well-defined. Moreover, is contained in the image of . Let and be the top and bottom boundaries of , respectively. Choose functions
such that and are the indices of a zero in and , respectively. By our assumption, the differences do not depend on the choice of and . The real Rel flow orbit through is obtained by twisting at a rate proportional to the difference . For , we have
Let , and consider the linear flow on . Recall that the closure of the flow orbit through is the smallest subtorus of containing . In other words, the closure is given by , where is the projection of the subspace of vectors whose components satisfy all homogeneous -linear relations satisfied by . By applying to a flow orbit, we obtain the following lemma.
Lemma 4.1.
Let be the subspace of vectors whose components satisfy all homogeneous -linear relations satisfied by . Let be the torus given by the projection of , and let . Then the closure of in is .
Corollary 4.2.
If are linearly independent over , then the closure of in contains the horocycle through .
In light of Theorem 3.2 and Corollary 4.2, we are interested in finding conditions under which the -orbit of a holomorphic -form in with a periodic horizontal foliation is dense in its connected component in . Note that for the hypothesis of Corollary 4.2 to hold, it must in particular be the case that every horizontal cylinder is twisted along .
Separatrix diagrams.
Associated to any holomorphic -form with a periodic horizontal foliation is a directed graph with a vertex for each zero of and a directed edge for each horizontal saddle connection oriented from left to right. The orientation on gives the structure of a ribbon graph, and the boundary components of the associated surface with boundary come in pairs, with one pair for each horizontal cylinder. The ribbon graph , together with the pairing of boundary components, is called a separatrix diagram. See Section 4 of [KZ] for more discussion, where this concept was introduced.
As before, let be the horizontal cylinders on , let be a saddle connection crossing from bottom to top, and let and be the top and bottom boundaries of , respectively. Each saddle connection has a length . For each horizontal cylinder , these lengths satisfy a homogeneous integral linear equation
| (2) |
The holomorphic -form is determined up to isomorphism by its separatrix diagram, the lengths of its horizontal saddle connections, and the heights and twist parameters of its horizontal cylinders. The height and twist parameter of are determined by , which lies in the upper half-plane . The positive solutions in to the equations in (2) form a simplicial cone of dimension , where is the number of horizontal saddle connections. In this way, we obtain a continuous map
such that any holomorphic -form in the image of has a periodic horizontal foliation and the associated separatrix diagram is isomorphic to .
Lemma 4.3.
There is a countable collection of -linear subspaces of positive codimension such that for , the -orbit of is dense in its connected component in .
Proof.
The set of such that the period coordinates of are linearly dependent over is a countable union of -linear subspaces of positive codimension. The lemma follows from Theorem 2.2. ∎
In particular, we can slightly perturb the lengths of the horizontal saddle connections in and the twist parameters of the horizontal cylinders in to obtain a holomorphic -form with a dense -orbit. Next, consider the length function
recording the circumference of the horizontal cylinder . The cone is an open subset of an -linear subspace of , and is the restriction of a linear functional on this subspace. We can choose a basis for of the form with for . With respect to this basis, the period coordinates of holomorphic -forms in the image of range over an open subset of . It follows that two length functions and are collinear over if and only if and are homologous.
Lemma 4.4.
Suppose that is nonzero and that has a periodic horizontal foliation with horizontal cylinders and separatrix diagram satisfying the following properties.
-
(1)
If and are the endpoints of a horizontal saddle connection, then .
-
(2)
If and are zeros in the top and bottom boundaries, respectively, of the same horizontal cylinder, then .
-
(3)
If , then and are not homologous.
Then there is a countable collection of zero sets of polynomials of positive codimension such that for , the closure of contains the horocycle through .
Proof.
The functions , , are reciprocals of linear functionals restricted to a nonempty open subset. Since and are not homologous for , no two of these functions are collinear over . Since for , the same holds for the functions . Then by Lemma 4.9 in [Wri2], the functions are linearly independent over , and in particular over . Then each choice of not all zero determines a relation
which holds only on a subspace of of positive codimension. After clearing denominators, the lemma follows from Corollary 4.2. ∎
Density criterion.
We conclude this section with a criterion for the existence of a dense real Rel flow orbit in a connected component of , based on the existence of certain holomorphic -forms with a periodic horizontal foliation.
Theorem 4.5.
Fix a nonzero , and let be a connected component of . Suppose there exists with a periodic horizontal foliation satisfying the following properties.
-
(1)
If and are the endpoints of a horizontal saddle connection, then .
-
(2)
If and are zeros in the top and bottom boundaries, respectively, of the same horizontal cylinder, then .
-
(3)
Distinct horizontal cylinders are not homologous.
Then there exists such that is dense in .
Proof.
Let be the separatrix diagram associated to , and let be the subspaces as in Lemmas 4.3 and 4.4. The complement of in is dense in and invariant under scaling by , so there is in the image of this complement under . The closure of in contains the horocycle through , and the -orbit of is dense in . Thus, by Theorem 3.2 there exists such that is dense in . ∎
5. Periodic horizontal foliations with non-homologous cylinders
In this section, we prove Theorem 1.1 and Theorem 1.5. Throughout, we fix , a partition of with , and a nonzero . To prove Theorem 1.1, by Theorem 4.5 it is enough to establish the following.
Theorem 5.1.
Let be a connected component of . There exists with a periodic horizontal foliation satisfying the following properties.
-
(1)
If and are the endpoints of a horizontal saddle connection, then .
-
(2)
If and are zeros in the top and bottom boundaries, respectively, of the same horizontal cylinder, then .
-
(3)
Distinct horizontal cylinders are not homologous.
Before beginning the proofs of Theorems 5.1 and 1.5, we refer to Figure 1 for an example in the simplest case where , which illustrates the basic idea of our constructions. In the top image, the holomorphic -form is presented as a connected sum of tori with periodic horizontal and vertical foliations. In the bottom image, the horizontal cylinders and the vertical cylinders are labelled. If is the circumference of and is the circumference of , then and . Let be the integral of along one of the slits from to . The horizontal foliation of clearly satisfies the conditions of Theorem 5.1, thus Theorem 1.1 holds in the case where . Regarding Theorem 1.5, note that the vertical foliation of satisfies analogous conditions. In other words, the horizontal foliation of the rotated holomorphic -form also satisfies the conditions of Theorem 5.1. We can choose such that the reciprocals are linearly independent over , the reciprocals are linearly independent over , and the period coordinates are linearly independent over . Then by Corollary 4.2, the closure of contains , and similarly the closure of contains . Then the closure of the leaf of through is -invariant. By Theorem 2.2, the -orbit of is dense in . Thus, Theorem 1.5 holds in the case where .
We will split the proof of Theorem 5.1 into 5 cases. Each case will build off of the construction in the first case, which is based on repeated use of the slit construction from Section 2. Our construction is not the simplest possible, but it does have some advantages. In particular, the holomorphic -forms we construct will also have periodic vertical foliations, which we will analyze along the way, in order to prove Theorem 1.5 afterward.
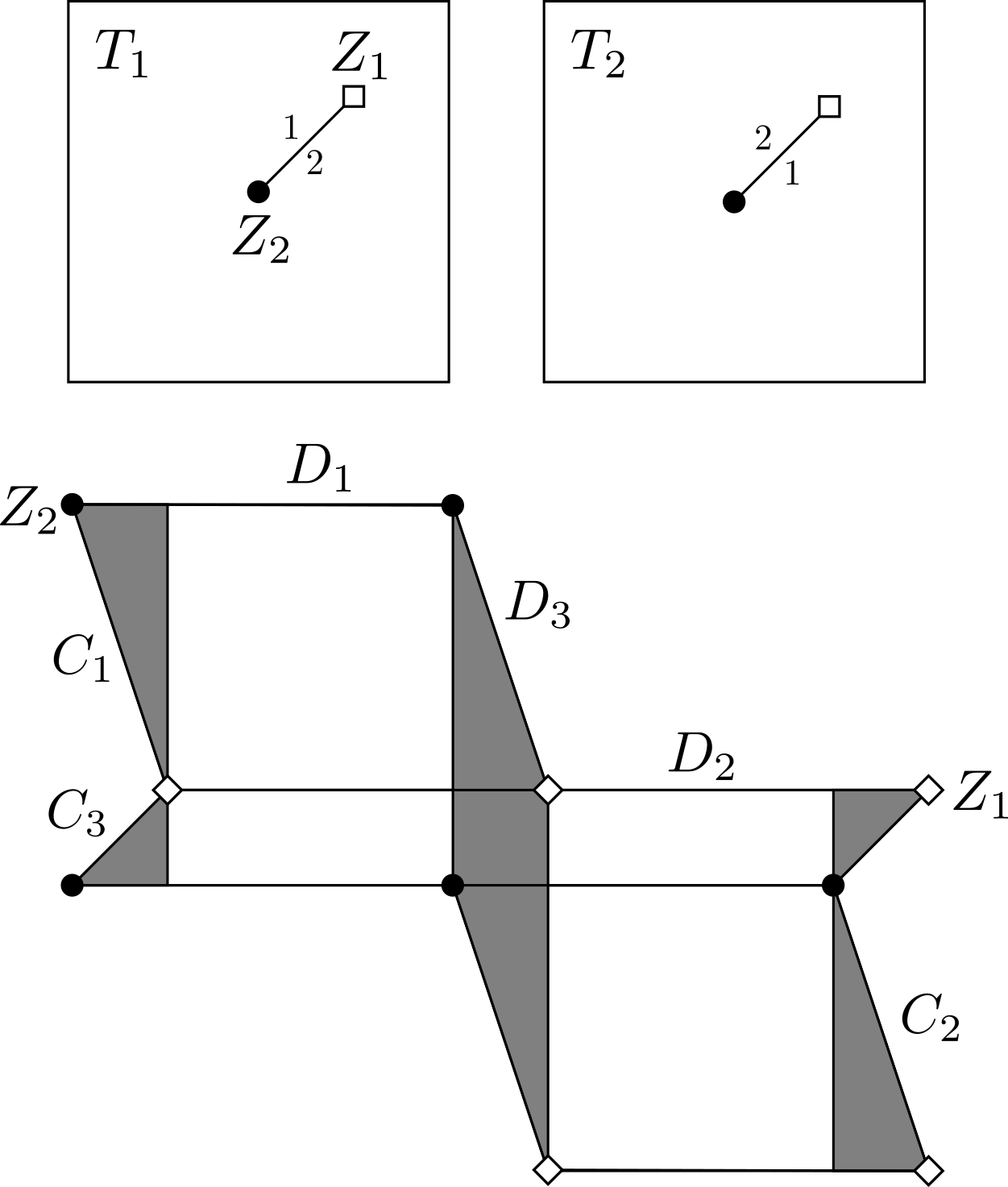
Proof.
(of Theorem 5.1)
The proof is given in cases.
Case 1:
We make the following assumptions.
-
•
The components of are distinct.
-
•
For all , we have .
-
•
If is even for all , then the associated parity of spin structure is .
-
•
If , then the image of in is a nonhyperelliptic component.
For , let
be a flat torus with periodic horizontal and vertical foliations, and let be the associated projection. Let be a closed geodesic with , and let be a closed geodesic with . Since for , and , there is a maximal such that and
and a minimal such that and
We have
Let
Choose for and , such that
| (3) | ||||
| (4) | ||||
| (5) |
and let . If , let . For and , let
be the oriented line segment from to . For and , and for , the projection is an embedded oriented segment. Moreover, the segments
are disjoint except at their common starting point , and are in counterclockwise order around . By replacing and with parallel closed geodesics, we may assume that and are disjoint from all of the segments .
Below, we will repeatedly apply the slit construction from Section 2 to the tori . Each application of the slit construction will involve a subset of the segments for some . The segments involved will always be embedded, disjoint except at a common starting point, and will not contain any zeros except at their starting point. Our construction takes place in steps. If , then there are steps, and if , then there are steps.
In step , we apply the slit construction to the segments
to obtain a holomorphic -form on a surface of genus , with a zero of order coming from the points , and a zero of order coming from the points . In step , we apply the slit construction to the segments
to obtain a holomorphic -form on a surface of genus . The order of the zero from step is unchanged. Additionally, has a zero of order coming from the points , and a zero of order coming from the points . We continue in this way through step . In step , where , we apply the slit construction to the segments
to obtain a holomorphic -form on a surface of genus . The orders of the zeros from steps through are unchanged. Additionally, has a zero of order coming from the points
and a zero of order coming from the points
In step , we apply the slit construction to the segments
to obtain a holomorphic -form . If
then has genus . In this case, has a zero of order coming from the points , and a zero of order coming from the points , . Otherwise, has genus . In this case, for
by (5) the counterclockwise angle from to around their common starting point in is . The orders of the zeros from steps through are unchanged. Additionally, has a zero of order coming from the points , and a zero of order
coming from some of the starting points of the slits. We continue in this way through step . In step , where , we apply the slit construction to the segments
to obtain a holomorphic -form . If
then has genus . In this case, the orders of the zeros , from steps through are unchanged. Additionally, has a zero of order coming from the points
and a zero of order coming from the points
Otherwise, has genus . In this case, for
by (5) the counterclockwise angle from to around their common starting point in is . The orders of the zeros from steps through are unchanged. Additionally, has a zero of order coming from the points
and a zero of order
coming from some of the starting points of the slits.
Now let
| (6) |
Note that is connected and of genus , since either , in which case , or and , in which case
If , then the points on arising from the starting points of the slits are not zeros of , and in particular is not a zero of . If , then letting , we have that is a zero of order coming from some of the starting points of the slits. Thus, the zeros of have orders , respectively, so
Next, we describe the horizontal cylinders on and we verify that satisfies conditions (1), (2), and (3) in Theorem 5.1. For the purpose of proving Theorem 1.5, we also describe the vertical cylinders on and we verify that satisfies conditions (1), (2), and (3) in Theorem 5.1. The horizontal and vertical foliations of are clearly periodic. Abusing notation, for , denote by the open subset arising from the complement of the slits in .
For , there is a unique horizontal cylinder contained in , and there is a unique vertical cylinder contained in . We have and . If , then let be minimal such that and
and otherwise, let . If , then let be maximal such that and
and otherwise, let . Letting be the height of and the height of , we have
Letting be the circumference of and the circumference of , we have
For , there is a unique horizontal cylinder such that intersects if and only if , and there is a unique vertical cylinder such that intersects if and only if . Letting be the height of and the height of , we have
Letting be the circumference of and the circumference of , we have
For , there is a unique horizontal cylinder such that intersects if and only if , and there is a unique vertical cylinder such that intersects if and only if . Letting be the height of and the height of , we have
Letting be the circumference of and the circumference of , we have
If , the cylinders and have been mentioned twice above. The cylinders and account for all of the horizontal and vertical cylinders on .
For , the top boundary of consists of a single saddle connection. If , this saddle connection joins to itself, and otherwise, this saddle connection joins to itself. The bottom boundary of also consists of a single saddle connection. If , this saddle connection joins to itself, and otherwise, this saddle connection joins to itself. At least one of and is nonzero. If , then and . If , then . If both and are nonzero, then . Thus, the zeros in the top and bottom boundaries of are distinct. The same holds for the left and right boundaries of , respectively.
For , the top boundary of consists of saddle connections joining to itself. If , these saddle connections lie in the bottom boundaries of
in cyclic order from left to right, and otherwise, these saddle connections lie in the bottom boundaries of
in cyclic order from left to right. If , the bottom boundary of consists of a single saddle connection joining to itself and lying in the top boundary of . If , the bottom boundary of consists of saddle connections joining to itself and lying in the top boundaries of
in cyclic order from left to right. Analogous statements hold for the left and right boundaries of .
For , the bottom boundary of consists of saddle connections joining to itself. If , these saddle connections lie in the top boundaries of
in cyclic order from left to right, and otherwise, these saddle connections lie in the top boundaries of
in cyclic order from left to right. If , the top boundary of consists of a single saddle connection joining to itself and lying in the bottom boundary of . If , the top boundary of consists of saddle connections joining to itself and lying in the bottom boundaries of
in cyclic order from left to right. If , the top boundary of was described in the previous paragraph, and the bottom boundary of was described in this paragraph. Again, analogous statements hold for the left and right boundaries of . We have verified that satisfies conditions (1) and (2), and we have verified that satisfies conditions (1) and (2).

For , let be a closed geodesic with , let be a closed geodesic with , and let
Clearly, is a symplectic basis for , and
so in the case where all are even, the parity of the associated spin structure is given by
For , we have
and for , we have
by considering algebraic intersection numbers with , . In particular, the homology classes and are distinct. We have verified that satisfies condition (3), and we have verified that satisfies condition (3).
Lastly, suppose that and , and suppose that the image of in lies in the hyperelliptic component. Then the hyperelliptic involution preserves each horizontal cylinder on , and so preserves for all . Since , each shares a unique saddle connection with and a unique saddle connection with , where indices are taken modulo . Each of these saddle connections must be preserved by . However, this is impossible since .
Letting , we are done with Case 1. Figure 1 shows an example in the simplest case , and Figure 2 shows an example in the case , with the presentation as a connected sum of tori as well as the horizontal and vertical cylinder decompositions. Figure 3 shows an additional example in the case .

Case 2:
We make the following assumptions.
-
•
The components of are distinct.
-
•
For all , we have and is even.
-
•
The associated parity of spin structure is .
-
•
The image of in is a nonhyperelliptic component.
By Theorem 2.1, these assumptions imply . Consider a holomorphic -form from Case 1 as in (6), and keep notation from Case 1. Suppose additionally that
Cut along , glue the top side of to the bottom side of to obtain a closed geodesic , and glue the top side of to the bottom side of to obtain a closed geodesic . Let
be the resulting holomorphic -form. For , the horizontal cylinder and the closed geodesic are preserved. For , let be the horizontal cylinder containing . The horizontal foliation of is periodic, and the horizontal cylinders are . For , the vertical cylinder and the closed geodesic are preserved. Since , for , the vertical cylinder and the closed geodesic are also preserved. Let be the region bounded by from above, by from below, and by the slits from . Let be the region bounded by from above, by from below, and by the slits from . Let be a smooth oriented closed loop going upward from the top side of in , then crossing the slit bordering and from right to left, then rotating counterclockwise around the slits in , and then going upward to the bottom side of and closing up. Let be a smooth oriented closed loop disjoint from going upward from the top side of , then crossing the slit bordering and from left to right, and then going upward to the bottom side of to close up. Figure 4 shows the configuration of in .

For , let
For , we have that is disjoint from . Moreover, is disjoint from and intersects once with , and is disjoint from and intersects once with . Therefore,
is a symplectic basis for . We have
and for we have . Therefore, the parity of the associated spin structure is given by
Since , for , we have
and since , for , we have
If , then has already been described. If , then
We have verified that satisfies condition (3). For , the bottom boundary of consists of a single saddle connection joining to itself. The top boundary of also consists of a single saddle connection. If , this saddle connection joins to itself, and otherwise, this saddle connection joins to itself. The zeros in the top and bottom boundaries of are distinct. Thus, since satisfies conditions (1) and (2), also satisfies conditions (1) and (2).
Next, we describe the vertical cylinders on . There is a vertical cylinder passing through and and crossing the slit bordering and . The left boundary of consists of a single saddle connection joining to itself, and the right boundary of consists of a single saddle connection joining to itself. There is a vertical cylinder passing through and and disjoint from the slits. The left boundary of consists of a single saddle connection joining to itself. The right boundary of also consists of a single saddle connection. If or , this saddle connection joins to itself, and otherwise, this saddle connection joins to itself. Thus, since satisfies conditions (1) and (2), also satisfies conditions (1) and (2).
For , let be a closed geodesic with . Letting , we have
For , there is a vertical cylinder passing through and , and passing through if and only if . Let be a closed geodesic with . Let . Since , we have
Since , for , we have
If , then we have addressed all of the vertical cylinders. If and , then the vertical cylinder and the closed geodesic are preserved, and we have
If and , then there is a vertical cylinder passing through . Let be a closed geodesic with . Letting , we have
We have verified that satisfies condition (3).
Lastly, when is odd and , a similar argument from Case 1 considering shows that does not admit a hyperelliptic involution.
Letting , we are done with Case 2.
Case 3:
We assume that the image of in is a hyperelliptic component, which implies the following.
-
•
We have .
-
•
The components of are distinct.
Consider a holomorphic -form from Case 1 as in (6), and keep notation from Case 1. Suppose additionally that for , we have
Cut along , reglue opposite sides of and , and let
be the resulting holomorphic -form. There is a holomorphic involution with that preserves each horizontal cylinder and exchanges the two zeros of . Each horizontal cylinder contains two fixed points of , and there are horizontal cylinders, so has fixed points and must be a hyperelliptic involution.
For , let be the closed geodesic on arising from the top side of , and let be the horizontal cylinder containing . The horizontal cylinder and the closed geodesic are preserved. The horizontal foliation of is periodic, and the horizontal cylinders on are . Letting , , and , we have
For , there is a loop which crosses and from bottom to top and is disjoint from the other horizontal cylinders. Thus, satisfies condition (3). For , the top boundary of consists of a single saddle connection joining to itself, and the bottom boundary of consists of a single saddle connection joining to itself. The top boundary of consists of saddle connections joining to itself, and the bottom boundary of consists of saddle connections joining to itself. Thus, satisfies conditions (1) and (2).
Next, we describe the vertical cylinders on . For , let be the region bounded by from below, by from above, and by the slits coming from . For , there is a vertical cylinder passing through and and disjoint from the slits. There is a vertical cylinder that passes through and is disjoint from the slits if is odd, and that passes through and the slit bordering if is even. For , there is a vertical cylinder passing through , as well as the slit bordering and the slit bordering . There is a vertical cylinder passing through , and the slit bordering . The vertical foliation of is periodic, and the vertical cylinders are . For , let be a closed geodesic with , and let . The nonzero algebraic intersection numbers are given by
We have verified that satisfies condition (3). Moreover, we note that the span of in contains homology classes such that is a symplectic basis for . For , the left boundary of consists of a single saddle connection joining to itself, and the right boundary of consists of a single saddle connection joining to itself. For , the left boundary of consists of a single saddle connection joining to itself, and the right boundary of consists of a single saddle connection joining to itself. Thus, satisfies conditions (1) and (2).
Letting , we are done with Case 3. See Figure 5 for an example in the case .

Case 4:
We make the following assumptions.
-
•
The components of are distinct.
-
•
For some , we have .
By relabelling zeros, we may assume that . Let . Then is a partition of for some , and we have . By Cases 1, 2, and 3, there is satisfying conditions (1), (2), and (3) in Theorem 5.1. Additionally, if the orders of the zeros are all even, we may assume that or according to whether the image of in is an even component or an odd component. We apply the following surgery to .
Let be a horizontal segment starting at and shorter than any saddle connection on . Slit along , and let be the top and bottom sides of the slit, respectively. Divide into segments, with the left segment having length and the right segment having length . Divide into segments, with the left segment having length and the right segment having length . Identify pairs of segments of equal length, and let be the resulting holomorphic -form. On , the order of is . The orders of the other zeros are unchanged, and no new zeros are created. No new horizontal cylinders are created, and the only horizontal saddle connections that are created are loops through . Since satisfies conditions (1), (2), and (3), also satisfies conditions (1), (2), and (3). By iterating this surgery times, we obtain a holomorphic -form
satisfying conditions (1), (2), and (3) in Theorem 5.1. If some zero order is odd, then we are done, so suppose that all of the orders of the zeros are even. The above surgery can be alternatively described by slitting along , gluing in a horizontal cylinder that does not contain a vertical saddle connection, and then vertically shrinking the cylinder to height . The first step is an instance of bubbling a handle from Section 4 of [KZ]. Since one of the endpoints of is not a zero, by Lemma 11 in [KZ], the above surgery does not change the parity of the associated spin structure. Thus, we are done with Case 4.
Case 5:
We assume that the components of are not distinct.
The components of determine a partition of the set , where and are in the same part of if and only if . Letting , we obtain a partition of with that is refined by . Choose a representative of , and let be represented by the vector such that for and , . Note that the components of are distinct. By Cases 1, 2, 3, and 4, there is with zeros of orders and satisfying conditions (1), (2), and (3) of Theorem 5.1. If is even for all , then is even for all , and we may additionally assume that or according to whether the image of in is an even component or an odd component. We apply the following surgery to .
For each , write . Apply the slit construction from Section 2 iteratively, using short horizontal segments on , in order to split the zero of order into zeros of orders . After relabelling the resulting zeros, we obtain a holomorphic -form . In each use of the slit construction above, we only modify a holomorphic -form on a contractible neighborhood of a zero. Thus, in the case where every is even, we do not change the parity of the associated spin structure. Therefore, .
By construction, since satisfies conditions (1) and (2), also satisfies conditions (1) and (2). No new horizontal cylinders are created during the surgery, so since satisfies condition (3), also satisfies condition (3). We are done with Case 5. ∎
The criteria in Theorems 3.2 and 4.5 can be readily verified for many other -orbit closures in strata. As an example, we briefly discuss the existence of dense orbits of real Rel flows on nonarithmetic eigenform loci in . See [BSW] and [McM1] for definitions and detailed discussions. Let be a non-square integer such that . Let
be the area- locus of eigenforms for real multiplication by the real quadratic order of discriminant . There is with a periodic horizontal foliation and horizontal cylinders, whose circumferences have irrational ratios. Each horizontal saddle connection on is a loop. Letting , is well-defined, and its closure is given by
By replacing with for some , we can ensure that the -orbit of is dense in . Theorem 3.2 then implies the following.
Theorem 5.2.
For any non-square integer such that , there exists such that is dense in .
Lastly, we use the constructions in our proof of Theorem 5.1 to prove Theorem 1.5. We refer to Figure 1 and the discussion preceding the proof of Theorem 5.1 for the simplest case where .
Theorem 5.3.
Suppose , fix a nonzero with distinct components, and let . Let be a connected component of . There is an explicit with periodic horizontal and vertical foliations, such that the leaf of through is dense in .
Proof.
First, suppose there is arising from the construction in Case 1 of the proof of Theorem 5.1, and keep notation from Case 1. Recall that has a periodic horizontal foliation with horizontal cylinders , and a periodic vertical foliation with vertical cylinders . The circumference of is , and the circumference of is . The circumferences and are parameters in the construction in Case 1, arising from the choice of tori with periodic horizontal and vertical foliations. This construction also depended on parameters for the slits joining the tori. Moreover, , , and provide period coordinates for . The valid choices of parameters yield period coordinates ranging over an open subset of . As in Section 4, choose functions
so that (respectively, ) is the index of a zero in the top (respectively, bottom) boundary of , and (respectively, ) is the index of a zero in the left (respectively, right) boundary of . Both and satisfy the conditions in Theorem 5.1. Then by the proofs of Lemmas 4.3 and 4.4, we can choose the parameters , , and so that the following four properties hold.
-
•
has area .
-
•
, , are linearly independent over .
-
•
, , are linearly independent over .
-
•
The period coordinates of are linearly independent over .
Let be the leaf of through , and recall that the -action on sends leaves of to leaves of . By Corollary 4.2, the closure of contains the horocycle . Similarly, by Corollary 4.2 applied to , the closure of contains the opposite horocycle . Since and generate , it follows that the closure is -invariant. By Theorem 2.2, the -orbit of is dense in . Thus, is dense in .
The argument when there is arising from Case 2 of the proof of Theorem 5.1 is similar. In the notation from Case 2, the horizontal and vertical foliations of are periodic, and there are horizontal cylinders with circumferences , and vertical cylinders with circumferences . The circumferences and are parameters in the construction, arising from the choice of tori . There are parameters arising from the slits. The circumferences arise from cylinders passing through and , and can be freely varied by changing the choices of horizontal closed geodesics in and to cut along. Lastly, in the beginning of the construction, we assumed . However, , , and provide period coordinates for , since the associated elements of are linearly independent, which is shown in Case 2. By perturbing these period coordinates within , we can perturb while preserving each of the horizontal and vertical cylinders and preserving the property of having periodic horizontal and vertical foliations, so that the four properties from the previous paragraph hold. Then the leaf of through is dense in . The argument when there is arising from Case 3 of the proof of Theorem 5.1 is also similar. The horizontal and vertical foliations of are periodic, and there are horizontal cylinders with circumferences , and vertical cylinders with circumferences . There is a parameter arising from the slits. As is shown in Case 3, , , and provide period coordinates for . Again, we can perturb these period coordinates within so that the four properties in the previous paragraph hold. Then the leaf of through is dense in .

We may now assume that some . By relabelling zeros, we may assume that . Let . Then is a partition of for some , and . Choose arising from the construction in Case 1, 2, or 3 of the proof of Theorem 5.1. If every is even, we additionally require that or according to whether the image of in lies in an even component or odd component.
We focus on the case where arises from the construction in Case 1, since the analysis in the other cases is similar. Keep notation from Case 1. Recall that has horizontal cylinders with heights and circumferences , and that has vertical cylinders with heights and circumferences . For , recall that and , and let
and let
For , as we travel along from to , the height of changes by , and we have . Therefore, all of the horizontal cylinders on persist on . Similarly, for , all of the vertical cylinders on persist on . We will apply a variant of the surgery from Case 4 to , after imposing some additional restrictions on the parameters in the construction of .
We will additionally assume that and for all . Recall that is constructed from flat tori by iteratively applying the slit construction from Section 2. Since , we have and . In this case, there are steps in the construction in Case 1. The torus is only slit in steps and . In step , is slit along the projection of the segment from to , and in step , is slit along the projection of the segment from to . There is a unique horizontal cylinder passing through all tori, and a unique vertical cylinder passing through all tori. The only other horizontal cylinder passing through is , and the only other vertical cylinder passing through is . For , choose satisfying
| (7) | |||
| (8) | |||
| (9) |
and let . The flat torus contains a closed geodesic satisfying . Let be the straight segment on emanating from and satisfying . Slit along , slit along , and reglue opposite sides. The result is a holomorphic -form . In the case where all are even, the associated parity of spin structure is unchanged by Lemma 11 in [KZ]. Every horizontal cylinder and every vertical cylinder on persists on . The height of is decreased, and the height of is decreased, while the heights of the other horizontal cylinders and vertical cylinders are unchanged. Additionally, for , has a horizontal cylinder passing through with circumference
and a vertical cylinder passing through with circumference
We also denote and .
The holomorphic -forms and satisfy conditions (1) and (3) in Theorem 5.1. The cylinders and only contain the zero in their boundary, and thus do not satisfy condition (2). However, , , and provide period coordinates for . Again, by the proofs of Lemmas 4.1 and 4.3, we can perturb these period coordinates within so that the following properties hold.
-
•
has area .
-
•
The collection
is linearly independent over .
-
•
The collection
is linearly independent over .
-
•
The period coordinates of are linearly independent over .
Replacing with if necessary, we may assume that . Then there exist
with the following property. On , as increases from to , the horizontal cylinder collapses to height and a new horizontal cylinder emerges, which we also denote . No other horizontal cylinders collapse, although their heights may change. Let . On , the cylinder has circumference . No other horizontal cylinder circumferences change. On , the cylinder contains in its top boundary and in its bottom boundary, the cylinder contains in its top boundary and in its bottom boundary, and the cylinder contains in its top boundary and in its bottom boundary. The zeros in the boundaries of all other horizontal cylinders remain the same. Similarly, for , on , as increases from to , the horizontal cylinder collapses to height and a new horizontal cylinder emerges, which we also denote . No other horizontal cylinders collapse. Let . On , the cylinder has circumference . No other horizontal cylinder circumferences change. On , the cylinder contains in its top boundary and in its bottom boundary, the cylinder contains in its top boundary and in its bottom boundary, and the cylinder contains in its top and bottom boundaries, where . The zeros in the boundaries of all other horizontal cylinders remain the same. See Figure 6 for an example in the case .
The horizontal cylinders on that are twisted along are . Since , , are linearly independent over , by Lemma 4.1, the closure of contains all holomorphic -forms obtained from by twisting arbitrarily. The horizontal cylinders on that are twisted along are , . Since , , , are linearly independent over , by Lemma 4.1, the closure of contains all holomorphic -forms obtained from by twisting , arbitrarily. Similarly, for , the closure of contains all holomorphic -forms obtained from by twisting the cylinders , arbitrarily. Now let be the leaf of through . For , by considering sequences of the form
with such that is close to and such that is close to , we see that the closure contains all holomorphic -forms obtained from by twisting arbitrarily. More generally, by considering appropriate sequences of the form
with , we conclude that contains the image of the horizontal twist map , and in particular contains the horocycle . An analogous argument, with and in place of and , and swapping and , shows that contains the opposite horocycle . Thus, is -invariant. By Theorem 2.2, the -orbit of is dense in . Thus, is dense in .
References
- [BSW] M. Bainbridge, J. Smillie, and B. Weiss. Horocycle dynamics: new invariants and the eigenform loci in the stratum . Mem. Amer. Math. Soc., to appear.
- [CDF] G. Calsamiglia, B. Deroin, and S. Francaviglia. A transfer principle: from periods to isoperiodic foliations. Preprint (2020).
- [CSW] J. Chaika, J. Smillie, and B. Weiss. Tremors and horocycle dynamics on the moduli space of translation surfaces. Preprint (2020).
- [EMZ] A. Eskin, H. Masur, and A. Zorich. Moduli spaces of abelian differentials: the principal boundary, counting problems, and the Siegel–Veech constants. Publ. Math. IHES 97 (2003), 61–179.
- [EM] A. Eskin and M. Mirzakhani. Invariant and stationary measures for the action on moduli space. Publ. Math. IHES 127 (2018), 95–324.
- [EMM] A. Eskin, M. Mirzakhani, and A. Mohammadi. Isolation, equidistribution, and orbit closures for the action on moduli space. Ann. of Math. 182 (2015), 673–721.
- [For] G. Forni. Limits of geodesic push-forwards of horocycle invariant measures. Ergod. Th. & Dynam. Sys. 41 (2021), 2782–2804.
- [Ham] U. Hamenstädt. Ergodicity of the absolute period foliation. Israel J. Math. 225 (2018), 661–680.
- [HW] P. Hooper and B. Weiss. Rel leaves of the Arnoux-Yoccoz surfaces. Select. Math. 24 (2018), 857–934.
- [KZ] M. Kontsevich and A. Zorich. Connected components of the moduli spaces of Abelian differentials with prescribed singularities. Invent. Math. 153 (2003), 631–678.
- [McM1] C. McMullen. Dynamics of over moduli space in genus two. Ann. of Math. 165 (2007), 397–456.
- [McM2] C. McMullen. Navigating moduli space with complex twists. J. Eur. Math. Soc. 5 (2013), 1223–1243.
- [McM3] C. McMullen. Moduli spaces of isoperiodic forms on Riemann surfaces. Duke Math. J. 163 (2014), 2271–2323.
- [McM4] C. McMullen. Cascades in the dynamics of measured foliations. Ann. Scient. Ec. Norm. Sup. 48 (2015), 1–39.
- [MW1] Y. Minsky and B. Weiss. Nondivergence of horocycle flows on moduli space. J. Reine Angew. Math. 552 (2002), 131–177.
- [MW2] Y. Minsky and B. Weiss. Cohomology classes represented by measured foliations, and Mahler’s question for interval exchanges. Ann. Scient. Ec. Norm. Sup. 47 (2014), 245–284.
- [Win] K. Winsor. Dynamics of the absolute period foliation of a stratum of holomorphic 1–forms. Preprint (2021).
- [Wri1] A. Wright. The field of definition of affine invariant submanifolds of the moduli space of abelian differentials. Geom. Top. 18 (2014), 1323–1341.
- [Wri2] A. Wright. Cylinder deformations in orbit closures of translation surfaces. Geom. Top. 19 (2015), 413–438.
- [Ygo] F. Ygouf. A criterion for the density of the isoperiodic leaves in rank 1 affine invariant orbifolds. Preprint (2020).
- [Zor] A. Zorich. Flat surfaces, from: “Frontiers in number theory, physics, and geometry. I”. Springer, Berlin (2006), 437–583.
Email: [email protected]
Department of Mathematics, Harvard University, Cambridge, Massachusetts, USA