Denoising Diffusion Autoencoders are Unified Self-supervised Learners
Abstract
Inspired by recent advances in diffusion models, which are reminiscent of denoising autoencoders, we investigate whether they can acquire discriminative representations for classification via generative pre-training. This paper shows that the networks in diffusion models, namely denoising diffusion autoencoders (DDAE), are unified self-supervised learners: by pre-training on unconditional image generation, DDAE has already learned strongly linear-separable representations within its intermediate layers without auxiliary encoders, thus making diffusion pre-training emerge as a general approach for generative-and-discriminative dual learning. To validate this, we conduct linear probe and fine-tuning evaluations. Our diffusion-based approach achieves 95.9% and 50.0% linear evaluation accuracies on CIFAR-10 and Tiny-ImageNet, respectively, and is comparable to contrastive learning and masked autoencoders for the first time. Transfer learning from ImageNet also confirms the suitability of DDAE for Vision Transformers, suggesting the potential to scale DDAEs as unified foundation models. Code is available at github.com/FutureXiang/ddae.
1 Introduction
Understanding data with limited human supervision is a crucial challenge in machine learning. To cope with massive amounts of data with scarce annotations, deep learning paradigms are shifting from supervised to self-supervised pre-training. Regarding natural language processing (NLP), self-supervised models such as BERT [31], GPTs [43, 44, 8] and T5 [45] have achieved outstanding performance across diverse tasks, and large language models like ChatGPT [40] are showing a profound impact beyond the machine learning community. Among these, BERT uses masked language modeling (MLM) as a pretext task to train encoders while which cannot generate full text samples. In contrast, GPTs and T5 have shown capabilities in generating long paragraphs autoregressively (AR). Moreover, they prove that decoder-only or encoder-decoder models can acquire deep language understandings via generative pre-training, without the need of training an encoder intentionally. With the rise of AI-Generated Content (AIGC), GPTs and T5 have been garnering more attention compared to pure encoders, which unify the generative (e.g. translation, summarization) and discriminative (e.g. classification) tasks [44, 45].


In computer vision, self-supervised learners have not yet achieved similar feats as GPTs in bridging the gap between generation and recognition. While generative adversarial networks (GAN) [20, 30, 7] and autoregressive Transformers [55, 19, 47] can synthesize high-fidelity images, they do not offer significant benefits for discriminative tasks. For recognition, contrastive methods [11, 12, 21, 9] build features through pretext tasks on augmented images. Masked autoencoders [23, 3, 60] introduce BERT-like masked image modeling (MIM) pre-training for Vision Transformers [16], but they seem not natural and practical for convolutional networks. Note that although MIM-based methods can recover masked image tokens, they are problematic in synthesizing full images, mainly because the complete data distribution is not directly modeled. These methods are not referred to as unified generative-and-discriminative models. Instead, we denote them as “semi-” generative for their partial similarities to full generative models (Table 1).
Theoretically, it is more practical to extend generative models for discriminative purposes and gain the benefit of both ways. Recently, we have witnessed the flourish of AI-generated visual content due to the emergence of diffusion models [26, 53], with state-of-the-art results reported in image synthesis [13, 29, 41], image editing [24] and text-to-image synthesis [46, 48, 50]. Considering such capability, versatility, and scalability in generative modeling, we ask: whether diffusion models can replicate the success of GPTs and T5, in becoming unified generative-and-discriminative learners? We regard them as very promising alternatives in the visual domain, based on the following observations:
(i) It has been demonstrated that discriminative image or text encodings can be learned through end-to-end generative pre-training [10, 36, 38], i.e. “analysis-by-synthesis”. Intuitively, the full generation task should contain, and be more challenging than the semi-generative masked modeling, suggesting that image (or language) generation is compatible with visual (or language) understanding, but not vice versa. The generative pre-training paradigm supports diffusion as a meaningful discriminative learning method.
(ii) Diffusion networks are trained as multi-level denoising autoencoders (DAE, Figure 1(a)). The idea of denoising autoencoding has been widely applied to discriminative visual representation learning [56, 57, 6]. More recently, masked autoencoders (MAE) [23] have further highlighted the effectiveness of denoising pre-training, which can also be inherited by diffusion networks — likewise, recovering images with large, multi-scale noise is nontrivial and may also require a high-level understanding of visual concepts.
(iii) The benefits of diffusion-based representation learning are evidenced. DDPM-seg [4] confirms that diffusion can capture pixel-wise semantic information, indicating the feasibility. Besides, previous attempts in GANs and Transformers, i.e. BigBiGAN [15] and iGPT [10], find that better image generation capability can translate to improved feature quality, suggesting that diffusion is even more capable of representation learning as the state-of-the-art generative model. Diffusion-based representation learners can also be facilitated by large AIGC projects if the learned knowledge can be conveniently transferred from pre-trained models.
| Model | Pre-training target and method | (i) Generative pre-training | (ii) Denoising autoencoding |
|---|---|---|---|
| Natural Language Processing | |||
| BERT [31] | Encoder-only, MLM | Semi- | Masked |
| GPT [43] | Decoder-only, AR | Full | – |
| T5 [45] | Enc-dec, MLM+AR | Full | Masked |
| Computer Vision | |||
| MAE [23] | Encoder-only, MIM | Semi- | Masked |
| iGPT [10] | Decoder-only, AR | Full | – |
| DDAE (ours) | Enc-dec, Diffusion | Full | Multi-level Gaussian |
Driven by this analysis, we investigate whether diffusion models, which incorporate the best practices of generative pre-training and denoising autoencoding (as summarized in Table 1), can learn effective representations for image classification. Our approach is straightforward: we evaluate diffusion pre-trained networks, namely denoising diffusion autoencoders (DDAE), as feature extractors by measuring the linear probe and fine-tuning accuracies of intermediate activations (Figure 1(b)). For linear probing, we pass noised images with specific scales (or timesteps) to DDAE and examine the activations at different layers. For fine-tuning, we truncate DDAE at the best representation layer as an image encoder and fine-tune it without additional noising.
We confirm that via end-to-end diffusion pre-training, DDAEs do learn strongly linear-separable features, which lie in the middle of up-sampling and can be extracted when images are perturbed with noises. Moreover, we validate the correlation between generative and discriminative performance of DDAEs through ablation studies on noise configurations, training steps, and the mathematical model. Evaluations on CIFAR-10 [33] and Tiny-ImageNet [34] show that the diffusion-based approach is comparable to supervised WideResNet [63], contrastive SimCLRs [11, 12] and MAE [23] for the first time. The transfer ability has also been verified on ImageNet [49] pre-trained models, including the ones constructed by pixel-space UNets and latent-space Vision Transformers such as DiT [41].
Our study highlights the underlying nature of diffusion models as unified vision foundation models. The revealed duality of DDAEs as state-of-the-art generative models and competitive recognition models may inspire improvements to vision pre-training and applications in both domains. With the insightful elucidation and observations presented in this paper, it is highly likely to transfer powerful discriminative knowledge from large-scale pre-trained AIGC models like Stable Diffusion [48] in the near future.
2 Related work
Diffusion models are becoming the most popular generative paradigm due to their high-fidelity performance and the ability to synthesize complex visual concepts [26, 53, 29, 48, 46, 50], without unstable adversarial training, mode collapse issues or architecture constraints. With improvements to computational efficiency [48], training [29], sampling [51, 39, 29] and guidance [13, 27], diffusion models become the state-of-the-art on unconditional CIFAR-10 [33], class-conditional ImageNet [49], and text-to-image on MS-COCO [35]. AIGC projects such as Stable Diffusion [48] and ControlNet [65] have achieved broad social impacts. Recent work on diffusion with ViTs [16, 2, 41] further explores diffusion models with scalable backbones.
Representation learning with generative models is a long-standing idea since they model the data distribution in an unsupervised manner. While VAEs [32, 54] can learn meaningful representations, they have proven more useful in generation than recognition. BigBiGAN [15] learns discriminative features from large-scale GANs [7] with jointly trained encoders [17, 14]. However, the feature quality may be compromised since GANs naturally capture less data diversity. iGPT [10] models next pixel prediction with Transformers and achieves competitive results with contrastive methods, but the lack of inductive bias for images makes its downstream applications restricted and inefficient.
Representation learning with diffusion models. A number of studies [42, 66] introduce auxiliary encoders to extract representations following GAN Inversion [59], but they focus on attribute manipulation rather than recognition. Other methods learn linear-separable features with modified diffusion frameworks [1, 37], while they underperform contrastive baselines by large margins. Training diffusion models with classification objectives has been explored [61], but it fails to rival pure recognition models and hurts generative performance heavily. Diffusion-based conditional likelihood estimation [67] is also straightforward, but its accuracy on CIFAR-10 is still below ResNet. In contrast, our approach is comparable to typical self-supervised and supervised models without modifying diffusion frameworks. Our study is partially inspired by DDPM-seg, which studies DDPM [26] on single super-class datasets for segmentation. However, we are the first to explore various diffusion models for classification on complex multi-class datasets.
3 Approach
3.1 Background: DDAEs as generative models
Diffusion models [26, 53, 29] define a series of data corruptions which apply Gaussian noise to data . Given timestep which indicates noise levels, the corruption is defined as , where and are hyper-parameters controlling the signal-to-noise ratio. When is large enough, data will be approximately corrupted to . With the reparameterization trick, a noised version of at an arbitrary level of can be obtained, by sampling and taking:
| (1) |
Diffusion models aim to invert the corruption and reconstruct samples. Specifically, a random is drawn from , and the model samples iteratively until getting . Diffusion models employ trainable networks to approximate the transitions with , whose mean is predicted by networks and variance is a constant. By simplifying the maximize likelihood objective, networks are equivalently trained with the denoising autoencoder objective [29]:
| (2) |
where is a function of and . Therefore, a denoising network trained by diffusion modeling can be seen as a multi-level and level-conditional version of DAEs, specifically Denoising Diffusion Autoencoders (DDAE).
DDPM [26] proposes the “Variance Preserving” parameterization, where and . are determined by a linear schedule from to . The network is trained to minimize the noise prediction error , which is a re-weighted version of Eq. 2, since the denoiser can be derived from . DDPM uses a UNet with 35.7M parameters, and achieves competitive performance on CIFAR-10.
EDM [29] proposes to use the “Variance Exploding” parameterization, where and is sampled by an improved schedule. Based on score-based stochastic differential equations [53], which extend the corruptions to infinite timesteps, EDM yields state-of-the-art results on CIFAR-10 using a larger DDPM++ network [53] with 56M parameters.
Apart from the mathematical formulation improvements, some studies explore efficient and scalable architectures for DDAEs. In particular, Latent Diffusion Models (LDM) [48] perform diffusion modeling within the compressed VAE latent space and outperform pixel-space models on high-resolution text-to-image synthesis. DiT [41] explores scalable backbones under the LDM framework, which replaces UNets with Vision Transformers and achieves state-of-the-art results on class-conditional ImageNet generation.
In this paper, we consider (i) the original DDPM UNet, (ii) DDPM++ trained by EDM, and (iii) latent-space DiT as representative DDAE implementations. DDPM(++) uses UNets with timestep embeddings to parameterize or . DiT uses latent-space ViTs with timestep and label embeddings to learn for conditional generation, and jointly learns an unconditional model to achieve classifier-free guidance [27] sampling.
3.2 Evaluating DDAEs as discriminative learners
Extracting meaningful and discriminative representations from DDAEs is not trivial. Although deterministic inference methods like DDIM [51] are able to derive uniquely identifiable encodings, the contained information is not compact enough for classification. There also exists a trend to employ additional encoders to learn representations for attribute manipulation [42, 66] or classification [1, 37]. In contrast, inspired by iGPT [10] and DDPM-seg [4] which evaluate learned features in autoregressive Transformers and diffusion UNets, we propose to directly take the intermediate activations in pre-trained DDAEs. This approach does not require modification to common diffusion frameworks and is compatible with all existing models.
Drawing from the connections with denoising autoencoders, it is possible that DDAEs can produce linear-separable representations at some implicit encoder-decoder interfaces, resembling MAE. Driven by this, we extend previous investigations on GPTs and DDPM [10, 4] to various network backbones (UNets and DiT) under different frameworks (DDPM and EDM). Considering that UNet with skip connections has been the de-facto design, we avoid splitting the encoder-decoder explicitly to prevent diminishing the generation performance. However, the best layer to extract features remains unknown. Additionally, to prevent the gap between pre-training and deploying, images have to be noised by certain scales for linear evaluations. Considering both the aforementioned facts, we investigate the relationship between feature qualities and layer-noise combinations through grid search, following DDPM-seg.


To apply noise, we randomly sample and use Eq. 1 to obtain , since no obvious differences can be observed between random and deterministic noising. Linear probe accuracies on the features after global average pooling are examined, as illustrated in Figure 1(b). Figure 2 shows that layer depths and noising scales affect feature quality jointly as a concave function, whose global maximum point can be found empirically. For the resolution of pixels, the best features lie in the middle of up-sampling, rather than at the lowest resolution as in common practices. Furthermore, we find that perturbing images with relatively small noises improves the linear probe performance, especially on DDPM++ trained by EDM, which achieves linear probe accuracy and surpasses classical AE or VAEs [1].
These properties have been verified across different datasets and models, but the optimal layer-noise combination may vary under different settings. In the remainder of this paper, linear probe accuracies are reported as the highest found in grid search. For fine-tuning, clean images are passed to DDAE encoders, which are truncated at the optimal layers. The timestep inputs are also fixed to the optimal values. Note that this may not perform best for fine-tuning, since we find the fine-tuning accuracy can be further improved if more layers are used, and it is less sensitive to timestep inputs. However, we keep the layer-noise setup consistent with linear probing to reduce notation overhead.
3.3 Label-free monitoring for layer selection



Although DDAE learns high quality representations for discriminative tasks, it may rely on probing with annotated data to search for proper configurations. Therefore, it would be valuable if label-free metrics can indicate the best performing layers at training. Inspired by feature distribution analysis [58] in contrastive learning, we normalize the features from each layer to be on the unit hypersphere and investigate their alignment and uniformity [58] properties.
In the context of contrastive learning, the alignment loss directly evaluates the distance between positive pairs, while the uniformity loss aims to measure the distribution uniformity on the unit hypersphere:
To apply them to DDAEs, we need to define the positive pairs properly. Considering that the feature extraction method proposed in Section 3.2 does not rely on deterministic noising, we assume that the representation should be independent to the noise sample used in Eq. 1. To this end, we adapt these two metrics as:
| (3) | ||||
| (4) |
where is the DDAE encoder, denotes the noised image using , and are independently sampled noise.
We present the metrics with respect to selected layers in Figure 3, to validate whether they align with the feature quality. We evaluate three DDAE implementations on the CIFAR-10 training set: DDPM, DDPM++ trained by DDPM, and DDPM++ trained by EDM. For each model, is fixed to the respective optimal value, and we monitor the trajectories of metrics during training. Figure 3 shows that overall, and agree with the linear probe results (near lower left corners). Moreover, features from the well-performing layers show consistent improvements to both metrics during training. These results indicate that diffusion training may share similarities with contrastive representation learning, and selecting layers by metrics may mitigate the layer searching issue.

4 Experiments
We firstly examine the impact of some core designs in diffusion models on both generative and discriminative performance through ablation studies. We then compare the results with counterparts on CIFAR-10 [33] and Tiny-ImageNet [34] datasets under linear probing, fine-tuning and ImageNet [49] transfer settings.
All models are retrieved or trained from official (or equivalent) codebases. For image classification, we do not use regularization methods such as mixup [64] or cutmix [62], and only employ lightweight augmentations. Implementation details as well as optimal layer-noise settings are provided in the code repository and the appendix.
4.1 Main properties
Previous research has demonstrated that in Transformers, better generative performance links to better representations, as measured by log-likelihood and linear probe accuracy [10]. Accordingly, we propose to investigate the correlation between generative and discriminative capabilities of DDAEs by plotting evaluation accuracy as a function of image quality calculated on 50k samples. In particular, the widely applied Fréchet Inception Distance (FID) [25] is used as the metric for generation quality. We conduct ablation studies from two perspectives: (i) denoising autoencoding, and (ii) generative pre-training, which correspond to the two sides of DDAEs as discussed in Section 1.
4.1.1 Denoising autoencoding
Diffusion models can be viewed as multi-level denoising autoencoders. Based upon the findings in Figure 2 that DDAEs learn strongly linear-separable features in an unsupervised manner, we explore what design in the multi-level denoising makes DDAEs stronger representation learners than classical AEs, VAEs [1] and DAEs. In particular, we consider two key factors in DDPM [26] that may contribute to improved denoising pre-training: (1) the number of noise levels () and (2) the range of noise scales ().
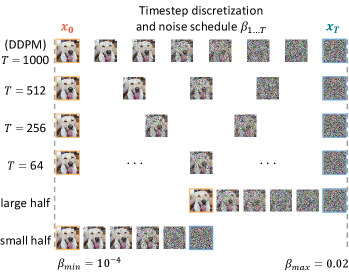
To investigate the effect of noise levels, we reduce the default to , , and . We opt not to decrease it further as DDPM cannot generate meaningful images when . For each configuration, the noise schedule is linearly spaced in the range of , where and , following DDPM default. Additionally, we examine the effect of the noise scales by using the larger half and the smaller half of default schedule range. We keep in these two scenarios for fair comparison. Figure 4(a) shows the influence of the noise configurations and training steps, and Figure 4(b) provides an illustration of ablated noising configurations. DDPM with the maximum number of noise levels and the broadest noise scale coverage, achieves best performance in both image generation and recognition.


Noise level and range. Reducing noise levels or narrowing the noise range weakens both generative and discriminative performances. Training handicapped diffusion models with only levels or the larger scales leads to more significant performance declines. Interestingly, we observe that the recognition ability seems to depend less on a dense and wide noise configuration than generation. As shown in Figure 4(a), while generation FID may suffer huge decreases, the highest linear probe accuracy drops slightly by less than 3%. The model with even produces stronger features than other handicapped models, despite its inability to generate meaningful images.
We attempt to explain these intriguing properties from a contrastive learning angle. Since the denoising objective (Section 3.1) demonstrates that DDAEs are forced to predict the very same given different versions of (Eq. 1), there exists an underlying constraint of alignment on these various noised versions. In other words, the time levels and random noises serve jointly as data augmentations, and different s are positive views of . Consequently, a denser and wider noise configuration can increase the diversity of positive samples and improve the representation quality. The high accuracy in the model with suggests that more noise levels could be an overkill for recognition-only purpose, but they still contribute significantly to generation. Unfortunately, such diversity may require longer training duration — Figure 4(a) shows that models with half level counts or ranges can be well-trained at around 1000 epochs, while the full model requires 2000 epochs for this simple CIFAR-10. EDM [29] even relies on a 400 A100 GPU days training to reach state-of-the-art results on ImageNet. Due to the revealed duality of generation and recognition, we hope the best practices in discriminative representation learning (e.g. self-distillation methods such as BYOL and DINO [21, 9]) will inspire future improvements to training efficiency in diffusion models beyond sampling, so that the scaling of diffusion models can be explored more efficiently. Introducing feature-level constraints to DDAEs could be helpful to accelerate training and boost discriminative performance, and we leave it to future work.
Training step. By tracking checkpoints throughout the training duration, it can be observed that better generative model learns better representations. Moreover, we observe that while linear probe accuracy tends to overfit after 1000 epochs in DDPM training, the generation performance continues to improve, indicating that it has not saturated. Similar observations can be found in other curves (Figure 4(a)), that recognition tends to overfit earlier than generation.
Since diffusion training is a pixel-to-pixel task, it is reasonable to assume that DDAEs firstly learn high-level understandings from the noised input at the deeper layers, and gradually learn to predict the exact pixels through decoding. Consequently, models may focus on fitting some imperceptible details after learning saturated semantic representations. These properties somewhat provide support for the theory of relationship between image generation and understanding, as claimed intuitively in Section 1.
In summary, by evaluating various checkpoints with different denoising pre-training setups, the positive correlation between the generative and discriminative capabilities of DDAEs is confirmed, aligning with the findings in iGPT.
4.1.2 Generative pre-training
To dive deeper into improved generative pre-training for recognition, we compare the basic 35.7M DDPM UNet with DDPM++ trained by EDM. With a larger network capacity, framework improvements, and data augmentation (CIFAR-10), we consider EDM as a better generative model, and examine whether it performs better in recognition similarly. Figure 5 shows the accuracies with respect to FIDs on two datasets. Note that the networks and hyper-parameters for Tiny-ImageNet are far from optimal, since the best practice is too expensive, that it may cost 32 A100 GPU days to train a ADM network [13] on Tiny-ImageNet, according to EDM. Therefore, our goal is to provide confirmation of the observations, rather than optimizing performances.
Recognition accuracy. Figure 5 demonstrates that EDM outperforms DDPM on both generative and discriminative metrics. On CIFAR-10, the linear probe accuracy increases dramatically from 88.5% to 95.9%. After fine-tuning, EDM achieves 97.2% accuracy, surpassing WideResNet-28-10 [63]. This superior classification performance confirms diffusion as a meaningful self-supervised pre-training approach. On Tiny-ImageNet, observations are similar. While the FID has limited improvements between DDPM and EDM, the recognition rates increase more significantly by 3.2% (linear probe) and 5.3% (fine-tuning). The fine-tuned EDM also slightly surpasses supervised WideResNet. The results suggest that improving diffusion models for better generation performance will naturally lead to better recognition models due to the effective generative pre-training.
Network backbone issues. Although the DDPM++ network in EDM has a larger model size than DDPM, their truncated versions fail to benefit from scaling when trained from scratch on both datasets (see “Scratch” in Figure 5). Moreover, even though we tune hyper-parameters and train them longer, these truncated UNets fail to reach comparable accuracies as ResNets and are often unstable to train. These results suggest that truncating diffusion UNets at up-sampling and appending global pooling are not optimal practices for classification. These incompetent backbones for recognition may have encumbered the performance of DDAE. Using general-purpose vision backbones without up-sampling (e.g. ViTs) or designing novel networks with explicit encoder-decoder split may overcome this issue.
However, ViT-based diffusion models are mainly operating in the latent space to achieve promising performance. We conduct preliminary experiments to compare pixel-space and latent-space image classification, and we find that the latter performs consistently worse on CIFAR-10 (96.3% v.s. 96.0%) and Tiny-ImageNet (69.3% v.s. 65.3%), suggesting that latent compression may lose information for recognition. Moreover, it may be an obstacle for downstream tasks such as object detection. We leave the exploration for unified pixel-space backbones to future work.


4.1.3 Noise-conditional classifier
Classifier guidance is a common manner to enhance conditional models [53, 13], which relies on a noise-conditional classifier to obtain the conditional gradients , or perturbed mean . Since the DDAE features are extracted with noise perturbation, our approach can naturally serve as such classifier. Specifically, we extract features in the same way as linear probing, and attach a two-layer MLP as the classifier head:
| (5) |
where is the frozen DDAE encoder, is the two-layer classifier, and denotes the timestep embedding.
Figure 6 shows the accuracies of noise-conditional classifiers based on DDPM UNet and EDM-trained DDPM++. Following [53], we train noise-conditional WideResNets on CIFAR-10 as supervised baselines and compare them to our DDAE-based approach. The curves show that a two-layer MLP head on frozen DDAE features can achieve promising accuracies, and outperforms supervised models over almost all noise scales. Most importantly, our simple approach can simultaneously obtain (or , ) and the classification logits in one single forward pass, reducing the time overhead in sampling caused by external classifiers.
4.2 Comparison with previous methods
| Method | Evaluation | Generation FID | Acc. % |
|---|---|---|---|
| on CIFAR-10 | |||
| WideResNet-28-10 [63] | Supervised | N/A | 96.3 |
| DRL/VDRL [1, 37] | Non-linear | 3.0 | <80.0 |
| HybViT [61] | Supervised | 26.4 | 95.9 |
| SBGC [67] | Supervised | * | 95.0 |
| DDAE (EDM) | Linear | 2.0 | 95.9 |
| DDAE (EDM) | Fine-tune | N/A | 97.2 |
| on Tiny-ImageNet | |||
| WideResNet-28-10 [63] | Supervised | N/A | 69.3 |
| HybViT [61] | Supervised | 74.8 | 56.7 |
| DDAE (EDM) | Linear | 19.5 | 50.0 |
| DDAE (EDM) | Fine-tune | N/A | 69.4 |
| * Negative log-likelihood (NLL) of 3.11 is reported. Similar model [53] achieves | |||
| 2.99 NLL and 2.92 FID, for reference. | |||
We compare EDM and DiT models with other diffusion-based representation learning methods and self-supervised discriminative methods. Since the generative performance is our first priority, we select checkpoints with the lowest FID for DDAEs, despite the recognition rates may overfit.
Comparison with diffusion-based methods. Table 2 shows that EDM-based DDAE outperforms all previous supervised or unsupervised diffusion-based methods on both generation and recognition. Moreover, our DDAE can be seen as the state-of-the-art hybrid model [61] on CIFAR-10, which can generate and classify (through linear classifier) with a single model. On Tiny-ImageNet, our self-supervised EDM yields significantly better generation FID than the supervised HybViT, despite a lower linear probe accuracy. After fine-tuning, DDAE catches up with supervised WideResNet and surpasses HybViT by large margins.
Comparison with contrastive learning methods. Table 3 presents the evaluation results on CIFAR-10. For linear probing, EDM-based DDAE is comparable with SimCLRs considering model sizes. After fine-tuning, EDM achieves 97.2% (w/o transfer) and 98.1% (w/ transfer) accuracies, outperforming SimCLRs with comparable parameters, despite underperforming the scaled 375M SimCLR model by 0.5%. Table 4 presents results on Tiny-ImageNet. Our EDM-based model significantly outperforms SimCLR pre-trained ResNet-18 under both linear probing and fine-tuning settings. However, DDAE is not as efficient as SimCLR on this dataset, that a slightly larger ResNet-50 can surpass our linear probe result with fewer parameters.
Transfer learning with Vision Transformers. To verify the transfer ability on scalable ViTs, we transfer the DiT model, which is pre-trained on ImageNet, to CIFAR-10 and Tiny-ImageNet. Since the DiT codebase only provides the largest DiT-XL/2 checkpoint for class-conditional generation, we use it in an unconditional manner by dropping label to null [27]. Although this may not be strictly fair due to the scale and supervision difference, we mainly aim to confirm the scalability of ViT-based DDAEs.
Table 3 and Table 4 show that the scaled DiT-XL/2 outperforms the smaller MAE ViT-B/16 under all settings by large margins except for linear probing on CIFAR-10. It also catches up with the 375M SimCLR and achieves 98.4% accuracy on CIFAR-10 after fine-tuning. These results indicate that similar to pixel-space ViTs, latent-space DiTs can also benefit from scaling and pre-training on larger datasets. However, diffusion pre-trained DiTs may not be as efficient as MAE pre-trained ViTs on recognition tasks, since the former is specifically designed for advanced image generation without optimizing its representation learning ability.
| Method | Evaluation | Params (M) | Acc. % |
| on CIFAR-10 | |||
| WideResNet-28-10 [63] | Supervised | 36 | 96.3 |
| DDAE (EDM) | Linear | 36 | 95.9 |
| SimCLR Res-50 [11] | Linear | 24 | 94.0 |
| SimCLRv2 Res-101-SK [12] | Linear | 65 | 96.4 |
| DDAE (EDM) | Fine-tune | 36 | 97.2 |
| SimCLRv2 Res-101-SK [12] | Fine-tune | 65 | 97.1 |
| on CIFAR-10, with ImageNet transfer | |||
| DDAE (EDM) | Linear | 36 | 91.4 |
| SimCLR Res-50 [11] | Linear | 24 | 90.6 |
| SimCLR Res-50-4x [11] | Linear | 375 | 95.3 |
| DDAE (EDM) | Fine-tune | 36 | 98.1 |
| SimCLR Res-50 [11] | Fine-tune | 24 | 97.7 |
| SimCLR Res-50-4x [11] | Fine-tune | 375 | 98.6 |
| \hdashlineDDAE (DiT-XL/2)† | Linear | 314 | 84.3 |
| MAE ViT-B/16 [22] | Linear | 86 | 85.2 |
| DDAE (DiT-XL/2)† | Fine-tune | 314 | 98.4 |
| MAE ViT-B/16 [22] | Fine-tune | 86 | 96.5 |
| † Trained as class-conditional model but evaluated in an unconditional manner. | |||
| Extra VAE encoder is used. | |||
| Method | Evaluation | Params (M) | Acc. % |
| on Tiny-ImageNet | |||
| WideResNet-28-10 [63] | Supervised | 36 | 69.3 |
| DDAE (EDM) | Linear | 40 | 50.0 |
| SimCLR Res-18 [18] | Linear | 12 | 48.8 |
| SimCLR Res-50 [5] | Linear | 24 | 53.5 |
| DDAE (EDM) | Fine-tune | 40 | 69.4 |
| SimCLR Res-18 [5] | Fine-tune | 12 | 54.8 |
| on Tiny-ImageNet, with ImageNet transfer | |||
| DDAE (DiT-XL/2)† | Linear | 338 | 66.3 |
| MAE ViT-B/16 [22] | Linear | 86 | 55.2 |
| DDAE (DiT-XL/2)† | Fine-tune | 338 | 77.8 |
| MAE ViT-B/16 [22] | Fine-tune | 86 | 76.5 |
| † Trained as class-conditional model but evaluated in an unconditional manner. | |||
| Extra VAE encoder is used. | |||
5 Discussion and conclusion
We propose diffusion pre-training as a unified approach to simultaneously acquire superior generation ability and deep visual understandings, which potentially leads to the development of unified vision foundation models. However, as the first study to investigate diffusion for recognition at scale, there remain some limitations and open questions.
Backbone issues. Truncating DDAEs in the middle is not an elegant and optimal practice for encoders, and our approach relies on probing to find the best layer. Though the metric-based method works well on CIFAR-10, it may fail on more complex datasets where features are less linear-separable. In constrast, ideal DDAE backbones may have explicit encoder-decoder disentanglement. Moreover, whether latent-based networks can rival pixel-space models on more recognition tasks needs more exploration.
Efficiency issues. Although DDAEs can achieve comparable accuracies to some pure recognition models, they rely on larger model sizes and are not efficient. Besides, diffusion models require longer training duration to achieve optimal generative performance, making them costly to scale.
Relation to other self-supervised methods. We hypothesize that the alignment between different images along the noising trajectory may implicitly contribute to the discriminative properties, which operates similarly to positive-only contrastive learning. The concurrent study named Consistency Models [52], which shares similarities to self-distillation-based contrastive learning [21, 9], has already exploited this idea on denoising outputs. Moreover, we believe there exists another possibility of integrating such consistency or self-predictive constraints to DDAE features, resembling studies combining MAEs with contrastive methods [28]. It may also mitigate the previous issues by aggregating discriminative features on a designated encoder-decoder interface, and improving the learning efficiency.
Acknowledgements
This work is partly supported by the National Key R&D Program of China (2021ZD0110503), the National Natural Science Foundation of China (No. 62022011, 62202031, U20B2069), the Beijing Natural Science Foundation (No. 4222049), and the Fundamental Research Funds for the Central Universities.
References
- [1] Korbinian Abstreiter, Sarthak Mittal, Stefan Bauer, Bernhard Schölkopf, and Arash Mehrjou. Diffusion-based representation learning. arXiv:2105.14257, 2021.
- [2] Fan Bao, Chongxuan Li, Yue Cao, and Jun Zhu. All are worth words: a vit backbone for score-based diffusion models. arXiv:2209.12152, 2022.
- [3] Hangbo Bao, Li Dong, Songhao Piao, and Furu Wei. Beit: Bert pre-training of image transformers. arXiv:2106.08254, 2021.
- [4] Dmitry Baranchuk, Ivan Rubachev, Andrey Voynov, Valentin Khrulkov, and Artem Babenko. Label-efficient semantic segmentation with diffusion models. arXiv:2112.03126, 2021.
- [5] Prashant Bhat, Elahe Arani, and Bahram Zonooz. Distill on the go: online knowledge distillation in self-supervised learning. In CVPRW, 2021.
- [6] Emmanuel Asiedu Brempong, Simon Kornblith, Ting Chen, Niki Parmar, Matthias Minderer, and Mohammad Norouzi. Denoising pretraining for semantic segmentation. In CVPR, 2022.
- [7] Andrew Brock, Jeff Donahue, and Karen Simonyan. Large scale gan training for high fidelity natural image synthesis. arXiv:1809.11096, 2018.
- [8] Tom Brown, Benjamin Mann, Nick Ryder, Melanie Subbiah, Jared D Kaplan, Prafulla Dhariwal, Arvind Neelakantan, Pranav Shyam, Girish Sastry, Amanda Askell, et al. Language models are few-shot learners. In NeurIPS, 2020.
- [9] Mathilde Caron, Hugo Touvron, Ishan Misra, Hervé Jégou, Julien Mairal, Piotr Bojanowski, and Armand Joulin. Emerging properties in self-supervised vision transformers. In ICCV, 2021.
- [10] Mark Chen, Alec Radford, Rewon Child, Jeffrey Wu, Heewoo Jun, David Luan, and Ilya Sutskever. Generative pretraining from pixels. In ICML, 2020.
- [11] Ting Chen, Simon Kornblith, Mohammad Norouzi, and Geoffrey Hinton. A simple framework for contrastive learning of visual representations. In ICML, 2020.
- [12] Ting Chen, Simon Kornblith, Kevin Swersky, Mohammad Norouzi, and Geoffrey E Hinton. Big self-supervised models are strong semi-supervised learners. In NeurIPS, 2020.
- [13] Prafulla Dhariwal and Alexander Nichol. Diffusion models beat gans on image synthesis. In NeurIPS, 2021.
- [14] Jeff Donahue, Philipp Krähenbühl, and Trevor Darrell. Adversarial feature learning. arXiv:1605.09782, 2016.
- [15] Jeff Donahue and Karen Simonyan. Large scale adversarial representation learning. In NeurIPS, 2019.
- [16] Alexey Dosovitskiy, Lucas Beyer, Alexander Kolesnikov, Dirk Weissenborn, Xiaohua Zhai, Thomas Unterthiner, Mostafa Dehghani, Matthias Minderer, Georg Heigold, Sylvain Gelly, et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv:2010.11929, 2020.
- [17] Vincent Dumoulin, Ishmael Belghazi, Ben Poole, Olivier Mastropietro, Alex Lamb, Martin Arjovsky, and Aaron Courville. Adversarially learned inference. arXiv:1606.00704, 2016.
- [18] Aleksandr Ermolov, Aliaksandr Siarohin, Enver Sangineto, and Nicu Sebe. Whitening for self-supervised representation learning. In ICML, 2021.
- [19] Patrick Esser, Robin Rombach, and Bjorn Ommer. Taming transformers for high-resolution image synthesis. In CVPR, 2021.
- [20] Ian Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair, Aaron Courville, and Yoshua Bengio. Generative adversarial nets. In NeurIPS, 2014.
- [21] Jean-Bastien Grill, Florian Strub, Florent Altché, Corentin Tallec, Pierre Richemond, Elena Buchatskaya, Carl Doersch, Bernardo Avila Pires, Zhaohan Guo, Mohammad Gheshlaghi Azar, et al. Bootstrap your own latent-a new approach to self-supervised learning. In NeurIPS, 2020.
- [22] Jie Gui, Zhengqi Liu, and Hao Luo. Good helper is around you: Attention-driven masked image modeling. arXiv:2211.15362, 2022.
- [23] Kaiming He, Xinlei Chen, Saining Xie, Yanghao Li, Piotr Dollár, and Ross Girshick. Masked autoencoders are scalable vision learners. In CVPR, 2022.
- [24] Amir Hertz, Ron Mokady, Jay Tenenbaum, Kfir Aberman, Yael Pritch, and Daniel Cohen-Or. Prompt-to-prompt image editing with cross attention control. arXiv:2208.01626, 2022.
- [25] Martin Heusel, Hubert Ramsauer, Thomas Unterthiner, Bernhard Nessler, and Sepp Hochreiter. Gans trained by a two time-scale update rule converge to a local nash equilibrium. In NeurIPS, 2017.
- [26] Jonathan Ho, Ajay Jain, and Pieter Abbeel. Denoising diffusion probabilistic models. In NeurIPS, 2020.
- [27] Jonathan Ho and Tim Salimans. Classifier-free diffusion guidance. arXiv:2207.12598, 2022.
- [28] Zhicheng Huang, Xiaojie Jin, Chengze Lu, Qibin Hou, Ming-Ming Cheng, Dongmei Fu, Xiaohui Shen, and Jiashi Feng. Contrastive masked autoencoders are stronger vision learners. arXiv preprint arXiv:2207.13532, 2022.
- [29] Tero Karras, Miika Aittala, Timo Aila, and Samuli Laine. Elucidating the design space of diffusion-based generative models. arXiv:2206.00364, 2022.
- [30] Tero Karras, Samuli Laine, Miika Aittala, Janne Hellsten, Jaakko Lehtinen, and Timo Aila. Analyzing and improving the image quality of stylegan. In CVPR, 2020.
- [31] Jacob Devlin Ming-Wei Chang Kenton and Lee Kristina Toutanova. Bert: Pre-training of deep bidirectional transformers for language understanding. In Proceedings of NAACL-HLT, 2019.
- [32] Diederik P Kingma and Max Welling. Auto-encoding variational bayes. arXiv:1312.6114, 2013.
- [33] Alex Krizhevsky, Geoffrey Hinton, et al. Learning multiple layers of features from tiny images. 2009.
- [34] Ya Le and Xuan Yang. Tiny imagenet visual recognition challenge. CS 231N, 7(7):3, 2015.
- [35] Tsung-Yi Lin, Michael Maire, Serge Belongie, James Hays, Pietro Perona, Deva Ramanan, Piotr Dollár, and C Lawrence Zitnick. Microsoft coco: Common objects in context. In ECCV, 2014.
- [36] Frederick Liu, Siamak Shakeri, Hongkun Yu, and Jing Li. Enct5: Fine-tuning t5 encoder for non-autoregressive tasks. arXiv:2110.08426, 2021.
- [37] Sarthak Mittal, Guillaume Lajoie, Stefan Bauer, and Arash Mehrjou. From points to functions: Infinite-dimensional representations in diffusion models. arXiv:2210.13774, 2022.
- [38] Jianmo Ni, Gustavo Hernández Ábrego, Noah Constant, Ji Ma, Keith B Hall, Daniel Cer, and Yinfei Yang. Sentence-t5: Scalable sentence encoders from pre-trained text-to-text models. arXiv:2108.08877, 2021.
- [39] Alexander Quinn Nichol and Prafulla Dhariwal. Improved denoising diffusion probabilistic models. In ICML, 2021.
- [40] Long Ouyang, Jeff Wu, Xu Jiang, Diogo Almeida, Carroll L Wainwright, Pamela Mishkin, Chong Zhang, Sandhini Agarwal, Katarina Slama, Alex Ray, et al. Training language models to follow instructions with human feedback. arXiv:2203.02155, 2022.
- [41] William Peebles and Saining Xie. Scalable diffusion models with transformers. arXiv:2212.09748, 2022.
- [42] Konpat Preechakul, Nattanat Chatthee, Suttisak Wizadwongsa, and Supasorn Suwajanakorn. Diffusion autoencoders: Toward a meaningful and decodable representation. In CVPR, 2022.
- [43] Alec Radford, Karthik Narasimhan, Tim Salimans, Ilya Sutskever, et al. Improving language understanding by generative pre-training. OpenAI blog, 2018.
- [44] Alec Radford, Jeffrey Wu, Rewon Child, David Luan, Dario Amodei, Ilya Sutskever, et al. Language models are unsupervised multitask learners. OpenAI blog, 2019.
- [45] Colin Raffel, Noam Shazeer, Adam Roberts, Katherine Lee, Sharan Narang, Michael Matena, Yanqi Zhou, Wei Li, and Peter J Liu. Exploring the limits of transfer learning with a unified text-to-text transformer. JMLR, 21(1):5485–5551, 2020.
- [46] Aditya Ramesh, Prafulla Dhariwal, Alex Nichol, Casey Chu, and Mark Chen. Hierarchical text-conditional image generation with clip latents. arXiv:2204.06125, 2022.
- [47] Aditya Ramesh, Mikhail Pavlov, Gabriel Goh, Scott Gray, Chelsea Voss, Alec Radford, Mark Chen, and Ilya Sutskever. Zero-shot text-to-image generation. In ICML, 2021.
- [48] Robin Rombach, Andreas Blattmann, Dominik Lorenz, Patrick Esser, and Björn Ommer. High-resolution image synthesis with latent diffusion models. In CVPR, 2022.
- [49] Olga Russakovsky, Jia Deng, Hao Su, Jonathan Krause, Sanjeev Satheesh, Sean Ma, Zhiheng Huang, Andrej Karpathy, Aditya Khosla, Michael Bernstein, et al. Imagenet large scale visual recognition challenge. IJCV, 115:211–252, 2015.
- [50] Chitwan Saharia, William Chan, Saurabh Saxena, Lala Li, Jay Whang, Emily Denton, Seyed Kamyar Seyed Ghasemipour, Burcu Karagol Ayan, S Sara Mahdavi, Rapha Gontijo Lopes, et al. Photorealistic text-to-image diffusion models with deep language understanding. arXiv:2205.11487, 2022.
- [51] Jiaming Song, Chenlin Meng, and Stefano Ermon. Denoising diffusion implicit models. arXiv:2010.02502, 2020.
- [52] Yang Song, Prafulla Dhariwal, Mark Chen, and Ilya Sutskever. Consistency models. arXiv:2303.01469, 2023.
- [53] Yang Song, Jascha Sohl-Dickstein, Diederik P Kingma, Abhishek Kumar, Stefano Ermon, and Ben Poole. Score-based generative modeling through stochastic differential equations. arXiv:2011.13456, 2020.
- [54] Aaron Van Den Oord, Oriol Vinyals, et al. Neural discrete representation learning. In NeurIPS, 2017.
- [55] Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N Gomez, Łukasz Kaiser, and Illia Polosukhin. Attention is all you need. In NeurIPS, 2017.
- [56] Pascal Vincent, Hugo Larochelle, Yoshua Bengio, and Pierre-Antoine Manzagol. Extracting and composing robust features with denoising autoencoders. In ICML, 2008.
- [57] Pascal Vincent, Hugo Larochelle, Isabelle Lajoie, Yoshua Bengio, Pierre-Antoine Manzagol, and Léon Bottou. Stacked denoising autoencoders: Learning useful representations in a deep network with a local denoising criterion. JMLR, 11(12), 2010.
- [58] Tongzhou Wang and Phillip Isola. Understanding contrastive representation learning through alignment and uniformity on the hypersphere. In ICML, 2020.
- [59] Weihao Xia, Yulun Zhang, Yujiu Yang, Jing-Hao Xue, Bolei Zhou, and Ming-Hsuan Yang. Gan inversion: A survey. PAMI, 2022.
- [60] Zhenda Xie, Zheng Zhang, Yue Cao, Yutong Lin, Jianmin Bao, Zhuliang Yao, Qi Dai, and Han Hu. Simmim: A simple framework for masked image modeling. In CVPR, 2022.
- [61] Xiulong Yang, Sheng-Min Shih, Yinlin Fu, Xiaoting Zhao, and Shihao Ji. Your vit is secretly a hybrid discriminative-generative diffusion model. arXiv:2208.07791, 2022.
- [62] Sangdoo Yun, Dongyoon Han, Seong Joon Oh, Sanghyuk Chun, Junsuk Choe, and Youngjoon Yoo. Cutmix: Regularization strategy to train strong classifiers with localizable features. In ICCV, 2019.
- [63] Sergey Zagoruyko and Nikos Komodakis. Wide residual networks. arXiv:1605.07146, 2016.
- [64] Hongyi Zhang, Moustapha Cisse, Yann N Dauphin, and David Lopez-Paz. mixup: Beyond empirical risk minimization. arXiv:1710.09412, 2017.
- [65] Lvmin Zhang and Maneesh Agrawala. Adding conditional control to text-to-image diffusion models. arXiv:2302.05543, 2023.
- [66] Zijian Zhang, Zhou Zhao, and Zhijie Lin. Unsupervised representation learning from pre-trained diffusion probabilistic models. In NeurIPS, 2022.
- [67] Roland S Zimmermann, Lukas Schott, Yang Song, Benjamin A Dunn, and David A Klindt. Score-based generative classifiers. arXiv:2110.00473, 2021.
Appendix A Implementation details
Diffusion pre-training. We follow official implementations of DDPM, EDM and DiT for generative diffusion pre-training. The networks used in DDPM and EDM are UNets based on WideResNet with multiple convolutional down-sampling and up-sampling stages. Single head self-attention layers are used in the residual blocks at some resolutions. For CIFAR-10, we retrieve official checkpoints111https://github.com/pesser/pytorch_diffusion222https://github.com/NVlabs/edm from their codebases. For Tiny-ImageNet, we use official (or equivalent) implementations and similar configurations to train unconditional diffusion models by ourselves. The setting is in Table 5. Transformer-based DiT-XL/2 pre-trained on ImageNet is retrieved from its official codebase333https://github.com/facebookresearch/DiT, and we do not train a smaller version (e.g. DiT-B/2) due to the high computational cost. The used off-the-shelf VAE model for latent compression is retrieved from Stable Diffusion444Hugging Face/Diffusers, which has a down-sample factor of 8.
Linear probing and fine-tuning. We use very simple settings for linear probing and fine-tuning experiments (see Table 6 and Table 7) and we intentionally do not tune the hyper-parameters such as Adam / or weight decays. In contrast with common practices in representation learning, we do not use additional normalization layers before linear classifiers since we find it also works well.
To train latent-space DiTs for recognition efficiently, we store the extracted latent codes through the VAE encoder and train DiTs in an offline manner. We encode 10 versions of the training set with data augmentations and randomly sample one version per epoch at the training. This approach may suffer from insufficient augmentation, and increasing augmentation versions or training with online VAE encoder may improve the recognition accuracy.
Supervised training from scratch. In Figure 5, we present recognition accuracies of truncated UNet encoders trained from scratch and compare them to supervised Wide ResNets. The setting is in Table 8. We intentionally train these supervised models for long duration (200 epochs) to reach maximum performance for fair comparisons.
Appendix B Layer-noise combinations in grid search
In Section 3.2 we have shown that the layer-noise combination affects representation quality heavily. We perform grid searching to find a good enough, if not the best, combination for each model and dataset. For 18-step or 50-step EDM models, we train linear classifiers for 10 epochs with each layer and timestep. For 1000-step DDPM or DiT, we increase the timestep by 5 or 10 to search more efficiently. Table 9 shows the combinations adopted in Section 4.
| dataset | CIFAR-10 | Tiny-ImageNet | ||
|---|---|---|---|---|
| model | DDPM | EDM | DDPM | EDM |
| architecture | DDPM | DDPM++ | DDPM | DDPM++ |
| base channels | 128 | 128 | 128 | 128 |
| channel multipliers | 1-2-2-2 | 2-2-2 | 1-2-2-2 | 1-2-2-2 |
| attention resolutions | {16} | {16} | {16} | {16} |
| blocks per resolution | 2 | 4 | 2 | 4 |
| full DDAE params | 35.7M | 55.7M | 35.7M | 61.8M |
| pre-training epochs | 2000 | 4000 | 2000 | 2000 |
| config | value | ||
|---|---|---|---|
| optimizer | Adam with default momentum & weight decay | ||
| base learning rate | 1e-3 | ||
| learning rate schedule | cosine decay | ||
| batch size per GPU | 128 | ||
| GPUs | 4 | ||
| augmentations | RandomHorizontalFlip() and | ||
| RandomCrop(32, 4) for CIFAR-10 or | |||
| RandomCrop(64, 4) for Tiny-ImageNet | |||
| training epochs | CIFAR-10 | Tiny-ImageNet | |
| DDPM | 10 | 20 | |
| EDM | 15 | 30 | |
| DiT | 30 | 30 | |
| config | value | ||
|---|---|---|---|
| optimizer | Adam with default momentum & weight decay | ||
| base learning rate | 1e-3 (DDPM and EDM), 8e-5(DiT) | ||
| learning rate schedule | cosine decay | ||
| batch size per GPU | 128 (DDPM and EDM), 8 (DiT) | ||
| GPUs | 4 (DDPM and EDM), 8 (DiT) | ||
| augmentations | RandomHorizontalFlip() and | ||
| RandomCrop(32, 4) for CIFAR-10 or | |||
| RandomCrop(64, 4) for Tiny-ImageNet | |||
| training epochs | CIFAR-10 | Tiny-ImageNet | |
| DDPM | 30 | 80 | |
| EDM | 50 | 100 | |
| DiT | 50 | 50 | |
| config | value |
|---|---|
| optimizer | Adam (DDAE encoder), SGD (WideResNet) |
| base learning rate | 5e-4 (DDAE encoder), 0.1 (WideResNet) |
| learning rate schedule | cosine decay |
| batch size per GPU | 128 |
| GPUs | 4 |
| augmentations | RandomHorizontalFlip() and |
| RandomCrop(32, 4) for CIFAR-10 or | |
| RandomCrop(64, 4) for Tiny-ImageNet | |
| training epochs | 200 |
| warmup epochs | 5 |
| model | dataset@resolution | layer | timestep |
|---|---|---|---|
| DDPM | CIFAR-10@32 | 7/12 (1st block@16) | 11/1000 |
| EDM | CIFAR-10@32 | 6/15 (1st block@16) | 4/18 |
| DiT | CIFAR-10@256 | 12/28 | 121/1000 |
| DDPM | Tiny-ImageNet@64 | 2/12 (2nd block@8) | 45/1000 |
| EDM | Tiny-ImageNet@64 | 7/20 (2nd block@16) | 14/50 |
| DiT | Tiny-ImageNet@256 | 13/28 | 91/1000 |