DenDrift: A Drift-Aware Algorithm for Host Profiling

Ali Sedaghatbaf RISE Research Institutes of SwedenVästeråsSweden [email protected] , Sima Sinaei RISE Research Institutes of SwedenVästeråsSweden [email protected] , Perttu Ranta-aho F-Secure CorporationHelsinkiFinland [email protected] and Marko Koskinen Techila TechnologiesTampereFinland [email protected]

Abstract.

Detecting and reacting to unauthorized actions is an essential task in security monitoring. What make this task challenging are the large number and various categories of hosts and processes to monitor. To these we should add the lack of an exact definition of normal behavior for each category. Host profiling using stream clustering algorithms is an effective means of analyzing hosts’ behaviors, categorizing them, and identifying atypical ones. However, unforeseen changes in behavioral data (i.e. concept drift) make the obtained profiles unreliable. DenStream is a well-known stream clustering algorithm, which can be effectively used for host profiling. This algorithm is an incremental extension of DBSCAN which is a non-parametric algorithm widely used in real-world clustering applications. Recent experimental studies indicate that DenStream is not robust against concept drift. In this paper, we present DenDrift as a drift-aware host profiling algorithm based on DenStream. DenDrift relies on non-negative matrix factorization for dimensionality reduction and Page-Hinckley test for drift detection. We have done experiments on both synthetic and industrial datasets and the results affirm the robustness of DenDrift against abrupt, gradual and incremental drifts.

clustering, evolving data streams, concept drift, matrix factorization, Page-Hinkley test, DenStream.

^†^†copyright: none

1. Introduction

F-Secure is known as a reliable cyber-security leader around the world. F-Secure has over 100,000 corporate customers, serves more than 300 enterprises through consulting, and tens of millions of consumer customers are protected via the security products provided by this corporation. Among other tasks, the detection and response system at F-Secure collects process execution data from a set of hosts monitored by this system. The collected data indicate when and how many times each process is executed by each host. Currently an offline clustering algorithm is used to group hosts based on their similarities in process execution. Anomaly detection based on offline clustering is challenging due to the statistical changes in data which are known as concept drift (see Section 3.1). Concept drift has a negative impact on the quality of clusters and imposes further effort for anomaly detection. In particular, the clusters obtained for one point of time might be much different from the previous point due to statistical changes in data over time. F-Secure is looking for a clustering algorithm for host profiling that can detect and adapt to concept drifts. No presumption should be made about the number of clusters, and the algorithm should be able to produce clusters of arbitrary shapes.

Our proposition is to use an incremental and non-parametric clustering algorithm that can maintain a high clustering quality by properly detecting concept drift in the input stream and retraining the underlying model after drift. In incremental clustering, efficient processing and memory consumption is of paramount importance. On one hand, data is constantly arriving and we have a limited time for data processing. On the other hand, we cannot store all data in memory since the data stream may exist for several months or years. Several incremental clustering algorithms have been developed in the past two decades. These algorithms can be categorized into the following four groups (Moulton et al., 2018): (1) partitioning algorithms (e.g. CluStream (Aggarwal et al., 2003), StreamKM++ (Ackermann et al., 2012)) which partition the data stream into a predefined number of groups, (2) density-based algorithms (e.g. DenStream (Cao et al., 2006), SDSttream (Ren and Ma, 2009)) which try to identify high-density regions in the data stream, (3) grid-based algorithms (e.g. DStream (Chen and Tu, 2007), DENGRIS (Amini et al., 2012)) which divide the feature space into grid cells and then map each data point to a cell, and (4) hierarchical algorithms (e.g. ClusTree (Kranen et al., 2011)) which rely on a hierarchical index structure to maintain stream summaries. Among these algorithms, we are more interested in DenStream, which is computationally efficient and makes no limiting assumption on the shape and number of clusters.

In this paper, we introduce DenDrift as an algorithm for host profiling under concept drift. As input, DenDrift receives a stream of process execution events. Each event in this stream records the number of process executions per host. Since we have thousands of hosts and processes, clustering hosts directly based on the host-process events is computationally intractable, DenDrift generates a host-process matrix for each time interval (with a user-defined duration), and uses non-negative matrix factorization (NMF) (Lee and Seung, 1999) to reduce the dimensionality of that matrix. In this way, the stream of execution events is transformed to a stream of matrices. For clustering this stream, DenDrift relies on DenStream. DenStream is simple, efficient, can generate clusters of arbitrary shape, can effectively detect anomalies, and has demonstrated a good clustering quality. However, experimental studies (Moulton et al., 2018) indicate that this algorithm is not robust against concept drift. In particular, concept drift leads to a decrease in the quality of clusters generated by this algorithm. To overcome this limitation, DenDrift uses the Page-Hinckley Test (PHT) (Mouss et al., 2004) for drift detection, and retrains the DenStream model for drift adaptation.

Our experimental results (see Section 5) affirm that not only DenDrift improves the robustness of DenStream against three prevalent forms of concept drift (i.e. abrupt, gradual and incremental), but also it can effectively distinguish abrupt drifts from outliers. In this paper, we report experiments on both synthetic and real-world data. The real-world data are obtained from the event log files recorded by the detection and response system at F-Secure. To generate synthetic data with controlled concept drift, we have developed a drifted stream generator using Gaussian mixture models. In summary, the contributions of this paper include the following:

•

Elaborating DenDrift as a new algorithm for host profiling, which is robust against abrupt, gradual and incremental drifts and can detect outliers,
•

Introducing a drifted stream generator based on Gaussian mixture models that can simulate concept drift and concept evolution,
•

Explaining the experiments performed on synthetic and industrial datasets, and
•

Discussing about the computational efficiency of DenDrift.

The rest of the paper is organized as follows. Section 2 is dedicated to discussion about the related work. Some background information about DenStream and concept drift is provided in Section 3. An overview of DenDrift is presented in Section 4. The implementation and experiments are detailed in Section 5, and finally some concluding remarks and future directions are pointed out in Section 6.

2. Related Work

The research contributions related to the scope of this paper can be categorized into two groups: (1) algorithms for dimensionality reduction, and (2) concept drift detection methods.

2.1. Dimensionality Reduction

Analyzing high dimensional data is a significant challenge in machine learning. On one hand, recent advances in data collection tools and techniques have led to the generation of huge amounts of data with several dimensions (or features). On the other hand, not all features may be relevant and useful to extract valuable information. Several Dimensionality Reduction (DR) algorithms (Ayesha et al., 2020) have been proposed to eliminate irrelevant features and improve the efficiency and accuracy of the machine learning algorithms processing the collected data.

Principal Component Analysis (PCA) (Jolliffe, 2011) is a well-known and unsupervised DR algorithm whose goal is to discover a set of features referred to as principal components. These features hold the highest variance hence the maximum information. PCA has been applied to several domains (e.g. image and voice processing), and several extensions have been introduced for this algorithm since introduction. Single Value Decomposition (SVD) (Modarresi, 2015) is another DR algorithm closely related to PCA, and specifically developed for matrix factorization. This algorithm transforms the input matrix to two orthogonal and one diagonal matrices. Latent Semantic Analysis (LSA) (Tang et al., 2005) is another DR technique based on SVD, which is typically used for extracting information from text documents.

In this paper we use NMF (Lee and Seung, 1999) for reducing the dimensionality of host-process matrices. NMF is an algorithm for factorizing matrices with non-negative elements, and has been widely applied in several fields such as topic discovery (Shi et al., 2018), age prediction (Varikuti et al., 2018), image clustering (Yang et al., 2018) and speech enhancement (Bando et al., 2018).We prefer NMF to PCA and SVD due to several reasons. It is more suitable for very sparse matrices (as in our case), and we do not need to make any assumption about the missing values. Furthermore, through non-negativity constraints, NMF allows only additive combinations, which makes it capable of learning parts-based representations. All the values recorded in the event log provided by F-Secure are non-negative. Therefore NMF is suitable for reducing the dimensionality of host-process matrices. Last but not the least, NMF has an inherent clustering property (Ding et al., 2005) which make it capable of discovering natural clusters and mislabeled records while PCA and SVD cannot.

2.2. Concept Drift Detection

Concept drift detection is essential to trigger stream adaptation strategies in data stream mining. Several drift detection methods have been proposed recently (Gonçalves Jr et al., 2014). The techniques can be divided into two categories based on their reliance on labeled data: explicit/supervised drift detectors and implicit/unsupervised drift detectors. Explicit drift detectors, which focus on real drifts (as defined in Section 3.1) rely on labeled data to compute performance metrics such as accuracy and F-measure, which they can monitor online over time. They detect a drop in performance and as such, are efficient in signaling drift when it occurs. Implicit drift detectors focus on virtual drifts (as defined in Section 3.1) and rely on properties of the unlabeled data’s feature values to signal deviations. They are prone to false alarms, but their ability to function without labeling makes them useful in applications where labeling is expensive, time-consuming, or not available. Our main focus in this paper is on virtual drifts and unsupervised drift detectors applied to clustering problems.

The OnLIne Drift Detection Algorithm (OLINDDA) uses K-means clustering to continuously monitor and adapt to emerging data distributions (Spinosa et al., 2007). Unknown samples are stored in a short-term memory queue and are periodically clustered and then either merged with existing similar clusters or added as a new cluster to the pool of clusters. When a new cluster forms, it will be considered either a novel concept or a drifted concept depending on the distance between its centroid and the global centroid (i.e. the centroid of centrods). If the distance is less than a given threshold, it’s a drifted concept and a novel concept otherwise. The MINAS algorithm (Faria et al., 2013) is another distance-based method for drift and novelty detection. This algorithm relies on CluStream for stream clustering. CluStream is an incremental extension of K-means. Instead of the distance from the global concept, the distance between the centroid of the newly-formed cluster and the centroid of its nearest cluster is investigated by MINAS for drift and novelty detection. Short distances indicate drift and long ones imply novelty.

In (Zgraja and Woźniak, 2018), the authors propose a solution to improve the robustness of ClusTree (Kranen et al., 2011) against concept drift. ClusTree is a hierarchical stream clustering algorithm that relies on R-trees to maintain a stream summary. The solution proposed in (Zgraja and Woźniak, 2018) relies on the sliding window model and the number of novelties for concept drift detection. In particular, if the new data point doe not belong to any of the micro-clusters live in the current window, it is recognized as a novelty, and we have a concept drift if the quantity of novelties is higher than a given threshold. DriftVis (Yang et al., 2020) is another solution based on sliding windows and distance measurement. In this method, the energy distance between the new data point and the most similar ones is calculated as a measure of concept drift. Gaussian mixture models are used to cluster data over time, and the points (in the latest window) that go to the same cluster with the new data point, are considered most similar to it. A high energy distance is then considered as an indicator of concept drift.

While most of the related work have focused on abrupt drifts (e.g. (Spinosa et al., 2007; Faria et al., 2013; Zgraja and Woźniak, 2018; Yang et al., 2018)), DenDrift can detect also incremental and gradual drifts. DenDrift relies on PHT (Mouss et al., 2004) for drift detection. PHT is a simple and efficient means of change detection. Furthermore, unlike OLINDDA, MINAS and the solution proposed in (Zgraja and Woźniak, 2018), drift detection in DenDrift is independent of the underlying clustering algorithm, which makes DenDrift extensible to other incremental clustering algorithms (e.g. CluStream) as well.

3. Background

3.1. Concept Drift

Assume that we have a stream of data points such that each point $d$ in this stream is defined as a pair $(x,y)$ where $x$ is the feature vector and $y$ is the class label of $d$ . Any change in the statistical properties of $x$ and/or the probability $p(y|x)$ is recognized as a concept drift. If the change occurs only in $p(x)$ without affecting $p(y|x)$ , then the concept drift is called virtual. On the other hand, changes in $p(y|x)$ which may occur with/without changes in $p(x)$ are called real drifts (Gama et al., 2014). In this paper we focus on virtual drifts since there is no class label in the dataset provided by F-Secure. To detect virtual drifts we investigate changes in data mean over time.

Virtual drifts may appear in several forms (Gama et al., 2014; Lemaire et al., 2014). In this paper we focus on three prevalent ones i.e. abrupt/sudden, gradual, and incremental (see Figure 1). In abrupt drift, we see a sudden change in the mean of data points. In other words, a new stable concept replaces the current concept immediately at some point of time. In gradual drift, we see some alternations between the two concepts for a short period of time, and finally some intermediate and temporary concepts appear between the stable concepts in incremental drift.

3.2. DenStream

DenStream (Cao et al., 2006) is an incremental extension of DBSCAN (Ester et al., 1996). DBSCAN is a well-known and density-based algorithm for offline clustering. In the online learning phase, DenStrean arranges the incoming records into micro-clusters such that each micro-cluster includes records whose density is more than the given threshold $\mu$ . In particular, upon the arrival of data record $R$ , DenStream tries to merge it with the nearest micro-cluster $MC$ . $R$ can be merged into $MC$ only if the radius of $MC$ after merging does not exceed the threshold specified by parameter $\epsilon$ . If there is no micro-cluster suitable for merging, then a new micro-cluster will be created for $R$ . To each micro-cluster a weight $w$ is assigned which decreases over time if the micro-cluster does not change. The forgetting rate is specified by parameter $\lambda$ . Micro-clusters are checked periodically and categorized into two groups based on the value of $w$ . The micro-clusters with a high $w$ form the group of potential micro-clusters. The weight of each potential micro-cluster is controlled by parameters $\beta$ and $\mu$ such that the least weight is $\beta\times\mu$ . Upon each request for offline clustering, the potential micro-clusters will be analyzed by DBSCAN to build the final clusters. On the other hand, the low-weight micro-clusters will be considered as outliers and will be removed from the set of final clusters. The lower limit of $w$ for a micro-cluster to be considered as a potential micro-cluster is computed as a function of the checking point and the point of time when the micro-cluster was created.

4. DenDrift

In this section, we elaborate DenDrift as a drift-aware host profiling algorithm. We assume that concept drift has a negative impact on the quality of clustering. In fact, if the incoming data are from a different distribution than the old data, then we expect a degradation in the quality of the generated clusters. Accordingly, we need to continuously monitor the changes in the input data and retrain the underlying cluster model (i.e. reinitialize the set of micro-clusters) if we have more changes than a given threshold. In DenDrift we use DenStream as the stream clustering algorithm and employ PHT and MNF for change detection and dimensionality reduction respectively. As input, DenDrift needs the streams’s dimensionality i.e. number of host latent features ( $N_{f}$ ), change threshold expected by PHT ( $Th_{c}$ ), and the minimum number of changed hosts to be considered as a potential concept drift ( $Th_{d}$ ). DenDrift works in two modes: normal mode where the number of changed hosts is lower than $Th_{d}$ , and change mode where the minimum number of changed hosts is $Th_{d}$ . DenDrift consists of the following steps presented in Algorithm 1:

Input:

N_{f},Th_{c},Th_{d}

1 E = EventLog.getEvents(

t

);

2 M = generateMatrix(E);

3 [W, H] = NMF(M,

N_{f}

);

4 C = 0;

5 if Mode is ”Normal” then

6 foreach $h\in H$ do

7 PrimaryPHT.add(h);

8 if PrimaryPHT.detectedChange( $Th_{c}$ ) then

9 C += 1;

11 end if

13 end foreach

14 if $C\geq Th_{d}$ then

15 Mode = ”Change”;

17 else

18 foreach $h\in H$ do

19 SparePHT.add(h);

21 end foreach

23 end if

25else

26 foreach $h\in H$ do

27 PrimaryPHT.add(h);

28 if PrimaryPHT.detectedChange( $Th_{c}$ ) then

29 C += 1;

31 end if

33 end foreach

34 if $C<Th_{d}$ then

35 Mode = ”Normal”;

36 foreach $h\in H$ do

37 SparePHT.add(h);

38 if SparePHT.detectedChange( $Th_{c}$ ) then

39 C += 1;

41 end if

43 end foreach

45 end if

46 if $C\geq Th_{d}$ then

47 DenStream.reset();

48 PrimaryPHT.reset();

49 SparePHT.reset();

51 end if

53 end if

54DenStream.merge(H);

55 if $t\%T_{p}=0$ then

56 DenStream.prunMicroClusters(

t

);

58 end if

59if clusteringRequested() then

60 DenStream.generateFinalClusters();

62 end if

Algorithm 1 DenDrift

(1)

In the first step (lines 1-3), DenDrift generates a host-process matrix based on the execution counts recorded in the event log on date $t$ for each pair of hosts and processes. Line 3 estimates the latent matrix of hosts by applying NMF to the matrix obtained in line 2. Given a matrix $M=[m_{ij}]\in{\mathbb{R}}^{h\times p}$ , NMF generates two matrices $H=[h_{ij}]\in{\mathbb{R}}^{h\times k}$ and $W=[w_{ij}]\in{\mathbb{R}}^{k\times p}$ such that $M\approx H\times W$ . In other words, NMF tries to minimize the following objective function.

(1) $O=\parallel M-HW\parallel^{2}_{F}$

where $\parallel.\parallel^{2}_{F}$ denotes the Frobenius norm.

In our context, $M$ is the host-process matrix obtained on a specific date $t$ such that each $m_{ij}\in M$ is a non-negative integer value expressing the number of times host $h_{i}$ has executed process $p_{j}$ during the period $[t-1,t)$ . After factorization, we are interested in matrix $H$ which encodes the latent features of hosts.
(2)

In the second step, first we check whether the current mode of DenDrift is normal or change. In the normal mode, first the number of changed hosts is calculated by applying PHT to $H$ (lines 6-11). Host $h$ is then considered changed if PHT detects changes in at least one of the features of the corresponding vector in $H$ . PHT can detect changes in the mean of a one-dimensional stream. Therefore, for each feature we train a distinct instance of PHT. Assume that we are interested to detect changes with a minimal magnitude of $\delta$ and allowed error of $\lambda$ in a one-dimensional stream $s={x_{1},x_{2},...,x_{n}}$ . Then, a PHT instance will alarm whenever $U_{n}-m_{n}\geq\lambda$ or $M_{n}-U_{n}\geq\lambda$ , where $m_{n}=min_{0\leq k\leq n}U_{k}$ and $M_{n}=max_{0\leq k\leq n}U_{k}$ such that $U_{k}$ is estimated using the following Equation.

(2) $U_{k}=\sum_{i=0}^{n}(x_{i}-\delta/2)$

In line 12, the number of changed hosts is compared with $Th_{d}$ . If at least $Th_{d}$ hosts have changed, DenDrift will enter the change mode. Otherwise, a spare PHT will be updated with $H$ . The spare PHT is used to detect outliers (see Figure 1(a)), while the primary one takes part in drift detection. Using two PHTs in parallel makes DenDrift capable of differentiating abrupt drifts from outliers. In the change mode, we continue using the primary PHT to detect the end of the change period (lines 20-25), which happens if the number of changed hosts goes below $Th_{d}$ . In this case, DenDrift enters the normal mode (line 17) and the spare PHT compares $H$ after the change period with $H$ before that. If the spare instance does not recognize a significant change ( $C<Th_{d}$ ), it means that the concept after the change period is similar to the one before that. Therefore, we have an outlier and a drift otherwise. Note that the spare PHT is updated only in the normal mode (lines 14-18), so it can effectively compare the post-change concept with the pre-change concept. If the concepts are different (i.e. we have a concept drift), DenStream and the PHT instances will be reinitialized to learn the new concept (lines 36-38).
(3)

Lines 41-47 express the typical steps in DenStream. First, the current matrix is merged with the micro-clusters (see Algorithm 1 in (Cao et al., 2006)) which are categorized into potential and outlier groups. Then, $t$ is compared with $T_{p}$ (as the minimal time span for pruning micro-clusters), to update the micro-clusters (see Algorithm 2 in (Cao et al., 2006)). Here, the set of potential/outlier micro-clusters gets updated with the current high-/low-weight micro-clusters. At the end and upon a request for offline clustering, DBSCAN will be invoked to extract the final clusters from the potential micro-clusters.

5. Experiments

In this section we assess the performance of DenDrift on both synthetic datasets and datasets generated by applying NMF to the log file provided by F-Secure. Before discussing the experimental results, we provide details about the implementation of DenDrift in Section 5.1. Then we describe the datasets in Section 5.2, and finally we demonstrate the robustness of DenDrift against concept drift in Section 5.3 by comparing the quality of clusters generated by DenDrift with those generated by DenStream.

5.1. Implementation

We have implemented DenDrift using Python 3.8. We utilized the well-known library scikit-learn for implementing DBSCAN and NMF. For PHT we employed the implementation provided in scikit-multiflow. To have a precise control over concept drift in our experiments on synthetic datasets, we implemented a drifted-stream generator. This generator is capable of synthesizing streams with abrupt, gradual or incremental concept drifts using Gaussian mixture models and the Jensen-Shannon distance (Endres and Schindelin, 2003; Fuglede and Topsoe, 2004). In this generator, the stable concepts before and after a drift are modeled as mixture models with one multi-variate normal distribution for each cluster, and the magnitude of the drift is controlled via the Jensen-Shannon distance. The Jensen-Shannon distance is the square root of the Jensen-Shannon divergence (Lin, 1991), and takes a value in $[0,1]$ . The Jensen-Shannon divergence is based on the Kullback–Leibler divergence, which can be used to measure the distance between two probability distributions. The benefit of the Jensen-Shannon divergence over Kullback–Leibler is being symmetric and having always a finite value. we can adjust different aspects of the drifts and clusters generated by the stream generator using the parameters listed in Table 1.

Table 1. Input parameters of the stream generator

$T_{d}$	drift type which could be ”abrupt”, ”gradual” or ”incremental”.
$D_{d}$	drift duration i.e. the number of instances generated between two stable concepts. Each instance includes a constant number of host latent vectors.
$M_{d}$	drift magnitude in terms of the Jensen-Shannon distance.
$P_{d}$	drift precision which indicates the amount of acceptable deviation between the magnitude of the generated drift and the value of $M_{d}$ .
$C_{b}$	number of clusters before drift.
$C_{a}$	number of clusters after drift.
$N_{f}$	number of host latent features.
$S_{i}$	size of each instance which indicates the number of host latent vectors included in each instance.
$N_{b}$	number of instances before drift.

Input:

C_{b},C_{a},M_{d},P_{d}

Output:

Mix_{pre},Mix_{pst}

Mix_{pre}

= genMixModel(

C_{b}

);

2 while true do

Mix_{pst}

= genMixModel(

C_{a}

);

4 Distance = JensenShannon(

Mix_{pre},Mix_{pst}

);

5 if $Distance=M_{d}\pm P_{d}$ then

6 break;

8 end if

10 end while

Algorithm 2 Mixture Model Generation Algorithm

Algorithm 2 presents the steps of generating Gaussian mixture models for stable concepts before and after the simulated drift. Method $genMixModel$ in this algorithm receives the number of clusters as input and samples from a multivariate normal distribution for each cluster. Then the parameters of the underlying mixture model are estimated using a goodness-of-fit test. After estimating the mixture model characterizing the pre-drift concept, we repeatedly generate a new model for the post-drift concept until the distance between the two models has an acceptable deviation from the expected drift magnitude.

The mixture models generated by Algorithm 2 can then used by the drifted-stream generator to synthesize a drifted data stream. The generator uses Algorithm 3 to create each instance of the stream. If the instance belongs to the pre-/post-drift concept, the generator samples from the pre-/post-drift mixture model respectively (lines 1-5). However, if the instance belongs to the time interval between the two concepts and the type of the drift is gradual, the generator chooses one of the concepts randomly such that the probability of choosing the pre-/post-drift concept decreases/increases as we move towards the end of the interval (lines 6-12). In case of an incremental drift, the generator assigns a weight to each mixture model based on the relative time gap between the instance and the pre- and post-drift concepts. Then, it uses that weight to determine the number of latent vectors to sample from each mixture model (lines 13-20).

As an illustrative example, assume that we have 200 hosts and want to divide them into two clusters, Figure 2(a) shows the clusters generated by the drifted-stream generator before applying concept drift. The impact of an abrupt drift (i.e. $D_{d}=0$ ) with a magnitude of $M_{d}=0.6$ on these clusters is reflected in Figure 2(b). Figure 2(c) shows another case where the number of clusters changes after concept drift (i.e. we have concept evolution), and finally Figure 2(d) shows the case without any change in the number of clusters but with a lower drift magnitude.

Input:

Stream,Mix_{pre},Mix_{pst},T_{d},D_{d}

Size_{s}=|Stream|

;

2 if $Size_{s}<N_{b}$ then

3 Inst =

Mix_{pre}

.sample(

S_{i}

);

5 else if $Size_{s}\geq N_{b}+D_{d}$ then

6 Inst =

Mix_{pst}

.sample(

S_{i}

);

8 else if $T_{d}$ = ”gradual” then

9 Rnd = random(0,1);

10 if $Rnd<(Size_{s}-N_{b})/D_{d}$ then

11 Inst =

Mix_{pst}

.sample(

S_{i}

);

13 else

14 Inst =

Mix_{pre}

.sample(

S_{i}

);

16 end if

18 else

Weight=(Size_{s}-N_{b})/D_{d}

;

Size_{pre}=(1-Weight)\times S_{i}

;

Size_{pst}=Weight\times S_{i}

;

Inst_{pre}=Mix_{pre}.sample(Size_{pre})

;

Inst_{pst}=Mix_{pst}.sample(Size_{pst})

;

Inst=Inst_{pre}\cup Inst_{pst}

;

26 end if

27Stream.add(Inst);

Algorithm 3 Instance Generation Algorithm

5.2. Datasets

We conducted experiments on both synthetic datasets generated using the drifted stream generator presented in Section 5.1 and two datasets generated by applying NMF to the event log provided by F-Secure.

5.2.1. F-Secure Datasets

The F-Secure event log includes events recorded over a 3-month period (i.e. 92 days). Each record is a tuple of the form (host_id, process_name, date, count), where count indicates the number of times the process with identifier process_name (hashed for rare processes) is executed by the host with hashed identifier host_id on the date specified by date. This log file includes data recorded for approximately 2000 hosts and 1,000,000 processes. We partitioned this log file by date, such that each partition included data recorded for a single day. Then we applied NMF to each partition to obtain the host latent vectors for the corresponding day. To be able to analyze the potential influence of the number of latent features on the performance of DenDrift, We considered two cases regarding the number of latent features for each host. One case with two and another with 10 latent features. At the end, we had two datasets consisting of 92 data instances. Each instance was a matrix with $N_{h}$ rows and two or 10 columns such that $N_{h}\approx 2000$ denotes the number of hosts. These datasets were label-less. To facilitate comparing the quality of clusters obtained by DenDrift with those found by DenStream, we utilized the inherent clustering property of NMF (Ding et al., 2005) and assigned the index of the feature with the maximum value as a class label to each row of these datasets.

5.2.2. Synthetic Datasets

We generated three synthetic datasets corresponding to the three forms of concept drift investigated in this paper (i.e. abrupt, gradual and incremental). Each of the synthetic datasets includes 100 instances with the same number of rows as the F-Secure datasets, and with two columns. In contrast to the F-Secure datasets, we know exactly the location, type and duration of concept drifts in the synthetic datasets. Furthermore, we have access to the ground truth (i.e. the correct label of each row), since we know which multi-variate normal distribution is used to generate each row. For all synthetic datasets, we considered two as the number of clusters before concept drift ( $C_{b}=2$ ), and we inserted a concept drift with magnitude $M_{d}=0.6$ in the 50th instance, such that the duration of gradual and incremental drifts was set to 10 ( $D_{d}=10$ ), and the minimum number of changed hosts to consider as a drift was 50 meaning that $Th_{d}\approx 0.03$ .

5.3. Observations

5.3.1. Synthetic Datasets

Figures 3(a)-3(c) show the number of changes detected by DenDrift in each synthetic dataset. The start and end points of concept drift are highlighted by a diamond, and the start/end points detected by DenDrift are indicated be a dashed line. According to these results, DenDrift can detect the three forms of concept drift with a short delay. In these experiments, we configured DenStream with $\lambda=0.1$ , $\epsilon=0.5$ , $\beta=0.8$ and $\mu=3$ . The impact of retraining (after drift detection) on the accuracy of clustering is demonstrated in Figures 4(a)-4(c). Accordingly, compared to DenStream, DenDrift is more robust against concept drift. In particular, we see a considerable degradation in the accuracy of DenStream due to concept drift. Even in some cases, (e.g. Figure 4(c)), the accuracy of DenStream stays very low after concept drift. On the contrary, DenDrift can recover quickly.

In the above experiments, we assumed that the number of clusters would not change due to concept drift. However, we also did experiments on cases with evolving concepts, where we had a different number of clusters before and after drift. Since the drift detection mechanism in DenDrift is independent of the number of clusters and clustering mechanism, any change in the number of clusters would not have a negative impact on the detection performance of DenDrift. As shown in Figure 5(a), DenDrift can effectively detect concept drift in spite of concept evolution. In this example, we have a gradual drift with a duration of 20 ( $D_{d}=20$ ) such that the number of cluster increases from two to four after the concept drift. Furthermore, Figures 5(b) and 5(c) compare the accuracy of DenDrift with DenStream in cases that we have an increase or decrease in the number of clusters respectively. In both cases, DenDrift has a better performance.

5.3.2. F-Secure Datasets

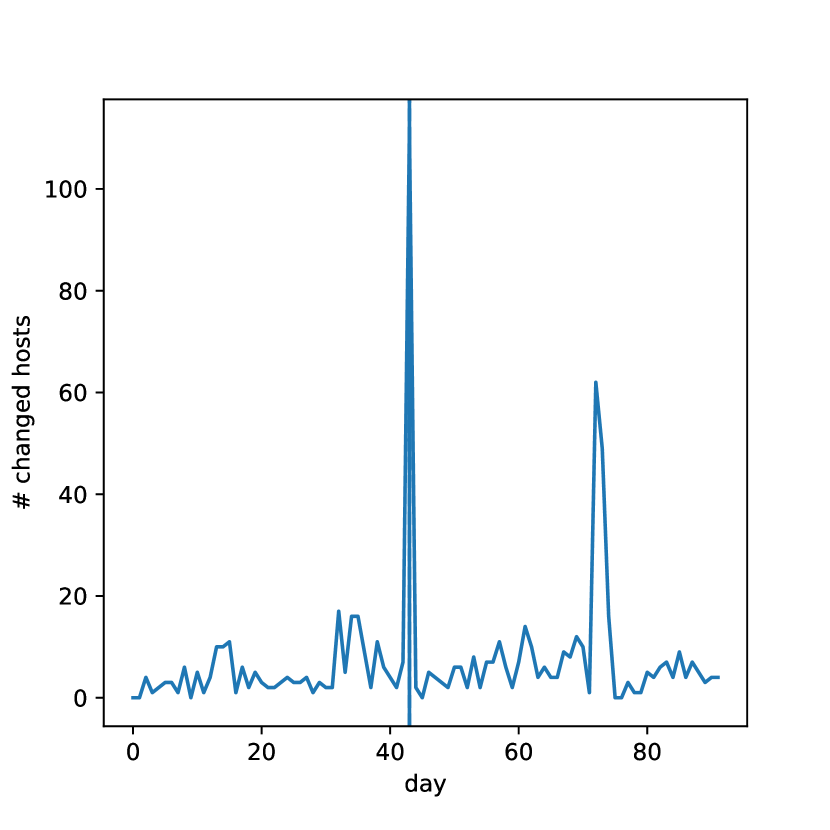
Figure 6 reports the results of the experiments performed on the F-Secure datasets. Accordingly, DenDrift has detected an abrupt drift on day 43 in both cases. In particular, more than 100 hosts have found to be changed on this day irrespective of the number of latent features. We found that this change was related to a pilot testing which was started a few days before and led to a change in the behavior of the employed hosts. As Figures 6(c)-6(d) demonstrate, this change did not have a significant negative impact on the quality of clusters. However, retraining DenStream for the new concept, improved its accuracy by approximately 10%. Another fact worth mentioning is the outlier detected on day 72 for the dataset with 10 latent features (Figure 6(b)). In particular, DenDrift detected a sudden change in more than 150 hosts. However, this change was not a true concept drift rather a temporary change (or an outlier). Since a temporary change does not change the concept (statistical properties), it is not necessary to retrain DenStream. In these experiments, we configured DenStream with $\lambda=\epsilon=0.1$ , $\beta=1$ and $\mu=9$ .

The results presented in Figure 6 highlight that the number of changed hosts may potentially differ depending on the number of latent features (i.e. $N_{f}$ ), and the thresholds for change and drift (i.e. $Th_{c}$ and $Th_{d}$ in Algorithm 1. Apparently, if we have very low thresholds, DenDrift may enter the change mode more frequently. However, the capability of DenDrift to distinguish drifts from outliers, would avoid false positives and unnecessary retrainings in most cases. Another fact worth discussion is the impact of $N_{f}$ on the efficiency and accuracy of NMF and hence DenDrift. If we pick a too small/large value, we would end up with underfitting/overfitting in the NMF model. We did an experiment on NMF regarding the relation between $N_{f}$ and both the efficiency and accuracy of factorization. In this experiment, we considered 200 as the maximum number of iterations until convergence. We observed that increasing the number of latent features would decrease reconstruction error (or increase factorization accuracy) and may also increase the execution overhead of NMF (see Figure 7). Reconstruction error measures the difference between the input host-process matrix $M$ and $W\times H$ , where $W$ and $H$ are the matrices generated by NMF in DenDrift (line 3 in Algorithm 1). Figure 7 indicates that 20 is an optimal choice for the F-Secure data if we take into account only the efficiency and accuracy of NMF. We performed another experiment to assess the impact of $N_{f}$ on the overall execution overhead of DenDrift. Figure 8 shows the relation between $N_{f}$ and both the overhead of NMF and the total execution time of DenDrift for processing one host-process matrix. Accordingly, in all cases the time spent for drift detection and clustering is negligible in comparison to the delay imposed by NMF, and the NMF computations may take more than five minutes due to the delay in convergence.

6. Concluding Remarks

In this paper, we presented DenDrift as a drift-aware algorithm for host profiling. DenDrift is an extension of an incremental clustering algorithm called DenStream and relies on Page-Hinckley test for concept drift detection. Furthermore, we have developed a concept drift simulator which can generate drifted streams with a user-defined dimensionality, duration and drift magnitude. Three prevalent forms of concept drift are supported by this simulator (i.e. abrupt, gradual and incremental), which can be injected at a user-defined point in the stream. Our experimental results indicate that DenDrift can detect and adapt to abrupt, gradual and incremental drifts in synthetic streams generated by our simulator. Furthermore, our experiments on real-world data with an abrupt drift also confirm the effectiveness of DenDrift for drift detection and adaptation. Furthermore, our experiments on high-dimensional streams indicate that DenDrift can effectively distinguish between drifts and outliers (or temporary changes), and avoid unnecessary retraining. DenDrift is principally an extension of DenStream, but the drift detection mechanism is independent of the clustering mechanism. Therefore, it is easy to use other algorithms (e.g. CluStream and StreamKM++) as the underlying clustering algorithm in DenDrift. Doing further experiments on those algorithms is considered as future work.

Acknowledgements.

This work was carried out during the tenure of an ERCIM ‘Alain Bensoussan’ Fellowship Program and has been partially supported and funded by the ITEA3 European IVVES project.

References

(1)
Ackermann et al. (2012) Marcel R Ackermann, Marcus Märtens, Christoph Raupach, Kamil Swierkot, Christiane Lammersen, and Christian Sohler. 2012. Streamkm++ a clustering algorithm for data streams. Journal of Experimental Algorithmics (JEA) 17 (2012), 2–1.
Aggarwal et al. (2003) Charu C Aggarwal, S Yu Philip, Jiawei Han, and Jianyong Wang. 2003. A framework for clustering evolving data streams. In Proceedings 2003 VLDB conference. Elsevier, 81–92.
Amini et al. (2012) Amineh Amini, Teh Ying Wah, and Ying Wah Teh. 2012. DENGRIS-Stream: A density-grid based clustering algorithm for evolving data streams over sliding window. In Proc. international conference on data mining and computer engineering. 206–210.
Ayesha et al. (2020) Shaeela Ayesha, Muhammad Kashif Hanif, and Ramzan Talib. 2020. Overview and comparative study of dimensionality reduction techniques for high dimensional data. Information Fusion 59 (2020), 44–58.
Bando et al. (2018) Yoshiaki Bando, Masato Mimura, Katsutoshi Itoyama, Kazuyoshi Yoshii, and Tatsuya Kawahara. 2018. Statistical speech enhancement based on probabilistic integration of variational autoencoder and non-negative matrix factorization. In 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). IEEE, 716–720.
Cao et al. (2006) Feng Cao, Martin Estert, Weining Qian, and Aoying Zhou. 2006. Density-based clustering over an evolving data stream with noise. In Proceedings of the 2006 SIAM international conference on data mining. SIAM, 328–339.
Chen and Tu (2007) Yixin Chen and Li Tu. 2007. Density-based clustering for real-time stream data. In Proceedings of the 13th ACM SIGKDD international conference on Knowledge discovery and data mining. 133–142.
Ding et al. (2005) Chris Ding, Xiaofeng He, and Horst D Simon. 2005. On the equivalence of nonnegative matrix factorization and spectral clustering. In Proceedings of the 2005 SIAM international conference on data mining. SIAM, 606–610.
Endres and Schindelin (2003) Dominik Maria Endres and Johannes E Schindelin. 2003. A new metric for probability distributions. IEEE Transactions on Information theory 49, 7 (2003), 1858–1860.
Ester et al. (1996) Martin Ester, Hans-Peter Kriegel, Jörg Sander, Xiaowei Xu, et al. 1996. A density-based algorithm for discovering clusters in large spatial databases with noise.. In Kdd, Vol. 96. 226–231.
Faria et al. (2013) Elaine R Faria, João Gama, and André CPLF Carvalho. 2013. Novelty detection algorithm for data streams multi-class problems. 795–800.
Fuglede and Topsoe (2004) Bent Fuglede and Flemming Topsoe. 2004. Jensen-Shannon divergence and Hilbert space embedding. In International Symposium onInformation Theory, 2004. ISIT 2004. Proceedings. IEEE, 31.
Gama et al. (2014) João Gama, Indrė Žliobaitė, Albert Bifet, Mykola Pechenizkiy, and Abdelhamid Bouchachia. 2014. A survey on concept drift adaptation. ACM computing surveys (CSUR) 46, 4 (2014), 1–37.
Gonçalves Jr et al. (2014) Paulo M Gonçalves Jr, Silas GT de Carvalho Santos, Roberto SM Barros, and Davi CL Vieira. 2014. A comparative study on concept drift detectors. Expert Systems with Applications 41, 18 (2014), 8144–8156.
Jolliffe (2011) Ian Jolliffe. 2011. Principal Component Analysis. Springer Berlin Heidelberg, Berlin, Heidelberg, 1094–1096. https://doi.org/10.1007/978-3-642-04898-2_455
Kranen et al. (2011) Philipp Kranen, Ira Assent, Corinna Baldauf, and Thomas Seidl. 2011. The ClusTree: indexing micro-clusters for anytime stream mining. Knowledge and information systems 29, 2 (2011), 249–272.
Lee and Seung (1999) Daniel D Lee and H Sebastian Seung. 1999. Learning the parts of objects by non-negative matrix factorization. Nature 401, 6755 (1999), 788–791.
Lemaire et al. (2014) Vincent Lemaire, Christophe Salperwyck, and Alexis Bondu. 2014. A survey on supervised classification on data streams. In European Business Intelligence Summer School. Springer, 88–125.
Lin (1991) Jianhua Lin. 1991. Divergence measures based on the Shannon entropy. IEEE Transactions on Information theory 37, 1 (1991), 145–151.
Modarresi (2015) Kourosh Modarresi. 2015. Unsupervised feature extraction using singular value decomposition. Procedia computer science 51 (2015), 2417–2425.
Moulton et al. (2018) Richard Hugh Moulton, Herna L Viktor, Nathalie Japkowicz, and João Gama. 2018. Clustering in the presence of concept drift. In Joint European Conference on Machine Learning and Knowledge Discovery in Databases. Springer, 339–355.
Mouss et al. (2004) Hayet Mouss, D Mouss, N Mouss, and L Sefouhi. 2004. Test of page-hinckley, an approach for fault detection in an agro-alimentary production system. In 2004 5th Asian Control Conference (IEEE Cat. No. 04EX904), Vol. 2. IEEE, 815–818.
Ren and Ma (2009) Jiadong Ren and Ruiqing Ma. 2009. Density-based data streams clustering over sliding windows. In 2009 Sixth international conference on fuzzy systems and knowledge discovery, Vol. 5. IEEE, 248–252.
Shi et al. (2018) Tian Shi, Kyeongpil Kang, Jaegul Choo, and Chandan K Reddy. 2018. Short-text topic modeling via non-negative matrix factorization enriched with local word-context correlations. In Proceedings of the 2018 World Wide Web Conference. 1105–1114.
Spinosa et al. (2007) Eduardo J Spinosa, André Ponce de Leon F. de Carvalho, and João Gama. 2007. Olindda: A cluster-based approach for detecting novelty and concept drift in data streams. In Proceedings of the 2007 ACM symposium on Applied computing. 448–452.
Tang et al. (2005) Bin Tang, Michael Shepherd, Evangelos Milios, and Malcolm I Heywood. 2005. Comparing and combining dimension reduction techniques for efficient text clustering. In Proceeding of SIAM international workshop on feature selection for data mining. Citeseer, 17–26.
Varikuti et al. (2018) Deepthi P Varikuti, Sarah Genon, Aristeidis Sotiras, Holger Schwender, Felix Hoffstaedter, Kaustubh R Patil, Christiane Jockwitz, Svenja Caspers, Susanne Moebus, Katrin Amunts, et al. 2018. Evaluation of non-negative matrix factorization of grey matter in age prediction. NeuroImage 173 (2018), 394–410.
Yang et al. (2020) Weikai Yang, Zhen Li, Mengchen Liu, Yafeng Lu, Kelei Cao, Ross Maciejewski, and Shixia Liu. 2020. Diagnosing concept drift with visual analytics. In 2020 IEEE Conference on Visual Analytics Science and Technology (VAST). IEEE, 12–23.
Yang et al. (2018) Zuyuan Yang, Yu Zhang, Yong Xiang, Wei Yan, and Shengli Xie. 2018. Non-negative matrix factorization with dual constraints for image clustering. IEEE Transactions on Systems, Man, and Cybernetics: Systems 50, 7 (2018), 2524–2533.
Zgraja and Woźniak (2018) Jakub Zgraja and Michał Woźniak. 2018. Drifted data stream clustering based on ClusTree algorithm. In International Conference on Hybrid Artificial Intelligence Systems. Springer, 338–349.