Delving into Probabilistic Uncertainty for
Unsupervised Domain Adaptive Person Re-identification
Abstract
Clustering-based unsupervised domain adaptive (UDA) person re-identification (ReID) reduces exhaustive annotations. However, owing to unsatisfactory feature embedding and imperfect clustering, pseudo labels for target domain data inherently contain an unknown proportion of wrong ones, which would mislead feature learning. In this paper, we propose an approach named probabilistic uncertainty guided progressive label refinery (P2LR) for domain adaptive person re-identification. First, we propose to model the labeling uncertainty with the probabilistic distance along with ideal single-peak distributions. A quantitative criterion is established to measure the uncertainty of pseudo labels and facilitate the network training. Second, we explore a progressive strategy for refining pseudo labels. With the uncertainty-guided alternative optimization, we balance between the exploration of target domain data and the negative effects of noisy labeling. On top of a strong baseline, we obtain significant improvements and achieve the state-of-the-art performance on four UDA ReID benchmarks. Specifically, our method outperforms the baseline by 6.5% mAP on the Duke2Market task, while surpassing the state-of-the-art method by 2.5% mAP on the Market2MSMT task. Code is available at: https://github.com/JeyesHan/P2LR.
Introduction
Person re-identification (ReID) aims to retrieve all images of the target person from non-overlapping camera views. It has broad applications in smart retail, searching missing children, and other person related scenarios. Although existing deep learning methods (Zhang, Zhang, and Liu 2021; Isobe et al. 2020; Luo et al. 2019; Guo et al. 2019; Hermans, Beyer, and Leibe 2017) have achieved remarkable performance, these methods rely heavily on manual annotations. Furthermore, they fail to generalize on other datasets when domain gap between the source and target domain exists. To address this critical issue, UDA person ReID where labeled source images and unlabeled target images are presented has attracted great attention in recent years.
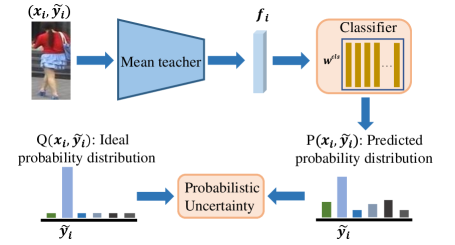
UDA person ReID methods include domain transfer based methods (Huang et al. 2020b; Ge et al. 2020; Deng et al. 2018; Wei et al. 2018; Zhong et al. 2018), ranking based methods (Zhong et al. 2019; Wang et al. 2020; Yu et al. 2019), and clustering based methods (Fan et al. 2018; Lin et al. 2019; Fu et al. 2019; Ge, Chen, and Li 2020; Zhai et al. 2020b). In general, clustering based methods can obtain superior performance. Typically, clustering based methods consist of three stages, i.e., i) pre-training with labeled source domain images, ii) generating pseudo labels for target domain images by clustering, and iii) fine-tuning with target domain images. The first stage is conducted only once and the latter two stages are repeated several times for mutual promotion. However, owing to unsatisfactory feature embedding and imperfect clustering quality, we are supposed to tackle an unknown proportion of wrong pseudo labels. On one hand, such noisy labels inherent with cross-domain pseudo labeling would mislead the network optimization in the fine-tuning stage. On the other hand, the negative effects caused by wrong pseudo labels will propagate and amplify as the training procedure proceeds. Therefore, it is crucial to identify wrong pseudo labels and alleviate the uncertainty of pseudo labeling to promote the UDA person ReID.
This paper addresses two key issues for clustering-based methods: 1) how to identify the wrong pseudo labels. 2) how to reduce the negative effects of wrongly-labeled samples in optimization. For the first issue, we observe that the probability distribution among identities of wrong-labeled samples is significantly different from that of samples with correct pseudo labels. Samples with correct pseudo labels are explicit, reaching high in the corresponding true identity and remain close to zero in other identities. In contrast, samples with wrong pseudo labels are ambiguous, with several peaks in several other identities. This obvious difference inspires us to model the probabilistic uncertainty by measuring the inconsistency between the predicted and ideal distributions of pseudo labels (Figure 1). For the second issue, we propose a probabilistic uncertainty guided progressive label refinery framework and solve it by Alternative Convex Search (Gorski, Pfeuffer, and Klamroth 2007). We alternatively include samples with high credibility and minimize the uncertainty of selected samples to boost the performance of domain adaptive person ReID.
Our main contributions can be summarized as follows:
-
•
We propose to measure the probabilistic uncertainty of pseudo labels for UDA person ReID. A quantitative criterion that estimates the probabilistic distance of the predicted distribution of samples against ideal ones, is established to serve as the standard for eliminating wrongly-labeled samples.
-
•
We propose a framework named Probabilistic uncertainty guided Progressive Label Refinery (P2LR) to determine and purify wrong labels of target domain samples for UDA person ReID.
-
•
We conduct extensive experiments and achieve the state-of-the-art performance on four benchmark datasets. P2LR outperforms the baseline by 6.5% mAP on the Duke2Market task and surpasses the state-of-the-art method by 2.5% mAP on the Market2MSMT task.

Related Work
UDA person ReID. To save exhaustive annotations, unsupervised domain adaptation (UDA) (Wei et al. 2021; Isobe et al. 2021; Cui et al. 2020; Gong et al. 2019) makes models trained on source domain adapt to target domain. Existing UDA ReID methods can be divided into three categories, i.e., domain transfer based methods, ranking based methods, and clustering based methods.
Domain transfer based methods (Huang et al. 2020b; Ge et al. 2020) leverage style-transfer techniques to transfer source images into target domain. Then the transferred images with inherited labels are utilized to fine-tune the model pre-trained on source domain. SPGAN (Deng et al. 2018) and PTGAN (Wei et al. 2018) use GANs to transform source-domain images to match the image styles of the target domain. HHL (Zhong et al. 2018) proposes to learn camera-invariant embeddings via transforming images according to target camera styles. However, the image generation quality is still unsatisfactory and the information of target domain is not fully explored because target domain images are only used for providing style supervision signals.
Ranking based methods build positive and negative sample pairs and use the contrastive loss to optimize neural networks with soft labels on the target domain. ECN (Zhong et al. 2019) builds a memory bank to store seen features. Exemplar, camera, and neighborhood invariance are modeled by pair learning with features in the memory bank. Wang et al. (Wang et al. 2020) use memory bank to mine hard negative instances across batches. MAR (Yu et al. 2019) exploits a set of reference persons to generate multiple soft labels. However, the constructed image pairs or feature pairs lacks global guidance over all identities. Additionally, the reference images or features might be outliers in some cases which mislead the feature learning.
Clustering based methods obtain superior performance to domain transfer based and ranking based methods to date. Clustering methods generate pseudo labels through clustering and then fine-tune models with generated pseudo labels. Fan et al. (Fan et al. 2018) propose to alternatively assign labels for unlabeled training samples and optimize the network with the generated targets. BUC (Lin et al. 2019) proposes a bottom-up clustering framework to gradually group similar clusters. SSG (Fu et al. 2019) employs both global body and local body part features for clustering and evaluation. DAAM (Huang et al. 2020a) introduces domain alignment constraints and an attention module. MMT (Ge, Chen, and Li 2020) introduces two sibling mutual mean teachers. MEB-Net (Zhai et al. 2020b) establishes three networks to perform mutual mean learning. However, these methods ignore noisy/wrong labels generated by clustering methods, which hinders the advancement of these approaches.
Pseudo label evaluation. Wrong pseudo label samples harm learning robust feature embedding for neural networks. To quantify and identify the correctness of pseudo labels, pseudo label evaluation becomes significantly crucial. Kendall et al. (Kendall and Gal 2017) and Chang et al. (Chang et al. 2020) establish an end-to-end framework to measure the observation noise and alleviate the negative influence for better network optimization. Zheng et al. (Zheng and Yang 2021) propose to estimate the correctness of predicted pseudo labels in semantic segmentation. As for clustering-based UDA person ReID, EUG (Wu et al. 2019), UNRN (Zheng et al. 2021a), and GLT (Zheng et al. 2021b) are uncertainty based methods. EUG employs the distance between samples and clustering centroids in feature space to determine the reliability of samples. UNRN measures the output consistency between mean teacher and student models as uncertainty, while we model the distribution of single-model clusters and measure the probabilistic distance to an ideal distribution as the uncertainty. GLT is a group-aware label transfer framework to explicitly correct noisy labels while we pick reliable pseudo labels to train the model progressively, which further correct noisy labels implicitly.
Methodology
Notation. The goal of UDA person ReID is to adapt the trained model from a source domain to an unsupervised target domain , where and denote the number of samples in the source and target domains, respectively. and denote the sample and its attached label in the source domain with supervisory information. denotes the sample in target domain without supervision. The pseudo label generated by clustering for sample in target is denoted as .
Figure 2 shows an overview of our proposed P2LR framework for UDA person ReID. We first construct a clustering baseline with mutual mean teachers (Ge, Chen, and Li 2020). On top of the baseline, we introduce the probabilistic uncertainty guided progressive label refinery to evaluate the noisy level of pseudo labels and reduce the negative influence of noisy samples. In the following parts, we first introduce the clustering baseline, and then elaborate on the label uncertainty modeling based on probabilistic uncertainty and the proposed P2LR framework.
Recap Clustering Baseline
We construct a clustering-based pipeline based on MMT (Ge, Chen, and Li 2020) for UDA person ReID. Following the general pipeline of clustering-based methods, three stages are consisted, such as: source-domain model pre-training, clustering, and target-domain fine-tuning. In the source pre-training stage, two sibling networks are established with the same architecture. They are initialized with different random seeds, trained with the same data yet experienced different data augmentations to reduce the dependence. The networks are optimized by the identity loss and triplet loss . In the clustering stage, pseudo labels for target-domain data are generated by clustering. In the target fine-tuning stage, two mean teachers and are established with the exponential moving average of student models over iterations. The prediction of one teacher model is taken as soft labels to mutually supervise the training of the other student. Apart from the identification and triplet loss with hard pseudo labels provided by clustering, each model is also guided by the Kullback–Leibler (KL) divergence loss and soft triplet loss with the soft labels.
The whole loss function in the fine-tuning stage is as:
| (1) |
where , , indicate corresponding loss weights.

Probabilistic Uncertainty Modeling
For clustering-based UDA person ReID, the pseudo labels are noisy, which would mislead the network training in the target fine-tuning stage and hurt the performance in target domain. To reduce the effects of noise, uncertainty estimation is a natural way to eliminate the unreliable pseudo labels. To establish the uncertainty criterion, we present the output probabilistic distribution of samples with correct and wrong labels for an investigative study. As shown in Figure 3a, the sample with wrong pseudo labels is associated with high probabilistic uncertainty, which has several peaks and generally reaches high in different identities. In contrast, the sample with correct pseudo labels is associated with low probabilistic uncertainty (Figure 3b). The assigned probability peaks high in the correct identity and remains nearly zero in other identities. This is consistent with the intuitive idea that the samples with wrong pseudo labels are ambiguous for model prediction, which is significantly distinct to correct pseudo labels.
Inspired by this observation, we leverage the distribution difference as the probabilistic uncertainty to softly evaluate the noisy level of samples. Each unlabeled sample in the target domain is assigned with a pseudo label by clustering. Based on the clustering at -th step, we build an external classifier , where is the parameterized weights of the external classifier. Note that the weights are generated dynamically and don’t need separate training. Here we employ cluster centroids of dimensions as classifier weights. For a feature of sample extracted by the mean teacher, we obtain classified probability distributions among identities with this classifier following Eq.2. Here is the temperature parameter.
| (2) |
In source domain, we obtain a single impulse distribution for samples after symmetrically arranging the probability from large to small while making as the center. This phenomenon motivates us to model the generalized ideal distributions for samples in the target domain. We find that the smoothed distribution associative with large temperature is highly stable and insensitive to specific datasets. When decreases ( controls the variety of distributions), another distribution might be better for some cases but hard to generalize. Therefore, we draw the smoothed distribution (Eq.LABEL:eq:qfunc) as the ideal distribution .
| (3) |
where is the identity index and is the number of identities (i.e. the number of clusters). is a hyperparameter and is set to 0.99.
We estimate the probabilistic distance of the predicted probability across identities and the ideal distribution to measure the uncertainty of samples. Rather than measuring the feature inconsistency of teacher-student models (Zheng et al. 2021a), we define a criterion named probabilistic uncertainty, which measures the inconsistency between predicted distribution and the ideal distribution . Moreover, we leverage the Kullback–Leibler (KL) divergence to measure the inconsistency and establish the probabilistic uncertainty as:
| (4) |
Larger indicates that the pseudo label generated by clustering is more likely to be wrong, which should be excluded in the target fine-tuning stages. As in Figure 3c, our probabilistic uncertainty is highly related to correctness.
Uncertainty Guided Alternative Optimization
We formulate the uncertainty guided domain adaption mathematically. The model can be denoted as , where is the associated parameters. Each model maps a sample to the prediction . An uncertainty score can be further obtained, as . is the label uncertainty estimation module. The uncertainty guided learning can be formulated as a joint optimization problem as:
| (5) |
where is the indicator for sample selection. is the age parameter to control the learning pace. That is, we need to reduce the overall uncertainty of select samples while selecting as many samples as possible for sufficient training. To optimize the above objective function, we adopt Alternative Convex Search (Gorski, Pfeuffer, and Klamroth 2007). In particular, and are alternatively optimized while fix the other. With the fixed , the global optimum is solved as:
| (6) |
When is fixed, the global optimum is solved as:
| (7) |
The two optimization steps are iteratively conducted, while is gradually increased to add more harder samples.
Uncertainty guided sample selection. With the proposed uncertainty measurement, the solution for Eq.7 is provided by gradient descent based network training. With fixed , finding the optimal is converted into a combinatorial optimization issue with the linear objective function. We can simply derive the global minimum by setting the partial derivative of Eq.6 to as zero. Considering is either 0 or 1, we obtain the close-formed solution as:
| (8) |
Since clustering and target fine-tuning stages are iterated in an alternative way for multiple steps, we need to determine how many samples are included. A sequence is predefined for this purpose, where is the number of selected examples at iteration time . Based on the predefined , the threshold is dynamically updated according to Eq.9 to ensure exactly samples are assigned with non-zero .
| (9) |
Note that as the training proceeds, the models become more reliable. Consequently, the measured uncertainty reduces drastically at the beginning, then converges slowly with larger (Figure 4(left)). As the result, should be enlarged as increases. To be consistent with the trends of uncertainty reduction, we design as a rescaled logarithm-exponential function:

| (10) |
is the initial proportion of samples for fine-tuning in target domain. The setting of enables the model to learn from sufficient easy samples at early steps, to avoid falling into the negative loop of degrading. is the hyper-parameter to control the increasing rate of samples (Figure 4(right)). Because the rate of adding examples is negatively correlated to the size of the current training set, the number of newly added examples is reduced as the training proceeds. More importantly, the uncertainty decreases dramatically when is small, we enlarge the set of samples in a fast way. As increases, the uncertainty converges and the set of samples for fine-tuning increases slowly for stable training. This progressive label refinery would help the model learn sufficiently from the newly added samples in target domain.
| Methods | DukeMTMCMarket1501 | Market1501DukeMTMC | ||||||
|---|---|---|---|---|---|---|---|---|
| mAP | R1 | R5 | R10 | mAP | R1 | R5 | R10 | |
| ATNet (Liu et al. 2019)(CVPR’19) | 25.6 | 55.7 | 73.2 | 79.4 | 24.9 | 45.1 | 59.5 | 64.2 |
| SPGAN+LMP (Deng et al. 2018)(CVPR’18) | 26.7 | 57.7 | 75.8 | 82.4 | 26.2 | 46.4 | 62.3 | 68.0 |
| BUC (Lin et al. 2019) (AAAI’19) | 38.3 | 66.2 | 79.6 | 84.5 | 27.5 | 47.4 | 62.6 | 68.4 |
| ECN (Zhong et al. 2019) (CVPR’19) | 43.0 | 75.1 | 87.6 | 91.6 | 40.4 | 63.3 | 75.8 | 80.4 |
| PDA-Net (Li et al. 2019) (ICCV’19) | 47.6 | 75.2 | 86.3 | 90.2 | 45.1 | 63.2 | 77.0 | 82.5 |
| PCB-PAST (Zhang et al. 2019) (ICCV’19) | 54.6 | 78.4 | - | - | 54.3 | 72.4 | - | - |
| SSG (Fu et al. 2019) (ICCV’19) | 58.3 | 80.0 | 90.0 | 92.4 | 53.4 | 73.0 | 80.6 | 83.2 |
| ACT (Yang et al. 2020) (AAAI’20) | 60.6 | 80.5 | - | - | 54.5 | 72.4 | - | - |
| MPLP (Wang and Zhang 2020) (CVPR’20) | 60.4 | 84.4 | 92.8 | 95.0 | 51.4 | 72.4 | 82.9 | 85.0 |
| DAAM (Huang et al. 2020a) (AAAI’20) | 67.8 | 86.4 | - | - | 63.9 | 77.6 | - | - |
| AD-Cluster (Zhai et al. 2020a) (CVPR’20) | 68.3 | 86.7 | 94.4 | 96.5 | 54.1 | 72.6 | 82.5 | 85.5 |
| MMT (Ge, Chen, and Li 2020) (ICLR’20) | 71.2 | 87.7 | 94.9 | 96.9 | 65.1 | 78.0 | 88.8 | 92.5 |
| NRMT (Zhao et al. 2020)(ECCV’20) | 71.7 | 87.8 | 94.6 | 96.5 | 62.2 | 77.8 | 86.9 | 89.5 |
| B-SNR+GDS-H (Jin et al. 2020)(ECCV’20) | 72.5 | 89.3 | - | - | 59.7 | 76.7 | - | - |
| MEB-Net (Zhai et al. 2020b)(ECCV’20) | 76.0 | 89.9 | 96.0 | 97.5 | 66.1 | 79.6 | 88.3 | 92.2 |
| UNRN (Zheng et al. 2021a) (AAAI’21) | 78.1 | 91.9 | 96.1 | 97.8 | 69.1 | 82.0 | 90.7 | 93.5 |
| GLT (Zheng et al. 2021b)(CVPR’21) | 79.5 | 92.2 | 96.5 | 97.8 | 69.2 | 82.0 | 90.2 | 92.8 |
| P2LR (Ours) | 81.0 | 92.6 | 97.4 | 98.3 | 70.8 | 82.6 | 90.8 | 93.7 |
| Methods | Marke1501MSMT17 | DukeMTMCMSMT17 | ||||||
|---|---|---|---|---|---|---|---|---|
| mAP | R1 | R5 | R10 | mAP | R1 | R5 | R10 | |
| ECN (Zhong et al. 2019) (CVPR’19) | 8.5 | 25.3 | 36.3 | 42.1 | 10.2 | 30.2 | 41.5 | 46.8 |
| SSG (Fu et al. 2019) (ICCV’19) | 13.2 | 31.6 | - | 49.6 | 13.3 | 32.2 | - | 51.2 |
| DAAM (Huang et al. 2020a) (AAAI’20) | 20.8 | 44.5 | - | - | 21.6 | 46.7 | - | - |
| NRMT (Zhao et al. 2020)(ECCV’20) | 19.8 | 43.7 | 56.5 | 62.2 | 20.6 | 45.2 | 57.8 | 63.3 |
| MMT (Ge, Chen, and Li 2020) (ICLR’20) | 22.9 | 49.2 | 63.1 | 68.8 | 23.3 | 50.1 | 63.9 | 69.8 |
| UNRN (Zheng et al. 2021a) (AAAI’21) | 25.3 | 52.4 | 64.7 | 69.7 | 26.2 | 54.9 | 67.3 | 70.6 |
| GLT (Zheng et al. 2021b)(CVPR’21) | 26.5 | 56.6 | 67.5 | 72.0 | 27.7 | 59.5 | 70.1 | 74.2 |
| P2LR (Ours) | 29.0 | 58.8 | 71.2 | 76.0 | 29.9 | 60.9 | 73.1 | 77.9 |
| Methods | DukeMarket | |||
| mAP | R1 | R5 | R10 | |
| Model pretraining | 29.6 | 57.8 | 73.0 | 79.0 |
| Base. | 58.0 | 78.1 | 89.0 | 92.2 |
| Base.+ML | 68.5 | 84.6 | 94.3 | 96.1 |
| Base.+ML+MT (Baseline) | 74.5 | 90.3 | 96.4 | 97.9 |
| Baseline + distance | 77.8 | 90.8 | 96.6 | 98.0 |
| Baseline + Internal classifier | 80.2 | 91.9 | 96.9 | 98.0 |
| Baseline + Consistency | 79.2 | 90.4 | 96.8 | 98.0 |
| Baseline + Reweighting | 77.7 | 90.6 | 96.6 | 97.6 |
| Baseline + P2LR(=0.95) | 74.8 | 89.9 | 95.7 | 97.1 |
| Baseline + P2LR(=0.97) | 77.1 | 90.0 | 96.4 | 97.5 |
| Baseline + P2LR(=1.00) | 80.8 | 91.8 | 97.4 | 98.2 |
| Baseline + P2LR (Ours) | 81.0 | 92.6 | 97.4 | 98.3 |
Experiments
Implementation Details
We implement our model based on MMT (Ge, Chen, and Li 2020) and train it on four Tesla XP GPUs. ADAM optimizer is adopted to optimize models with the weight decay of 5e-4. We employ ImageNet (Deng et al. 2009) pre-trained ResNet50 (He et al. 2016) as the backbone. We obey normal sampling in person ReID, where and in each mini-batch. Then we perform data augmentation of random cropping, flipping, and erasing. Note that random erasing is not utilized in the source pre-training stage. All person images are resized to . We use the clustering algorithm of k-means where the number of clusters () is set as 500, 700, and 1500 for Market, Duke, and MSMT datasets, respectively. The temperature parameter in Eq.2 is set to 20. The parameter and in Eq.10 are set to 0.3 and 1.5, respectively. Overall alternative optimization steps are set to 100. In source pre-training stage, the initial learning rate is set to and is decreased by 1/10 on the 40th and 70th epoch in the total 80 epochs. In target fine-tuning stage, the learning rate is fixed to .
Datasets and Protocols
We evaluate our method on three main-stream person ReID datasets, i.e., Market-1501 (Market) (Zheng et al. 2015), DukeMTMC-reID (Duke) (Ristani et al. 2016), and MSMT17 (MSMT) (Wei et al. 2018). The Market-1501 dataset contains 32,668 annotated images of 1,501 identities shot from 6 cameras, where 12,936 images of 751 identities are used for training and 19,732 images of 750 identities for testing.The DukeMTMC-reID dataset consists of 36,411 images collected from 8 cameras, where 702 identities are used for training and 702 identities for testing. MSMT17 is the most challenging and largest person ReID dataset consisting of 126,441 images of 4,101 identities, where 1,041 identities and 3,060 identities are used for training and testing, respectively. We adopt mean average precision (mAP) and CMC Rank-1/5/10 (R1/R5/R10) accuracy without re-ranking (Zhong et al. 2017) for evaluation.
Comparison with State-of-the-Arts
We compare our method against the state-of-the-art (SOTA) methods on four UDA ReID settings and present the results in Table 1. Among existing methods for UDA person ReID, DAAM (Huang et al. 2020a) introduces domain alignment constraints and an attention module. SSG (Fu et al. 2019), MMT (Ge, Chen, and Li 2020), MEB-Net (Zhai et al. 2020b), and UNRN (Zheng et al. 2021a) are all clustering-based methods. SSG (Fu et al. 2019) employs both global body and local body part features for clustering and evaluation. We construct the baseline based on MMT (Ge, Chen, and Li 2020) which introduces mutual mean teacher for UDA person ReID. Compared to the baseline MMT (Ge, Chen, and Li 2020), our proposed P2LR significantly improves the UDA ReID accuracy, with 9.8%, 5.7%, 6.1%, and 6.6% mAP improvements on four UDA ReID settings. Compared to MEB-Net (Zhai et al. 2020b) which establishes three networks to perform mutual mean learning, we increase the mAP by 5.0%, 4.7% with a simpler architecture design. Notably, UNRN and GLT leverage source data during target fine-tuning stage and build an external support memory to mine hard pairs. Our P2LR still achieves 3.7% and 3.7% mAP gains to UNRN, 2.5% and 2.2% mAP gains to GLT on the MSMT dataset. In general, our method P2LR achieves the state-of-the-art performance on all datasets, which verifies the effectiveness of P2LR.


Ablation Studies
In this section, we carry out extensive ablation studies to validate the effectiveness of each component in P2LR.
Effectiveness of progressive label refinery. To alleviate the negative effects of noisy/wrong pseudo labels, we exploit the characteristics of probability distribution among identities to evaluate probabilistic uncertainty of pseudo labels and refine the pseudo labels by alternative optimization. We validate the effectiveness of the proposed progressive label refinery module by comparing the performance of Baseline and Baseline+P2LR. Without P2LR, the achieved mAP and Rank-1 accuracy are 74.5% and 90.3%, respectively. With P2LR, the achieved mAP is 81.0% and Rank-1 accuracy is 92.6%, respectively. The mAP is significantly improved by 6.5% with the sole P2LR on the Duke2Market task. The results show that the proposed method is effective to alleviate the negative effects caused by noisy/wrong pseudo labels and significantly improves UDA person ReID performance.
Different designs of label correctness estimation. A straightforward way to evaluate the uncertainty of pseudo labels is referring to the distance to the nearest centroid in feature space. As shown in Table 2, the mAP and Rank-1 accuracy is improved by 3.2% and 1.8% with the probabilistic uncertainty criterion. That is because the probability distribution based uncertainty evaluation considers more global references than distance in local feature space. Besides, we find introducing an external classifier with cluster centroid for uncertainty evaluation outperforms internal classifiers in . It can be attributed to the fact that internal classifiers are more easily misled by noisy labeling during training. External classifiers whose weights are generated by clustering could correct the misleading to some extent.
We compare our label evaluation method to prediction consistency based method UNRN. Our method surpasses UNRN with large margins. The uncertainty (noise level) of pseudo labels should be measured from the intrinsic property of its own probabilistic distribution, especially for UDA ReID. Since noise already exists in teacher models, the consistency-based uncertainty as in UNRN might overfit biased teacher models.
Progressive label refinery vs Sample Reweighting. We compare the label refinery with reweighting method proposed in UNRN (Zheng et al. 2021a). In general, our method filters out wrong labels with the guidance of uncertainty, while the reweighting-based method reduces the negative influence in loss functions. The comparative results are presented in Table 2. The proposed progressive label refinery significantly outperforms reweighting method. It indicates that removing wrong labeled samples in training is more effective for reducing their negative influence.
Parameter analysis. We experiment with different ideal distribution by setting different . We present the mAP/R1/R5/R10 in Table 2 and mAP curves with the number of refinery steps in Figure 6a, respectively. It can be seen has important impacts while the mAP curve of =0.99 grows fastest and highest. Therefore, we set =0.99 for all other experiments. We then explore the influence of temperature parameter in the uncertainty measurement while setting in Figure 6b. The achieved mAP and Rank-1 accuracy maintain high when is set to . When , the achieved mAP is 80.4% and Rank-1 accuracy is 91.4%. When , the achieved mAP is 80.2% and Rank-1 accuracy is 92.0%. Afterwards, we present the influence of in progressive label refinery Figure 6c setting . The mAP and Rank-1 accuracy reach peak (81.0% and 92.6%) when is around 0.3. It indicates we preserve about 30% of samples and eliminate 70% ones in the early refinery steps. We progressively exploit more uncertain samples in later refinery steps for strong performance.
Visualization. We present the visualization results to validate the effectiveness of probabilistic uncertainty measurement for selecting samples. The selected certain samples and un-selected uncertain samples of three clusters determined by the proposed criterion in the first refinery step are presented in Figure 5. It can be observed that most selected samples are from the same identity while un-selected samples are hard samples of the identity or from other identities. By combining the selected certain samples with high confidence into target domain fine-tuning, the proposed P2LR can achieve superior UDA person ReID performance.
Conclusion
In this paper, we aim to find wrong pseudo labels and reduce their negative effects for clustering-based UDA person ReID. We observe that the probability distributions of samples with wrong pseudo labels are ambiguous with multiple peaks, which is different from that of correctly-labeled samples. This inspires us to propose a probabilistic uncertainty guided progressive label refinery (P2LR) framework for UDA person ReID. We solve it by alternative optimization, which balances between the target domain exploitation and noise label overfitting. The proposed method brings significant improvements over a strong baseline and achieves the state-of-the-art performance on four benchmarks.
Acknowledgments
This work was supported by the Cross-Media Intelligent Technology Project of Beijing National Research Center for Information Science and Technology (BNRist) under Grant No.BNR2019TD01022, National Natural Science Foundation of China under Grant No.61771288, and the research fund under Grant No. 2019GQG0001 from the Institute of GuoQiang, Tsinghua University.
References
- Chang et al. (2020) Chang, J.; Lan, Z.; Cheng, C.; and Wei, Y. 2020. Data uncertainty learning in face recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 5710–5719.
- Cui et al. (2020) Cui, S.; Wang, S.; Zhuo, J.; Su, C.; Huang, Q.; and Tian, Q. 2020. Gradually vanishing bridge for adversarial domain adaptation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 12455–12464.
- Deng et al. (2009) Deng, J.; Dong, W.; Socher, R.; Li, L.-J.; Li, K.; and Fei-Fei, L. 2009. Imagenet: A large-scale hierarchical image database. In 2009 IEEE conference on computer vision and pattern recognition, 248–255. Ieee.
- Deng et al. (2018) Deng, W.; Zheng, L.; Ye, Q.; Kang, G.; Yang, Y.; and Jiao, J. 2018. Image-image domain adaptation with preserved self-similarity and domain-dissimilarity for person re-identification. In Proceedings of the IEEE conference on computer vision and pattern recognition, 994–1003.
- Fan et al. (2018) Fan, H.; Zheng, L.; Yan, C.; and Yang, Y. 2018. Unsupervised person re-identification: Clustering and fine-tuning. ACM Transactions on Multimedia Computing, Communications, and Applications (TOMM), 14(4): 1–18.
- Fu et al. (2019) Fu, Y.; Wei, Y.; Wang, G.; Zhou, Y.; Shi, H.; and Huang, T. S. 2019. Self-similarity grouping: A simple unsupervised cross domain adaptation approach for person re-identification. In Proceedings of the IEEE/CVF International Conference on Computer Vision, 6112–6121.
- Ge, Chen, and Li (2020) Ge, Y.; Chen, D.; and Li, H. 2020. Mutual Mean-Teaching: Pseudo Label Refinery for Unsupervised Domain Adaptation on Person Re-identification. In International Conference on Learning Representations.
- Ge et al. (2020) Ge, Y.; Zhu, F.; Zhao, R.; and Li, H. 2020. Structured domain adaptation with online relation regularization for unsupervised person Re-ID. arXiv preprint arXiv:2003.06650.
- Gong et al. (2019) Gong, R.; Li, W.; Chen, Y.; and Gool, L. V. 2019. Dlow: Domain flow for adaptation and generalization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2477–2486.
- Gorski, Pfeuffer, and Klamroth (2007) Gorski, J.; Pfeuffer, F.; and Klamroth, K. 2007. Biconvex sets and optimization with biconvex functions: a survey and extensions. Mathematical methods of operations research, 66(3): 373–407.
- Guo et al. (2019) Guo, J.; Yuan, Y.; Huang, L.; Zhang, C.; Yao, J.-G.; and Han, K. 2019. Beyond human parts: Dual part-aligned representations for person re-identification. In Proceedings of the IEEE/CVF International Conference on Computer Vision, 3642–3651.
- He et al. (2016) He, K.; Zhang, X.; Ren, S.; and Sun, J. 2016. Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition, 770–778.
- Hermans, Beyer, and Leibe (2017) Hermans, A.; Beyer, L.; and Leibe, B. 2017. In defense of the triplet loss for person re-identification. arXiv preprint arXiv:1703.07737.
- Huang et al. (2020a) Huang, Y.; Peng, P.; Yi Jin, Y. L.; Xing, J.; and Ge, S. 2020a. Domain Adaptive Attention Model for Unsupervised Cross-Domain Person Re-Identification. In Proceedings of the AAAI Conference on Artificial Intelligence.
- Huang et al. (2020b) Huang, Y.; Zha, Z.-J.; Fu, X.; Hong, R.; and Li, L. 2020b. Real-world person re-identification via degradation invariance learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 14084–14094.
- Isobe et al. (2020) Isobe, T.; Han, J.; Zhuz, F.; Liy, Y.; and Wang, S. 2020. Intra-clip aggregation for video person re-identification. In 2020 IEEE International Conference on Image Processing (ICIP), 2336–2340. IEEE.
- Isobe et al. (2021) Isobe, T.; Jia, X.; Chen, S.; He, J.; Shi, Y.; Liu, J.; Lu, H.; and Wang, S. 2021. Multi-target domain adaptation with collaborative consistency learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 8187–8196.
- Jin et al. (2020) Jin, X.; Lan, C.; Zeng, W.; and Chen, Z. 2020. Global distance-distributions separation for unsupervised person re-identification. In European Conference on Computer Vision, 735–751. Springer.
- Kendall and Gal (2017) Kendall, A.; and Gal, Y. 2017. What Uncertainties Do We Need in Bayesian Deep Learning for Computer Vision? Advances in Neural Information Processing Systems, 30: 5574–5584.
- Li et al. (2019) Li, Y.-J.; Lin, C.-S.; Lin, Y.-B.; and Wang, Y.-C. F. 2019. Cross-dataset person re-identification via unsupervised pose disentanglement and adaptation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, 7919–7929.
- Lin et al. (2019) Lin, Y.; Dong, X.; Zheng, L.; Yan, Y.; and Yang, Y. 2019. A bottom-up clustering approach to unsupervised person re-identification. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 33, 8738–8745.
- Liu et al. (2019) Liu, J.; Zha, Z.-J.; Chen, D.; Hong, R.; and Wang, M. 2019. Adaptive transfer network for cross-domain person re-identification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 7202–7211.
- Luo et al. (2019) Luo, H.; Jiang, W.; Gu, Y.; Liu, F.; Liao, X.; Lai, S.; and Gu, J. 2019. A strong baseline and batch normalization neck for deep person re-identification. IEEE Transactions on Multimedia, 22(10): 2597–2609.
- Ristani et al. (2016) Ristani, E.; Solera, F.; Zou, R.; Cucchiara, R.; and Tomasi, C. 2016. Performance measures and a data set for multi-target, multi-camera tracking. In European conference on computer vision, 17–35. Springer.
- Wang and Zhang (2020) Wang, D.; and Zhang, S. 2020. Unsupervised person re-identification via multi-label classification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 10981–10990.
- Wang et al. (2020) Wang, X.; Zhang, H.; Huang, W.; and Scott, M. R. 2020. Cross-batch memory for embedding learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 6388–6397.
- Wei et al. (2021) Wei, G.; Lan, C.; Zeng, W.; and Chen, Z. 2021. MetaAlign: Coordinating Domain Alignment and Classification for Unsupervised Domain Adaptation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 16643–16653.
- Wei et al. (2018) Wei, L.; Zhang, S.; Gao, W.; and Tian, Q. 2018. Person transfer gan to bridge domain gap for person re-identification. In Proceedings of the IEEE conference on computer vision and pattern recognition, 79–88.
- Wu et al. (2019) Wu, Y.; Lin, Y.; Dong, X.; Yan, Y.; Bian, W.; and Yang, Y. 2019. Progressive learning for person re-identification with one example. IEEE Transactions on Image Processing, 28(6): 2872–2881.
- Yang et al. (2020) Yang, F.; Li, K.; Zhong, Z.; Luo, Z.; Sun, X.; Cheng, H.; Guo, X.; Huang, F.; Ji, R.; and Li, S. 2020. Asymmetric co-teaching for unsupervised cross-domain person re-identification. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 34, 12597–12604.
- Yu et al. (2019) Yu, H.-X.; Zheng, W.-S.; Wu, A.; Guo, X.; Gong, S.; and Lai, J.-H. 2019. Unsupervised person re-identification by soft multilabel learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2148–2157.
- Zhai et al. (2020a) Zhai, Y.; Lu, S.; Ye, Q.; Shan, X.; Chen, J.; Ji, R.; and Tian, Y. 2020a. Ad-cluster: Augmented discriminative clustering for domain adaptive person re-identification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 9021–9030.
- Zhai et al. (2020b) Zhai, Y.; Ye, Q.; Lu, S.; Jia, M.; Ji, R.; and Tian, Y. 2020b. Multiple expert brainstorming for domain adaptive person re-identification. In Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, August 23–28, 2020, Proceedings, Part VII 16, 594–611. Springer.
- Zhang et al. (2019) Zhang, X.; Cao, J.; Shen, C.; and You, M. 2019. Self-training with progressive augmentation for unsupervised cross-domain person re-identification. In Proceedings of the IEEE/CVF International Conference on Computer Vision, 8222–8231.
- Zhang, Zhang, and Liu (2021) Zhang, Z.; Zhang, H.; and Liu, S. 2021. Person Re-Identification Using Heterogeneous Local Graph Attention Networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 12136–12145.
- Zhao et al. (2020) Zhao, F.; Liao, S.; Xie, G.-S.; Zhao, J.; Zhang, K.; and Shao, L. 2020. Unsupervised domain adaptation with noise resistible mutual-training for person re-identification. In European Conference on Computer Vision, 526–544. Springer.
- Zheng et al. (2021a) Zheng, K.; Lan, C.; Zeng, W.; Zhang, Z.; and Zha, Z.-J. 2021a. Exploiting Sample Uncertainty for Domain Adaptive Person Re-Identification. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 35, 3538–3546.
- Zheng et al. (2021b) Zheng, K.; Liu, W.; He, L.; Mei, T.; Luo, J.; and Zha, Z.-J. 2021b. Group-aware label transfer for domain adaptive person re-identification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 5310–5319.
- Zheng et al. (2015) Zheng, L.; Shen, L.; Tian, L.; Wang, S.; Wang, J.; and Tian, Q. 2015. Scalable person re-identification: A benchmark. In Proceedings of the IEEE international conference on computer vision, 1116–1124.
- Zheng and Yang (2021) Zheng, Z.; and Yang, Y. 2021. Rectifying pseudo label learning via uncertainty estimation for domain adaptive semantic segmentation. International Journal of Computer Vision, 129(4): 1106–1120.
- Zhong et al. (2017) Zhong, Z.; Zheng, L.; Cao, D.; and Li, S. 2017. Re-ranking person re-identification with k-reciprocal encoding. In Proceedings of the IEEE conference on computer vision and pattern recognition, 1318–1327.
- Zhong et al. (2018) Zhong, Z.; Zheng, L.; Li, S.; and Yang, Y. 2018. Generalizing a person retrieval model hetero-and homogeneously. In Proceedings of the European Conference on Computer Vision (ECCV), 172–188.
- Zhong et al. (2019) Zhong, Z.; Zheng, L.; Luo, Z.; Li, S.; and Yang, Y. 2019. Invariance matters: Exemplar memory for domain adaptive person re-identification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 598–607.