Delay-induced spontaneous dark- state generation from two distant excited atoms

Large-scale interconnected quantum systems offer promising applications in quantum information processing and distributed quantum sensing [1, 2, 3]. As the experimental capabilities for directly interconnecting distant quantum nodes grow [4], we have yet to develop the theoretical toolbox to efficiently analyze systems of multiple qubits collectively exchanging photons over large distances, where delay effects cannot be neglected. Such many-body systems exhibit rich non-Markovian and nonlinear dynamics, arising from delayed and multiphoton interactions. Given the complexity associated with such systems, even the simplest scenarios, e.g., the spontaneous decay of two fully excited distant atoms, remains unexplored.

The most studied cases of coupled emitters consider nearby atoms, neglecting the delay time the field needs to propagate between them. This scenario is a landmark of quantum optics across platforms, such as atoms in free space [5, 6], inside a leaky cavity [7], and near waveguides [8]. In all of these cases, ensembles of initially fully excited two-level atoms decay into their ground state. As atoms decay, correlations among them spontaneously and momentarily emerge, leading to the well-known collective phenomenon of superfluorescence  [9, 10, 11, 6]¹¹1We use the term superfluorescence [9] as a particular case of superradiance when considering a fully inverted sample. Broadly speaking, superradiance is the collective enhancement of the decay rate of an atom in an atomic ensemble beyond the spontaneous emission rate of a single atom [96, 5]. Such atom-atom correlations, which are absent in the initial state, emerge without external driving fields or post-selection  [5].

Platforms based on waveguide QED present an effective way to go beyond the zero-delay approximation, enabling tunable, efficient, and long-ranged interactions in the optical and microwave regime [13, 14, 15, 16, 17, 18, 19, 20, 21]. For example, state-of-the-art experiments allow one to tune out dispersive dipole-dipole interactions by strategically positioning the atoms along a waveguide [22, 23, 24] while highly reducing coupling to non-guided modes [25, 26, 27, 28, 29]. Furthermore, waveguide-coupled quantum emitters enable chiral interactions due to strong spin-momentum coupling, and directional routing of photons [30, 31, 32, 33, 34, 35].

When the time taken by a photon to propagate between two distant emitters becomes comparable to their characteristic lifetimes, the system exhibits surprisingly rich delay-induced non-Markovian dynamics even in the single-photon regime [36, 37, 38, 39, 40, 32]. Some examples of such dynamics include collective spontaneous emission rates exceeding those of Dicke superradiance and formation of highly delocalized atom-photon bound states [41, 42, 43, 44, 45, 46, 47, 48, 49, 50]. In addition, time-delayed feedback can assist in preparing photonic cluster states [51] and single-photon sources with improved coherence and indistinguishability [52].

Recent studies of the effects emerging from delayed interactions considered either many atoms with a single photon [53, 54, 45, 41, 55], many photons with a single atom [44, 56, 57, 58], or numerical exploration of three-photons and three-atoms [50], inviting us to revisit the theoretical description of other canonical quantum optical phenomena, such as superfluorescence, in the context of waveguide-coupled emitters in a large-scale quantum network.

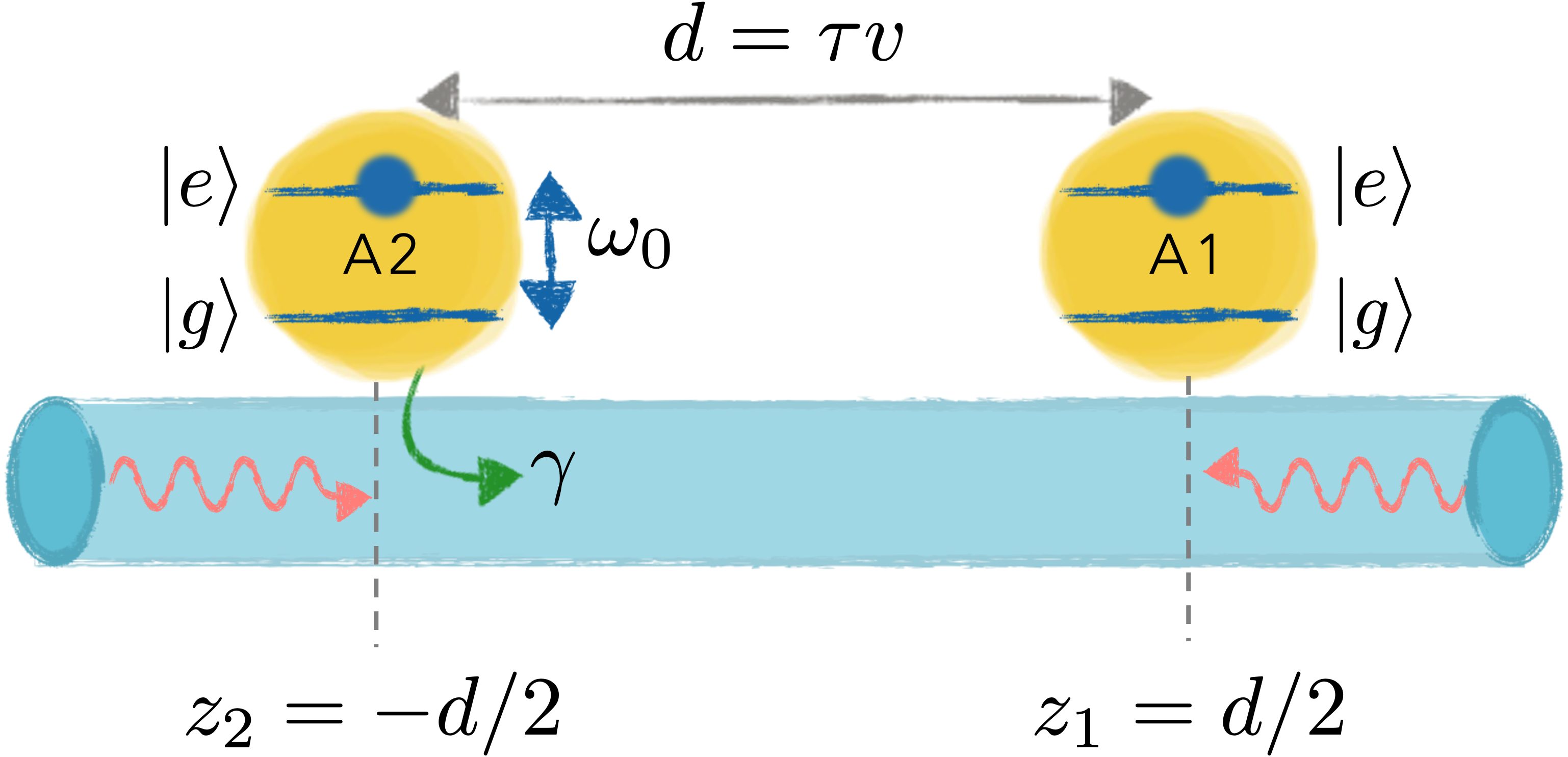
In this paper, we show that a system of two-atoms, with two-excitations, and delayed-interactions (see Fig. 1) exhibits novel non-Markovian collective dynamics. In particular, for fully inverted atoms, the instantaneous decay can be faster than in superfluorescence and steady-state entanglement can suddenly emerge. In the latter case, the electromagnetic (EM) field can have two photons trapped between the two atoms, an effect that can not be captured by Markovian dynamics. We refer to this phenomenon, which leads to the spontaneous generation of a dark state, as delayed-induced subfluorescence –the subradiant counterpart of the well-known superfluorescence effect. The resulting steady state is a delocalized hybrid atom-photon state, requiring a description beyond the usual Born and Markov approximations and qualitatively different from the case without delay, where the system always ends in the ground state. The rich and unique dynamics in such a seemingly simple system demonstrates non-Markovian delay as a mechanism for trapping light, entanglement generation and stabilization in long-distance interacting quantum nodes.

We consider two two-level atoms, with transition frequency $\omega_{0}$ between the ground $\left|g\right\rangle$ and excited $\left|e\right\rangle$ states, coupled through a waveguide. In this work, our emphasis is on the case of perfectly coupled atoms, the free Hamiltonian of the total atoms+field system is given by $H_{0}=(\hbar\omega_{0}/2)\sum_{r=1}^{2}\hat{\sigma}_{z}^{(r)}+\sum_{\alpha,\eta}\hbar\omega_{\alpha}\hat{a}^{\dagger}_{\alpha,\eta}\hat{a}_{\alpha,\eta}$. The interaction Hamiltonian in the interaction picture is (having made the electric-dipole and rotating-wave approximations):

where $g_{\alpha}$ is the coupling between atoms and the guided mode $\alpha$ with frequency $\omega_{\alpha}$, $\Delta_{\alpha}=\omega_{\alpha}-\omega_{0}$, and $k_{\alpha\eta}=\eta\omega_{\alpha}/v$, with $\eta=\pm 1$ specifying the direction of propagation. The position of the atoms is $z_{1,\,2}=\pm d/2$, $\hat{\sigma}_{z}^{(r)}=\left|e\right\rangle_{r}\left\langle e\right|_{r}-\left|g\right\rangle_{r}\left\langle g\right|_{r}$ and the raising and lowering operators for the $r$-th atom are defined as $\hat{\sigma}_{+}^{(r)}=\left(\hat{\sigma}_{-}^{(r)}\right)^{\dagger}=\left|e\right\rangle_{r}\left\langle g\right|_{r}$.

We consider the initial state with both atoms excited and the field in the vacuum state, $\left|e_{1}e_{2},\{0\}\right\rangle$. As a consequence of the rotating-wave approximation, the total number of atomic and field excitations are conserved, suggesting the following ansätz for the state of the system at time $t$:

where $\left|g_{1}g_{2},\{0\}\right\rangle$ is the ground state of the system. The complex coefficients $a(t)$, $b_{\alpha\eta}^{(r)}(t)$, and $c_{\alpha\eta,\beta\eta^{\prime}}(t)$ correspond to the probability amplitudes of having an excitation in both the atoms, $r^{\mathrm{th}}$ atom and field mode $\left\{\alpha,\eta\right\}$, and field modes $\left\{\alpha,\eta\right\}$ and $\left\{\beta,\eta^{\prime}\right\}$, respectively. The coefficients $c_{\alpha\eta}(t)$ represent the probability amplitude of exciting two photons in modes $\left\{\alpha,\eta\right\}$. The Hamiltonian in Eq. (1) models two emitters interacting via the quantized electromagnetic field; their distance, codified in the phase $e^{ik_{\alpha\eta}z_{r}}$, has the effect of introducing a delay in the equations of motion for the quantum state coefficients. This delayed interaction between the emitters results from the finite propagation speed of light.

Defining $B_{\alpha\eta}^{(r)}=b_{\alpha\eta}^{(r)}(t)e^{-i\Delta_{\alpha}t}$ and $C_{\alpha\eta}=c_{\alpha\eta}(t)e^{-2i\Delta_{\alpha}t}$, and formally integrating the equation for $c_{\alpha\eta,\beta\eta^{\prime}}(t)$, the Schrödinger equation yields the following system of delay-differential equations for the excitation amplitudes:

where $\gamma$ is the decay rate of the emitters into the guided modes. We present a detailed derivation in Appendix A. We solve the system of equations via Laplace transforms considering the initial conditions $a(0)=1$ and $B_{\alpha\eta}(0)=C_{\alpha\eta}(0)=0$.

The Laplace transform of $a(t)$ is (see Appendix B)

where $\phi=\omega_{0}\tau$ is the resonance field propagation phase.

We write the sum over modes on the right-hand side (RHS) of Eq. (6) as an integral over frequencies by introducing the density of modes $\rho(\omega_{\alpha})$. Additionally, we use the Wigner-Weisskopf approximation and set $\rho(\omega_{\alpha}),\,g_{\alpha}\approx\rho(\omega_{0}),\,g_{0}$, evaluated at the atomic resonance frequency, a good approximation in the presence of delay effects in waveguide QED [40]. With these considerations we obtain $\tilde{a}(s)=1/(s+\gamma)$ for all $\tau$. Taking the inverse Laplace transform we get $a(t)=e^{-\gamma t}$, which gives the time-dependent probability of having two atomic excitations

We remark that the probability of having two atomic excitations is independent of the delay between atoms.

The probability of having only one of the atoms excited is

where the time-dependent solutions $b_{\alpha\eta}^{(1,2)}(t)$ are derived in Appendix B and given by (42). In the limits of two coincident atoms with $\tau=0$, and two infinitely distant atoms with $\tau\to\infty$, we obtain the expected Markovian dynamics [59, 60]:

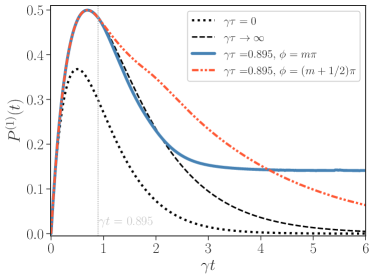
Figure 2 shows $P^{(1)}(t)$ for different values of the delay $\tau$ and the propagation phase $\phi$. For times $t<\tau$, the atoms decay independently. At time $t=\tau$, the field emitted by one atom reaches the other, modifying their decay dynamics depending on the value of the propagation phase $\phi$. Their instantaneous decay rate, given by the negative slope of $P^{(1)}(t)$, could momentarily exceed that of standard superfluorescence ($\tau=0$). The delay condition $\gamma\tau\approx 0.375$ and $\phi=n\pi$ maximizes the instantaneous decay rate. This phenomenon is a signature of superduperradiance, reported in Ref. [41]. Notably, in this case the atom-atom coherence that is necessary to modify the instantaneous decay emerges spontaneously.

In the late-time limit, the following steady state appears when $\phi=n\pi$ for any delay $\tau$ between the atoms (see Appendix C):

where we have removed the explicit time dependence of the steady-state coefficients. The steady-state amplitude for the mode $\left\{\alpha,\eta\right\}$ is

and $c_{\alpha\eta,\beta\eta^{\prime}}$ is given in Eq. (50)in Appendix C. The last two terms in Eq. (III) represent a bound state in the continuum (BIC) that corresponds to having one shared excitation between the atoms and one propagating photon mode in between them [44]. Using the Born rule and Eq. (11), we obtain that its probability is $2P^{(1)}\left(t\to\infty\right)$, where:

We note that the probability of ending up in a BIC state is maximum for $\gamma\tau\approx 0.895$ with a probability of $0.282$.

The fact that the atoms+field state is non-separable shows that one cannot use the Born-Markov approximation to solve for the dynamics of the system. Using Eq. (III) and Eq. (11) we obtain the following reduced density matrix for the atomic subsystem

with $+$ corresponding to the case when $n$ is odd and $-$ when it is even and $\left|\Psi^{\pm}\right\rangle=(\left|e_{1}g_{2}\right\rangle\pm\left|g_{1}e_{2}\right\rangle)/\sqrt{2}$ are single excitation Bell states. As the initially inverted atoms evolve into a superposition of radiative and non-radiative states upon delayed-interactions, the atoms decay into a superposition of ground state and an entangled dark steady state. For a field propagation phase $\phi=2n\pi$ $(\phi=(2n+1)\pi)$, the dark state that appears in the late-time limit corresponds to the antisymmetric state $\left|\Psi^{-}\right\rangle$ (symmetric state $\left|\Psi^{+}\right\rangle$).

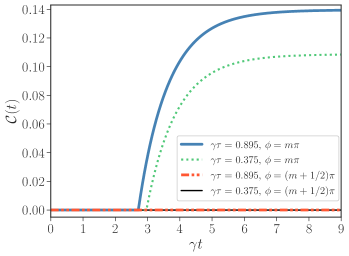
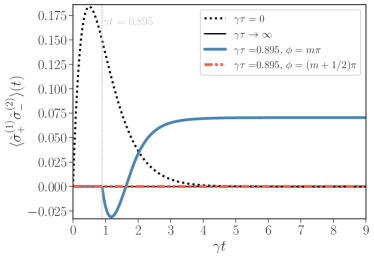
Delayed interactions create quantum correlations between the atoms. We quantify it using the concurrence $\mathcal{C}(t)$ of the reduced density matrix of the atoms $\hat{\rho}_{A}(t)=Tr_{F}(|\psi(t)\rangle\langle\psi(t)\lvert)$ [61]. For $\tau\to\infty$, the concurrence is zero throughout the evolution since the initially uncorrelated atoms evolve independently. Remarkably, when $\tau=0$, the concurrence is also zero throughout the evolution, even when atoms transition to a superradiant behavior. This case exemplifies that entanglement is not necessary for superradiance. For intermediate values of $\tau$, we numerically study the dynamics of concurrence, shown in Fig. 3 (a). We begin studying its behavior for $\gamma\tau\approx 0.895$ (corresponding to the maximum value of $P^{(1)}\left(t\to\infty\right)$) and $\gamma\tau\approx 0.375$ (corresponding to the largest instantaneous decay rate). Since the system lacks initial correlations, the concurrence is zero from $t=0$ to a certain time, $t_{\text{SBE}}$, when there is a sudden birth of entanglement (SBE) [62, 63, 64, 65, 66, 67, 68]. For $\phi=n\pi$, the concurrence increases until reaching a stationary value, whereas for $\phi=(n+\frac{1}{2})\pi$, it always remains zero. In general, for other values of $\phi$, the concurrence suddenly departs from zero and slowly decays after reaching a maximum value. For $\gamma\tau\approx 0.895$, we obtain the maximum value for the concurrence. Figure 3 (b) shows the emergence of atom-atom correlations defined by $\mathrm{Tr}\left[\hat{\rho}_{A}(t)\hat{\sigma}_{+}^{(1)}\hat{\sigma}_{-}^{(2)}\right]$. We note that the atom-atom correlations develop as soon as the atoms “see” each other, while the concurrence takes longer to emerge. Delayed atom-atom interactions couple the fully excited state of the atoms to both single excitation symmetric and antisymmetric states. After the build-up of correlations, the most radiative state collectively decays, while the non-radiative atomic state remains. The system, therefore, spontaneously evolves into an entangled dark state in the presence of retardation. Such appearance of quantum correlations is a striking example of environment-assisted spontaneous entanglement generation.

We now focus on the dynamics of the field sourced by the non-Markovian behavior of the atoms. Field operators are often described through mode expansion, as shown in Eq. (51), or Green’s functions [69]. Its expectation values involve integrating over all the modes or knowing the Green’s function for the field, which for waveguides is usually given by a mode expansion [70]. When the system is Markovian, an input-output relation simplifies the calculation of field observables, and the sum over field modes is replaced by a sum over atomic operators: $\hat{{\mathbf{E}}}^{+}({\mathbf{r}})={\hat{{\mathbf{E}}}}^{+}_{\textrm{Input}}({\mathbf{r}})+\sum_{i}f({\mathbf{r}},{\mathbf{r}_{i}})\hat{\sigma}_{-}^{i}$, where the positive part of the field operator, $\hat{{\mathbf{E}}}^{+}({\mathbf{r}})$, at ${\mathbf{r}}$, is proportional to the input field, $\hat{{\mathbf{E}}}^{+}_{\textrm{Input}}({\mathbf{r}})$, plus the field sourced by the atomic operators $\hat{\sigma}_{-}^{i}$. Here ${\mathbf{r}_{i}}$ is the position of atom $i$, and $f({\mathbf{r}},{\mathbf{r}_{i}})$ is a complex function that depends on the modes of the system [14, 71].

The probability of measuring two photons at the same time at position $z$ is proportional to the second-order correlation function [72]

where we take the maximum over the distance between the atoms, in the normalization constant, to compare the second-order correlation function for different time lags. By substituting the input-output relation for the Markovian case into $g^{(2)}$ and replacing it with the stationary solution, Eq. (III), we see that the dynamics does not lead to a two-photon bound state. However, the system under consideration is non-Markovian, and one must calculate the field observables from the full expression for the field operator.

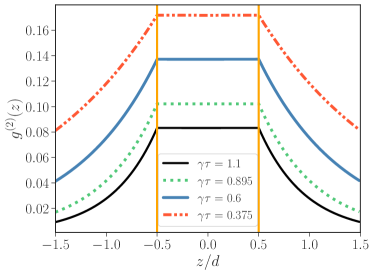
Figure  4 shows the second-order correlation function in the stationary regime ($t\to\infty$) (see Appendix D for details), for different distances between the atoms. It can be seen that two photons are trapped between the atoms, a result that is distinctly non-Markovian, demonstrating the rich interplay of non-Markovianity and nonlinear atom-photon interactions. Although the maximum probability of having the atoms excited is given at a distance $\gamma\tau\approx 0.895$, the probability of having two photons excited at a particular $z$ is greater at $\gamma\tau\approx 0.375$, where the instantaneous decay is maximum. This is explained by the fact that the probability of having two photons trapped in a particular position increases when the probability of the atomic excitation diminishes, because the energy from the atomic excitation should go to the field.

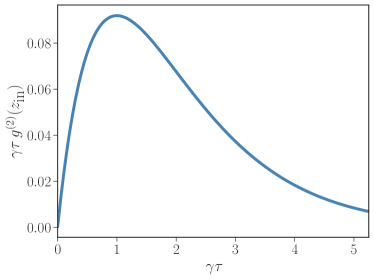
A salient question pertains to the maximum probability of having two photons between the atoms. This probability depends on the value of the autocorrelation function and the distance between the two atoms. Figure 5 depicts $\gamma\tau\,g^{(2)}(z_{\textrm{in}})$, which is proportional to the probability of having two photons in the waveguide region separating the two atoms as a function of the delay. The distance between the atoms where the probability of having two photons is maximum is $\gamma\tau\approx 1.0$.

Note that we chose a normalization that does not depend on the transverse profile (see Appendix D for details). To obtain the actual probability that two photon detection happen at the same time and position, it is useful to calculate the field energy in the guided field modes, in the limit $t\to\infty$ (see Appendix C)

where $P^{(1)}\left(t\to\infty\right)$ is the probability of having one atomic excitation in the long time limit (see Eq. (12)). This result states that the total field energy corresponds to the energy of two photons with frequency $\omega_{0}$ (the total energy) minus the energy accumulated in the atoms that has not been emitted into the waveguide. The normalization constant, $\int dz\langle\hat{{\mathbf{E}}}^{(+)}(z)\hat{{\mathbf{E}}}^{(-)}(z)\rangle$, is given by the total energy around the fiber, $\mathcal{E}_{\textrm{total}}$ (see Eq. (15)) multiplied by the square of the mode profile at the atomic frequency transition $\omega_{0}$.

We have analyzed the spontaneous decay of two fully inverted atoms coupled through a waveguide in the presence of retardation effects. A remarkable result is the spontaneous creation of a steady delocalized atom-photon bound state, with sudden birth of entanglement between the atoms. Furthermore, we demonstrate that such a delay can create two-photon bound states, wherein one can have two photons in the waveguide region between the two atoms. Such states appear as a result of the non-Markovian time-delayed feedback of the spontaneously radiated EM field acting on the emitters. Additionally, the collective decay of the two atoms can be momentarily enhanced beyond standard superfluorescence and subsequently inhibited, demonstrating the rich non-Markovian dynamics of such a system.

Such delay-induced spontaneous steady state entanglement generation can have implications in the rapidly growing field of waveguide QED, a field with promising applications in quantum information processing [73, 3, 74, 75, 76, 77, 78, 79] that benefit from preparing and manipulating long-lived dark-states. In this context, there have been several proposals to generate a steady entangled state; compared to delay-induced subfluorescence, these schemes necessitate extra degrees of control, such as external driving fields [80, 81, 82, 36], initial entanglement [41], or chiral emission in front of a mirror [39, 83].

It is not only the generation [84] but also the stabilization of entangled states that are critical to developing efficient quantum devices. In contrast to the idea that the interaction of quantum systems with their environment leads to decoherence and can degrade the entanglement between the components of a quantum system [85], the environment can also be proposed as a generator [86, 87] and stabilizer of entanglement [88]. Our results demonstrate that non-Markovian time-delayed feedback can be a mechanism for environment-assisted entanglement generation and stabilization.

Adding delay to the most straightforward collective system of two two-level atoms leads to different phenomenology, breaking the Born and Markov approximations, non-trivially modifying the dynamics, and spontaneously creating steady-state quantum correlations between the atoms and multiphoton bound states. Our results further the understanding of the significant role delay plays in quantum optics and present the outset of studying more complex phenomena involving many-body interactions [6, 89, 90]. However, studying this scenario is challenging as the complexity of the problem increases with the number of emitters, and known methods based on master equation approaches fail because neither the Markov nor the Born approximations are valid. Furthermore, although we neglect dispersive dipole-dipole interactions and coupling to non-guided modes to highlight the consequences of delay-induced non-Markovianity, all these effects can coexist, creating richer dynamics that will increase in complexity as the system scales up.

We acknowledge helpful discussions with Saikat Guha and Elizabeth Goldschmidt. P.S. is a CIFAR Azrieli Global Scholar in the Quantum Information Science Program. This work was supported by DGAPA-UNAM under grant IG101421 and IG101324 from Mexico, as well as CONICYT-PAI grant 77190033, and FONDECYT grant N^∘ 11200192 from Chile. K.S. acknowledges funding support from the John Templeton Foundation Award No. 62422, the National Science Foundation under Grant No. PHY-2309341 and the Army Research Office through Grant No. W911NF2410080.