Degree sequence condition for Hamiltonicity in tough graphs

Songling Shan¹¹1Auburn University, Department of Mathematics and Statistics, Auburn, AL 36849. Email: [email protected]. Supported in part by NSF grant DMS-2345869. Arthur Tanyel²²2Auburn University, Department of Mathematics and Statistics, Auburn, AL 36849. Email: [email protected].

Abstract

Generalizing both Dirac’s condition and Ore’s condition for Hamilton cycles, Chvátal in 1972 established a degree sequence condition for the existence of a Hamilton cycle in a graph. Hoàng in 1995 generalized Chvátal’s degree sequence condition for 1-tough graphs and conjectured a $t$ -tough analogue for any positive integer $t\geq 1$ . Hoàng in the same paper verified his conjecture for $t\leq 3$ and recently Hoàng and Robin verified the conjecture for $t=4$ . In this paper, we confirm the conjecture for all $t\geq 4$ .

Keywords. Degree sequence; Hamiltonian cycle; Toughness

1 Introduction

Graphs considered in this paper are simple, undirected, and finite. Let $G$ be a graph. Denote by $V(G)$ and $E(G)$ the vertex set and edge set of $G$ , respectively. The degree of a vertex $v$ in $G$ is denoted by $\deg(v)$ . If $u$ and $v$ are non-adjacent in $G$ , then $G+uv$ is obtained from $G$ by adding the edge $uv$ . We write $u\sim v$ if two vertices $u$ and $v$ are adjacent in $G$ ; and write $u\not\sim v$ otherwise. For $S\subseteq V(G)$ , denote by $G[S]$ and $G-S$ the subgraph of $G$ induced on $S$ and $V(G)\setminus S$ , respectively. For $v\in V(G)$ , we write $G-v$ for $G-\{v\}$ . For two integer $p,q$ , we let $[p,q]=\{i\in\mathbb{Z}:p\leq i\leq q\}$ .

Let $n\geq 1$ be an integer. The non-decreasing sequence $d_{1},d_{2},\dots,d_{n}$ is a degree sequence of graph $G$ if the vertices of $G$ can be labeled as $v_{1},v_{2},\dots,v_{n}$ such that $\deg(v_{i})=d_{i}$ for all $i\in[1,n]$ . In 1972, Chvátal [3] proved the following well known result.

Theorem 1.

Let $G$ be a graph with degree sequence $d_{1},d_{2},\dots,d_{n}$ , where $n\geq 3$ is an integer. If for all $i<\frac{n}{2}$ , $d_{i}\leq i$ implies $d_{n-i}\geq n-i$ , then $G$ is Hamiltonian.

Hoàng [5, Conjecture 1] in 1995 conjectured a toughness analogue for the theorem above. We let $c(G)$ denote the number of components of $G$ . For a real number $t\geq 0$ , we say $G$ is t-tough if $|S|\geq t\cdot c(G-S)$ for all $S\subseteq V(G)$ such that $c(G-S)\geq 2$ . The largest $t$ for which $G$ is $t$ -tough is called the toughness of $G$ and is denoted $\tau(G)$ . If $G$ is complete, $\tau(G)$ is defined to be $\infty$ . Chvátal [4] defined this concept in 1973 as a measure of a graph’s “resilience” under the removal of vertices. Hoàng’s conjecture can now be stated as follows.

Conjecture 2.

Let $n\geq 3$ and $t\geq 1$ be integers, and $G$ be a graph with degree sequence $d_{1},d_{2},\dots,d_{n}$ . Suppose that $G$ satisfies the following predicate $P(t)$ :

P(t):\forall i,t\leq i<\frac{n}{2},d_{i}\leq i\Rightarrow d_{n-i+t}\geq n-i.

Then, if $G$ is $t$ -tough, $G$ is Hamiltonian.

Hoàng in the same paper [5, Theorem 3] proved that the Conjecture holds for $t\leq 3$ . Since every hamiltonian graph must necessarily be 1-tough, the statement for $t=1$ generalizes Theorem 1. Recently, Hoàng and Robin [6] proved that the Conjecture is true for $t=4$ . In this paper, we confirm Conjecture 2 for all $t\geq 4$ .

Theorem 3.

Let $t\geq 4$ be an integer and $G$ be a $t$ -tough graph on $n\geq 3$ vertices with degree sequence $d_{1},d_{2},\dots,d_{n}$ . If for all $i<\frac{n}{2}$ it holds that $d_{i}\leq i$ implies $d_{n-i+t}\geq n-i$ , then $G$ is Hamiltonian.

A graph $G$ is pancyclic if $G$ contains cycles of any length from $3$ to $|V(G)|$ . As a consequence of Theorem 3 and a result of Hoàng [5, Theorem 7] that if a $t$ -tough graph $G$ satisfies $P(t)$ and is Hamiltonian, then $G$ is pancyclic or bipartite, we also obtain the following result.

Corollary 4.

The proof of Theorem 3 relies on our closure lemma for $t$ -tough graphs $G$ : if $x$ and $y$ are non-adjacent in $G$ and $\deg(x)+\deg(y)\geq n-t$ , then $G+xy$ is Hamiltonian implies that $G$ is Hamiltonian. We will prove Theorem 3 in the next section by applying this closure lemma and then prove the closure lemma in the subsequent section.

2 Proof of Theorem 3

We will need the following result by Bauer et al. [1] and our closure lemma for $t$ -tough graphs with $t\geq 4$ .

Theorem 5.

Let $t\geq 0$ be any real number and $G$ be a $t$ -tough graph on $n\geq 3$ vertices . If $\delta(G)>\frac{n}{t+1}-1$ , then $G$ is Hamiltonian.

Theorem 6 (Toughness Closure Lemma).

Let $t\geq 4$ be an integer, $G$ be a $t$ -tough graph on $n\geq 3$ vertices, and let distinct $x,y\in V(G)$ be non-adjacent with $\deg(x)+\deg(y)\geq n-t$ . Then $G$ is Hamiltonian if and only if $G+xy$ is Hamiltonian.

The following toughness closure concept was given by Hoàng and Robin [6]. Let $t\geq 1$ be an integer, and $G$ be a $t$ -tough graph on $n\geq 3$ vertices. Then the $t$ -closure of $G$ is formed by repeatedly adding edges joining vertices $x$ and $y$ such that $x$ and $y$ are non-adjacent in the current graph and their degree sum is at least $n-t$ in the current graph, until no such pair remains. By the same argument as showing that the Hamiltonian closure of a graph is well defined (e.g., see [2, Lemma 4.4.2]), the $t$ -closure of $G$ is well defined. Thus by Theorem 6, we will consider the $t$ -closure of $G$ instead when we prove Theorem 3. We mostly adopted the ideas used by Hoàng and Robin in [6].

Proof of Theorem 3.

As $G$ satisfies the property $P(t)$ implies that any supergraph of $G$ obtained from $G$ by adding missing edges also satisfies the property $P(t)$ , by Theorem 6, it suffices to work with the $t$ -closure of $G$ . For the sake of notation, we just assume that $G$ itself is its $t$ -closure. We may assume that $G$ is not Hamiltonian. Thus $G$ is not complete and so $\delta(G)\geq 8$ by $G$ being 4-tough.

Let $v_{1},v_{2},\dots,v_{n}$ be all the vertices of $G$ such that $\deg(v_{i})=d_{i}$ for all $i\in[1,n]$ . Thus, we have that $\deg(v_{i})+\deg(v_{j})\geq n-t$ implies $v_{i}v_{j}\in E(G)$ . By Theorem 1, if $d_{i}>i$ for all $i<\frac{n}{2}$ , then $G$ is Hamiltonian. So, we assume that there exists some positive integer $k<\frac{n}{2}$ such that $d_{k}\leq k$ . Then as $\delta(G)\geq 8$ , we have $k\geq 8$ . Choose $k$ to be minimum with the property that $d_{k}\leq k$ . Then $d_{i}>i$ for all $i\in[1,k-1]$ . Since $d_{k-1}\leq d_{k}\leq k$ , we must have $d_{k-1}=d_{k}=k$ .

Let $S,T\subseteq V(G)$ . We say that $S$ is complete to $T$ if for all $u\in S$ and $v\in T$ such that $u\neq v$ , we have $u\sim v$ . If $u\sim v$ for all $u\in S$ and $v\in V(G)$ such that $u\neq v$ , we call $S$ a universal clique of $G$ . Clearly, vertices in a universal clique have degree $n-1$ in $G$ . We will show that $G$ has a universal clique of size larger than $\frac{n}{t+1}-1$ . In particular, this gives that $\delta(G)>\frac{n}{t+1}-1$ . By Theorem 5, this proves that $G$ is Hamiltonian, a contradiction to the assumption that $G$ is not Hamiltonian. Let

U^{\alpha}=\{v_{i}:d_{i}\geq n-\alpha,i\in[1,n]\}\quad\text{for any integer $\alpha$ with $1\leq\alpha<\frac{n}{2}$.}

Claim 2.1.

For all positive integer $\alpha<\frac{n}{2}$ , $U^{\alpha}$ is a clique complete to $\{v_{i}:d_{i}\geq\alpha-t,i\in[1,n]\}$ .

Proof of Claim 2.1.

If $v_{j}\in U^{\alpha}$ for some $j\in[1,n]$ and $v_{\ell}\in\{v_{i}:d_{i}\geq\alpha-t,i\in[1,n]\}$ for some $\ell\in[1,n]$ , then $d_{j}+d_{\ell}\geq n-\alpha+\alpha-t=n-t$ . Thus, $v_{j}\sim v_{\ell}$ . This in turn implies that $U^{\alpha}$ is a clique in $G$ , since $U^{\alpha}\subseteq\{v_{i}:d_{i}\geq\alpha-t,i\in[1,n]\}$ . ∎

Claim 2.2.

Let $\alpha<\frac{n}{2}$ be any positive integer. If for every $i\in[1,n]$ , it holds that $d_{i}<\alpha-t$ implies $d_{i}\geq i-t+1$ , then $U^{\alpha}$ is a universal clique in $G$ .

Proof of Claim 2.2.

Assume there exists a positive integer $\alpha<\frac{n}{2}$ that satisfies the hypothesis, but $U^{\alpha}$ is not a universal clique. Choose $p\in[1,n]$ to be maximum such that there exists $v_{q}\in U^{\alpha}$ for some $q\in[1,n]$ such that $v_{p}\not\sim v_{q}$ . By Claim 2.1, $v_{p}\notin\{v_{i}:d_{i}\geq\alpha-t,i\in[1,n]\}$ . Thus $d_{p}\geq p-t+1$ by the assumption of this claim. By the maximality of $p$ , we have $v_{q}\sim v_{\ell}$ for all $\ell\in[p+1,n]$ . So, $d_{q}\geq n-p-1$ , which gives $d_{p}+d_{q}\geq p-t+1+n-p-1=n-t$ . But, this implies $v_{p}\sim v_{q}$ , a contradiction. ∎

Let $\Omega\subseteq V(G)$ be a universal clique in $G$ of maximum size.

Claim 2.3.

We have $|\Omega|\leq k-2$ .

Proof of Claim 2.3.

Suppose that $|\Omega|\geq k-1$ . As $\Omega$ is a universal clique in $G$ , we have $d_{i}\geq|\Omega|\geq k-1$ for all $i\in[1,n]$ . If $|\Omega|>k$ , then $d_{1}>k$ , which contradicts $d_{1}\leq d_{k}=k$ . Thus $|\Omega|\leq k$ . Note that $v_{i}\not\in\Omega$ for any $i\in[1,k]$ as every vertex of $\Omega$ has degree $n-1>\frac{n}{2}>k$ . Let $S=\left(\bigcup_{i\in[1,k]}N(v_{i})\right)\setminus\{v_{1},\ldots,v_{k}\}$ . As $d_{i}\leq k$ for all $i\in[1,k]$ , each $v_{i}$ has at most $k-|\Omega|$ neighbor from $\{v_{k+1},\ldots,v_{n}\}\setminus\Omega$ in $G$ , and so we have

	$\displaystyle\|S\|\leq$	$\displaystyle\|\Omega\|=k$	if $\|\Omega\|=k$ ,
	$\displaystyle\|S\|\leq$	$\displaystyle\|\Omega\|+k\leq 2k-1$	if $\|\Omega\|=k-1$ .

Since $\Delta(G[\{v_{1},\ldots,v_{k}\}])\leq 1$ , we have $c(G-S)\geq c(G[\{v_{1},\ldots,v_{k}\}])\geq\frac{k}{2}\geq 4$ . However, we get $\frac{|S|}{c(G-S)}<4$ , contradicting the toughness of $G$ . Thus, Claim 2.3 must hold. ∎

Claim 2.4.

For all positive integer $\alpha<\frac{n}{2}$ such that $d_{\alpha}\leq\alpha$ , we have $|U^{\alpha}|\geq\alpha-t$ .

Proof of Claim 2.4.

Suppose $v_{\alpha}\in V(G)$ such that $d_{\alpha}\leq\alpha<\frac{n}{2}$ . By the hypothesis, $d_{n-\alpha+t}\geq n-\alpha$ . That is, there are at least $n-(n-\alpha+t)+1=\alpha-t+1$ vertices of degree at least $n-\alpha$ , indicating $|U^{\alpha}|\geq\alpha-t$ . ∎

Claim 2.5.

We have $d_{\alpha}>\alpha$ for all integer $\alpha$ with $k+t-1\leq\alpha<\frac{n}{2}$ .

Proof of Claim 2.5.

Assume there exists $\alpha$ such that $k+t-1\leq\alpha<\frac{n}{2}$ and $d_{\alpha}\leq\alpha$ . Choose such an $\alpha$ to be minimum. It suffices to show that $U^{\alpha}$ is a universal clique: by Claims 2.3 and 2.4, we have $k-2\geq|\Omega|\geq|U^{\alpha}|\geq\alpha-t$ . Rearranging gives $k+t-2\geq\alpha\geq k+t-1$ , a contradiction. Thus we show that $U^{\alpha}$ is a universal clique in the following. By Claim 2.1, $U^{\alpha}$ is a clique complete to $\{v_{i}:d_{i}\geq\alpha-t,i\in[1,n]\}$ . Therefore, to apply Claim 2.2, we show that every vertex $v_{j}$ for $j\in[1,n]$ belongs to the set $\{v_{i}:d_{i}\geq\alpha-t,i\in[1,n]\}$ or satisfies $d_{j}<\alpha-t$ but $d_{j}\geq j-t+1$ .

We first show that $d_{j}\geq\alpha-t$ for all $j\in[\alpha,n]$ . Consider for now that $j=\alpha$ . If $\alpha>k+t-1$ , then $\alpha-1\geq k+t-1$ . By the minimality of $\alpha$ , we get $\alpha-1<d_{\alpha-1}\leq d_{\alpha}\leq\alpha$ . Thus $d_{\alpha}=\alpha>\alpha-t$ . If $\alpha=k+t-1$ , then $d_{\alpha}\geq d_{k}=k>\alpha-t$ . In either case, we have shown $d_{\alpha}\geq\alpha-t$ . For any $j\in[\alpha+1,n]$ , we have $d_{j}\geq d_{\alpha}\geq\alpha-t$ . Now for $j\in[1,\alpha-1]$ , suppose $d_{j}<\alpha-t$ . By the minimality of $k$ , we have $d_{j}\geq j\geq j-t+1$ if $j\in[1,k]$ . We have $d_{j}\geq d_{k}=k>k-1\geq j-t+1$ if $j\in[k+1,k+t-2]$ . By the minimality of $\alpha$ , we have $d_{j}>j>j-t+1$ for all $j\in[k+t-1,\alpha-1]$ . This completes the proof. ∎

Claim 2.6.

We have $k\geq\frac{n}{2}-t$ .

Proof of Claim 2.6.

We suppose to the contrary that $k<\frac{n}{2}-t$ . Let $p=\lfloor\frac{n-1}{2}\rfloor$ . Then $k+t-1\leq p<n/2$ . By Claim 2.5, we have $d_{p}>p$ . If $d_{p}=n-1$ , then all vertices from $\{v_{p},\ldots,v_{n}\}$ are contained in a universal clique of $G$ and so we have $|\Omega|>\frac{n}{2}$ . This gives $k\geq|\Omega|>\frac{n}{2}$ , a contradiction of the assumption that $k<\frac{n}{2}-t$ . Thus there exists $i\in[1,n]$ such that $v_{p}\not\sim v_{i}$ . We choose such an $i$ to be maximum. Since $v_{i}\nsim v_{p}$ , we have $d_{i}<n-t-d_{p}<n-t-(\frac{n-1}{2}-1)=\frac{n+1}{2}-t+1\leq d_{p}$ , which gives $i<p$ . Then by Claim 2.5 and the argument in the second paragraph in the proof of Claim 2.5, we have $d_{i}\geq i-t+1$ . By the maximality of $i$ , we have $v_{p}\sim v_{j}$ for all $j\in[i+1,n]$ and so $d_{p}\geq n-i-1$ . This gives $d_{i}+d_{p}\geq n-i-1+i-t+1=n-t$ , which contradicts that $v_{p}\nsim v_{i}$ . ∎

Claim 2.7.

We have $\delta(G)>\frac{n}{t+1}-1$ .

Proof of Claim 2.7.

Assume $\delta(G)\leq\frac{n}{t+1}-1$ . Then, as $2t\leq\delta(G)$ , we have $(2t+1)(t+1)\leq n$ . By Claim 2.2 and the choice of $k$ , we know that $U^{k}$ is a universal clique. Therefore, by Claims 2.4 and 2.6, we get $\delta(G)\geq|U^{k}|\geq k-t\geq\frac{n}{2}-2t$ . Observe that for $t\geq 3$ , we have

	$\displaystyle\frac{n}{2}-\frac{n}{t+1}$	$\displaystyle=$	$\displaystyle\frac{n(t-1)}{2(t+1)}\geq\frac{(2t+1)(t+1)(t-1)}{2(t+1)}$
		$\displaystyle=$	$\displaystyle(t+0.5)(t-1)>2t-1.$

This gives $\frac{n}{2}-2t>\frac{n}{t+1}-1$ . Thus $\delta(G)\geq k-t>\frac{n}{t+1}-1$ , a contradiction. ∎

As $\delta(G)>\frac{n}{t+1}-1$ , Theorem 5 implies that $G$ is Hamiltonian, a contradiction to our assumption that $G$ is not Hamiltonian. This completes the proof. $\blacksquare$

3 Proof of Theorem 6

Denote by $\overset{\rightharpoonup}{C}$ an orientation of a cycle $C$ . We assume that the orientation is clockwise throughout the rest of this paper. For $u,v\in V(C)$ , $u\overset{\rightharpoonup}{C}v$ denotes the path from $u$ to $v$ along $\overset{\rightharpoonup}{C}$ . Similarly, $u\overset{\leftharpoonup}{C}v$ denotes the path between $u$ and $v$ which travels opposite to the orientation. We use $u^{+}$ to denote the immediate successor of $u$ on $\overset{\rightharpoonup}{C}$ and $u^{-}$ to denote the immediate predecessor of $u$ on $\overset{\rightharpoonup}{C}$ . If $S\subseteq V(C)$ , then $S^{+}=\{u^{+}:u\in S\}$ and $S^{-}=\{u^{-}:u\in S\}$ . We use similar notation for a path $P$ when it is given an orientation. Theorem 7 is needed in the proof of Theorem 6, and we prove Theorem 7 in the last section.

Theorem 7.

Let $t\geq 4$ be rational and $G$ be a $t$ -tough graph on $n\geq 3$ vertices. Suppose that $G$ is not Hamiltonian, but there exists $z\in V(G)$ such that $G-z$ has a Hamilton cycle $C$ . Then, for any distinct $x,y\in N(z)$ , we have that $\deg(x^{+})+\deg(y^{+})<n-t$ .

Theorem 6 (Toughness Closure Lemma).

Proof.

It is clear that $G$ is Hamiltonian implies that $G+xy$ is Hamiltonian. For the converse, we suppose that $G+xy$ is Hamiltonian but $G$ is not. Then again, this implies that $G$ is not complete and so $\delta(G)\geq 2t$ .

As $G+xy$ is Hamiltonian, $G$ has a Hamilton path connecting $x$ and $y$ . Let $P=v_{1}\ldots v_{n}$ be such a path, where $v_{1}=x$ and $v_{n}=y$ . We will orient $P$ to be from $x$ to $y$ , and write $u\preceq v$ for two vertices $u$ and $v$ such that $u$ is at least as close to $x$ along $\overset{\rightharpoonup}{P}$ as $v$ is. Our goal is to find a cutset $S$ of $G$ with size less than $2t$ and so arriving a contradiction to the toughness of $G$ . For this purpose, based on the assumption that $G$ is not Hamiltonian, we look at how the neighbors of $x$ and $y$ are arranged along this path $P$ , and their adjacency relations.

The first two assertions below follow directly from the assumption that $G$ is not Hamiltonian, and the last two are corollaries of the first two.

Claim 3.1.

Let distinct $i,j\in[2,n-1]$ and suppose $x\sim v_{i}$ and $y\sim v_{j}$ . Then the following holds.

(1)

If $i<j$ , then $v_{i}^{-}\not\sim v_{j}^{+}$ and $y\not\sim v_{i}^{-}$ .
(2)

If $i>j$ , then $v_{i}^{+}\not\sim v_{j}^{+}$ and $v_{i}^{-}\not\sim v_{j}^{-}$ .
(3)

If $i\leq n-3$ and additionally $x\sim v_{i+2}$ , then $v_{i+1}\not\sim v_{k}^{+}$ for any $v_{k}$ with $v_{k}\sim y$ .
(4)

If $j\leq n-3$ and additionally $y\sim v_{j+2}$ , then $v_{j+1}\not\sim v_{k}^{-}$ for any $v_{k}$ with $v_{k}\sim x$ .

Since $\deg(x)+\deg(y)\geq n-t$ and $x$ and $y$ do not have two common neighbors that are consecutive on $P$ by Claim 3.1(1) above, each of $x$ and $y$ is expected to have many neighbors that are consecutive on $P$ . Thus we define neighbor intervals for $x$ and $y$ , respectively, as set of consecutive vertices on $P$ that are all adjacent to $x$ or $y$ . For $z\in\{x,y\}$ , and $v_{i},v_{j}$ with $i,j\in[2,n-1]$ and $i\leq j$ such that $z\sim v_{i},v_{j}$ , we call $V(v_{i}Pv_{j})$ a $z$ -interval and denote it by $I_{z}[v_{i},v_{j}]$ if $V(v_{i}Pv_{j})\subseteq N(z)$ but $v_{i}^{-},v_{j}^{+}\not\sim z$ .

Given $I_{x}[v_{i},v_{j}]$ and $I_{y}[v_{k},v_{\ell}]$ , by Claim 3.1(1), we know that the two intervals can have at most one vertex in common. In case that they do have a common vertex, then it must be the case that $v_{j}=v_{k}$ . In this case, we let $I_{xy}[v_{i},v_{j},v_{k}]=I_{x}[v_{i},v_{j}]\cup I_{y}[v_{k},v_{\ell}]$ and call it a joint-interval. Finally, for $i,j\in[3,n-2]$ with $i\leq j$ , we define interval-gaps to be sets of consecutive vertices on $P$ that are all not adjacent to either $x$ or $y$ . A parallel-gap is $J[v_{i},v_{j}]:=V(v_{i}Pv_{j})$ such that $V(v_{i}Pv_{j})\cap(N(x)\cup N(y))=\emptyset$ and that $v_{i}^{-},v_{j}^{+}\in N(x)$ , or $v_{i}^{-},v_{j}^{+}\in N(y)$ , or $v_{i}^{-}\in N(x)$ but $v_{j}^{+}\in N(y)$ . A crossing-gap is $J[v_{i},v_{j}]:=V(v_{i}Pv_{j})$ such that $V(v_{i}Pv_{j})\cap(N(x)\cup N(y))=\emptyset$ and that $v_{i}^{-}\in N(y)$ and $v_{j}^{+}\in N(x)$ . By the range of $i$ and $j$ in the above definition, we see that each of $x$ and $y$ is not contained in any interval-gaps.

Let $\mathcal{I}_{x}$ be the set of $x$ -intervals that are not joint-intervals, $\mathcal{I}_{y}$ be the set of $y$ -intervals that are not joint-intervals, and $\mathcal{I}_{xy}$ be the set of joint-intervals. Let

p=|\mathcal{I}_{x}\cup\mathcal{I}_{y}|,\quad\text{and}\quad q=|\mathcal{I}_{xy}|.

Claim 3.2.

Each crossing-gap contains at least two vertices and there are at least $q-1$ distinct crossing-gaps when $q\geq 1$ .

Proof of Claim 3.2.

For the first part, suppose $\{v_{i}\}$ for some $i\in[2,n-1]$ is a crossing-gap with a single vertex. Then $C=v_{i+1}x\overset{\rightharpoonup}{P}v_{i-1}y\overset{\leftharpoonup}{P}v_{i+1}$ gives a Hamilton cycle of $G-v_{i}$ . We have $v_{i}\sim v_{i-1},v_{i+1}$ , and with respect to the cycle $\overset{\rightharpoonup}{C}$ , we have $x=v_{i+1}^{+}$ and $y=v_{i-1}^{+}$ . However, $\deg(x)+\deg(y)\geq n-t$ , contradicting Theorem 7. For the second part, assume that $q\geq 2$ . Let the $q$ common neighbors of $x$ and $y$ be $u_{1},\ldots u_{q}$ with $u_{1}\preceq u_{2}\ldots\preceq u_{q}$ . Thus $V(u_{i}Pu_{i+1})$ for each $i\in[1,q-1]$ is a set of vertices such that $u_{i}\sim y$ and $u_{i+1}\sim x$ . By the first part of this claim and Claim 3.1(1), we know that each of $V(u_{i}^{+}Pu^{-}_{i+1})$ for $i\in[1,q-1]$ contains at least two vertices that are adjacent to neither $x$ nor $y$ . By finding a minimal sub-path of $u_{i}^{+}\overset{\rightharpoonup}{P}u^{-}_{i+1}$ such that the predecessor of its left end is a neighbor of $y$ , the successor of its right end is a neighbor of $x$ , we can find two distinct vertices $w_{1},w_{2}\in V(u_{i}^{+}Pu^{-}_{i+1})$ with the following properties: $w_{1}\preceq w_{2}$ , $w_{1}^{-}\sim y$ , $w_{2}^{+}\sim x$ , and $V(w_{1}Pw_{2})\cap(N(x)\cap N(y))=\emptyset$ . Then $J[w_{1},w_{2}]$ is a crossing-gap. Since $V(u_{i}^{+}Pu^{-}_{i+1})$ and $V(u_{j}^{+}Pu^{-}_{j+1})$ are disjoint for distinct $i,j\in[1,q-1]$ , we can find $q-1$ distinct crossing-gaps. ∎

Let $p^{*}$ be the total number of distinct parallel-gaps and $q^{*}$ be the total number of distinct crossing-gaps. We let the set of $p^{*}$ parallel-gaps be $\{J[u_{i},w_{i}]:i\in[1,p^{*}],u_{1}\preceq w_{1}\preceq u_{2}\preceq w_{2}\preceq\ldots\preceq u_{p^{*}}\preceq w_{p^{*}}\}$ , and let $|J[u_{i},w_{i}]|=p_{i}$ . We also let the set of $q^{*}$ crossing-gaps be $\{J[r_{i},s_{i}]:i\in[1,q^{*}],r_{1}\preceq s_{1}\preceq r_{2}\preceq s_{2}\ldots\preceq r_{q^{*}}\preceq s_{q^{*}}\}$ , and let $|J[r_{i},s_{i}]|=q_{i}$ .

Claim 3.3.

We have $|\mathcal{I}_{x}\cup\mathcal{I}_{y}\cup\mathcal{I}_{xy}|=p+q\leq t-\sum\limits_{i=1}^{p^{*}}(p_{i}-1)-\sum\limits_{i=1}^{q^{*}}(q_{i}-2)$ .

Proof of Claim 3.3.

By the definition, the three sets $\mathcal{I}_{x},\mathcal{I}_{y},\mathcal{I}_{xy}$ are pairwise disjoint. Thus $|\mathcal{I}_{x}\cup\mathcal{I}_{y}\cup\mathcal{I}_{xy}|=p+q$ . Also, by our definition, we have $|N(x)\cap N(y)|=|\mathcal{I}_{xy}|=q$ and so $|N(x)\cup N(y)|\geq n-t-q$ . Since $|\mathcal{I}_{x}\cup\mathcal{I}_{y}\cup\mathcal{I}_{xy}|=p+q$ , and $v_{2}$ and $v_{n-1}$ are contained in an $x$ -interval, $y$ -interval, or joint-interval, it follows that there are exactly $p+q-1=p^{*}+q^{*}$ interval-gaps. By Claim 3.2, $q^{*}\geq q-1$ . As $x$ and $y$ are not contained in any interval-gaps, we get

	$\displaystyle t+q$	$\displaystyle\geq$	$\displaystyle\|V(G)\setminus(N(x)\cup N(y))\|\geq 2+\sum_{i=1}^{p^{}}p_{i}+\sum_{i=1}^{q^{}}q_{i}$
		$\displaystyle\geq$	$\displaystyle 2+p^{}+\sum\limits_{i=1}^{p^{}}(p_{i}-1)+2q^{}+\sum\limits_{i=1}^{q^{}}(q_{i}-2).$

As $p+q-1=p^{*}+q^{*}$ and $q^{*}\geq q-1$ , we get $p+q\leq t-\sum\limits_{i=1}^{p^{*}}(p_{i}-1)-\sum\limits_{i=1}^{q^{*}}(q_{i}-2)$ . Therefore,

|\mathcal{I}_{x}\cup\mathcal{I}_{y}\cup\mathcal{I}_{xy}|=p+q\leq t-\sum_{i=1}^{p}(p_{i}-1)-\sum_{i=1}^{q-1}(q_{i}-2),

as desired. ∎

Claim 3.4.

For any $i\in[2,n-2]$ , if $\{v_{i},v_{i+1}\}$ is a crossing-gap of size 2, then $v_{i}\not\sim v_{j}$ for any $j\in[3,n-2]$ such that $y\sim v_{j-1},v_{j+1}$ .

Proof of Claim 3.4.

We will show that $v_{i+1}$ has less than $2t$ neighbors in $G$ , to arrive a contradiction to $G$ being $t$ -tough.

By Claim 3.1(1)-(2), we know that for any $v_{k}\sim y$ with $v_{k}\preceq v_{i}$ on $P$ , we have $v_{i+1}\not\sim v_{k-1}$ ; and for $v_{k}\sim y$ with $v_{i}\preceq v_{k}$ on $P$ , we have $v_{i+1}\not\sim v_{k+1}$ . Thus vertices from $(N(y)\cap V(v_{2}Pv_{i}))^{-}$ and $(N(y)\cap V(v_{i+2}Pv_{n-1}))^{+}$ are non-neighbors of $v_{i+1}$ . Let

	$\displaystyle C=$	$\displaystyle v_{j}v_{i}\overset{\leftharpoonup}{P}xv_{i+2}\overset{\rightharpoonup}{P}v_{j-1}y\overset{\leftharpoonup}{P}v_{j}$	if $i<j$ ,
	$\displaystyle C=$	$\displaystyle v_{j}v_{i}\overset{\leftharpoonup}{P}v_{j+1}y\overset{\leftharpoonup}{P}v_{i+2}x\overset{\rightharpoonup}{P}v_{j}$	if $i>j$ .

Then $C$ is a Hamilton cycle of $G-v_{i+1}$ . The predecessors and successors of vertices below are all taken with respect to $\overset{\rightharpoonup}{C}$ . As $G$ is not Hamiltonian, both $N(v_{i+1})^{-}$ and $N(v_{i+1})^{+}$ are independent sets in $G$ . When $i<j$ , since $v_{i+1}\sim v_{i+2}$ and $x=v_{i+2}^{-}$ , it then follows that $v_{i+1}\not\sim z^{+}$ for any $z\in N(x)$ . As a consequence, we get $N(x)^{+}\cap N(v_{i+1})=\emptyset$ . When $i>j$ , since $v_{i+1}\sim v_{i+2}$ and $x=v_{i+2}^{+}$ , it then follows that $v_{i+1}\not\sim z^{-}$ for any $z\in N(x)$ . As a consequence, we get $N(x)^{-}\cap N(v_{i+1})=\emptyset$ .

The arguments above indicate that for every distinct vertex $z\in N(x)\cup N(y)$ , there is a unique non-neighbor of $v_{i+1}$ that is corresponding to $z$ . Thus $v_{i+1}$ has at least $|N(x)\cup N(y)|$ non-neighbors on $C$ . Then by Claim 3.3 that $q\leq t$ , we get

$\displaystyle\deg(v_{i+1})$	$\displaystyle\leq$	$\displaystyle n-1-\|N(x)\cup N(y)\|$
	$\displaystyle\leq$	$\displaystyle n-1-(n-t-q)$
	$\displaystyle\leq$	$\displaystyle 2t-1,$

a contradiction. ∎

We now construct a cutset $S$ of $G$ such that $|S|<2t$ . To do so, we define the following sets:

$\displaystyle S_{x}$	$\displaystyle=$	$\displaystyle\{v_{j},v_{j+1}:\text{$v_{j}$ is the right endvertex of an $x$-interval that is not a joint-interval}\},$
$\displaystyle S_{y}$	$\displaystyle=$	$\displaystyle\{v_{i},v_{j}:\text{$I_{y}[v_{i},v_{j}]$ is a $y$-interval that is not a joint-interval}\},$
$\displaystyle S_{xy}$	$\displaystyle=$	$\displaystyle\{v_{j},v_{k}:\text{$I_{xy}[v_{i},v_{j},v_{k}]$ is a joint-interval}\},$
$\displaystyle T_{1}$	$\displaystyle=$	$\displaystyle\bigcup_{\text{ $J[v_{i},v_{j}]$ is a parallel-gap of size at least 2}}J[v_{i},v_{j}],$
$\displaystyle T_{2}$	$\displaystyle=$	$\displaystyle\bigcup_{\text{ $J[v_{i},v_{j}]$ is a crossing-gap of size 3}}\left(J[v_{i},v_{j}]\setminus\{v_{j}\}\right),$
$\displaystyle T_{3}$	$\displaystyle=$	$\displaystyle\bigcup_{\text{ $J[v_{i},v_{j}]$ is a crossing-gap of size at least 4}}J[v_{i},v_{j}].$

Let

	$\displaystyle S=$	$\displaystyle S_{x}\cup S_{y}\cup S_{xy}\cup T_{1}\cup T_{2}\cup T_{3}$	if $\{v_{n-1}\}$ is a $y$ -interval,
	$\displaystyle S=$	$\displaystyle\left(S_{x}\cup S_{y}\cup S_{xy}\cup T_{1}\cup T_{2}\cup T_{3}\right)\setminus\{v_{n-1}\}$	otherwise.

We prove the following claims regarding what vertices are in $V(G)\setminus S$ and the size of $S$ .

Claim 3.5.

Let $v_{i}\in V(G)\setminus S$ for some $i\in[2,n-2]$ . Then $x\sim v_{i},v_{i+1}$ , or $y\sim v_{i-1},v_{i+1}$ , or $v_{i}$ is contained in a parallel-gap of size one such that $y\sim v_{i-1},v_{i+1}$ , or $v_{i}$ is contained in a crossing-gap of size two, or $v_{i}$ is the right endvertex of a crossing-gap of size three.

Proof of Claim 3.5.

By the definition of $S$ , we know that either $v_{i}$ is a neighbor of $x$ or $y$ , or $v_{i}$ is contained in a parallel-gap of size one, or a crossing-gap of size two or three. If $x\sim v_{i}$ , then by the definition of $S_{x}$ , we have $x\sim v_{i+1}$ . If $y\sim v_{i}$ , then by the definition of $S_{y}$ , we have $y\sim v_{i-1},v_{i+1}$ . If $v_{i}$ is contained in a parallel-gap of size one, then by the definition of $S_{x}$ , we know that $y\sim v_{i-1}$ . As $\{v_{i}\}$ is a parallel-gap, $y\sim v_{i-1}$ implies $y\sim v_{i+1}$ . If $v_{i}$ is contained in crossing-gap of size three, then $v_{i}$ is the right endvertex of a crossing-gap of size three by the definition of $T_{3}$ . ∎

Claim 3.6.

We have $|S|\leq 2t-1$ .

Proof of Claim 3.6.

For each crossing-gap $J[r_{i},s_{i}]$ of size $q_{i}$ , we let $q_{i}^{*}=q_{i}$ if $q_{i}\geq 4$ , $q_{i}^{*}=q_{i}-1$ if $q_{i}=3$ , and $q_{i}^{*}=0$ if $q_{i}=2$ . Note that by the definition of $S$ , only one vertex was deleted from the $y$ -interval containing $v_{n-1}$ . Now by the definition of $S$ and Claim 3.3, we have

$\displaystyle\|S\|$	$\displaystyle\leq$	$\displaystyle 2(p+q)-1+\sum_{i=1,p_{i}\geq 2}^{p^{}}p_{i}+\sum_{i=1}^{q^{}}q_{i}^{*}$
	$\displaystyle\leq$	$\displaystyle 2\left(t-\sum\limits_{i=1}^{p^{}}(p_{i}-1)-\sum\limits_{i=1}^{q^{}}(q_{i}-2)\right)-1+\sum_{i=1,p_{i}\geq 2}^{p^{}}p_{i}+\sum_{i=1}^{q^{}}q_{i}^{*}$
	$\displaystyle=$	$\displaystyle 2t-1+\sum_{i=1,p_{i}\geq 2}^{p^{}}\left(p_{i}-2(p_{i}-1)\right)+\sum\limits_{i=1}^{q^{}}\left(q_{i}^{*}-2(q_{i}-2)\right)$
	$\displaystyle\leq$	$\displaystyle 2t-1,$

where the last inequality follows as $p_{i}-2(p_{i}-1)\leq 0$ when $p_{i}\geq 2$ , and $q_{i}^{*}-2(q_{i}-2)\leq 0$ by the definition of $q_{i}^{*}$ and the fact that $q_{i}\geq 2$ for all $i\in[1,q^{*}]$ from Claim 3.2. ∎

Claim 3.7.

We have $c(G-S)\geq 2$ .

Proof of Claim 3.7.

For the sake of contradiction, suppose $G^{\prime}=G-S$ is connected. Let $X^{\prime}=N_{G^{\prime}}(x)\cup\{x\}$ and $Y^{\prime}=N_{G^{\prime}}(y)\cup\{y\}$ . Then, there must exists a path $P^{\prime}$ in $G^{\prime}$ connecting a vertex of $X^{\prime}$ and a vertex $Y^{\prime}$ and is internally-disjoint with $X^{\prime}\cup Y^{\prime}$ . Suppose that $P^{\prime}=uu_{1}\ldots u_{h}v$ for some $u\in X^{\prime}$ and $v\in Y^{\prime}$ . By Claim 3.5, we know that $v=y$ , or $v^{-},v^{+}\sim y$ , or $y=y_{n-1}$ when the $y$ -interval containing $y_{n-1}$ has size at least two, and that $u^{+}\sim x$ . By Claim 3.1(1) and (4), we know that $P^{\prime}\neq uv$ . Thus $P^{\prime}$ contains at least three vertices. As $P^{\prime}$ is internally-disjoint with $X^{\prime}\cup Y^{\prime}$ , $u_{1},\ldots,u_{h}$ are from interval-gaps of $P$ .

As again, $v=y$ , or $v^{-},v^{+}\sim y$ , or $y=y_{n-1}$ when the $y$ -interval containing $y_{n-1}$ has size at least two. Since $u_{h}\sim v$ , Claim 3.1(4) implies that $u_{h}^{+}\not\sim x$ . Thus $u_{h}$ is not the right endvertex of any crossing-gap. By Claim 3.4, $u_{h}$ is not the left endvertex of any crossing-gap of size two. Thus by Claim 3.5, $\{u_{h}\}$ is a parallel-gap of size one such that $y\sim u_{h}^{-},u_{h}^{+}$ . Now with $u_{h}$ in the place of $v$ , the same arguments as above imply that $\{u_{h-1}\}$ , if exists, is a parallel-gap of size one such that $y\sim u_{h-1}^{-},u_{h-1}^{+}$ . Similarly, for any $i\in[1,h-2]$ , if exists, we deduce that $\{u_{i}\}$ is a parallel-gap of size one such that $y\sim u_{i}^{-},u_{i}^{+}$ . As $u_{1}\sim u$ and $u^{+}\sim x$ , we get a contradiction to Claim 3.1(4). ∎

Now Claims 3.6 and 3.7 together give a controduction to the toughness of $G$ , completing the proof of Theorem 6. $\blacksquare$

4 Proof of Theorem 7

Theorem 7.

Proof.

Suppose to the contrary that there are distinct $x,y\in N(z)$ for which $\deg(x^{+})+\deg(y^{+})\geq n-t$ . As $G$ is not hamiltonian, $G$ is not a complete graph. Thus $\deg(z)=\deg(z,C)\geq 2t$ .

For $S\subseteq V(G)$ and $x\in V(G)$ , let $N(S)=\bigcup_{v\in S}N(v)$ and $N(x,S)=N(x)\cap S$ . For $u,v\in V(C)$ , we let $V_{uv}^{+}=V(u\overset{\rightharpoonup}{C}v)$ and $V_{uv}^{-}=V(u\overset{\leftharpoonup}{C}v)$ . We will construct a cutset $S$ of $G$ such that $\frac{|S|}{c(G-S)}<t$ . For this purpose, we define the following sets:

\begin{array}[]{lll}Y_{1}=N(y^{+},V^{+}_{y^{+}x})^{-},&Y_{2}=N(y^{+},V^{-}_{y^{+}x})^{+},&Y=Y_{1}\cup Y_{2},\\ X=N(x^{+}),&Z=N(z)^{+},&R=V(G)\setminus(X\cup Y\cup Z).\end{array}

In the following, we prove some properties of these sets.

Claim 4.1.

We have $X\cap Y=\emptyset$ .

Proof of Claim 4.1.

Suppose to the contrary that there exists $a\in X\cap Y$ . If $a\in Y_{1}$ , then $y^{+}\overset{\rightharpoonup}{C}ax^{+}\overset{\rightharpoonup}{C}yzx\overset{\leftharpoonup}{C}a^{+}y^{+}$ is a Hamilton cycle of $G$ . If $a\in Y_{2}$ , then $y^{+}\overset{\rightharpoonup}{C}ax^{+}\overset{\rightharpoonup}{C}yzx\overset{\leftharpoonup}{C}a^{+}y^{+}$ is a Hamilton cycle of $G$ . ∎

If there are $u,v\in Z$ with $u\in N(v)$ , then $uv\overset{\rightharpoonup}{C}u^{-}zv^{-}\overset{\leftharpoonup}{C}u$ is a Hamilton cycle in $G$ . Thus we have the following claim.

Claim 4.2.

The set $Z$ is an independent set in $G$ .

Claim 4.3.

We have $|R\cup(Z\setminus Y)|\leq t$ and $|Y\cap Z|\geq|R|+t$ .

Proof of Claim 4.3.

Clearly $|X\cup Y\cup Z|\leq n-|R|$ . Observe that $|X|=\deg(x^{+})$ and $|Y|=\deg(y^{+})$ . By Claim 4.1, we have $|X\cup Y|=|X|+|Y|\geq n-t$ ; and by Claim 4.2, we have $X\cap Z=\emptyset$ . Thus,

	$\displaystyle n-\|R\|\geq\|X\cup Y\cup Z\|$	$\displaystyle\geq$	$\displaystyle\|X\|+\|Y\|+\|Z\|-\|X\cap Z\|-\|Y\cap Z\|$		(1)
		$\displaystyle\geq$	$\displaystyle n-t+\|Z\|-\|Y\cap Z\|=n-t+\|Z\setminus Y\|,$		(1)

which gives $|R\cup(Z\setminus Y)|\leq t$ . For the second part, it follows from (1) by noting that $|Z|\geq 2t$ . ∎

We will take a subset $U$ of $(Y\cap X^{+})\cup(Y\cap X^{-})$ with size at least $t$ and show that deleting less than $4t$ vertices from $G$ produces at least $t$ components, and thus contradicts the assumption that $G$ is 4-tough. We let

U_{1}=Y\cap X^{+}\cap V^{+}_{yx},\quad U_{2}=Y\cap X^{-}\cap V^{-}_{yx},\quad U=U_{1}\cup U_{2}.

Claim 4.4.

We have $|U|\geq t$ .

Proof of Claim 4.4.

As $|Z\cap Y|\geq|R|+t$ , it suffices to show $|(Z\cap Y)\setminus U|\leq|R|$ . Let $u\in(Y\cap Z\cap V_{yx}^{+})\setminus U_{1}$ . Then we have $u^{-}\not\in X$ by the definition of $U_{1}$ . Also, we have $u^{-}\not\in Z$ because $u\in Z$ and $Z$ is an independent set by Claim 4.2. Furthermore, $u^{-}\not\in Y$ , as otherwise $y^{+}\sim u$ that contradicts $Z$ being independent in $G$ . Thus $u^{-}\in R\cap V(y^{+}\overset{\rightharpoonup}{C}x^{-})$ . Consider next that $u\in(Z\cap Y\cap V_{yx}^{-})\setminus U_{2}$ . Then we have $u^{+}\not\in X$ by the definition of $U_{2}$ . Also, we have $u^{+}\not\in Z$ and $u^{+}\not\in Y$ by the same argument as above. Thus $u^{+}\in R\cap V(x^{+}\overset{\rightharpoonup}{C}y)$ . Therefore we have

$\displaystyle\|(Z\cap Y)\setminus U\|$	$\displaystyle=$	$\displaystyle\|(Y\cap Z\cap V_{yx}^{+})\setminus U_{1}\|+\|(Z\cap Y\cap V_{yx}^{-})\setminus U_{2}\|$
	$\displaystyle=$	$\displaystyle\|\left((Z\cap Y\cap V_{yx}^{+})\setminus U_{1}\right)^{-}\|+\|\left((Z\cap Y\cap V_{yx}^{-}\right)\setminus U_{2})^{+}\|$
	$\displaystyle\leq$	$\displaystyle\|R\cap V(y^{+}\overset{\rightharpoonup}{C}x^{-})\|+\|R\cap V(x^{+}\overset{\rightharpoonup}{C}y)\|\leq\|R\|,$

as desired. ∎

Claim 4.5.

The set $U\cup\{z\}$ is an independent set in $G$ .

Proof of Claim 4.5.

Since $Z$ is an independent set by Claim 4.2, for any $u\in U_{1}$ , since $y^{+}\sim u^{+}$ and $y^{+}\in Z$ , it follows that $z\not\sim u$ ; and for any $u\in U_{2}$ , since $x^{+}\sim u^{+}$ and $x^{+}\in Z$ , it follows that $z\not\sim u$ . Thus $z$ it not adjacent to any vertex from $U$ . Next, let distinct $u,v\in U$ such that $u\sim v$ . Consider first that $u,v\in U_{1}$ . By symmetry, we assume that $u$ is in between $y$ and $v$ along $\overset{\rightharpoonup}{C}$ . Then $x\overset{\leftharpoonup}{C}vu\overset{\leftharpoonup}{C}y^{+}u^{+}\overset{\rightharpoonup}{C}v^{-}x^{+}\overset{\rightharpoonup}{C}yzx$ is a Hamilton cycle of $G$ . Next consider $u,v\in U_{2}$ . By symmetry, we assume that $u$ is in between $x$ and $v$ along $\overset{\rightharpoonup}{C}$ . Then $x\overset{\leftharpoonup}{C}y^{+}v^{-}\overset{\leftharpoonup}{C}u^{+}x^{+}\overset{\rightharpoonup}{C}uv\overset{\rightharpoonup}{C}yzx$ is a Hamilton cycle of $G$ . Finally, consider $u\in U_{1}$ and $v\in U_{2}$ . Then $x\overset{\leftharpoonup}{C}u^{+}y^{+}\overset{\rightharpoonup}{C}uv\overset{\leftharpoonup}{C}x^{+}v^{+}\overset{\rightharpoonup}{C}yzx$ is a Hamilton cycle in $G$ . Therefore, $U\cup\{z\}$ is an independent set in $G$ . ∎

We show that all except at most $2t$ vertices of $N(U)$ correspond to a vertex from $U$ . For this purpose, we introduce three new sets as follows.

$\displaystyle N^{*}(U_{1})$	$\displaystyle=$	$\displaystyle\bigcup_{u\in U_{1}}(N(u,V^{+}_{ux})^{-}\cup N(u,V^{-}_{ux})^{+}),$
$\displaystyle N^{*}(U_{2})$	$\displaystyle=$	$\displaystyle\bigcup_{u\in U_{2}}(N(u,V^{+}_{uy})^{-}\cup N(u,V^{-}_{uy})^{+}),$
$\displaystyle N^{*}(U)$	$\displaystyle=$	$\displaystyle N^{}(U_{1})\cup N^{}(U_{2})$

We can think of the definition of $N^{*}(U)$ above as a mapping from $N(U)$ to vertices in $N(U)^{+}\cup N(U)^{-}$ . For $v\in N^{*}(U)$ , we say that a vertex $u\in U$ generates $v$ if $v\in N(u,V^{+}_{ux})^{-}\cup N(u,V^{-}_{ux})^{+}$ when $u\in U_{1}$ , and if $v\in N(u,V^{+}_{uy})^{-}\cup N(u,V^{-}_{uy})^{+}$ when $u\in U_{2}$ .

A chord of $C$ is an edge $uv$ with $u,v\in V(C)$ and $uv\not\in E(C)$ . Two chords $ua$ and $vb$ of $C$ that do not share any endvertices form a crossing if the four vertices $u,a,v,b$ appear along $\overset{\rightharpoonup}{C}$ in the order $u,v,a,b$ or $u,b,a,v$ . We say that $u\in N^{*}(U)$ form a crossing with $v\in\{x^{+},y^{+}\}$ if there exist distinct vertices $a\in N(u)$ and $b\in N(v)$ such that such that $ua$ and $vb$ are crossing chords of $C$ .

Claim 4.6.

For $u\in U$ and $v\in\{x^{+},y^{+}\}$ , there exist no $a,b\in V(C)$ such that $ab\in E(C)$ , $a\in N^{*}(U)$ , and $ua$ and $vb$ form a crossing.

Proof of Claim 4.6.

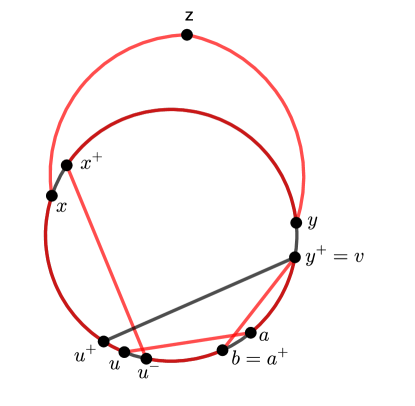
We proceed by contradiction. Assume that $u,v,a$ , and $b$ are as described in the claim. The definitions of $U_{1}$ and $U_{2}$ are symmetric up to reversing the direction of $\overset{\rightharpoonup}{C}$ and exchanging the roles of $x$ and $y$ . Thus we assume that $u\in U_{1}$ and consider two cases regarding $v=x^{+}$ or $v=y^{+}$ below. In each case, we construct a Hamilton cycle of $G$ , thereby achieving a contradiction to the assumption that $G$ is not Hamiltonian.

Consider first that $v=x^{+}$ . We let a Hamilton cycle $C^{*}$ of $G$ be defined as follows according to the location of the vertex $a$ on $\overset{\rightharpoonup}{C}$ :

$\displaystyle C^{*}=$	$\displaystyle ua\overset{\leftharpoonup}{C}y^{+}u^{+}\overset{\rightharpoonup}{C}xzy\overset{\leftharpoonup}{C}x^{+}b\overset{\rightharpoonup}{C}u$	if $a\in V_{y^{+}u}^{+}$ (in this case $b=a^{+}$ ). See Figure 1(a).
$\displaystyle C^{*}=$	$\displaystyle ua\overset{\leftharpoonup}{C}xzy\overset{\rightharpoonup}{C}x^{+}b\overset{\rightharpoonup}{C}u^{+}y^{+}\overset{\leftharpoonup}{C}u$	if $a\in V_{u^{+}x}^{+}$ (in this case $b=a^{-}$ ).
$\displaystyle C^{*}=$	$\displaystyle ua\overset{\leftharpoonup}{C}x^{+}b\overset{\rightharpoonup}{C}yzx\overset{\leftharpoonup}{C}u^{+}y^{+}\overset{\rightharpoonup}{C}u$	if $a\in V_{x^{+}y}^{+}$ (in this case $b=a^{+}$ ).

Consider then that $v=y^{+}$ . We let a Hamilton cycle $C^{*}$ of $G$ be defined as follows according to the location of the vertex $a$ on $\overset{\rightharpoonup}{C}$ :

	$\displaystyle C^{*}=$	$\displaystyle ua\overset{\leftharpoonup}{C}y^{+}b\overset{\rightharpoonup}{C}u^{-}x^{+}\overset{\rightharpoonup}{C}yzx\overset{\leftharpoonup}{C}u$	if $a\in V_{y^{+}u}^{+}$ (in this case $b=a^{+}$ ). See Figure 1(b).
	$\displaystyle C^{*}=$	$\displaystyle ua\overset{\leftharpoonup}{C}xzy\overset{\rightharpoonup}{C}x^{+}u^{-}\overset{\rightharpoonup}{C}y^{+}b\overset{\rightharpoonup}{C}u$	if $a\in V_{u^{+}x}^{+}$ (in this case $b=a^{-}$ ).

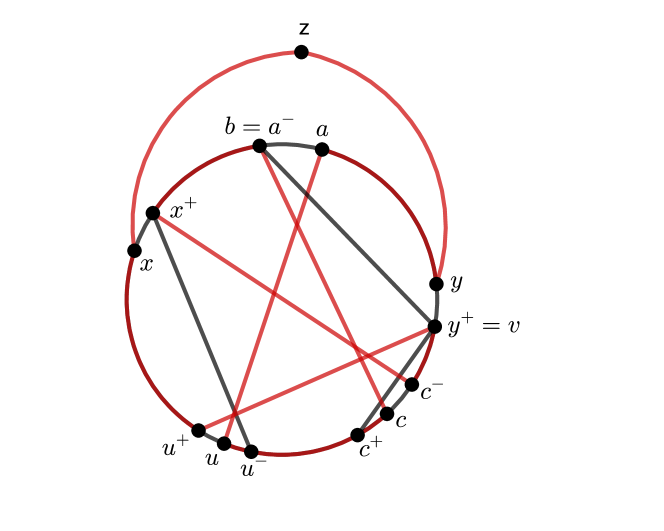
Refer to caption — Figure 1: Illustration of the cycle $C^{*}$ , drawn in red.

Lastly, let $a\in V_{x^{+}y}^{+}$ . In this case, we have $b=a^{-}$ . Let $c\in U$ be the vertex that generates $a$ . Then $C^{*}$ is constructed according to the location of $c$ on $\overset{\rightharpoonup}{C}$ :

$\displaystyle C^{*}=$	$\displaystyle ua\overset{\rightharpoonup}{C}yzx\overset{\leftharpoonup}{C}u^{+}y^{+}\overset{\rightharpoonup}{C}c^{-}x^{+}\overset{\rightharpoonup}{C}bc\overset{\rightharpoonup}{C}u$	if $c\in V_{y^{+}u}^{+}$ . See Figure 2.
$\displaystyle C^{*}=$	$\displaystyle ua\overset{\rightharpoonup}{C}yzx\overset{\leftharpoonup}{C}cb\overset{\leftharpoonup}{C}x^{+}c^{-}\overset{\leftharpoonup}{C}u^{+}y^{+}\overset{\rightharpoonup}{C}u$	if $c\in V_{u^{+}x}^{+}$ .
$\displaystyle C^{*}=$	$\displaystyle ua\overset{\leftharpoonup}{C}ac^{+}x^{+}\overset{\rightharpoonup}{C}ca^{+}\overset{\rightharpoonup}{C}yzx\overset{\leftharpoonup}{C}u^{+}y^{+}\overset{\rightharpoonup}{C}u$	if $c\in V_{x^{+}a}^{+}$ .
$\displaystyle C^{*}=$	$\displaystyle ua\overset{\rightharpoonup}{C}cb\overset{\leftharpoonup}{C}x^{+}c^{+}\overset{\rightharpoonup}{C}yzx\overset{\leftharpoonup}{C}u^{+}y^{+}\overset{\rightharpoonup}{C}u$	if $c\in V_{a^{+}y}^{+}$ .

∎

We will show next that $|N(U)|\leq 4|U|$ . In this way, after deleting $N(U)$ of at most $4|U|$ vertices, we will get at least $|U|+1$ components and so get a contradiction to the toughness of $G$ .

Claim 4.7.

We have $|N(U)|\leq 2t+2|U|$ .

Proof of Claim 4.7.

By the definition of $N^{*}(U)$ , we know that $N(U)\subseteq(N^{*}(U))^{+}\cup(N^{*}(U))^{-}$ . Now to prove Claim 4.7, it suffices to show that $|N^{*}(U)\setminus U|\leq t$ because if this is true then we get

\displaystyle|N(U)|

\displaystyle\leq

\displaystyle|(N^{*}(U)\setminus U)^{+}|+||(N^{*}(U)\setminus U)^{-}|+|U^{+}|+|U^{-}|\leq 2t+2|U|.

We show that $|N^{*}(U)\setminus U|\leq|R\cup(Z\setminus Y)|$ , which would get us the desired upper bound by the first part of Claim 4.3.

The proof requires several cases. In most cases, we show that for each distinct element of $N^{*}(U)\setminus U$ in the given case, there is a distinct element of $R\cup(Z\setminus Y)$ . Let $u\in N^{*}(U)\setminus U$ and $v\in U$ such that $v$ generates $u$ . Recall that $U_{1}=Y\cap X^{+}\cap V^{+}_{yx}$ and $U_{2}=Y\cap X^{-}\cap V^{-}_{yx}$ . Since the definitions of $U_{1}$ and $U_{2}$ are symmetric up to reversing the direction of $\overset{\rightharpoonup}{C}$ and exchanging the roles of $x$ and $y$ , we prove the case $v\in U_{1}$ only.

Consider first that $u\not\in Y$ . We may assume $u\not\in Z$ as otherwise $u\in Z\setminus Y$ . Now we must have $u\not\in X$ since otherwise $x^{+}u$ and $vu^{-}$ form a crossing if $u^{-}\in N(v)$ and $x^{+}u$ and $vu^{+}$ form a crossing if $u^{+}\in N(v)$ , contradicting Claim 4.6. Therefore $u\not\in X\cup Y\cup Z$ and so $u\in R$ . Thus in the following cases, we assume $u\in Y$ . Recall that we assumed $v\in U_{1}$ .

Suppose first that $u\in V_{vx}^{+}$ . Then $u\in N^{*}(U)\setminus U$ implies $u\not\in Y\cap X^{+}$ . Since $u\in Y$ , we must have $u\not\in X^{+}$ . This implies that $u^{-}\not\in X$ . We next claim that $u^{-}\not\in Y$ , as otherwise $y^{+}u^{-}$ and $vu^{+}$ form a crossing. Thus $u^{-}\in(Z\setminus Y)\cup R$ .

Suppose then that $u\in V_{x^{+}y}^{+}$ . Then $u\in N^{*}(U)\setminus U$ implies $u\not\in Y\cap X^{-}$ . As $u\in Y$ , we get $u^{+}\notin X$ . Also, $u^{+}\notin Y$ . Otherwise, $y^{+}u\overset{\rightharpoonup}{C}yzx\overset{\leftharpoonup}{C}vu^{-}\overset{\leftharpoonup}{C}x^{+}v^{-}\overset{\leftharpoonup}{C}y^{+}$ is a Hamilton cycle in $G$ . Thus $u^{+}\in R\cup(Z\setminus Y)$ . In particular, in this case, $u\neq y$ . For otherwise, suppose $u=y$ , then $vy^{-}\overset{\leftharpoonup}{C}x^{+}v^{-}\overset{\leftharpoonup}{C}yzx\overset{\leftharpoonup}{C}v$ is a Hamilton cycle in $G$ . Thus $u^{+}\neq y^{+}$ .

Lastly, consider $u\in V_{y^{+}v}^{+}$ . Then $u\in N^{*}(U)\setminus U$ implies $u\not\in Y\cap X^{+}$ . As $u\in Y$ , we must have $u\not\in X^{+}$ , which gives $u^{-}\not\in X$ . By Claim 4.6, $u^{-}\notin Y$ . Lastly, $u^{-}\notin Z$ , as otherwise $zu^{--}\overset{\leftharpoonup}{C}x^{+}v^{-}\overset{\leftharpoonup}{C}u^{-}v\overset{\rightharpoonup}{C}xz$ is a Hamilton cycle in $G$ . Thus $u^{-}\in(Z\setminus Y)\cup R$ . Since $u\neq y^{+}$ , it follows that $u^{-}\neq y$ .

The three sets $V_{vx}^{+}$ , $V_{x^{+}y}^{+}$ , and $V_{y^{+}v}^{+}$ are disjoint, we have $u^{+}\neq y^{+}$ when $u\in V_{x^{+}y}^{+}$ , and we have $u^{-}\neq y$ when $u\in V_{y^{+}v}^{+}$ . Thus the argument above implies that distinct vertices from $N^{*}(U)\setminus U$ correspond to distinct vertices from $(Z\setminus Y)\cup R$ . Therefore $|N^{*}(U)\setminus U|\leq|R\cup(Z\setminus Y)|$ , as desired. ∎

Now, set $S=N(U)$ . Then $|S|\leq 2t+2|U|\leq 4|U|$ by Claims 4.7 and 4.4. By Claim 4.5, $c(G-S)\geq|U|+1$ , where $|U|$ of the components are isolated vertices from $U$ , and one component contains the vertex $z$ . This gives $\frac{|S|}{c(G-S)}\leq\frac{4|U|}{|U|+1}<4$ , which contradicts that $G$ is 4-tough. This completes the proof of Theorem 7. $\blacksquare$

References

[1] D. Bauer, H. J. Broersma, J. van den Heuvel, and H. J. Veldman. Long cycles in graphs with prescribed toughness and minimum degree. Discrete mathematics, 141(1-3):1–10, 1995.
[2] J. A. Bondy and U. S. R. Murty. Graph theory with applications. American Elsevier Publishing Co., Inc., New York, 1976.
[3] V. Chvátal. On hamilton’s ideals. Journal of Combinatorial Theory, Series B, 12(2):163–168, 1972.
[4] V. Chvátal. Tough graphs and hamiltonian circuits. Discrete Mathematics, 5(3):215–228, 1973.
[5] C. T. Hoàng. Hamiltonian degree conditions for tough graphs. Discrete mathematics, 142(1-3):121–139, 1995.
[6] C. T. Hoàng and C. Robin. A closure lemma for tough graphs and hamiltonian degree conditions. Discrete Mathematics, 347(4):113872, 2024.

	$\displaystyle\|S\|\leq$	$\displaystyle\|\Omega\|=k$	if $\|\Omega\|=k$ ,
	$\displaystyle\|S\|\leq$	$\displaystyle\|\Omega\|+k\leq 2k-1$	if $\|\Omega\|=k-1$ .

$\displaystyle\|(Z\cap Y)\setminus U\|$	$\displaystyle=$	$\displaystyle\|(Y\cap Z\cap V_{yx}^{+})\setminus U_{1}\|+\|(Z\cap Y\cap V_{yx}^{-})\setminus U_{2}\|$
	$\displaystyle=$	$\displaystyle\|\left((Z\cap Y\cap V_{yx}^{+})\setminus U_{1}\right)^{-}\|+\|\left((Z\cap Y\cap V_{yx}^{-}\right)\setminus U_{2})^{+}\|$
	$\displaystyle\leq$	$\displaystyle\|R\cap V(y^{+}\overset{\rightharpoonup}{C}x^{-})\|+\|R\cap V(x^{+}\overset{\rightharpoonup}{C}y)\|\leq\|R\|,$