Deformation dynamics of an oil droplet into a crescent shape during intermittent motion

(+)-Camphor and oil red O (dye) were purchased from FUJIFILM Wako Pure Chemical Corporation (Japan), and paraffin was purchased from Sigma-Aldrich (USA). The chemicals were used without further purification. Ion-free water was obtained using Elix UV3 (Merck, Germany). We prepared a paraffin solutions of camphor and oil red O at different concentrations by stirring using a vortex mixer and sonication.

We observed the time evolution of $20~{}\mu\mathrm{L}$ droplets located on the water surface in a Petri dish with an inner diameter of $194.5~{}\mathrm{mm}$. The time evolution of the system was recorded from above for an hour at $50~{}\mathrm{fps}$ with the CMOS camera (STC-MBS43U3V, OMRON SENTECH Co., LTD., Japan) equipped with the objective lens (3Z4S-LE SV-0814H, OMRON Co., LTD., Japan). The Petri dish was illuminated by a light panel placed below.

All experiments were performed at room temperature ($22\pm 2{}^{\circ}\mathrm{C}$). The recorded videos were analyzed using an image-processing software ImageJ[43].

The interfacial tension between pure water and oil was measured using the pendant drop method. Paraffin containing oil red O was ejected through a hook-shaped needle (4983 PD 22G, Kyowa Interface Science Co., Japan) into the aqueous phase. The droplet image was recorded from the side with the above-mentioned camera equipped with the objective lens (TEC-M55, CBC Co., Ltd., Japan). It was illuminated by the LED lamp (AS3000, AS ONE Co., Japan) located at the opposite side to the camera. The interfacial tension was calculated by fitting the shape of an oil droplet to a theoretical curve. The details are described in Appendix A.

The motion of a $20~{}\mu\mathrm{L}$ droplet of paraffin with dissolved camphor (concentration $0.06~{}\mathrm{M}$) and oil red O (concentration $1.0~{}\mathrm{g/L}$) clearly demonstrated the transient character of the phenomenon. Three different types of motion could be easily distinguished for different times $t$ elapsed from the moment when the droplet was placed on the water surface. At the beginning of the experiment, the droplet showed self-propelled motion along a straight line perturbed by reflections with the dish wall, as illustrated in Fig. 1(a-1). Approximately at $t=30~{}\mathrm{s}$, the droplet began to rotate along the wall (Fig. 1(a-2)). Such type of motion was observed for over $1500~{}\mathrm{s}$. The droplet speed began to oscillate with an increasing amplitude and a decreasing average as illustrated in Fig. 1(b). Then, at $t\sim 2000~{}\mathrm{s}$, the droplet motion switched to intermittent one (Fig. 1(a-3)). At this stage, short intervals of time when a droplet moved (less than $10~{}\mathrm{s}$) were separated by periods when it was standing. The droplet had a circular shape when it did not move, and it became elongated and exhibited deformation into a crescent shape during intermittent motion. We observed a monotonic decrease in the peak speed as a function of time. It can be anticipated that the changes in the character of motion are related to the rate of camphor release, which decreases the water surface tension around it. However, as we discuss below, the slow modification of interfacial tension of the oil-water interface resulting from the presence of dye molecules near the surface is another factor leading to intermittent motion.

Hereafter, we focus on the intermittent motion shown in Fig. 1(a-3). We defined a single phase of intermittent motion based on the droplet speed as a function of time (cf. Fig. 3(b)). If the droplet stopped ($v\leq 2~{}\mathrm{mm/s}$) for more than $4~{}\mathrm{s}$, then we assumed that the droplet was at the rest state. If the droplet at the rest state accelerated and its speed exceeded $10~{}\mathrm{mm/s}$, then we considered this moment as the start of the intermittent phase. In the case that the time duration between the start of motion and the return to the rest state was less than $10~{}\mathrm{s}$, we defined that the droplet had performed an intermittent motion, and we analyzed the time series during each intermittent motion in detail. To minimize the boundary effect we did not analyze the intermittent motion if the droplet got closer than $20~{}\mathrm{mm}$ to the wall of the Petri dish. In case that a droplet exhibited fission, we excluded the data after the fission.

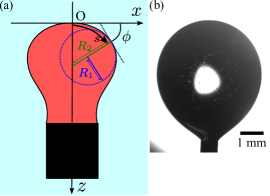
In the following analysis, we focused on the correlations between the droplet speed and dynamic deformation into a crescent shape observed during the intermittent motion (Fig. 1(a-3)). The observed droplet elongation was always perpendicular to the direction of motion. For quantitative study on the deformation dynamics, we introduced the local coordinates associated with the direction of motion. Each frame of the observed time evolution was processed so that pixels representing the droplet were black (the logical value $1$) and all the others were white (the logical value $0$). For each frame, we calculated the droplet center $\bm{r}_{\mathrm{c}}(t)$ as the center of mass (COM) of the black pixels. The set of droplet centers defined the droplet trajectory. The origin of the local coordinate system was set at $\bm{r}_{\mathrm{c}}(t)$. The $Y$-axis was defined as parallel to a fitting line to the droplet trajectory with a least-square method and directed as the net displacement vector. The $X$-axis was set perpendicular to the $Y$-axis. Using these coordinates, we defined the time-dependent aspect ratio $R=a/b$, where $b$ is the width of the droplet measured on the $Y$-axis and $a$ is the length of the droplet projected on the $X$-axis as illustrated in Fig. 2(a). The second quantity describing time-dependent droplet shape is the front-back asymmetric parameter $A=\Delta\Sigma/(2\Sigma)$, where $\Sigma$ is the area (the number of black pixels) of the droplet image and $\Delta\Sigma$ is the area of the figure obtained by applying XOR operation to the original droplet image and its image reflected with respect to the $X$-axis as shown in Fig. 2(b). It should be noted that $0\leq A\leq 1$ and $A=0$ for a droplet with mirror symmetry on the $X$-axis.

Figure 3(a) shows the speed $v(t)$ of the droplet center $(\bm{r}_{\mathrm{c}}(t))$ and the deformations $R(t)$ and $A(t)$ as functions of time during a single phase of intermittent motion illustrated in Fig. 3(b). The time $\Delta t=0$ corresponds to the moment when $v(t)$ has the maximum value. As shown in Fig. 3(a), the deformations began almost simultaneously when motion started. The speed $v(t)$ reached its maximum before the maxima of $R(t)$ and $A(t)$, which means that deformations still developed after the droplet started to slow down. The comparison between $v(t)$, $R(t)$ and $A(t)$ shows that the maximum acceleration appeared when the values of both the parameters describing deformation were around $50\%$ of their maximum.

The behavior illustrated in Fig. 3(a) was reproduced in many observations of intermittent motion, as shown in Fig. 4, in which the scatter plot of the time $\Delta t_{R}$ for the maximum of $R(t)$ and $\Delta t_{A}$ for the maximum of $A(t)$ is displayed. In almost all analyzed cases, both $\Delta t_{R}$ and $\Delta t_{A}$ were positive, and $\Delta t_{A}$ was slightly greater than $\Delta t_{R}$.

Next, we investigated the dependence of the droplet deformation on the oil red O concentration. We performed experiments at oil red O concentrations in the range of $0.5$–$1.1~{}\mathrm{g/L}$. The maximum values of $R(t)$ and $A(t)$ ($R_{\mathrm{max}}$ and $A_{\mathrm{max}}$) increased for oil red O concentrations larger than $0.8~{}\mathrm{g/L}$ as shown in Fig. 5.

To understand the role of oil red O during the droplet evolution, we measured the interfacial tension $\gamma_{\mathrm{ow}}(t)$ between a paraffin droplet containing oil red O and pure water using the pendant drop method[44] as a function of time. The method is described in Appendix A. The measurements were performed for various oil red O concentrations. For the oil red O concentration $\geq 0.5~{}\mathrm{g/L}$, the interfacial tension gradually decreased in time after the interface was formed as shown in Fig. 6. Assuming that the diffusional transport of oil red O molecules and the linear absorption process of them at the droplet interface are responsible for the decrease in the interfacial tension, the time evolution of the interfacial tension should be described as an exponential relaxation. Thus, for quantitative evaluation, we fitted time-dependent interfacial tension $\gamma_{\mathrm{ow}}(t)$ to an exponential function

where $\gamma_{\mathrm{ow}}^{(0)}$ is the interfacial tension at the initial stage, $\Delta\gamma_{\mathrm{ow}}=(\gamma_{\mathrm{ow}}^{(0)}-\gamma_{\mathrm{ow}}(\infty))$ is the difference in interfacial tension between the initial and final stages , and $\tau$ is the characteristic time for the decrease in interfacial tension. This functional form comes from the model describing the rate of relaxation of interfacial tension towards its stable value as proportional to $(\gamma_{\mathrm{ow}}(\infty)-\gamma_{\mathrm{ow}}(t))$. Such behavior can be expected when the dye is absorbed on the droplet surface. We plotted $\gamma_{\mathrm{ow}}^{(0)}$, $\Delta\gamma_{\mathrm{ow}}$ and $\tau$ against oil red O concentration in Fig. 7. $\gamma_{\mathrm{ow}}^{(0)}$ and $\Delta\gamma_{\mathrm{ow}}$ were decreasing and increasing functions of oil red O concentration, respectively. In the case when the decrease in interfacial tension was clearly observed (oil red O concentrations: $0.5$, $0.8$, and $1.0~{}\mathrm{g/L}$), $\tau$ was approximately equal to $800~{}\mathrm{s}$. In addition, we performed the same measurement for the oil droplet that contained both oil red O ($1.0~{}\mathrm{g/L}$) and camphor ($0.06~{}\mathrm{M}$). The decrease in interfacial tension was also observed, and $\gamma_{\mathrm{ow}}^{(0)}$ was lower compared to paraffin droplet with oil red O ($1.0~{}\mathrm{g/L}$) but without camphor.

To better understand the droplet deformation phenomenon, we evaluated two related dimensionless numbers. First, the capillary number $\mathrm{Ca}$ is the ratio of the viscous force and interfacial tension, $\mathrm{Ca}=\mu v/\gamma_{\mathrm{ow}}$, where $\mu$ is the viscosity of the liquid, $v$ is the characteristic velocity, and $\gamma_{\mathrm{ow}}$ is the characteristic value for oil/water interfacial tension. By substituting $\mu\simeq 2\times 10^{-1}~{}\mathrm{Pa\,s}$ (paraffin), $v\simeq 10^{-2}~{}\mathrm{m/s}$, and $\gamma_{\mathrm{ow}}\simeq 60\times 10^{-3}~{}\mathrm{N/m}$, we obtain $\mathrm{Ca}\simeq 3\times 10^{-2}\ll 1$. This means that during an intermittent motion, the relative effect of viscous drag forces is much smaller than that of surface tension.

Next, the Weber number $\mathrm{We}$ is the relative importance of the fluid inertia compared to its surface tension. $\mathrm{We}=\rho rv^{2}/\gamma_{\mathrm{ow}}$, where $\rho$ is the mass density of the liquid and $r$ is the characteristic length. For $\rho\simeq 10^{3}~{}\mathrm{kg/m^{3}}$, $r\simeq 10^{-2}~{}\mathrm{m}$ and other parameter values listed above, we obtained $\mathrm{We}\simeq 2\times 10^{-5}\ll 1$. This means that the inertial effects are negligible during an intermittent motion. Considering both the dimensionless numbers, we concluded that the surface tension difference around the droplet plays the most important role in droplet deformation.

In the following, we use the approximation of droplet free energy to derive the energy condition for a spontaneous deformation of droplet shape. If we neglect the contribution of the periphery, then the free energy of a floating droplet shown in Fig. 8 is estimated as:

Here, $S=\gamma_{\mathrm{aw}}-(\gamma_{\mathrm{ow}}+\gamma_{\mathrm{ao}})$ is the spreading coefficient, $\gamma_{\mathrm{aw}}$ and $\gamma_{\mathrm{ao}}$ are the interfacial tensions between air and water and between air and oil, respectively, $g$ is the gravitational acceleration, $\Sigma$ is the area of the droplet, and $\Delta\rho_{\mathrm{ao}}$ and $\Delta\rho_{\mathrm{ow}}$ are the density differences between air and oil and that between oil and water, respectively, as shown in Fig. 8. In Eq. (2), $e_{\mathrm{ao}}$ and $e_{\mathrm{ow}}$ are the differences in height between the water level at infinity and the air/oil interface, and that between the water level at infinity and the oil/water interface, respectively. For the following analyses, we neglected the second term in Eq. (2) as it is much smaller than the first term since the thickness of a droplet is of the order of $100~{}\mu\mathrm{m}$, thus much smaller than the droplet size.

The second contribution to droplet energy comes from the curvature of its outer edge. The excess energy of the triple line per unit length equals:

where $\kappa_{\mathrm{ao}}^{-1}$ and $\kappa_{\mathrm{ow}}^{-1}$ are capillary lengths of air/oil and oil/water interfaces, respectively. $\theta_{\mathrm{ao}}(x=0)$ is the angle between the air/oil interface and the $x$-axis at the triple line, and $\theta_{\mathrm{ow}}(x=0)$ is that between the oil/water interface and the $x$-axis. We calculated the excess energy of the triple line using the relationships linking the angles $\theta_{\mathrm{ao}}(x=0)$, $\theta_{\mathrm{ow}}(x=0)$ with the interfacial tensions derived in Appendix A.3.

The change in free energy related to droplet deformation can be approximated as:

where the first term is the energy for an increase in droplet area by $\Delta\Sigma$, and the second describes the energy for an increase in droplet periphery $\Delta l$. If the surface tension difference between the front and back of the droplet is $\delta\gamma_{\mathrm{aw}}$ and the droplet moved on a water surface by an area of $\sigma$, then the work exerted on the droplet is estimated as

To support self-motion with deformation, the energy gain due to the surface tension gradient should exceed the free energy increase due to the droplet deformation depending on the interfacial tension. If the excess energy of the triple line dominates, the system relaxes towards a circular shape as, for example, demonstrated in the case of soap films[45]. In our system, the quasi-elastic laser scattering (QELS) measurements shown in Appendix B suggested that the value of $\delta\gamma_{\mathrm{aw}}$ does not exceed $0.3~{}\mathrm{mN/m}$, though we were not able to measure this value directly. For the following calculations, we used $\delta\gamma_{\mathrm{aw}}=0.25~{}\mathrm{mN/m}$. During the intermittent motion shown in Fig. 3, we observed $\Delta\Sigma=3.3~{}\mathrm{mm}^{2}$, $\Delta l=17.2~{}\mathrm{mm}$ and $\sigma=1288.5~{}\mathrm{mm}^{2}$. For these parameters and values of interfacial tensions measured by the Wilhelmy method: $\gamma_{\mathrm{ao}}=31.6~{}\mathrm{mN/m}$ and $\gamma_{\mathrm{aw}}=73.5~{}\mathrm{mN/m}$, the values of $\Delta E_{\Sigma}=S\Delta\Sigma$, $\Delta E_{l}=\mathcal{T}\Delta l$ and $W$ are plotted as functions of $\gamma_{\mathrm{ow}}$ in Fig. 9(a). For these realistic values of parameters ($\gamma_{\mathrm{ow}}\sim 50~{}\mathrm{mN/m}$), $\Delta E_{\Sigma}+\Delta E_{l}$, and $W$ are of the same order, which implies that the deformation of a droplet can occur. $\Delta E_{\Sigma}(\gamma_{\mathrm{ow}})$ and $\Delta E_{l}(\gamma_{\mathrm{ow}})$ are increasing functions of interfacial tension $\gamma_{\mathrm{ow}}$, while $W$ does not depend on it. The increase in $\Delta E_{l}(\gamma_{\mathrm{ow}})$ is faster than that in $\Delta E_{\Sigma}(\gamma_{\mathrm{ow}})$, which means that the line energy is the most important for droplet deformation. Figure 9(b) shows the deformation energy normalized by the work exerted on the droplet. For the selected parameter values, the spontaneous droplet deformation can occur when $\Delta E/W<1$, which happens if $\gamma_{\mathrm{ow}}\lesssim 47~{}\mathrm{mN/m}.$ Having in mind that $\gamma_{\mathrm{ow}}$ is a decreasing function of oil red O concentration (cf. Fig. 6), we can see why droplet deformation occurs for droplets with a higher concentration of oil red O. The estimated threshold for deformation is a bit lower than expected from the results discussed in the previous chapter. There could be many reasons for this. First, the estimation is based on a simple model. Second, the local inhomogeneities in oil red O concentration, especially those near the droplet boundary, can trigger local shape changes. And finally, there may be possible errors in the measurements of interfacial tension. For example, the threshold should increase for the lower value of $\gamma_{\mathrm{ao}}$.

The discussion of energetic aspects of droplet deformation indicates that a deformation occurs easier for a long time $t$ after the droplet is placed on the water surface. To verify this observation, we investigated deformations of paraffin droplets with oil red O that do not contain camphor. Of course, if such droplets are placed on the water surface they do not move and do not change their shapes. The surface tension gradient necessary for the motion was induced by touching the water surface close to the droplet with a camphor piece at time $T$ after the droplet had been placed on water. The experiment with a $20~{}\mu\mathrm{L}$ paraffin droplet containing oil red O (concentration $1.0~{}\mathrm{g/L}$) is illustrated in Fig. 10. As a camphor source, we used a $3~{}\mathrm{mm}$-diameter camphor disk located around $5~{}\mathrm{mm}$ away from the droplet boundary. After the camphor disk touched the surface, the droplet moved away from the source with deformation into a crescent shape, as shown in Fig. 10(a). We performed experiments for $T=30,180,300,600~{}\mathrm{s}$ and plotted the characteristic parameters describing the droplet shape dynamics in Fig. 10(b). The time $\Delta T=0$ corresponds to when the droplet COM speed $v$ has the maximum value. The maximum magnitude of deformation $A_{\mathrm{max}}$ increased with $T$ as shown in Fig. 10(b-2). The shape of the droplet was the most curved when $T=600~{}\mathrm{s}$, which can explain why $R_{\mathrm{max}}(T=600~{}\mathrm{s})$ was smaller than that when $T=300~{}\mathrm{s}$. Figure 10(b-3) shows a scatter plot of the times $\Delta T_{R}$ and $\Delta T_{A}$, at which the maximum values of $R$ and $A$ ($R_{\mathrm{max}}$ and $A_{\mathrm{max}}$) were observed. Both $\Delta T_{R}$ and $\Delta T_{A}$ were positive and had almost the same value. This result is similar to those for the spontaneous deformation of a droplet with camphor shown in Fig. 4, though the relationship between $\Delta T_{R}$ and $\Delta T_{A}$ was slightly different from that between $\Delta t_{R}$ and $\Delta t_{A}$. However, the times $\Delta T_{R}$ and $\Delta T_{A}$ were over twice as large as $\Delta t_{R}$ and $\Delta t_{A}$. The difference can be attributed to the larger surface concentration gradient in the case of a camphor-free droplet than the one appearing for the paraffin droplet with camphor. When $T=30$ s, the droplet hardly deformed, as shown in Fig. 10(c), and the characteristic parameters could not be appropriately obtained. These results indicate that for longer $T$ of the order of $10$ minutes, the modification of the droplet interface becomes more efficient, leading to more pronounced droplet deformation.

In this subsection, we focus our attention on time-dependent velocity and deformation during the intermittent droplet motion. In particular, we focus our attention on the role of the oil red O because in the previous study, a large deformation of a droplet shape without fission has not been observed without oil red O[41].

The results shown in Figs. 3, 4 and 10 indicate complex interactions between camphor and oil red O. For a droplet forced to move by an external source, $\Delta T_{A}$ and $\Delta T_{R}$ seem perfectly correlated. In this case, the time difference between the peak of velocity and that of the deformation can be as long as $4~{}\mathrm{s}$ and increases with time $T$. For a droplet containing camphor, $\Delta t_{A}$ and $\Delta t_{R}$ are much shorter ($<1.5~{}\mathrm{s}$). Moreover, $\Delta t_{R}<\Delta t_{A}$, but the values are weakly correlated. The different relationship between the peaks can be attributed to the presence of surface active molecules inside a droplet.

To learn more about the intermittent motion mechanism and understand the relationship between time-dependent droplet velocity and shape deformation (cf. Figs. 3 and 4), we observed surface flows around the droplet exhibiting an intermittent motion. The flows were traced by small plastic particles (HP20SS, DIAION SEPABEADS, Mitsubishi Chemical, Japan), whose diameters were in the range of $60$–$150~{}\mu\mathrm{m}$ and the density was $1.01~{}\mathrm{kg/L}$. The particles were floating at the water surface due to the hydrophobic properties of their surfaces.

The snapshots illustrating the evolution of droplets and flows are shown in Fig. 11. Before the droplet started the intermittent motion, the particles were still on the water surface, which means that no strong surface flow was induced around the droplet (see Fig. 11(a)). The evolution towards intermittent motion should be ruled by fluctuations in camphor release. A small region without tracer particles can be seen up-left of the droplet. The tracer particle-free area grows in time as seen in Figs. 11(b)–(c) and generates a difference in surface tension between the upper and the lower boundaries of the droplet. The resulting force is large enough to drive the droplet towards the region with low camphor concentration. After more camphor molecules are released, the camphor-rich area (the one without tracer particles) grows large and contacts with almost a half of the droplet periphery. At this stage, the droplet acceleration reaches the maximum (Figs. 11(c)–(d)). The droplet moves to the area with low camphor concentration and, as a consequence, the gradient of surface tension becomes low. In this phase of motion, the droplet slowed down and returned to the disk shape as shown in Figs. 11(e)–(f).

In the experiments, the continuous motion changed to the intermittent motion circa half an hour after a droplet was placed on the water surface as shown in Fig. 1. In the continuous motion, asymmetric concentration driving the droplet is supported by coupling between motion and high rate of camphor release. The transition to intermittent motion can be explained by combination of two factors. One is a decrease in camphor release rate due to declining camphor concentration in the droplet. However, the decrease alone does not fully explain the transition because paraffin droplets with small camphor concentration did not show intermittent motion. Our analysis shows that the modification of the water-oil interface by the presence of oil red O molecules is the factor allowing for moderation of camphor release as well as for changes in droplet shape. The release rate may be additionally affected by the flow around the droplet[46]. For the clarification of the more detailed mechanism of this droplet deformation phenomenon, we need more precise measurement of the dynamics of camphor and oil red O molecules. We also need to construct a mathematical model that reproduces the time evolution of motion and deformation including hydrodynamics in future study.