Deep inelastic scattering as a probe of entanglement:
confronting experimental data
Abstract
Parton distributions can be defined in terms of the entropy of entanglement between the spatial region probed by deep inelastic scattering (DIS) and the rest of the proton. For very small , the proton becomes a maximally entangled state. This approach leads to a simple relation between the average number of color-singlet dipoles in the proton wave function and the entropy of the produced hadronic state . At small , the multiplicity of dipoles is given by the gluon structure function, . Recently, the H1 Collaboration analyzed the entropy of the produced hadronic state in DIS, and studied its relation to the gluon structure function; poor agreement with the predicted relation was found. In this letter we argue that a more accurate account of the number of color-singlet dipoles in the kinematics of H1 experiment (where hadrons are detected in the current fragmentation region) is given not by but by the sea quark structure function . Sea quarks originate from the splitting of gluons, so at small , but in the current fragmentation region this proportionality is distorted by the contribution of the quark-antiquark pair produced by the virtual photon splitting. In addition, the multiplicity of color-singlet dipoles in the current fragmentation region is quite small, and one needs to include corrections to asymptotic formula. Taking both of these modifications into account, we find that the data from the H1 Collaboration in fact agree well with the prediction based on entanglement.
pacs:
13.60.Hb, 12.38.CyIn our paper KHLE (see also Tu:2019ouv ; GOLE ) we computed the von Neumann entropy of the system of partons resolved by deep inelastic scattering (DIS) at a given Bjorken and momentum transfer . We then proposed to interpret it as the entropy of entanglement between the spatial region probed by deep inelastic scattering and the rest of the proton. We found that in the small , large rapidity regime, all partonic micro-states have equal probabilities – the proton is composed by an exponentially large number of micro-states that occur with equal and small probabilities . This yields a simple relation between the entanglement entropy and the multiplicity of partons (dominated by gluons at small ):
| (1) |
where is an average number of color-singlet dipoles. In the region of small the gluons dominate and where is the gluon structure function111Note that this relation is a quantum analog of the Boltzmann formula underlying statistical physics.. Assuming that the multiplicity of produced hadrons is proportional to the multiplicity of color-singlet dipoles (“local parton-hadron duality” LHPD ; MULIB ), eq. (1) imposes a relation between the parton structure function (extracted from the inclusive cross section of DIS) and the entropy of produced hadrons; this relation can be directly tested in experiment. The comparison to the experimental data on hadron multiplicity distributions from CMS Collaboration at the LHC provided encouraging results KHLE ; Tu:2019ouv .
However, recent dedicated experimental analysis performed by the H1 collaboration H1EE shows a disagreement with Eq. (1) if one assumes (see Fig. 12 in Ref. H1EE and the dotted curves in our Fig. 1). In this letter we demonstrate that the H1 data in fact are in a good agreement with our approach, once two important effects are taken into account. Both of them are implied by the kinematics of the H1 measurements that are performed in the current fragmentation region (see also Refs.H1EE ; H1MULT1 ; H1MULT2 ; ZEUSMULT ), and thus at moderate values of Bjorken . First, since the experimental hadron multiplicities are not large, we need to take into account corrections of the order of to Eq. (1). Second, because the H1 data are concentrated in the current fragmentation region and not at very small , we need to reconsider our claim in Ref.KHLE that the multiplicity of the color-singlet dipoles is equal to . Indeed, the hadrons produced in the current fragmentation region of DIS originate from the hadronization of the struck quark (a constituent of the color-singlet dipole) and the multiplicity of color-singlet dipoles is thus determined by the sea quark structure function, see Fig. 2. Therefore the correct relation between the number of dipoles and the experimentally measured entropy of hadrons (valid for large ) is
| (2) |
The sea quark and gluon distributions are related to each other at small by (see Fig. 2)
| (3) |
where the function describes the splitting of the virtual photon into the quark-antiquark pair. In the region of very small , as we will now show, , and so the sea quark distribution is proportional to the gluon one. Therefore, with a logarithmic accuracy at very small we recover our original relation
| (4) |
To show that at very small , let us use the leading order DGLAP evolution equation DGLAP that gives for the sea quark structure function (see Fig. 2)
| (5) |
where . At small values of , the gluon structure function takes the form (see Ref.KOLEB for a review)
| (6) |
where is the number of colors, , and the BFKL kernel has the form:
| (7) |
should be calculated from the initial conditions. Plugging Eq. (6) in Eq. (5) we can take the integrals over and . Taking the integral over in the diffusion approximation, and using the method of steepest descent , we obtain the following result:
| (8) |
We evaluated Eq. (8) for small neglecting terms in proportional to . Note that does not depend on and numerically is about 0.3. Actually, the next -to-leading order correction increases the value of this and, as we can see from Fig. 1 (panel with ), in the NNLO fit for the region of smallest . However, away from the region of very small and in the kinematics of H1 measurement, the proportionality (8) is violated, and one should use the relation (2) instead of (4).
 |
 |
 |
 |

In addition, away from small , where the multiplicity of color-singlet dipoles is not large, one should take into account corrections to (4). In Refs.KHLE ; GOLE it is shown that in QCD cascade the multiplicity distribution has the following form:
| (9) |
where is the average multiplicity of color-singlet dipoles. The distribution (9) leads to the following von Neumann entropy:
| (10) |
One can see that at large we obtain , but corrections are sizable when (see Fig. 3). It should be noted that the distribution of Eq. (9) describes quite well the experimental hadron multiplicity distributions in proton-proton collisions (see Refs. KHLE ; Tu:2019ouv ; GOLE ).
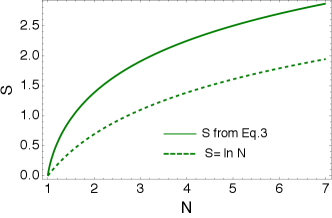
For comparison with the H1 experimental data H1EE (see Fig. 1), we first assume, following KHLE , that the hadron multiplicity is equal to the number of color-singlet dipoles. This assumption is based on “parton liberation” picture MULIB and on the ”local parton-hadron duality” LHPD . For sea quark and gluon structure functions in Fig. 1 we use NNLO fit H1ZEUS ; KATARZYNA to the combined H1 and ZEUS data.
One can see that our approach in fact describes the H1 data quite well – this is the first test of the relation between entanglement and the parton model in DIS enabled by the H1 analysis. We stress that once the data in the target fragmentation region at smaller value of becomes available at the Electron-Ion Collider, one should be able to use in the relation (1), as it has been done in Refs. KHLE ; Tu:2019ouv ; Baker:2017wtt ; GOLE ; GOLE1 . However, the general formula is given by Eq. (2) which at small reduces to since .
Acknowledgements: We thank Kong Tu, Thomas Ullrich and our colleagues at BNL, Stony Brook University, Tel Aviv University and UTFSM for stimulating discussions. We are very grateful to Aharon Levy and Katarzyna Wichmann for help in finding and extracting the parton distributions in the NNLO fit to HERA data. This work was supported in part by the U.S. Department of Energy under Contracts No. DE-FG88ER40388 and DE-SC0012704, BSF grant 2012124, ANID PIA/APOYO AFB180002 (Chile) and Fondecyt (Chile) grants 1180118.
References
- (1) D. E. Kharzeev and E. M. Levin, “Deep inelastic scattering as a probe of entanglement,” Phys. Rev. D 95 (2017) no.11, 114008 doi:10.1103/PhysRevD.95.114008 [arXiv:1702.03489 [hep-ph]].
- (2) Z. Tu, D. E. Kharzeev and T. Ullrich, “Einstein-Podolsky-Rosen Paradox and Quantum Entanglement at Subnucleonic Scales,” Phys. Rev. Lett. 124, no.6, 062001 (2020) doi:10.1103/PhysRevLett.124.062001 [arXiv:1904.11974 [hep-ph]].
- (3) E. Gotsman and E. Levin, “High energy QCD: multiplicity distribution and entanglement entropy,” Phys. Rev. D 102 (2020) no.7, 074008 doi:10.1103/PhysRevD.102.074008 [arXiv:2006.11793 [hep-ph]].
- (4) Y. L. Dokshitzer, V. A. Khoze, S. I. Troian and A. H. Mueller, “QCD Coherence in High-Energy Reactions,” Rev. Mod. Phys. 60, 373 (1988). doi:10.1103/RevModPhys.60.373
- (5) A. H. Mueller, “Toward equilibration in the early stages after a high-energy heavy ion collision,” Nucl. Phys. B 572 (2000), 227-240 doi:10.1016/S0550-3213(99)00502-7 [arXiv:hep-ph/9906322 [hep-ph]].
- (6) V. Andreev et al. [H1], “Measurement of charged particle multiplicity distributions in DIS at HERA and its implication to entanglement entropy of partons,” [arXiv:2011.01812 [hep-ex]].
- (7) C. Adloff et al. [H1], “Multiplicity structure of the hadronic final state in diffractive deep inelastic scattering at HERA,” Eur. Phys. J. C 5 (1998), 439-452 doi:10.1007/s100529800963 [arXiv:hep-ex/9804012 [hep-ex]].
- (8) C. Adloff et al. [H1], “Evolution of e p fragmentation and multiplicity distributions in the Breit frame,” Nucl. Phys. B 504 (1997), 3-23 doi:10.1016/S0550-3213(97)00585-3 [arXiv:hep-ex/9707005 [hep-ex]].
- (9) S. Chekanov et al. [ZEUS], “Energy dependence of the charged multiplicity in deep inelastic scattering at HERA,” JHEP 06 (2008), 061 doi:10.1088/1126-6708/2008/06/061 [arXiv:0803.3878 [hep-ex]].
- (10) V. N. Gribov and L. N. Lipatov, “Deep inelastic e p scattering in perturbation theory,” Sov. J. Nucl. Phys. 15, 438 (1972), [Yad. Fiz.15,781(1972)]; G. Altarelli and G. Parisi, “Asymptotic Freedom in Parton Language,” Nucl. Phys. B 126 (1977) 298. doi:10.1016/0550-3213(77)90384-4 Y. L. Dokshitzer, “Calculation of the Structure Functions for Deep Inelastic Scattering and e+ e- Annihilation by Perturbation Theory in Quantum Chromodynamics.,” Sov. Phys. JETP 46, 641 (1977), [Zh. Eksp. Teor. Fiz.73,1216(1977)].
- (11) Yuri V Kovchegov and Eugene Levin, “ Quantum Choromodynamics at High Energies”, Cambridge Monographs on Particle Physics, Nuclear Physics and Cosmology, Cambridge University Press, 2012 .
- (12) H. Abramowicz et al. [H1 and ZEUS], “Combination of measurements of inclusive deep inelastic scattering cross sections and QCD analysis of HERA data,” Eur. Phys. J. C 75 (2015) no.12, 580 doi:10.1140/epjc/s10052-015-3710-4 and https://lhapdf.hepforge.org/ .
- (13) K. Wichmann, private communication, 2021
- (14) O. K. Baker and D. E. Kharzeev, “Thermal radiation and entanglement in proton-proton collisions at energies available at the CERN Large Hadron Collider,” Phys. Rev. D 98, no.5, 054007 (2018) doi:10.1103/PhysRevD.98.054007 [arXiv:1712.04558 [hep-ph]].
- (15) E. Gotsman and E. Levin, “Thermal radiation and inclusive production in the CGC/saturation approach at high energies,” Eur. Phys. J. C 79 (2019) no.5, 415 doi:10.1140/epjc/s10052-019-6923-0 [arXiv:1902.07923 [hep-ph]].