Deep imaging inside scattering media through virtual spatiotemporal wavefront shaping
Abstract
The multiple scattering of light makes materials opaque and obstructs imaging. Wavefront shaping can reverse the scattering process, but imaging with physical wavefront shaping has limitations such as requiring physical guidestars, being restricted within a small isoplanatic volume, and relying on slow wavefront updates, with some approaches only working for planar targets outside the scattering media. Here, we introduce scattering matrix tomography (SMT): measure the hyperspectral scattering matrix of the sample, use it to digitally scan a synthesized confocal spatiotemporal focus and construct a volumetric image of the sample, and then use the tomograms as virtual guidestars in a nonconvex optimization to find the pulse shape, input wavefront, and output wavefront that can compensate for aberrations and scattering. SMT combines the strengths of wavefront shaping, spatiotemporal gating, and computational adaptive optics, eliminating physical guidestars and enabling digital double-path wavefront corrections tailored for every isoplanatic volume. We demonstrate sub-micron lateral resolution and one-micron axial resolution at one millimeter beneath ex vivo mouse brain tissue and over three transport mean free paths inside an opaque colloid, where existing imaging methods all fail due to the overwhelming multiple scattering. As a noninvasive and label-free method that works both inside and outside the scattering media, SMT may be applied broadly across medical imaging, biological science, device inspection, and colloidal physics.
I Introduction
Light scattering from inhomogeneities scrambles the wavefront and attenuates the signal exponentially while obscuring it with a speckled multiple-scattering background 1, 2. Overcoming light scattering to image at high resolution deep inside opaque media is a grand challenge that can enable through-skull optical imaging and stimulation, surgery-free biopsy, observation of cellular processes in their natural state, optical characterization of bulk colloids, high-resolution nondestructive device testing, and many other applications.
Traditional imaging methods tackle this problem by filtering away the multiple-scattering background. The reflectance confocal microscopy (RCM) 3, 4 uses spatial gating. Optical coherence tomography (OCT) 5 applies a coherence gate. The axial span of the spatial beam (which is twice the Rayleigh range) must cover the axial span of the image (i.e., the depth of field ), so OCT operates with a small numerical aperture (NA), leading to a coarse lateral resolution (typically 5–20 µm). Optical coherence microscopy (OCM) 6 combines spatial filtering and coherence gating while trading off the depth of field. Interferometric synthetic aperture microscopy 7 extends the depth of field, though its signal decreases with the loss of confocal gates away from the focal plane. Hardware 8, computational 9, 10, 11, 12, and hybrid 13 adaptive optics can restore the resolution of images blurred by aberrations but cannot overcome severe scattering as they do not control the numerous scattering modes in both the incident and the return paths. Multiphoton microscopy adopts longer wavelengths where scattering is weaker but requires fluorescence labeling and high-power lasers 14, 15. Tomographic phase microscopy quantitatively obtains the refractive index distribution 16, 17, 18, 19, 20 but requires thin specimens and access to both sides of the sample for transmission measurements. Selective detection of the forward scattered photons 21, 22 and photoacoustic tomography 23 allow imaging deeper at reduced resolution. The depth-over-resolution ratio stays around or below 200 in biological tissue across most label-free imaging methods (including non-optical ones such as ultrasound, X-ray CT, and MRI) 23, 24, 25, 26.
Over the past decade, a paradigm shift came with the appreciation that light scattering is deterministic and controllable. Given enough control elements, a suitable incident wavefront can reverse multiple scattering 27, 28 thanks to the time-reversal symmetry of Maxwell’s equations. Adopting such wavefronts can, in principle, allow imaging at much deeper depths. But the initial methods to determine these special wavefronts come with serious limitations as they introduce physical guidestars at the imaging site 29 such as invasive cameras 30, 31 or photorefractive crystals 32, 33, fluorescence labels 34, 35, 36, 37, acoustic foci with greatly reduced spatial resolution 38, 39, or isolated moving particles 40, 41. Additionally, each wavefront is only valid within a volume called the isoplanatic patch 8, whose size shrinks with depth and is less than 10 µm at 1 mm deep inside biological tissue 42, 43. Most of these methods also require a spatial light modulator (SLM) with a limited update speed. Such physical-guidestar-based schemes are schematically illustrated in Fig. 1a. To avoid using physical guidestars, researchers developed incoherent imaging methods based on angular correlations 44, 45 and optimization 46, 47, 48, 49. However, they only apply to planar targets at a large distance away from the scattering media because there is no gating mechanism for depth sectioning and because the small angular memory effect range limits the field of view. Reflection matrix measurement is another way to avoid physical guidestars. One can accumulate single-scattering signals using correlations in the reflection matrix 50 and remove aberrations and scattering through singular value decomposition 51, 52 or iterative phase conjugation 53, 54, 55, 56, 57, 58, culminating in the “volumetric reflection-matrix microscopy” (VRM) method 58 that performs both spectral and angular corrections at multiple depths. These matrix-based methods show great potential but, to date, have yet to deliver the drastic beyond-adaptive-optics scattering reversal promised by wavefront shaping.
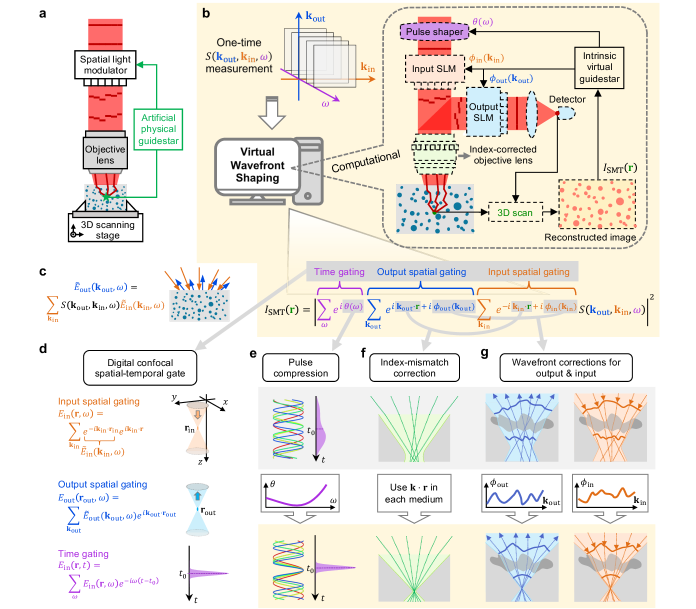
Here we use the scattering matrix to unify different approaches and combine the advantages of both the traditional and the recent methods, realizing label-free volumetric high-resolution imaging across a large depth of field deep inside the scattering media, with multi-isoplanatic spatiotemporal wavefront corrections on top of confocal and temporal gates while avoiding the restrictions of physical guidestars and slow SLMs. As illustrated in Fig. 1b, we measure the hyperspectral scattering matrix of the sample and use it to synthesize a spatiotemporal focus with pulse compression, refractive index mismatch correction, and wavefront correction for every isoplanatic volume. The focus is scanned digitally to yield a 3D image of the sample with no trade-off between the lateral resolution and the depth of field. We use the reconstructed image as virtual guidestars intrinsic to the sample and develop an optimization with regularization and progression strategies to find the optimal dispersion compensation and input/output wavefronts. This enables a depth-over-resolution ratio of 910 when imaging a resolution target at one millimeter beneath ex vivo mouse brain tissue—the highest reported in the literature (including both optical and non-optical label-free methods) to our knowledge. We attain diffraction-limited resolution when the signal is reduced by over ten-million-fold due to multiple scattering. We maintain the ideal transverse and axial resolutions across a depth of field of over 70 times the Rayleigh range at depths beyond three transport mean free paths inside an opaque colloid—the deepest reported to our knowledge. By formulating the problems of imaging and reversing light scattering as reconstruction and optimization problems, this approach offers a versatile platform that uses wave physics and computation to reveal hidden information.
II Scattering matrix tomography
The scattering matrix encapsulates the sample’s complete linear response 59, 60 (Fig. 1c). Any incident wave is a superposition of plane waves: , where is the position, is time, and is the amplitude of its plane-wave component with incoming momentum at frequency . The amplitudes that form the resulting outgoing wave are given by the scattering matrix through . The angular summations are restricted to in a background medium with speed of light ; we use “angle” interchangeably with “momentum.”
After measuring a subset of , one can digitally synthesize the sample’s response with tailored measurements in space-time given customized spatiotemporal inputs, which we collectively refer to as “virtual spatiotemporal wavefront shaping.” As illustrated in Fig. 1d, summing over incident angles with incoming plane-wave amplitudes creates an incident beam spatially focused at , forming an input spatial gate; summing over outgoing angles with outgoing plane-wave amplitudes from the scattering matrix yields the scattered field given a virtual detector at position , forming an output spatial gate; summing over frequency with an phase creates an incident pulse that arrives at at time , forming a temporal gate. Given a spatiotemporal focus arriving at at time , the scattered field is therefore . We then perform a virtual experiment with a confocal spatial focus () and with the temporal focus aligned with the spatial one (evaluating at time ), which yields the triply-gated scattering amplitude of the sample at position , denoted as
| (1) |
Digitally scanning (Fig. 1b) forms a phase-resolved image of the sample where the input spatial gate, output spatial gate, and temporal gate all align at every point in the absence of aberrations and scattering. The lateral spread of in the summation (typically set by the NA) determines the lateral resolution, with no degradation away from any particular focal plane. The axial spread (typically set by the spectral bandwidth) determines the axial resolution. The triple summation averages away random noises, providing a signal-to-noise ratio advantage akin to that of frequency-domain OCT over time-domain OCT 61. We use the non-uniform fast Fourier transform (NUFFT) 62 to efficiently evaluate these summations and the 3D spatial scan. Eq. (1) is the minimal, optimization-free version of what we call “scattering matrix tomography” (SMT).
VRM used an object momentum conservation principle 50, 58 to reconstruct images at multiple en-face slices by performing time gating at one depth, summing over incident angles while fixing the in-plane momentum transfer, performing a 2D inverse Fourier transform, and then looping over the depth 58. In comparison, SMT uses a virtual scanning of a confocal spatiotemporal focus, which results in a simpler and more intuitieve formalism, enables slicing in any orientation or direct volumetric reconstruction, generalizes the use of reflection matrix to any subset of the scattering matrix (can also be transmission, remission 21, 63, or a combination of them), adopts NUFFT which is much faster than brute-force summations and loops, and offers a rigorous basis for performing the index-mismatch correction and focus-quality-based spatiotemporal wavefront corrections below.
The triple gating suppresses multiple scattering. The single-scattering field at output for an input from is given by the Born approximation as proportional to , namely the component of the 3D Fourier transform of the sample’s permittivity contrast profile 64, 16, 17, 5. Such single-scattering contributions add up in phase in Eq. (1) to form the image, similar to an inverse Fourier transform from to . The multiple-scattering contributions do not add up in phase. Therefore, the triple summations over , , and boost the single-to-multiple-scattering ratio in compared to the raw measurement data .
To remove aberrations and scattering, we perform digital spatiotemporal wavefront corrections. The chromatic aberrations in the optical elements of the system and the frequency dependence of the refractive index in the sample create a frequency-dependent phase that misaligns and broadens the temporal gate. In SMT, we digitally compensate for such dispersion using a spectral phase acting as a virtual pulse shaper (Fig. 1e), similar to the dispersion compensation in spectral-domain OCT 65. The refractive index mismatch between the sample medium (e.g., biological tissue), the far field (e.g., air), and the coverslip (if there is one) refracts the rays, degrades the input and output spatial gates 66, and misaligns the spatial gates and the temporal gate. By using the appropriate propagation phase shift in each medium and the appropriate arrival time, SMT achieves an ideal spatiotemporal focus at all depths even in the presence of refraction, effectively creating a virtual dry objective lens that reverses both the spatial and the chromatic aberrations arising from the index mismatch (Fig. 1f) without liquid immersion (Supplementary Sect. III C). Importantly, we also digitally introduce angle-dependent phase profiles and that act as two virtual SLMs, one for the incident wave and one for the outgoing wave (Fig. 1g), which can adopt any wavefront to compensate for scattering and additional aberrations. This yields the general form of SMT,
| (2) |
By measuring the reflection from a mirror, we remove the dispersion and aberrations in the input path of the optical system (Supplementary Sect. III B).
To find the digital corrections , , and , we recognize that a good spatiotemporal focus at enhances the scattering intensity from targets at that position, so acts as a virtual noninvasive guidestar at (Fig. 1b). Therefore, we maximize an image quality metric ,
| (3) |
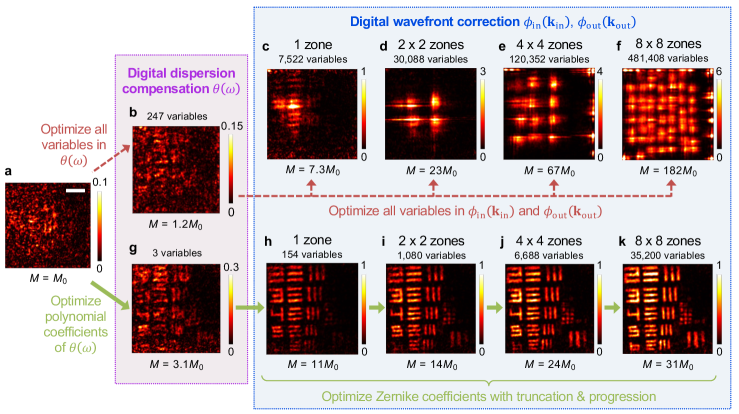
with being a constant; the logarithm factor promotes image sharpness 67, 12. Image-metric-based optimizations have long been used in adaptive optics 8, 9, 10, 11, 12, 13 and more recently with wavefront shaping without a time gate 46, 48, 37; motivated by the versatility of optimization problems, here we generalize this approach to perform double-path spatiotemporal digital wavefront correction. We derive the gradient of with respect to the parameters and adopt a quasi-Newton method, the low-storage Broyden–Fletcher–Goldfarb–Shanno (L-BFGS) method 68, in the NLopt library 69. Since a wavefront or can only remain optimal within an isoplanatic volume 8, 42, 43, we divide the space into zones (both axially and laterally) and use different for different zones.
A direct optimization, however, performs poorly when the scattering is sufficiently strong that signals from the target are initially buried under the speckled multiple-scattering background (Fig. 2a–f). This happens because (1) the problem is high-dimensional and nonconvex with numerous poor local optima, (2) the large number of parameters in , , and in the many zones can lead to overfitting, and (3) the optimization may inadvertently enhance unintended contributions like the speckled background instead of signals from a target at the specified position . To overcome these challenges, we employ five strategies to regularize the problem, lower its dimension, and guide the search away from poor local optima associated with unintended contributions (Supplementary Sect. III E–F): (i) Restrict to a third-order polynomial 65, 12. (ii) Expand and in Zernike polynomials 70, 10, 11, 12, 13, 8. (iii) First optimize over the full volume and then progressively optimize over smaller zones while using the previous as the initial guess. (iv) Truncate the scattering matrix to within the respective spatial zone to avoid overfitting. (v) Increase the number of Zernike terms as we progress to smaller zones, since the low-order terms correct for slowly varying aberrations with a large isoplanatic volume, while the high-order terms correct for the sharp variations from localized scattering with a small isoplanatic volume. These strategies work together to enable an effective optimization (Fig. 2g–k).
Since all targets within an isoplanatic volume share the same optimal wavefront while the speckled backgrounds do not, the summation over space in Eq. (3) promotes the target-to-speckle weight in the gradient and makes the optimization landscape smoother. As discussed earlier, the triple gating through summations over , , and in Eq. (2) also promotes the target-to-speckle ratio. Without one of these quadruple summations in and when scattering is sufficiently strong, the optimization landscape may not reflect the target contribution and may exhibit many local optima associated with the multiple-scattering background (Supplementary Fig. 14).
Previous matrix-based imaging methods used singular value decomposition 52 or iterative phase conjugation 53, 54, 55, 56, 57, 58 to perform angular wavefront corrections. They were not formulated as an image-metric optimization like Eq. (3) and did not have the above-mentioned regularization and progression strategies, which limited their performance when scattering is strong. The VRM method 58 also employed dispersion compensation, but it did so using an iterative phase conjugation scheme with a single angular summation instead of quadruple summations, which further restricted it to situations with less scattering.
III Experimental demonstration
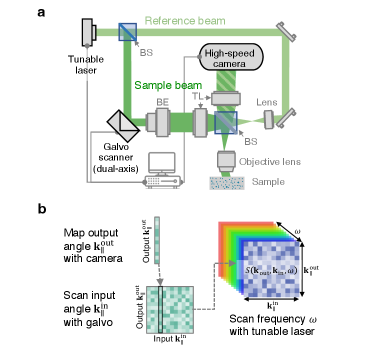
We use off-axis holography 71 to measure the field scattered from the sample to the incident side (Fig. 3) through a dry objective lens (Mitutoyo M Plan Apo NIR 100X, NA 0.5). Here, reduces to the reflection matrix . A CMOS camera (Photron Fastcam Nova S6) captures 64,000 columns of the reflection matrix per second, a dual-axis galvo scanner (ScannerMAX Saturn 5B) scans the incident angle , and a tunable laser (M Squared SolsTiS 1600) scans the frequency . The data acquisition here is two to three orders of magnitude faster than previous measurements of broadband scattering matrices 60, 72, 58. The power onto the sample ranges from 0.02 mW to 0.2 mW. We measure around 250 wavelengths from 740 nm to 940 nm, 2,900 outgoing angles, and 3,900 incident angles within the NA, over a µm2 area. The detection sensitivity, currently limited by the residual reflection from the objective lens, is 90 dB. See Supplementary Sects. I–II for details.
III.1 Planar Imaging
We first image the 8th group (whose 6th element has a bar width and separation of 1.1 µm) of a 1951 USAF resolution target underneath a 0.98-mm-thick tissue slice from the cerebral cortex of a mouse brain (Fig. 4a). A standard bright-field microscope image (with incoherent white-light illumination) shows no feature (Fig. 4b).
Using the measured hyperspectral reflection matrix, we first mimic existing reflection-based imaging methods virtually (Supplementary Sect. IV): restricting the frequency summation of Eq. (2) to one frequency yields a synthetic RCM image where time gating is absent (Fig. 4c); restricting the angular summations of Eq. (2) to small angles (we use NA 0.1 here) and fixing the depth of the spatial focus yields a synthetic OCT image (Fig. 4d); for OCM (Fig. 4e), we sum over all frequencies and all angles. The depth of the focal plane is chosen to maximize the total signal. All of these images include corrections for the input aberrations of the optical system. For OCT and OCM, we also perform digital dispersion compensation (following the same steps as in SMT). Despite the confocal spatial gate, temporal gate, corrections, and even computational adaptive optics (Supplementary Sect. IV C), none of these methods reveals any group-8 element due to the overwhelming scattering from the tissue. To compare to the most state-of-the-art, we also implement the VRM method 58. VRM fails (Fig. 4f) and performs worse than SMT without the five regularization and progression strategies (Fig. 2c) because its dispersion compensation is determined through a single angular summation without time gating and without confocal gating (Supplementary Sect. IV D).
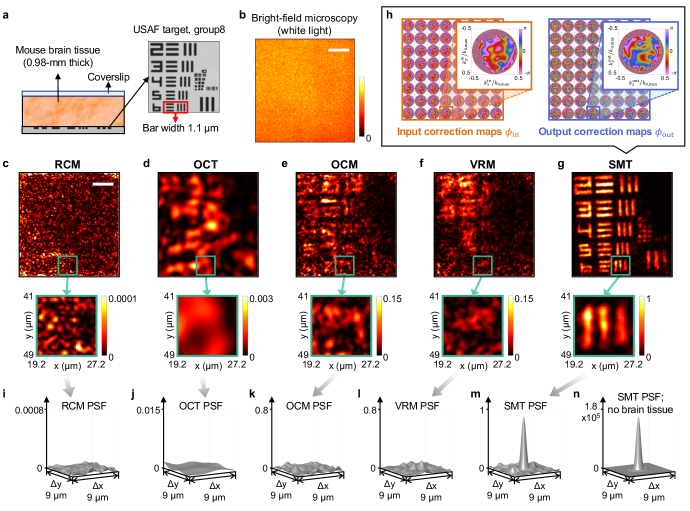
The SMT image resolves the 8th group of the USAF target with near perfection down to the smallest 6th element (Fig. 4g). Here, the progression goes down to 88 zones, with up to 22 Zernike radial orders (275 Zernike polynomials) per zone in both and , for a total of 35,200 wavefront correction variables. The optimized correction patterns and are shown in Fig. 4h. Here, because the former includes the optical-system aberration. The wavefronts vary faster at larger angles due to the longer propagation length through the medium and subsequently more severe scattering. These large-angle fast-oscillation patterns correct for the strongest scattering and are key to the wavefront correction (Supplementary Fig. 12).
The triple gating is essential. Supplementary Sects. V–VI show that when one of the three gates is removed, the image reconstruction would completely fail even after the optimizations. It is also crucial to perform corrections for both the incident path and the return path; Supplementary Sect. IV C shows that in the reciprocal space of the image, only low-order aberrations can be corrected because high-order terms require double-path wavefront corrections in both and 13. No existing computational adaptive optics methods 9, 10, 11, 12, 13 performs double-path corrections, so they would not be able to handle a strongly scattering system like this even if they adopt the optimization strategies here.
To quantify the imaging performance, we obtain the point spread function (PSF) by evaluating Eq. (2) with a variable output position given a fixed input position on the sixth element: ; see Supplementary Sect. VII. The PSFs of RCM, OCT, OCM, and VRM (Fig. 4i–l) have no discernible peak near , indicating a complete failure to image. The speckled OCM PSF averages to be 70 dB below the peak PSF of a mirror without the brain tissue (Fig. 4n), so the signal (which is buried beneath the speckled background and not visible here) has been reduced by at least ten-million-fold due to multiple scattering. The PSF of SMT (Fig. 4m) exhibits a sharp peak at with 7-times the height of the tallest speckle in the background, showing we have not reached the depth limit (where the signal strength equals the background strength) of SMT yet. The SMT peak’s full width at half maximum (FWHM) is 1.08 µm, close to the mirror PSF’s 0.93 µm FWHM, demonstrating diffraction-limited resolution despite the overwhelming multiple scattering. To our knowledge, the depth-over-FWHM ratio of 910 here is the highest reported in the literature for imaging high-contrast targets inside or behind ex vivo biological tissue, which scatters about twice as much as in vivo tissue 73.
III.2 Volumetric Imaging
We next perform 3D tomography of a dense colloid consisting of high-index titanium dioxide (TiO2, refractive index 2.5) nanoparticles dispersed in polydimethylsiloxane (PDMS, refractive index 1.4). The nanoparticles (Sigma-Aldrich, 914320) have a typical diameter of 500 nm, and we use Mie theory to estimate the scattering and transport mean free paths to be mm and mm at nm (Supplementary Sect. VIII). We measure the reflection matrix over a µm2 field of view with the reference plane at depth mm. Using the reflection matrix, we reconstruct SMT image over a µm3 volume inside the colloid by dividing the depth of field (DOF) µm into 16 sub-volumes vertically.
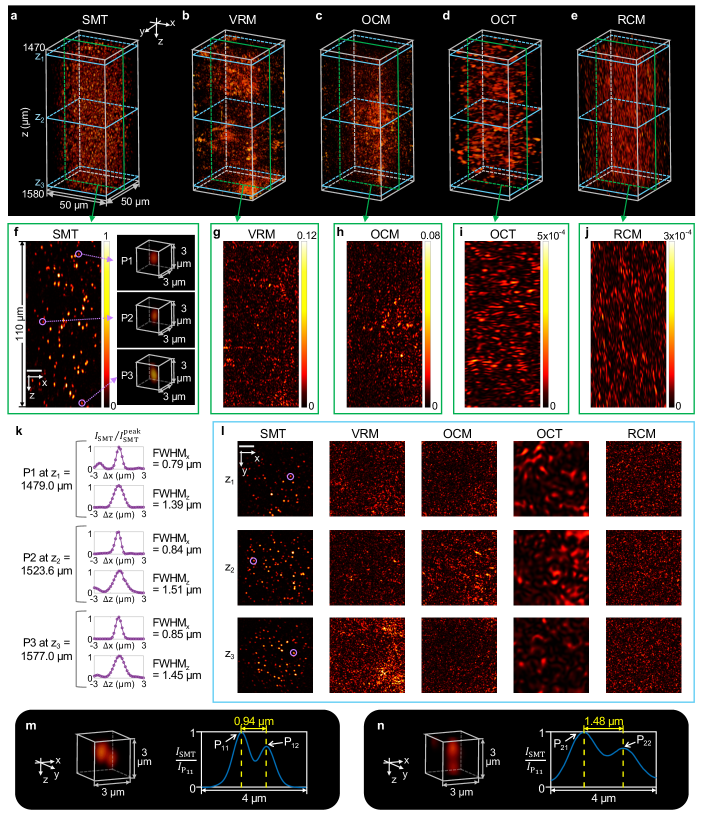
SMT creates a detailed 3D image of all the nanoparticles in this volume (Fig. 5a), with zoom-ins and cross sections of individual particles shown in Fig. 5f,k,l. A statistical analysis of these particles finds the lateral FWHM to vary from 0.7 µm to 1.0 µm within the µm DOF and the axial FWHM very close to the theoretical estimate of 1.42 µm given the spectral bandwidth of nm here (Supplementary Sect. IX). Fig. 5m,n shows examples of SMT images of nearby particle pairs, with one pair separated horizontally by 0.94 µm and one pair separated vertically by 1.48 µm. The SMT DOF covers approximately the volume of overlap among the input/output beams in the scattering matrix measurement; it grows with the field of view and is not restricted by the Rayleigh range (Supplementary Sect. IX B). Here, µm (with center wavelength nm and for PDMS), while the SMT DOF is 73 times larger.
We also construct VRM (generalized from multi-slice to volumetric) and synthetic OCM, OCT, and RCM images (Fig. 5b–e) for comparison, with longitudinal and transverse slices shown in Fig. 5g–j,l. For OCM and OCT, the depth of the spatial gate is fixed on one focal plane at mm when the temporal gate is scanned in (Supplementary Sect. IV B). All of these methods fail and cannot identify any of the nanoparticles at these depths. The VRM image exhibits bright artifacts at several constant- slices because its dispersion compensation maximizes the intensity at those isolated slices (Supplementary Sect. IV D).
IV Discussion
SMT provides a conceptually and mathematically simple framework that combines the advantages of existing methods while offering versatile capabilities. The main aspect not considered in this work is the frequency dependence of the wavefront correction. It is well known that the optimal wavefront for focusing behind scattering media depends sensitively on the frequency 74. Future work can explore optimization strategies that incorporate the frequency dependence in and while avoiding overfitting due to the additional degrees of freedom. One may also adopt a progressive increase of the NA 12 to utilize the deeper penetration of the forward scattered photons 21, 22, and/or a progressive increase of the depth 58. Global optimization can be used when the scattering is so strong that a local optimization loses its consistency. Future work may also explore other optimization schemes beyond using an image quality metric.
Validation against the ground truth is nontrivial for volumetric imaging 75. Using the recent “augmented partial factorization” simulation method 76, we have validated SMT through full-wave numerical simulations 77.
One can interpret RCM, OCT, and OCM as measuring the diagonal elements of the reflection matrix in a spatial basis. SMT utilizes the additional off-diagonal elements to digitally refocus to different planes and to enable double-path wavefront corrections. The price is having to measure those off-diagonal elements.
Motion artifacts make wavefront shaping in vivo a challenge 78. While the virtual wavefront shaping of SMT dispenses with slow SLMs, a coherent synthesis still requires measuring the matrix elements before the scatterer arrangement changes substantially. The speckle decorrelation time, primarily limited by the blood flow, is estimated as 5 ms at nm wavelength 1 mm deep inside the mouse brain where blood is rich 79 but can go beyond 30 seconds for the skull where there is less blood 55. Currently, our total measurement time for the USAF-target-under-tissue sample is three minutes, with the majority of which spent on the mechanical acceleration and deceleration of a birefringent filter during a scan-and-stop operation of the tunable laser. Scanning the filter continuously can reduce the measurement time to 5 seconds (Supplementary Sec. I D). One can further accelerate by orders of magnitude through truncating the spatial measurement 57, parallelizing the spectral acquisition 80, and reducing the number of frequencies or incident angles (Supplementary Sect. V–VI).
While SMT uses contrasts in the scattering strength, digital staining 81, 82 may be used to infer other contrasts. The phase information in can help detect sub-nm displacements 83, 84. One may incorporate polarization gating to select birefringent objects such as directionally oriented tissues. The hyperspectral scattering matrix can additionally resolve spectral information of the sample, such as the oxygenation of the hemoglobin. Applications that require feedback to identify the region of interest can use a subset of the matrix data to reconstruct a coarse image in real time.
Note: After we posted a preprint of this paper 85, a related preprint was posted by an independent group 86.
Data availability: The datasets generated and analyzed during the current study are available on Zenodo 87.
Code availability: The codes used to produce the results of the study are available on GitHub 88.
Acknowledgments: We thank B. Applegate, S. Fraser, O. D. Miller, F. Xia, and B. Flanagan for helpful discussions. This work was supported by the Chan Zuckerberg Initiative, the National Science Foundation CAREER award (ECCS-2146021), and the University of Southern California.
Author contributions: Y.Z. and C.W.H. designed the experimental setup. Y.Z. built the setup, prepared the samples, and carried out the measurements with help from M.D. M.D. and Y.Z. developed and carried out the dispersion compensation. M.D. developed and carried out the SMT wavefront optimization with regularization and progression. Z.W. developed fast 3D reconstruction using the non-uniform fast Fourier transform. Y.Z. and Z.W. developed the index-mismatch correction. Y.Z., T.Z., and T.C. developed the control and automation of the instruments. M.D. and Y.Z. implemented the synthesis of RCM, OCT, and OCM. M.D. implemented VRM. Y.Z. performed the 3D visualization and the analyses on phase stability, sensitivity, and resolution. C.W.H. conceived the project and supervised research. C.W.H., Y.Z., and M.D. wrote the manuscript with inputs from the other coauthors. All authors discussed the results.
Competing interests: C.W.H, Z.W., Y.Z., and M.D. are inventors of US patent applications 17/972,073 and 63/472,900 titled “Multi-spectral scattering-matrix tomography” filed by the University of Southern California.
References
- [1] Yoon, S. et al. Deep optical imaging within complex scattering media. Nat. Rev. Phys 2, 141–158 (2020).
- [2] Bertolotti, J. & Katz, O. Imaging in complex media. Nat. Phys. 18, 1008–1017 (2022).
- [3] Calzavara-Pinton, P., Longo, C., Venturini, M., Sala, R. & Pellacani, G. Reflectance confocal microscopy for in vivo skin imaging. Photochem. Photobiol. 84, 1421–1430 (2008).
- [4] Xia, F. et al. In vivo label-free confocal imaging of the deep mouse brain with long-wavelength illumination. Biomed. Opt. Express 9, 6545–6555 (2018).
- [5] Fercher, A. F., Drexler, W., Hitzenberger, C. K. & Lasser, T. Optical coherence tomography—principles and applications. Rep. Prog. Phys. 66, 239 (2003).
- [6] Aguirre, A. D., Zhou, C., Lee, H.-C., Ahsen, O. O. & Fujimoto, J. G. Optical coherence microscopy. In Drexler, W. & Fujimoto, J. G. (eds.) Optical Coherence Tomography: Technology and Applications, chap. 28, 865–911 (Springer, Cham, 2015).
- [7] Ralston, T. S., Marks, D. L., Scott Carney, P. & Boppart, S. A. Interferometric synthetic aperture microscopy. Nat. Phys. 3, 129–134 (2007).
- [8] Hampson, K. M. et al. Adaptive optics for high-resolution imaging. Nat. Rev. Methods Primers 1, 68 (2021).
- [9] Tippie, A. E., Kumar, A. & Fienup, J. R. High-resolution synthetic-aperture digital holography with digital phase and pupil correction. Opt. Express 19, 12027–12038 (2011).
- [10] Adie, S. G., Graf, B. W., Ahmad, A., Carney, P. S. & Boppart, S. A. Computational adaptive optics for broadband optical interferometric tomography of biological tissue. Proc. Natl. Acad. Sci. U.S.A. 109, 7175–7180 (2012).
- [11] Shemonski, N. D. et al. Computational high-resolution optical imaging of the living human retina. Nat. Photon. 9, 440–443 (2015).
- [12] Hillmann, D. et al. Aberration-free volumetric high-speed imaging of in vivo retina. Sci. Rep. 6, 35209 (2016).
- [13] Liu, S. et al. Closed-loop wavefront sensing and correction in the mouse brain with computed optical coherence microscopy. Biomed. Opt. Express 12, 4934–4954 (2021).
- [14] Horton, N. G. et al. In vivo three-photon microscopy of subcortical structures within an intact mouse brain. Nat. Photon. 7, 205–209 (2013).
- [15] Streich, L. et al. High-resolution structural and functional deep brain imaging using adaptive optics three-photon microscopy. Nat. Methods 18, 1253–1258 (2021).
- [16] Jin, D., Zhou, R., Yaqoob, Z. & So, P. T. Tomographic phase microscopy: principles and applications in bioimaging. J. Opt. Soc. Am. B 34, B64–B77 (2017).
- [17] Park, Y., Depeursinge, C. & Popescu, G. Quantitative phase imaging in biomedicine. Nat. Photon. 12, 578–589 (2018).
- [18] Tahir, W., Kamilov, U. S. & Tian, L. Holographic particle localization under multiple scattering. Adv. Photonics 1, 036003 (2019).
- [19] Lim, J., Ayoub, A. B., Antoine, E. E. & Psaltis, D. High-fidelity optical diffraction tomography of multiple scattering samples. Light Sci. Appl. 8, 82 (2019).
- [20] Chen, M., Ren, D., Liu, H.-Y., Chowdhury, S. & Waller, L. Multi-layer Born multiple-scattering model for 3D phase microscopy. Optica 7, 394–403 (2020).
- [21] Zhao, Y. et al. Dual-axis optical coherence tomography for deep tissue imaging. Opt. Lett. 42, 2302–2305 (2017).
- [22] Cua, M., Blochet, B. & Yang, C. Speckle-resolved optical coherence tomography for mesoscopic imaging within scattering media. Biomed. Opt. Express 13, 2068–2081 (2022).
- [23] Wang, L. V. & Hu, S. Photoacoustic tomography: in vivo imaging from organelles to organs. Science 335, 1458–1462 (2012).
- [24] Pian, Q. et al. Multimodal biomedical optical imaging review: towards comprehensive investigation of biological tissues. Curr. Mol. Imaging 3, 72–87 (2014).
- [25] Lal, C. & Leahy, M. J. An updated review of methods and advancements in microvascular blood flow imaging. Microcirculation 23, 345–363 (2016).
- [26] Gigan, S. Optical microscopy aims deep. Nat. Photon. 11, 14–16 (2017).
- [27] Rotter, S. & Gigan, S. Light fields in complex media: Mesoscopic scattering meets wave control. Rev. Mod. Phys. 89, 015005 (2017).
- [28] Cao, H., Mosk, A. P. & Rotter, S. Shaping the propagation of light in complex media. Nat. Phys. 18, 994–1007 (2022).
- [29] Horstmeyer, R., Ruan, H. & Yang, C. Guidestar-assisted wavefront-shaping methods for focusing light into biological tissue. Nat. Photon. 9, 563–571 (2015).
- [30] Vellekoop, I. M. & Mosk, A. Focusing coherent light through opaque strongly scattering media. Opt. Lett. 32, 2309–2311 (2007).
- [31] Popoff, S., Lerosey, G., Fink, M., Boccara, A. C. & Gigan, S. Image transmission through an opaque material. Nat. Commun. 1, 81 (2010).
- [32] Yaqoob, Z., Psaltis, D., Feld, M. S. & Yang, C. Optical phase conjugation for turbidity suppression in biological samples. Nat. Photon. 2, 110–115 (2008).
- [33] Cheng, Z., Li, C., Khadira, A., Zhang, Y. & Wang, L. V. High-gain and high-speed wavefront shaping through scattering media. Nat. Photon. 17, 299–305 (2023).
- [34] Tang, J., Germain, R. N. & Cui, M. Superpenetration optical microscopy by iterative multiphoton adaptive compensation technique. Proc. Natl. Acad. Sci. U.S.A. 109, 8434–8439 (2012).
- [35] Papadopoulos, I. N., Jouhanneau, J.-S., Poulet, J. F. & Judkewitz, B. Scattering compensation by focus scanning holographic aberration probing (F-SHARP). Nat. Photon. 11, 116–123 (2017).
- [36] May, M. A. et al. Fast holographic scattering compensation for deep tissue biological imaging. Nat. Commun. 12, 4340 (2021).
- [37] Aizik, D. & Levin, A. Non-invasive and noise-robust light focusing using confocal wavefront shaping. Preprint at https://arxiv.org/abs/2301.11421 (2023).
- [38] Xu, X., Liu, H. & Wang, L. V. Time-reversed ultrasonically encoded optical focusing into scattering media. Nat. Photon. 5, 154–157 (2011).
- [39] Wang, Y. M., Judkewitz, B., DiMarzio, C. A. & Yang, C. Deep-tissue focal fluorescence imaging with digitally time-reversed ultrasound-encoded light. Nat. Commun. 3, 928 (2012).
- [40] Ma, C., Xu, X., Liu, Y. & Wang, L. V. Time-reversed adapted-perturbation (TRAP) optical focusing onto dynamic objects inside scattering media. Nat. Photon. 8, 931–936 (2014).
- [41] Zhou, E. H., Ruan, H., Yang, C. & Judkewitz, B. Focusing on moving targets through scattering samples. Optica 1, 227–232 (2014).
- [42] Judkewitz, B., Horstmeyer, R., Vellekoop, I. M., Papadopoulos, I. N. & Yang, C. Translation correlations in anisotropically scattering media. Nat. Phys. 11, 684–689 (2015).
- [43] Osnabrugge, G., Horstmeyer, R., Papadopoulos, I. N., Judkewitz, B. & Vellekoop, I. M. Generalized optical memory effect. Optica 4, 886–892 (2017).
- [44] Bertolotti, J. et al. Non-invasive imaging through opaque scattering layers. Nature 491, 232–234 (2012).
- [45] Katz, O., Heidmann, P., Fink, M. & Gigan, S. Non-invasive single-shot imaging through scattering layers and around corners via speckle correlations. Nat. Photon. 8, 784–790 (2014).
- [46] Yeminy, T. & Katz, O. Guidestar-free image-guided wavefront shaping. Sci. Adv. 7, eabf5364 (2021).
- [47] Feng, B. Y. et al. NeuWS: Neural wavefront shaping for guidestar-free imaging through static and dynamic scattering media. Sci. Adv. 9, eadg4671 (2023).
- [48] Haim, O., Boger-Lombard, J. & Katz, O. Image-guided computational holographic wavefront shaping. Preprint at https://arxiv.org/abs/2305.12232 (2023).
- [49] Weinberg, G., Sunray, E. & Katz, O. Noninvasive megapixel fluorescence microscopy through scattering layers by a virtual reflection-matrix. Preprint at https://arxiv.org/abs/2312.16065 (2023).
- [50] Kang, S. et al. Imaging deep within a scattering medium using collective accumulation of single-scattered waves. Nat. Photon. 9, 253–258 (2015).
- [51] Badon, A. et al. Smart optical coherence tomography for ultra-deep imaging through highly scattering media. Sci. Adv. 2, e1600370 (2016).
- [52] Badon, A. et al. Distortion matrix concept for deep optical imaging in scattering media. Sci. Adv. 6, eaay7170 (2020).
- [53] Kang, S. et al. High-resolution adaptive optical imaging within thick scattering media using closed-loop accumulation of single scattering. Nat. Commun. 8, 2157 (2017).
- [54] Yoon, S., Lee, H., Hong, J. H., Lim, Y.-S. & Choi, W. Laser scanning reflection-matrix microscopy for aberration-free imaging through intact mouse skull. Nat. Commun. 11, 5721 (2020).
- [55] Kwon, Y. et al. Computational conjugate adaptive optics microscopy for longitudinal through-skull imaging of cortical myelin. Nat. Commun. 14, 105 (2023).
- [56] Li, B. et al. Efficient framework of solving time-gated reflection matrix for imaging through turbid medium. Opt. Express 31, 15461–15473 (2023).
- [57] Najar, U. et al. Non-invasive retrieval of the time-gated transmission matrix for optical imaging deep inside a multiple scattering medium. Preprint at https://arxiv.org/abs/2303.06119 (2023).
- [58] Lee, Y.-R., Kim, D.-Y., Jo, Y., Kim, M. & Choi, W. Exploiting volumetric wave correlation for enhanced depth imaging in scattering medium. Nat. Commun. 14, 1878 (2023).
- [59] Popoff, S. M. et al. Measuring the transmission matrix in optics: an approach to the study and control of light propagation in disordered media. Phys. Rev. Lett. 104, 100601 (2010).
- [60] Mounaix, M. et al. Spatiotemporal coherent control of light through a multiple scattering medium with the multispectral transmission matrix. Phys. Rev. Lett. 116, 253901 (2016).
- [61] De Boer, J. F., Leitgeb, R. & Wojtkowski, M. Twenty-five years of optical coherence tomography: the paradigm shift in sensitivity and speed provided by Fourier domain OCT. Biomed. Opt. Express 8, 3248–3280 (2017).
- [62] Barnett, A. H., Magland, J. & af Klinteberg, L. A parallel nonuniform fast Fourier transform library based on an “exponential of semicircle” kernel. SIAM J. Sci. Comput. 41, C479–C504 (2019).
- [63] Bender, N. et al. Coherent enhancement of optical remission in diffusive media. Proc. Natl. Acad. Sci. U.S.A. 119, e2207089119 (2022).
- [64] Wolf, E. Three-dimensional structure determination of semi-transparent objects from holographic data. Opt. Commun. 1, 153–156 (1969).
- [65] Wojtkowski, M. et al. Ultrahigh-resolution, high-speed, Fourier domain optical coherence tomography and methods for dispersion compensation. Opt. Express 12, 2404–2422 (2004).
- [66] Hell, S., Reiner, G., Cremer, C. & Stelzer, E. H. Aberrations in confocal fluorescence microscopy induced by mismatches in refractive index. J. Microsc. 169, 391–405 (1993).
- [67] Muller, R. A. & Buffington, A. Real-time correction of atmospherically degraded telescope images through image sharpening. J. Opt. Soc. Am. 64, 1200–1210 (1974).
- [68] Liu, D. C. & Nocedal, J. On the limited memory BFGS method for large scale optimization. Math. Program. 45, 503–528 (1989).
- [69] Johnson, S. G. The NLopt nonlinear-optimization package. http://github.com/stevengj/nlopt.
- [70] Noll, R. J. Zernike polynomials and atmospheric turbulence. J. Opt. Soc. Am. 66, 207–211 (1976).
- [71] Verrier, N. & Atlan, M. Off-axis digital hologram reconstruction: some practical considerations. Appl. Opt. 50, H136–H146 (2011).
- [72] Xiong, W., Hsu, C. W. & Cao, H. Long-range spatio-temporal correlations in multimode fibers for pulse delivery. Nat. Commun. 10, 2973 (2019).
- [73] Kobat, D. et al. Deep tissue multiphoton microscopy using longer wavelength excitation. Opt. Express 17, 13354–13364 (2009).
- [74] Van Beijnum, F., Van Putten, E. G., Lagendijk, A. & Mosk, A. P. Frequency bandwidth of light focused through turbid media. Opt. Lett. 36, 373–375 (2011).
- [75] Krauze, W. et al. 3D scattering microphantom sample to assess quantitative accuracy in tomographic phase microscopy techniques. Sci. Rep. 12, 19586 (2022).
- [76] Lin, H.-C., Wang, Z. & Hsu, C. W. Fast multi-source nanophotonic simulations using augmented partial factorization. Nat. Comput. Sci 2, 815–822 (2022).
- [77] Wang, Z., Zhang, Y. & Hsu, C. W. Full-wave simulations of tomographic optical imaging inside scattering media. Preprint at https://arxiv.org/abs/2308.07244 (2023).
- [78] Liu, Y., Ma, C., Shen, Y., Shi, J. & Wang, L. V. Focusing light inside dynamic scattering media with millisecond digital optical phase conjugation. Optica 4, 280–288 (2017).
- [79] Qureshi, M. M. et al. In vivo study of optical speckle decorrelation time across depths in the mouse brain. Biomed. Opt. Express 8, 4855–4864 (2017).
- [80] Gao, L. & Smith, R. T. Optical hyperspectral imaging in microscopy and spectroscopy – a review of data acquisition. J. Biophotonics 8, 441–456 (2015).
- [81] Rivenson, Y. et al. PhaseStain: the digital staining of label-free quantitative phase microscopy images using deep learning. Light Sci. Appl. 8, 23 (2019).
- [82] Chen, X. et al. Artificial confocal microscopy for deep label-free imaging. Nat. Photon. 17, 250–258 (2023).
- [83] Akkin, T., Davé, D. P., Milner, T. E. & Rylander III, H. G. Detection of neural activity using phase-sensitive optical low-coherence reflectometry. Opt. Express 12, 2377–2386 (2004).
- [84] Kim, W., Kim, S., Huang, S., Oghalai, J. S. & Applegate, B. E. Picometer scale vibrometry in the human middle ear using a surgical microscope based optical coherence tomography and vibrometry system. Biomed. Opt. Express 10, 4395–4410 (2019).
- [85] Zhang, Y. et al. Deep imaging inside scattering media through virtual spatiotemporal wavefront shaping. Preprint at https://arxiv.org/abs/2306.08793 (2023).
- [86] Balondrade, P. et al. Multi-spectral reflection matrix for ultra-fast 3D label-free microscopy. Preprint at https://arxiv.org/abs/2309.10951 (2023).
- [87] https://doi.org/10.5281/zenodo.8231064.
- [88] https://github.com/complexphoton/SMTexperiment.