Decoherence control of a single-photon optomechanical system in phase-sensitive reservoirs.
Abstract
Recent advancements in strong single-photon optomechanical coupling also demand a deeper understanding of environmental interactions in this regime. The inadequacy of the standard Lindblad master equation necessitates the use of the Dressed-State Master Equation (DSME), which accounts for the correct eigenstates. This work investigates the impact of squeezed vacuum and thermal reservoirs on the decoherence of cavity photon Fock states in the strong coupling regime. We demonstrate that decoherence can be effectively controlled by tuning reservoir parameters, with the control mediated through a cavity dephasing term that becomes significant at high temperatures. The findings presented provide critical insights into reservoir engineering for precise control of quantum decoherence, advancing the understanding of strongly coupled optomechanical systems in engineered environments.
- Keywords
-
Dressed-state master equation, decoherence, optomechanical nonlinearity, quantum photonics, single-photon strong coupling, squeezed reservoir.
I Introduction
There is an increasing focus on utilizing optical photons as a foundation for quantum information processing, communication systems, and advanced sensing technologies. Central to these applications are photonic system components, such as single-photon sources (Luc, ; Ina, ; Luk, ; Ama, ), generators of nonclassical states of light (Gui, ; Lin, ), interferometers (Alb, ; Hyo, ), and sensors (Tia, ; Tor, ; Feng, ; Ali, ), some of which rely on photon-phonon interactions for their functionality. These interactions are particularly critical in the quantum regime, where nonlinear photon-photon interactions mediated by phonons enable phenomena such as photon blockade Hai ; Dong1 ; kai ; Dong2 ; Rabl , characterized by sub-Poissonian photon statistics. As optomechanical nonlinearity plays an essential role in the operation of future quantum devices, a deeper understanding of the dynamics of open quantum optomechanical systems in the strong single-photon coupling regime is imperative. Previous studies have explored the influence of vacuum and thermal reservoirs on the dynamics of optomechanical systems in the strong single-photon coupling regime (Hu, ). These investigations revealed critical insights into how environmental interactions affect system coherence and dynamics. However, the potential of squeezed vacuum and squeezed thermal reservoirs, known to provide additional control over the dynamics of open quantum systems (Hou, ; Ami, ; Rog, ; Chun, ), remains underexplored. Squeezed environments are particularly intriguing as they introduce new degrees of freedom, such as adjustable squeezing parameters and reservoir phase, offering enhanced flexibility for mitigating decoherence and manipulating quantum states. In this article, we extend a previous study (Hu, ) by analyzing the effect of single-photon strong coupling on the time evolution of an optomechanical system’s density operator under the influence of squeezed vacuum and squeezed thermal reservoirs (Gon, ). Interestingly, for specific reservoir parameters, including the squeezing strength and phase, the decoherence rate can exhibit a dramatic reduction, suggesting the possibility of controlling decoherence through reservoir engineering. The simulations presented in this work utilize the Dressed-State Master Equation (DSME), which is well-suited for analyzing systems in the strong coupling regime and has been successfully applied in previous studies of strongly coupled systems (Pon, ; Cho, ). This approach allows us to accurately account for the modified eigenstates of the system, which are critical for capturing the dynamics in the strong coupling regime. Additionally, we propose modifications to the Standard Master Equation (SME) in the interaction picture to incorporate the effects of squeezed thermal reservoirs, providing a more comprehensive framework for analyzing such systems.
Our results are compared with the dynamics observed under thermal reservoirs (Hu, ), highlighting the unique effects introduced by squeezed environments. This comparison underscores the importance of squeezing parameters in controlling quantum system dynamics, particularly in the context of photon-phonon interactions. By quantifying the impact of reservoir phase and squeezing strength on decoherence, we provide valuable insights into the potential of squeezed reservoirs for mitigating decoherence and enhancing coherence in optomechanical systems. These findings pave the way for further exploration of reservoir engineering strategies to optimize quantum devices operating in the strong coupling regime. The article is organized as follows: Section II and Section III provide brief descriptions of the Hamiltonian and eigenbasis relevant to the strong photon-phonon coupling regime. In Section IV, we introduce the Dressed-State Master Equation (DSME) for the evolution of the reduced density matrix, followed by an exploration of its modifications in Section V. The main results are presented and discussed in Section VI, and the article concludes with a summary in Section VII.
II Non-Quadratic Hamiltonian
In optomechanical systems, dressed states serve as the eigenstates of the Hamiltonian that accounts for the interaction between optical and mechanical modes. These states are essential for understanding the system’s behavior under varying laser drive conditions. In the regime of a strong laser drive and weak single=photon optomechanical coupling, the dressed states arise from superpositions of photon-phonon product states, which lead to a splitting of the normal modes associated with the non-interacting Hamiltonian (Mar, ). This splitting reflects the strong coupling between optical and mechanical degrees of freedom, resulting in modified system dynamics that deviate significantly from those of the uncoupled Hamiltonian. Conversely, under a weak laser drive, the influence of single-photon optomechanical coupling , becomes prominent. In the strong coupling regime the cavity photons are effectively ”dressed” by mechanical excitations. In this scenario, the dressed states approximate the eigenstates of the complete Hamiltonian (including the interaction term) when analyzed in the photon-number basis. A unitary transformation of the system Hamiltonian can rigorously demonstrate this behavior, providing a clearer view of the system’s optomechanical response in the weak driving regime. This transformation enables the analytical diagonalization of the Hamiltonian in the dressed state basis, offering a foundation for exploring interaction-driven modifications to system behavior. In this work, we consider a single-mode optomechanical system, consisting of a Fabry-Perot cavity with one end mirror that is free to oscillate under the radiation pressure exerted by the cavity photons. The mechanical degree of freedom associated with this mirror is modeled as a simple harmonic oscillator, while the optomechanical coupling arises from the radiation pressure force that depends on the photon number in the cavity mode. The Hamiltonian of this system, expressed in a frame rotating at the laser drive frequency , is formulated as:
| (1) |
where is the detuning between the laser drive frequency and the intrinsic cavity frequency . Here, represents the natural frequency of the mechanical oscillator, while corresponds to the frequency of the external driving laser. The operators and denote the annihilation and creation operators for the cavity mode, while and represent the annihilation and creation operators for the mechanical mode of the movable mirror. The term describes the single-photon optomechanical coupling strength, quantifying the interaction between the cavity photon number and the mechanical displacement. The final term, , the external laser drive of amplitude . This term provides the energy input to the cavity, facilitating a controlled excitation of the optical mode, and serves as a tunable parameter for investigating optomechanical effects under variable driving strengths. Eq.1 thus encapsulates the dynamics of the optomechanical system, where the non-quadratic term introduces significant non-linearities. These non-linearities are essential for studying complex optomechanical phenomena, including photon blockade, squeezed states, and cooling of the mechanical mode via radiation pressure.
III Polaron Transform
In the context of cavity optomechanics, exploring the system’s eigenstates in the absence of an external drive provides insight into its fundamental nonlinear interactions. To determine the eigenstates of the Hamiltonian under these conditions, we apply a polaron transformation. When the external drive field is removed, the Hamiltonian transforms as follows:
| (2) |
where denotes a unitary operator, with the generator given by
| (3) |
as shown in Nun . Here, and are the frequencies of the cavity mode and mechanical mode, respectively, while represents the single-photon optomechanical coupling strength. This transformation isolates the intrinsic nonlinear interactions between photons and phonons by removing the linear optomechanical terms.
With the transformed Hamiltonian , we can express the total energy of the system in terms of photon and phonon occupation numbers. The energy of the system is then given by
| (4) |
where and denote the expectation values of the photon and phonon number operators, respectively. The term captures the nonlinear energy shift induced by photon-photon interactions mediated by the mechanical mode. This nonlinearity is quadratic in photon number and becomes pronounced in regimes of high photon occupation or strong optomechanical coupling.
The eigenstates of the transformed Hamiltonian can be represented as product states involving both the photon and phonon components. These eigenstates take the form:
| (5) |
where and is the photon number operator. Here, represents a displaced mechanical state , where the displacement amplitude is proportional to the photon number, given by . The term denotes the photon Fock state.
In this framework, a dressed state arises when the mechanical state becomes dependent on the photon number, effectively allowing the cavity photons to “dress” the mechanical state. This coupling mechanism leads to a second-order nonlinearity within the system, manifesting as photon-photon interactions mediated by phonons. The dressing of the mechanical state by cavity photons introduces a nonlinear interaction of a quantum nature, often termed quantum or intrinsic nonlinearity. In the single-photon regime, where the occupation number remains low, these nonlinear effects are subtle but can be amplified in systems with strong to ultrastrong optomechanical coupling (large ).
We can now express the total energy of the system in the dressed state picture as:
| (6) |
where is as defined above. Here, denotes the dressed state in which the mechanical state has been displaced by the cavity photon field. For simplicity, we assume the photon-phonon states, , are represented as a tensor product of individual Fock states.
IV Dressed-State Master Equation
In studying the dynamics of an open quantum system, a typical approach is to use the Standard Master Equation (SME) under the Born-Markov approximation. For systems with weak single-photon coupling, the photon-phonon interaction can be neglected, allowing us to approximate the system’s eigenmodes and use the SME. However, in the strong single-photon coupling regime, intermodal interactions become significant and cannot be ignored, necessitating an alternative approach known as the Dressed-State Master Equation (DSME) (Hu, ; Aga, ; Tah, ). The DSME is formulated within the photon-phonon eigenbasis introduced in Section III, where we consider the strong coupling between the cavity mode and the mechanical mode. In this basis, the Hamiltonian incorporates the shifts in energy levels caused by the photon-phonon interaction, producing dressed states that reflect the altered eigenstructure of the system. Additionally, it is assumed that the thermal bath coupled to the mechanical resonator interacts with both mechanical and optical degrees of freedom, while the bath coupled to the optical resonator affects only the optical degree of freedom.
In the interaction picture, the mechanical operator takes the form,
| (7) |
where is given by Eq.2. By introducing completeness of the dressed-state basis from Eq.5 into Eq.7, we get a “bookkeeping” term, for the definition of in the interaction picture. This allows us to rewrite Eq.(7),
| (8) |
We call it bookkeeping since the term aligns the interpretation of across the DSME and SME. In the SME framework Eq.8 converts back to its usual form in the non-dressed photon-phonon basis ,
| (9) |
It is evident from Eqs.8 and 9 that in the interaction picture for DSME, resolves into two terms rotating with different frequencies and zero. In Eq.8, the first term changes in the energy of the optomechanical system by exchanging one phonon with the mechanical thermal bath while the second term shifts the system energy levels without exchanging any energy. On the other hand the it is fairly straightforward to proveHu that the photon annihilation operator in the interaction picture, is similar for both DSME and the SME at optical frequencies, viz,
| (10) |
For a system in dressed basis (where ), the SME approach introduces additional term in the interaction picture, namely;
| (11) |
where is the density matrix in the interaction picture, is the thermal occupancy number at temperature , and are the mechanical and optical decay rates, respectively, and is the cavity photon number operator. The term represents dissipator, defined here as
| (12) |
where is a system eigen-operator.
The last term in Eq.(11) corresponds to dephasing in density matrix , as it does not affect photon or phonon populations directly but still contributes to the decoherence of . For , terms involving can be neglected. This reduces Eq.(11) to SME in the unperturbed eigenbasis. Assuming Ohmic reservoirs the DSME in the interaction picture can be written as;
| (13) |
where . Note here that an additional approximation is applied to cavity photons in the DSME approach. The cavity frequency should be much larger than the mechanical frequency (), an assumption generally valid for optical photons inside the cavity. In the case of microwave photons, however, this approximation may not hold, requiring the use of the Global Master Equation (GME) (Tah, ). Comparing Eqs.(11) and (13) we see that the SME has an extra dephasing term in the dressed-state basis and strong coupling regime as compared to the DSME. At a high reservoir temperature, , which leads to a larger dephasing in the DSME than the SME. This was first noted in Hu where they showed increasing tends to an increase in decoherence for the DSME. At low reservoir temperature, the last term in Eq.(13) can be neglected, restoring a higher coherence for the DSME compared to the SME. In the following sections we look at whether this comparison holds for the case of squeezed thermal reservoirs and how can it be controlled.
V Dressed-State Master Equation for a Squeezed Thermal Reservoir
In open quantum systems, the non-unitary evolution of the state density matrix arises from interactions with an external reservoir. A well-established method to study system-reservoir interactions is through the Born-Markov approximation, where the coupling between the system and reservoir is assumed to be weak, and the reservoir correlation functions exhibit ”memory-less” behavior. In other words, the characteristic time scale for interactions among reservoir components is much shorter than that of the system. Experimental studies typically involve vacuum or thermal reservoirs. However, non-thermal reservoirs, such as squeezed thermal reservoirs, are more challenging to construct experimentally but have shown promising theoretical applications. Squeezed thermal reservoirs, for instance, have been demonstrated to mitigate quantum coherence decay rates, thus aiding in the preservation of non-classical effects (Ser, ; Kim, ). Recent studies have highlighted the utility of squeezed thermal reservoirs as resources for enhancing the performance of nanomechanical quantum engines, allowing them to exceed the Carnot efficiency limit and improve both power output and efficiency in quantum heat engines (Jan, ; Aba, ). While there is extensive understanding of how squeezed reservoirs influence decoherence in individual quantum states (e.g., coherent or Fock states), there remains a significant gap in the literature regarding the effects of squeezed reservoirs on the decoherence properties of strongly coupled systems. Understanding this role becomes especially relevant for optomechanical systems operating in the strong photon-phonon coupling regime.
V.1 Properties and Realization of Squeezed Thermal Reservoirs
A squeezed thermal reservoir can be realized by introducing a modulated signal to a nanobeam resonator, where the signal noise is manipulated to be suppressed along one quadrature and amplified along the orthogonal quadrature (Jan, ). The phase-space distribution of such a signal then exhibits a squeezed thermal state. Similarly, thermal noise produced by a laser passed through a parametric amplifier can yield squeezed thermal noise. Another method, proposed by Zoller et al. (Zol, ), suggests engineering a squeezed vacuum reservoir via interference between the spontaneous decays of two different excited states in atomic systems. However, this approach requires multiple ground states, which can complicate its practical implementation.
Squeezed thermal reservoirs are categorized as non-stationary reservoirs (Hei, ), in contrast to stationary thermal reservoirs. This classification arises because the correlation functions of the electric field operators for the radiation modes in squeezed reservoirs are time-dependent, breaking the time-homogeneity characteristic of thermal reservoirs. Consequently, in the rotating wave approximation, the master equation governing the evolution of optical and mechanical operators includes additional terms that account for this time-dependence. These modifications have significant implications for the decoherence behavior of systems interacting with squeezed thermal reservoirs, particularly under strong coupling conditions. We examine the Standard Master Equation (SME) in quantum optics for a system interacting with a squeezed thermal reservoir (Hei, ). In the context of our study, this corresponds to the SME in the unperturbed eigenbasis, or equivalently, the system’s eigenbasis in the weak photon-phonon coupling regime (). The SME under these conditions is given by
| (14) |
The terms and characterize the squeezed thermal reservoir and encapsulate the effects of thermal and squeezing parameters on the system dynamics. arise since the electric field operator for squeezed thermal reservoir is not homogeneous in time(Hei, ). Specifically, and are defined as follows:
where represents the thermal occupancy of the mechanical mode, while and denote the squeezing parameters. Here, quantifies the degree of squeezing, and represents the phase of the squeezed quadrature. For optical photons, the thermal occupancy at the cavity frequency is negligible (); thus, and reduce to simpler forms,
for the optical operator . These simplifications capture the effective noise parameters for the optical mode when it is subjected to a squeezed vacuum environment.
The terms proportional to and introduce unique contributions to the system’s dissipative dynamics due to the non-classical properties of the squeezed thermal reservoir. In particular, the presence of reflects the phase-sensitive correlations in the noise spectrum of the reservoir, a hallmark of squeezed states. Such correlations can lead to reduced decoherence rates for certain system states, thereby helping preserve quantum coherence. This characteristic has implications for applications that rely on long-lived quantum states, such as quantum information processing and precision sensing.
V.2 DSME for under the influence of squeezed thermal reservoir
In this section, we extend the discussion from previous sections to consider optomechanical systems operating in the strong to ultrastrong photon-phonon coupling regime. As highlighted in Section IV, in this regime, the Standard Master Equation (SME) for the system density matrix in the interaction picture , introduces an additional dephasing term due to inability of the mechanical operator to resolve distinct frequency components . By contrast, the Dressed-State Master Equation (DSME) effectively resolves these frequency distinctions, thereby eliminating the need for additional dephasing terms. To examine the behavior of the DSME under the influence of squeezed reservoirs, we follow a procedure similar to that outlined by Hu et al. (Hu, ). We begin by writing down the correlation function for a squeezed thermal reservoir. As previously mentioned, the electric field operator is no longer homogeneous in time, we get terms in the correlation function which are independent/dependent in time(Hei, ). Rearranging them we get;
| (15) | ||||
where,
where is the system-reservoir coupling for the reservoir mode having polarization . The correlation function in Eq.(15) leads to additional terms proportional to operators , , and in the dressed state. Since for the cavity mode, and are replaced by and respectively, while for the mechanical mode(where ) they are replaced by and respectively. Under these assumptions we derive the DSME in the strong to ultrastrong photon-phonon coupling regime interacting with a squeezed thermal reservoir. This is shown in Appendix A. The final equation can then be written as;
| (16) | ||||
where, . As expected, Eq.(16) is very similar to Eq.(14) except that is replaced by for the dressed-state basis. We see a similar last term to that in Eq.(13), where now, we have the temperature and dependent term also depending on the reservoir squeezing parameters . From the definitions of , , and we see that for (no squeezing), Eq.(16) reduces to Eq.(13). On the other hand for different values of and we can control the amount of photon dephasing contribution to the decoherence of the density operator . In SectionVI we exploit this control to demonstrate that the decoherence rates of coherent superposition states can be lowered for certain values of and .
V.3 SME for under the influence of squeezed thermal reservoir
In Section IV, we highlighted that for a strong single-photon optomechanical coupling(), the SME in the interaction picture for a thermal reservoir contains an additional cavity dephasing term(Eq.(11)). This is true even for a squeezed thermal reservoir. Infact two additional terms should be included for SME as shown in Appendix B,
| (17) | ||||
Comparing with Eq.(11), in the last term is replaced by while the second last term in Eq.(17) is proportional to cosine of reservoir phase(Appendix B). Both these terms in the weak photon-phonon coupling limit().
VI Results and discussion
In this section, we present a comparative analysis of the decoherence of the system’s density operator for both phase-sensitive (squeezed) and thermal reservoirs within the framework of the DSME. We investigate how these reservoirs influence the decoherence of cavity photon Fock states in coherent superpositions within an optomechanical system. Additionally, we examine the impact of the squeezing parameters and on the decoherence rate of the system’s density operator for cavity photon Fock states. For these simulations, we employ the mesolve routine from the Quantum Toolbox in Python (QuTiP) (Qut1, ), utilizing appropriate Lindblad superoperators and the Hamiltonian given in Eq. (2).
To simulate the evolution of the cavity photons, we first define a general initial state of the optomechanical system as
| (18) |
where and denote the cavity photon and mechanical Fock states, respectively. As demonstrated in Section III, these states are eigenstates of the Hamiltonian . While using superpositions of coherent states instead of Fock states does not alter the final results and is experimentally more feasible, we opt for Fock states here for technical clarity. In the interaction picture, the coherence of the cavity photon state is represented by the off-diagonal element of the time-evolved density operator after performing a partial trace over the mechanical Fock states. This is expressed as,
| (19) |
where is the initial density operator.
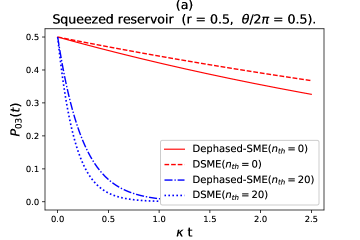
is the partial trace over the mechanical state. For brevity we choose and , and . This state is similar to the one used in Hu et. al.(Hu, ). Fig.1 shows the evolution of as a function of dimensionless unit for depahsed-SME and DSME in vacuum and thermal reservoirs corresponding to master equations given in Eq.(11) and Eq.(13) above. It is qualitatively similar to the one produced in Hu et al.(Hu, ) i.e. the effect of cavity dephasing becomes dominant at high temperatures in the DSME than that for the SME in the interaction picture. A similar trend can be seen Fig.2 where the evolution occurs under the influence of a squeezed reservoir. Fig.2(a) indicates a decrease in the difference between evolution under SME and DSME at high reservoir temperature (), as compared to Fig.1 while Fig.2(b) indicates an opposite effect.


|
Further, at low reservoir temperatures() it can be seen that the rate of decay of under DSME is slower than that for the SME. This is because DSME at low temperature is devoid of any temperature dependent dephasing, Eq.(16) while the last term for SME in Eq.(17) does not vanish causing additional dephasing at . Also from Fig.2 we notice that thermal reservoirs do not provide any control over this decoherence while the squeezed reservoirs do by changing the squeezing parameters and . This shouldn’t come as a surprise for a quantum system weakly interacting with a squeezed thermal reservoir as this topic has been vastly covered in the literature. The interesting part here is that we can clearly quantify this control in terms of the phase of the reservoir in the strong photon-phonon coupling regime, .
It is seen from Fig.2 that for the same value of , the decoherence drastically changes for different values of . This is due to the dependence of decoherence on the cosine of the phase of the reservoir. In the weak photon-phonon coupling regime, , the terms connected to in Eqs.(16) and (17) vanish which makes it harder to establish such an explicit dependence on phase of the reservoir at least at high temperatures. This is not so for . By setting up an appropriate reservoir phase one can increase/decrease the overall coherence of the cavity mode of the optomechanical system density matrix. Fig.3 indicates the dependence of squeezing parameters, and on DSME for interaction with the squeezed thermal reservoir. We choose the value of for which goes below as a function of and in Fig.3(a) and 3(b) respectively.
 
|
We see that the value of for a thermal reservoir does not change with respect to or (shown as solid blue line) which is expected. In Fig.3(a), for a squeezed reservoir we can see that a maximum is reached near and in the ultrastrong coupling regime, . From Fig.3(b) we also see that for values of the coherence time gradually decreases towards that for thermal DSME. This means that for values greater than , decreases faster towards of its initial value even though we set reservoir phase at .
VII Conclusion
In this article we have demonstrated the effects squeezed thermal reservoirs have on a single cavity optomechanical system in the strong single-photon coupling regime. In the strong single-photon optomechanical coupling regime, the appropriate master equation is the dressed-state master equation(DSME) as long as it is applied for the situation where the frequency of cavity photons is much larger than the natural frequency of the mechanical resonator. Such an optomechanical system interacting with a squeezed thermal reservoir gives additional terms in the master equation which depend on the cosine of the reservoir phase. We have shown that by setting the squeezed thermal reservoir phase to we can increase coherence times for strongly coupled optomechanical systems which otherwise is not possible for thermal reservoir. On the other hand we have also shown that increasing reservoir squeezing parameter does not always lead to an increase in coherence time and that a maximum is reached for particular values of and upto an order of magnitude for strongly coupled photon-phonon systems. For values of there is a drastic increase in coherence under the influence of squeezed thermal reservoir with its phase near , as compared to a thermal reservoir. It would be further interesting to analyse the effect of reservoir phase on the time evolution of Wigner functions of Fock states used in our study since negative densities of Wigner functions have been known to be related to coherence and non-classicality. Our study might be useful in understanding systems which are reservoir engineered to increase coherence. It might also help in understanding entanglement in strongly coupled systems under the influence of phase-sensitive reservoirs. Although the current state-of-the-art experiments are far from reaching such strong single-photon optomechanical coupling strengths this study becomes necessary to demonstrate what can be achieved once there is such a technology in place.
Appendix A Mechanical damping.
Calculations for cavity field damping are pretty straightforward and similar to the case for a squeezed vacuum reservoir for operator and . Hence we do not present it here again. They can be found in any standard quantum optics textbook. Instead we begin straightaway with operators representing mechanical oscillation and damping. From Eq.(15) in Section V.1,
| (20) |
| (21) |
| (22) |
where we have assumed approximately equal contributions from the spectral density near and . If the spectral density , the contribution of Equation (22) is negligible as compared to Equations (20) and (21). Recalling, (ohmic reservoir), Equation (22) for high temperatures () becomes,
| (23) |
We define a hermitian operator in the interaction picture, where in the interaction picture and dressed basis. Our aim is to calculate terms in,
| (24) |
for a squeezed thermal reservoir. Let us consider the first term in Equation (24),
| (25) |
Next we use Equations (20) to (23) to piece-wise calculate the above integral for a squeezed thermal reservoir and neglect fast oscillating terms under the rotating wave approximation(RWA),
| (26) |
| (27) |
| (28) |
| (29) |
Substituting the above equations in Equation (24) and similarly calculating the Hermitian conjugate, we get the mechanical part of Eq.(LABEL:12).
Appendix B Cavity dephasing in SME
Emergence of cavity dephasing terms in Equation (17) can be understood as follows; The unitary transformation of the dissipator from Schrodinger picture of the standard master equation(SME) to interaction its picture in dressed basis is,
| (30) |
where , being the system hamiltonian in Eq.2). Similarly for a squeezed thermal reservoir,
| (31) | ||||
where .
References
- (1) L. Caspani, C. Xiong, B. J. Eggleton, D. Bajoni, M. Liscidini, M. Galli, R. Morandotti, and D. J Moss, Light Sci. Appl. 6, e17100 (2017).
- (2) I. Yeo, H. J. Kim, J. D. Song, and K. S. Yi, Phys. Rev. B 94, 165422 (2016).
- (3) Ł Dusanowski, Soon-Hong Kwon, C. Schneider, and S. Höfling, Phys. Rev. Lett. 122, 173602 (2019).
- (4) B. Sarma, and A. K. Sarma, J. Phys. B: At. Mol. Opt. Phys. 51, 075505 (2018).
- (5) G. Huang, W. Deng, H. Tan, and G. Cheng, Phys. Rev. A 99, 043819 (2019).
- (6) L. Liu, B.-P. Hou, X.-H. Zhao, and B. Tang, Opt. Express 27, 8361-8374 (2019).
- (7) A. Barchielli, and M. Gregoratti, Phys. Rev. A 104, 013713 (2021).
- (8) C.-W. Lee, J. H. Lee, and H. Seok, Scientific Reports, 10, 17496 (2020).
- (9) T. Liu, F. Pagliano, René van Veldhoven, V. Pogoretskiy, Yuqing Jiao, and A. Fiore, Nature Communications 11, 2407 (2020).
- (10) M. Toroš, and T. S. Monteiro, Phys. Rev. Research 2, 023228 (2020).
- (11) F. Zhou, Y. Bao, R. Madugani, D. A. Long, J. J. Gorman, and T. W. LeBrun, Optica 8, 350 (2021).
- (12) A. Motazedifard, A. Dalafi, and M. H. Naderi, AVS Quantum Sci. 3, 024701 (2021).
- (13) H.-Q. Shi1, X.-T. Zhou, X.-W. Xu, and N.-H. Liu1, Scientific Reports 8, 2212 (2018).
- (14) D.-Y. Wang, C.-H. Bai, X. Han, S. Liu, S. Zhang, and H.-Fu Wang, Opt. Lett. 45, 2604 (2020).
- (15) K. Wang, Y.-P. Gao, T.-T. Pang, T.-J. Wang, and C. Wang, EPL 131, 24003 (2020).
- (16) D.-Y. Wang, C.-H. Bai, S. Liu, S. Zhang, and H.-Fu Wang, New J. Phys. 22, 093006 (2020).
- (17) P. Rabl, Phys. Rev. Lett. 107, 063601 (2011).
- (18) D. Hu, S.-Y. Huang, J.-Q. Liao, L. Tian, and H.-S. Goan, Phys. Rev. A 91, 013812 (2015).
- (19) Q. Z. Hou, C. J. Yang, C. Y. Chen, J. H. An, W. L. Yang, and M. Feng, Phys. Rev. A 100, 032302 (2019).
- (20) A. Joshi, S. S. Hassan, and M. Xiao, Phys. Rev. A 72, 055803 (2005).
- (21) R. J. de Assis, J. S. Sales, J. A. R. da Cunha, and N. G. de Almeida, Phys. Rev. E 102, 052131 (2020).
- (22) C.-J. Yang, J.-H. An, W. Yang, and Y. Li Phys. Rev. A 92, 062311 (2015).
- (23) G. Manzano, Phys. Rev. E 98, 042123 (2018).
- (24) M. A. de Ponte, M. C. de Oliveira, and M. H. Y. Moussa, Phys. Rev. A 70, 022324 (2004).
- (25) C.-H. Chou, T. Yu, and B. L. Hu, Phys. Rev. E 77, 011112 (2008).
- (26) M. Aspelmeyer, T. J. Kippenberg, and F. Marquardt, Rev. Mod. Phys. 86, 1391 (2014).
- (27) A. Nunnenkamp, K. Børkje, and S. M. Girvin, Phys. Rev. Lett. 107, 063602 (2011).
- (28) A. Serafini, S. De Siena and F. Illuminati, Modern Physics Letters B 18, 687 (2004).
- (29) M. S. Kim, and V. Bužek, Phys. Rev. A 47, 610 (1993).
- (30) J. Klaers, S. Faelt, A. Imamoglu, and E. Togan Phys. Rev. X 7, 031044 (2017).
- (31) J. Roßnagel, O. Abah, F. Schmidt-Kaler, K. Singer, and E. Lutz Phys. Rev. Lett. 112, 030602 (2014).
- (32) Heinz-Peter Breuer, and F. Petruccione, Theory of open quantum systems (Oxford University Press, 2002), p.136.
- (33) S. Agarwal, S. M. Hashemi Rafsanjani, and J. H. Eberly, J. Phys. B: At. Mol. Opt. Phys. 46, 224017 (2013).
- (34) M. Tahir Naseem, A. Xuereb, and Ö. E. Müstecaplıoğlu, Phys. Rev. A 98, 052123 (2018).
- (35) N. Lütkenhaus, J. I. Cirac, and P. Zoller, Phys. Rev. A 57, 548 (1998).
- (36) J. R. Johansson, P. D. Nation, and F. Nori, Comp. Phys. Comm. 183, 1760 (2012).