e-mail: [email protected] 22institutetext: Department of Astronomy, Stockholm University, AlbaNova University Centre, SE-106 91, Stockholm, Sweden 33institutetext: Minnesota Institute for Astrophysics, School of Physics and Astronomy, University of Minnesota, 316 Church Str. SE, Minneapolis, MN 55455, USA
Deciphering Lyman blob 1 with deep MUSE observations††thanks: Based on observations made with ESO Telescopes at the La Silla Paranal Observatory under programme ID 094.A-0605, programme ID 095.A-0570, and programme ID 097.A-0831.
Abstract
Context. Lyman blobs (LABs) are large-scale radio-quiet Lyman (Ly) nebula at high- that occur predominantly in overdense proto-cluster regions. Especially the prototypical SSA22a-LAB1 at has become an observational reference for LABs across the electromagnetic spectrum.
Aims. We want to understand the powering mechanisms that drive the LAB to gain empirical insights into galaxy formation processes within a rare dense environment at high-. Thus we need to infer the distribution, the dynamics, and the ionisation state of LAB 1’s Ly emitting gas.
Methods. LAB 1 was observed for 17.2 h with the VLT/MUSE integral-field spectrograph. We produced optimally extracted narrow band images in Ly , He ii , and we tried to detect C iv emission. By utilising a moment based analysis we mapped the kinematics and the line profile characteristics of the blob. We also linked the inferences from the line profile analysis to previous results from imaging polarimetry.
Results. We map Ly emission from the blob down to surface-brightness limits of erg s-1cm-2arcsec-2. At this depth we reveal a bridge between LAB 1 and its northern neighbour LAB 8, as well as a shell-like filament towards the south of LAB 1. Complexity and morphology of the Ly profile vary strongly throughout the blob. Despite the complexity, we find a coherent large scale east-west 1000 km s-1 velocity gradient that is aligned perpendicular to the major axis of the blob. Moreover, we observe a negative correlation of Ly polarisation fraction with Ly line width and a positive correlation with absolute line-of-sight velocity. Finally, we reveal He ii emission in three distinct regions within the blob, but we can only provide upper limits for C iv.
Conclusions. Various gas excitation mechanisms are at play in LAB 1: Ionising radiation and feedback effects dominate near the embedded galaxies, while Ly scattering is contributing at larger distances. However, He ii/Ly ratios combined with upper limits on C iv/Ly can not discriminate between AGN ionisation and feedback driven shocks. The alignment of the angular momentum vector parallel to the morphological principal axis appears odds with the predicted norm for high-mass halos, but likely reflects that LAB 1 resides at a node of multiple intersecting filaments of the cosmic web. LAB 1 can thus be thought of as a progenitor of present day massive elliptical within a galaxy cluster.
Key Words.:
Cosmology: observations – Galaxies: high-redshift – Galaxies: halos – Techniques: imaging spectroscopy1 Introduction
Lyman (Ly) blobs (LABs) are very luminous ( erg s-1) and very extended ( kpc in projection) Ly emitting nebulae. They were unexpectedly revealed in narrow-band imaging campaigns targeting Lyman emitting galaxies (LAEs) at (Francis et al., 1996; Steidel et al., 2000). LABs have now been found in numerous, sometimes LAB-dedicated, high- galaxy surveys (e.g. Matsuda et al., 2004; Nilsson et al., 2006; Prescott et al., 2012, 2013). Their presence is confirmed from (Barger et al., 2012) up to (Ouchi et al., 2009; Sobral et al., 2015; Shibuya et al., 2018; Zhang et al., 2019). Moreover, a very rare class of extended [O iii] nebulae have been proposed to share similarities with high-redshift LABs (Schirmer et al., 2016).
The distinctive observational feature of LABs with respect to similarly extended and luminous high- Ly nebulae around radio-galaxies (e.g. Morais et al., 2017; Vernet et al., 2017; Marques-Chaves et al., 2019), radio-loud quasars (e.g. Smith et al., 2009; Roche et al., 2014), or radio-quiet quasars (e.g. Christensen et al., 2006; Borisova et al., 2016; Ginolfi et al., 2018; Husemann et al., 2018; Arrigoni Battaia et al., 2019; Drake et al., 2019; Farina et al., 2019; Travascio et al., 2020) is that the primary powering source driving their Ly emission is usually not detected or not obvious from the rest-frame UV and rest-frame optical discovery data (see also review by Cantalupo, 2017, and references therein). However, the defining physical characteristic of LABs is their preferential occurrence within overdense high- proto-cluster regions. In fact, the first LABs were found in narrow-band searches targeting known or presumed high-density structures (Francis et al., 1996; Steidel et al., 2000). Following these initial discoveries, other narrow-band surveys targeting redshift overdensities were able to replicate the success in unveiling LABs (e.g. Palunas et al., 2004; Erb et al., 2011; Mawatari et al., 2012; Cai et al., 2017; Kikuta et al., 2019). Conversely, LABs found in blind searches could be linked to over-densities (Prescott et al., 2008; Yang et al., 2009, 2010; Bădescu et al., 2017). Given that their preferred habitats are proto-cluster regions and their sizes are enormous, it appears natural to suspect LABs as the progenitors of extremely massive, if not the most-massive galaxies in present day cluster environments (see also review by Overzier, 2016).
The required amount of hydrogen ionising photons to drive the observed Ly output of the blobs via recombinations is s-1 for a erg s-1 LAB in a standard case-B recombination scenario. This would correspond to star-formation rates M⊙yr-1 and absolute UV magnitudes using canonical conversion factors (e.g. Kennicutt, 1998). The absence of such bright UV galaxies in the vicinity of the nebulae may indicate that the powering sources are heavily dust-obscured along the line of sight. Moreover, it might also hint at an additional source of Ly photons in LABs: collisional excitations of neutral hydrogen by free electrons, a process which also cools the heated electron gas. As a coolant, Ly is most effective for gas temperatures around K. In the case of LABs, potential heating sources could be star-burst driven super-winds from the heavily obscured central galaxies (e.g. Taniguchi & Shioya, 2000; Mori et al., 2004) or the gravitational potential of the halo hosting the blob (“gravitational cooling”, see e.g. Haiman et al., 2000; Rosdahl & Blaizot, 2012).
The gravitational cooling mechanism was initially deemed the dominant powering source for driving Ly emission from LABs (Haiman et al., 2000; Dijkstra & Loeb, 2009). This idea is especially intriguing, as theoretical models predict that gas accretion onto galaxies forms dense cold flow filaments (e.g., Kereš et al., 2005; Dekel & Birnboim, 2006; Brooks et al., 2009; Stewart et al., 2017). Despite its theoretical importance, empirical evidence for this processes in high- galaxies remains circumstantial (e.g. Rauch et al., 2016). The filamentary Ly morphology of LABs as well as the alignment of their major axes with the surrounding large scale structure are regarded as observational support for the gravitational cooling scenario (Erb et al., 2011; Matsuda et al., 2011).
The polarisation of the observed Ly emission from the blob could potentially distinguish between the central engine hypothesis or the in-situ powering by gravitational cooling (Dijkstra & Loeb, 2008; Eide et al., 2018). In the former case the polarisation fraction is expected to increase with distance from the embedded sources. And indeed, for Lyman blob 1, the object examined in detail in this study, such a polarisation characteristic was detected (Hayes et al., 2011; Beck et al., 2016). These observations were thought to rule out the gravitational cooling scenario, but Trebitsch et al. (2016) showed that also gravitational cooling may be responsible for the observed polarisation pattern.
Regardless, follow-up campaigns with X-ray, sub-mm, IR, and radio-facilities revealed that a significant fraction of LABs indeed harbour highly obscured star-bursts with star-formation rates M⊙yr-1 or AGNs (e.g. Yang et al., 2011; Ao et al., 2015, 2017). Thus, mechanical heating and/or ionising radiation from these buried systems are definitely contributing and possibly dominating the energy budget that powers Ly in LABs. In such a scenario the filamentary morphology can still be reconciled with the cooling flow interpretation, as those flows are expected to fuel star-formation and AGN activity in the first place. But rather than being lit-up in Ly by gravitational cooling, these filamentary flows could simply be illuminated from the systems that they are feeding (Prescott et al., 2015b). However, a potential counterargument to this scenario is that the gas in the cold flows is self-shielded from ionising radiation given the expected typical densities (cm-3; Dijkstra & Loeb 2009). Moreover, it appears counter-intuitive that the heavily obscured embedded sources have high escape fractions of ionising photons into large enough solid angles to power the blobs. As yet, there is still no consensus on the importance of the possible Ly powering mechanisms in LABs.
Integral-field spectroscopic (IFS; Bacon & Monnet, 2017) observations are an especially promising observational line of attack for such studies. Disentangling the different Ly powering mechanisms at work in LABs is warranted, as the relevant Ly emission processes are linked to the physical processes that regulate the build-up of stellar mass and growth of super-massive black holes in the most-massive galaxies of the present day universe. The modern integral-field spectrographs on 10 m class telescopes, i.e. the “Keck Cosmic Web Imager” (Morrissey et al., 2018) at the Keck II telescope and the “Multi Unit Spectroscopic Explorer” (MUSE, Bacon et al., 2010, 2014) at ESO’s Very Large Telescope UT4, are ideally suited to cover the projected sizes of LABs. Analyses of combined spectral and spatial information from IFS can provide a detailed view of the Ly morpho-kinematics. Specifically, cold-mode accretion filaments are expected to leave imprints on the velocity fields compared to simple Keplarian motions (Arrigoni Battaia et al., 2018; Martin et al., 2019). Moreover, gas which is not affected by star-formation or AGN driven feedback is expected to be kinematically more quiescent than feedback heated gas. Thus, these processes can potentially be distinguished by spatially mapping the observed Ly line width.
A difficultly in interpreting line-of-sight velocities and line-widths from Ly emission, is that resonant scattering diffuses the intrinsic Ly radiation field in real and frequency-space (see review by Dijkstra, 2019). The spatial diffusion can be envisioned as a projected smoothing processes (Bridge et al., 2018), that can enhance the apparent size of the Ly blobs by reducing the steepness of their surface brightness profiles (Zheng et al., 2011; Gronke & Bird, 2017). Moreover, it can also “wash-out” cold-accretion features of small angular size (Smith et al., 2019). The diffusion in frequency space, which is dependent on the kinematics and column densities of the scattering medium, can lead to significant modulations of the spectral profile (e.g., Laursen et al., 2009). Additionally, the transmission of the Ly photons through the intergalactic medium will also modify the line profile (e.g., Laursen et al., 2011). However, the observed low-velocity shifts between Ly and optically thin emission lines for galaxies within LABs appear at odds with the expectations from Ly radiative transfer theory (e.g. McLinden et al., 2013). This might indicate that Ly scattering does not significantly modulate the observable velocity field of LABs. Thus, it is possible to obtain a measure the angular momentum of the gas in the early formation stage of a massive halo, which directly relates to the action of tidal torques from the surrounding large scale structure and the cosmic web (e.g. Forero-Romero et al., 2014; Lee et al., 2018).
Further insights into the thermodynamic properties of the emitting gas of blobs can be gained from ground based IFS data due to the potential detectability of other rest-frame UV emission lines. Especially He ii and C iv emission lines have been used as diagnostics for LABs (Prescott et al., 2009; Scarlata et al., 2009a; Arrigoni Battaia et al., 2015). Both lines act as gas-coolants, but for a higher temperature ( K) gas phase compared to Ly which cools the K phase (Yang et al., 2006). Heating sources driving this phase could be feedback effects from the embedded galaxies (Mori et al., 2004; Cabot et al., 2016) or the gravitational potential of the halo hosting the blob (Yang et al., 2006; Dijkstra & Loeb, 2009). Both lines can also be powered via photo-ionisation, but require the abundance of higher energy photons to produce the recombining species. Such hard ionising radiation is only expected in the vicinity of extreme low metallicity stellar populations (e.g. Schaerer, 2013) or in the surroundings of an AGN (e.g. Humphrey et al., 2019). Analysing relative line strengths and comparing the spatial distribution of the He ii and C iv emitting gas to the positions of potential ionising sources within blob may help to distinguish between photo-ionisation and cooling-radiation scenarios.
With the aim to decipher the physical processes at work in LABs we present the deepest IFS observations of a giant LAB obtained so far. Our target is the prototypical giant Steidel et al. LAB – SSA-22a Lyman blob 1 (LAB1). LAB 1 lives in one of the most overdense regions known at . This region, referred to as the SSA 22 proto-cluster, shows a significant density peak of Lyman break galaxies (Steidel et al., 1998, 2003; Saez et al., 2015), Lyman emitting galaxies (LAEs, Hayashino et al., 2004; Yamada et al., 2012), sub-mm galaxies (Tamura et al., 2009), AGNs (Lehmer et al., 2009b; Alexander et al., 2016), and also LABs (Matsuda et al., 2004, 2011). Interestingly, with an estimated cluster mass of 2-4M⊙, the SSA 22 proto-cluster may actually be a unique structure within the horizon (Kubo et al., 2015).
Since its discovery LAB 1 became the target of numerous follow-up observations and is thus the most well studied LAB to-date. We will provide an overview of those results in the following Sect. 2 before describing our new 17.2 h MUSE observations in Sect. 3. In Sect. 4 we detail how we reduced the MUSE data. We present our analysis and results in Sect. 5, and in Sect. 6 we discuss the interpretations of our findings. Lastly, we summarise and present our conclusions in Sect. 7.
Throughout the paper we assume a canonical 737-cosmology, i.e. , , and H km s-1Mpc-1. Adopted reference line wavelengths stem from the atomic line list compiled by van Hoof (2018), all wavelengths Å refer to vacuum wavelengths, and for conversions between air- and vacuum wavelengths we follow the prescriptions adopted in the Vienna Atomic Line Database (Ryabchikova et al., 2015).
2 Summary of previous results on LAB 1
| Name | RA | Dec | Refs. | |
|---|---|---|---|---|
| SSA22a-C11 | 22h17m25.70s | +00∘12′34.4″ | 3.09990.0004 | (1),(2) |
| SSA22a-C15 | 22h17m26.15s | +00∘12′54.7″ | 3.09860.0003 | (1),(2) |
| LAB1-ALMA1 | 22h17m25.94s | +00∘12′36.6″ | (3) | |
| LAB1-ALMA2 | 22h17m26.01s | +00∘12′36.4″ | (3) | |
| LAB1-ALMA3 | 22h17m26.11s | +00∘12′36.4″ | 3.09930.0004 | (3) |
| VLA-LAB1a | 22h17m25.95s | +00∘12′35.3″ | (4) | |
| LAB01-K15b | 22h17m25.70s | +00∘12′38.7″ | 3.10070.0002 | (5) |
| S1 | 22h17m26.08s | +00∘12′34.2″ | 3.0968 | (5),(6) |
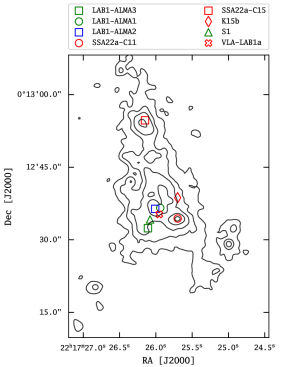
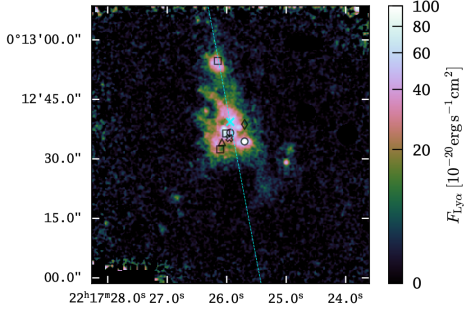
LAB 1 (RA: 22h17m26.0s, Dec: +00∘12′36″) was discovered in a narrow-band image by Steidel et al. (2000). These observations targeted Ly emission of a previously identified redshift overdensity at that was revealed as a peak in the redshift distribution of a spectroscopic follow-up campaign for Lyman break selected galaxies in the SSA-22 field (Steidel et al., 1998). With an isophotal area of 181 arcsec2 (10523 kpc2 in projection) and a total Ly luminosity of erg s-1 LAB 1 is one of the largest and one of most luminous LABs known (Matsuda et al., 2011). Directly north of LAB 1, offset by ″ from its photometric centre, Matsuda et al. (2004) identified a companion blob: LAB 8 (RA: 22h17m26.1s, Dec: +00∘12′55″, erg s-1, isophotal area 40 arcsec2). As will be demonstrated in the present analysis LAB 1 and LAB 8 are, in fact, a contiguous structure (see Figure 1).
Two of the Lyman break galaxies from Steidel et al. (1998) are within the combined LAB 1 / LAB 8 structure. Adopting the nomenclature of Steidel et al. (2003), these are SSA22a-C11 and SSA22a-C15. We list the coordinates of both galaxies in Table 1222We note the coordinates for these Lyman break galaxies provided in Steidel et al. (2003) – RA22h17m25.67s/Dec+00∘12′35.2″ for SSA22a-C11, and RA22h17m26.127s/Dec+00∘12′55.3″ for SSA22a-C15 – appear to be offset by ″ to the north-west with respect to where these galaxies are located in our data. As described in Sect. 4.2, we aligned our data with the 2MASS reference frame, while Steidel et al. (2003) tied their astrometry the HST guide star catalogue. Earlier versions of the HST guide star catalogue were known to contain systematic errors of up to 1″ (Morrison et al., 2001). We thus speculate that this is the reason for the coordinate offsets. Here we revise the coordinates of SSA22a-C11 and SSA22a-C15 according to our adopted reference frame (Table 1). . SSA22a-C11 is located in the south-west of LAB 1, while SSA22a-C15 is found close to the Ly photometric centre of LAB 8. Both galaxies have their redshift confirmed via near-IR detections of their [O iii] lines (McLinden et al., 2013). Interestingly, McLinden et al. (2013) find no offset between Ly emission line redshifts and [O III] redshifts. This is not commonly the case for high- Ly emitting galaxies where the Ly line is typically found to be offset by km s-1 with respect to the systemic redshift (e.g. Rakic et al., 2011; Chonis et al., 2013; Trainor et al., 2015). Since positive Ly redshift offsets are usually interpreted as signs of outflowing expanding gas, McLinden et al. (2013) argue that C11 and C15 have no such prominent outflows. Moreover, C11 has an inferred star-formation rate of M⊙yr-1 (Steidel et al., 1998, 2003), thus falls short by more than a factor of ten in producing the required amount of ionising photons to power LAB 1.
Given the potential of obscured star-formation or AGN activity in the blob, it became naturally the target of several sub-mm and radio campaigns (Chapman et al., 2001, 2003; Matsuda et al., 2007; Yang et al., 2012; Geach et al., 2014, 2016; Umehata et al., 2017; Ao et al., 2017). Initial studies provided a confusing picture with purported detections by some that were vastly incommensurate with upper limits reached by others (see Sect. 2 of Geach et al., 2014). Nevertheless, advances in sub-mm detector technology and collecting area lead to a significant detection of three 850m sources within the blob (Geach et al., 2014, 2016; Umehata et al., 2017). Adopting the nomenclature of Umehata et al. (2017), these ALMA detected systems are denoted LAB1-ALMA1, LAB1-ALMA2, and LAB1-ALMA3. We list their coordinates in Table 1. LAB1-ALMA1 and LAB1-ALMA2 are in close vicinity to each other and close to the peak of Ly surface brightness. LAB1-ALMA3 is located in the south-eastern part of LAB 1. The total measured 850 m flux density from these three resolved ALMA sources is mJy. This corresponds to star-formation rates of M⊙yr-1 under standard dust-heating assumptions. Moreover, hints for an extended low-surface brightness dust-component which is not detected by ALMA are seen in the fact that the single-dish SCUBA-2 observations (Geach et al., 2014) yield a factor of higher flux compared to the interferometric measurement.
Ao et al. (2017) report 3 GHz radio-continuum detection slightly south of LAB 1-ALMA1 and LAB1-ALMA2. This Jy radio source is denoted VLA-LAB1a and we list its coordinates in Table 1. Given the proximity to LAB 1-ALMA1 and LAB1-ALMA2 the radio source is believed to be physically associated with the mJy sub-mm galaxies. According to Ao et al. (2017) the ratio is atypical for a purely star-forming system and thus could be indicative of AGN activity. Both systems have no spectroscopic redshift confirmation independent of Ly. However, sources at the positions of LAB1-ALMA1 and LAB1-ALMA2 are reported as K-Band selected galaxies with photometric redshifts in the range (Uchimoto et al., 2012, their Figure 10).
LAB1-ALMA3 is spectroscopically confirmed as a [C II] 158 m emitting source with ALMA (Jy km s-1, ; Umehata et al., 2017). It is also detected as a 3 GHz radio-continuum source with the VLA (Jy; Ao et al., 2017). As the coordinates of this radio counterpart are identical with LAB1-ALMA3 we do not list it as a separate source. Moreover, Ao et al. (2017) report a tentative X-Ray signal at the position of LAB1-ALMA3 using the deep (400 ks) Chandra full-band (0.5 - 8 keV) image from Lehmer et al. (2009a). From these observations Ao et al. (2017) suggest the potential existence of an AGN in this source. Moreover, LAB1-ALMA3 appears as a K-Band selected galaxy in the sample of Uchimoto et al. (2012) and has been spectroscopically confirmed via H and [OIII] emission with MOIRCS on the Subaru telescope (Kubo et al., 2015, 2016). The redshift derived from those rest-frame optical lines () is commensurate with the [C II]-based redshift.
Two more galaxies are spectroscopically confirmed members of the blob. LAB01-K15b is a K-Band selected galaxy detected in [O iii] emission (Kubo et al., 2015, 2016) and S1 is a serendipitous [O iii] detection from Geach et al. (2016). The coordinates and redshifts of both sources were presented by Umehata et al. (2017) and are reproduced in Table 1. Lastly, Kubo et al. (2016) display a faint K-Band selected galaxy slightly south-west of SSA22a-C11 at a compatible photometric redshift (their Figure 2), however, no coordinates for this potential member of LAB 1 are provided.
In summary, the LAB 1/LAB 8 system contains 5 spectroscopically confirmed galaxies. Guided by the systemic redshifts of the galaxies associated with the blob (Table 1) we fix as its systemic redshift in the following. One of the spectroscopically confirmed systems, LAB1-ALMA3, is detected in 850m dust-continuum, [C ii] 158m emission, 3GHz radio continuum, and tentatively in X-Rays (Ao et al., 2017). Additionally, two 850m sources (LAB1-ALMA1 and LAB1-ALMA2) which are accompanied by a 3GHz sources (VLA-LAB1a) are detected in the centre of LAB 1. While these sources are not spectroscopically confirmed members of the blob, their physical association with the system appears likely, especially given their prominent central position within the blobs structure. To provide a visual overview of the with the LAB 1/LAB 8 system associated galaxies we plot their positions with respect to the Ly surface brightness contours in Figure 1. For the latter we made already use of the MUSE data discussed in the remainder of the paper.
The interpretation that LAB1-ALMA1 and LAB1-ALMA2 are physically associated with the blob is further supported by results from imaging-polarimetry with FORS2 on the VLT by Hayes et al. (2011). The radial polarisation profile, as well as the orientation of the polarisation vectors from those observations are consistent with predictions from Ly radiative-transfer theory for Ly scattering from a central Ly powering source (Dijkstra & Loeb, 2008). Interestingly, LAB1-ALMA1 and LAB1-ALMA2 are at the centre of the circular pattern denoted by the polarisation vectors from Hayes et al. (2011). More recent spectro-polarimetry with FORS2 by Beck et al. (2016) appears consistent with this scenario, although the interpretation of spectro-polarimetric Ly data is more complex (Lee & Ahn, 1998), as different scattering geometries and kinematics are degenerate with respect to observable polarisation signal (Eide et al., 2018). Especially, Trebitsch et al. (2016) challenged the interpretation of Hayes et al. (2011) by showing that the observed polarisation signal can be reproduced in a pure cooling-flow scenario. Thus, despite significant observational efforts and numerous counterpart identifications, there is still considerable debate regarding the mechanisms that power the Ly emission of the blob.
Previous IFS observations of LAB 1 were obtained with the SAURON instrument at the WHT (Bower et al., 2004; Weijmans et al., 2010). These observations revealed a complex morpho-kinematic structure of the system in Ly. The identification of multiple clump-like features in these data was seen as evidence for the presence of multiple galaxies in the system, while the chaotic motions where interpreted as signs for galaxy-galaxy interactions. Moreover, Weijmans et al. (2010) found signatures of coherent velocity shear at the positions of the Lyman break galaxies C11 and C15. While these observations provided first insights into the complex kinematic structure of the system, they were limited in depth and spatial resolution. Here we will present the new deep MUSE observations of the system, that will allow us to map the spatial and kinematic structure of blob in unprecedented detail.
3 ESO VLT/MUSE Observations of LAB 1
| Date-Time | AM | DS | SGS | Sky | PID | |
|---|---|---|---|---|---|---|
| [yy/mm/dd-UT] | [″] | [″] | [s] | |||
| 14/11/13-00:33:06 | 1.14 | 0.61 | 0.69 | 1498 | 2 | a† |
| 14/11/13-00:59:29 | 1.19 | 0.82 | 0.73 | 1498 | 2 | a |
| 15/05/22-08:15:40 | 1.47 | 1.26 | 1.00 | 1500 | 3 | b |
| 15/05/22-08:42:34 | 1.34 | 0.94 | 0.94 | 1500 | 3 | b |
| 15/05/29-07:55:36 | 1.43 | — | 0.72 | 1500 | 3 | b |
| 15/05/29-08:22:31 | 1.31 | 0.59 | 0.71 | 1500 | 3 | b |
| 15/05/29-08:53:20 | 1.22 | 0.51 | 0.68 | 1500 | 3 | b |
| 15/05/29-09:20:15 | 1.16 | 0.54 | 0.65 | 1500 | 3 | b |
| 15/05/30-08:58:17 | 1.20 | 0.92 | 0.84 | 1500 | 3 | b |
| 15/05/30-09:25:11 | 1.15 | 0.67 | 0.82 | 1500 | 3 | b |
| 15/06/12-08:25:02 | 1.16 | 0.94 | 0.75 | 1500 | 2 | b |
| 15/06/12-08:51:58 | 1.13 | 1.21 | 0.78 | 1500 | 2 | b† |
| 15/06/12-09:21:56 | 1.11 | 1.06 | 0.79 | 1500 | 2 | b |
| 15/06/12-09:48:52 | 1.10 | 0.92 | 0.79 | 1500 | 2 | b† |
| 15/06/19-08:32:25 | 1.12 | 0.77 | 0.66 | 1498 | 2 | a |
| 15/06/19-08:59:09 | 1.10 | 0.80 | 0.68 | 1498 | 2 | a† |
| 15/06/19-09:37:28 | 1.11 | 0.88 | 0.63 | 1498 | 2 | a |
| 15/06/19-10:04:12 | 1.13 | 0.95 | 0.65 | 1498 | 2 | a |
| 15/06/20-07:40:02 | 1.19 | 0.78 | 0.70 | 1498 | 2 | a |
| 15/06/20-08:06:46 | 1.14 | 0.82 | 0.68 | 1498 | 2 | a |
| 15/06/20-08:38:08 | 1.11 | 0.93 | 0.66 | 1498 | 2 | a |
| 15/06/20-09:04:52 | 1.10 | 0.83 | 0.70 | 1498 | 2 | a |
| 15/06/22-08:01:52 | 1.14 | 1.14 | 0.63 | 1498 | 2 | a‡ |
| 15/06/22-08:28:34 | 1.11 | 1.69 | 0.77 | 1498 | 2 | a |
| 15/06/24-06:39:13 | 1.32 | 0.60 | 0.68 | 1498 | 2 | a |
| 15/06/24-07:05:55 | 1.23 | 0.55 | 0.69 | 1498 | 2 | a |
| 15/09/17-02:35:33 | 1.12 | 1.10 | 0.71 | 1498 | 1 | a |
| 15/09/17-03:02:18 | 1.11 | 0.66 | 0.67 | 1498 | 1 | a |
| 16/07/15-09:09:06 | 1.23 | 1.10 | 1.14 | 1495 | 2 | c |
| 16/07/15-09:35:50 | 1.31 | 0.83 | 1.14 | 1495 | 2 | c |
| 16/08/12-06:47:59 | 1.16 | 1.12 | 0.89 | 1510 | 1 | c |
| 16/08/12-07:14:59 | 1.22 | 1.03 | 0.93 | 1510 | 1 | c |
| 16/09/02-02:33:13 | 1.22 | 0.84 | 1.00 | 1485 | 2 | c |
| 16/09/02-03:00:08 | 1.16 | 0.76 | 0.93 | 1485 | 2 | c |
| 16/09/05-01:57:24 | 1.29 | 0.87 | 1.00 | 1495 | 2 | c |
| 16/09/05-02:24:08 | 1.21 | 0.71 | 0.90 | 1495 | 2 | c |
| 16/09/25-00:19:41 | 1.36 | 0.91 | 1.01 | 1485 | 2 | c |
| 16/09/25-00:46:14 | 1.26 | 0.95 | 0.89 | 1485 | 2 | c |
| 16/09/30-00:11:15 | 1.32 | 1.76 | 1.02 | 1495 | 2 | c |
| 16/09/30-00:38:10 | 1.23 | 0.89 | 0.96 | 1495 | 2 | c |
| 16/10/04-00:43:00 | 1.18 | 1.56 | 1.39 | 510 | 2 | c |
| 16/10/04-01:55:53 | 1.10 | 0.85 | 1.02 | 1495 | 2 | c |
| 16/10/04-02:22:48 | 1.10 | 0.94 | 0.92 | 1495 | 2 | c |
LAB 1 was observed with MUSE (Bacon et al., 2010) in its wide field mode configuration without adaptive optics at the European Southern Observatories Unit Telescope 4 (Antu) in three service-mode programmes from 2014 to 2016 (ESO Programme IDs 094.A-0605, 095.A-0570, and 097.A-0831 with principal investigators Hayes, Bower, and Hayes, respectively). A log of these observations is given in Table 2. The individual exposure times are typically 1500 s, only with one exposure being significantly shorter (510 s). In total the three programmes accumulated a total open-shutter time of 63390 s (17.6 h) on the target.
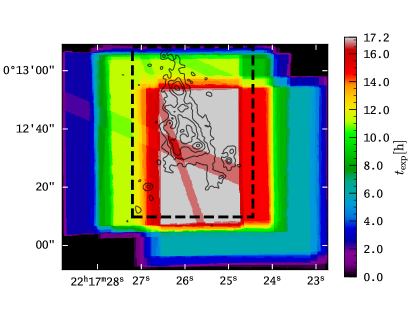
The three different programmes centred the instrument on different regions of the blob. While programmes 094.A-0605 and 095.A-0570 centred the 1′1′ MUSE field of view slightly north of LAB 1 to encompass also the northern neighbouring Ly blob LAB 8, programme 097.A-0831 centred on a region south-west of the brightest blob structure. This off-set was motivated by a detection of a previously unknown low-surface brightness extension of the blob in a reduction of the data from programme 094.A-0605 (see Geach et al., 2016). Each programme used the dithering and rotation pattern that is recommended in the MUSE observing manual444http://www.eso.org/sci/facilities/paranal/instruments/muse/doc.html. Unfortunately, one exposure suffered from a severe tracking error and could not be used in the final analysis. Thus the total integration time of the analysable dataset is 17.2 h.
The DIMM seeing reported by ESO for the observation ranges from 0.5″ to 1.7″, but with the majority of exposures taken at sub-arcsecond seeing (mean: 0.87″, median: 0.88″). A potentially more accurate measurement of the seeing is provided by the FHWM measurements of stars in the meteorology fields recorded by MUSE’s slow-guiding system (SGS column of Table 2). Albeit having a slightly larger scatter, the measured image quality by the SGS is often a bit better than the site-wide values provided by the DIMM (mean: 0.83″, median: 0.78″),
Programmes 094.A-0605 and 097.A-0831 were taken without the blue cut-off filter in the fore-optics (extended wavelength mode), thus allowing the wavelength range from 465 nm to 930 nm to be sampled (although at the cost of second-order contaminations at nm), while programme 095.A-0570 was taken with the blue cut-off filter within the light path (nominal wavelength mode), thus sampling the wavelength range from 480 nm to 930 nm.
All observational raw data and the associated calibration frames where retrieved from the ESO Science Archive Facility using the raw-data query form555http://archive.eso.org/cms/eso-data.html and the cal-selector tool. For all exposures the associated calibration frames (bias frames, arc lamp frames, continuum lamp frames, twilight flats, standard star exposures, and astrometric standard fields) were taken as part of the standard calibration plan for MUSE observations. This means especially, that twilight flats were taken typically once a week, while standard-star exposures are usually obtained daily. Nevertheless, some retrieved exposures were associated to standard star666The to our science observations associated spectrophotometric standards are Feige110, GJ754.1A, GD153, EG274, LTT3218, GD108, and LTT7987. exposure that were taken one night before or after the science observations.
4 Data reduction
4.1 Production of the datacube
For the reduction of the 17.6 h of MUSE observations into a science-ready datacube we used version 2.4.2 of the MUSE Instrument Pipeline (MUSE DRS – Weilbacher et al., 2016) provided by ESO777https://www.eso.org/sci/software/pipelines/muse/muse-pipe-recipes.html and version 3.0 of the MUSE Python Data Analysis Framework (MPDAF – Bacon et al., 2016; Piqueras et al., 2017) provided by the MUSE consortium888https://mpdaf.readthedocs.io/. The here MUSE DRS version used here incorporates the so-called self-calibration procedure to improve the flat-fielding accuracy for deep datasets (Conseil et al., 2016). For our data reduction we adopted a similar strategy as the one used for the reduction of the MUSE Hubble Ultra Deep Field (Bacon et al., 2017).
We first ran the MUSE DRS calibration recipes muse_bias, muse_flat, muse_wavecal, and muse_lsf on the calibration frames that are associated to each science and standard star exposure. We also used the muse_twilight recipe on the twilight frames. Next, we applied the resulting calibration data products to each science and standard star exposure using the recipe muse_scibasic. The resulting standard-star pixtables where then fed into muse_standard to create response curves. Those were the applied to each science exposure with the muse_scipost task, using its self-calibration feature, but not using its sky-subtraction capabilities. When running muse_scipost we used the associated astrometric calibrations provided from the ESO archive instead of the astrometric calibrations shipped with the pipeline. This approach was necessary, as the instrument underwent several interventions during the long period over which observations were taken. Not using the correct astrometric calibrations would result in uncorrected geometric distortions within the pixtables.
In order for self-calibration to work optimally, regions containing sources that are bright in the continuum needed to be masked. While in principle the DRS can automatically detect such regions, we manually masked out bright continuum objects a bit more conservatively compared to the DRS generated mask. Manual masking was performed by visual inspection of the datacubes with the ds9 software (Joye & Mandel, 2003) using polygon-shaped and circular regions. These regions where then converted into datacube masks using the pyregion python package999https://pyregion.readthedocs.io/. Additionally, four science exposures contained continuum bright linear trails from moving objects (likely satellite flares, meteors or aeroplanes – affected exposures are marked by a in Table 2). These trails were also masked manually for the self-calibration.
We then removed night sky-emission with muse_create_sky and muse_subtract_sky. During this step we iteratively masked out regions that contained emission from the Ly blob, so that the blob’s emission is not subtracted from the final data.
Next we resampled the individual sky-subtracted and flux-calibrated exposure tables to the final 3D grid with muse_scipost_make_cube. We defined this final grid via an initial run of muse_expcombine on a subset of pointings from each observing programme. Using MPDAF’s combine method we then produced an unweighted mean stack of those individual datacubes to produce the final science-ready datacube. Prior to this stack we masked out bright linear trails that were present in some observations (marked by a in Table 2). We also ensured that remaining cosmic-ray residuals in the individual datacubes were filtered out in the final stack by using the - clipping algorithm in the combine task (2 maximum iterations with ).
The resulting final datacube has spatial elements (spaxels) that sample the sky parallel to right ascension and declination at 0.2″0.2″. Each spaxel consists of 3802 spectral elements that sample the spectral domain from 4599.6 Å to 9350.8 Å linearly with steps of 1.25 Å.
Throughout the above procedure a formal variance propagation is also carried out by each of the used routines, thus a second datacube containing the variance for each volume pixel (voxel) is also produced. However, the resampling procedure in muse_scipost_make_cube produces correlated noise between neighbouring voxels (see Figure 5 in Bacon et al., 2017). Since this co-variance term between neighbouring voxels can not easily be accounted for in the final reduction, the formal variance cube contains underestimates of the true variances. By processing artificial pixtables filled only with Gaussian noise, Bacon et al. (2017) demonstrate that the variance for a voxel in an individual exposure datacube must be corrected by a factor of (see Figure 6 in Bacon et al., 2017). Following Bacon et al. (2017) we apply this correction to our final variance cube.
We display a map of the integration time for each spaxel in the MUSE datacube of LAB1 in Figure 2. The maximum integration time of 61920 s (17.2h) is reached in a 32″48″ central region of our datacube. In this region all three ESO observing programmes overlap. This region completely encompassed the known extend of LAB 1 and LAB 8 prior to the here presented observations. Moreover, Figure 2 also illustrates the location of the masked out regions due to continuum-bright meteor trails or satellite tracks.
Lastly, we produce an emission line only datacube by subtracting a running median filter in spectral direction. This simple method for continuum removal has been proven effective in previous MUSE studies for isolating emission line signals (e.g. Borisova et al., 2016; Herenz & Wisotzki, 2017; Herenz et al., 2017a, b; Arrigoni Battaia et al., 2019). Here we set the width of the median filter conservatively to 301 spectral layers (376.25 Å).
4.2 Astrometric alignment
We register the MUSE datacube to an absolute astrometric frame by using the 2MASS point-source catalogue (Skrutskie et al., 2006). Unfortunately, there are only two 2MASS sources within the limited FoV of the MUSE and STIS observations, with one of those sources actually being an extended galaxy. We therefore use the only real 2MASS point source (2MASS J22172397+0012359) to anchor our astrometric reference frame in both observational datasets.
By tying the astrometric reference frame only to one source there remain in principle still several degrees of freedom with respect to geometrical distortions and rotation. However, rotation geometrical distortion are corrected for MUSE data at the pipeline level, and the accuracy of this procedure is constantly monitored by ESO using astrometric calibration fields.
We verified our absolute astrometry against an archival HST/STIS 50CCD clear-filter image that is partially overlapping with our MUSE data (Proposal ID: 9174, presented and analysed in Chapman et al., 2001, 2004). We tied the absolute astrometry of this image also to the 2MASS point source. By visual inspection via blinking in ds9 we then ensured that no offsets exist between both datasets. We conservatively estimate that the absolute astrometric accuracy of our data to be on the order of one MUSE pixel (0.2″).
5 Analysis and results
5.1 Velocity sliced Ly emission maps
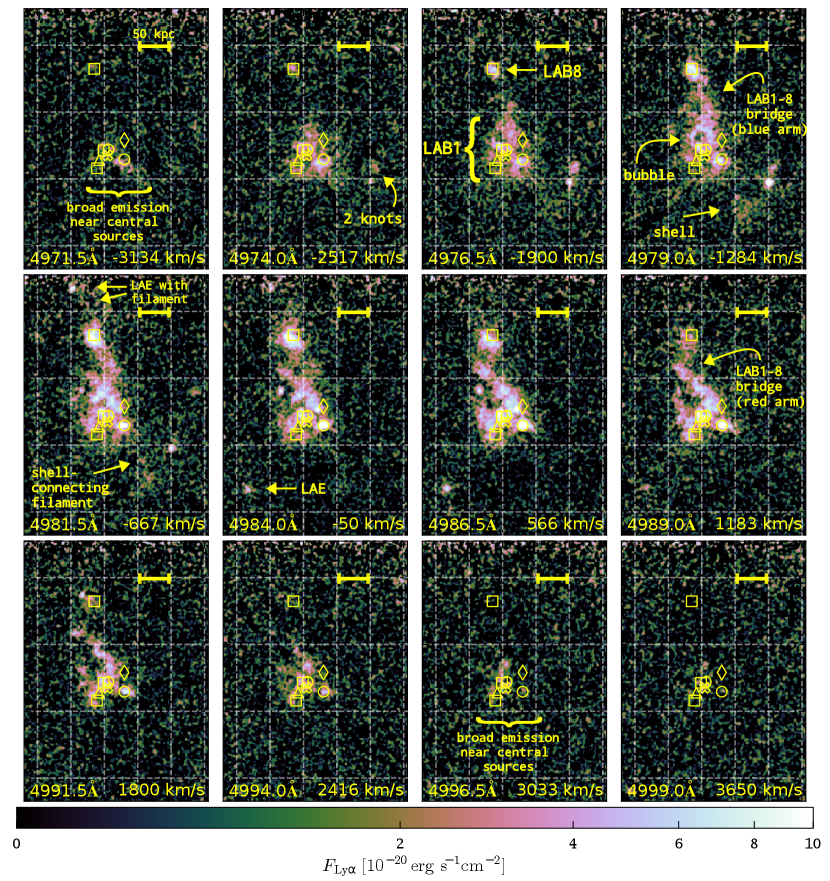
We present a spectral sequence of pseudo-narrowband images over the Ly line in Figure 3. These images show that we can trace Ly emission from LAB 1 over a bandwidth of Å (km s-1 around ). As can be seen from Figure 3, the highest velocity gas emitting Ly is located in vicinity of the central sources LAB1-ALMA1, LAB1-ALMA2, and VLA-LAB1a. However, numerous other features with narrower spectral width appear only in a few velocity slices. Overall the velocity slices reveal a complex spectral and morphological structure of Ly emission throughout different parts of the blob. We labelled notable features in Figure 3, where we point at:
-
1.
A circular structure devoid of strong Ly emission towards the north of the sub-mm sources. This feature is labelled as “bubble” in Figure 3. It is most clearly seen in the slice around 4979 Å, where we indicate this feature with an arrow. In subsequent redder slices this “bubble” appears with less contrast. It appears as if its radius increases from kpc at 4979 Å to up to kpc towards redder wavelengths.
-
2.
A filamentary narrow bridge connecting LAB 1 to LAB 8 in the north. This bridge becomes visible in the slice at 4979 Å and can be clearly followed until the 4989 Å slice. For LAB 8 the flux shears from the north-west to the south-east with increasing wavelength and the filament shows the same velocity shearing. We indicate this by labelling it as “LAB1-8 bridge (blue arm)” and “LAB1-8 bridge (red arm)” of the bridge in the panel displaying the 4979 Å slice and 4989 Å slice, respectively.
-
3.
A compact emission knot towards the north of LAB 8, that connects to LAB 8 via a faint low-surface brightness filament. This feature is seen in the slices at 4981.5 Å and 4984 Å, and we label it as “LAE with filament” in the 4984 Å slice. This newly discovered LAE and filament is close to the edge of the field of view of the observations, and thus only exposed at 8 h to 12 h, thus the noise in this part of the datacube is significantly larger. Nevertheless, as we will discuss in the following Sect. 5.4, the compact emitter and the filament are significant detections.
-
4.
A faint extended, slightly curved, shell-like region towards the south-west of LAB 1. Along the major axis the extent of the shell is kpc, and its projected thickness is kpc. This low-surface brightness emission is visible in the slices from 4976.5 Å to 4981.5 Å where we label it simply as “shell”. The indicated previously undetected Ly emitting region appears to be connected to the main area of LAB 1 via a low-surface brightness filament trailing from the north-east to the south-west. The filament is most prominently visible in the 4981.5Å slice where we label it “shell connecting filament”. In the northern part of this shell-like region a compact high-surface brightness knot is visible. This knot is accompanied by another slightly more diffuse knot. These two knots in the northern part of the shell can be traced in the velocity slices from 4974Å to 4981.5Å, and we label both features as “2 knots” in the 4974Å slice.
-
5.
Another compact isolated Ly line emitter towards the south-east of LAB 1 seen in the slices from 4984 Å to 4989 Å. We will show in the following Sect. 5.2, that this emitter is one of four newly detected Ly emitters in the proximity of the LAB 1/LAB 8. We label this emitter “LAE” in the 4984Å slice.
A closer inspection of the velocity slices reveals that there appears to be an overall velocity shear. The bluer km s-1 slices show predominantly emission towards the west, while the redder km s-1 slices are dominated by emission from the east. This structure of the velocity shear becomes more clear in our moment based analysis of the Ly line profiles (Sect. 5.3).
5.2 Detection and photometric measurements of Ly emission
5.2.1 Method
To determine the overall Ly surface-brightness morphology of LAB 1 from our MUSE datacube it would not be optimal to create a simple narrow-band image by summing over a certain number of datacube layers. Choosing a single bandwidth for such an image would either decrease the signal-to-noise ratio (S/N) for regions where the Ly profiles are very broad if the bandwidth is chosen too narrow or, conversely, decrease the S/N in regions where Ly is narrow if the adopted bandwidth would optimally encompass the broader profiles. Furthermore, such a simple summation would also not account for the presence of velocity shear. We thus create an adaptive narrow-band image. For this image we sum for only over voxels that contain Ly flux. Our method is similar to the creation of the narrow-band images in the analysis of extended Ly emission around QSOs from MUSE data (e.g. Borisova et al., 2016; Arrigoni Battaia et al., 2019).
In order to find the spectral pixels over which we need to sum we utilised the 3D cross-correlation procedure of the LSDCat software101010LSDCat is publicly available via the Astrophysics Source Code Library: http://ascl.net/1612.002 (Herenz & Wistozki, 2016). (Herenz & Wisotzki, 2017). LSDCat produces an S/N datacube by cross-correlating the continuum subtracted datacube with a 3D Gaussian template. The parameters of the template are the amount of spatial and spectral dispersion of the 3D Gaussian. Cross-correlation suppresses high-frequency noise while maximising the S/N of signals within the data that match the template. Hence, the method is commonly called “matched filtering” (e.g., Vio & Andreani, 2016; Loomis et al., 2018).
LSDCat was originally developed for the detection of Ly emitting galaxies in blind MUSE surveys (see Herenz et al., 2017b; Urrutia et al., 2019). For this application the parameters of the template are optimally chosen when they match the width of the seeing point spread function (PSF) and the average line width of LAEs (see Sects. 4.2 and 4.3 in Herenz & Wisotzki, 2017). However, our goal here is not to optimise the template for compact emission line sources, but to maximise the detectability of faint low-surface brightness filaments in the outskirts of the blob. Simultaneously, we want to preserve the morphology of small scale surface-brightness variations. As there is no optimal a priori solution to this problem, the final set of adopted parameters had to be chosen by parameter variation and visual inspection of the resulting images. By experimenting with different spatial filter widths, we found that a spatial FWHM of 1.8″ preserved most of the contrast of compact features and significantly enhanced the S/N of the extended filamentary features in the outskirts of the blob. The adopted filter FWHM is roughly twice the seeing PSF FWHM111111We determined the PSF FWHM via fitting a 2D Gaussian profile to the bright star within our field of view in a 45 Å wide narrow-band image centred at . of 0.95″. As derived by Zackay & Ofek (2017), a filter width of twice of the seeing FWHM will reduce121212In general for compact point-sources the relation , with holds, where and denote the adopted width of the filter and the width of the point-spread function, respectively (Herenz & Wisotzki, 2017). the maximum S/N of compact sources only by 20%. Similarly, we varied the FWHM of the spectral part and found that 300 km/s is well suited for enhancing the detectability of the blobs low-surface brightness features.
5.2.2 Maximum S/N image
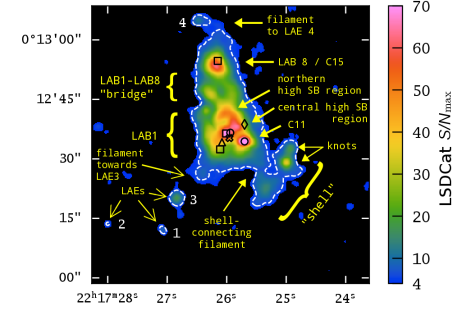
In Figure 4 we show the resulting map when taking the maximum S/N in from the LSDCat S/N datacube around . We adopt an S/N threshold of six as detection threshold to identify reliable regions from which Ly emission is detected. These regions are demarcated by a white dashed line in Figure 4. An S/N threshold of six has previously been proven effective to maximise the ratio of real- to spurious detections in blind emission line searches with MUSE (Herenz & Wisotzki, 2017; Herenz et al., 2017b; Urrutia et al., 2019). This is also visualised in Figure 4, where we include spaxels in the display down to a S/N of four. Inspecting spectra extracted in the regions revealed that in all those cases a possible emission line signature is at most marginal, while the regions are confident detections.
While our goal is to use the S/N datacube from the 3D cross-correlation as a mask to produce an optimally extracted narrow-band image, its 2D representation in the form of maximum S/N map in Figure 4 provides us with a schematic visualisation of the main morphological features of the system. We annotate these in Figure 4. Most of the features were already hinted at in the display of the velocity slices in Figure 3
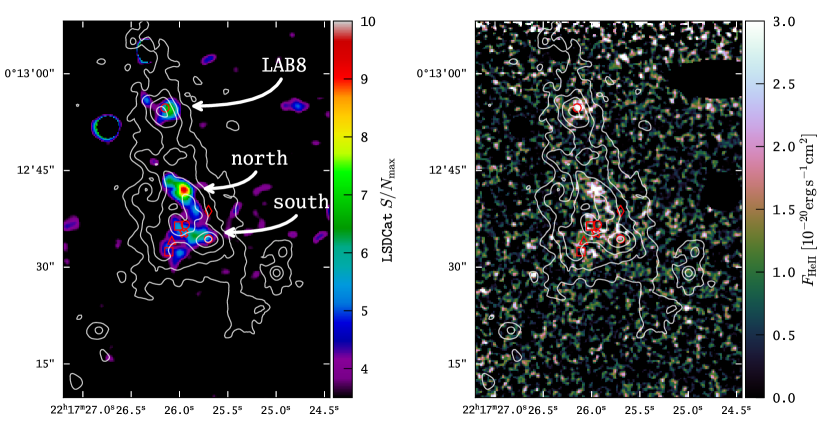
Marked S/N peaks are found at the position of the LBG SSA22a-C11 in LAB 1 and near the LBG SSA22a-C15 in LAB 8. We point out that the LAB 8 peak shows a slight offset towards the south of SSA22a-C15. The centre of LAB 1 shows an extended region of high S/N, that exhibits its peak values at LAB1-ALMA2. This area is labelled “central high SB region” in Figure 4. Interestingly, the sub-mm, [CII ] and potentially X-Ray detected source LAB1-ALMA3 do not have an associated prominent peak in the S/N map, and neither have the spectroscopically confirmed sources S1 and K15b associated peaks. But, these three sources (LAB1-ALMA3, S1, and K15b) demarcate the central high surface-brightness region from the south-east (LAB1-ALMA3, S1) to the north-west (K15b). In the north-west another high surface-brightness region then curves back to the north-east. This feature is labelled “northern high surface-brightness region” in Figure 4 and does not contain known sources. It is, however, spatially coincident with the northern edge of the “bubble” that we pointed out in Section 5.1 (see Figure 3).
Our maximum S/N map also accentuates the two filamentary features that form a bridge between LAB 1 and LAB 8. Moreover, the newly detected “shell” region in the south west is clearly connected via a significantly detected filament to the central region of the blob. This shell harbours a compact high-S/N knot, accompanied by more diffuse emission knots towards the north and the south. We also find four isolated peaks (labelled 1 to 4 in the figure) that are not connected to the central large region. These isolated peaks represent newly identified Ly emitters in close vicinity to the blob, and they will be analysed separately in Sect. 5.4. LAE 4, to the north of LAB 8, appears to be connected by a filamentary structure to the main body of the blob, but this potential filament is detected at lower significance than our adopted detection threshold. The map also hints a potential filament pointing towards LAE 3.
5.2.3 Adaptive narrow-band image
Equipped with the S/N datacube from LSDCat we constructed the optimal 3D extraction mask for our adaptive narrow-band image. We do so by summing the flux datacube in the spectral direction only over voxels that contain at least an S/N value above 4 in the S/N datacube. We note, that spaxels that do not contain a single voxel with are blacked out in Figure 4, thus the displayed spaxels in Figure 4 can be interpreted as a 2D projection of the 3D extraction mask. The choice of this analysis threshold is motivated by our observation that some regions in Figure 4 may contain a marginal Ly signal. The use of a second S/N threshold that is lower than the detection threshold is also core principle of the LSDCat software, which uses a detection threshold for finding emission lines and an analysis threshold for performing measurements on the detected lines (Herenz & Wisotzki, 2017). In order to provide a visual representation of the background noise in source free regions we adopt the strategy from Borisova et al. (2016) and sum over 4 spectral bins. We centre the summation around 4983.4 Å (the wavelength of Ly at ). The so constructed adaptive narrow-band image is displayed in Figure 5. The noise of the image estimated from placing random apertures in empty sky regions in the central parts of the image is erg s-1cm-2arcsec-2.
The adaptive narrow-band image allows us to characterise the features that were pointed out above (Figures 3) and 4) by Ly surface brightness131313All measurements were obtained within an circular aperture of 2″diameter. (). We distinguish three fragments in the shell: (1) A bright compact knot with erg s-1cm-2arcsec-2, (2) a fainter more diffuse knot to the north of the bright knot with erg s-1cm-2arcsec-2, and (3) an even more diffuse extended fragment in the south of the shell with erg s-1cm-2arcsec-2. The filament connecting the diffuse part of the shell (labelled as shell-connecting filament in Figure 5) is characterised by erg s-1cm-2arcsec-2 emission, while the central- and northern high-surface brightness regions of LAB 1 show erg s-1cm-2arcsec-2. The high- regions clearly demarcate a central circular region of lower ( erg s-1cm-2arcsec-2). This apparent cavity, first seen by Bower et al. (2004), was labelled “bubble” in Figure 3. To the north of LAB 1 we find the two filaments connecting LAB 1 with LAB 8, with the eastern one showing higher ( erg s-1cm-2arcsec-2) than the western one ( erg s-1cm-2arcsec-2). LAB 8 is characterised by erg s-1cm-2arcsec-2, and for the filament towards LAE 4 in the north we measure erg s-1cm-2arcsec-2. However, in the northern part of the image, due to the lower number of contributing exposures (see Figure 2), the background noise of the image is higher ( erg s-1cm-2arcsec-2). With values after the 3D cross-correlation procedure it missed the adopted detection threshold and we regard this filament conservatively only as a tentative feature.
5.2.4 Size and total Ly luminosity
We define the size of the unveiled LAB 1 + LAB 8 + shell structure as the area of the region above the adopted detection threshold of (white contour in Figure 4), excluding the isolated LAEs. In terms of surface brightness this threshold corresponds to a limit of erg s-1cm-2arcsec-2. The corresponding limit in surface luminosity is erg s-1kpc-2. At this threshold Ly emission from the LAB 1/LAB 8 structures covers an area of 553 arcsec2. This corresponds to a projected surface of kpc2 at . The total measured Ly flux from the structure is erg s-1cm-2, which corresponds to a Ly luminosity of erg s-1.
While the Ly structure revealed here is enormous, two even larger Ly nebulae, namely the “Slug” nebulae with an extent of kpc (Cantalupo et al., 2014) and the MAMMOTH-1 nebula with an extent of kpc (Cai et al., 2017), are known. While the “Slug” nebulae surrounds a luminous ( erg s-1) type-I quasar, the MAMMOTH-1 nebulae surrounds a relatively faint broad-band source whose emission line spectrum appears to be consistent with a quasar. Nevertheless, both the “Slug” and the MAMMOTH-1 nebulae are also characterised by a factor of 3.4 and 1.5 higher luminosity than the LAB 1 + LAB 8 + shell structure, respectively. Both nebulae are at , and thus the effect of cosmological surface brightness dimming is reduced by a factor of compared to our observations. While no limiting surface brightness for the “Slug” observations is published, Cai et al. (2017) report a surface brightness detection limit of erg s-1cm-2arcsec-2 for MAMMOTH-1. This translates to limiting surface luminosity of erg s-1kpc-2 , which is comparable to our physical limit. The projected maximum extend of our structure, measured from the northernmost tip in LAB 8 to the southernmost point in the shell, is 45.4″ or, correspondingly, 346.3 kpc in projection, which is a factor of smaller that the extent of the MAMMOTH-1 nebula. Similar to the LAB 1 - LAB 8 structure, MAMMOTH-1 exists in an extreme overdense region of the universe.
5.2.5 Photometric centre and photometric principal axis
We applied the formalism of image moments (Hu, 1962; Stobie, 1980, 1986) to the adaptive narrow-band image to calculate the photometric centre as well as the angle of the principal axis, , of the LAB. In pixel-coordinates of the adaptive narrow-band image the photometric centre is defined as
| (1) |
and the angle of the principal axis is defined as
| (2) |
with
| (3) |
and
| (4) |
For these calculations we only considered pixels in the narrowband image that have a corresponding pixel above a S/N of six in the maximum S/N map. Moreover, the definition of the angle of the principal axis in Eq. (2) is such that 0∘ corresponds to the axis from S to N, and that the angle increases anticlockwis to the east. The in this way obtained photometric centre, converted to celestial coordinates (J2000), is located at RA22h17m25.94s, Dec+00∘12′39.338″, and for the angle of the principal axis we find east of north.
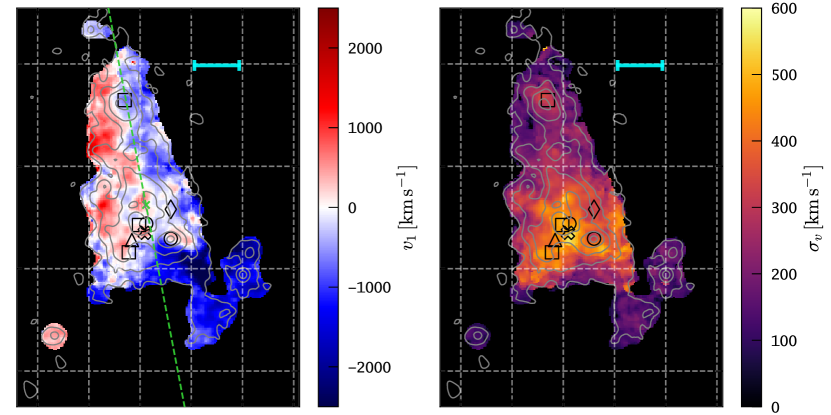
We show the position of the photometric centre in Figure 5 by a cyan cross. As can be seen, the photometric centre is located slightly west to the “bubble”. We also indicate the principal axis in Figure 5 by a dashed cyan line. Figuratively speaking, the principal axis is the axis along which the blob appears most elongated. Formally, it describes axis along which the variance in flux is maximised. For a light distribution of elliptical shape, the so defined principal axis would be oriented along the major axis of the ellipse. Thus, our measurement is comparable to the measurements of LAB position angles via ellipse fitting in Erb et al. (2011). We discuss the alignment between principal axis and gas kinematics in Sect. 6.3.1.
5.3 Moment based maps of the Ly line profile
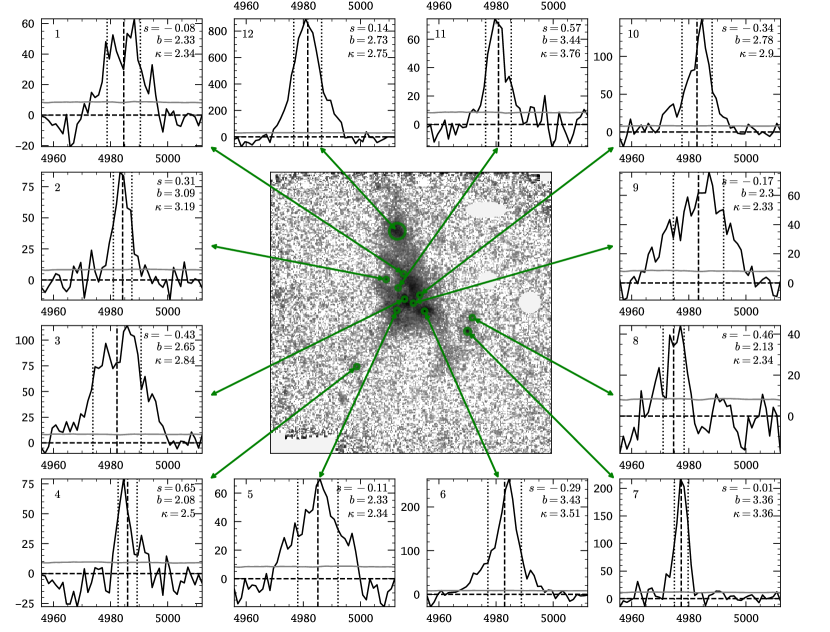
By visually inspecting the Ly spectral profile as a function of position with the QFitsView software141414The QFitsView software is publicly available via the Astrophysics Source Code Library: http://ascl.net/1210.019. (Davies et al., 2010; Ott, 2012), we find that the line profile complexity varies strongly throughout the blob. We illustrate this by showing a selection of representative profiles in Figure 6. As can be seen, in some region the profiles appear very broad and with a dominating peak (e.g. panel 12 in Figure 6), while other regions are characterised by clearly double- (e.g. panel 3) or even multi-component profiles (e.g. panel 5 or panel 9). The isolated LAEs in the outskirts (example in panel 4, see also Figure 9), or in the shell-like region (panel 7) show narrower Ly profiles.
The varying complexity of the Ly profiles as a function of position prohibit parametric fits of a simple model to the spaxels of the datacube in order to create maps of, e.g., the velocity centroid () or line-width (). Such an analysis was presented for the much shallower SAURON data of LAB 1 (Bower et al., 2004; Weijmans et al., 2010), but the increased sensitivity and resolution of our MUSE data warrant a different approach. We thus resort on a moment-based non-parametric analysis. Our method is rooted in descriptive statistics (e.g. Ivezić et al., 2014), but we need to account for two differences when describing spectroscopic line profiles instead of statistical data with such an ansatz. First, formal validity of the summarising parameters is only given when positive values are considered in the calculations. Second, the presence of noise and the usage of small sets of input values can lead to non-trivial biases in moment-based quantities, especially if the analysed profiles are of low S/N. To ensure positive values and in order to minimise low-S/N biases we first applied three preprocessing steps to the continuum-subtracted datacube:
-
1.
We used the 3D mask that was already used for the creation of the adaptive narrow band image in Sect. 5.2.2. We recall that this 3D mask was constructed by thresholding the matched-filtered datacube with . Voxels that do not fulfil this criterion will be set to 0 in the analysis.
-
2.
We smoothed each layer of the flux datacube with a circular 2D Gaussian ( 0.8″). This is done to reduce the spaxel-to-spaxel noise in the final maps, especially in low surface-brightness regions. This value significantly improved the S/N ratio of the Ly profiles in the filaments and low surface-brightness regions of the blob.
-
3.
We used a 2D mask by thresholding the maximum S/N map shown in Figure 4 to exclude spaxels were only a very small number of spectral bins would contribute to the resulting moments. After visual inspection we set this “display threshold” to , i.e. the analysed regions are exactly the regions that we regarded as confident detections in Sect. 5.2.2.
After these preparatory steps we created a 2D array of the central flux-weighted moment (first moment) from the processed datacube voxels ,
| (5) |
as well as 2D arrays of the -th flux-weighted moments,
| (6) |
for , and . In Eqs. (5) and (6), as well as in the following equations below, and denote the indices of spatial axes of the flux datacube , while indexes the spectral direction.
The first moment map resulting from Eq. (5) directly translates into a line-of-sight velocity map
| (7) |
where is the speed of light, is the non-linear translation between MUSE spectral pixel coordinate and vacuum wavelength151515We use the air-to-vacuum wavelength conversion that has been adopted in the Vienna Atomic Line Database (Ryabchikova et al., 2015): https://www.astro.uu.se/valdwiki/Air-to-vacuum\%20conversion. and is the systemic redshift of LAB 1. For this translation we fix the systemic redshift of LAB 1 to , in agreement with known redshifts of the galaxies within the blob. The so created map is shown in the left panel of Figure 7. There we also show the photometric centre and the principal axis that were computed from the adaptive narrow band image as described in the previous section. We point out that the principal axis is oriented orthogonal to the direction of the apparent large scale velocity gradient. This feature will be further discussed in Sect. 6.3.
By taking the square root of second moment map (Eq. 6, with ) we compute a map that provides a measure of the width of the spectral profiles:
| (8) |
This map is shown in the right panel of Figure 7. We express the width of the profiles in km s-1, but caution that this measurement can not be directly interpreted as velocity dispersion as it is often done for non-resonant emission lines. For example, double- or multiple peaked profiles generally have larger second moments than single peaked profiles. Moreover, radiative transfer effects are also known to broaden the single-peaked Ly line profiles when compared to non-resonant emission lines (see also Sect. 5.5). We thus call the second moment based measure “apparent velocity dispersion”. Lastly, the spectral resolution of MUSE also has an effect on the apparent velocity dispersion. Given the complexity of the profiles and the non-parametric nature of our measurement the effect of broadening the profiles via convolution with the spectrograph’s line spread function is not easily quantifiable. The measured instrumental width for MUSE at 4980Å is km s-1 (Bacon et al., 2017). As a figure of merit estimate, this translates into resolution corrections of -34 km s-1, -20 km s-1, -15 km s-1, and -10 km s-1 for apparent velocity dispersions of 100 km s-1, 150 km s-1, 200 km s-1, and 300 km s-1, respectively, if the observed line profiles and the line spread function are well approximated by a Gaussian profile i.e.
| (9) |
Creating such moment-based maps of line-of-sight velocity and apparent velocity dispersion is common in the analysis of synthesised datacubes from radio-interferometric 21 cm observations of galaxies (e.g. Thompson et al., 2017, Section 10.5.4). It now is also routinely used in the analyses of extended Ly nebulae surrounding quasars (e.g. Borisova et al., 2016; Arrigoni Battaia et al., 2018, 2019; Drake et al., 2019). Moreover, recent theoretical work by Remolina-Gutiérrez & Forero-Romero (2019) and Smith et al. (2019) resort on a moment-based analysis in the analysis of Ly profiles from Ly radiative transfer simulations. However, in order to create maps that characterise the varying complexity of the Ly profile as a function of position in the blob, we use measurements involving higher-moments. Remolina-Gutiérrez & Forero-Romero (2019) suggest to use the skewness , the kurtosis , and the bimodality . These measurements will be detailed in the following. To provide a visual guide on how to interpret these quantities we also display their values next to the example profiles from the blob shown in Figure 6.
We calculate a map of the Ly profile skewness via
| (10) |
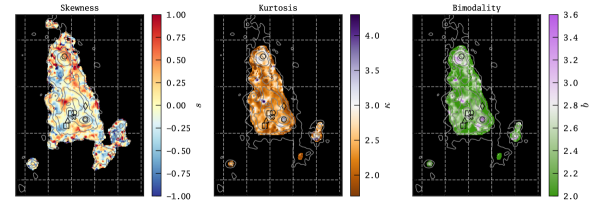
The so defined skewness () quantifies the asymmetry of the spectral profile with respect to . If the profile is symmetric around (panel 1 in Figure 6), while for a tail is found redwards of (e.g. panels 4 and 11 in Figure 6) and for a tail is bluewards of (e.g. panels 6, 8, and 10 Figure 6). We show our computed map for in the left panel of Figure 8.
We note that other definitions than Eq. (10) have been used in the literature to quantify the asymmetric Ly line-profile morphology of LAEs. For example, Shimasaku et al. (2006) quantified the observed skewness in spectral profiles from Lyman emitting galaxies by multiplying the definition given in Eq. (10) with a measure of the width of the line, however, we prefer to not entangle those two quantities. Other authors (Mallery et al., 2012; U et al., 2015) quantified skewness by fitting a skewed Gaussian profile. But this approach does not capture the complex Ly spectral profiles seen here in LAB 1. Additionally, Childs & Stanway (2018) showed recently that the skewness values derived from fitting an asymmetric Gaussian do not accurately capture the true skewness of Ly profiles in the presence of finite spectral resolution and background noise. Two other alternative definitions have been put forward by Dawson et al. (2007). These authors quantify asymmetry either via the ratio of flux blue- and redwards of the peak or via the ratio of the widths than encompass 90% of the flux blue- and redwards of the peak. However, given that the profiles in LAB 1 sometimes show multiple peaks at substantial spectral distance (e.g. panel 1 and 3 in Figure 6), quantifying asymmetry around the higher peak would exaggerate the skew measure compared to the visual perception of symmetry in those profiles.
We obtain a map of the kurtosis of the Ly profiles via
| (11) |
Kurtosis quantifies how much flux is in the wings of the profiles in comparison to the wings of Gaussian profile (i.e. their tail extremity). For the tails are comparable to the Gaussian profile, while profiles with show more pronounced tails (e.g. panels 6 and 11 in Figure 6), while indicates the absence of pronounced tails (e.g. panels 1, 5, and 9 in Figure 6). Of course, only wings that are significantly above the noise can contribute to this statistic. As a corollary, regions of low S/N are biased towards to low kurtosis values. We avoid these biases by increasing the display threshold to . We show the resulting map for in the centre panel of Figure 8.
Following Remolina-Gutiérrez & Forero-Romero (2019) we calculate a map of the bi-modality of the Ly line profiles using
| (12) |
Remolina-Gutiérrez & Forero-Romero (2019) introduced this quantity to discriminate whether their Ly radiative transfer models result in single- or double component profiles. We point out that this measure is not a formal statistical test for bi-modality, but it can capture the visual appearance of the Ly profile morphologies. We find that for profiles appear mostly to have clearly distinct double component structures (e.g. panels 1 and 4 in Figure 6, but see panel 5 and 9), while profiles with appear single peaked (e.g. panel 2, 6, and 7 in Figure 6). However, some profiles may also have a subdominant second component, that is mainly contributing to the kurtosis (e.g. panel 11 in Figure 6). In the range , however, the discriminatory power of appears not strong, and visual inspection of those profiles indicates a high complexity with possible multiple components or peaks (see e.g. panels 3 and 10 in Figure 6). Despite its potential lack of accuracy, qualitatively captures the visual complexity of the profiles, with higher values indicating simple single component profiles and lower values indicating more complex profiles, and with the lowest values often corresponding to the presence of double component profiles. Moreover, since the is biased towards low values in regions of low S/N, also will be biased low in those regions. Thus, we hide the biased regions by setting the display threshold to . We show our computed map for in the right panel of Figure 8.
It can be seen that most of the blob shows low values of indicative of double component Ly profiles. This impression is also on par with our visual inspection of the line profile variations throughout the blob. Moreover, in the central high surface-brightness region of LAB, where also the broadest profiles are observed, we obtain values in the intermediate range – these profiles often appear to exhibit a high-degree of complexity. Lastly, only a few small island regions can be characterised by high values of . These regions show clearly distinct single peaked profiles, often with very pronounced tails. We will describe and discuss the here derived and presented maps from the moment based analysis further in Sect. 6.3.
5.4 Newly discovered faint LAEs at in proximity to LAB 1
| ID | RA | Dec | ||||
|---|---|---|---|---|---|---|
| 1 | 22h17m27.08s | 0∘12′12.2″ | 0.6″ | -17.2 | +3690 | 127 |
| 2 | 22h17m28.01s | 0∘12′13.7″ | 0.7″ | -17.1 | -1445 | 94 |
| 3 | 22h17m26.83s | 0∘12′20.1″ | 1.5″ | -16.7 | +804 | 222 |
| 4 | 22h17m26.48s | 0∘13′05.0″ | 1.3″ | -16.6 | -275 | 105 |
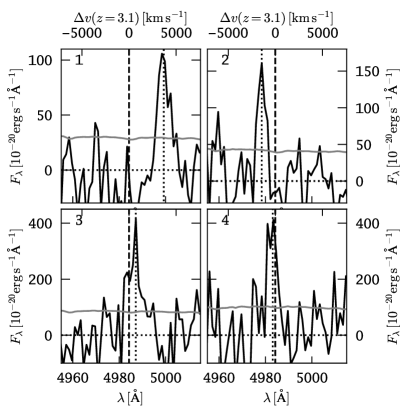
As mentioned in Section 5.2, our S/N map revealed four detections that are not embedded in the extended Ly radiation from the blob. We labelled those sources 1 – 4 in Figure 4. These sources are detected with S/N in the LSDCat cross-correlated datacube. Formally there exists one more detection with S/N at close to the eastern border of Figure 4, however this detection turned out to be an artefact near the edge of our field of view.
The coordinates, Kron-radii, and fluxes of the newly detected LAEs are listed in Table 16. These measurements have been obtained with the LSDCat software (Herenz & Wisotzki, 2017). In Figure 9 we show the spectral profiles of the detections. These 1D spectra have been extracted within a circular aperture of radius . No other lines are detected at these positions and thus we are confident that the sources are LAEs in physical proximity to the blob. Additionally, two of the line-profiles (LAE 3 & LAE 4) are reminiscent of the characteristic red-asymmetric line-profiles seen typically in LAEs (e.g. Dawson et al., 2007; Yamada et al., 2012). At the range of the measured fluxes is , which corresponds to Ly luminosities . Hence those galaxies occupy the faint-end () of the LAE luminosity function (Drake et al., 2017a, b; Herenz et al., 2019) and are thus below the detection limit of classical narrow-band imaging surveys.
From the spectral profiles we measure the LAEs redshifts using the first flux-weighted moment (Eq. 5). These redshifts are indicated as a vertical dotted lines in Figure 9. We list the velocity difference with respect to in Table 16. The two galaxies 1 and 3 south-east of the blob show large positive . In fact, their redshifts appear to be a continuation of the overall west-to-east line-of-sight velocity gradient seen in the blob. For such large values of radiative transfer effects are unlikely the main cause for the redshift offsets. We speculate, that the peculiar motion of those galaxies are driven by the gravitation potential of LAB 1’s dark matter halo. The peculiar motion of the compact sources embedded in the northern part of the south-western shell-like structure (labelled as “knots” in Figure 4) could also be explained by this scenario. Moreover, the small blue-shift of our LAE 4 to the north of LAB 8 appears consistent with a smooth continuation of the overall blob velocity field. However, the base of the blob’s filament which points towards the LAE 3 shows blue-shifts and thus deviates from a smooth velocity-field continuation. As we will discuss in more detail in Sect. 6, such small scale modulations of a velocity field could be interpreted as peculiar motions of individual galaxies or filamentary cooling flows. Lastly, the eastern-most galaxy (2) is significantly blue-shifted and does not follow any trend. This galaxy might thus be at a larger distance from LAB 1’s halo and thus not subject to its gravitational potential.
We quantify the line widths of the LAEs from the square root of the second flux-weighted moment (Eq. 8). As already discussed in Sect. 5.3, the moment-based measurement is not readily corrected for the instrumental resolution. Nevertheless, compared to the complexity of the line profiles seen in the blob, the profiles of the isolated LAEs appear relatively simple, hence the prescription for the figure-of-merit estimate in Eq. (9) provides a valid approximation here. The so corrected Ly line-widths are 102 km s-1, 57 km s-1, 208 km s-1, and 73 km s-1 for our LAEs 1, 2, 3, and 4, respectively. These line-widths are within the range of typical values obtained for a sample of brighter LAEs in the SSA22 field (Yamada et al., 2012, mean km s-1, median km s-1). Moreover, Yamada et al. (2012) also found that the line-widths for some less extreme LABs in SSA22 are significantly broader than those of the isolated LAEs. We thus may consider these faint LAEs as an extension of the known SSA22 LAE population that exists below the detection limits of narrow-band selected samples.
5.5 Detection of He ii 1640 emission
| Name | RA | Dec | Area | He ii/Ly | C iv/Ly | ||||
|---|---|---|---|---|---|---|---|---|---|
| [J2000] | [J2000] | ″ | [ erg/s/cm2] | [km/s] | [km/s] | [km/s] | |||
| south | 22h17m25.89s | +00∘12′35.3″ | 13.9 | 10.51.8 | 1368 | 28955 | 4649 | 0.060.01 | |
| north | 22h17m26.01s | +00∘12′42.2″ | 12.6 | 7.21.1 | 4251 | 15224 | 3684 | 0.070.01 | |
| LAB8 | 22h17m26.12s | +00∘12′54.1″ | 8.8 | 6.70.9 | 10922 | 20744 | 2986 | 0.110.02 |
We detect low-SB He ii emission from three distinct regions within the Ly blob. We visualise this detection in Figure 10, where we show the resulting maximum S/N map from the LSDCat 3D cross-correlated datacube (Sect. 5.2.2). Here we evaluated the S/N datacube between Å and Å (i.e. Å around He ii at ). We also show in Figure 10 an adaptive narrow-band image for He ii constructed similarly as the adaptive Ly image in Sect. 5.2.3. Due to the faintness of the emission we lowered the extraction threshold a bit, i.e. here the image was extracted by using voxels with from the S/N datacube. We provide a visual representation of the noise level in regions not containing any detected signal in the same manner as we did for the adaptive Ly image, i.e. we sum spaxels by Å (4 spectral bins) around 6724 Å.
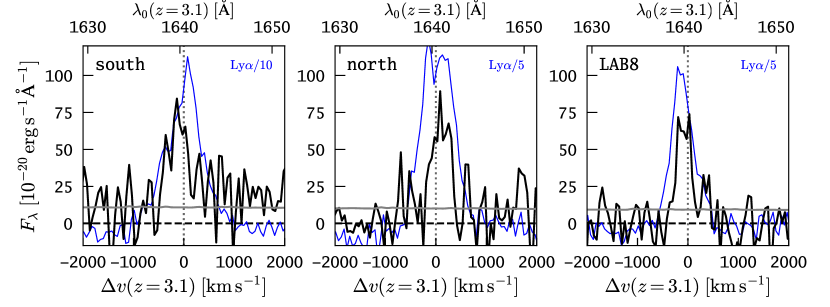
We label the three regions where He ii is detected with “south”, “north”, and “LAB8” in Figure 10. The “south” region is located south-west in proximity the ALMA continuum sources LAB1-ALMA1 and LAB1-ALMA2 while being slightly north-east of the Lyman break galaxy SSA22a-C11. The “north” He ii region can not be associated with any known source in LAB 1. This region is co-spatial with the feature labelled “northern high SB region” in Fig. 4. It is also co-spatial with the region labelled R2 in Weijmans et al. (2010) and McLinden et al. (2013). Lastly, the “LAB8” region appears in proximity to the Lyman break galaxy SSA22a-C15. We report in Table 4 positions of those regions. These positions are S/N-weighted, i.e. calculated according to Eq. (1) with replaced by the pixel values of the maximum S/N map and only considering pixels satisfying for each region. All He ii peaks are within regions of Ly surface-brightness above erg s-1cm-2arcsec-2. But the morphological features seen in He ii are considerably different compared to the morphology of Ly above this surface brightness limit.
In order to extract 1D spectra from those regions we created apertures consisting of contiguous regions with in the maximum S/N image. The corresponding areas of these He ii morphology-matched apertures are also listed in Table 4. The in those regions extracted spectral profiles of the He ii emission are shown in the bottom panels of Figure 10. We furthermore compare in this figure the He ii spectral profiles to the Ly profiles extracted in the same regions.
We measured the He ii fluxes in those regions by summing the spectral profiles shown in Figure 10 over their full width at zero intensity. The error on the fluxes was obtained from Monte-Carlo (MC) realisations of the profile, where we used the propagated variances as input for adding noise to each spectral bin. The so obtained flux measurements are listed in Table 4. Given the areas of the extraction apertures, the measured fluxes correspond to He ii surface-brightness values of 7.6erg s-1cm-2arcsec-2, 5.7erg s-1cm-2arcsec-2, and 7.6 erg s-1cm-2arcsec-2 for region “south”, “north”, and “LAB8”, respectively. The measured He ii surface-brightness is times fainter than the upper limits reported for a previous attempt to detect He ii emission in LAB 1 using narrow-band imaging (Arrigoni Battaia et al., 2015).
To quantify the He ii/Ly flux ratios we measured the Ly fluxes over their full width at zero intensity within the three He ii emitting regions. We obtained erg s-1cm-2, erg s-1cm-2, and erg s-1cm-2, corresponding to He ii/Ly , , and , for region “south”, “north”, and “LAB8”, respectively (see also Table 4). The errors on those ratios have also been computed from MC simulations for the individual He ii and Ly flux measurements. From the previous non-detection of He ii Arrigoni Battaia et al. (2015) determined upper limits He ii/Ly for LAB 1 and He ii/Ly for LAB8, thus the measured He ii/Ly ratios are a factor of two lower.
Using the first flux-weighted moment (Eq. 5) on the extracted profiles, we determined the relative redshift offset between He ii and the Ly . Again, the errors have been computed from MC realisations.
A significant offset between Ly and He ii is only detected for the LAB 8 region, where Ly appears modestly blue-shifted. Blue-shifted Ly emission with respect to non-resonant nebular lines is atypical for normal Ly emitting galaxies, that show often km s-1 (e.g. Rakic et al., 2011; Song et al., 2014), although few exceptions exist (e.g. Trainor et al., 2015). Interestingly, our non-detections of velocity offsets between Ly and He ii around C11 and LAB 8 is consistent with the non-detection of offsets between Ly and [O iii] for those systems by McLinden et al. (2013). Moreover, Prescott et al. (2015a) also report similar low velocity offsets between He ii and Ly in a He ii detected LAB at . These authors also compile data from the literature to show that LABs exhibit generally lower kinematic offsets between Ly and optically thin lines and the here presented measurements on He ii emitting regions in LAB1 corroborate this fact.
Lastly, it is visible in Figure 10 that in all three regions the Ly profile appears broader compared to He ii. To quantify this we measured the width of the He ii and Ly lines, and , using the second flux-weighted moment (Eq. 6, with ). The measurements obtained are reported in Table 4. We find that Ly is 1.6, 2.4, and 1.4 broader than He ii in the “south”, “north” and “LAB8” region, respectively. These values are in agreement with the broadening for Ly with respect to He ii observed in a LAB by Prescott et al. (2015a). As pointed out by these authors, the absence of significant velocity offsets between Ly and He ii and the presence of line broadening in Ly with respect to He ii are consistent with a scenario where a significant fraction of the extended Ly emission is produced in situ. We will discuss this physical interpretation further in Sect. 6.4.
5.6 Non-detection of the C iv 1548,1550 doublet
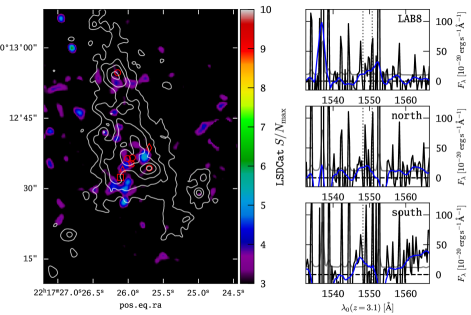
We detect no significant signal from the C iv doublet (1548.203 Å and 1550.777 Å) in the MUSE data of LAB 1. This can be seen in Figure 11 where we show the maximum S/N map for C iv from evaluation of the 3D cross-correlated S/N datacube (see Sect. 5.2). Here the S/N cube was evaluated between Å and Å. While there are a few patches within the blob that indicate possible signal at , this spectral region of the datacube is highly contaminated by sky-subtraction residuals. As these systematic residuals are not accounted for in the variance datacube, our S/N estimates are biased high. These sky-subtraction residuals appear especially pronounced at the edges of the individual observational datasets (see exposure map in Figure 2). These edge-residuals are apparent as a patchy horizontal stripe of values slightly south of the photometric centre of LAB 8, as well as a vertical stripe on the western edge of the displayed region. A few pixels in the maximum S/N map show values above 5 in regions within the blob, but the extracted spectra in those regions do not show signal. We show in Figure 11 the spectral region of interest around C iv for the spectra extracted within the three He ii emitting regions (Sect. 5.5). In order to suppress the high-frequency sky-noise and residuals we also smoothed those spectra with a Å wide Gaussian. Interestingly, the smoothed spectrum – shown as a blue line in Figure 11 – indeed appears to exhibit a small bump at the position of the line in all three regions. However, from the noise in those three regions (shown as a grey line in Figure 11), it is obvious that these features are not significant and can be only considered as a hint of C iv emission.
To provide upper limits on C iv emission we perform a source insertion and recovery experiment. For this experiment we assume that the C iv emission would be co-spatial with the He ii emitting regions. As noted in Sect. 5.5, each of the three He ii emitting region is defined by a cluster of connected spaxels that have . For simplicity we assume constant surface brightness within each region. Furthermore, we model the spectral profile of the doublet by two Gaussians, where the dispersion is set to the average width measured from the He ii line: km s-1 and we fix the ratio to 1.7 between and . We implant the so generated C iv emitting regions at surface-brightness levels from erg s-1cm-2arcsec-2 to erg s-1cm-2arcsec-2 in steps of erg s-1cm-2arcsec-2 prior to median-filter subtracting the fully reduced datacube. After median-filter subtracting each datacube with artificial C IV sources we ran the 3D cross-correlation procedure from LSDCat. From this experiment we found that we would detect the C iv emission significantly in all three regions at surface-brightness levels erg s-1cm-2arcsec-2. Given the areas of the three He ii emitting regions, our surface-brightness limit corresponds upper limits in C iv flux of erg s-1cm-2, erg s-1cm-2, and erg s-1cm-2 for region “south”, “north”, and “LAB 8”, respectively. Given the measured Ly fluxes in those regions (see Sect. 5.5), this corresponds to upper limits in C iv/Ly ratios of 0.06, 0.1, and 0.11 for region “south”, “north”, and “LAB 8”, respectively. Our upper limits on C iv translate into upper limits of , , of C IV / He ii in region “south”, “north”, and “LAB 8”, respectively.
Our upper limit for C iv emission within the He ii emitting zones appears, at first sight, less constraining than the previous upper limit of 7.4erg s-1cm-2arcsec-2 from narrow-band observations Arrigoni Battaia et al. (2015). However, the comparison has to be treated with caution, as the previous estimate assumed constant C iv emission over the whole area of the blob (200 arcsec2). But, we assumed here that C IV emission is confined to the three He ii emitting regions (10 arcsec2). The assumption of overlapping C IV and He ii emission appears a good first-order approximation in scenario where C IV and He ii act as a coolant of shock heated gas, as for both lines the maximum emissivity is obtained in a similar gas phase of K (Cabot et al., 2016), where C iv is driven through collisional excitations of C3+ (ionisation potential 47.9 eV) while He ii is originating from the recombination cascade of collisionally ionised He2+ (ionisation potential 54.4 eV). Nevertheless, the C iv emissivity also peaks in a region of slightly lower density ( cm-3) compared to He ii ( cm-3), thus C iv could potentially also be more extended (Cabot et al., 2016). This effect could be further enhanced by the resonant nature of C iv (see also Berg et al., 2019). On the other hand, if photo-ionisation from a AGN produces C4+ (ionisation potential 64.4 eV) that emits C iv as a result of recombinations, the C4+ zone would be confined within the He2+ zone. Lastly, we will show below (Sect. 6.4) that under certain conditions C IV might be even brighter than He ii. For this reason some detections of extended C IV without corresponding He II around quasars have been reported (Borisova et al., 2016; Travascio et al., 2020).
6 Discussion
6.1 On interpreting the moment maps of Ly from LAB 1 as a tracer of gas kinematics
Before interpreting flux-weighted moment maps from Ly as a tracer of gaseous motions, we need to asses how Ly radiative transfer effects may have influenced these measurements. Ly velocity fields found to exhibit coherent large-scale kinematics have been observed around known (e.g. Arrigoni Battaia et al., 2018; Martin et al., 2019) or suspected (Prescott et al., 2015a) quasars. Details on the density distribution of the gas within those systems are still not settled, but it has been asserted that the strong ionisation field from the quasar produces a large fraction of Ly photons in situ throughout the nebula via recombinations (e.g. Martin et al., 2014, 2019; Cantalupo et al., 2014, 2019). Nevertheless, even small residual neutral H i fractions () within the ionised halo will result in high Ly optical depths. Still, we suspect that the radiative transfer modulation of the Ly profile for an extended intrinsic Ly radiation field is less dramatic compared to the effect of an integrated spectrum within a compact Ly emitting source. The reason is that the profile measured at each position in the nebula only reflects small local velocity offsets between point of emission and surface of last scattering (Prescott et al., 2015a). At typical spectral resolving powers then only a broadening of the Ly line may be observed. This expectation appears consistent with our results for the He ii emitting regions in LAB 1. Moreover, systemic literature redshifts of the galaxies associated with LAB 1 do not show significant offsets with respect to those determined from Ly (McLinden et al., 2013; Kubo et al., 2016; Umehata et al., 2017). From this we conclude that the first-moment map traces the gas-kinematics close to the embedded sources. For those galaxy near zones we then can assume that significant amounts of Ly photons must be produced in situ.
For interpreting the entire first-moment map as a tracer of the underlying gas kinematics, especially in regions far from known galaxies in LAB 1, we can not resort to the argument above. The detection of polarised Ly emission, both in imaging polarimetry (Hayes et al., 2011) and spectro-polarimetry (Beck et al., 2016), shows that significant fractions of the observed Ly photons must have scattered into the line of sight after being emitted from a central source. According to radiative transfer theory the observed polarisation signal in Ly stems from scattered photons within the wing of the absorption profile (e.g. Dijkstra & Loeb, 2008; Eide et al., 2018). Hence, while these photons preserve information regarding the kinematics of the surface of last scattering, they appear red- or blue-shifted (depending on the kinematics of the scattering medium) with respect to the overall kinematics of the gas. Therefore, in a scenario where only scattered Ly photons are observed at large distance to the embedded sources, the measured first-moments would be biased towards higher or lower velocities compared to the true gas kinematics. This could potentially increase the observed amplitude of the observed velocity gradient.
However, the above scenario also requires that significant amounts of Ly photons are released by the dust-rich ALMA 850m detected galaxies in LAB 1 (see also Geach et al., 2016). The possibility of this process is indicated by the detection of Ly emission from nearby ultra-luminous infrared galaxies (Martin et al., 2015a). Feedback driven outflows powered by star-formation is believed to create the required Ly escape channels. Evidence for the required feedback effects at the positions of the galaxies comes from our higher-moment analysis discussed below (Sect. 6.3), but also from the spectro-polarimetry measurements by Beck et al. (2016). These authors find that the polarisation signal is increased in the wings of the Ly profile, especially near the embedded galaxies. According to recent Ly radiative transfer models of Eide et al. (2018) this is an expected polarisation signature in the presence of outflowing gas. Moreover, the Ly escape channels produced by gaseous outflows can potentially also act as escape channels for ionising photons from the embedded systems, thus a significant fraction of those photons might indeed be available to power the emission from the blob via recombination. Empirical evidence for such a process have also been observed in the nearby universe (Herenz et al., 2017a; Bik et al., 2018; Menacho et al., 2019). Thus, in addition to Ly scattering far from the embedded galaxies, we also expect that also in LAB 1 a significant fraction of Ly radiation is produced in-situ at larger distances from the known embedded sources. Hence, the observed emission from the galaxy far-zones is likely superposition of scattered and in-situ produced Ly emission. This potentially mitigates biases in the first moment maps that would result from pure Ly scattering.
To summarise, we presented qualitative arguments in favour of interpreting large-scale coherent features in the first-moment map from Ly as tracers of the gaseous motion in the system. These qualitative arguments are, as of yet, not tested for Ly radiative transfer simulations in realistic Ly blob environments. As we will also discuss further below, radiative transfer effects are, however, expected to strongly influence the Ly line-width and the derived moments of higher order. We suggest that the here presented non-parametric moment-based measurements of the line profiles present a starting point to summarise the complexity of the encountered profiles in LAB environments. Guided by radiative transfer simulations then these measurements may help to disentangle scattering processes from in-situ Ly photon production.
6.2 Combined analysis of Ly line profile morphology and imaging polarimetry
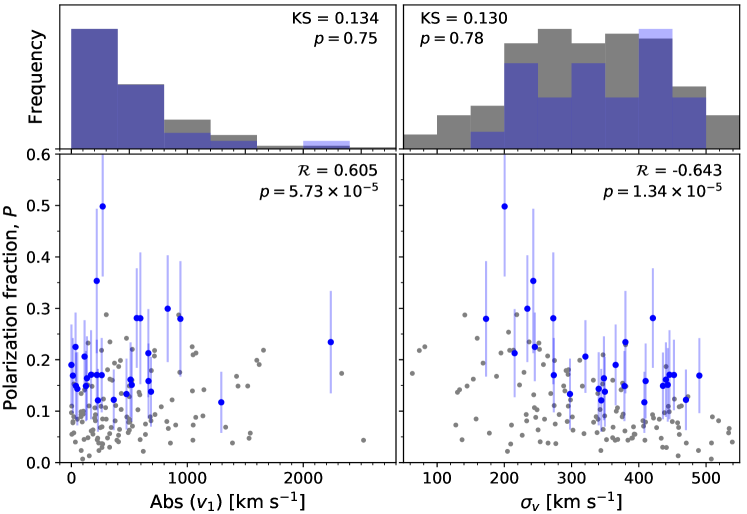
Hayes et al. (2011) studied LAB1 using the FORS2 polarimeter at VLT in order to spatially map the polarimetric properties of the Ly emission, including the Stokes vectors ( and ), the polarised light fraction () and angle of the linear polarisation vector (). The resulting maps of and were qualitatively consistent with theoretical predictions by Lee & Ahn (1998), Rybicki & Loeb (1999), and Dijkstra & Loeb (2008), and implied a geometry in which Ly is produced inside, or close to the central regions of the highest Ly surface brightness (at the positions of the later-discovered ALMA sources 1 and 2) and scattered at large impact parameters, from vectors in the plane of the sky to the sightline of the observer. However the narrowband imaging polarimetry data contained no information regarding the kinematic properties of the Ly emission, and we could not study where in the Ly line profile the polarisation signal is imparted. To remedy this Beck et al. (2016) conducted spectroscopic polarisation observations with the same instrument, to study and as a function of frequency. Those observations showed that the wavelength dependence of is small near line centre, but rises towards the line wings. This is again qualitatively consistent with the numerical predictions of Dijkstra & Loeb (2008). Those slit data contained the necessary frequency information, but only at eight positions identified along the 1″ wide slit. Moreover, those studies were limited to the regions of highest surface brightness (Beck et al. 2016, their Figure 3).
In this Section we use the 3D spectroscopy provided by MUSE to shed further light on the origin of the polarisation pattern. We perform a hybrid study, and contrast the spatially known (but spectrally-unknown) measurements of and with the Ly kinematics using 3D spectroscopy. Hayes et al. (2011) used Voronoi tessellation to locally enhance the SNR in the images taken in individual beams (‘ordinary & extraordinary’), and we apply the same binning patterns to the MUSE data: we aligned the FORS2 Ly intensity images with the MUSE data, and propagate the recovered astrometric information into the maps of and . For every Voronoi tessellated cell we then extract the corresponding spaxels from the MUSE datacube, and compute the moments described in Section 5.3.
Figure 12 shows the results, where we display the absolute velocity offset from (left panel) and the velocity dispersion (right panel). We show the absolute value of the first moment because the polarisation signal is imparted by wing scatterings, and scatterings in both the blue and red wings manifest in the same (the quantity measured in our polarimetry data Dijkstra & Loeb, 2008). We find a positive correlation between and the absolute line-of-sight velocity, and also an anti-correlation between and the velocity dispersion. The -values of suggest that correlations of this magnitude or larger are very unlikely to have arisen by a random process. That Ly should exhibit higher degrees of polarisation for narrow lines is a curious result, and may stem from several effects.
The polarisation data show a high , and a pattern in that is close-to tangentially aligned with a central source, and follows contours of surface brightness at smaller scales (Hayes et al., 2011, Figure 2). To impart such a pattern, scattering in the wing of the redistribution profile needs to be promoted, so as to in turn enhance scattering through the excited level (Dijkstra & Loeb, 2008; Eide et al., 2018). will instead decrease if too many core (resonance) scattering events occur (through the level). Such an enhancement of wing events cannot be the case for a static medium, where the gas would absorb Ly close to line-centre (core). Some velocity offset is needed, which implies that high should avoid (the original motivation for the outflowing shell models of Dijkstra & Loeb 2008). Moreover, even if large bulk velocity offsets are present, the velocity dispersion cannot be significantly larger than the absolute : the consequence of a broad velocity range of absorbing material will always leave some high column density gas close to line-centre, and maintain significant core scattering. In a complicated, 3-dimensional environment with multiple sources of Ly and many velocity components of scattering gas, highly polarised regions should favour larger velocity shifts and narrower lines, and we would expect to correlate with and anti-correlate with the line width. This is precisely what Figure 12 shows and the combination of 2D polarimetric data and 3D spectroscopic data supports a scenario in which preferential scattering outside the Doppler core is enhanced by velocity differences.
6.3 Insights into LAB 1 from the spatially resolved line-profile analysis
6.3.1 Large-scale gas kinematics from the first-moment map
We concluded in Sect. 6.1 that the first-moment map from Ly (Figure 7, left panel) can be used to trace the large scale kinematics of the gas within the blob. As apparent from that map, the blob shows a coherent large-scale velocity gradient from receding velocities on its eastern side to approaching velocities on its western side. This large scale velocity gradient encompasses LAB 1 and the northern neighbour LAB 8. Moreover, the newly detected shell-like region in the south-west (SW) of the blob is completely blue-shifted, thus seemingly follows the large scale E–W velocity gradient. Furthermore, also within the shell a gradient from NW to SE is seen. The velocity field is mostly coherent over kpc and shows significant perturbations only on smaller (kpc) scales.
We quantify the amplitude of the large-scale velocity shear as km s-1, where and are the lower and upper 5th percentile of the observed first moments throughout the blob (this choice of percentiles is robust against outliers while sampling the true extremes of the distribution). Coherent large scale velocity fields of such large amplitude appear to be rare amongst extended Ly nebulae around quasars at redshifts similar to LAB 1 (Borisova et al., 2016; Arrigoni Battaia et al., 2019). Nevertheless, a few comparable examples do exist: object 3 (Q0042-2627) in Borisova et al. (2016), the QSO UM 287 studied in Martin et al. (2015b) and Martin et al. (2019), as well as object 13 from Arrigoni Battaia et al. (2019) that was described in detail in Arrigoni Battaia et al. (2018). Moreover, two of the four QSOs in the recent sample by Drake et al. (2019) show coherent kinematics, while the other two objects show highly irregular and disturbed velocity fields.
We hypothesise that the preponderance of disturbed velocity fields around QSOs could be related to large-scale AGN feedback effects. As an additional hypothesis we state that the large fraction of chaotic velocity fields around QSOs is driven by the short exposure times that are typically used in those studies (e.g. 1 h in Borisova et al. 2016; 45 min in Arrigoni Battaia et al. 2019). These short exposures result in lower S/N for low-SB Ly emission in the outskirts of the halos and potentially even miss the faintest regions, where large scale kinematics may become most apparent. Comparing our observations with previous IFS observations of LAB 1 by Bower et al. (2004) and Weijmans et al. (2010), which additionally have a coarser spatial resolution (0.4″ per spaxel, and seeing FWHM1.5″) compared with our data (0.2″ per spaxel, and seeing FWHM0.9″), we indeed find that their velocity fields represent just a coarser and more noisy representation of the here observed velocity field in the high SB regions of the blob. Nevertheless, Bower et al. (2004) described the overall velocity structure of LAB 1 as chaotic with a lack of velocity shear. And undeniably, the velocity field of LAB 1 within the high-SB regions (erg s-1cm-2arcsec-2) appears complicated. As noted by Weijmans et al. (2010) the observed complexity in this region can be broken down into several sub-regions that show coherent velocity shear and some of these regions are associated to known galaxies within the LAB. These small-scale perturbations, now observed at higher spatial resolution in the MUSE data, might be related coherent motions of the gas in the individual sub-halos. But they also could be caused by kinematic perturbations due to inflowing cold gas, or they could be driven by feedback effects (see Sect. 6.3.2 below).
The most striking feature of the newly revealed large-scale velocity field is that the shear is observed perpendicular to the morphological principal axis (Figure 7, left panel). The existence of such a large-scale coherent velocity field of high-amplitude appears in qualitative agreement with theoretical predictions of hydro-dynamical simulations in a CDM framework. In particular it is a natural outcome of the filamentary nature of the cosmic web and the predicted existence of dense cold-gas streams that can penetrate deeply into dark-matter potential wells without being shock-heated by the gravitational potential (see review by Stewart, 2017). However, the perpendicular alignment between the velocity field and the morphological principal axis implies that the angular momentum vector of the gas in LAB 1 is aligned parallel with the morphological principal axis. Simulations in the CDM framework predict that the angular momentum vector and the elongation of the dark matter halos – including their gaseous and stellar contents – show correlated properties with the surrounding large-scale structure of the cosmic-web (e.g., Forero-Romero et al., 2014; Libeskind et al., 2018; Codis et al., 2018; Wang & Kang, 2018, and references therein). These studies predict that the angular-momentum of high-mass halos (M⊙) is expected, on average, to be orthogonal to the major axis of the halo, and the halo’s major axis is expected to be aligned parallel with the connecting filament of the cosmic web. Thus, the observed alignment between morphological principal axis, which we naively interpret as the direction of the major cosmic web filament (as suggested by Erb et al., 2011), renders LAB 1 as an outlier from the theoretically expected average for high-mass halos.
We speculate that the deviation from the theoretically expected norm in LAB 1 is caused by the complexity of the surrounding large-scale structure. We regard the observed multi-filamentary morphology of the blob, with one filament extending to the SE in the direction of the two newly identified LAEs (labelled “filament towards LAE 3” in Figure 4), another filament extending to the north (“filament to LAE 4” in Figure 4), and another filament connecting to the shell-like region in SW (“shell-connecting filament” in Figure 4) as evidence for such a complex environment. In fact, the SSA 22 proto-cluster, which hosts LAB 1 and LAB 8, is one of the most-massive structure known in the high-redshift universe (see Kikuta et al. 2019 for another extreme overdensity at ). In such a high- high-density peak of the universe a complex interwoven network of filaments is expected. Indeed, recent MUSE observations ( h) by Umehata et al. (2019) have revealed such a cold-gas network in Ly at the core of SSA 22, located 4.8 ′ (2.19 Mpc) north-east of LAB 1. Interestingly, also this structure shows a mix of perpendicular and parallel aligned large-scale velocity gradients with respect to the filamentary structure (Umehata et al., 2019, their Fig. 3).
The complexity of angular momentum alignments in dense cosmic regions was studied in simulations by Lee et al. (2018), who also showed that in these environments the orientation of angular momentum vector is expected to change frequently and significantly. In such a scenario the observed alignment of LAB 1’s angular momentum can be reconciled as an early evolutionary stage of a massive galaxy.
6.3.2 Small-scale kinematical perturbations in the first-moment map
As mentioned before, the coherent velocity field of LAB 1 shows also various perturbations on smaller scales. One prominent perturbation occurs at the position of the Lyman break galaxy SSA22a-C11, where the velocity shears from north-west to south-east, i.e. almost perpendicular to the apparent large-scale motion. The coherent small-scale velocity shear at the position of SSA22a-C11 was already noted by Weijmans et al. (2010). In this region the velocity field varies from km s-1 to km s-1 just within 2″ or 15 kpc in projection. It appears as if Ly traces the velocity field of this individual bright galaxy that is not aligned with the blob’s large scale velocity field. Such misalignments of sub-halos are also in qualitative agreement with the theoretical studies mentioned in the previous section (e.g. Codis et al., 2018). However, especially given the large amplitude on small physical scale, this disturbance of the velocity field may also be caused by feedback effects (galactic outflows, as proposed by Weijmans et al. 2010). Less prominent disturbances are apparent near the sub-mm detected sources LAB1-ALMA1 and LAB1-ALMA2. Here, as we will discuss below in Sect. 6.3.3, the analysis of the higher order moment map will provide arguments in favour star-formation driven winds and/or outflows.
While the small-scale perturbations may be caused by individual velocity fields of the embedded galaxies and/or star-formation driven winds or outflows, we also have to consider the alternative (but not competing) hypothesis that they may in fact represent evidence for cold-flow multi-filamentary inflows. Recently, Martin et al. (2019) presented a quantitative framework to fit the expected kinematic signatures from cold-flow accretion streams to Ly intensity weighted velocity maps. These authors motivate their parametric ansatz by numerical simulations of a galaxy that exhibits cold filamentary inflows. The velocity field of this simulation was found to be optimally described by a large-scale rotating component that is modulated by radially and azimuthally varying components. These modulations are shown to capture the kinematic perturbations caused by the filamentary cooling flows. Martin et al. (2019) show that these parametric models also provide an excellent fit to the observed Ly velocity fields of two large extended Ly nebulae around radio-quiet quasars. We find that the qualitative appearance of velocity field modulations caused by the cooling flows in the Martin et al. ansatz bear similarity to the small scale perturbations seen in LAB 1’s first-moment map. A quantitative treatment with the Martin et al. ansatz is, however, beyond the scope of the present analysis.
6.3.3 Interpretation of higher-order moment maps
Empirical insights into the Ly photon production and/or scattering mechanisms within the blob can be gained from our maps of the Ly line-width (Figure 7, right panel), its skewness, its kurtosis , as well as its bi-modality (Figure 8). In the following we will discuss several notable features in those maps. By visually inspecting the spaxels in each of the discussed regions we ensured that the mapped values are indeed representative of the observed line profile morphology.
The highest line-widths ( km s-1) are observed N and S of LAB1-ALMA1 and LAB1-ALMA2. Towards the north this high dispersion regions shows a V-shaped morphology that traces the edges of the prominent “bubble” feature seen in the narrow-band image (Figure 5). While Ly shows no pronounced double peaked profile () at the position of LAB1-ALMA1 and LAB1-ALMA2, more pronounced double peaks are observed in the V-shaped region (), with the NE arm showing the most pronounced double peaks (). Thus, while it is tempting to interpret the broad widths close to the sub-mm source as gas that is kinematically hotter due to feedback from the galaxies, the measured large width of the profiles in those regions is rather the result of double component Ly profiles, i.e. Ly radiative transfer.
However, we might witness possible signatures of outflowing gas traced by the Ly skewness at the position of LAB1-ALMA1, where the Ly profiles show a pronounced skew towards the blue (). Interestingly, the Ly profiles in some of the Martin et al. (2015a) ULIRGs show profiles with a blue tail. Martin et al. (2015a) interpret these blue tails as outflow signatures, with the Ly in the wing being produced by gas cooling within the outflow. Also, SE of LAB1-ALMA3 strong blue-skewed profiles that are indicative of an outflow are observed. This is corroborating the inference by Umehata et al. (2017) who argued that the properties of the [C ii] 158m emission from LAB1-ALMA3 are suggestive of an interaction between a galactic outflow with an intergalactic gas stream.
As can be seen from Figure 7 the line-width of Ly is narrower in the outskirts of the blob. Both the shell-like region in the SW, the filament emanating to the N and connecting to LAB 8, as well as the filament emanating to the NE are characterised by km s-1. However, as traced by the higher-moment based statistics (Figure 8), even in those regions the observed Ly line profiles appear to be quite complex. For example along the LAB 1 - LAB 8 connecting filament the line profile is strongly skewed to the red (). Most prominently this structure emerges as a red band in the skewness map. Throughout most of this filament the discriminatory power of the adopted bi-modality indicator is weak (). However, visual inspection of the line profile hints at least in some places at the appearance of a secondary weaker red peak as cause for the measured red skew. For the NE filament observationally the situation is more clear, here the profile is clearly double peaked (, see also example spectrum in panel 1 of Figure 6), mostly with a weaker blue component. Both the red-skewed profiles with a potential secondary peak and the double peaked profiles are likely caused by radiative transfer. As we discussed above (Sect. 6.2), the strongest polarisation signal arises in regions of smaller line-width ( km s-1), also supportive of Ly scattering from a central source. Hence, the low-line width regions in the outskirts and in the filamentary regions hint at dense patches of gas where Ly scattering takes place. The filamentary morphology of some of these patches is morphological reminiscent of cooling-flows, but whether the dominant Ly signal is produced by cooling or photo-ionisation in those regions remains unclear. At least the line profiles in those regions appear consistent with a super-position of in-situ produced Ly photons (dominant peak) and scattered Ly radiation (wing or second component).
Another peculiar and outstanding feature in our higher moment-based maps is found at the N edge of the bubble. Here the profile is significantly skewed () and described by a single-component () profile with a pronounced wing (). An aperture extracted Ly spectral profile from this region is shown in panel 11 of Figure 6. The bubble or cavity was already remarked as a peculiar feature in LAB 1 by Bower et al. (2004). As a possible scenario Bower et al. (2004) discuss, that the bubble is filled by hot ionised gas. Bower et al. (2004) speculate that a potential radio-jet from the central sub-mm sources could have heated this gas. In this scenario the skewed Ly line arises in the region where the beamed emission is being slowed down by the denser cold-gas. Observational evidence for radio-emitting gas influencing the Ly spectral properties have been presented for radio loud quasars and radio galaxies (e.g. Maxfield et al., 2002; Humphrey et al., 2007; Roche et al., 2014; Morais et al., 2017). However, no extended powerful radio-lobes are seen in the VLA 10cm radio-continuum images and with Jy the nearby compact radio-continuum source is weaker compared to typical radio-loud quasars (Ao et al., 2017). Moreover, Ao et al. (2017) remark a slight radio-excess compared to the expectation from the sub-mm determined star-formation, but they conclude that star-formation is a significant contributor in heating the gas. These observations appear compatible with the alternative hypotheses from Bower et al. (2004) that the cavity has been blown by a star-formation driven wind. The emergence of He ii emission in the vicinity of the bubble may be linked to shock heated gas within the compressed shell of the bubble, although photo-ionisation by a potentially obscured radio-quiet AGN can not be ruled out (see Sect. 6.4 below). Nevertheless, the Ly profile in this region also shows a bump on the blue side, and such a profile appears consistent with theoretically expected Ly radiative transfer modulations within shock fronts (Chung et al., 2016).
Lastly, we note that at the position of C11 the Ly profile is single-peaked (), but shows significant tails towards both the blue and red (). Inspecting the profile from C11 we find that these wings appear to have substructure in the form of two additional peaks (see also panel 6 in Figure 6). This triple-peaked structure is reminiscent of the Ly profile from a multiply lensed-galaxy by Rivera-Thorsen et al. (2017), although not as extreme. Rivera-Thorsen et al. (2017) showed, that triple peaked Ly profiles are indicative of low-covering fractions of neutral gas along the sight-line (see also Behrens et al., 2014). Thus, such galaxies potentially leak ionising radiation along the sight-line. Indeed, recently Rivera-Thorsen et al. (2019) confirmed the ionising photon leakage from their system. Thus, although C11 is located in an extremely dense environment, at least in its vicinity most of the gas appears highly ionised, thereby possibly promoting the escape of ionising radiation.
6.4 He ii emission from the LAB: Driven by feedback, cooling flows, or hard ionising radiation?
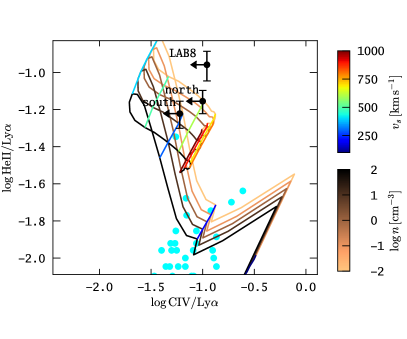
In Sect. 5.5 we reported on the detection of three distinct extended He ii emitting zones with erg s-1cm-2arcsec-2. Extended He II emission is commonly observed within the extended Ly emitting regions surrounding high- radio galaxies (e.g., Maxfield et al., 2002; Villar-Martín et al., 2007a, b; Morais et al., 2017; Marques-Chaves et al., 2019). Broad line profiles and alignments with the radio-jet axes indicate that He ii is, at least partly, powered by jet-gas interactions in those objects. Detections of He ii emitting zones within the extended Ly nebulae surrounding radio quiet quasars or in LABs not directly associated with an AGN appear less frequent and more difficult to interpret (Scarlata et al., 2009b; Prescott et al., 2009; Cai et al., 2017; Cantalupo et al., 2019; Humphrey et al., 2019). Different explanations have been put forward, e.g. with Scarlata et al. (2009b) favouring cooling-radiation in their system, Prescott et al. (2009) arguing for photo-ionisation by an AGN or an extremely metal poor stellar population in their object, while Cai et al. (2017) reason that their extended He ii zone is powered by shocks. We now try to constrain the physical mechanisms responsible for the extended He ii emission in the blob. To this aim we will also consider the upper limits on C IV emission from the He ii emitting zones (Sect. 5.6).
To place our result in context with previous observations (or upper limits) of He ii and C iv emission from high- sources with extended Ly emission we compare in Figure 13 our measured He ii/Ly ratios and our derived upper limits on C iv/Ly to the literature. The majority of comparison objects in Figure 13 harbour a bright active galactic nucleus. We observe that that the ratios and upper limits in LAB 1 appear not unusual with respect to other extended Ly objects, i.e, some objects exhibit significantly higher ratios both in He ii/Ly and C iv/Ly, but also significantly lower ratios or upper-limits have been reported. The diversity in ratios observed for nebulae with known powering source imply that varying physical conditions (e.g. metallicity, temperature, and density) within the emitting gas significantly influences the observed ratios. Additionally, radiative transfer effects in both Ly and C iv (Berg et al., 2019, their Sect. 2.3) can also bias conclusions drawn from this diagram (e.g. Caminha et al., 2016). This diagram has now been frequently used in the literature for attempting to understand the physical conditions of the ionised gas.
We show in Figure 13 the track of a photo-ionisation model from Villar-Martín et al. (2007a) that appears to be in good agreement with the He ii/Ly ratios and C iv/Ly ratios from our observations. This track was computed for gas of solar metallicity at a density of cm-3 as a function of varying (dimensionless) ionisation parameter
| (13) |
where denotes the rate of hydrogen ionising photons produced by the source and denotes the distance of the ionised gas cloud to the source. As spectral energy distribution of the ionising source Villar-Martín et al. (2007a) assumed an idealised quasar described by a power-law continuum with slope . Along the displayed track varies from -2.3 (start of the upper branch) to 0 (end of the lower branch); the inflection point in C iv/Ly is at (the model is adopted from Figure 1 of Villar-Martín et al., 2007a).
While the predicted line-ratios show some agreement with our observation, for region “north” the assumptions in this model require extremely high photo-ionisation rates: Region “north” is 50 kpc in projection towards LAB-ALMA1, LAB-ALMA2, and VLA-LAB1a. Thus, according to Eq. (13), even the smallest in the Villar-Martín et al. (2007a) model corresponds s-1 if we assume a galaxy at the position of LAB-ALMA1, LAB-ALMA2, or VLA-LAB1a as the ionising source. This value would be similar to the photo-ionisation rate inferred for the luminous quasar UM 287 that powers the “Slug” nebulae (Cantalupo et al., 2014) and two orders of magnitude higher than the s-1 that would be required to power the whole blob via photo-ionisation (under case-B assumptions). While the photo-ionisation model might be more fitting for the zones “south” and “LAB 8”, as they are in close vicinity to known galaxies, existing deep multi-wavelength data does not find strong evidence in favour of such a luminous AGN (Ao et al., 2017). Thus, we also explore different mechanism that have been put forward to explain He ii in LABs.
The co-spatial occurrence of He ii emitting gas with embedded galaxies in the blob is qualitatively consistent with hydrodynamic simulations from Cabot et al. (2016) that do not contain photo-ionisation by an AGN. The Cabot et al. (2016) models predict that the main source of He ii emission in LABs should be shock-heated gas from supernovae driven winds. Included in the simulations are both Ly radiative transfer and dust-extinction effects, as well as photo-ionisation from a star-forming population at star-formation rates compatible with typical LABs (). In Figure 14 we compare our measured He ii/Ly ratios and C iv/Ly upper limits with the results from the 48 simulated LABs by Cabot et al. (2016). As can be seen our measured He ii/Ly ratios are significantly above the ratios predicted by the models, while our upper limits on C iv/Ly are compatible with the models. The discrepancy between models and data may indicate that, contrary to the assumption simulations, shock heating is not the dominant mechanism in producing the observed He ii/Ly ratios. Alternatively, the physical properties of the 46 simulated halos by Cabot et al. (2016) might be significantly different from that of the halo hosting LAB 1.
We find a similar discrepancy between the He ii/Ly ratios in LAB 1 and recent AGN photo-ionisation models by Humphrey et al. (2019). As shown in Figure 14, these models also predict significantly lower He ii/Ly than what is observed here. The Humphrey et al. (2019) photo-ionisation tracks where computed for different ionising sources illuminating low-metallicity () gas. Similar to the calculations by Villar-Martín et al. (2007a) a gas density of cm-3 was adopted. The aim of these computations was to find an explanation of the extreme ratios and/or upper limits found for some nebulae around AGN or radio-galaxies that appeared incompatible with previous photo-ionisation attempts (see Figure 13). We show in Figure 14 the resulting predictions for photo-ionisation by an idealised quasar (described by a power-law continuum spectral energy distribution with , blue curve), whose ionising continuum also has been modified by intervening cold-gas that absorbs 50% of the ionising photons (green curve) and a fiducial zero-metallicity stellar population (modelled by a K black body) for varying ionisation parameters. In Figure 14 the tracks are shown from for the highest C iv/Ly ratios to where C iv/Ly. Within the displayed range the He ii/Ly ratio exhibits a weak dependence on , while the C iv/Ly ratio rapidly decreases with decreasing . The reason for the almost constant He ii/Ly ratio is that in the simulated low-metallicity gas the fraction of He++ ions remains saturated for an photo-ionisation field. On the other hand, the large decrease in C IV/Ly for decreasing is driven by both the reduction in electron temperature (resulting in lower collision rates for C3+) and the decreasing fraction of ions for smaller values of . We remark also that for (outside of the displayed range in Fig. 14, see Humphrey et al. 2019) the He ii/Ly ratios will also start to decrease significantly. As explained above, for cm3 gas in region “north” only would be compatible with a scenario where the whole blob is powered by photo-ionisation, but also at these extreme ionisation parameters the Humphrey et al. (2019) model are incompatible with our observations. Thus, photo-ionisation of low-metallicity gas by an AGN or Pop-III stellar population under the assumptions made in the Humphrey et al. (2019) models appears not to be a valid scenario to explain the He ii emitting zones in LAB 1.
It is also apparent in Figure 14 that the photo-ionisation tracks overlap with the predictions from the ab-initio simulations by Cabot et al. (2016) in which shock-heated emission dominates. A similar degeneracy was commented upon by Arrigoni Battaia et al. (2015), who computed a different set of AGN photo-ionisation models. Similar to Villar-Martín et al. (2007a), these authors modelled the expected line ratios in solar-metallicity optically-thick and optically-thin gas. Their optically-thin models are compatible with our He ii/Ly ratios at very low ionisation parameters (), where C iv/Ly (Figure 12 in Arrigoni Battaia et al., 2015), i.e. times below our upper limit for this ratio. As discussed above, such low values of are not unrealistic for the He ii emitting zones within the LAB. On the other hand, their optically thick models () would require relatively high ionisation parameters to reproduce our observed He ii/Ly ratios. For those models then, the predicted C iv/Ly values would be slightly below our upper limits. Unfortunately, this region of the He ii/Ly vs. C iv/Ly parameter space is also covered by shock models. This is illustrated by Figure 15, where we compare our measurements and upper limits to the predictions from shock models at solar metallicity by Allen et al. (2008). For those models we use the same parameters motivated by Arrigoni Battaia et al. (2015), and we refer to Sect. 5.2 of their publication for an in-depth discussion of the motivation and description of the models.
As evident by Figure 15, both shock and shock+precursor models can reproduce the observed He ii/Ly ratios for C IV/Ly ratios that would be consistent with our upper limits for shock velocities of km s-1. While for region “south” the observed line-width in He ii appears compatible with those velocities, the other two regions show significantly narrower He ii emission. However, especially the emission stemming from the pre-cursor arises in kinematically more quiescent gas which is photo-ionised by the hard-UV radiation from the shock. The measured line-widths might thus indicate that we observe He ii emission from the pre-shock phase.
A third interpretation for our He ii detection is provided in the models from Yang et al. (2006). These models suggest that extended zones of narrow ( km s-1) He ii emission within Ly blobs are a signature of gravitational cooling radiation. We here observe He ii in close vicinity to star-forming galaxies (regions “south” and “LAB 8”) and next to the expanding bubble within the blob (region “north”). The Yang et al. (2006) models also predict the highest He ii and Ly surface brightness in close vicinity of the star-forming galaxies within the blobs. Considering only Ly emission, a similar conclusion was recently reached by Trebitsch et al. (2016). Hence, our observations do not rule out contributions from cooling radiation within two of our three detected He ii patches. But again, region “north” is an exception as it not close to a known galaxy.
To summarise, the detection of faint extended He II emission is consistent with all mechanisms that are suggested to power the Ly blob – i.e. cooling radiation, feedback driven shocks, and/or photo-ionisation from an embedded active galactic nuclei. For the latter two scenarios we compared He ii/Ly ratios and upper limits on C iv/Ly with observed ratios from the literature and models. He ii/Ly and C iv/Ly ratios comparable to our measurements have been found in extended Ly halos around high- radio galaxies and AGNs, and these ratios can be explained by some photo-ionisation models. However, our ratios are not as extreme as the ratios that would be expected from quasar photo-ionisation of extremely metal deficient gas at very low ionisation parameters (Humphrey et al., 2019).
A potential caveat when comparing our measured line ratios with photo-ionisation models is that measurements were obtained within apertures that cover a projected area of kpc2. We expect realistically that gas within those regions exhibits a range of different densities and temperatures. However, the observed He ii/Ly ratios from photo-ionised gas from an embedded quasar will depend sensitively on the density distribution of the line emitting gas (Cantalupo et al., 2019). In fact, for any realistic density distribution the aperture integrated He ii/Ly ratio will always be lower than the intrinsic ratios within the volume covered by the aperture. Thus, the quantitative comparison between our measured line ratios and upper limits to photo-ionisation models must be treated with caution, as these models always assumed constant densities.
7 Summary and conclusions
We presented an analysis of 17.2 h MUSE observations of the prototypical SSA22a LAB 1 at . Our analysis revealed many previously unknown features of this enigmatic high- object and provided detailed look into the early formation stage of a massive galaxy within an extremely dense environment. The main results of our study are the following:
-
1.
Our IFS data reaches a limiting depth of erg s-1cm-2arcsec-2 in Ly. This is a factor ten deeper than previous IFS observations of LAB 1 by Weijmans et al. (2010) that revealed Ly down to erg s-1cm-2arcsec-2. At this unprecedented depth we uncover several hitherto unknown features of the blob. Most prominently we find a filamentary bridge connecting LAB 1 with its northern neighbour LAB 8 and a shell-like arc towards the SW of LAB 1. Potentially another filament is emanating to the SE in the direction of two newly identified faint LAEs. These filamentary features are visible both in the sequence of 2.5 Å narrow-band slices (Figure 3) as well as in the adaptive Ly image (Figure 5). The newly uncovered structures are morphologically reminiscent of cold streams that are predicted to funnel cool gas into the potential wells of massive halos. As cooling flows are expected to align with the underlying filamentary large scale structure, the presence of multiple filaments pointing into various directions may imply that LAB 1 harbours a node in the cosmic web where a complex interwoven network of filaments arrives from various directions.
-
2.
We find a ring-like structure slightly west of the photometric centre that is deprived in Ly emission. While previous observations hinted already at the existence of this feature (Bower et al., 2004; Weijmans et al., 2010), the improved spatial resolution and sensitivity of our observations allow to slice through this shell in velocity space (Figure 3). The detection of He ii emission at a He ii/Ly ratio consistent with expectations for shock heated gas in regions directly demarcating the “bubble” appears supportive of the hypothesis that we are observing a genuine cavity filled by hot ionised gas. However, the line ratio is also consistent with photo-ionisation models that assume an AGN as ionising source, but the required photo-ionisation rates for those models appear too high when an AGN is assumed at the position of the central most plausible AGN sources (Sect. 6.4). Moreover, as seen in our higher-order moment maps (Figure 8), the Ly profile at this position is markedly different than in the surrounding regions – it is strongly skewed with a pronounced red tail, but not bi-modal. Such a profile is reminiscent of the Ly radiative transfer simulations for expanding shells (Verhamme et al., 2006; Gronke & Dijkstra, 2016), and furthermore the faint blue-wing seen in the profile (Figure 6, panel 11) appears consistent with predictions for the Ly profiles in shock-fronts (Chung et al., 2016). These results may indicate that pressure exerted by the hot ionised gas drives an expanding bubble (Sect. 6.3.3). Potential driving mechanisms for this expansion are a star-formation driven wind or radio emission from an obscured or faded AGN associated to the central sub-mm/radio sources.
-
3.
The Ly profiles observed from the blob exhibit varying degrees of complexity (Figure 6). We tried to map the varying complexity of the blob by utilising a moment-based non-parametric analysis of the profiles (Sect. 5.3). This analysis provided us with maps of the line of sight velocity (central moment), the width of the line, its skewness, kurtosis, and bi-modality (Figure 7 and Figure 8). Especially within the central regions of the blob we find broad double- or even triple peaked profiles. Unfortunately, however, for these complex broad profiles the used bi-modality measure from Remolina-Gutiérrez & Forero-Romero (2019) appeared to be not very precise. However, it spatially pinpoints three compact regions that are characterised single peaked profiles that are sometimes skewed towards the blue or the red. Two of these regions are associated with the known Lyman break galaxies SSA22a-C11 and SSA22a-C15, and the third is associated with the edge of the expanding bubble. Interestingly, these single peaked features appear in the vicinity of the He ii emitting zones. The spatially varying complexity of the profiles likely encodes a mix of different Ly photon production mechanisms: in-situ production from ionising sources and gravitational cooling, or both simultaneously. Moreover, projection effects from the line-of-sight passing through multiple filaments may also be responsible for the appearance of multiple peaks. Single peaked profiles might indicate a small residual fraction of neutral gas at line centre, and therefore pinpoint a high degree of ionisation. Quantitatively disentangling the production mechanisms and projection effects based on the line profiles appears notoriously difficult. An analysis of realistic Ly blob simulations in a cosmological context, as e.g. very recently presented by Kimock et al. (2020), could reveal whether the here presented moment based moment has diagnostic power in this respect.
-
4.
We find the highest degrees of Ly polarisation in regions that exhibit high velocity shifts and narrow line profiles (Sect. 6.2 and Figure 12). These regions are far from known embedded galaxies. It appears that this result is consistent with theoretical expectations for Ly scattering from a central source (Eide et al., 2018), although numerical simulations for Ly spectro-polarimetry in complex 3D environments have yet to be performed.
-
5.
The line-of-sight velocity field of the blob is characterised by a large-scale velocity gradient that is oriented perpendicular to the morphological major axis of the blob (Figure 7, left panel). The observed shearing amplitude is km s-1. The orientation of the velocity gradient implies a parallel alignment between angular momentum vector and major axis. This parallel alignment between major axis and angular momentum appears at odds with the theoretically expected average for massive halos (Sect. 6.3.1). We argue that this peculiar alignment reflects the complexity of the dense environment in which the blob resides. This leads us to speculate that LAB 1 is formed at the node of multiple intersecting filaments of the cosmic web. The kinematic interpretation of the large-scale velocity field relies on the assumption that the first-moment map from Ly is a good tracer of the large-scale kinematics (Sect. 6.3.1), an assumption that has of yet not been tested against radiative-transfer simulations.
-
6.
We detect extended He ii 1640 emission at three disjunct regions in the blob (Sect. 5.5 and Figure 10). The He ii emission from those regions shows a surface brightness of erg s-2cm-2arcsec-2. Two of those regions surround known embedded galaxies, and the third region demarcates the expanding bubble. Our observations do not reveal C iv 1549 emission from those regions (Sect. 5.6). A comparison between predicted He ii/Ly and C iv/Ly ratios from shock- and photo-ionisation models from the literature with our measurements and upper limits is consistent with both photo-ionisation from an AGN (Villar-Martín et al., 2007a) and fast radiative shocks (Allen et al., 2008). However, the observed ratios were found to be incompatible with recent AGN photo-ionisation models by Humphrey et al. (2019), that assume low-gas metallicity, an ionising source partly covered by optically thick neutral gas, or very low ionisation parameters. Moreover, our observed He ii/Ly ratios are also significantly above the predicted ratios from the hydrodynamic simulations of Cabot et al. (2016) that predict feedback driven shocks and gas accretion shocks as main source for the observed He ii emission in LABs.
Our new observations provide the most detailed view of a Ly blob to date. Given the numerous galaxies within the blob and the surrounding dense proto-cluster environment it appears natural to suspect LAB 1 as the progenitor of a massive cluster elliptical. The detection of He ii emission may hint at the importance of feedback effects in the early evolutionary stage of such systems, but AGN powering can not be ruled out. Moreover, we find no clear evidence for gravitational cooling, but we can also not rule this mechanism out. We suggest that simulations of Ly blobs in cosmological environments should be compared to the non-parametric line profile analysis presented here. Moreover, rest-frame optical emission line studies, e.g. with the James Webb Space Telescope, will help to better constrain the powering mechanisms. Finally, our study also highlights the potential importance of environmental effects on the kinematic properties of massive halos that lie at the intersection of multiple filaments of the cosmic web. As our study focused on a single object we can not establish any empirical trends in this respect, hence future studies of LAB samples at sufficient depth in proto-cluster environments are desirable.
Acknowledgements.
We thank the anonymous referee for a careful report that contained many suggestions that helped to improve this paper. E.C.H. thanks the extragalactic group at Stockholm University for a wonderful time and many insightful discussions during this project. E.C.H. also thanks Aaron Smith and Peter Laursen for useful comments during early stages of this project. This research made extensive use of the astropy package (Astropy Collaboration et al., 2018). All figures in this paper were created using matplotlib (Hunter, 2007).References
- Alexander et al. (2016) Alexander, D. M., Simpson, J. M., Harrison, C. M., et al. 2016, MNRAS, 461, 2944
- Allen et al. (2008) Allen, M. G., Groves, B. A., Dopita, M. A., Sutherland, R. S., & Kewley, L. J. 2008, ApJS, 178, 20
- Ao et al. (2015) Ao, Y., Matsuda, Y., Beelen, A., et al. 2015, A&A, 581, A132
- Ao et al. (2017) Ao, Y., Matsuda, Y., Henkel, C., et al. 2017, ApJ, 850, 178
- Arrigoni Battaia et al. (2019) Arrigoni Battaia, F., Hennawi, J. F., Prochaska, J. X., et al. 2019, MNRAS, 482, 3162
- Arrigoni Battaia et al. (2018) Arrigoni Battaia, F., Prochaska, J. X., Hennawi, J. F., et al. 2018, MNRAS, 473, 3907
- Arrigoni Battaia et al. (2015) Arrigoni Battaia, F., Yang, Y., Hennawi, J. F., et al. 2015, ApJ, 804, 26
- Astropy Collaboration et al. (2018) Astropy Collaboration, Price-Whelan, A. M., Sipőcz, B. M., et al. 2018, AJ, 156, 123
- Bacon et al. (2010) Bacon, R., Accardo, M., Adjali, L., et al. 2010, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, Vol. 7735, Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series
- Bacon et al. (2017) Bacon, R., Conseil, S., Mary, D., et al. 2017, A&A, 608, A1
- Bacon & Monnet (2017) Bacon, R. & Monnet, G. J. 2017, Optical 3D‐Spectroscopy for Astronomy (Wiley‐VCH Verlag GmbH & Co. KGaA)
- Bacon et al. (2016) Bacon, R., Piqueras, L., Conseil, S., Richard, J., & Shepherd, M. 2016, MPDAF: MUSE Python Data Analysis Framework, Astrophysics Source Code Library
- Bacon et al. (2014) Bacon, R., Vernet, J., Borisiva, E., et al. 2014, The Messenger, 157, 13
- Barger et al. (2012) Barger, A. J., Cowie, L. L., & Wold, I. G. B. 2012, ApJ, 749, 106
- Beck et al. (2016) Beck, M., Scarlata, C., Hayes, M., Dijkstra, M., & Jones, T. J. 2016, ApJ, 818, 138
- Behrens et al. (2014) Behrens, C., Dijkstra, M., & Niemeyer, J. C. 2014, A&A, 563, A77
- Berg et al. (2019) Berg, D. A., Chisholm, J., Erb, D. K., et al. 2019, ApJ, 878, L3
- Bik et al. (2018) Bik, A., Östlin, G., Menacho, V., et al. 2018, A&A, 619, A131
- Borisova et al. (2016) Borisova, E., Cantalupo, S., Lilly, S. J., et al. 2016, ApJ, 831, 39
- Bower et al. (2004) Bower, R. G., Morris, S. L., Bacon, R., et al. 2004, MNRAS, 351, 63
- Bridge et al. (2018) Bridge, J. S., Hayes, M., Melinder, J., et al. 2018, ApJ, 852, 9
- Brooks et al. (2009) Brooks, A. M., Governato, F., Quinn, T., Brook, C. B., & Wadsley, J. 2009, ApJ, 694, 396
- Bădescu et al. (2017) Bădescu, T., Yang, Y., Bertoldi, F., et al. 2017, ApJ, 845, 172
- Cabot et al. (2016) Cabot, S. H. C., Cen, R., & Zheng, Z. 2016, MNRAS, 462, 1076
- Cai et al. (2017) Cai, Z., Fan, X., Yang, Y., et al. 2017, ApJ, 837, 71
- Caminha et al. (2016) Caminha, G. B., Karman, W., Rosati, P., et al. 2016, A&A, 595, A100
- Cantalupo (2017) Cantalupo, S. 2017, in Astrophysics and Space Science Library, Vol. 430, Gas Accretion onto Galaxies, ed. A. Fox & R. Davé, 195
- Cantalupo et al. (2014) Cantalupo, S., Arrigoni-Battaia, F., Prochaska, J. X., Hennawi, J. F., & Madau, P. 2014, Nature, 506, 63
- Cantalupo et al. (2019) Cantalupo, S., Pezzulli, G., Lilly, S. J., et al. 2019, MNRAS, 483, 5188
- Chapman et al. (2001) Chapman, S. C., Lewis, G. F., Scott, D., et al. 2001, ApJ, 548, L17
- Chapman et al. (2004) Chapman, S. C., Scott, D., Windhorst, R. A., et al. 2004, ApJ, 606, 85
- Chapman et al. (2003) Chapman, S. C., Windhorst, R., Odewahn, S., Yan, H., & Conselice, C. 2003, ApJ, 599, 92
- Childs & Stanway (2018) Childs, H. J. T. & Stanway, E. R. 2018, MNRAS, 480, 1938
- Chonis et al. (2013) Chonis, T. S., Blanc, G. A., Hill, G. J., et al. 2013, ApJ, 775, 99
- Christensen et al. (2006) Christensen, L., Jahnke, K., Wisotzki, L., & Sánchez, S. F. 2006, A&A, 459, 717
- Chung et al. (2016) Chung, A. S., Dijkstra, M., Ciardi, B., & Gronke, M. 2016, MNRAS, 455, 884
- Codis et al. (2018) Codis, S., Jindal, A., Chisari, N. E., et al. 2018, MNRAS, 481, 4753
- Conseil et al. (2016) Conseil, S., Bacon, R., Piqueras, L., & Shepherd, M. 2016 [1612.05308]
- Davies et al. (2010) Davies, R., Agudo Berbel, A., Wiezorrek, E., Ott, T., & Förster-Schreiber, N. M. 2010, in Proc. SPIE, Vol. 7735, Ground-based and Airborne Instrumentation for Astronomy III, 77356V
- Dawson et al. (2007) Dawson, S., Rhoads, J. E., Malhotra, S., et al. 2007, ApJ, 671, 1227
- Dekel & Birnboim (2006) Dekel, A. & Birnboim, Y. 2006, MNRAS, 368, 2
- Dijkstra (2019) Dijkstra, M. 2019, Saas-Fee Advanced Course, 46, 1
- Dijkstra & Loeb (2008) Dijkstra, M. & Loeb, A. 2008, MNRAS, 386, 492
- Dijkstra & Loeb (2009) Dijkstra, M. & Loeb, A. 2009, MNRAS, 400, 1109
- Drake et al. (2019) Drake, A. B., Farina, E. P., Neeleman, M., et al. 2019, ApJ, 881, 131
- Drake et al. (2017a) Drake, A. B., Garel, T., Wisotzki, L., et al. 2017a, A&A, 608, A6
- Drake et al. (2017b) Drake, A. B., Guiderdoni, B., Blaizot, J., et al. 2017b, MNRAS, 471, 267
- Eide et al. (2018) Eide, M. B., Gronke, M., Dijkstra, M., & Hayes, M. 2018, ApJ, 856, 156
- Erb et al. (2011) Erb, D. K., Bogosavljević, M., & Steidel, C. C. 2011, ApJ, 740, L31
- Farina et al. (2019) Farina, E. P., Arrigoni-Battaia, F., Costa, T., et al. 2019, ApJ, 887, 196
- Forero-Romero et al. (2014) Forero-Romero, J. E., Contreras, S., & Padilla, N. 2014, MNRAS, 443, 1090
- Francis et al. (1996) Francis, P. J., Woodgate, B. E., Warren, S. J., et al. 1996, ApJ, 457, 490
- Geach et al. (2014) Geach, J. E., Bower, R. G., Alexander, D. M., et al. 2014, ApJ, 793, 22
- Geach et al. (2016) Geach, J. E., Narayanan, D., Matsuda, Y., et al. 2016, ApJ, 832, 37
- Ginolfi et al. (2018) Ginolfi, M., Maiolino, R., Carniani, S., et al. 2018, MNRAS, 476, 2421
- Gronke & Bird (2017) Gronke, M. & Bird, S. 2017, ApJ, 835, 207
- Gronke & Dijkstra (2016) Gronke, M. & Dijkstra, M. 2016, ApJ, 826, 14
- Haiman et al. (2000) Haiman, Z., Spaans, M., & Quataert, E. 2000, ApJ, 537, L5
- Hayashino et al. (2004) Hayashino, T., Matsuda, Y., Tamura, H., et al. 2004, AJ, 128, 2073
- Hayes et al. (2011) Hayes, M., Scarlata, C., & Siana, B. 2011, Nature, 476, 304
- Herenz et al. (2017a) Herenz, E. C., Hayes, M., Papaderos, P., et al. 2017a, A&A, 606, L11
- Herenz et al. (2017b) Herenz, E. C., Urrutia, T., Wisotzki, L., et al. 2017b, A&A, 606, A12
- Herenz & Wisotzki (2017) Herenz, E. C. & Wisotzki, L. 2017, A&A, 602, A111
- Herenz et al. (2019) Herenz, E. C., Wisotzki, L., Saust, R., et al. 2019, A&A, 621, A107
- Herenz & Wistozki (2016) Herenz, E. C. & Wistozki, L. 2016, LSDCat: Line Source Detection and Cataloguing Tool, Astrophysics Source Code Library
- Hu (1962) Hu, M. K. 1962, IRE Transactions on Information Theory, 8, 179
- Humphrey et al. (2013) Humphrey, A., Binette, L., Villar-Martín, M., Aretxaga, I., & Papaderos, P. 2013, MNRAS, 428, 563
- Humphrey et al. (2019) Humphrey, A., Villar-Martín, M., Binette, L., & Raj, R. 2019, A&A, 621, A10
- Humphrey et al. (2007) Humphrey, A., Villar-Martín, M., Fosbury, R., et al. 2007, MNRAS, 375, 705
- Hunter (2007) Hunter, J. D. 2007, Computing In Science & Engineering, 9, 90
- Husemann et al. (2018) Husemann, B., Worseck, G., Arrigoni Battaia, F., & Shanks, T. 2018, A&A, 610, L7
- Ivezić et al. (2014) Ivezić, Ž., Connelly, A. J., VanderPlas, J. T., & Gray, A. 2014, Statistics, Data Mining, and Machine Learningin Astronomy
- Joye & Mandel (2003) Joye, W. A. & Mandel, E. 2003, in Astronomical Society of the Pacific Conference Series, Vol. 295, Astronomical Data Analysis Software and Systems XII, ed. H. E. Payne, R. I. Jedrzejewski, & R. N. Hook, 489–492
- Kennicutt (1998) Kennicutt, Jr., R. C. 1998, ARA&A, 36, 189
- Kereš et al. (2005) Kereš, D., Katz, N., Weinberg, D. H., & Davé, R. 2005, MNRAS, 363, 2
- Kikuta et al. (2019) Kikuta, S., Matsuda, Y., Cen, R., et al. 2019, PASJ, 71, L2
- Kimock et al. (2020) Kimock, B., Narayanan, D., Smith, A., et al. 2020, arXiv e-prints, arXiv:2004.08397
- Kubo et al. (2015) Kubo, M., Yamada, T., Ichikawa, T., et al. 2015, ApJ, 799, 38
- Kubo et al. (2016) Kubo, M., Yamada, T., Ichikawa, T., et al. 2016, MNRAS, 455, 3333
- Laursen et al. (2009) Laursen, P., Razoumov, A. O., & Sommer-Larsen, J. 2009, ApJ, 696, 853
- Laursen et al. (2011) Laursen, P., Sommer-Larsen, J., & Razoumov, A. O. 2011, ApJ, 728, 52
- Lee & Ahn (1998) Lee, H.-W. & Ahn, S.-H. 1998, ApJ, 504, L61
- Lee et al. (2018) Lee, J., Kim, S., Jeong, H., et al. 2018, ApJ, 864, 69
- Lehmer et al. (2009a) Lehmer, B. D., Alexander, D. M., Chapman, S. C., et al. 2009a, MNRAS, 400, 299
- Lehmer et al. (2009b) Lehmer, B. D., Alexander, D. M., Geach, J. E., et al. 2009b, ApJ, 691, 687
- Libeskind et al. (2018) Libeskind, N. I., van de Weygaert, R., Cautun, M., et al. 2018, MNRAS, 473, 1195
- Loomis et al. (2018) Loomis, R. A., Öberg, K. I., Andrews, S. M., et al. 2018, AJ, 155, 182
- Mallery et al. (2012) Mallery, R. P., Mobasher, B., Capak, P., et al. 2012, ApJ, 760, 128
- Marques-Chaves et al. (2019) Marques-Chaves, R., Pérez-Fournon, I., Villar-Martín, M., et al. 2019, A&A, 629, A23
- Martin et al. (2015a) Martin, C. L., Dijkstra, M., Henry, A., et al. 2015a, ApJ, 803, 6
- Martin et al. (2014) Martin, D. C., Chang, D., Matuszewski, M., et al. 2014, ApJ, 786, 106
- Martin et al. (2015b) Martin, D. C., Matuszewski, M., Morrissey, P., et al. 2015b, Nature, 524, 192
- Martin et al. (2019) Martin, D. C., O’Sullivan, D., Matuszewski, M., et al. 2019, Nature Astronomy
- Matsuda et al. (2007) Matsuda, Y., Iono, D., Ohta, K., et al. 2007, ApJ, 667, 667
- Matsuda et al. (2004) Matsuda, Y., Yamada, T., Hayashino, T., et al. 2004, AJ, 128, 569
- Matsuda et al. (2011) Matsuda, Y., Yamada, T., Hayashino, T., et al. 2011, MNRAS, 410, L13
- Mawatari et al. (2012) Mawatari, K., Yamada, T., Nakamura, Y., Hayashino, T., & Matsuda, Y. 2012, ApJ, 759, 133
- Maxfield et al. (2002) Maxfield, L., Spinrad, H., Stern, D., Dey, A., & Dickinson, M. 2002, AJ, 123, 2321
- McLinden et al. (2013) McLinden, E. M., Malhotra, S., Rhoads, J. E., et al. 2013, ApJ, 767, 48
- Menacho et al. (2019) Menacho, V., Östlin, G., Bik, A., et al. 2019, MNRAS, 487, 3183
- Morais et al. (2017) Morais, S. G., Humphrey, A., Villar-Martín, M., et al. 2017, MNRAS, 465, 2698
- Mori et al. (2004) Mori, M., Umemura, M., & Ferrara, A. 2004, ApJ, 613, L97
- Morrison et al. (2001) Morrison, J. E., Röser, S., McLean, B., Bucciarelli, B., & Lasker, B. 2001, AJ, 121, 1752
- Morrissey et al. (2018) Morrissey, P., Matuszewski, M., Martin, D. C., et al. 2018, ApJ, 864, 93
- Nilsson et al. (2006) Nilsson, K. K., Fynbo, J. P. U., Møller, P., Sommer-Larsen, J., & Ledoux, C. 2006, A&A, 452, L23
- Ott (2012) Ott, T. 2012, QFitsView: FITS file viewer, astrophysics Source Code Library
- Ouchi et al. (2009) Ouchi, M., Ono, Y., Egami, E., et al. 2009, ApJ, 696, 1164
- Overzier (2016) Overzier, R. A. 2016, A&A Rev., 24, 14
- Palunas et al. (2004) Palunas, P., Teplitz, H. I., Francis, P. J., Williger, G. M., & Woodgate, B. E. 2004, ApJ, 602, 545
- Piqueras et al. (2017) Piqueras, L., Conseil, S., Shepherd, M., et al. 2017 [1710.03554]
- Prescott et al. (2009) Prescott, M. K. M., Dey, A., & Jannuzi, B. T. 2009, ApJ, 702, 554
- Prescott et al. (2012) Prescott, M. K. M., Dey, A., & Jannuzi, B. T. 2012, ApJ, 748, 125
- Prescott et al. (2013) Prescott, M. K. M., Dey, A., & Jannuzi, B. T. 2013, ApJ, 762, 38
- Prescott et al. (2008) Prescott, M. K. M., Kashikawa, N., Dey, A., & Matsuda, Y. 2008, ApJ, 678, L77
- Prescott et al. (2015a) Prescott, M. K. M., Martin, C. L., & Dey, A. 2015a, ApJ, 799, 62
- Prescott et al. (2015b) Prescott, M. K. M., Momcheva, I., Brammer, G. B., Fynbo, J. P. U., & Møller, P. 2015b, ApJ, 802, 32
- Rakic et al. (2011) Rakic, O., Schaye, J., Steidel, C. C., & Rudie, G. C. 2011, MNRAS, 414, 3265
- Rauch et al. (2016) Rauch, M., Becker, G. D., & Haehnelt, M. G. 2016, MNRAS, 455, 3991
- Remolina-Gutiérrez & Forero-Romero (2019) Remolina-Gutiérrez, M. C. & Forero-Romero, J. E. 2019, MNRAS, 482, 4553
- Rivera-Thorsen et al. (2019) Rivera-Thorsen, T. E., Dahle, H., Chisholm, J., et al. 2019, arXiv e-prints [arXiv:1904.08186]
- Rivera-Thorsen et al. (2017) Rivera-Thorsen, T. E., Dahle, H., Gronke, M., et al. 2017, A&A, 608, L4
- Roche et al. (2014) Roche, N., Humphrey, A., & Binette, L. 2014, MNRAS, 443, 3795
- Rosdahl & Blaizot (2012) Rosdahl, J. & Blaizot, J. 2012, MNRAS, 423, 344
- Ryabchikova et al. (2015) Ryabchikova, T., Piskunov, N., Kurucz, R. L., et al. 2015, Phys. Scr, 90, 054005
- Rybicki & Loeb (1999) Rybicki, G. B. & Loeb, A. 1999, ApJ, 520, L79
- Saez et al. (2015) Saez, C., Lehmer, B. D., Bauer, F. E., et al. 2015, MNRAS, 450, 2615
- Scarlata et al. (2009a) Scarlata, C., Colbert, J., Teplitz, H. I., et al. 2009a, ApJ, 706, 1241
- Scarlata et al. (2009b) Scarlata, C., Colbert, J., Teplitz, H. I., et al. 2009b, ApJ, 704, L98
- Schaerer (2013) Schaerer, D. 2013, in Astrophysics and Space Science Library, Vol. 396, Astrophysics and Space Science Library, ed. T. Wiklind, B. Mobasher, & V. Bromm, 345
- Schirmer et al. (2016) Schirmer, M., Malhotra, S., Levenson, N. A., et al. 2016, MNRAS, 463, 1554
- Shibuya et al. (2018) Shibuya, T., Ouchi, M., Konno, A., et al. 2018, PASJ, 70, S14
- Shimasaku et al. (2006) Shimasaku, K., Kashikawa, N., Doi, M., et al. 2006, PASJ, 58, 313
- Skrutskie et al. (2006) Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163
- Smith et al. (2019) Smith, A., Ma, X., Bromm, V., et al. 2019, MNRAS, 484, 39
- Smith et al. (2009) Smith, D. J. B., Jarvis, M. J., Simpson, C., & Martínez-Sansigre, A. 2009, MNRAS, 393, 309
- Sobral et al. (2015) Sobral, D., Matthee, J., Darvish, B., et al. 2015, ApJ, 808, 139
- Song et al. (2014) Song, M., Finkelstein, S. L., Gebhardt, K., et al. 2014, ApJ, 791, 3
- Steidel et al. (1998) Steidel, C. C., Adelberger, K. L., Dickinson, M., et al. 1998, ApJ, 492, 428
- Steidel et al. (2000) Steidel, C. C., Adelberger, K. L., Shapley, A. E., et al. 2000, ApJ, 532, 170
- Steidel et al. (2003) Steidel, C. C., Adelberger, K. L., Shapley, A. E., et al. 2003, ApJ, 592, 728
- Stewart (2017) Stewart, K. R. 2017, in Astrophysics and Space Science Library, Vol. 430, Gas Accretion onto Galaxies, ed. A. Fox & R. Davé, 249
- Stewart et al. (2017) Stewart, K. R., Maller, A. H., Oñorbe, J., et al. 2017, ApJ, 843, 47
- Stobie (1980) Stobie, R. S. 1980, in Proc. SPIE, Vol. 264, Conference on Applications of Digital Image Processing to Astronomy, ed. D. A. Elliott, 208–212
- Stobie (1986) Stobie, R. S. 1986, Pattern Recognition Letters, 4, 317
- Tamura et al. (2009) Tamura, Y., Kohno, K., Nakanishi, K., et al. 2009, Nature, 459, 61
- Taniguchi & Shioya (2000) Taniguchi, Y. & Shioya, Y. 2000, ApJ, 532, L13
- Thompson et al. (2017) Thompson, A. R., Moran, J. M., & Swenson, Jr., G. W. 2017, Interferometry and Synthesis in Radio Astronomy, 3rd Edition
- Trainor et al. (2015) Trainor, R. F., Steidel, C. C., Strom, A. L., & Rudie, G. C. 2015, ApJ, 809, 89
- Travascio et al. (2020) Travascio, A., Zappacosta, L., Cantalupo, S., et al. 2020, A&A, 635, A157
- Trebitsch et al. (2016) Trebitsch, M., Verhamme, A., Blaizot, J., & Rosdahl, J. 2016, A&A, 593, A122
- U et al. (2015) U, V., Hemmati, S., Darvish, B., et al. 2015, ApJ, 815, 57
- Uchimoto et al. (2012) Uchimoto, Y. K., Yamada, T., Kajisawa, M., et al. 2012, ApJ, 750, 116
- Umehata et al. (2019) Umehata, H., Fumagalli, M., Smail, I., et al. 2019, Science, 366, 97
- Umehata et al. (2017) Umehata, H., Matsuda, Y., Tamura, Y., et al. 2017, ApJ, 834, L16
- Urrutia et al. (2019) Urrutia, T., Wisotzki, L., Kerutt, J., et al. 2019, A&A, 624, A141
- van Hoof (2018) van Hoof, P. A. M. 2018, Galaxies, 6, 63
- Verhamme et al. (2006) Verhamme, A., Schaerer, D., & Maselli, A. 2006, A&A, 460, 397
- Vernet et al. (2017) Vernet, J., Lehnert, M. D., De Breuck, C., et al. 2017, A&A, 602, L6
- Villar-Martín et al. (2007a) Villar-Martín, M., Humphrey, A., De Breuck, C., et al. 2007a, MNRAS, 375, 1299
- Villar-Martín et al. (2007b) Villar-Martín, M., Sánchez, S. F., Humphrey, A., et al. 2007b, MNRAS, 378, 416
- Vio & Andreani (2016) Vio, R. & Andreani, P. 2016, A&A, 589, A20
- Wang & Kang (2018) Wang, P. & Kang, X. 2018, MNRAS, 473, 1562
- Weijmans et al. (2010) Weijmans, A.-M., Bower, R. G., Geach, J. E., et al. 2010, MNRAS, 402, 2245
- Weilbacher et al. (2016) Weilbacher, P. M., Streicher, O., & Palsa, R. 2016, MUSE-DRP: MUSE Data Reduction Pipeline
- Yamada et al. (2012) Yamada, T., Matsuda, Y., Kousai, K., et al. 2012, ApJ, 751, 29
- Yang et al. (2012) Yang, Y., Decarli, R., Dannerbauer, H., et al. 2012, ApJ, 744, 178
- Yang et al. (2010) Yang, Y., Zabludoff, A., Eisenstein, D., & Davé, R. 2010, ApJ, 719, 1654
- Yang et al. (2011) Yang, Y., Zabludoff, A., Jahnke, K., et al. 2011, ApJ, 735, 87
- Yang et al. (2009) Yang, Y., Zabludoff, A., Tremonti, C., Eisenstein, D., & Davé, R. 2009, ApJ, 693, 1579
- Yang et al. (2006) Yang, Y., Zabludoff, A. I., Davé, R., et al. 2006, ApJ, 640, 539
- Zackay & Ofek (2017) Zackay, B. & Ofek, E. O. 2017, ApJ, 836, 187
- Zhang et al. (2019) Zhang, H., Ouchi, M., Itoh, R., et al. 2019, arXiv e-prints [arXiv:1905.09841]
- Zheng et al. (2011) Zheng, Z., Cen, R., Weinberg, D., Trac, H., & Miralda-Escudé, J. 2011, ApJ, 739, 62