Decentralized and Communication-Free Multi-Robot
Navigation through Distributed Games
Abstract
Effective multi-robot teams require the ability to move to goals in complex environments in order to address real-world applications such as search and rescue. Multi-robot teams should be able to operate in a completely decentralized manner, with individual robot team members being capable of acting without explicit communication between neighbors. In this paper, we propose a novel game theoretic model that enables decentralized and communication-free navigation to a goal position. Robots each play their own distributed game by estimating the behavior of their local teammates in order to identify behaviors that move them in the direction of the goal, while also avoiding obstacles and maintaining team cohesion without collisions. We prove theoretically that generated actions approach a Nash equilibrium, which also corresponds to an optimal strategy identified for each robot. We show through extensive simulations that our approach enables decentralized and communication-free navigation by a multi-robot system to a goal position, and is able to avoid obstacles and collisions, maintain connectivity, and respond robustly to sensor noise.
I Introduction
Multi-robot teams are a viable solution for a variety of applications that involve distributed or simultaneous tasks, such as disaster response [1], area exploration [2], and search and rescue [3]. To effectively address such applications, robots must be able to move through complex environments and arrive at waypoints and goal positions [4]. While planning its own navigation actions, each robot must avoid obstacles as well as collisions with its teammates who are making their own movements. Accordingly, each robot needs the capability to anticipate both the actions of their local teammates and how their own actions will affect their neighbors.
In order to ensure the resilience of multi-robot teams, robots must be able to work in a decentralized manner in the real world [5, 6]. Complex environments can be dangerous, and relying on a single robot to provide centralized control can cause an entire multi-robot system to fail due to the failure of only that single robot [7]. Decentralized systems are resilient to this, continuing to operate despite failure of individual robots [8]. In addition, in a resilient multi-robot system robots should be able to operate without requiring the capability to communicate with their teammates. Multi-robot teams are often composed of low-cost robots that may lack expensive communication capabilities, or multi-robot teams may lose members due to obstacles and adversaries that interfere with communication. Together, enabling decentralized behaviors and allowing robots to operate without communication to their neighbors is vital for the success of the multi-robot team.
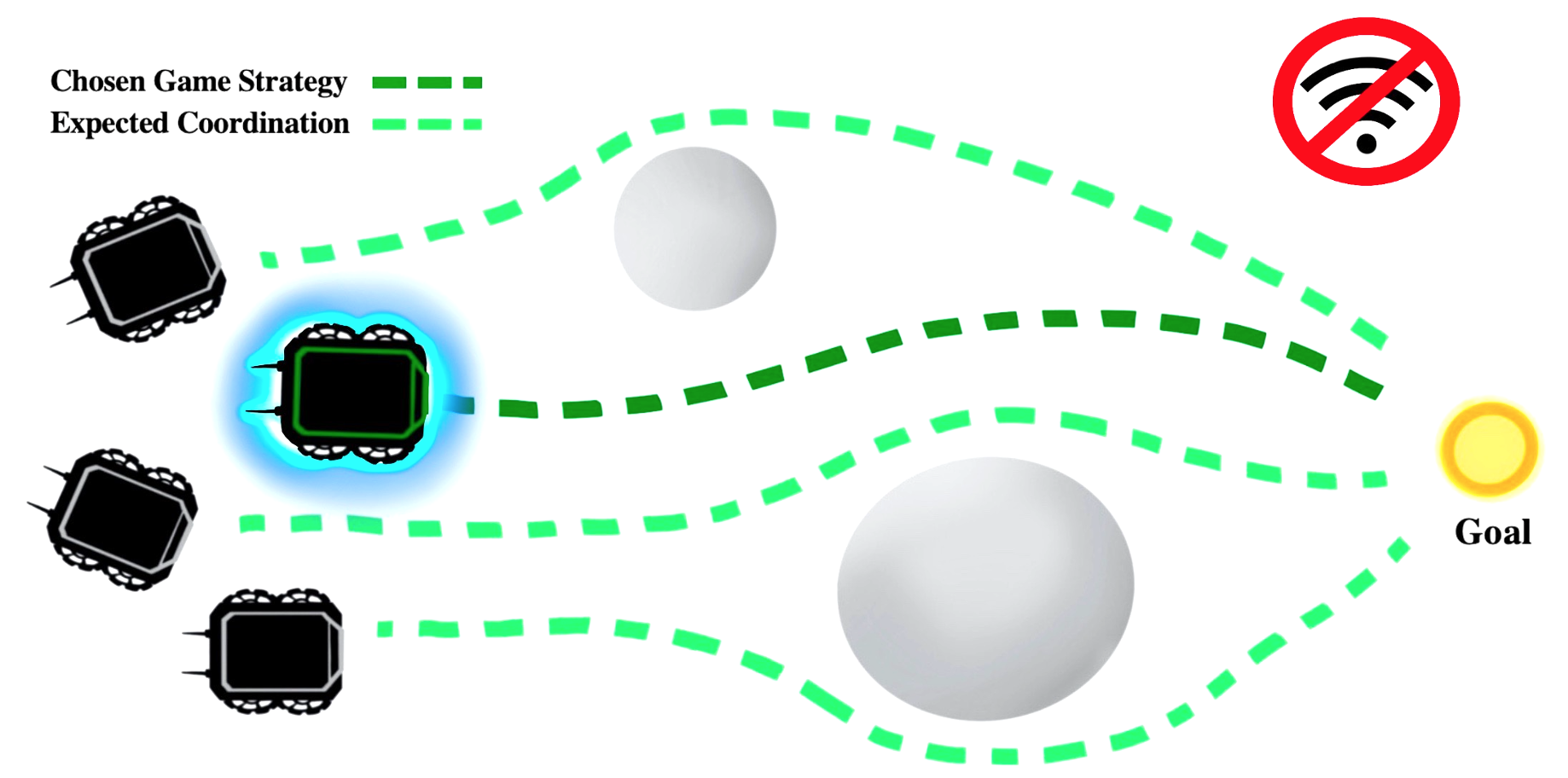
Due to its importance, multi-robot navigation has been explored by a wide variety of methods. Many methods have been designed based on centralized planning and control, which require a master robot for centralized computing and communication among all teammates [9, 10, 11]. Multiple other methods have been developed to work in a decentralized manner, but still rely on communication among robots [12, 13]. The problem of navigating multiple robots towards a goal in a completely decentralized and communication-free manner has not been well addressed, mainly because without communication it is challenging for a robot to anticipate actions of neighboring robots that dynamically make independent decisions [14, 15]. Recently, game theory has attracted increasing attention in coordinating robots without communication [16]. Game theoretic methods have been developed to identify actions in the context of their effect on teammates and adversaries for two-player applications such as driving [17, 18], or racing [19], as well as larger games in known environments for surveillance [20]. However, they have not been previously utilized to address the problem of navigating a variable size multi-robot system through a complex environment to a goal position.
In this paper, we propose a novel game theoretic and communication-free approach to multi-robot navigation. Our approach assumes that a robot is able to locally observe locations of nearby obstacles and robots in the multi-robot system, but does not require communication with teammates or knowledge of the entire system. Then, our approach models each robot and its neighboring teammates with a strategic game, formulating multi-robot navigation as a problem of solving a game for each robot at each time step. These games are solved in a distributed fashion, with each robot playing its own individual game. In each game, illustrated in Figure 1, a robot estimates the behaviors of its neighbors in order to identify movements that avoid collisions, while also progressing towards stationary or dynamic goal positions and avoiding obstacles. Collision-free actions are determined by the robot to minimize a cost function, which is theoretically proved to approach a Nash equilibrium, i.e., a state in the game where no player can unilaterally improve their outcome.
The contribution of this paper is twofold.
-
1.
We propose a novel formulation that models multi-robot navigation as multiple distributed normal-form games, allowing individual robots to form precise expectations about the actions of their neighbors and the effects of their own actions, which then enables communication-free and decentralized multi-robot navigation.
-
2.
We theoretically prove that these games approach stable Nash equilibria, which also enables each robot in the team to identify its optimal strategy without the requirement of communication with other teammates.
II Related Work
II-A Multi-Robot Maneuver
Many multi-robot navigation methods require explicit communication among robots, either to avoid collisions with obstacles by generating a consensus behavior among robots [21] or to calculate a global gradient that controls the overall shape of the multi-robot formation [9]. Several methods have used leader and follower models to navigate a multi-robot system. By controlling the movements of a number of robots, the overall behavior of the system was influenced [22]. A single leader was utilized in [23], basing its movements on influencing nearby naive agents to follow it to goal positions. A single leader was also utilized in [24] and multiple leaders were used in [10], but both required guaranteed connectivity with the leader. A consistent drawback of these models is a required communication, either for centralized control or for knowledge of follower positions in the environment.
Recently, several decentralized methods have been implemented. Graph neural networks have enabled decentralized behavior policies [13, 25], but relied on local communication that allowed information to propagate globally. Graph temporal logic was applied to swarm guidance in order to create policies that scale to large numbers of agents [26], but relies on knowledge of the overall agent distribution. Deep reinforcement learning was used to learn navigation policies around complex obstacles, allowing decentralized policies but requiring full knowledge of the state of the multi-robot system for training [27, 12].
II-B Game Theory for Robotics
Game theory seeks to explain and analyze the interaction of rational agents accommodating their own preferences and expectations. Modelling systems as games enables agents to analyze actions based on how they impact other agents. Many methods have been designed to find solutions to games, including optimization and reinforcement learning [28, 29, 30]. Game theory has been applied in several multi-robot system applications [31], due to its ability to consider the interaction of multiple agents and their competing motivations.
In autonomous driving, game theory has been applied to the problem of lane changing and merging [18]. Deep reinforcement learning was used to solve two player merging games in [17], which relied on defining drivers as proactive or passive. Roles for two players were also used in [32], which modelled lane changing as a Stackleberg game that has implicit leaders and followers. Multiple drivers were modelled in [33], which solved games through optimization by converting constraints such as collision avoidance to Lagrangian multiplier terms. In addition to lane changing, game theory was also used to generate racing trajectories which would avoid collisions while still competing with other agents [19, 34].
Despite the exploration of game theory in autonomous driving, previous research has mostly been limited to only two player systems (i.e., two cars). Recently, game theory has been applied to several multi-robot scenarios. Many approaches have considered task allocation, both with the requirement of communication [35] and enabling this without communication being necessary [36, 37, 38]. Collision avoidance has been considered, but has required the agents to be capable of communicating with each other [mylvaganam2017differential]. Multi-robot sensing and patrolling has been the other main scenario explored with game theoretic models, but approaches have required prior mappings of the environment [39, 20] or still require communication between agents [40].
Game theoretic models have been used due to their useful ability to model other agents in a system, but have not been theoretically well studied in generating navigational behaviors for a large multi-robot system without the ability to communicate between robots in complex environments.
III Our Proposed Approach
III-A Multi-Robot Navigation as a Decentralized Game
We consider a multi-robot system consisting of robots. Each robot has a position , where is the position of the -th robot. At each time step , each robot makes a decision to take an action and update its position. We define a goal that is the position that the multi-robot system is attempting to navigate to, which is known to each robot. This goal can be stationary (e.g., a fixed location in the environment) or dynamic (e.g., a moving human whom the multi-robot system must follow). We define the multi-robot system to have reached the goal state when , where is the geometric center of the robot system and is a distance threshold.
We define an ideal interaction distance between robots, where if then the -th and -th robots are at risk of collision (with the collision risk rising as approaches ) and if then there is a risk of losing cohesion between robots and (with this risk rising as moves further away from ). Successful cohesion in the multi-robot system results from maintaining . Finally, we consider a set of obstacles in the environment. Robots should take actions such that , so as to avoid collisions with obstacles. We assume each robot is able to locally perceive neighboring robots and obstacles.
Then, we formulate the problem of multi-robot navigation with multiple distributed and differentiable simultaneous strategic games , where each robot is the main player of a game based on its local environment. Each game is simultaneous as the robot plays its game at each time step without knowledge of how other robots will move. Each game is also strategic, where players are unable to coordinate through explicit communication. represents the set of players, where the cardinality of is denoted as . This set of players is defined as the main player robot and the neighboring robots within sensing distance. represents the strategy set for game , where represents the set of available strategies of the -th player. We define a strategy to be a movement update available to the -th robot given and actions
| (1) |
where satisfies and is a hyperparameter controlling the importance of the action. Values of are discussed later in the paper when consider the theoretical aspects of the games.
We define as the set of differentiable cost functions that govern the action of each player, where is the strategy of the -th player and is the strategy set of all other players, i.e. . Each player is assumed to be rational, i.e., each player will select a strategy that minimizes its cost function , while expecting that every other player is selecting strategies in that minimize their own cost functions. We denote the optimal strategy for player as and the optimal strategies for the other players as . The formulated cost function common to each player is defined as:
| (2) |
where represents a cost related to cohesion with other players within sensing distance, which can be defined as , where defines a point that is on the axis between a sensed robot and robot and is distance from robot (e.g., if the distance between robots is less than , this cost will encourage robot to move away from robot ). This is calculated from the position of robot using the estimated strategy of the neighboring robot , such that .
Hyperparameters balance the different influences and are valued such that . controls the weighting of progress towards the goal. This part of the cost function decreases as the -th robot makes progress towards the goal. controls the weighting of cohesion with neighboring robots. This cohesion cost is minimized when the -th robot is at a distance from every neighbor. controls the weighting of navigating to avoid obstacles. As robots move away from obstacles, this term minimizes the overall cost function.
III-B Solution and Analysis of the Game
In order to identify optimal behaviors for each robot, our approach constructs the described game for each robot at each time step. Algorithm 1 solves the game required to enable decentralized and communication-free multi-robot navigation. The algorithm identifies the players involved in each game , consisting of only the local neighbors of robot , and initializes a null strategy for the main player. Then, it minimizes each neighboring player’s cost function to identify optimal strategies . From this, it updates the main player’s cost function and identifies the optimal strategy that minimizes it. When Algorithm 1 converges after iteration, is adopted as the strategy for robot . In empirical evaluation, Algorithm 1 converges quickly, typically in less than iterations.
For each game, we have two objectives for the main player (denoted as robot ). First, our approach should minimize the cost function described in Eq. (2), in order to identify the best strategy for this main player. Second, our approach should generate strategies that move in the direction of a Nash equilibrium for the game, or a state where no player can improve their strategy without other players changing their strategies. If every player acts rationally, as we are assuming, then a Nash equilibrium means that robot has identified a strategy that cannot be improved upon, assuming its expectations of its neighbors’ optimal strategies are accurate.
III-B1 Minimizing the Cost Function
First, we consider the objective of minimizing the cost function for the main player of the game . We have defined our game and our cost functions as differentiable, and so we are able to utilize derivative-based methods in order to identify minima which correspond to equilibria in the game. To take advantage of this fact, we define an action that is part of a strategy with the gradient of the cost function:
| (3) |
with the exact gradient of Eq. (2) omitted for space. Just as gradient descent moves in the direction that minimizes a function, by defining our actions this way robots will take physical moves in the direction of minimizing their cost functions. Then, is normalized to be a unit vector by in order to represent real-world restrictions on robot movements at a single time step.
We now introduce constraints on to include explicit collision avoidance, both with obstacles and neighboring robots. These constraints ensure that the valid set of strategies for robot does not allow actions that would move it within the estimated position of a neighbor or obstacle:
| (4) | ||||
where is a distance defined as that where collision occurs and is dependent on the physical dimensions of the robots. Though we propose a general solution where valid movements can occur in any direction (as with a holonomic robot), additional constraints can be applied here in correspondence with a robot’s physical and kinematic limitations.
Given Eqs. (3) and (4), we prove in Theorem 1 that our approach minimizes the cost function of each robot.
Theorem 1.
The inner loop of Algorithm 1 minimizes the value of at each iteration for the main player .
Proof.
Eq. (1) computes a strategy for the -th player by . From Eq. (1), we can also define the null strategy as that with an action is equal to , meaning that returns the cost at the current position of robot . Finally, Eq. (3) computes . Combining these terms together results in:
| (5) |
Thus, for sufficiently small step sizes of , Eq. (5) is equivalent to gradient descent, and thus decreases the cost function:
| (6) |
Further proof that gradient descent decreases function values is omitted for brevity. ∎
III-B2 Approaching a Nash Equilibrium
We now prove the objective of generating strategies for all players such that each game moves in the direction of a Nash equilibrium. A Nash equilibrium results when no single agent can improve its position without other agents changing their strategies. In our case, when all agents are rational in being motivated to minimize their defined cost function, the Nash equilibrium is also the optimal solution to a game. Formally, a Nash equilibrium is achieved when an optimal strategy is identified such that:
| (7) |
Mathematically, a Nash equilibrium occurs when the first derivative of equals :
| (8) |
The set of first derivatives of all cost functions is defined as the game gradient:
It is necessary for a Nash equilibrium that the game gradient . Additionally, a stable Nash equilibrium occurs when the second derivative of each cost function is positive; that is, when the Jacobian of the cost functions is positive, or:
| (9) |
In light of the above rigorous conditions, and given that all defined by Eq. (2) are parameterized by the cascading strategies of neighboring robots (i.e., when a neighboring robot moves, it effects the cost functions of all nearby robots), a Nash equilibrium may not be theoretically possible to achieve in an individual game (i.e., since a game is played at each time step and robots can only move so far physically at a time step). Instead, we prove that strategies identified by Algorithm 1 approach a stable Nash equilibrium.
Theorem 2.
Algorithm 1 decides strategies for each player such that approaches a stable Nash equilibrium.
Proof.
In Eq. (3), we define the action taken using the gradient of the cost function. From Theorem 1, we have proven that defining our action in such a way minimizes the cost function and thus approaches . By taking this action (or an action in the direction of it, after normalizing to unit length), the -th robot moves in the direction of minimizing this cost function. As Theorem 1 holds for all , the result of applying Algorithm 1 for each robot is that:
| (10) |
Thus, our approach results in each game approaching a Nash equilibrium.
Additionally, we earlier define that the hyperparameters of the cost function must be chosen such that . In order for a Nash equilibrium to be stable, the Jacobian of the cost functions is positive, requiring . The second derivative of our cost function is:
| (11) |
Therefore, when the above condition for setting the hyperparameter values is met, the Jacobian of the cost function is positive. Thus, each robot in the game moves in the direction of a stable Nash equilibrium, which corresponds to an optimal movement for each robot. ∎
Theorems 1 and 2 prove that our approach minimizes the cost function for each robot in each game and that every game moves robots in the direction of a stable Nash equilibrium, or an optimal strategy for each robot. Thus, our approach enables optimal multi-robot navigation with our defined cost function which moves towards the goal, maintains ideal system cohesion, and avoids collisions with obstacles.
IV Experimental Results
We perform extensive evaluation of our approach, comparing it to two baseline versions (setting either or equal to 0), a greedy approach that moves towards the goal without consideration of obstacles or collisions, and a random approach to provide a worst case comparison (as widely used in other works [23, 10]). Both the greedy and random approaches are restricted to be collision-free, similar to the strategy constraints in Eq. (4). We also evaluate with added sensor noise to make robots less certain of the locations of their neighbors and obstacles. Each scenario is simulated 100 times to gain an understanding of performance with a variety of starting formations, obstacle arrangements, and goal locations.
We evaluate and compare our approach using four metrics. First, Cohesion quantifies the average distance between all robots in the system. Ideally, the cohesion distance of a system is equal to , the defined interaction distance that avoids collisions and preserves cohesion. Second, Connectivity quantifies the connectivity of the system. We define a binary adjacency matrix where the -th element equals if the -th and -th robot are within sensing distance of each other, and otherwise. We then calculate the 2nd smallest eigenvalue of the Laplacian of this, known as the algebraic connectivity of the graph [41]. We present this metric as a percentage, where indicates the system is not connected and indicates the system is fully connected. Though our approach does not require communication, connectivity has other benefits, such as relaying information about malfunctions or events. Third, the Nearest Obstacle reports the average nearest distance to an obstacle at each iteration. Fourth, the Distance to Goal shows the progress of each compared approach towards the goal position, showing at each time step.
IV-A Evaluation in Obstacle Field
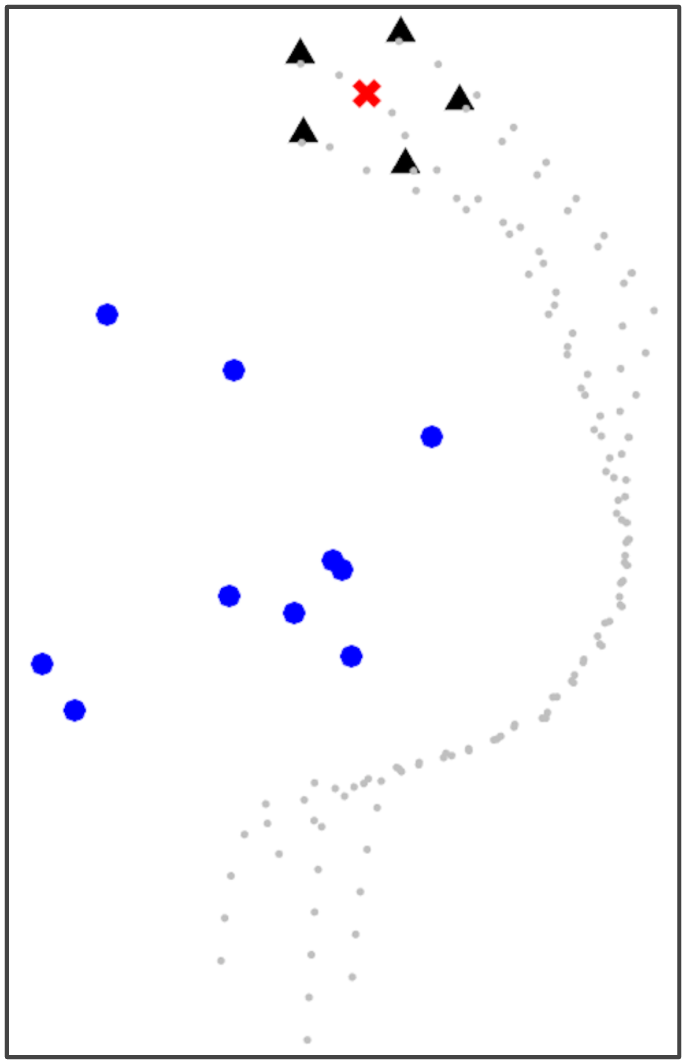
We first evaluated the Obstacle Field scenario seen in Figure 2(a), with quantitative results seen in Figure 3. We see that our full approach completes simulations with the closest to the ideal interaction distance in Figure 3(a), while maintaining it well as time progresses. The approach performs similarly well, as this still considers system cohesion. The greedy approach and approach, which do not value cohesion, result in robots grouped much too close together. Figure 3(b) displays the connectivity status achieved by different methods over the course of the simulation. Both our full approach and our approach maintain connectivity well, as does the greedy approach, which indirect causes robots to move towards one another at the goal. Our approach is less able to maintain a connected system as it moves through obstacles due to it not valuing spacing between robots, but increases connectivity as the system reaches the goal position.
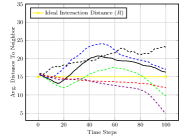
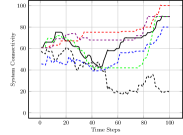
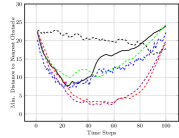
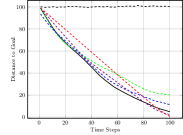
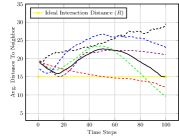
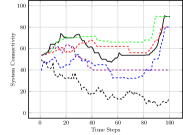
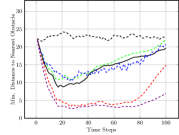
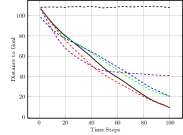
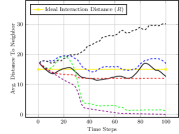
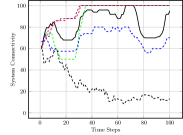
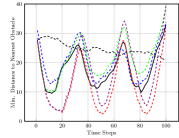
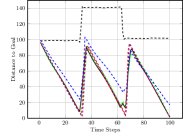
Figure 3(c) shows the average nearest obstacle to any robot. Here, we see that our approach performs poorly for the first time, with it and the greedy approach moving very near to obstacles. Our full approach and our approach perform well, as they value distance from obstacles. Finally, Figure 3(d) shows the distance to the goal over time for each approach. Only the random approach fails to make progress towards the goal. Overall, we see that our full approach performs the best, making progress towards the goal while staying close to the ideal system cohesion, maintaining connectivity, and avoiding obstacles. Each baseline version performs poorly somewhere, with maintaining a poor interaction distance and connectivity and navigating much closer to obstacles.
IV-B Evaluation in Area Obstacles
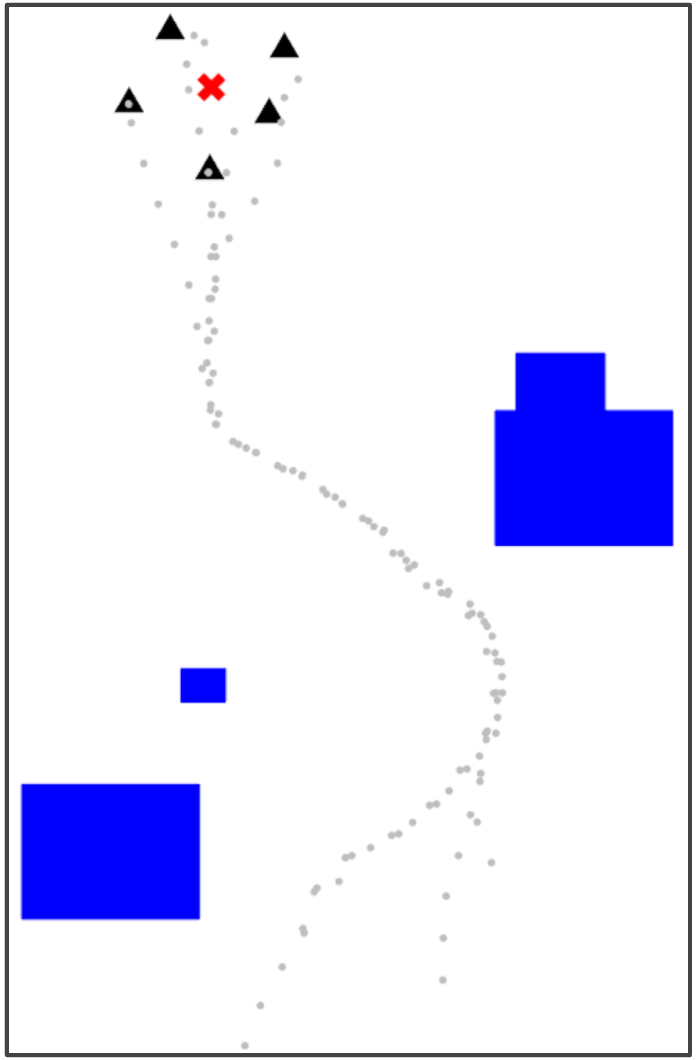
We next evaluated the Area Obstacles scenario seen in Figure 2(b), in which large square obstacles lie between the multi-robot system and the goal position. These larger obstacles interfere with robot movement much more than point obstacles, and so cause larger variation in evaluation. First, in Figure 4(a) we see that our approach is the only one capable of ending a simulation with robots distributed at the ideal cohesion distance. The alternate versions of our approach result in robots grouped much too closely together, while the greedy approach ends with robots spaced too far apart, as robots become stuck navigating through the large obstacles. Figure 4(b) shows a similar result when considering the connectivity status. All approaches struggle to maintain a fully connected system as the robots move through the large obstacles. Our approach and its variations perform the best, ensuring the multi-robot system stays together instead of separating around obstacles and resulting in the highest connectivity scores. The greedy approach, which attains high connectivity through simple point obstacles, has much more trouble maintaining connectivity as robots become stuck without an algorithm to plan navigational behaviors around the large obstacles.
In Figure 4(c) we see the distance to the nearest obstacle as robots progress through the environment. As with the Obstacle Field scenario, our full approach and the approach are able to maintain significant distance from the large obstacles, showing the importance of the obstacle avoidance term in the cost function. Again we see the and greedy approaches result in the lowest average distance to an obstacle, indicating a high risk of being stuck behind an obstacle or nearing a collision. Finally, in Figure 4(d) we see that our approach and its variations are the only approaches able to consistently reach a goal position through the Area Obstacles. These approaches, because of their ability to plan actions in the context of their environments and their neighbors, allow the multi-robot system to effectively navigate the large obstacles. The greedy approach, as can be expected by its poor maintenance of system cohesion and its nearness to obstacles, regularly fails to navigate the entire system to the goal position.
IV-C Evaluation with Dynamic Goal
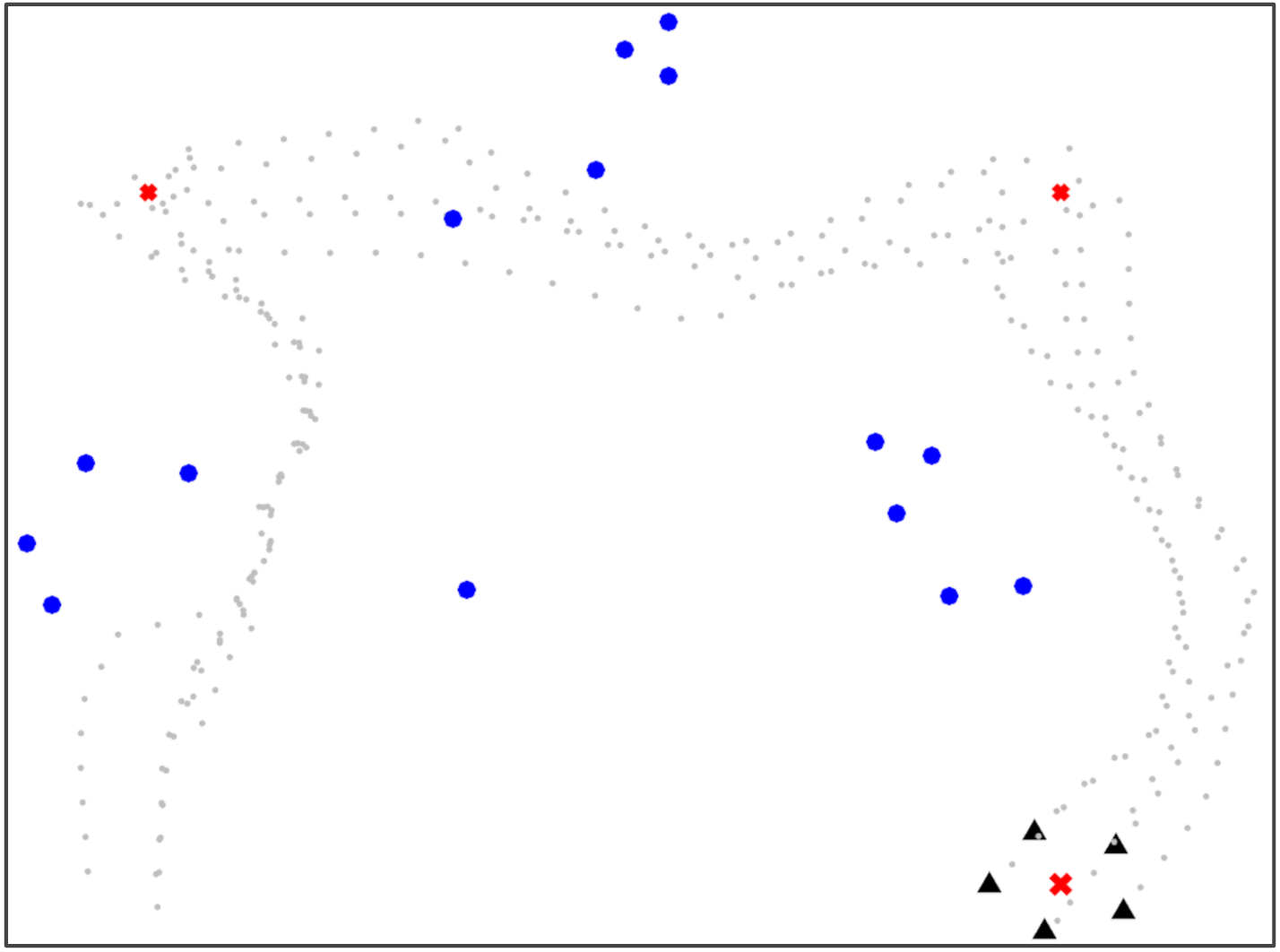
Finally, we evaluate the scenario seen in Figure 2(c) in which there is a Dynamic Goal, as if the multi-robot system was tasked with following waypoints or a human through an environment. We see similar results to earlier scenarios. The naive greedy approach causes robots to bunch together, maintaining cohesion but making the system at risk for collisions. Our baseline approaches again each struggle in the cost areas that their hyperparameters omit. When , we see that the system maintains connectivity at the expense of allowing robots to become dangerously close together. When , we see that the system maintains a safe distance between robots but risks collisions with obstacles.
However, our full approach again balances the evaluated metrics. It is able to maintain an ideal interaction distance among robots, keeping them at a safe distance to avoid collisions but still achieving full connectivity. This full approach is also able to maintain a safe distance from obstacles in the environment, while still making progress towards the waypoints.
IV-D Robustness to Noise
In order to understand how our approach would perform with the noise inherent in physical robot operations (i.e., uncertainty about the positions of detected neighbors and obstacles), we conduct evaluations with locations in the environment modified with sensor noise. Results with this added noise can be seen in blue in Figures 3-5. We can see that our approach does lose performance when noise is added, but is still able to outperform both of our baseline methods and the greedy method. Due to robots being able to play their games before each action, errors in observation do not build up or persist and cause long term issues. Additionally, as our approach is decentralized, errors from the added noise do not propagate through the system, and are restricted to individual robots. Accordingly, our approach is very robust to the sensor and movement noise encountered in physical multi-robot systems.
V Conclusion
In this paper, we propose a novel game theoretic method for decentralized and communication-free multi-robot navigation. Our approach is proven to identify strategies that approach a stable Nash equilibrium, resulting in optimal behaviors for each robot. We show that our approach enables a multi-robot system to navigate to a goal position, with changes to hyperparameter values showing the importance of terms that encourage both avoiding obstacles and collisions with neighboring robots and maintaining connectivity, while remaining robust to errors from sensor noise.
References
- [1] M. Erdelj, M. Król, and E. Natalizio, “Wireless sensor networks and multi-UAV systems for natural disaster management,” Computer Networks, vol. 124, pp. 72–86, 2017.
- [2] B. Bayat, N. Crasta, A. Crespi, A. M. Pascoal, and A. Ijspeert, “Environmental monitoring using autonomous vehicles: a survey of recent searching techniques,” Current Opinion in Biotechnology, vol. 45, pp. 76–84, 2017.
- [3] A. Goldhoorn, A. Garrell, R. Alquézar, and A. Sanfeliu, “Searching and tracking people with cooperative mobile robots,” Autonomous Robots, vol. 42, no. 4, pp. 739–759, 2018.
- [4] T. Manderson, J. C. Gamboa, S. Wapnick, J.-F. Tremblay, F. Shkurti, D. Meger, and G. Dudek, “Vision-based goal-conditioned policies for underwater navigation in the presence of obstacles,” in Robotics: Science and Systems (RSS), 2020.
- [5] M. Smyrnakis and S. M. Veres, “Coordination of control in robot teams using game-theoretic learning,” IFAC Proceedings Volumes, vol. 47, no. 3, pp. 1194–1202, 2014.
- [6] J. Banfi, N. Basilico, and S. Carpin, “Optimal redeployment of multirobot teams for communication maintenance,” in International Conference on Intelligent Robots and Systems (IROS), 2018.
- [7] W. Luo and K. Sycara, “Minimum k-connectivity maintenance for robust multi-robot systems,” in International Conference on Intelligent Robots and Systems (IROS), 2019.
- [8] J. Li, W. Abbas, M. Shabbir, and X. Koutsoukos, “Resilient distributed diffusion for multi-robot systems using centerpoint,” in Robotics: Science and Systems (RSS), 2020.
- [9] M. Aranda, J. A. Corrales, and Y. Mezouar, “Deformation-based shape control with a multirobot system,” in International Conference on Robotics and Automation (ICRA), 2019.
- [10] B. Reily, C. Reardon, and H. Zhang, “Leading multi-agent teams to multiple goals while maintaining communication,” in Robotics: Science and Systems (RSS), 2020.
- [11] A. Varava, K. Hang, D. Kragic, and F. T. Pokorny, “Herding by caging: a topological approach towards guiding moving agents via mobile robots.,” in Robotics: Science and Systems (RSS), 2017.
- [12] J. Lin, X. Yang, P. Zheng, and H. Cheng, “Connectivity guaranteed multi-robot navigation via deep reinforcement learning,” in Conference on Robot Learning (CoRL), 2019.
- [13] E. Tolstaya, F. Gama, J. Paulos, G. Pappas, V. Kumar, and A. Ribeiro, “Learning decentralized controllers for robot swarms with graph neural networks,” in Conference on Robot Learning (CoRL), 2019.
- [14] R. Emery-Montemerlo, Game-Theoretic Control for Robot Teams. PhD thesis, Rutgers, The State University of New Jersey, 2005.
- [15] R. Emery-Montemerlo, G. Gordon, J. Schneider, and S. Thrun, “Game theoretic control for robot teams,” in International Conference on Robotics and Automation (ICRA), 2005.
- [16] S. Bansal, J. Xu, A. Howard, and C. Isbell, “A bayesian framework for nash equilibrium inference in human-robot parallel play,” in Robotics: Science and Systems (RSS), 2020.
- [17] G. Ding, S. Aghli, C. Heckman, and L. Chen, “Game-theoretic cooperative lane changing using data-driven models,” in International Conference on Intelligent Robots and Systems (IROS), 2018.
- [18] A. Liniger and L. Van Gool, “Safe motion planning for autonomous driving using an adversarial road model,” in Robotics: Science and Systems (RSS), 2020.
- [19] M. Wang, Z. Wang, J. Talbot, J. C. Gerdes, and M. Schwager, “Game theoretic planning for self-driving cars in competitive scenarios,” in Robotics: Science and Systems (RSS), 2019.
- [20] E. Hernández, A. Barrientos, and J. Del Cerro, “Selective smooth fictitious play: An approach based on game theory for patrolling infrastructures with a multi-robot system,” Expert Systems with Applications, vol. 41, no. 6, pp. 2897–2913, 2014.
- [21] J. Alonso-Mora, E. Montijano, M. Schwager, and D. Rus, “Distributed multi-robot formation control among obstacles: A geometric and optimization approach with consensus,” in International Conference on Robotics and Automation (ICRA), 2016.
- [22] L. Sabattini, C. Secchi, M. Lotti, and C. Fantuzzi, “Coordinated motion for multi-robot systems under time varying communication topologies,” in International Conference on Robotics and Automation (ICRA), 2016.
- [23] M. Kwon, M. Li, A. Bucquet, and D. Sadigh, “Influencing leading and following in human-robot teams,” in Robotics: Science and Systems (RSS), 2019.
- [24] C. Vrohidis, C. P. Bechlioulis, and K. J. Kyriakopoulos, “Safe decentralized and reconfigurable multi-agent control with guaranteed convergence,” in International Conference on Robotics and Automation (ICRA), 2017.
- [25] A. Khan, E. Tolstaya, A. Ribeiro, and V. Kumar, “Graph policy gradients for large scale robot control,” in Conference on Robot Learning (CoRL), 2019.
- [26] F. Djeumou, Z. Xu, and U. Topcu, “Probabilistic swarm guidance subject to graph temporal logic specifications,” in Robotics: Science and Systems (RSS), 2020.
- [27] J. Lin, X. Yang, P. Zheng, and H. Cheng, “End-to-end decentralized multi-robot navigation in unknown complex environments via deep reinforcement learning,” in International Conference on Mechatronics and Automation (ICMA), 2019.
- [28] P. Mertikopoulos and W. H. Sandholm, “Learning in games via reinforcement and regularization,” Mathematics of Operations Research, vol. 41, no. 4, pp. 1297–1324, 2016.
- [29] M. T. Basar, A. Haurie, and G. Zaccour, “Nonzero-sum differential games,” in Handbook of Dynamic Game Theory, pp. 61–110, 2018.
- [30] J. Y. Halpern and Y. Moses, “Characterizing solution concepts in terms of common knowledge of rationality,” International Journal of Game Theory, vol. 46, no. 2, pp. 457–473, 2017.
- [31] C. Robin and S. Lacroix, “Multi-robot target detection and tracking: taxonomy and survey,” Autonomous Robots, vol. 40, no. 4, pp. 729–760, 2016.
- [32] J. F. Fisac, E. Bronstein, E. Stefansson, D. Sadigh, S. S. Sastry, and A. D. Dragan, “Hierarchical game-theoretic planning for autonomous vehicles,” in International Conference on Robotics and Automation (ICRA), 2019.
- [33] S. L. Cleac’h, M. Schwager, and Z. Manchester, “Algames: A fast solver for constrained dynamic games,” in Robotics: Science and Systems (RSS), 2020.
- [34] Z. Wang, R. Spica, and M. Schwager, “Game theoretic motion planning for multi-robot racing,” in Distributed Autonomous Robotic Systems, pp. 225–238, 2019.
- [35] J. J. Roldán, J. Del Cerro, and A. Barrientos, “Should we compete or should we cooperate? applying game theory to task allocation in drone swarms,” in International Conference on Intelligent Robots and Systems (IROS), 2018.
- [36] A. Kanakia, B. Touri, and N. Correll, “Modeling multi-robot task allocation with limited information as global game,” Swarm Intelligence, vol. 10, no. 2, pp. 147–160, 2016.
- [37] T. Gao and S. Bhattacharya, “Multirobot charging strategies: A game-theoretic approach,” IEEE Robotics and Automation Letters, vol. 4, no. 3, pp. 2823–2830, 2019.
- [38] W. Dai, H. Lu, J. Xiao, and Z. Zheng, “Task allocation without communication based on incomplete information game theory for multi-robot systems,” Journal of Intelligent & Robotic Systems, vol. 94, no. 3-4, pp. 841–856, 2019.
- [39] Y. Meng, “Multi-robot searching using game-theory based approach,” International Journal of Advanced Robotic Systems, vol. 5, no. 4, p. 44, 2008.
- [40] V. Ramaswamy, S. Moon, E. W. Frew, and N. Ahmed, “Mutual information based communication aware path planning: A game theoretic perspective,” in International Conference on Intelligent Robots and Systems (IROS), 2016.
- [41] M. Fiedler, “Algebraic connectivity of graphs,” Czechoslovak Mathematical Journal, vol. 23, no. 2, pp. 298–305, 1973.