Data-Free Adversarial Knowledge Distillation for Graph Neural Networks
Abstract
Graph neural networks (GNNs) have been widely used in modeling graph structured data, owing to its impressive performance in a wide range of practical applications. Recently, knowledge distillation (KD) for GNNs has enabled remarkable progress in graph model compression and knowledge transfer. However, most of the existing KD methods require a large volume of real data, which are not readily available in practice, and may preclude their applicability in scenarios where the teacher model is trained on rare or hard to acquire datasets. To address this problem, we propose the first end-to-end framework for data-free adversarial knowledge distillation on graph structured data (DFAD-GNN). To be specific, our DFAD-GNN employs a generative adversarial network, which mainly consists of three components: a pre-trained teacher model and a student model are regarded as two discriminators, and a generator is utilized for deriving training graphs to distill knowledge from the teacher model into the student model. Extensive experiments on various benchmark models and six representative datasets demonstrate that our DFAD-GNN significantly surpasses state-of-the-art data-free baselines in the graph classification task.
1 Introduction
An increasing number of machine learning tasks require dealing with a large amount of graph data, which capture rich and complex relationships among potentially billions of elements. Graph Neural Networks (GNNs) have become an effective way to address the graph learning problem by converting the graph data into a low dimensional space while keeping both the structural and property information to the maximum extent. Recently, the rapid evolution of GNNs has led to a growing number of new architectures as well as novel applications Lu et al. (2021); Sun et al. (2018); Wu et al. (2021).
However, training a powerful GNN often requires heavy computation and storage. Hence it is hard to deploy them into resource-constrained devices, such as mobile phones. There has been a large literature Bahri et al. (2021) aiming to compress and speed-up the cumbersome GNNs into lightweight ones. Among those methods, knowledge distillation Hinton et al. (2015) is one of the most popular paradigms for learning a portable student model from the pre-trained complicated teacher by directly imitating its outputs.
Knowledge distillation (KD) is proposed by Hinton et al. Hinton et al. (2015) for supervising the training of a compact yet efficient student model by capturing and transferring the knowledge from a large complicated teacher model. KD has received significant attention from the community in the recent years Yang et al. (2021); Gou et al. (2021). Despite its successes, KD in its classical form has a critical limitation. It assumes that the real training data is still available in the distillation phase. However, in practice, the original training data is often unavailable due to privacy concerns. Besides, many large models are trained on millions or even billions of graphs Lu et al. (2021). While the pre-trained models might be made available for the community at large, making training data available also poses a lot of technical and policy challenges.
An effective way to avert the above-mentioned issue is using the synthetic graphs, i.e., data-free knowledge distillation Lopes et al. (2017); Liu et al. (2021). Just as “data free” implies, there is no training data. Instead, the data is reversely generated from the pre-trained models. Data-free distillation has received a lot of attention in the field of computer vision Fang et al. (2019); Lopes et al. (2017); Fang et al. (2021), which is however rarely been explored in graph mining. Note that Deng et al. Deng and Zhang (2021) have made some pilot studies on this problem and proposed graph-free knowledge distillation (GFKD). Unfortunately, GFKD is not an end-to-end approach. It only takes the fixed teacher model into account, ignoring the information from the student model when generating graphs. Moreover, their method is based on the assumption that an appropriate graph usually has a high degree of confidence in the teacher model. In fact, the model maps the graphs from the data space to a very small output space, thus losing a large amount of information. Therefore, these generated graphs are not very useful for distilling the teacher model efficiently which leads to an unsatisfactory performance.
In this work, we propose a novel data-free adversarial knowledge distillation framework for GNNs (DFAD-GNN). DFAD-GNN uses a knowledge distillation method based on GAN Goodfellow et al. (2014). As illustrated in Figure 1, DFAD-GNN contains one generator and two discriminators: one fixed discriminator is the pre-trained teacher model, the other is the compact student model that we aim to learn. The generator generates graphs to help transfer teachers’ knowledge to students. Unlike previous work Deng and Zhang (2021), our generator can fully utilize both the intrinsic statistics from the pre-trained teacher model and the customizable information from the student model, which can help generate high quality and diverse training data to improve the student model’s generalizability. The contributions of our proposed framework can be summarized as follows: 1) We study a valuable yet intractable problem: how to distill a portable and efficient student model from a pre-trained teacher model when the original training data is not available; 2) We propose a novel data-free adversarial knowledge distillation framework for GNNs (DFAD-GNN) in order to train a compact student model using the generated graphs and a fixed teacher model. To the best of our knowledge, DFAD-GNN is the first end-to-end framework for data-free knowledge distillation on graph structured data; and 3) Extensive experiments demonstrate that our proposed framework significantly outperforms existing state-of-the-art data-free methods. DFAD-GNN can successfully distill a student model with 81.8%-94.7% accuracy of the teacher model on all six datasets.
2 Preliminary and Related Work
2.1 Graph Neural Networks
Graph Neural Networks (GNNs) have received considerable attention for a wide variety of tasks Wu et al. (2020); Zhou et al. (2020). Generally, GNN models can be unified by a neighborhood aggregation or message passing schema Gilmer et al. (2017), where the representation of each node is learned by iteratively aggregating the embeddings (“message”) of its neighbors.
As one of the most influential GNN models, Graph Convolutional Network (GCN) Kipf and Welling (2016) performs a linear approximation to graph convolutions. Graph Attention Network (GAT) Veličković et al. (2017) introduces an attention mechanism that allows weighing nodes in the neighborhood differently during the aggregation step. GraphSAGE Hamilton et al. (2017) is a comprehensive improvement on the original GCN which replaced full graph Laplacian with learnable aggregation functions. Graph Isomorphism Network (GIN) Xu et al. (2018) uses a simple but expressive injective multiset function for neighbor aggregation. These GNNs above will be employed as our teacher models and student models in the experiments.
2.2 Knowledge Distillation
Knowledge distillation (KD) aims to transfer the knowledge of a (larger) teacher model to a (smaller) student model Hinton et al. (2015); Wu et al. (2022). It was originally introduced to reduce the size of models deployed on devices with limited computational resources. Since then, this line of research has attracted a lot of attention Gou et al. (2021). Recently, there are a few attempts that try to combine knowledge distillation with graph convolutional networks (GCNs). Yang et al. Yang et al. (2021) proposed a knowledge distillation framework which can extract the knowledge of an arbitrary teacher model and inject it into a well-designed student model. Jing et al. Jing et al. (2021) proposed to learn a lightweight student GNN that masters the complete set of expertise of multiple heterogeneous teachers. These works aim to improve the performance of student models on semi-supervised node classification task, rather than the graph classification task we considered in this work. Furthermore, although the above-mentioned methods obtained promising results, they cannot be effectively launched without the original training dataset. In practice, the training dataset could be unavailable for some reasons, e.g. transmission limitations, privacy, etc. Therefore, it is necessary to consider a data-free approach for compressing neural networks.
Techniques addressing data-free knowledge distillation have relied on training a generative model to synthesize fake data. One recent work named graph-free KD (GFKD) Deng and Zhang (2021) has proposed a data-free knowledge distillation for graph neural network. GFKD learns graph topology structures for knowledge distillation by modeling them with a multinomial distribution. The training processes include two independent steps: (1) first, it uses a pre-trained teacher model to generate fake graphs; (2) afterwards, it uses these fake graphs to distill knowledge into the compact student model. However, those fake graphs are optimized by an invariant teacher model without considering the student model. Therefore, they are not very useful for distilling the student model efficiently. In order to generate high quality diverse training data to improve the student model’s generalizability, we propose a data-free adversarial knowledge distillation framework for GNNs (DFAD-GNN). Our generator is trained end-to-end which not only uses the pre-trained teacher’s intrinsic statistics but also obtains the discrepancy between teacher model and student model. We remark that the key differences between GFKD and our model lies in the training process and the generator.
2.3 Graph Generation
Data-free knowledge distillation involves the generation of training data. Motivated by the power of Generative Adversarial Networks (GANs) Goodfellow et al. (2014), researchers have used them for generating graphs. Bojchevski et al. proposed NetGAN Bojchevski et al. (2018), which uses the GAN framework to generate random walks on graphs. De Cao and Kipf proposed MolGAN De Cao and Kipf (2018), which generates molecular graphs using a simple multi-layer perceptron (MLP).
In this work, we build on a min-max game between two adversaries who try to optimize opposite loss functions. This approach is analogous to the optimization performed in GANs to train the generator and discriminator. The key difference is that GANs are generally trained to recover an underlying fixed data distribution. However, our generator chases a moving target: the distribution of data which is most indicative of the discrepancies of the current student model and its teacher model.

3 DFAD-GNN Framework
As shown in Figure 1, DFAD-GNN mainly consists of three components: one generator and two discriminators. One fixed discriminator is the pre-trained teacher model , the other is the compact student model that we aim to learn. More specifically, the generator takes samples from a prior distribution and generates fake graphs. Then the generated graphs are used to train a student model under the supervision of the teacher model.
3.1 Generator
The generator is used to synthesize fake graphs that maximize the disagreement between the teacher and the student . takes -dimensional vectors sampled from a standard normal distribution and outputs graphs. For each , outputs an object: that defines node features, where is the node number and is node feature dimension. Then we calculate adjacency matrix as follows:
| (1) |
where is the logistic sigmoid function. We transform the range of from to with a threshold . If the element in is larger than , it is set as 1, otherwise 0.
The loss function used for is the same as that used for , except that the goal is to maximize it. In other words, the student is trained to match the teacher’s predictions and the generator is trained to generate difficult graphs for the student. The training process can be formulated as:
| (2) |
where indicates the discrepancy between the teacher and the student . If generator keeps generating simple and duplicate graphs, student model will fit these graphs, resulting in a very low model discrepancy between student model and teacher model. In this case, the generator is forced to generate difficult and different graphs to enlarge the discrepancy.
3.2 Adversarial Distillation
Overall, the adversarial training process consists of two stages: the distillation stage that minimizes the discrepancy ; and the generation stage that maximizes the discrepancy , as shown in Figure 1. We detail each stage as follows.
Input: A pre-trained teacher model,
Output: A comparable student model,
3.2.1 Distillation Stage
In this stage, we fix the generator and only update the student in the discriminator. We sample a batch of random noises and construct fake graphs with generator . Then each graph is fed to both the teacher and the student model to produce the output and , where is a vector indicating the scores of different categories.
In our approach, the choice of loss involves similar factors to those outlined in GANs: multiple works have discussed the problem of vanishing gradients as the discriminator becomes strong in case of GAN training Arjovsky and Bottou (2017). Most prior work in model distillation optimized over the KullbackLeibler Divergence (KLD) and Mean Square Error (MSE) between the student and the teacher model. However, as the student model matches more closely the teacher model, these two loss functions tend to suffer from vanishing gradients. Specifically, back-propagating such vanishing gradients through the generator can harm its learning. For our approach, we minimize the Mean Absolute Error (MAE) between and , which provides stable gradients for the generator so that the vanishing gradients can be alleviated. In our experiment, we empirically find that this significantly improves student’s performance over other possible losses. Now we can define the loss function for distillation stage as follows:
| (3) |
3.2.2 Generation Stage
The goal of the generation stage is to push the generation of new graphs. In this stage, we fix the two discriminators and only update the generator. We encourage the generator to produce more confusing training graphs. The loss function used for generator is the same as for student except that the goal is to maximize it:
| (4) |
With the generation loss, the error first back-propagates through the discriminator (the teacher and the student model), then through the generator to optimize it.
3.3 Optimization
The whole distillation process is summarized in Algorithm 1. DFAD-GNN trains the student and the generator by iterating over the distillation stage and the generation stage. Based on the learning progress of the student model, the generator crafts new graphs to further estimate the model discrepancy. The competition in this adversarial game drives the generator to discover more knowledge. In the distillation stage, we update the student model for times so as to ensure its convergence. Note that compared with the conventional method GFKD Deng and Zhang (2021), the time complexity of DFAD-GNN mainly lies on the matrix multiplication of the generator, i.e., where is the number of nodes and is the node feature dimension. Although our method has higher time complexity, the performances are much better. In addition, because there are not too many nodes in most real world graph-level applications (usually less than 100), we remark that our complexity is acceptable in practice.
4 Experiments
4.1 Datasets
We adopt six graph classification benchmark datasets including three bioinformatics graph datasets, i.e., MUTAG, PTC_MR, and PROTEINS, and three social network graph datasets, i.e., IMDB-BINARY, COLLAB, and REDDIT-BINARY. The statistics of these datasets are summarized in Table 1. To remove the unwanted bias towards the training data, for all experiments on these datasets, we evaluate the model performance with a 10-fold cross validation setting, where the dataset split is based on the conventionally used training/test splits Niepert et al. (2016); Zhang et al. (2018); Xu et al. (2018) with LIBSVM Chang and Lin (2011). We report the average and standard deviation of validation accuracies across the 10 folds within the cross-validation.
| Dataset | #Graphs | #Classes | Avg#Graph Size |
|---|---|---|---|
| MUTAG | 188 | 2 | 17.93 |
| PTC_MR | 344 | 2 | 14.29 |
| PROTEINS | 1113 | 2 | 39.06 |
| IMDB-BINARY | 1000 | 2 | 19.77 |
| COLLAB | 5000 | 3 | 74.49 |
| REDDIT-BINARY | 2000 | 2 | 427.62 |
| Datasets | MUTAG | PTC_MR | PROTEINS | IMDB-BINARY | COLLAB | REDDIT-Binary | ||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Teacher | GIN-5-128 | GIN-5-128 | GIN-5-128 | GIN-5-128 | GIN-5-128 | GIN-5-128 | ||||||||||||||||||||||||||||||
| 96.7±3.7 | 75.0±3.5 | 78.3±2.9 | 80.1±3.7 | 83.5±1.2 | 92.2±1.2 | |||||||||||||||||||||||||||||||
| Student | GIN-5-32 | GIN-1-128 | GIN-5-32 | GIN-1-128 | GIN-5-32 | GIN-1-128 | GIN-5-32 | GIN-1-128 | GIN-5-32 | GIN-1-128 | GIN-5-32 | GIN-1-128 | ||||||||||||||||||||||||
| (6.7%) | (20.6%) | (6.7%) | (20.6%) | (6.7%) | (20.6%) | (6.7%) | (20.6%) | (6.7%) | (20.6%) | (6.7%) | (20.6%) | |||||||||||||||||||||||||
| KD | 96.7±5.1 | 95.3±4.6 | 76.6±5.9 | 77.0±8.1 | 76.0±5.1 | 78.8±3.2 | 80.4±3.4 | 82.0±3.5 | 82.8±1.6 | 83.6±1.9 | 90.4±2.2 | 91.7±1.9 | ||||||||||||||||||||||||
| RANDOM | 67.9±8.0 | 62.9±8.5 | 60.1±9.1 | 61.0±8.5 | 60.8±9.4 | 60.2±9.2 | 61.6±5.8 | 60.2±6.4 | 57.3±4.3 | 59.9±3.4 | 69.6±4.3 | 64.5±5.6 | ||||||||||||||||||||||||
| GFKD | 77.8±11.1 | 72.6±10.4 | 65.2±7.7 | 62.1±7.0 | 61.3±4.0 | 62.5±3.6 | 67.2±5.5 | 65.1±5.4 | 64.7±3.3 | 64.1±3.0 | 70.2±3.4 | 68.1±3.9 | ||||||||||||||||||||||||
| DFAD-GNN | 87.8±6.9 | 85.6±6.7 | 71.0±3.1 | 69.7±3.5 | 70.0±4.2 | 69.9±5.3 | 73.1±4.3 | 74.9±3.1 | 72.1±2.7 | 71.2±2.0 | 75.4±2.4 | 75.7±2.3 | ||||||||||||||||||||||||
| (90.8%) | (88.5%) | (94.7%) | (92.9%) | (89.4%) | (89.3%) | (91.3%) | (93.5%) | (86.3%) | (85.3%) | (81.8%) | (82.1%) | |||||||||||||||||||||||||
| Student | GCN-5-32 | GCN-1-128 | GCN-5-32 | GCN-1-128 | GCN-5-32 | GCN-1-128 | GCN-5-32 | GCN-1-128 | GCN-5-32 | GCN-1-128 | GCN-5-32 | GCN-1-128 | ||||||||||||||||||||||||
| (3.3%) | (10.6%) | (3.3%) | (10.6%) | (3.3%) | (10.6%) | (3.3%) | (10.6%) | (3.3%) | (10.6%) | (3.3%) | (10.6%) | |||||||||||||||||||||||||
| KD | 86.7±9.4 | 82.2±10.2 | 70.9±7.3 | 70.0±6.9 | 74.5±3.8 | 75.5±4.0 | 79.7±3.6 | 81.1±3.2 | 81.7±1.1 | 82.1±2.2 | 88.2±2.3 | 87.8±2.4 | ||||||||||||||||||||||||
| RANDOM | 58.9±19.3 | 55.6±21.1 | 59.4±10.1 | 55.6±8.1 | 59.2±8.4 | 57.9±8.0 | 52.3±2.4 | 55.1±2.8 | 55.6±4.4 | 55.3±5.5 | 59.3±3.7 | 57.7±4.2 | ||||||||||||||||||||||||
| GFKD | 70.0±11.2 | 69.1±10.3 | 65.0±8.2 | 61.9±8.5 | 62.9±7.7 | 61.4±8.8 | 63.5±5.3 | 65.2±5.7 | 65.7±2.6 | 64.2±1.9 | 65.3±2.6 | 65.1±2.7 | ||||||||||||||||||||||||
| DFAD-GNN | 74.1±9.3 | 76.4±8.8 | 67.7±2.9 | 67.9±3.5 | 67.2±5.0 | 65.7±3.7 | 69.5±4.8 | 68.6±5.4 | 70.3±1.2 | 69.8±1.8 | 69.9±1.3 | 70.4±1.9 | ||||||||||||||||||||||||
| (76.2%) | (79.0%) | (90.3%) | (90.5%) | (85.8%) | (83.9%) | (86.8%) | (85.6%) | (84.2%) | (83.6%) | (75.8%) | (76.4%) | |||||||||||||||||||||||||
| Student | GAT-5-32 | GAT-1-128 | GAT-5-32 | GAT-1-128 | GAT-5-32 | GAT-1-128 | GAT-5-32 | GAT-1-128 | GAT-5-32 | GAT-1-128 | GAT-5-32 | GAT-1-128 | ||||||||||||||||||||||||
| (164.6%) | (84.5%) | (164.6%) | (84.5%) | (164.6%) | (84.5%) | (164.6%) | (84.5%) | (164.6%) | (84.5%) | (164.6%) | (84.5%) | |||||||||||||||||||||||||
| KD | 87.8±8.9 | 82.2±10.2 | 73.2±5.5 | 69.7±6.8 | 76.6±3.4 | 74.5±4.6 | 80.7±3.0 | 79.9±2.8 | 80.3±1.5 | 81.5±1.2 | 90.9±1.9 | 90.6±2.0 | ||||||||||||||||||||||||
| RANDOM | 63.9±17.3 | 57.5±20.3 | 60.0±7.1 | 59.4±6.7 | 59.8±6.4 | 60.6±5.6 | 53.6±4.5 | 52.9±2.1 | 56.3±3.6 | 58.1±3.3 | 57.6±4.1 | 55.8±4.3 | ||||||||||||||||||||||||
| GFKD | 72.5±13.8 | 70.4±11.9 | 63.2±6.5 | 62.7±7.0 | 62.2±6.8 | 62.8±7.9 | 63.7±4.6 | 64.4±5.2 | 66.2±2.3 | 64.9±3.7 | 67.8±3.5 | 68.3±4.4 | ||||||||||||||||||||||||
| DFAD-GNN | 76.9±6.9 | 77.3±5.9 | 66.4±3.9 | 68.0±4.7 | 67.8±4.9 | 66.0±4.7 | 68.4±3.9 | 68.0±4.7 | 71.1±1.6 | 70.5±2.5 | 73.5±2.6 | 72.3±2.7 | ||||||||||||||||||||||||
| (79.5%) | (79.9%) | (88.5%) | (90.7%) | (86.6%) | (84.3%) | (85.4%) | (84.9%) | (85.1%) | (84.4%) | (79.7%) | (78.4%) | |||||||||||||||||||||||||
| Student |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
| (5.9%) | (11.1%) | (5.9%) | (11.1%) | (5.9%) | (11.1%) | (5.9%) | (11.1%) | (5.9%) | (11.1%) | (5.9%) | (11.1%) | |||||||||||||||||||||||||
| KD | 87.8±12.1 | 82.8±9.8 | 75.6±5.3 | 70.3±6.6 | 76.3±3.5 | 75.7±4.5 | 80.8±2.6 | 80.1±2.5 | 81.2±1.7 | 81.5±2.5 | 90.1±1.7 | 89.5±1.9 | ||||||||||||||||||||||||
| RANDOM | 62.2±17.4 | 57.8±22.7 | 61.1±7.0 | 59.9±6.9 | 57.4±8.5 | 55.7±6.3 | 52.6±2.8 | 53.2±2.9 | 54.6±3.6 | 55.5±2.7 | 54.6±4.5 | 54.4±4.0 | ||||||||||||||||||||||||
| GFKD | 67.7±12.9 | 68.1±12.1 | 62.5±5.9 | 63.0±6.6 | 63.3±7.7 | 61.8±7.9 | 62.3±5.2 | 63.1±6.0 | 63.3±2.3 | 64.7±3.2 | 63.6±3.8 | 64.0±3.7 | ||||||||||||||||||||||||
| DFAD-GNN | 76.5±7.3 | 75.9±6.5 | 66.9±3.7 | 67.5±3.9 | 69.0±6.1 | 67.8±5.4 | 67.5±4.9 | 69.0±3.4 | 68.9±1.1 | 69.6±2.1 | 71.3±3.1 | 69.1±2.9 | ||||||||||||||||||||||||
| (79.1%) | (78.5%) | (89.2%) | (90.0%) | (88.1%) | (86.6%) | (84.3%) | (86.1%) | (82.5%) | (83.4%) | (77.3%) | (74.9%) | |||||||||||||||||||||||||
4.2 Generator Architecture
We adopt a generator with fixed architecture for all experiments. The generator takes a 32-dimensional vector sampled from a standard normal distribution . We process it with a 3-layer MLP of [64,128,256] hidden units respectively, tanh is taken as the activation function. Finally, a linear layer is used to map the 256-dimensional vectors to -dimensional vectors and reshape them as node features . Throughout our experiments, we take the average number of nodes in the training data as and test the effect of in the ablation experiment.
4.3 Teacher/Student Architecture
To demonstrate the effectiveness of our proposed framework, we consider four GNN models as teacher and student models for a thorough comparison, including: GIN, GCN, GAT and GraphSAGE. Although the GNN model does not always require a deep network to achieve good results, however, from Appendix B, there is no fixed layer and hidden units that can make six datasets achieve the best performance on four different models. For fair comparison, we use 5 layers with 128 hidden units for teacher models. For the student model, we conduct experiments to gradually reduce the number of layers and gradually reduce the number of hidden units . We use a graph classifier layer which first builds a graph representation by averaging all node features extracted from the last GNN layer and then passing this graph representation to an MLP.
4.4 Implementation
For training, we use Adam optimizer with weight decay 5e-4 to update student models. The generator is trained with Adam without weight decay. Both student and generator are using a learning rate scheduler that multiplies the learning rate by a factor 0.3 at 10%, 30%, and 50% of the training epochs. The number of updates of the student model in Algorithm 1 is set to 5. The threshold is empirically set to 0.5.
4.5 Baselines
We compare with the following baselines to demonstrate the effectiveness of our proposed framework.
Teacher: The given pre-trained model which serves as the teacher in the distillation process.
KD: The generator is removed, and the student model is trained on 100% original training data in our framework.
RANDOM: The generator’s parameters are not updated and the student model is trained on the noisy graphs generated by the randomly initialized generator.
GFKD: GFKD is a data-free KD for GNNs by modeling the topology of graph with a multinomial distribution Deng and Zhang (2021).


4.6 Experimental Results
We have pre-trained all datasets on GCN, GIN, GAT and GraphSAGE with 5 layers and 128 hidden units (5-128 for short), and found that GIN performs best on all datasets (Detailed experimental results can be found in the Appendix B). Therefore, we adopt GIN as the teacher model in Table 2. We choose two representative architecture 1-128 and 5-32 for four kinds of student models (More experiments with other architectures can be found in the Appendix D).






From Table 2, it can be observed that KD’s performance is very close to even outperforms the teacher model. That’s because KD is a data-driven method which uses the same training data as the teacher model for knowledge distillation. This also implies that the loss function of our DFAD-GNN is very effective in distilling knowledge from the teacher model to the student model, as we apply the same loss function in both KD and our DFAD-GNN.
We also observe that RANDOM delivers the worst performance as the generator is not updated during the training process, thus the generator will not be able to generate difficult graphs as the student model progresses. Consequently, the student model fail to learn enough knowledge from the teacher, resulting in poor results.
In terms of the efficacy of our DFAD-GNN, Table 2 shows that our DFAD-GNN consistently outperforms the recent data-free method GFKD Deng and Zhang (2021). We conjecture the potential reason that DFAD-GNN can significantly outperform GFKD is the teacher encodes the distribution characteristics of the original input graphs under its own feature space. Simply inverting graphs in GFKD tends to overfit to the partial distribution information stored in this teacher model. As a consequence, their generated fake graphs are lacking of generalizability and diversity. In contrast, our generated graphs are more conducive to transferring the knowledge of the teacher model to the student model.
In terms of the stability, it can be seen from Table 2 that the standard deviation of our DFAD-GNN is the smallest among all the data-free baselines and across all datasets, indicating that our model can obtain relatively stable prediction results.
Another interesting observation is that the performance of the compressed model is not necessarily worse than the more complex model. As can be seen from Table 2, that performance of a more compressed student model with 5-32 is not necessarily worse than the student model with 1-128. Therefore, we speculate that the performance of the student model may have no obvious relationship with the degree of model compression, which requires further investigation.
4.7 Model Analysis
Model Comparison.
Here, we select PROTEINS and COLLAB with the most training data on molecular datasets and social datasets respectively for cross-training among the four kinds of models. It can be seen from Figure 2, when GIN is used as a teacher model, the overall performance of the student model is better, no matter which type of the student model is adopted. When GIN is used as a student model, the performance of the student model is significantly improved compared to other student models. We speculate there may be two reasons: (1) Under the same number of layers and hidden units, the GIN model has more parameters than GCN and GraphSAGE, so GIN owns more powerful learning capability. Note that although GAT has more parameters than GIN, it may be better at calculating node attention weights and then performing node classification tasks; (2) GIN is proposed to solve the problem of graph isomorphism. For our small molecule graphs and social network graphs, GIN is more powerful than other models in graph classification tasks.
Choice of Loss Function.
The choice of loss is of paramount importance to a successful distillation. We explore five potential loss functions, including logit-MAE (calculate MAE with pre-softmax activations, L-MAE for short), softmax-MAE (calculate MAE with softmax outputs, S-MAE for short), MSE, KLD, and Cross Entropy (CE for short). These losses are commonly used in the knowledge distillation literature Gou et al. (2021). Figure 3 shows that using the MAE achieves significantly better test accuracies compared to other loss functions. Generally speaking, it is better to calculate MAE before softmax, because logits contain more information. As mentioned earlier, when the student model matches more closely to the teacher model, other loss functions tend to suffer from vanishing gradients Fang et al. (2019). Specifically, backpropagating such vanishing gradients through the generator can harm its learning. To prevent gradients from vanishing, we use the MAE computed with the teacher and student logits.
Percentage of Training Data.
Although in the above reported results, we assume that the student cannot obtain any training data. However, in practice, student may have partial access to the training data. To reflect the practical scenario of knowledge distillation, we conduct extra experiments on PTC_MR and IMDB-B, by varying the percentage of training data from 0.5% to 100%, while keeping other hyper-parameters the same as in the previous experiments. As illustrated in Figure 4, PTC_MR requires 17.1% of real data to achieve our results, while IMDB-B requires only 5.6%. This is because PTC_ MR has less data, thus the percentage of real data required is higher than IMDB-B.
Number of generated nodes.
To explore the influence of node number on the model performance, we conduct experiments with varying sizes of on PTC_MR and IMDB-B. It can be seen from Figure 5 that the model performs better when takes the value near the average number of nodes in the training set. Far from the average number, the performance will decrease correspondingly due to a large deviation from real data.
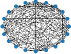
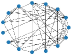
Visualization of Generated Graphs.
The generated graphs and real graphs of IMDB-B and PTC_MR are shown in Figure 6. Although the generated graphs are not exactly the same as the real graphs, they can be used to generate a student model with relatively good performance.










5 Conclusion
This paper introduces a data-free adversarial knowledge distillation framework on graph neural network for model compression. Without any access to real data, we successfully reduce the discrepancy and obtain a student model with relatively good performance. Our extensive experiments on graph classification demonstrate that our framework can be effectively applied to different network architectures. In the future, we will extend this work to multi-teacher scenarios and continue to explore how to generate more complex graphs under various generator structures.
Acknowledgments
This work is supported in part by the National Natural Science Foundation of China (No. 62192784, U20B2045, 62172052, 61772082, 62002029, U1936104). It is also supported in part by The Fundamental Research Funds for the Central Universities 2021RC28.
References
- Arjovsky and Bottou [2017] Martin Arjovsky and Léon Bottou. Towards principled methods for training generative adversarial networks. arXiv preprint arXiv:1701.04862, 2017.
- Bahri et al. [2021] Mehdi Bahri, Gaétan Bahl, and Stefanos Zafeiriou. Binary graph neural networks. In CVPR, pages 9492–9501, 2021.
- Bojchevski et al. [2018] Aleksandar Bojchevski, Oleksandr Shchur, Daniel Zügner, and Stephan Günnemann. Netgan: Generating graphs via random walks. In ICML, pages 610–619. PMLR, 2018.
- Chang and Lin [2011] Chih-Chung Chang and Chih-Jen Lin. Libsvm: a library for support vector machines. ACM transactions on intelligent systems and technology (TIST), 2(3):1–27, 2011.
- De Cao and Kipf [2018] Nicola De Cao and Thomas Kipf. Molgan: An implicit generative model for small molecular graphs. arXiv preprint arXiv:1805.11973, 2018.
- Deng and Zhang [2021] Xiang Deng and Zhongfei Zhang. Graph-free knowledge distillation for graph neural networks. ArXiv, abs/2105.07519, 2021.
- Fang et al. [2019] Gongfan Fang, Jie Song, Chengchao Shen, Xinchao Wang, Da Chen, and Mingli Song. Data-free adversarial distillation. arXiv preprint arXiv:1912.11006, 2019.
- Fang et al. [2021] Gongfan Fang, Kanya Mo, Xinchao Wang, Jie Song, Shitao Bei, Haofei Zhang, and Mingli Song. Up to 100x faster data-free knowledge distillation. arXiv preprint arXiv:2112.06253, 2021.
- Gilmer et al. [2017] Justin Gilmer, Samuel S Schoenholz, Patrick F Riley, Oriol Vinyals, and George E Dahl. Neural message passing for quantum chemistry. In ICML, pages 1263–1272. PMLR, 2017.
- Goodfellow et al. [2014] Ian Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair, Aaron Courville, and Yoshua Bengio. Generative adversarial nets. NeurIPS, 27, 2014.
- Gou et al. [2021] Jianping Gou, Baosheng Yu, Stephen J Maybank, and Dacheng Tao. Knowledge distillation: A survey. International Journal of Computer Vision, 129(6):1789–1819, 2021.
- Hamilton et al. [2017] William L Hamilton, Rex Ying, and Jure Leskovec. Inductive representation learning on large graphs. In Proceedings of the 31st International Conference on Neural Information Processing Systems, pages 1025–1035, 2017.
- Hinton et al. [2015] Geoffrey Hinton, Oriol Vinyals, and Jeff Dean. Distilling the knowledge in a neural network. arXiv preprint arXiv:1503.02531, 2015.
- Jing et al. [2021] Yongcheng Jing, Yiding Yang, Xinchao Wang, Mingli Song, and Dacheng Tao. Amalgamating knowledge from heterogeneous graph neural networks. In CVPR, pages 15709–15718, 2021.
- Kipf and Welling [2016] Thomas N Kipf and Max Welling. Semi-supervised classification with graph convolutional networks. arXiv preprint arXiv:1609.02907, 2016.
- Liu et al. [2021] Yuang Liu, Wei Zhang, Jun Wang, and Jianyong Wang. Data-free knowledge transfer: A survey. arXiv preprint arXiv:2112.15278, 2021.
- Lopes et al. [2017] Raphael Gontijo Lopes, Stefano Fenu, and Thad Starner. Data-free knowledge distillation for deep neural networks. arXiv preprint arXiv:1710.07535, 2017.
- Lu et al. [2021] Yuanfu Lu, Xunqiang Jiang, Yuan Fang, and Chuan Shi. Learning to pre-train graph neural networks. In AAAI, volume 35, pages 4276–4284, 2021.
- Niepert et al. [2016] Mathias Niepert, Mohamed Ahmed, and Konstantin Kutzkov. Learning convolutional neural networks for graphs. In International conference on machine learning, pages 2014–2023. PMLR, 2016.
- Sun et al. [2018] Lichao Sun, Yingtong Dou, Carl Yang, Ji Wang, Philip S Yu, Lifang He, and Bo Li. Adversarial attack and defense on graph data: A survey. arXiv preprint arXiv:1812.10528, 2018.
- Veličković et al. [2017] Petar Veličković, Guillem Cucurull, Arantxa Casanova, Adriana Romero, Pietro Lio, and Yoshua Bengio. Graph attention networks. arXiv preprint arXiv:1710.10903, 2017.
- Wu et al. [2020] Zonghan Wu, Shirui Pan, Fengwen Chen, Guodong Long, Chengqi Zhang, and S Yu Philip. A comprehensive survey on graph neural networks. IEEE transactions on neural networks and learning systems, 32(1):4–24, 2020.
- Wu et al. [2021] Chuhan Wu, Fangzhao Wu, Yang Cao, Lingjuan Lyu, Yongfeng Huang, and Xing Xie. Fedgnn: Federated graph neural network for privacy-preserving recommendation. arXiv preprint arXiv:2102.04925, 2021.
- Wu et al. [2022] Chuhan Wu, Fangzhao Wu, Lingjuan Lyu, Yongfeng Huang, and Xing Xie. Communication-efficient federated learning via knowledge distillation. Nature Communications, 13(1):1–8, 2022.
- Xu et al. [2018] Keyulu Xu, Weihua Hu, Jure Leskovec, and Stefanie Jegelka. How powerful are graph neural networks? arXiv preprint arXiv:1810.00826, 2018.
- Yang et al. [2021] Cheng Yang, Jiawei Liu, and Chuan Shi. Extract the knowledge of graph neural networks and go beyond it: An effective knowledge distillation framework. In WWW, pages 1227–1237, 2021.
- Zhang et al. [2018] Muhan Zhang, Zhicheng Cui, Marion Neumann, and Yixin Chen. An end-to-end deep learning architecture for graph classification. In Thirty-Second AAAI Conference on Artificial Intelligence, 2018.
- Zhou et al. [2020] Jie Zhou, Ganqu Cui, Shengding Hu, Zhengyan Zhang, Cheng Yang, Zhiyuan Liu, Lifeng Wang, Changcheng Li, and Maosong Sun. Graph neural networks: A review of methods and applications. AI Open, 1:57–81, 2020.