D³Fields: Dynamic 3D Descriptor Fields for Zero-Shot Generalizable Rearrangement

We formulate our problem as a zero-shot rearrangement problem given a 2D goal image $\mathcal{I}$ and RGBD images from multiple fixed viewpoints. We denote the workspace scene representation as $\bm{s}_{\text{goal}}$. Our goal is to find an optimal action sequence $\{a^{t}\}$ to minimize the task objective:

	$\displaystyle\min_{\{a_{t}\}}$	$\displaystyle c(\bm{s}^{T},\bm{s}_{\text{goal}}),$			(1)
	s.t.	$\displaystyle\bm{s}^{t}=g(\bm{o}^{t}),$	$\displaystyle\bm{s}^{t+1}=f(\bm{s}^{t},a^{t}),$

where $c(\cdot,\cdot)$ is the cost function measuring the distance between the terminal representation $\bm{s}^{T}$ and the goal representation $\bm{s}_{\text{goal}}$. Representation extraction function $g(\cdot)$ takes in the current multi-view RGBD observations $\bm{o}^{t}$ and outputs the current representation $\bm{s}^{t}$. $f(\cdot,\cdot)$ is the dynamics function that predicts the future representation $\bm{s}^{t+1}$, conditioned on the current representation $\bm{s}^{t}$ and action $a^{t}$. The optimization aims to find the action sequence $\{a_{t}\}$ that minimizes the cost function $c(\bm{s}^{T},\bm{s}_{\text{goal}})$.

Section 3.2 describes how to construct representation extraction function $g(\cdot)$. Section 3.3 elaborates on the dynamics function $f(\cdot,\cdot)$. In Section 3.4, we show how to define the cost function $c(\cdot,\cdot)$.

We assume that we can access multiple RGBD cameras with fixed viewpoints to construct D³Fields. Multi-view RGBD observations are first fed into visual foundational models. Then we obtain 2D feature volumes $\mathcal{W}$. D³Fields are implicit functions $\mathcal{F}(\cdot|\mathcal{W})$ defined as follows:

$\displaystyle(d,\mathbf{f},\mathbf{p})=\mathcal{F}(\mathbf{x}|\mathcal{W}),$

(2)

where $\mathbf{x}$ can be an arbitrary 3D coordinate in the world frame, and $(d,\mathbf{f},\mathbf{p})$ corresponds to the signed distance $d\in\mathbb{R}$, the semantic descriptor $\mathbf{f}\in\mathbb{R}^{N}$, and the instance probability distribution $\mathbf{p}\in\mathbb{R}^{M}$ of $M$ instances. $M$ could be different across scenarios.

As an overview, our pipeline first projects $\mathbf{x}$ into the image space of each camera. Then, we can obtain the truncated depth difference between projected depth and real depth reading using Equation 3. Afterwards, we assign weights to each viewpoint using Equation 4 and interpolate the semantic features and instance masks for each camera using Equation 5. Finally, we fuse features from all viewpoints to obtain the final descriptor using Equation 6.

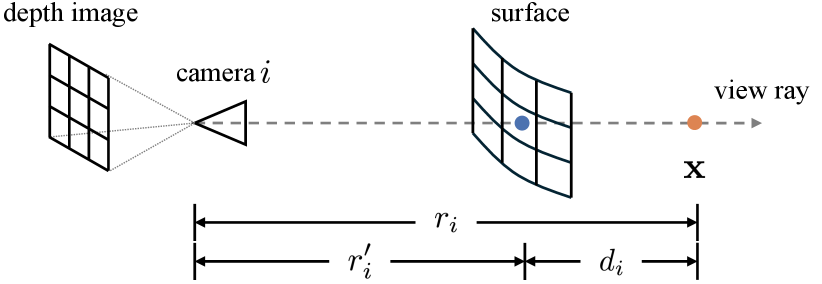
More concretely, we map an arbitrary 3D point $\mathbf{x}$ to the $i$th viewpoint’s image space. We denote the projected pixel as $\mathbf{u}_{i}$ and the distance from $\mathbf{x}$ to the $i$th viewpoint as $r_{i}$ (Figure 3). By interpolating the $i$th viewpoint’s depth image $\mathcal{R}_{i}$, we compute the corresponding depth reading from the depth image as $r^{\prime}_{i}=\mathcal{R}_{i}[\mathbf{u}_{i}]$. Then we can compute the truncated depth difference as

$\displaystyle d_{i}=r_{i}-r^{\prime}_{i},$

$\displaystyle\quad d_{i}^{\prime}=\textrm{max}(\textrm{min}(d_{i},\mu),-\mu),$

(3)

where $\mu$ specifies the truncation threshold for the Truncated Signed Distance Function (TSDF). Given the truncated depth difference, we compute weights $v_{i}$ and $w_{i}$ for each viewpoint as

$\displaystyle v_{i}=\mathds{1}_{d_{i}<\mu},\quad w_{i}=\exp{\left(\frac{\min\left(\mu-|d_{i}|,0\right)}{\mu}\right)}.$

(4)

Here is the explanation and design justification for each term.

• $v_{i}$:

  It represents the visibility of $\mathbf{x}$ in camera $i$. $\mathds{1}_{d_{i}<\mu}$ is the indicator function, which equals to 1 when $d_{i}<\mu$ and equals to 0 otherwise. When $d_{i}=r_{i}-r^{\prime}_{i}\geq\mu$, $\mathbf{x}$ is behind the surface, which means $\mathbf{x}$ is not visible in camera $i$ and $v_{i}=0$.

• $w_{i}$:

  It is the weight for the $i$th viewpoint. Since we only have a confident estimation when $\mathbf{x}$ is close to the surface, $w_{i}$ will decay as $|d_{i}|$ increases. For $\mathbf{x}$ that is far away, $w_{i}$ degrades to $0$.

Then we extract the semantic feature $\mathbf{f}_{i}$ and instance mask $\mathbf{p}_{i}$ in each viewpoint using

$\displaystyle\mathbf{f}_{i}=\mathcal{W}_{i}^{\mathbf{f}}[\mathbf{u}_{i}],$

$\displaystyle\quad\mathbf{p}_{i}=\mathcal{W}_{i}^{\mathbf{p}}[\mathbf{u}_{i}],$

(5)

where DINOv2 [17] extracts the semantic feature volume $\mathcal{W}_{i}^{\mathbf{f}}\in\mathbb{R}^{H\times W\times N}$ from RGB image. $\mathcal{W}_{i}^{\mathbf{p}}\in\mathbb{R}^{H\times W\times M}$ is the instance mask volume using Grounded-SAM [14, 15]. Note that $\bm{p}_{i}$ is a one-hot vector and already associated to ensure consistent instance indexing across different views. Finally, we fuse the semantic features and instance masks from all $K$ viewpoints using

$\displaystyle d=\frac{\sum_{i=1}^{K}v_{i}d_{i}^{\prime}}{\delta+\sum_{i=1}^{K}v_{i}},\quad\mathbf{f}=\frac{\sum_{i=1}^{K}v_{i}w_{i}\mathbf{f}_{i}}{\delta+\sum_{i=1}^{K}v_{i}},\quad\mathbf{p}=\frac{\sum_{i=1}^{K}v_{i}w_{i}\mathbf{p}_{i}}{\delta+\sum_{i=1}^{K}v_{i}},$

(6)

where $\delta$ is a small number to avoid numeric issues. Since the process of projection, interpolation, and fusion is differentiable, $\mathcal{F}(\cdot|\mathcal{W})$ is differentiable when $\mathbf{x}$ is within the truncation threshold.

This section will present how to use the dynamic implicit 3D descriptor field $\mathcal{F}(\cdot|\mathcal{W})$ to track keypoints and train dynamics. Without loss of generality, consider the tracking of a single object instance $\bm{s}^{t}\in\mathbb{R}^{3\times n_{\bm{s}}}$. For clarity, we denote $\mathbf{f}$ and $d$ from $\mathcal{F}(\cdot|\mathcal{W})$ as $\mathcal{F}_{\mathbf{f}}(\cdot|\mathcal{W})$ and $\mathcal{F}_{d}(\cdot|\mathcal{W})$. We initialize the tracked keypoints $\bm{s}^{0}$ by sampling points close to the surface of the desired instance. To track keypoints $\bm{s}^{0}$, we formulate the tracking problem as an optimization problem:

$\displaystyle\min_{\bm{s}^{t+1}}$

$\displaystyle||\mathcal{F}_{\mathbf{f}}(\bm{s}^{t+1}|\mathcal{W})-\mathcal{F}_{\mathbf{f}}(\bm{s}^{0}|\mathcal{W})||_{2}.$

(7)

As $\mathcal{F}(\cdot|\mathcal{W})$ is differentiable, we could use a gradient-based optimizer. This method could be naturally extended to multiple-instance scenarios. We found that relying solely on features for tracking can be unstable. Therefore, if we know that the tracked object is rigid, we can apply additional rigid constraints and distance regularization for more stable tracking.

Keypoint tracking enables dynamics model training on real data. We instantiate the dynamics model $f(\cdot,\cdot)$ as graph neural networks (GNNs). We follow [48] to predict object dynamics. Please refer to [49, 48] for more details on how to train the graph-based neural dynamics model. The trained dynamics model will be used for trajectory optimization in Section 3.4.

In this section, we will describe how to define the planning cost for our zero-shot rearrangement framework. As shown in Figure 2 (c), we first find the correspondence between the descriptor fields and goal image using Equation 8. Then we define the cost function $c(\cdot,\cdot)$ in Equation 9 to measure the distance between the current state and the goal state. Finally, we optimize the action sequence $\{a_{t}\}$ to minimize the cost function as described in Section 3.1.

As described in Section 3.2, we initially sample points $\bm{s}^{0}\in\mathbb{R}^{3\times n_{\bm{s}}}$ and obtain the associated features $\mathbf{f}^{0}\in\mathbb{R}^{f\times n_{\bm{s}}}$ from the descriptor fields. We correspond $\bm{s}^{0}$ to the goal image $\mathcal{I}_{\text{goal}}$ to define 2D goal points $\bm{s}_{\text{goal}}\in\mathbb{R}^{2\times n_{\bm{s}}}$. Firstly, we compute the feature distance $\alpha_{ij}$ between $i$th pixel $\mathbf{u}_{i}$ of $\mathcal{I}_{\text{goal}}$ and $j$th sampled point of $\bm{s}^{0}$. Then we normalize $\alpha_{ij}$ using the softmax over the whole image and obtain the weight $\beta_{ij}$. Lastly, we find the 2D point $\bm{s}_{\text{goal},j}$ corresponding to the $j$th 3D point using weighted sum. The computation process is summarized in the following:

$\displaystyle\alpha_{ij}=||\mathcal{W}^{\mathbf{f}}_{\text{goal}}[\mathbf{u}_{i}]-\mathbf{f}_{j}^{0}||_{2},\quad\beta_{ij}=\frac{\exp{\left(-s\alpha_{ij}\right)}}{\sum_{i=1}^{H\times W}\exp{\left(-s\alpha_{ij}\right)}},\quad\bm{s}_{\text{goal},j}=\sum_{i=1}^{H\times W}\beta_{ij}\mathbf{u}_{i},$

(8)

where $\mathcal{W}^{\mathbf{f}}_{\text{goal}}$ is the feature volume extracted from $\mathcal{I}_{\text{goal}}$ using DINOv2, and $s$ is the hyperparameter to determine whether the heatmap $\beta_{ij}$ is more smooth or concentrating. Although Equation. 8 only shows a single instance case, it could be naturally extended to multiple instances by using instance mask information.

Note that $\bm{s}_{\text{goal}}$ is in the image space, and the current state representation, $\bm{s}^{t}$ is in 3D space. To reconcile this discrepancy, we introduce a virtual reference camera. We project $\bm{s}^{t}$ into the reference image and obtain its 2D positions $\bm{s}^{t}_{\text{2D}}$. Consequently, we define the task cost function as follows:

$\displaystyle c(\bm{s}^{t},\bm{s}_{\text{goal}})=||\bm{s}^{t}_{\text{2D}}-\bm{s}_{\text{goal}}||_{2}^{2}.$

(9)

Given the planning cost, we could use an MPC framework to derive the action sequence $\{a_{t}\}$ to minimize the cost function. Specifically, we use MPPI to optimize the action sequence [50]. At each time step, we sample a set of action sequences and evaluate the cost function. Then we update the action sequence using the cost function and repeat the process until convergence. This process will be repeated for each time step until the task is completed. More details regarding the method are included in the supplementary material.

In the real world, we use four RGBD cameras positioned at the corners of the workspace and employ the Kinova^® Gen3 arm for action execution. In the simulation, we use OmniGibson and the Fetch robot for mobile manipulation tasks [51]. Our evaluations span various tasks, including organizing shoes, collecting debris, tidying the table, and so on. More details are in the supplementary material.

In this section, we compare our D³Fields with two baselines, Distilled Feature Fields (F3RM) [19] and FeatureNeRF [18]. For F3RM, we use four camera views as inputs and the DINOv2 features as the supervision and stop the distillation process at 2,000 steps, which is defaulted by the authors [19]. We first compare our D³Fields with F3RM and FeatureNeRF in terms of the correspondence accuracy, as shown in Figure 5. We reconstruct the mesh from our 3D implicit representation using marching cubes. We then select DINOv2 features from the source image and visualize the corresponding heatmap on the reconstructed feature mesh. We could see that our D³Fields could reconstruct the mesh with high quality and highlight semantically similar areas across different instances and contexts, while F3RM fails to reconstruct the mesh accurately, which leads to an inaccurate correspondence heatmap. Since FeatureNeRF is only pre-trained on a small dataset, it fails to construct an accurate mesh of the scene and find accurate correspondence in novel scenes, demonstrating our representation’s effectiveness in reconstructing meshes and encoding semantic features. Quantitative comparisons are included in the supplementary material.

We also evaluate the time efficiency of constructing the implicit representation given four RGBD views across four scenes on the machine with A6000 GPU. Our method takes $0.166\pm 0.002$ seconds, which is significantly more efficient than F3RM, which takes $88.379\pm 5.306$ seconds.

We conduct a qualitative evaluation of D³Fields in common robotic rearrangement tasks in a zero-shot manner, with partial results displayed in Figure 1 and Figure 6. We observed several key capabilities of our framework, which are as follows:

Generalization to AI-Generated Goal Images. In Figure 1, the goal image is rendered in a Van Gogh style, which is distinctly different from those in the workspace. Since D3Fields encode semantic information, capturing shoes with varied appearances under similar descriptors, our framework can manipulate shoes based on AI-generated goal images.

Compositional Goal Images. In the office desk organization task in Figure 1, the robot first arranges the mouse and pen to match the goal image. Then, the robot repositions the mug from the top of a box to the mug pad, guided by a separate goal image of the upright mug. This example illustrates that our system can accomplish tasks using compositional goal images.

Generalization across Instances and Materials. Figure 4 and Figure 1 also show our framework’s ability to generalize across various instances and materials. For example, the debris collection in Figure 1 shows our framework’s ability to handle granular objects. Figure 6 further shows our framework’s instance-level generalization, where the goal instances distinct from ones in the workspace.

Generalization across Simulation and Real World. We evaluated our framework in the simulator, as shown in the utensil organization and mug organization examples in Figure 6. Given goal images from the real world, our framework can also manipulate objects to the goal configurations. This underscores our framework’s generalization capabilities between simulation and the real world.

To obtain a more thorough understanding of our D³Fields, we first extract the mesh using the marching cube algorithm. We evaluate vertices from the extracted mesh using our D³Fields and obtain the associated segmentation information and semantic features, as visualized in Figure 7. Mask fields in Figure 7 show a distinct 3D instance segmentation in different scenarios, even clustering scenes like cans and toothpaste. The 3D instance segmentation enables the downstream planning module to distinguish and manipulate multiple instances, as shown in the mug organization tasks.

Additionally, we visualize the semantic features by mapping them to RGB space using PCA. We observe that our semantic fields show consistent color patterns across different instances. In the provided shoe example, even though various shoes have distinct appearances and poses, they exhibit similar color patterns: shoe heels are represented in green, and shoe toes in red. We observed similar patterns for other object categories such as mugs and forks. The consistent semantic features across various instances help our manipulation framework to achieve category-level generalization. When encountering novel instances, our D³Fields can still establish the correspondence between the workspace and the goal image using semantic features. In addition, we analyze in the supplementary to show that D³Fields have better 3D consistency compared to simple point cloud stitching.