D2RL: Deep Dense Architectures in Reinforcement Learning
Abstract
While improvements in deep learning architectures have played a crucial role in improving the state of supervised and unsupervised learning in computer vision and natural language processing, neural network architecture choices for reinforcement learning remain relatively under-explored. We take inspiration from successful architectural choices in computer vision and generative modeling, and investigate the use of deeper networks and dense connections for reinforcement learning on a variety of simulated robotic learning benchmark environments. Our findings reveal that current methods benefit significantly from dense connections and deeper networks, across a suite of manipulation and locomotion tasks, for both proprioceptive and image-based observations. We hope that our results can serve as a strong baseline and further motivate future research into neural network architectures for reinforcement learning. The project website is at this link https://sites.google.com/view/d2rl/home
1 Introduction
Deep Reinforcement Learning (DRL) is a general purpose framework for training goal-directed agents in high dimensional state and action spaces. There have been plenty of successes from DRL for robotic control tasks, spanning across locomotion and navigation tasks, both in simulation and in the real world (Schulman et al., 2015; Akkaya et al., 2019; Kalashnikov et al., 2018).
While the generality of the DRL framework lends itself to be applicable to a wide variety of tasks, one has to address issues such as the sample-efficiency and generalization of the agents trained with this framework. Sample-efficiency is fundamentally critical to agents trained in the real world, particularly for robotic control tasks. Baking in minimal inductive biases into the framework is one effective mechanism to address the issue of sample-efficiency of DRL agents and make them more efficient.
The generality of the framework makes it difficult to control particular behaviours and inductive biases for DRL algorithms. Inductive biases are important for learning algorithms, as they are able to induce desirable behaviour in the learned agents. Recent work has sought to improve the sample efficiency of DRL by adding an inductive bias of invariance, when learning from images, through techniques such as data augmentations (Laskin et al., 2020; Kostrikov et al., 2020) and contrastive losses (Srinivas et al., 2020). Similarly, another important inductive bias in DRL is the choice of the architectures for function approximators, for example how to parameterize the neural network for the policy and value functions. However, the problem of choosing architecture designs in DRL and robotics, for planning and control, has been largely ignored.
Modern computer vision and language processing research have shown the disproportionate advantage of the size and depth of the neural networks used (He et al., 2016b; Radford et al., ) wherein very deep neural networks can be trained such that they learn better and more generalizable representations. Furthermore, recent evidence suggests that deeper neural networks can not only learn more complex functions but also have a smoother loss landscape (Rolnick & Tegmark, 2017). Learning function approximators which enable better optimization and expressivity is an important inductive bias, which is greatly exploited in vision and language processing by using clever neural network architecture choices such as residual connections (He et al., 2016a), normalization layers (Santurkar et al., 2018), and gating mechanisms (Hochreiter & Schmidhuber, 1997), to name a few. It would be ideal to incorporate similar inductive biases in modern DRL algorithms in robotics in order to allow for better sample efficiency as that would significantly aid the deployment of real world robot learning agents.
In this paper, we first highlight the problems that occur when learning policies and value functions using vanilla deep neural networks. Then we propose D2RL; an architecture that addresses these problems while benefiting from the utility of inductive biases added by more expressive function approximators. We show how our proposed architecture scales effectively to a wide variety of off-policy RL algorithms, for proprioceptive-feature and image based inputs across a diverse set of challenging robotic control and manipulation environments. Our approach is motivated by utilizing a form of dense-connections similar to the ones found in modern deep learning, such as DenseNet (Huang et al., 2017), Skip-VAE (Dieng et al., 2019) and U-Nets (Ronneberger et al., 2015). We demonstrate that the proposed parameterization significantly improves sample efficiency of RL agents (as measured by the number of environment interactions required to obtain a level of performance) in continuous control tasks.
Our contributions can be summarized as:
-
1.
We investigate the problem with increasing the number of layers used to parameterize policies and value functions.
-
2.
We propose a general solution based on dense-connections to overcome the problem.
-
3.
We extensively evaluate our proposed architecture on a diverse set of robotics tasks from proprioceptive features and images across multiple standard algorithms.
2 Related work
Learning efficient representations for sample-efficient RL
Several recent papers have sought to improve representation learning of observations for control. CURL (Srinivas et al., 2020) augments the usual RL loss with a contrastive loss that seeks to learn a latent representation which enforces the inductive bias of encodings of augmentations of the same image being closer in latent space than embeddings of augmentations of different images. RAD (Laskin et al., 2020) and DrQ (Kostrikov et al., 2020) showed that simple data augmentations like random crop, color jitter, patch cutout, and random convolutions can alone help improve sample-efficiency and generalization of RL from pixel inputs. Some other algorithms learn latent representations decoupled from policy learning, through a variational autoencoder based loss (Higgins et al., 2017; Hafner et al., 2019; Nair et al., 2018). OFENet (Ota et al., 2020) shows that learning a higher dimensional feature space helps learn a more informative representation when learning from states. SAC-AE (Yarats et al., 2019) showed the utility of wide MLP layers (1024) in the actor and critic networks for SAC (Haarnoja et al., 2018) in pixel-based RL (Appendix B1 of Yarats et al. (2019)) . This architecture later propagated to CURL, RAD, and DrQ. Song et al. (2019) analyzed overfitting in model-free RL and found that using wider neural net architectures for the policy helps improve generalization.
Inductive biases in deep learning
Inductive biases in deep learning have been long explored in different contexts such as temporal relations (Hochreiter & Schmidhuber, 1997), spatial relations (LeCun et al., 1998; Krizhevsky et al., 2012), translation invariance (Berthelot et al., 2019; He et al., 2020; Chen et al., 2020; Srinivas et al., 2020; Laskin et al., 2020) and learning contextual representations (Vaswani et al., 2017). These inductive biases are injected either directly through the network parameterization (LeCun et al., 1998; Hochreiter & Schmidhuber, 1997; Vaswani et al., 2017) or by implicitly changing the objective function (Berthelot et al., 2019; Srinivas et al., 2020).
Learning very deep networks
Deep neural networks are useful for extracting features from data relevant for various downstream tasks. However, simply increasing the depth of a feed-forward neural network leads to instability in training due to issues such as vanishing gradients (Hochreiter & Schmidhuber, 1997), or a a loss of mutual information (He et al., 2016a). To mitigate this, residual connections were proposed which involve an alternate path between layers through an identity mapping (He et al., 2016a). Skip-VAEs (Dieng et al., 2019) tackle a similar issue of posterior collapse in typical VAE training by adding skip connections in the architecture of the VAE decoder. U-Nets (Ronneberger et al., 2015) consider a contractive path of convolutions and maxpooling layers followed by an expansive path of up-convolution layers. There are copy and crop identity mapping from layers of the contractive path to layers in the expansive path. Normalization techniques such as batch normalization are also important in learning deep networks (Ioffe & Szegedy, 2015). Combining residual connections with batch normalization have been used to successfully train networks with layers (He et al., 2016b). Our proposed architecture closely resembles DenseNet (Huang et al., 2017), which uses skip connections from feature maps of previous layers through concatenation, allowing for efficient learning and inference.
3 Preliminaries
In this section, we describe the actor-critic formulation of RL algorithms, which serves as the basic framework for our setup. We then describe the Data-Processing Inequality which is relevant for explaining and motivating the proposed architecture.
3.1 Actor-Critic methods
Actor-critic methods learn two models, one for the policy function and the other for the value function such that the value function assists in the learning of the policy. These are TD-learning (Tesauro, 1995) methods that have an explicit representation for the policy independent of the value function. We consider the setting where the critic is an state-action value function parameterized by a neural network, and the actor is also parameterized by a neural network. Let the current state be and denote the reward obtained after executing action in state , and transitioning to state . After sampling action in the next state , the policy parameters are updated in the direction suggested by the critic
The parameters are updated using the TD correction as follows:
Although the basic formulation above requires on-policy samples for gradient updates, a number of off-policy variants of the algorithm have been proposed (Haarnoja et al., 2018; Fujimoto et al., 2018) that incorporate importance weighting in the policy’s gradient update. Let the observed samples be sampled by a behavior policy , and be the policy to be optimized. The gradient update rule changes as
3.2 Data-processing inequality
The Data processing inequality (DPI) states that the information content of a signal cannot be increased via a local physical operation. So, given a Markov chain , the mutual information (MI) between and is not less than the MI between and i.e.
A vanilla feed-forward neural network has successive layers depend only on the output of the previous layer and so there is a Markov chain of the form from the input to the final output . In practice the last layer contains less information than the previous layer . By using dense connections (Huang et al., 2017), we are able to overcome the problem of DPI, as the original input is simply concatenated with the intermediate layers of the networks. We postulate that using dense connections are also important when parameterizing policies and value networks in RL and robotics. By preserving important information about the input across layers explicitly through dense connections, we can achieve faster convergence in solving complex tasks.
3.3 Implicit under-parameterization in Deep Q-Learning
Kumar et al. (2020) showed that using MLPs for function approximation of the policy and value functions in deep RL algorithms that use bootstrapping, leads to an implicit-underparameterization phenomena that causes poor-er performance. Implicit under-parameterization refers to a reduction in the effective rank of the feature, that occurs implicitly due to using MLPs for approximating Q-functions. This causes rank collapse for the feature matrix which are the weights of the penultimate layer of the Q network during training.
We believe that adding skip connections to the network architecture, as in D2RL could help alleviate this rank collapse issue, and improve performance. We empirically verify this in Section 5.2 and Table 3.
4 Method
In this section, we first show the issues with using deeper Multi-layered Perceptons (MLPs) to parameterize the policies and Q-networks in RL and robotics due to the Data Processing Inequality (DPI). We then propose a simple and effective architecture which overcomes the issues, using dense-connections. We will denote our proposed method as: Deep Dense architectures for Reinforcement Learning or D2RL in the subsequent sections.
4.1 Problem with deeper networks in Reinforcement Learning
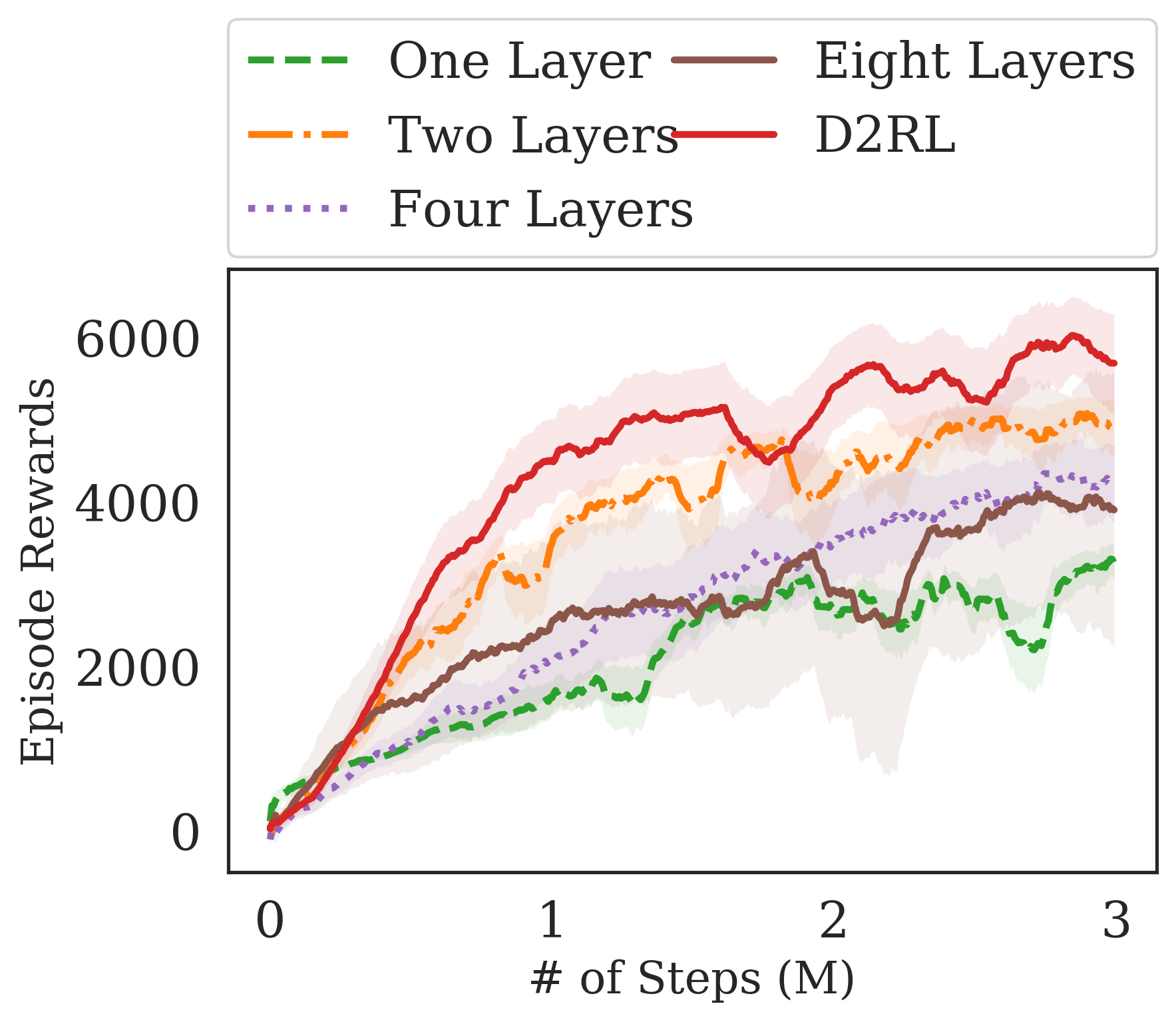
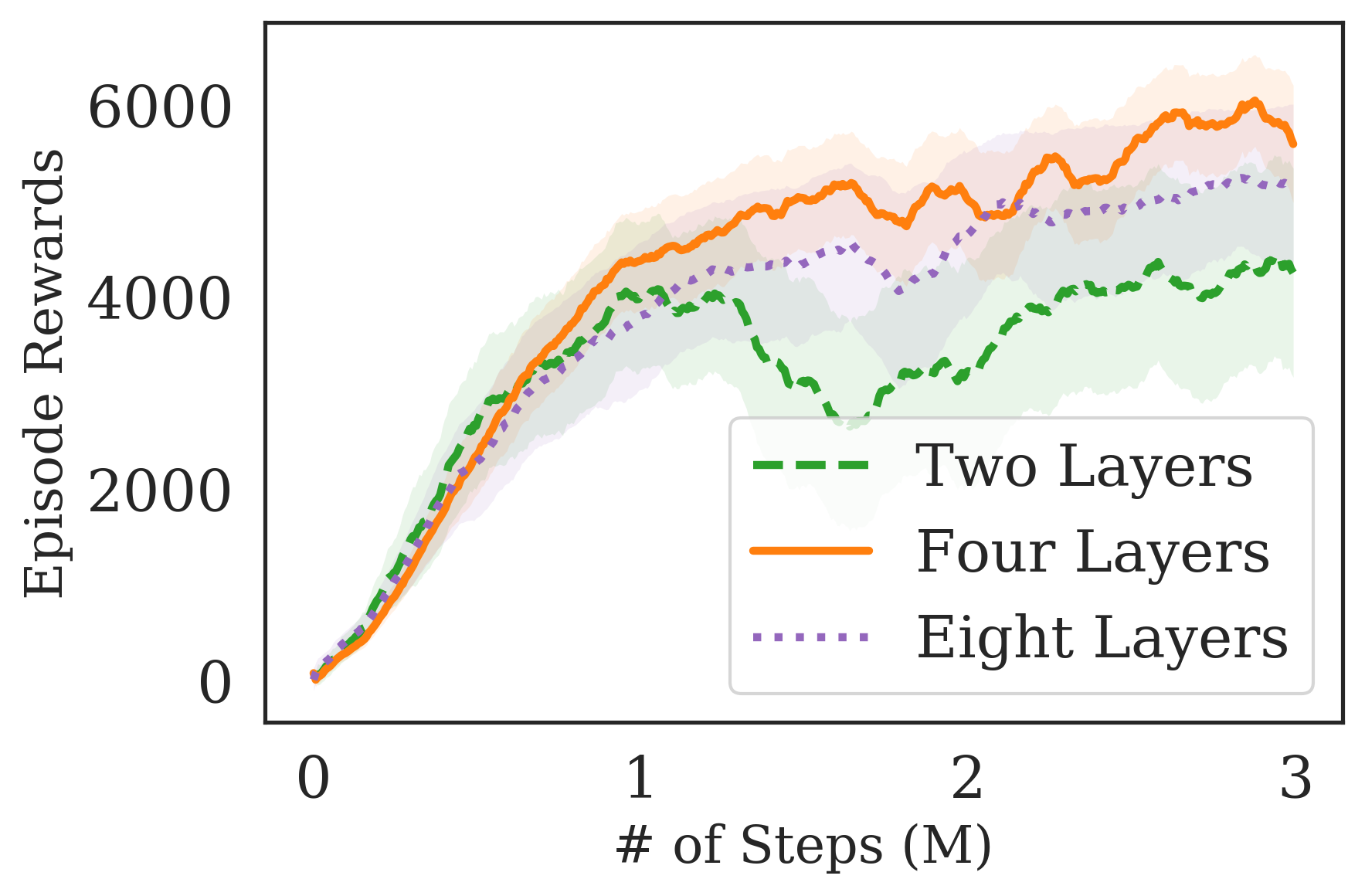
To test whether we can use the expressive power of deeper networks in RL for robotic control, we train a SAC agent (Haarnoja et al., 2018), while increasing the number of layers in the MLP used to parameterize the policy and the Q-networks, on the Ant-v2 environment of the OpenAI Gym suite (Brockman et al., 2016). The results are shown in Fig. 2. The results suggest that by simply increasing the number of layers used to parameterize the networks, we are unable to benefit from the inductive bias of deeper feature extractors in RL, like we see in computer vision. As we increase the number of layers in the network, the mutual information between the output and input likely decreases due to the non-linear transformations used in deep learning as explained by the DPI (see Section 3.2). Increasing the number of layers from 2 to 4 significantly decreases the sample efficiency of the agent and furthermore, increasing the number of layers from 2 to 8 decreases the sample efficiency while also making the agent less stable during training. As expected, when instead decreasing the number of layers from 2 to 1 the vanilla MLPs are not sufficiently expressive to perform well on the Ant-v2 task. This simple experiment suggests that even though the expressivity of the function approximators is important, by simply adding more layers in a vanilla MLP, the agent’s performance and sample complexity significantly deteriorates. However, it is desirable to use deeper networks to increase the network expressivity and to enable better optimization for the networks.
4.2 D2RL
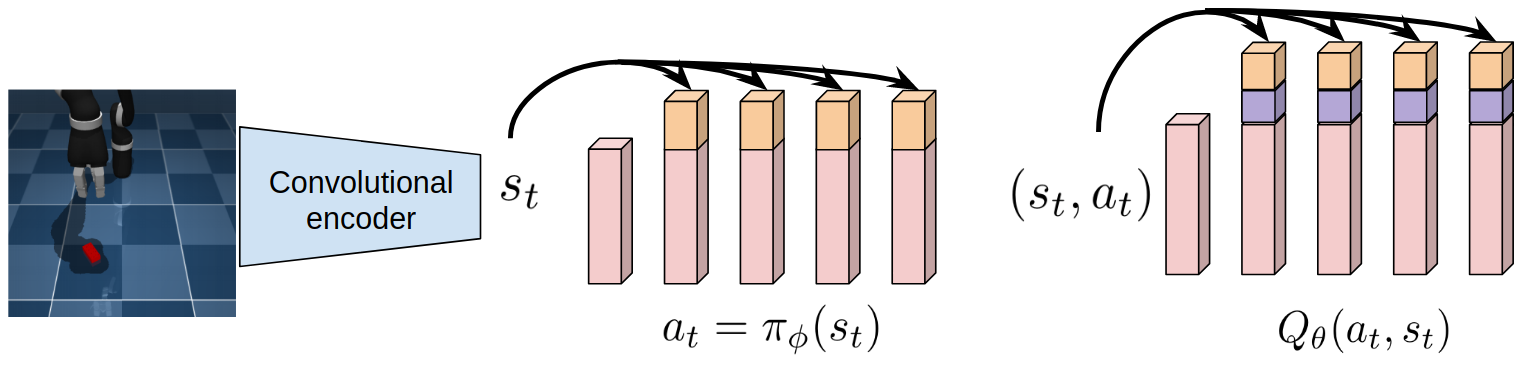
Our proposed D2RL variant incorporates dense connections (input concatenations) from the input to each of the layers of the MLP used to parameterize the policy and value functions. We simply concatenate the state or the state-action pair to each hidden layer of the networks except the last output linear layer, since that is just a linear transformation of the output from the previous layer. In case of pixel observations, we consider the states to be the encodings of a CNN encoder, as shown in Fig. 1. Our simple architecture enables us to increase the depth of the networks while also satisfying DPI. Fig 1 is a visual illustration and we provide a PyTorch-like pseudo-code below to promote clarity of the proposed method. We also include the actual PyTorch code (Paszke et al., 2019) for the policy and value networks to allow for fast-adoption and reproducibility in Appendix A.
5 Experiments
We experiment across a suite of different environments, some of which are shown in Fig. 8, each simulated using the MuJoCo simulator. We were unable to do real robot experiments due to COVID-19 and have included a 1-page statement along with the Appendix describing how our method can conveniently scale to physical robots. Through the experiments, we aim to understand the following questions:
-
•
How does D2RL compare with the baseline algorithms in terms of both asymptotic performance and sample efficiency on challenging robotic environments?
-
•
Are the benefits of D2RL consistent across a diverse set of algorithms and environments?
-
•
Is D2RL important for both the policy and value networks? How does D2RL perform with increasing depth?
5.1 Experimental details
To enable fair comparison between the current standard baselines and D2RL, we simply replace the 2-layer MLPs that are commonly parameterize the policy and value function(s) in widely used actor-critic algorithms such as SAC (Haarnoja et al., 2018; Yarats et al., 2019), TD3 (Fujimoto et al., 2018), DDPG (Qiu et al., 2019) and HIRO (Nachum et al., 2018). Instead, we use 4-layer D2RL to parameterize both the policies and the value function(s) in each of the actor-critic algorithms. Outside of the network architecture, we do not change any hyperparameters, and use the exact same values as reported in the original papers and the corresponding open-source code repositories. The details of all the hyperparameters used are in Appendix C. We perform ablation studies in Section 5.4 to investigate the importance of parameterizing both the policy and value function(s) using D2RL and see how varying the number of layers of D2RL affects performance. We also perform further experiments with a ResNet style architecture and additional experiments with Hindsight Experience Replay (Andrychowicz et al., 2017) on simpler manipulation environments which can be found in Appendix B.
5.2 Experimental Results
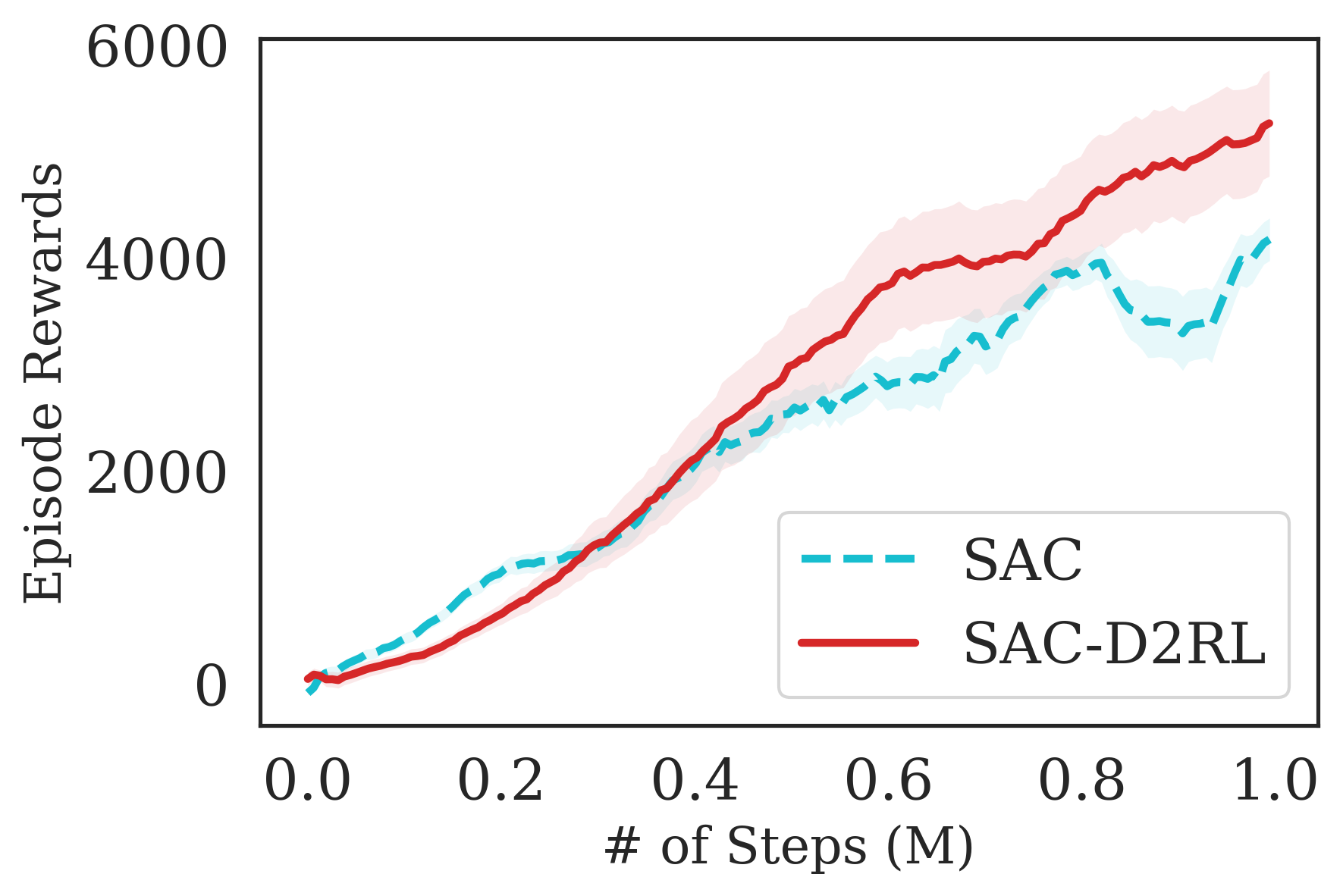
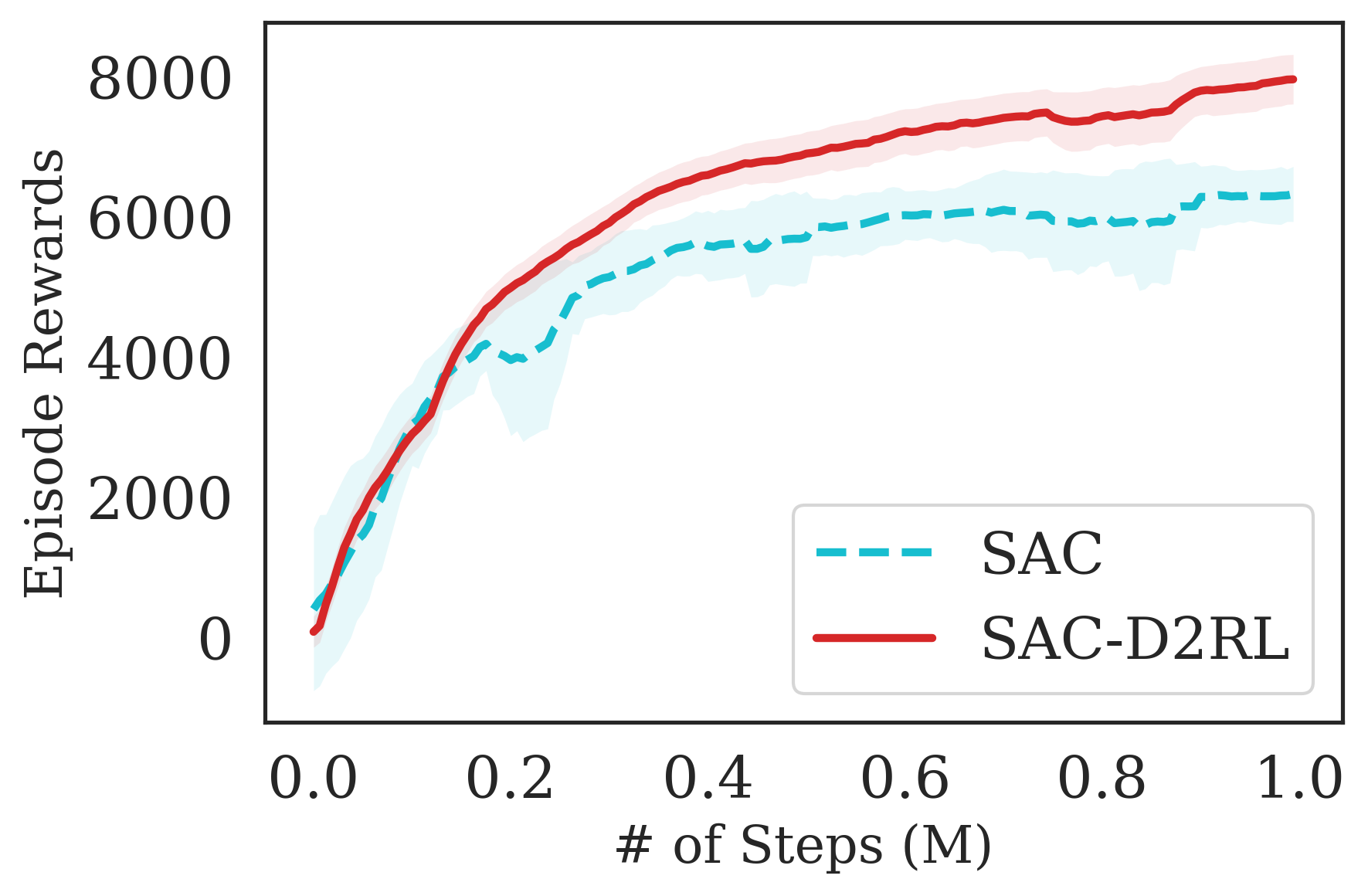
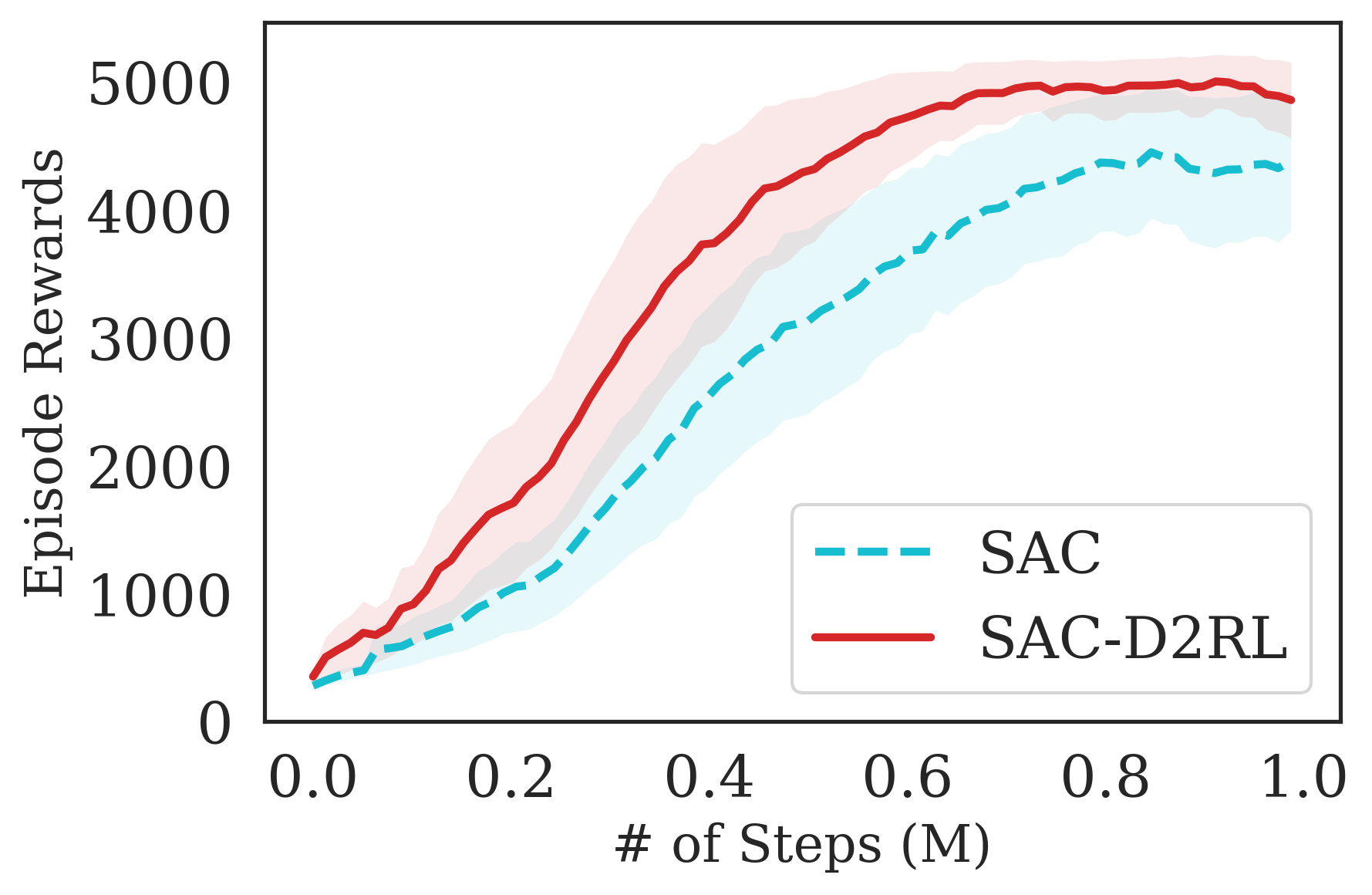
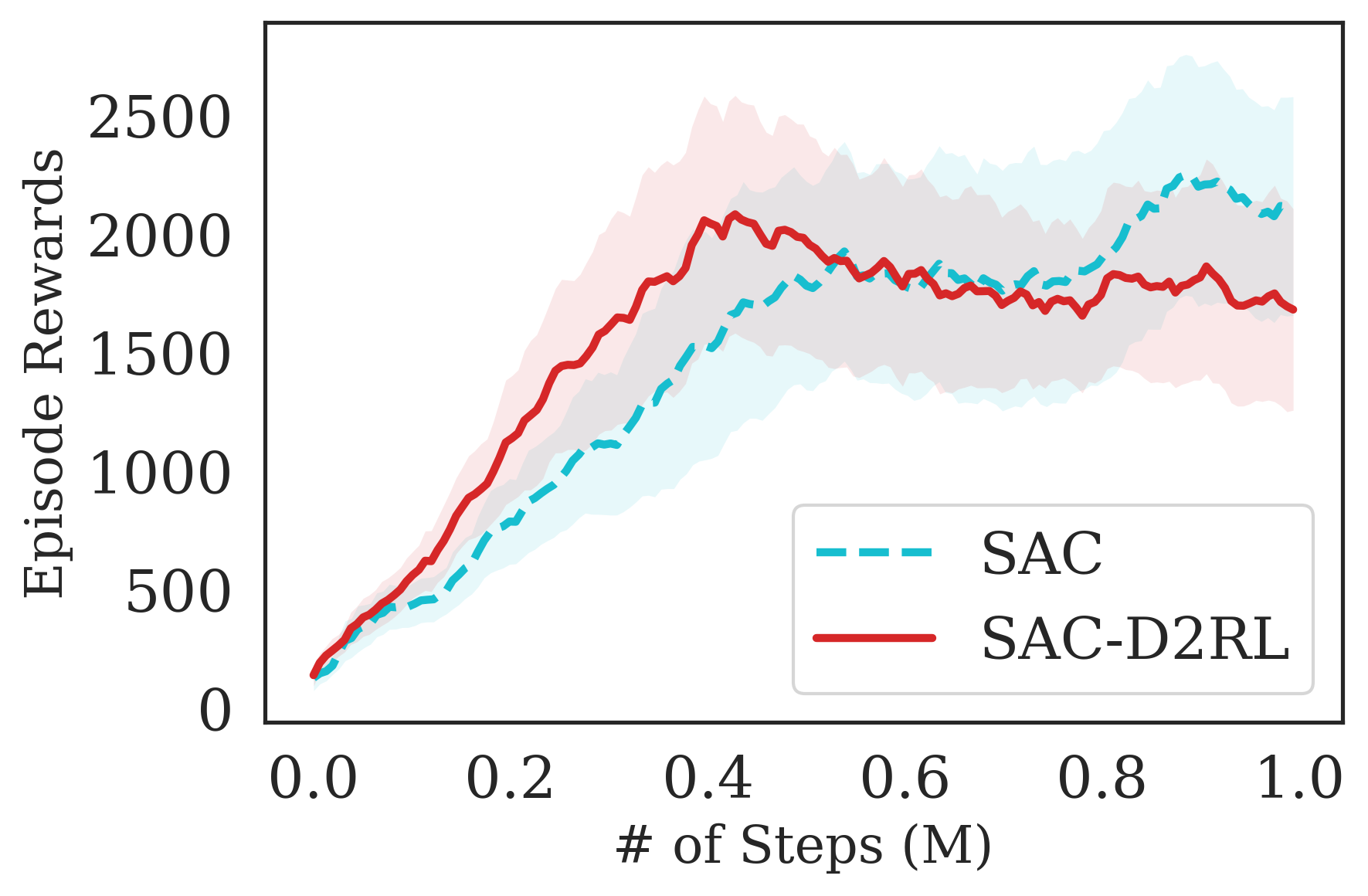
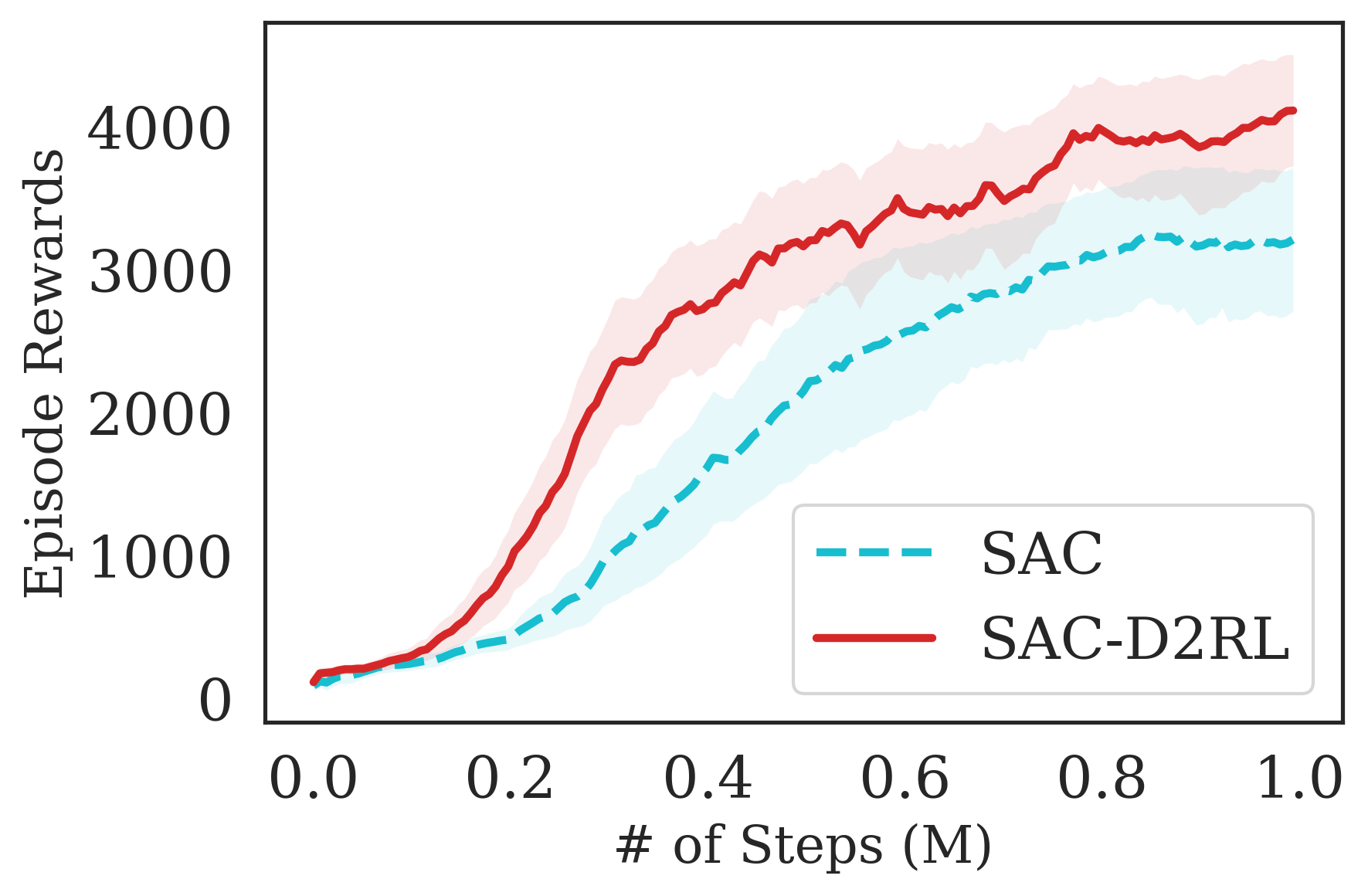
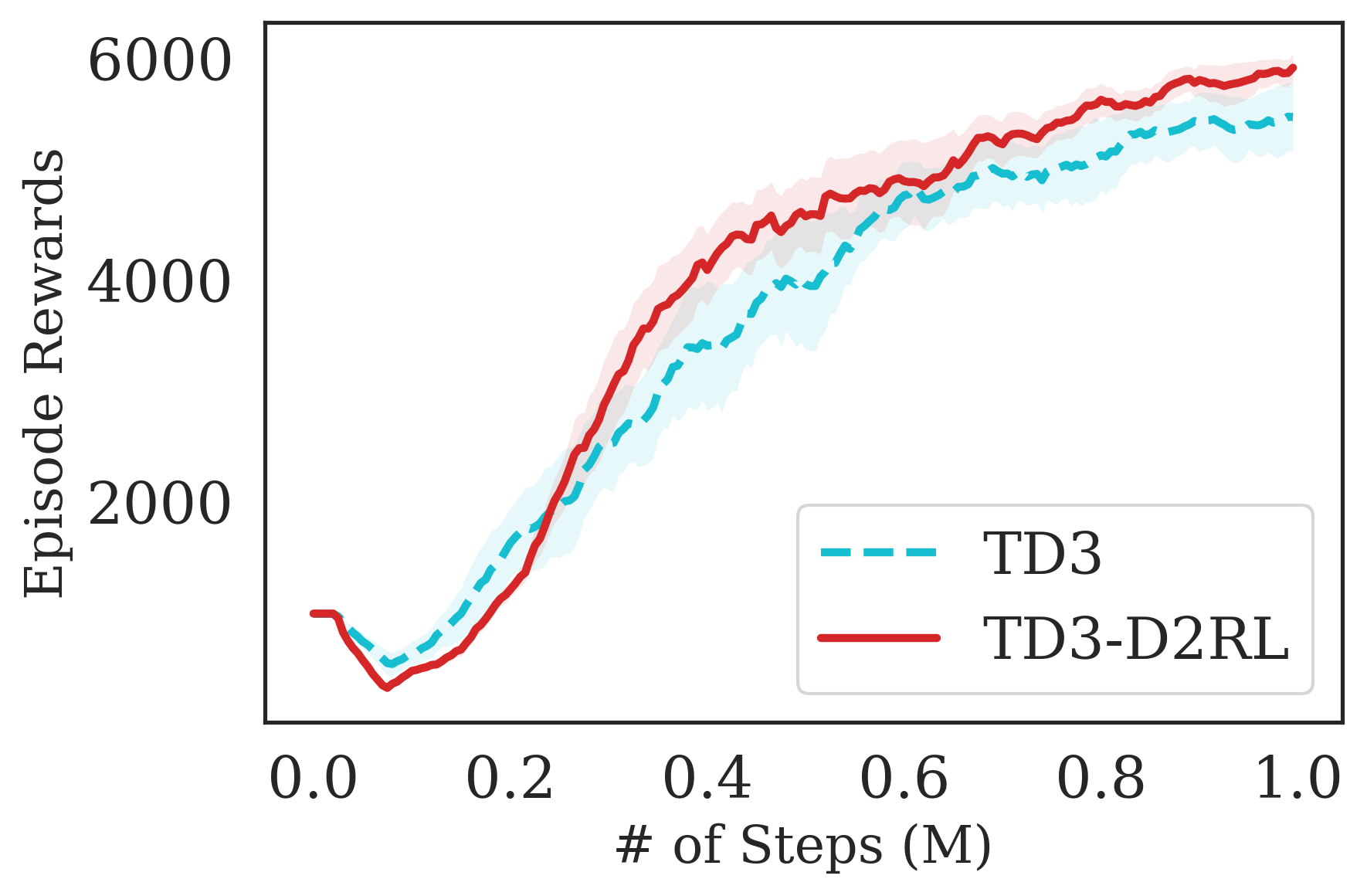
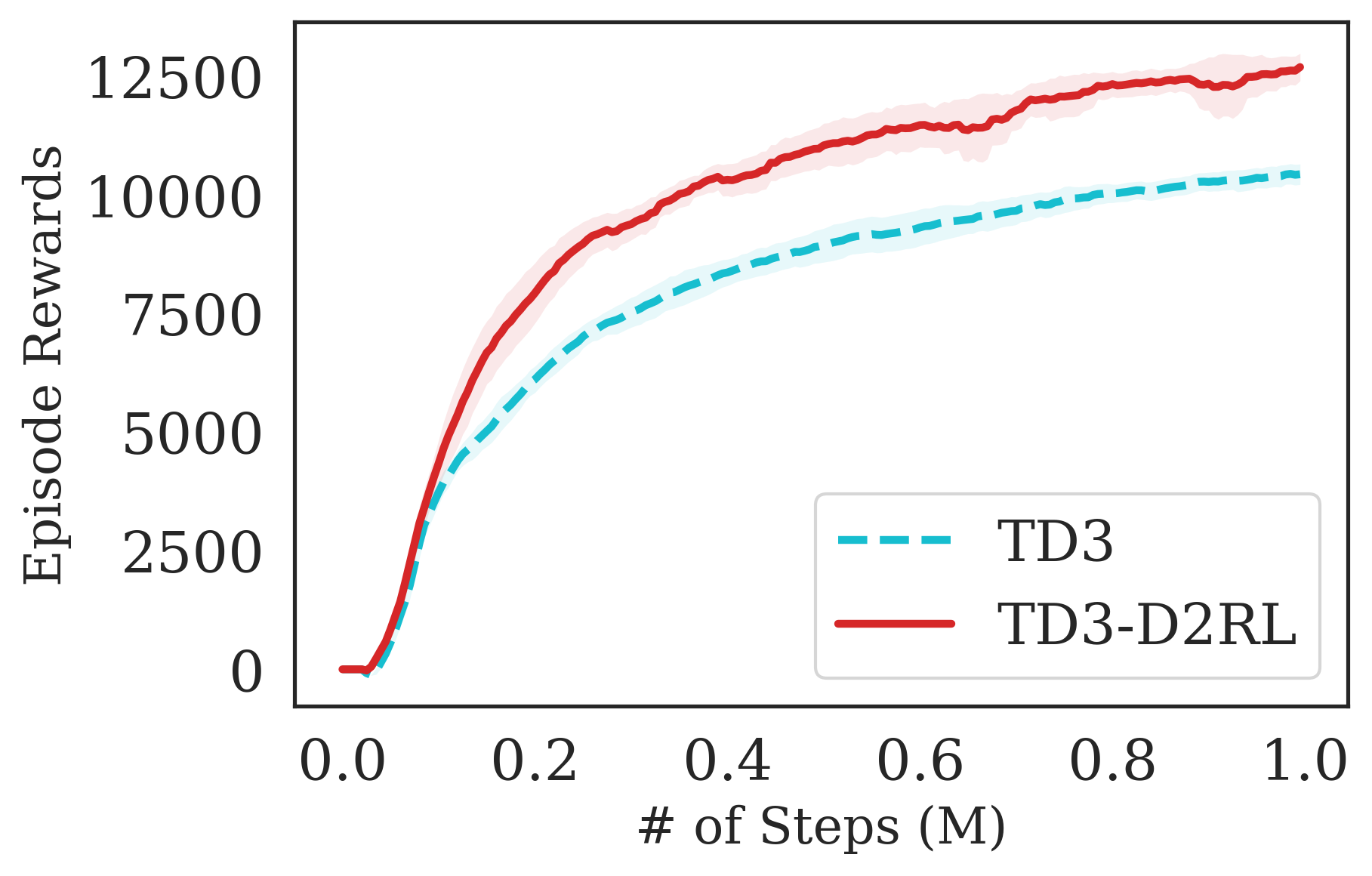
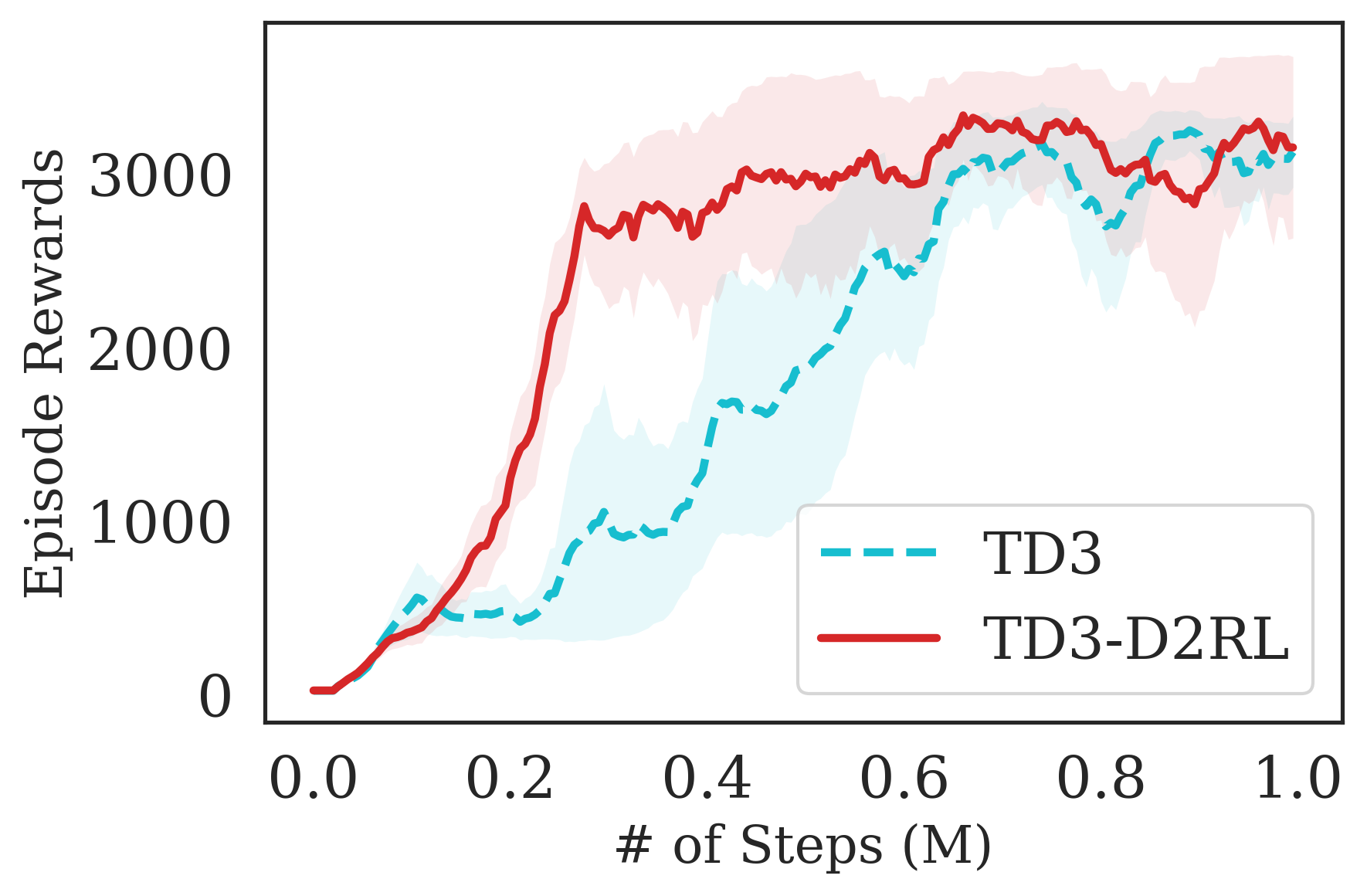
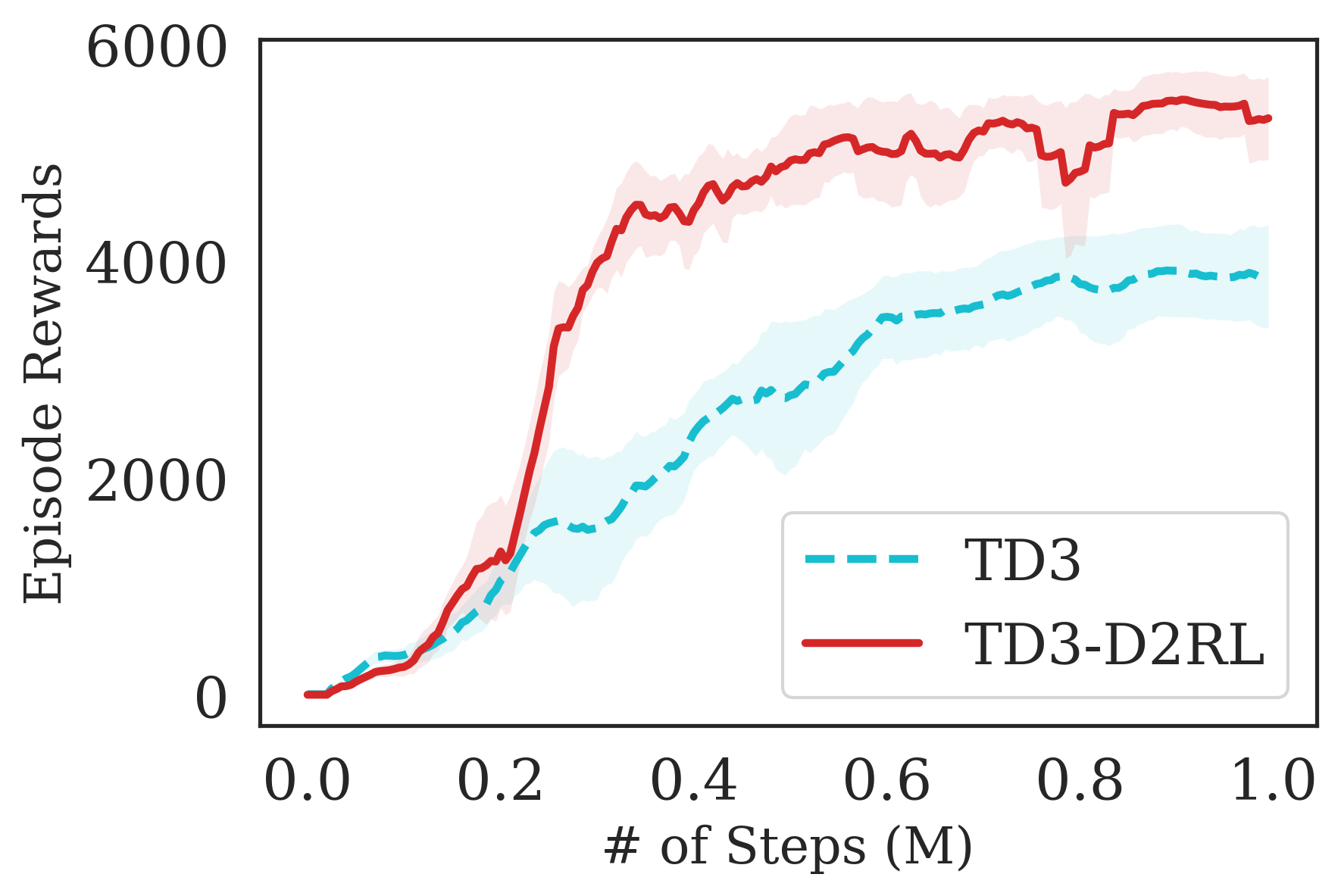
The proposed D2RL variant achieves superior performance compared to the baselines on state-based OpenAI Gym MuJoCo environments. We benchmark the proposed D2RL variant on a suite of OpenAI Gym (Brockman et al., 2016) environments by applying the modification to two standard RL algorithms, SAC (Haarnoja et al., 2018) and TD3 (Fujimoto et al., 2018). For all the environments, namely Ant, Cheetah, Hopper, Humanoid, and Walker, the observations received by the agent are state vectors consisting of the positions and velocities of joints of the agent. Additional details about the state-space and action-space are in the Appendix. From Fig. 4, we see that the proposed D2RL modification converges to significantly higher episodic rewards in most environments, and in others is competitive with the baseline. Also, these benefits can be seen across both the algorithms, SAC and TD3.
| From Images | From States | |||||
|---|---|---|---|---|---|---|
| 100K Step score | CURL | CURL-ResNet | CURL-D2RL | SAC | SAC-ResNet | SAC-D2RL |
| Finger, Spin | 767 57 | 548 120 | 837 18 | 459 48 | 551 57 | 627 107 |
| Cartpole, Swing | 582 142 | 327 101 | 836 34 | 717 14 | 701 24 | 751 12 |
| Reacher, Easy | 538 233 | 526 79 | 754 168 | 752 121 | 626 112 | 675 203 |
| Cheetah, Run | 299 48 | 230 17 | 253 57 | 587 58 | 633 28 | 721 43 |
| Walker, Walk | 403 24 | 275 57 | 540 143 | 132 43 | 456 89 | 354 159 |
| Ball in Cup, Catch | 769 43 | 450 169 | 880 48 | 867 42 | 880 22 | 891 33 |
| 500K Step score | CURL | CURL-ResNet | CURL-D2RL | SAC | SAC-ResNet | SAC-D2RL |
| Finger, Spin | 926 45 | 896 59 | 970 14 | 899 29 | 917 21 | 961 8 |
| Cartpole, Swing | 841 45 | 833 9 | 859 8 | 884 2 | 885 4 | 885 2 |
| Reacher, Easy | 929 44 | 900 48 | 929 62 | 973 23 | 969 34 | 952 30 |
| Cheetah, Run | 518 28 | 459 108 | 386 115 | 781 65 | 807 69 | 842 75 |
| Walker, Walk | 902 43 | 807 134 | 931 24 | 959 16 | 972 8 | 964 14 |
| Ball in Cup, Catch | 959 27 | 960 8 | 955 15 | 976 12 | 970 19 | 972 13 |
| 100K Step Score | TD3 | TD3-D2RL | 500K Step Score | TD3 | TD3-D2RL |
|---|---|---|---|---|---|
| Walker, Walk-Easy | 67 8 | 69 11 | Walker, Walk-Easy | 79 10 | 77 8 |
| Walker, Walk-Medium | 38 8 | 60 9 | Walker, Walk-Medium | 44 8 | 69 6 |
| Cartpole, Swing-Easy | 96 24 | 142 18 | Cartpole, Swing-Easy | 102 24 | 171 32 |
| Cartpole, Swing-Medium | 67 2 | 102 13 | Cartpole, Swing-Medium | 68 2 | 138 16 |
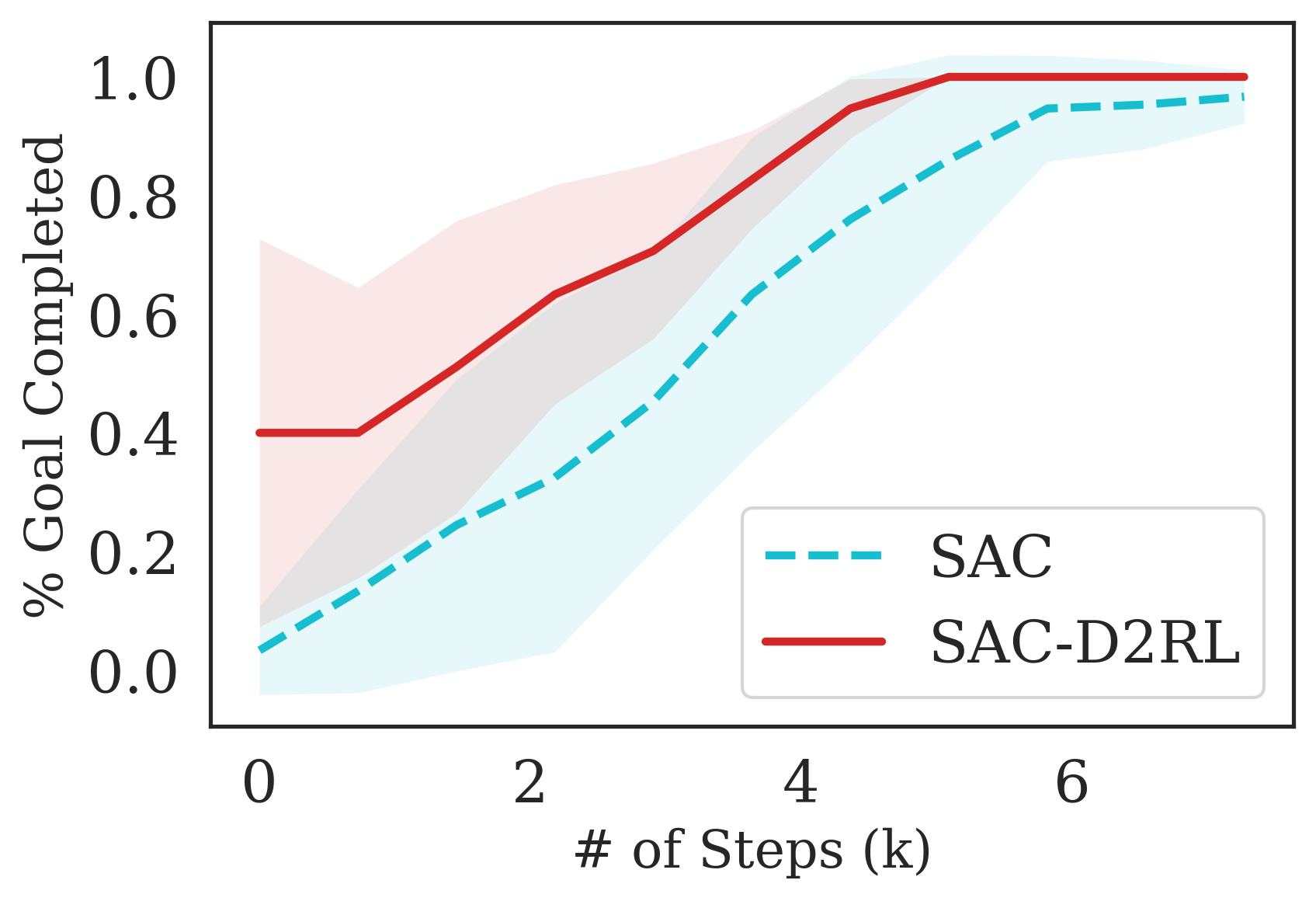
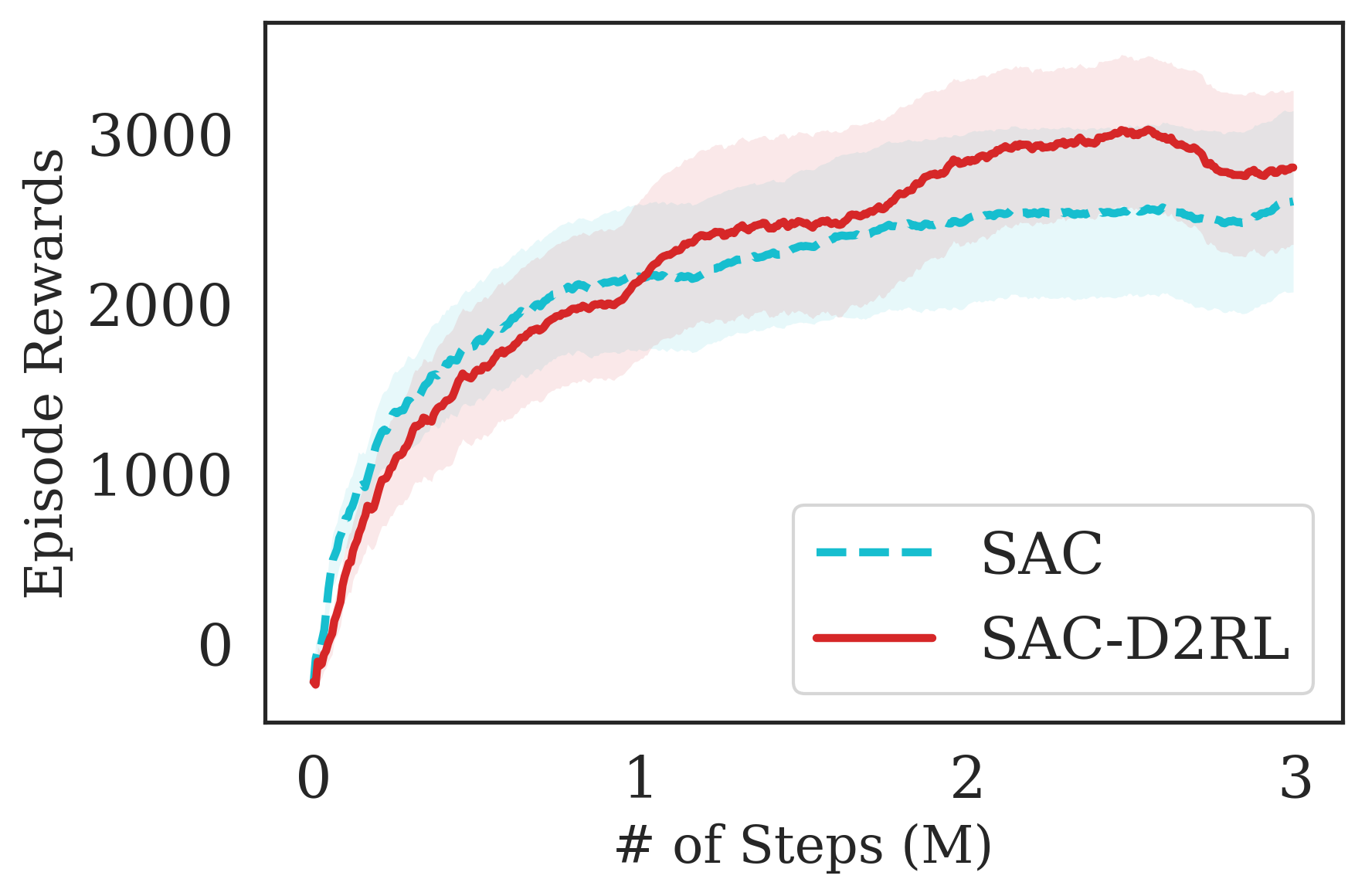
D2RL is more sample efficient compared to baseline state-of-the-art algorithms on both image-based and state-based DM Control Suite benchmark environments. We compare the proposed D2RL variant with SAC and state-of-the-art pixel-based CURL algorithms on the benchmark environments of DeepMind Control Suite (Tassa et al., 2020). For CURL, and CURL-D2RL, we train using only pixel-based observations from the environment. For SAC and SAC-D2RL, we train using proprioceptive features from the environment. The action spaces are the same in both the cases, pixels and state features based observations. The environments we consider are part of the benchamrk suite, and include Finger Spin, Cartpole Swing, Reacher Easy, Cheetah Run, Walker Walk, Ball in Cup Catch. Additional details are in the Appendix.
In Table 1, we tabulate results for all the algorithms after 100K environment interactions, and after 500K environment interactions. To report the results of the baseline, we simply use the results as reported in the original paper (Srinivas et al., 2020). From this Table, we observe that the D2RL variant performs better than the baselines for both 100K and 500K environment interactions, and the performance gains are especially significant in the 100K step scores. This indicates that D2RL is significantly more sample-efficient than the baseline.
D2RL performs significantly better in challenging environments with various modalities of noise, system delays, physical perturbations and dummy-dimensions (Dulac-Arnold et al., 2020). Dulac-Arnold et al. (2019) propose a set of challenges in the DM Control Suite environments that are more “realistic” by introducing the aforementioned problems. We train a TD3 agent Fujimoto et al. (2018) from states, on the “easy” and “medium” challenges for the walker-walk, and cartpole-swingup environments with and without D2RL. We present the results in Table 2. We see how the baseline TD3 agent gets significantly worse in the “medium” challenge compared to the “easy” version of the same environment. The agent trained with TD3-D2RL significantly outperforms the baseline TD3 agent on 3 of the 4 challenges, and the drop between the “easy” and “medium” challenges is significantly less severe, compared to the baseline. This experiment demonstrates how by using D2RL, we are able to get significantly better performance on environments which have been constructed to be more realistic by adding difficult problems that the agent must learn to reason with. The increased robustness to such problems further validates the general utility of D2RL in many different circumstances.
Verifying the alleviation of implicit underparameterization with D2RL. In Table 3, we compare effective ranks of the feature matrices for D2RL and a normal MLP, with the TD3 algorithm after 1M interactions, corresponding to Fig. 4. We observe that the effective ranks for D2RL are higher across environments. For this computation, we use the same formula of from (Kumar et al., 2020), where is the learned weight matrix of the penultimate layer of the nwtwork (i.e. the feature matrix). Kumar et al. (2020) showed that lower effective rank of the feature matrix correlates negatively with performance, and we believe this might help explain some of the empirical observations of better performance of D2RL. Using skip connections as in D2RL leads to higher effective rank feature matrices compared to standard MLPs used in deep RL, as can be seen from Table 3.
| Walker2d-v2 | Ant-v2 | Hopper-v2 | Cheetah-v2 | |||||
|---|---|---|---|---|---|---|---|---|
| 1M Steps | TD3 | TD3-D2RL | TD3 | TD3-D2RL | TD3 | TD3-D2RL | TD3 | TD3-D2RL |
| Policy | 153 | 161 | 165 | 178 | 145 | 159 | 157 | 161 |
| Q-network | 138 | 165 | 153 | 180 | 123 | 157 | 143 | 164 |
The sample efficiency and asymptotic performance of D2RL scale to complex robotic manipulation and locomotion environments. Additionally, we consider some challenging manipulation and locomotion environments with different robots, the details of which are discussed below:
Fetch-{Reach, Pick, Push, Slide}: There are four environments, where a Fetch robot is tasked with solving the tasks of reaching a goal location, picking an object and placing it at a goal location, pushing a puck to a goal location, and sliding a puck to a goal location. The the Fetch-Slide environment, it is ensured that sliding occurs instead of pusing because the goal location is beyong the end-effector’s reach. The observations to the agent consist of proprioceptive state features and the action space is the (x,y,z) position of the end-effector and the distance between the grippers.
Jaco-Reach: A Jaco robot arm with a three finger gripper is tasked with reaching a location location indicated by a red brick. The observations to the agent consist only of proprioceptive state features and the arm is joint torque controlled.
Ant-Maze: An Ant robot with four legs is tasked with navigating a U-shaped maze while being joint torque controlled. This is a challenging locomotion environment with a temporally-extended task, that requires the agent to move around the maze to reach the goal.
Baxter-Block Join and Lift: One arm of a Baxter robot with two fingers must be controlled to grasp a block, join it to another block and lift the combination above a certain goal height. The observations to the agent consist of proprioceptive state features and the action space is the (x,y,z) position of the end-effector and the distance between the grippers.
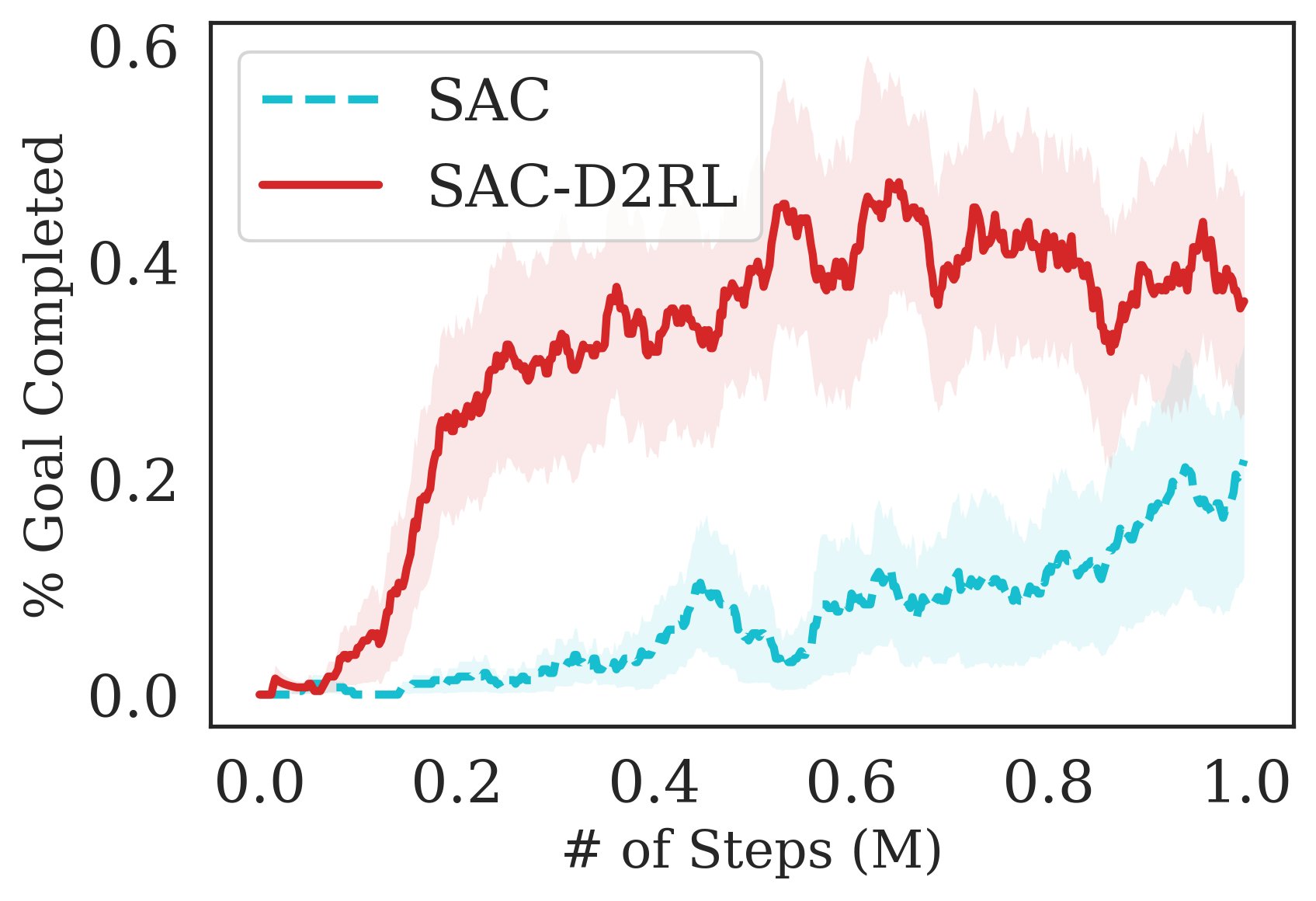
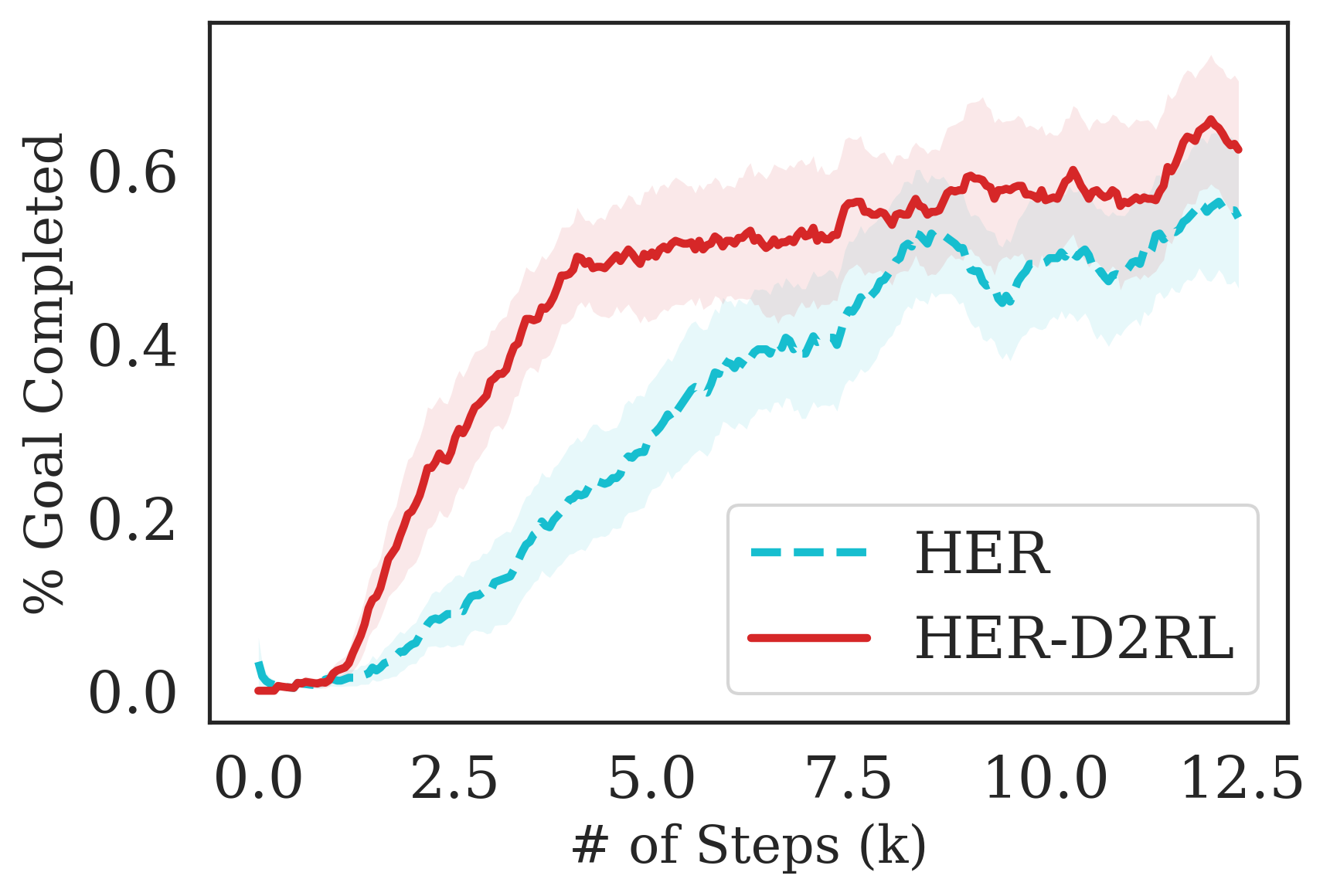
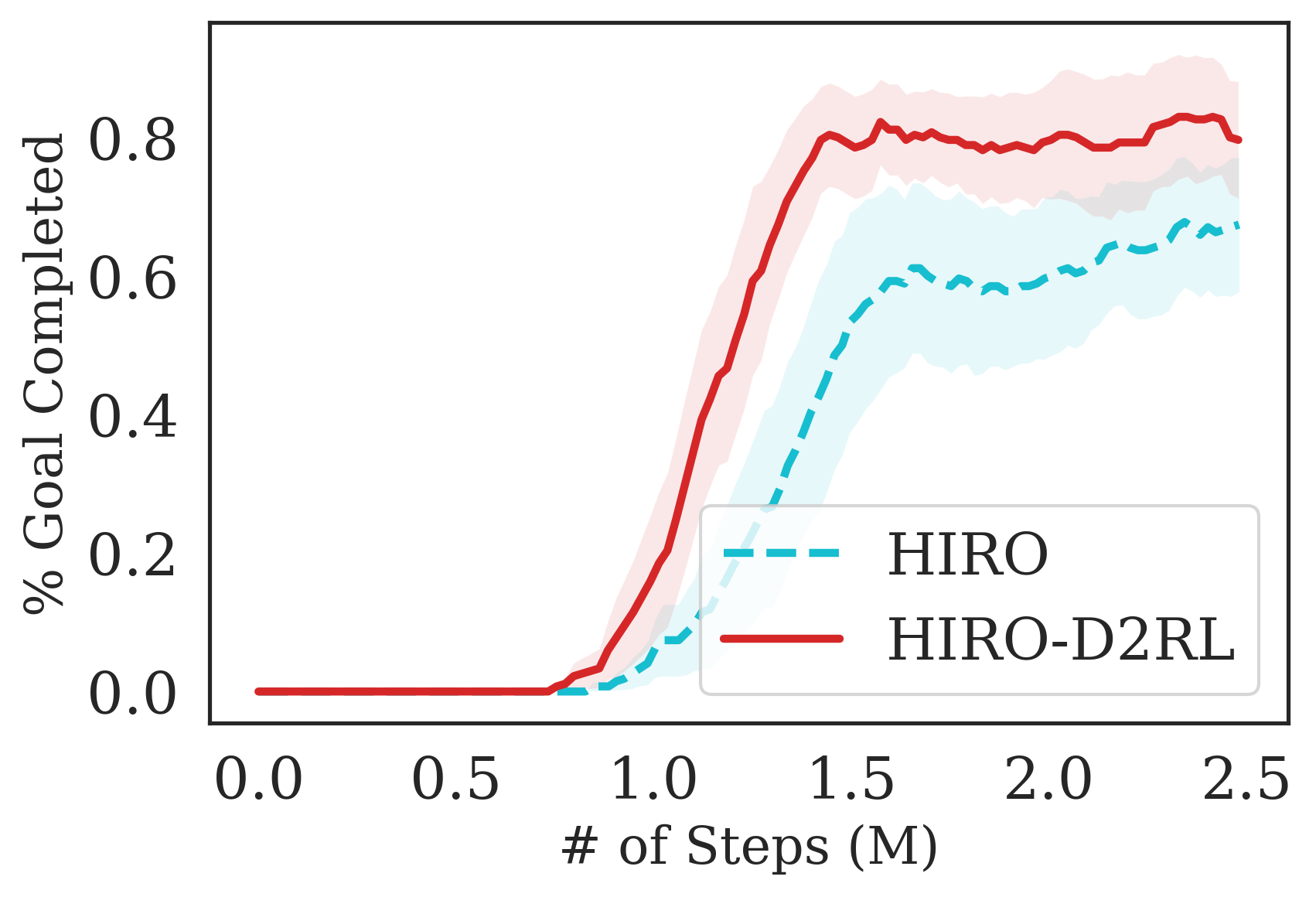
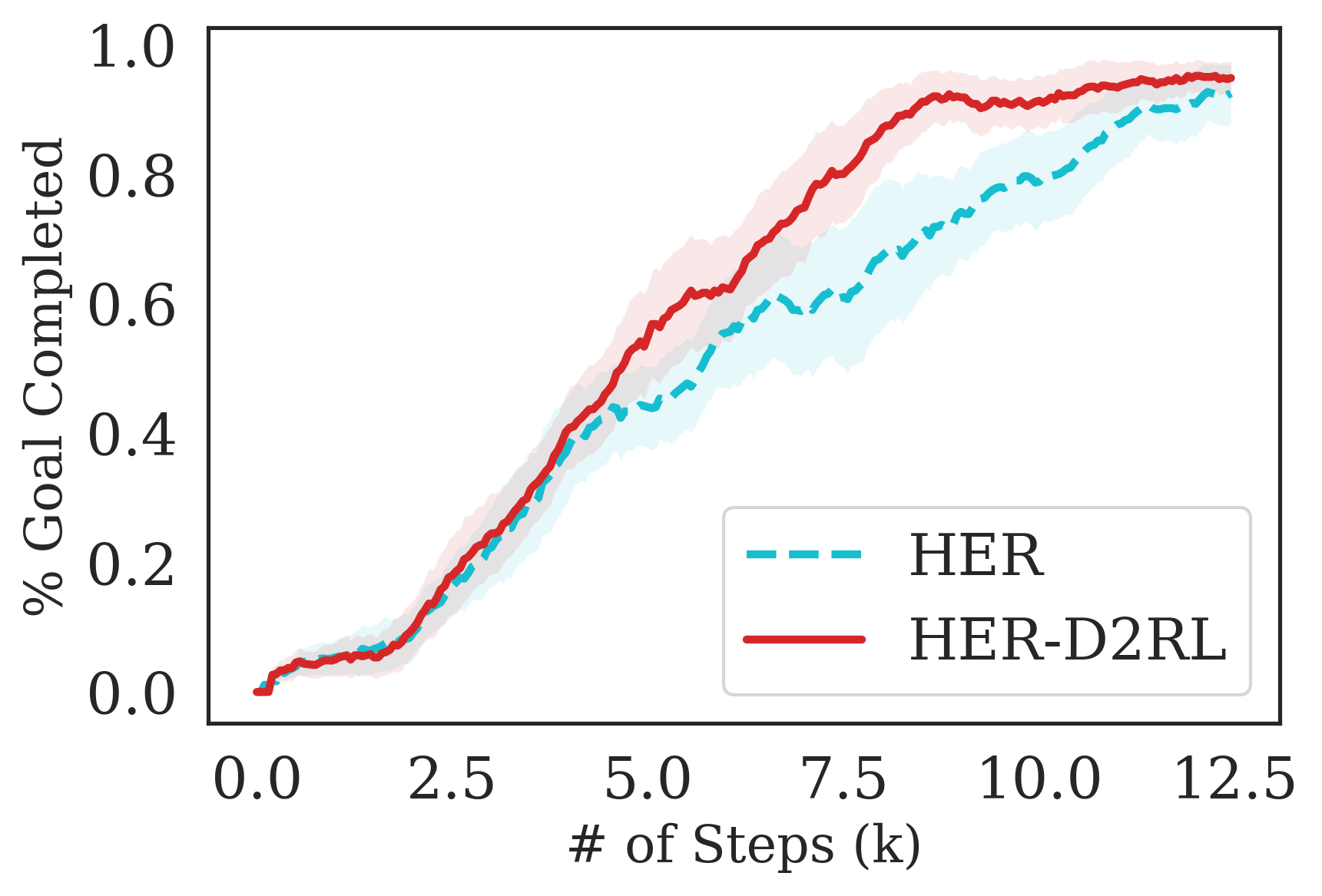
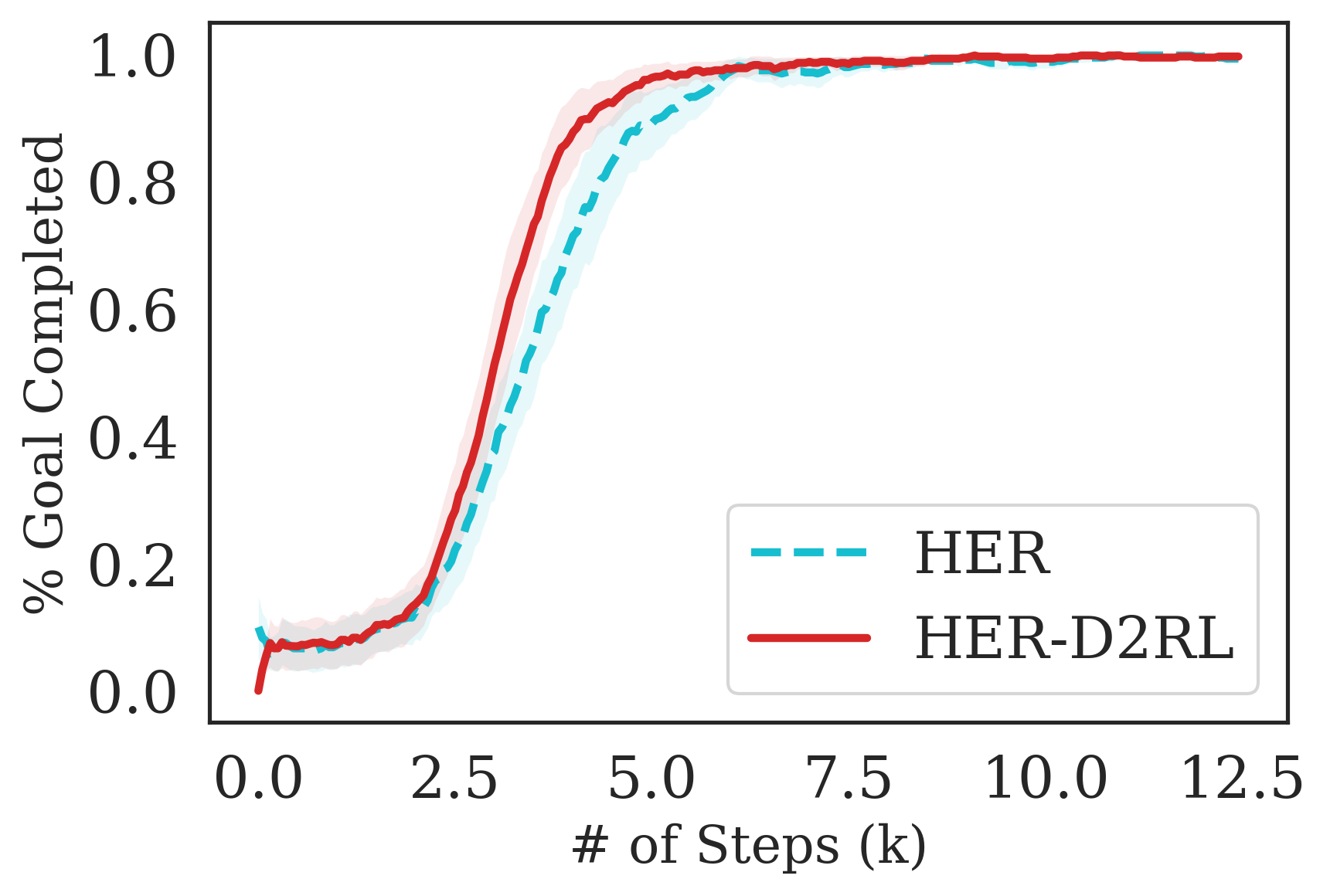
For the Fetch-{Reach, Pick, Push, Slide} environments, we consider the HER (Andrychowicz et al., 2017) algorithm (with DDPG (Qiu et al., 2019)) trained with sparse rewards that was shown to achieve state-of-the-art results in these environments. The plots for Fetch- Pick and Fetch-Push are in the Appendix, sue to space constraint here. In addition, we also show results with SAC on Fetch-Reach and Fetch-Slide trained using a SAC agent. For Ant-Maze, we consider the hierarchical RL algorithm HIRO (Nachum et al., 2018) that was shown to be successful in this very long horizon task. For Jaco-Reach and Baxter-Block Join and Lift, we consider the default SAC algorithm released with the environment codebase https://github.com/clvrai/furniture
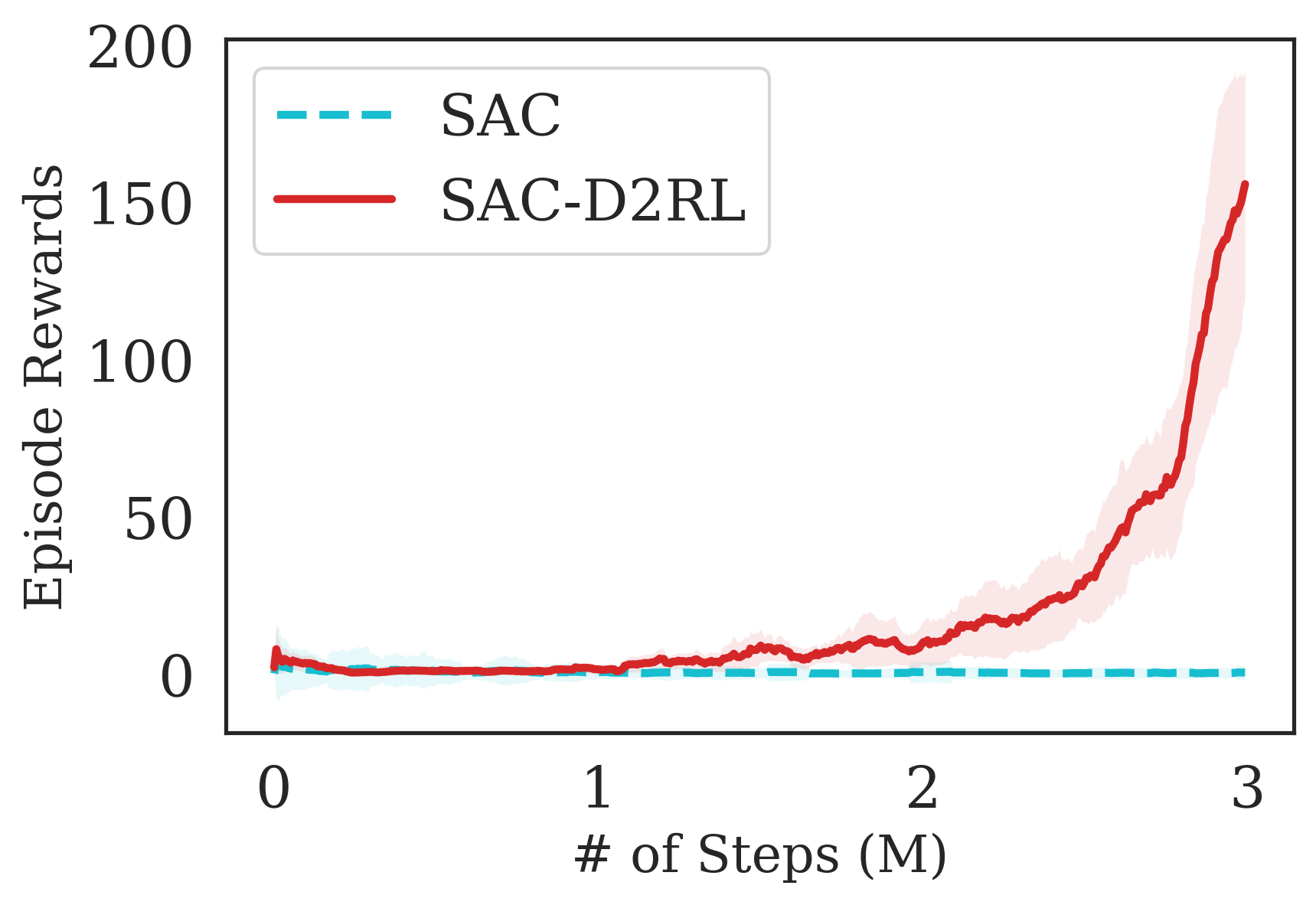
The results are summarized in Fig. 7, where we see that the proposed D2RL modification converges to higher episodic rewards and converges significantly faster in most environments. By performing a wide range of experiments on challenging robotics environments, we further notice significantly better sample efficiency on all environments which suggests the wide generality and applicability of D2RL. Interestingly, we also observe in 5(d) that SAC is unable to train the agent to perform the Jaco-Reach task in 3M environment steps, while SAC trained with D2RL policy and -networks is able to succesfully train an agent and starts outperforming the SAC baseline as early as 1M environment steps. This shows how crucial parameterization is in some environments as a simple 2-layer MLPs may not be sufficiently expressive or optimization using deeper network architectures may be necessary to solve such environments.
5.3 Comparisons with ResNet
Table 1 tabulates experiments with a ResNet-like MLP which utilizes residual connections instead of dense connections He et al. (2016a). We experiment with images using a base CURL agent Srinivas et al. (2020), and directly from proprioceptive features using a base SAC agent Haarnoja et al. (2018) on the DM Control Suite. We see that using D2RL clearly outperforms the ResNet agent on most tasks from images and state features. Residual connections add the features of a previous layer to the current layer instead of concatenating them (as done in D2RL). The same hyperparameters are used as D2RL for all experiments.
5.4 Ablation Studies
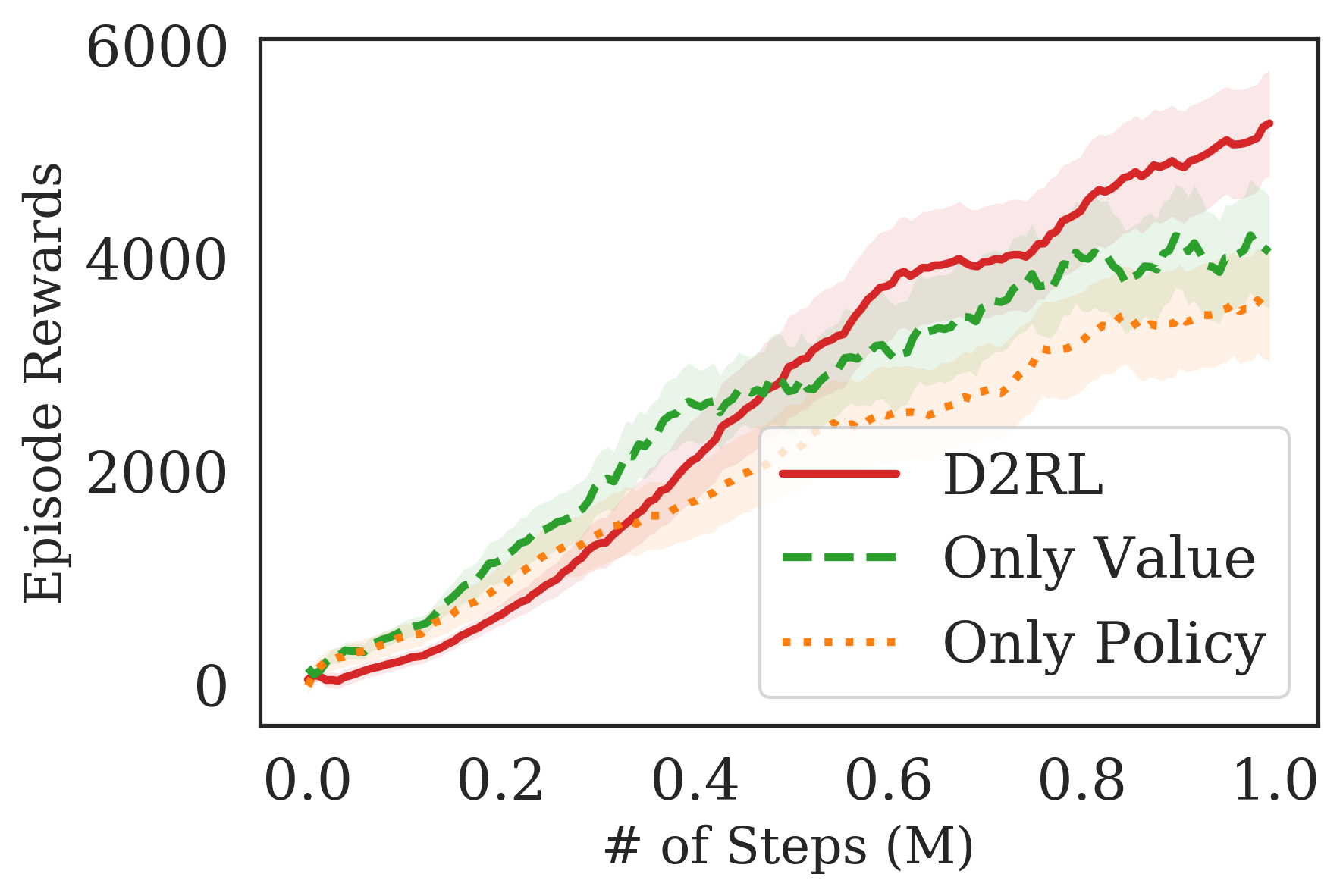
In this section, we look to answer the various components of using D2RL. We first analyze how the agent performs when only the policy or the value functions are parameterized as D2RL, while the other one is a vanilla 2-layer MLP. The results for training an SAC agent on Ant-v2 are present in Fig. 6(a), where we see that parameterizing both the networks as D2RL significantly outperforms when only one of the two use D2RL. However, one noteworthy observation can be made that when only the value functions are parameterized using D2RL, the agent significantly outperforms the variant where only the policy is parameterized using a D2RL. This suggests that it may be more important to parameterize the value function, but more research is required to give a more conclusive statement.
Similarly we train the same agent but instead vary the number of layers used while parameterizing the policies and value functions using D2RL. The results in Fig. 6(b) show that even when 8 layer D2RL is used, the results are only moderately worse that when using 4 layers, even though it has twice the depth and therefore twice as many parameters. These results are notably different from the results in Fig. 2, where as we increase the number of layers for vanilla MLPs to be greater than 2, we see a worsening results. The difference suggests that by using D2RL we are able to circumvent the issue of DPI that may hinder the performance for vanilla MLPs, as we postulated.
6 Discussion, Future Work, and Conclusion
In this paper, we investigated the effect of building better inductive biases into the architectures of the function approximators in deep reinforcement learning. We first looked into the effect of varying the number of layers to parameterize policies and value functions, and how the performance deteriorates as the number of layers increase. To overcome this problem, we proposed a generally applicable solution that significantly improves the sample efficiency of the state-of-the-art DRL baselines over a variety of manipulation, and locomotion environments with different robots, from both states and images. Studying the effect of network architectures has been long explored in computer vision and deep learning, and its benefits on performance have been well established. The effect of the network architectures, however, have not yet been studied in DRL and robotics. Improving the network architectures for a variety of popular standard actor-critic algorithms demonstrates the importance of building better inductive biases in the network paramterization such that we can improve the performance for the otherwise identical algorithms. In future work, we are interested in building better network architectures and further improving the underlying algorithms for robotic learning.
Acknowledgement
We thank Vector Institute Toronto for compute support, and Mayank Mittal, Irene Zhang, Alexandra Volokhova, Kevin Xie, and other members of the UofT CS Robotics group for helpful discussions and feedback on the draft. We thank Denis Yarats (NYU) for feedback on a previous version of the paper and for pointing out the findings about network architecture in SAC-AE. We thank Richard Song (Google) for providing insights on using wider networks in RL and the implications this could have in terms of generalization. We are grateful to Kei Ohta (Mitsubishi) for independently reproducing a Tensorflow 2 version of D2RL. HB thanks Aviral Kumar (UC Berkeley) for suggesting the connection D2RL might have in alleviating implicit under-parameterization in Deep Q learning.
References
- Akkaya et al. (2019) Ilge Akkaya, Marcin Andrychowicz, Maciek Chociej, Mateusz Litwin, Bob McGrew, Arthur Petron, Alex Paino, Matthias Plappert, Glenn Powell, Raphael Ribas, et al. Solving rubik’s cube with a robot hand. arXiv preprint arXiv:1910.07113, 2019.
- Andrychowicz et al. (2017) Marcin Andrychowicz, Filip Wolski, Alex Ray, Jonas Schneider, Rachel Fong, Peter Welinder, Bob McGrew, Josh Tobin, OpenAI Pieter Abbeel, and Wojciech Zaremba. Hindsight experience replay. In Advances in neural information processing systems, pp. 5048–5058, 2017.
- Berthelot et al. (2019) David Berthelot, Nicholas Carlini, Ian Goodfellow, Nicolas Papernot, Avital Oliver, and Colin A Raffel. Mixmatch: A holistic approach to semi-supervised learning. In Advances in Neural Information Processing Systems, pp. 5049–5059, 2019.
- Brockman et al. (2016) Greg Brockman, Vicki Cheung, Ludwig Pettersson, Jonas Schneider, John Schulman, Jie Tang, and Wojciech Zaremba. Openai gym. arXiv preprint arXiv:1606.01540, 2016.
- Chen et al. (2020) Ting Chen, Simon Kornblith, Mohammad Norouzi, and Geoffrey Hinton. A simple framework for contrastive learning of visual representations. arXiv preprint arXiv:2002.05709, 2020.
- Dieng et al. (2019) Adji B Dieng, Yoon Kim, Alexander M Rush, and David M Blei. Avoiding latent variable collapse with generative skip models. In The 22nd International Conference on Artificial Intelligence and Statistics, pp. 2397–2405, 2019.
- Dulac-Arnold et al. (2019) Gabriel Dulac-Arnold, Daniel Mankowitz, and Todd Hester. Challenges of real-world reinforcement learning. arXiv preprint arXiv:1904.12901, 2019.
- Dulac-Arnold et al. (2020) Gabriel Dulac-Arnold, Nir Levine, Daniel J Mankowitz, Jerry Li, Cosmin Paduraru, Sven Gowal, and Todd Hester. An empirical investigation of the challenges of real-world reinforcement learning. arXiv preprint arXiv:2003.11881, 2020.
- Fujimoto et al. (2018) Scott Fujimoto, Herke Van Hoof, and David Meger. Addressing function approximation error in actor-critic methods. arXiv preprint arXiv:1802.09477, 2018.
- Haarnoja et al. (2018) Tuomas Haarnoja, Aurick Zhou, Pieter Abbeel, and Sergey Levine. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. arXiv preprint arXiv:1801.01290, 2018.
- Hafner et al. (2019) Danijar Hafner, Timothy Lillicrap, Jimmy Ba, and Mohammad Norouzi. Dream to control: Learning behaviors by latent imagination. arXiv preprint arXiv:1912.01603, 2019.
- He et al. (2016a) Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 770–778, 2016a.
- He et al. (2016b) Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Identity mappings in deep residual networks. In European conference on computer vision, pp. 630–645. Springer, 2016b.
- He et al. (2020) Kaiming He, Haoqi Fan, Yuxin Wu, Saining Xie, and Ross Girshick. Momentum contrast for unsupervised visual representation learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 9729–9738, 2020.
- Higgins et al. (2017) Irina Higgins, Arka Pal, Andrei A Rusu, Loic Matthey, Christopher P Burgess, Alexander Pritzel, Matthew Botvinick, Charles Blundell, and Alexander Lerchner. Darla: Improving zero-shot transfer in reinforcement learning. arXiv preprint arXiv:1707.08475, 2017.
- Hochreiter & Schmidhuber (1997) Sepp Hochreiter and Jürgen Schmidhuber. Long short-term memory. Neural computation, 9(8):1735–1780, 1997.
- Huang et al. (2017) Gao Huang, Zhuang Liu, Laurens Van Der Maaten, and Kilian Q Weinberger. Densely connected convolutional networks. In Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 4700–4708, 2017.
- Ioffe & Szegedy (2015) Sergey Ioffe and Christian Szegedy. Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv preprint arXiv:1502.03167, 2015.
- Kalashnikov et al. (2018) Dmitry Kalashnikov, Alex Irpan, Peter Pastor, Julian Ibarz, Alexander Herzog, Eric Jang, Deirdre Quillen, Ethan Holly, Mrinal Kalakrishnan, Vincent Vanhoucke, et al. Qt-opt: Scalable deep reinforcement learning for vision-based robotic manipulation. arXiv preprint arXiv:1806.10293, 2018.
- Kostrikov et al. (2020) Ilya Kostrikov, Denis Yarats, and Rob Fergus. Image augmentation is all you need: Regularizing deep reinforcement learning from pixels. arXiv preprint arXiv:2004.13649, 2020.
- Krizhevsky et al. (2012) Alex Krizhevsky, Ilya Sutskever, and Geoffrey E Hinton. Imagenet classification with deep convolutional neural networks. In Advances in neural information processing systems, pp. 1097–1105, 2012.
- Kumar et al. (2020) Aviral Kumar, Rishabh Agarwal, Dibya Ghosh, and Sergey Levine. Implicit under-parameterization inhibits data-efficient deep reinforcement learning. arXiv preprint arXiv:2010.14498, 2020.
- Laskin et al. (2020) Michael Laskin, Kimin Lee, Adam Stooke, Lerrel Pinto, Pieter Abbeel, and Aravind Srinivas. Reinforcement learning with augmented data. arXiv preprint arXiv:2004.14990, 2020.
- LeCun et al. (1998) Yann LeCun, Léon Bottou, Yoshua Bengio, and Patrick Haffner. Gradient-based learning applied to document recognition. Proceedings of the IEEE, 86(11):2278–2324, 1998.
- Nachum et al. (2018) Ofir Nachum, Shixiang Shane Gu, Honglak Lee, and Sergey Levine. Data-efficient hierarchical reinforcement learning. In Advances in Neural Information Processing Systems, pp. 3303–3313, 2018.
- Nair et al. (2018) Ashvin V Nair, Vitchyr Pong, Murtaza Dalal, Shikhar Bahl, Steven Lin, and Sergey Levine. Visual reinforcement learning with imagined goals. In Advances in Neural Information Processing Systems, pp. 9191–9200, 2018.
- Ota et al. (2020) Kei Ota, Tomoaki Oiki, Devesh K Jha, Toshisada Mariyama, and Daniel Nikovski. Can increasing input dimensionality improve deep reinforcement learning? arXiv preprint arXiv:2003.01629, 2020.
- Paszke et al. (2019) Adam Paszke, Sam Gross, Francisco Massa, Adam Lerer, James Bradbury, Gregory Chanan, Trevor Killeen, Zeming Lin, Natalia Gimelshein, Luca Antiga, et al. Pytorch: An imperative style, high-performance deep learning library. In Advances in neural information processing systems, pp. 8026–8037, 2019.
- Qiu et al. (2019) Chengrun Qiu, Yang Hu, Yan Chen, and Bing Zeng. Deep deterministic policy gradient (ddpg)-based energy harvesting wireless communications. IEEE Internet of Things Journal, 6(5):8577–8588, 2019.
- (30) Alec Radford, Jeffrey Wu, Rewon Child, David Luan, Dario Amodei, and Ilya Sutskever. Language models are unsupervised multitask learners.
- Rolnick & Tegmark (2017) David Rolnick and Max Tegmark. The power of deeper networks for expressing natural functions. arXiv preprint arXiv:1705.05502, 2017.
- Ronneberger et al. (2015) Olaf Ronneberger, Philipp Fischer, and Thomas Brox. U-net: Convolutional networks for biomedical image segmentation. In International Conference on Medical image computing and computer-assisted intervention, pp. 234–241. Springer, 2015.
- Santurkar et al. (2018) Shibani Santurkar, Dimitris Tsipras, Andrew Ilyas, and Aleksander Madry. How does batch normalization help optimization? In Advances in Neural Information Processing Systems, pp. 2483–2493, 2018.
- Schulman et al. (2015) John Schulman, Sergey Levine, Pieter Abbeel, Michael Jordan, and Philipp Moritz. Trust region policy optimization. In International conference on machine learning, pp. 1889–1897, 2015.
- Song et al. (2019) Xingyou Song, Yiding Jiang, Yilun Du, and Behnam Neyshabur. Observational overfitting in reinforcement learning. arXiv preprint arXiv:1912.02975, 2019.
- Srinivas et al. (2020) Aravind Srinivas, Michael Laskin, and Pieter Abbeel. Curl: Contrastive unsupervised representations for reinforcement learning. arXiv preprint arXiv:2004.04136, 2020.
- Tassa et al. (2020) Yuval Tassa, Saran Tunyasuvunakool, Alistair Muldal, Yotam Doron, Siqi Liu, Steven Bohez, Josh Merel, Tom Erez, Timothy Lillicrap, and Nicolas Heess. dm_control: Software and tasks for continuous control, 2020.
- Tesauro (1995) Gerald Tesauro. Temporal difference learning and td-gammon. Communications of the ACM, 38(3):58–68, 1995.
- Vaswani et al. (2017) Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N Gomez, Łukasz Kaiser, and Illia Polosukhin. Attention is all you need. In Advances in neural information processing systems, pp. 5998–6008, 2017.
- Yarats et al. (2019) Denis Yarats, Amy Zhang, Ilya Kostrikov, Brandon Amos, Joelle Pineau, and Rob Fergus. Improving sample efficiency in model-free reinforcement learning from images. arXiv preprint arXiv:1910.01741, 2019.
Appendix A Pytorch Code
Appendix B Additional Experiments

Appendix C Hyperparameters and Environment details
| Hyperparameter | Value |
|---|---|
| Hidden units (MLP) | for Gym |
| for DM Control (Yarats et al., 2019) | |
| Evaluation episodes | |
| Optimizer | Adam |
| Learning rate | |
| Learning rate () | |
| MiniBatch Size | |
| Non-linearity | ReLU |
| Discount | |
| Initial temperature |
| Hyperparameter | Value |
|---|---|
| Random crop | True |
| Observation rendering | |
| Observation downsampling | |
| Replay buffer size | |
| Initial steps | |
| Stacked frames | |
| Action repeat | finger, spin; walker, walk |
| cartpole, swingup | |
| otherwise | |
| Hidden units (MLP) | (Yarats et al., 2019) |
| Evaluation episodes | |
| Optimizer | Adam |
| Learning rate | |
| Learning rate () | |
| Batch Size | (cheetah), 128 (rest) |
| function EMA | |
| Critic target update freq | |
| Convolutional layers | |
| Number of filters | |
| Non-linearity | ReLU |
| Encoder EMA | |
| Latent dimension | |
| Discount | |
| Initial temperature |
| Environment | Type | Controller | Inputs | Action dim. | Input dim. |
|---|---|---|---|---|---|
| Gym Cheetah | Locomotion | Joint torque | States | 6 | 17 |
| Gym Hopper | Locomotion | Joint torque | States | 3 | 11 |
| Gym Humanoid | Locomotion | Joint torque | States | 17 | 376 |
| Gym Walker | Locomotion | Joint torque | States | 6 | 17 |
| Gym Ant | Locomotion | Joint torque | States | 8 | 111 |
| Finger, Spin | Classical control | Joint torque | States/Images | 2 | 9 / 84x84x3 |
| Cartpole, Swing | Classical control | Joint torque | States/Images | 1 | 5 / 84x84x3 |
| Reacher, Easy | Classical control | Joint torque | States/Images | 2 | 6 / 84x84x3 |
| Cheetah, Run | Locomotion | Joint torque | States/Images | 6 | 17 / 84x84x3 |
| Walker, Walk | Locomotion | Joint torque | States/Images | 6 | 24 / 84x84x3 |
| Ball in a Cup, Catch | Manipulation | Joint torque | States/Images | 2 | 8 / 84x84x3 |
| Fetch Reach | Manipulation | EE position | States | 4 | 10 |
| Fetch Pick and Place | Manipulation | EE position | States | 4 | 25 |
| Fetch Push | Manipulation | EE position | States | 4 | 25 |
| Fetch Slide | Manipulation | EE position | States | 3 | 25 |
| Jaco Reach | Manipulation | Joint torque | States | 9 | 45 |
| Baxter JoinLift | Manipulation | Joint torque | States | 15 | 42 |
| Ant Maze | Locomotion | Joint torque | States | 8 | 30 |