Cyclotron resonance in Kondo insulator

We consider a simple model of a Kondo insulator composed of single orbital conduction electrons and $f$-electrons with pseudo-spins in two dimensions  Knolle and Cooper (2015); Zhang et al. (2016); Pal et al. (2016); Ram and Kumar (2017); Shen and Fu (2018); Grubinskas and Fritz (2018); Peters et al. (2019); Erten et al. (2016); Knolle and Cooper (2017a); Sodemann et al. (2018). Effects of three dimensionality will be discussed later. Since our primary purpose is to clarify the cyclotron resonance in a general Kondo insulator, we consider both of a non-topological insulator and topological insulator on an equal footing. The Hamiltonian is $H=\int d^{2}x\psi^{\dagger}(\mbox{\boldmath$x$}){\mathcal{H}}\psi(\mbox{\boldmath$x$})$,

$\displaystyle{\mathcal{H}}$

$\displaystyle=\left(\begin{array}[]{cc}\frac{\pi^{2}}{2m_{c}}+\frac{g_{c}\mu_{B}}{2}\sigma_{z}B&v_{0}+v_{1}a\mbox{\boldmath$\pi$}\cdot\mbox{\boldmath$\sigma$}^{t}\\ v_{0}+v_{1}a\mbox{\boldmath$\pi$}\cdot\mbox{\boldmath$\sigma$}^{t}&-\frac{\pi^{2}}{2m_{f}}+\epsilon_{f0}+\frac{g_{f}\mu_{B}}{2}\sigma_{z}B\end{array}\right),$

(3)

where $\psi(\mbox{\boldmath$x$})=(\psi_{c\uparrow},\psi_{c\downarrow},\psi_{f\uparrow},\psi_{f\downarrow})$ is the field operator for the conduction and $f$-electrons. $\mbox{\boldmath$\pi$}=-i\hbar\nabla+e\mbox{\boldmath$A$}$ with the electric charge $-e<0$ is the dynamical momentum and $A$ is a vector potential for a uniform magnetic field $\mbox{\boldmath$B$}=\nabla\times\mbox{\boldmath$A$}=(0,0,B)$ with $B>0$. $m_{c},m_{f}$ are effective masses for the conduction electrons and $f$-electrons respectively, and $m_{c}$ is assumed to equal the bare electron mass $m_{0}$ and $m_{f}=0.1m_{c}$ for brevity. $\epsilon_{f0}$ is the $f$-electron energy level, and $v_{0},v_{1}$ represent hybridization strength with a characteristic lattice length scale $a\sim$ few Å which is taken to be the length unit. The system is a topological Kondo insulator when $v_{0}=0,v_{1}\neq 0$, while it is a non-topological one for $v_{0}\neq 0,v_{1}=0$ Dzero et al. (2010, 2016). $\mu_{B}=e\hbar/2m_{0}$ is the Bohr magneton and $g$-factors are assumed to be $g_{c}=g_{f}=2$ for simplicity. We use the energy unit $t_{0}\equiv\hbar^{2}/(2m_{0}a^{2})$, and set $\hbar=1$ and the Boltzmann constant $k_{B}=1$. We fix the model parameters as $\epsilon_{f0}=0.5t_{0}$, and $(v_{0},v_{1})=(0.05t_{0},0)$ for a non-topological insulator and $(v_{0},v_{1})=(0,0.05t_{0})$ for a topological insulator, where the activation gaps at zero magnetic field are $\Delta_{0}=2v_{0}=0.1t_{0}$ and $\Delta_{1}=\sqrt{\epsilon_{f0}^{2}-(4(v_{1}a)^{2}m_{c}m_{f}/(m_{c}+m_{f}))^{2}}\simeq 0.067t_{0}$, respectively. Although these parameters may be too large when considering the Kondo insulators SmB₆ and YbB₁₂, they will be renormalized by the strong Coulomb interactions between the $f$-electrons as $m_{f}\rightarrow m_{f}/z,v_{0,1}\rightarrow\sqrt{z}v_{0,1}$ with a renormalization factor $z\ll 1$. We have confirmed that our results are qualitatively unchanged when we use different parameter values.

It is straightforward to diagonalize the Hamiltonian (3). We expand the field operator as $\psi_{i}(\mbox{\boldmath$x$})=\sum_{nk}a_{nki}\phi_{nk}(\mbox{\boldmath$x$})$ ($i$ represents $i=(c,\uparrow)$ etc.) by using the harmonic oscillator single-particle wave functions $\phi_{nk}$ with a Landau level $n$ and an index for degeneracy $k$. $a_{nk}$ is the corresponding annihilation operator. For a system in the infinite cylinder geometry with the size $L_{x}=\infty,L_{y}<\infty$, the lowest Landau level wave function is $\phi_{0k}=1/\sqrt{\sqrt{\pi}l_{B}L_{y}}\exp(iky-(x-kl_{B}^{2})^{2}/2l_{B}^{2})$ under the Landau gauge $\mbox{\boldmath$A$}=(0,Bx,0)$. They satisfy $l_{B}\pi_{+}\phi_{nk}=\sqrt{n+1}\phi_{n+1k},l_{B}\pi_{-}\phi_{nk}=\sqrt{n}\phi_{n-1k}$, where $\pi_{\pm}=(\pi_{x}\pm i\pi_{y})/\sqrt{2}$ and $l_{B}=1/\sqrt{eB}$ is the magnetic length. We suppress the index $k$ because it is not directly involved in the following discussions. The Hamiltonian ${\mathcal{H}}_{n,ij}$ in the Landau level basis gives eigenvalues $\{\varepsilon_{nm}\}_{m=1}^{4}$ and eigenvectors $\{u_{n,im}\}_{m=1}^{4}$Knolle and Cooper (2015); Zhang et al. (2016). The energy spectra for both the non-topological and topological cases are shown in Fig. 1. The gap closes at a critical value $b_{c}\simeq 0.058$ with $b\equiv eB/(m_{0}t_{0})=4\pi Ba^{2}/\phi_{0}$ ($\phi_{0}=h/e$ is the magnetic flux quantum) for both $(v_{0},v_{1})=(0.05t_{0},0),(v_{0},v_{1})=(0,0.05t_{0})$ and the system becomes metallic for $b>b_{c}$, corresponding to a field induced metallic phase as seen in SmB₆ and YbB₁₂  Cooley et al. (1999); Chen et al. (2015); Shahrokhvand et al. (2017); Wolgast et al. (2017); Sugiyama et al. (1988); Terashima et al. (2017, 2018). For simplicity, we set the chemical potential so that it coincides with the energy where the gap closes, $\mu=0.454t_{0}$ for the non-topological case and $\mu=0.45t_{0}$ for the topological case, respectively. The Landau level structure is complicated, but roughly speaking, it is a combination of $\varepsilon_{cn}=\omega_{c}(n+1/2)$ and $\varepsilon_{fn}=-\omega_{f}(n+1/2)+\epsilon_{f0}$ with Zeeman shifts, and Landau levels change their characters between conduction-electron-like one and $f$-electron-like one successively as $b$ increases. Because of the hybridization $v_{0,1}$, energy spacing between the neighboring Landau levels is not exactly $\omega_{c},\omega_{f}$ but can be in between them especially when the crossover in Landau level’s character takes place, which is responsible for quantum oscillations in static qunatities. We will see in the following that the magneto-optical conductivity can faithfully reflect these characteristic structures, providing rich information on the unusual Landau levels.

Before going to the discussion on cyclotron resonance, we first give a brief overview on the quantum oscillations of orbital magnetization at zero temperature (de Haas-van Alphen (dHvA) effect) to provide an intuitive insight of the characteristic Landau levels  Knolle and Cooper (2015). This will be helpful for understanding the intimate relationship between the quantum oscillations and cyclotron resonance discussed in the next section. In this section, we keep the Planck constant $\hbar$ explicitely. For simplicity we ignore the Zeeman effect and consider $m_{f}\rightarrow\infty,v_{0}\neq 0,v_{1}=0$ (a similar discussion holds for the topological $v_{0}=0,v_{1}\neq 0$ case). In this case, the energy spectrum is given by

$\displaystyle\varepsilon_{n\pm}=\frac{1}{2}[\varepsilon_{cn}+\epsilon_{f0}\pm\sqrt{(\varepsilon_{cn}-\epsilon_{f0})^{2}+4v_{0}^{2}}],$

(4)

where $\varepsilon_{cn}=\hbar\omega_{c}(n+1/2)$. At zero temperature limit $T\rightarrow 0$, only the lower energies $\varepsilon_{n-}<\mu$ contribute to the ground state energy. In the limit of small hybridization $v_{0}\ll\epsilon_{f0}$, it behaves as $\varepsilon_{n-}\simeq\varepsilon_{nc}-(\varepsilon_{cn}^{2}+4v_{0}^{2})/\epsilon_{f0}$ for $B\ll B_{n}$, while $\varepsilon_{n-}\simeq\epsilon_{f0}-(\epsilon_{f0}^{2}+4v_{0}^{2})/\varepsilon_{cn}$ for $B\gg B_{n}$, where $B_{n}$ is the crossover scale between the conduction-electron-like character and $f$-electron-like character defined by $\hbar\omega_{c}(n+1/2)=\epsilon_{f0}$, or equivalently $B_{n}=m_{c}\epsilon_{f0}/(e\hbar(n+1/2))$. To perform a simple analytical calculation, we introduce an approximation where $\varepsilon_{n-}$ is replaced by

$\displaystyle\varepsilon_{n-}=\left\{\begin{array}[]{ll}\varepsilon_{cn}&(B\leq B_{n})\\ \epsilon_{f0}&(B>B_{n})\end{array}\right..$

(7)

The schematic behavior of $\varepsilon_{n-}$ is shown in Fig. 2.

When the magnetic field is $B_{n+1}<B<B_{n}$, the ground state energy density is

	$\displaystyle u(B)$	$\displaystyle=D\sum_{l=0}^{n}\varepsilon_{l-}+\tilde{u}$
		$\displaystyle=D\frac{\hbar\omega_{c}}{2}[n(n+1)+n+1]+\tilde{u},$		(8)

where $D=2/(2\pi l_{B}^{2})=eB/\pi\hbar$ is the degeneracy per area including spin degrees of freedom and $\tilde{u}=D\sum_{l>n}\varepsilon_{l-}=D\sum_{l>n}\epsilon_{f0}$ is the contribution from higher Landau levels $n+1,n+2,\cdots$ with an appropriate regularization to avoid unphysical divergence. Similarly, the ground state energy density for $B_{n}<B<B_{n-1}$ is

$\displaystyle u(B)$

$\displaystyle=D\frac{\hbar\omega_{c}}{2}[(n-1)n+n]+D\epsilon_{f0}+\tilde{u},$

(9)

where the second term is the contribution from $\varepsilon_{n-}$ and the functional form of $\tilde{u}$ is the same as above. Correspondingly, the orbital magnetization $M=-\partial u/\partial B$ is given by

	$\displaystyle M(B_{n+1}<B<B_{n})$	$\displaystyle=-\frac{e\omega_{c}}{\pi}[n(n+1)+n+1]+\tilde{M},$		(10)
	$\displaystyle M(B_{n}<B<B_{n-1})$	$\displaystyle=-\frac{e\omega_{c}}{\pi}[(n-1)n+n]-\frac{e\epsilon_{f0}}{\pi\hbar}+\tilde{M},$		(11)

where $\tilde{M}(B)=-\partial\tilde{u}/\partial B$ and does not have a singularity. From these expressions, we see that the magnetization jumps at $B=B_{n}$ and oscillates with the period $\delta(1/B)=1/B_{n}-1/B_{n-1}=e\hbar/(m_{c}\epsilon_{f0})$ which is inversely proportional to the area of a Fermi surface cross section without hybridization when $\epsilon_{f0}\simeq\mu$. The size of the jump gives the oscillation amplitude, $\delta M(B=B_{n})=M(B_{n}+0)-M(B_{n}-0)=e\epsilon_{f0}/(\pi\hbar)$. Note that the sharp discontinuity of $M(B)$ is due to the approximation Eq. (7) where $\varepsilon_{n-}$ is not differentiable at $B=B_{n}$, and $M(B)$ is smooth for the original spectrum Eq. (4). Note also that the condition $m_{f}\rightarrow\infty$ can be relaxed and the quantum oscillation can be described by a similar argument for $m_{f}<\infty$.

From the above derivation of the oscillating magnetization $M(B)$ where all the states below the chemical potential contribute, it is clear that the crossover of a Landau level character as a function of $B$ from conduction-electron-like one to $f$-electron-like one is the most important key. This observation holds true also for the quantum oscillation for static transport (Shubnikov-de Haas effect) where an effective density of states thermally smeared around the chemical potential will play a central role Zhang et al. (2016). The smeared density of states oscillates also due to the crossover of the Landau level character as easily expected from Fig. 1 where a Landau level energy approaches the band edge and goes away from it as $B$ increases. Therefore, we conclude that the quantum oscillations in static quantities are essentially due to the Landau level crossover in the present model. Note that there are densely distributed Landau levels near the edges of upper/lower bands in Fig. 1, because energy level spacings becomes narrower when the slope of a Landau level energy changes around the crossover field strength. In the next section, we will see that this characteristic structure of the Landau levels leads to low energy cyclotron resonance, sharing essentially same origin with the quantum oscillations of static quantities. .

We calculate the magneto-optical conductivity for a circularly polarized light with frequency $\omega$  Mahan (2000),

	$\displaystyle\textrm{Re}\sigma_{-+}(\omega)$	$\displaystyle=\frac{1}{\omega}\left(\textrm{Im}K_{-+}^{R}(\omega)-\textrm{Im}K_{-+}^{R}(0)\right),$		(12)
	$\displaystyle K_{-+}^{R}(\omega)$	$\displaystyle=\frac{-i}{V}\int dt\theta(t)\langle[J_{-}(t),J_{+}(0)]\rangle e^{i\omega t}$
		$\displaystyle=\sum_{nmm^{\prime}}M^{-+}_{n,mm^{\prime}}\chi^{-+}_{n,mm^{\prime}}(\omega),$		(13)
	$\displaystyle\chi^{-+}_{n,mm^{\prime}}(\omega)$	$\displaystyle=\frac{f(\varepsilon_{n+1,m})-f(\varepsilon_{nm^{\prime}})}{\omega-\varepsilon_{n+1,m}+\varepsilon_{nm^{\prime}}+i\gamma},$		(14)

where $V$ is the volume of the system and $f(\varepsilon)=(e^{(\varepsilon-\mu)/T}+1)^{-1}$. Similarly, the conductivity for the opposite polarization $\sigma_{+-}(\omega)$ is given by the correlation function $K^{R}_{+-}(\omega)=\frac{-i}{V}\int dt\theta(t)\langle[J_{+}(t),J_{-}(0)]\rangle e^{i\omega t}$, and satisfies $\textrm{Re}\sigma_{-+}(\omega)=\textrm{Re}\sigma_{+-}(-\omega)$. The current operators are given by $J_{+}=J_{-}^{\dagger}=J_{x}+iJ_{y}=\sum{\mathcal{J}}_{+n,ij}a^{\dagger}_{n+1,i}a_{nj}$ with $J_{x,y}=\int d^{2}x\psi^{\dagger}\partial{\mathcal{H}}/\partial A_{x,y}\psi$, and ${\mathcal{J}}_{n+}={\mathcal{J}}_{n-}^{\dagger}$ is defined by

$\displaystyle{\mathcal{J}}_{n+}$

$\displaystyle=-\sqrt{2}e\left(\begin{array}[]{cccc}\frac{\sqrt{n+1}}{m_{c}l_{B}}&0&0&\sqrt{2}v_{1}a\\ 0&\frac{\sqrt{n}}{m_{c}l_{B}}&0&0\\ 0&\sqrt{2}v_{1}a&-\frac{\sqrt{n+1}}{m_{f}l_{B}}&0\\ 0&0&0&-\frac{\sqrt{n}}{m_{f}l_{B}}\end{array}\right).$

(19)

The matrix $M$ is defined as $M_{n,mm^{\prime}}^{-+}=\textrm{tr}[{\mathcal{J}}_{n-}{\mathcal{U}}_{n+1m}{\mathcal{J}}_{n+}{\mathcal{U}}_{nm^{\prime}}]/(2\pi l_{B}^{2})$ with $({\mathcal{U}}_{nm})_{ij}=u_{n,im}u_{n,jm}^{\ast}$. We fix the phenomenological broadening parameter $\gamma=0.0005t_{0}$ and results are essentially independent of $\gamma$.

Figure 3 shows the magneto-optical conductivity $\sigma(\omega)$ at a low temperature $T=0.007t_{0}=0.07\Delta_{0}$ for the non-topological case and $T=0.0047t_{0}\simeq 0.07\Delta_{1}$ for the topological case. The calculated cyclotron resonance is qualitatively similar for these two cases, although there are some quantitative differences.

For the small magnetic field $b=0.02\simeq 0.33b_{c}$, the conductivity is strongly suppressed and there are only small spectral weights in a low energy region below the activation gap $\omega<\Delta_{0,1}$. At high energy, a series of large peaks are located for $\omega\gtrsim\Delta_{0,1}$. On the other hand, when the magnetic field is close to the critical value, $b=0.05\simeq 0.83b_{c}$, $\sigma(\omega)$ at low energy is enhanced and there exist clear peaks well below the gap $\Delta_{0,1}$ even in the insulating states. More precisely, the low energy peaks are located in the region $\omega_{f}=0.005t_{0}\leq\omega\leq\omega_{c}=0.05t_{0}$ and will be called anomalous cyclotron resonance. The peak height is relatively larger in the topological case than in the non-topological case, and we conclude that existence of the anomalous peaks is a universal property of Kondo insulators with band inversion. Furthermore, we will see later that the anomalous cyclotron resonance shares common features in both non-topological and topological cases. Such anomalous low energy peaks are absent in non-band inverted insulators, but are made possible because of the characteristic Landau level structures in the Kondo insulators. As seen in Fig. 1, there are Landau levels densely distributed near the edges of the lowest positive energy band ($\varepsilon_{nm}>\mu$, shown in red) and the highest negative energy band ($\varepsilon_{nm}<\mu$, shown in blue), corresponding to the previously mentioned crossover in Landau level’s character. Transitions between the $n\leftrightarrow n+1$ Landau levels within each band edge in the same color are allowed at finite temperature, resulting in the low energy peaks in $\sigma(\omega)$, while such band edge Landau levels are absent in a non-band inverted insulator. Therefore, these anomalous peaks are a direct consequence of the unusual Landau level structure, essentially sharing the common origin with quantum oscillations within the present model.

An observation of these peaks will strongly support the mechanism for quantum oscillations proposed in the previous theories Knolle and Cooper (2015); Zhang et al. (2016); Pal et al. (2016); Ram and Kumar (2017); Shen and Fu (2018); Grubinskas and Fritz (2018); Peters et al. (2019), and hence provide a clue for the origin of the experimentally observed quantum oscillations. If the magnetic field is increased further, $b>b_{c}$, so that the system is metallic, one can see that the low energy peaks are further enhanced, corresponding to heavy fermion formation in the metallic regime. For the Kondo insulators SmB₆ and YbB₁₂, the frequency of the light should be smaller than $1\sim 2$ meV corresponding to their insulating gaps, and also in between $\omega_{f}$ and $\omega_{c}$ (they are $\omega_{f}\sim 0.1$ meV, $\omega_{c}\sim 1$ meV for example at $B=10$ T in the present model). Besides, a large magnetic field $B>10$ T would be required to observe the anomalous cyclotron resonance.

Next, we discuss temperature dependence of the conductivity. Figure 4 shows $\sigma(\omega)$ for different temperatures at the magnetic field $b=0.05\simeq 0.83b_{c}$.

At an intermediate temperature $T=0.5\Delta_{0,1}$, the anomalous low energy peaks are now comparable to the high energy peaks. Similarly to the $T=0.07\Delta_{0,1}$ case, these low energy peaks in $\sigma_{-+}(\omega)$ are located in the region $\omega_{f}=0.005t_{0}\leq\omega\leq\omega_{c}=0.05t_{0}$, while there is only one low energy peak at $\omega\simeq\omega_{f}$ in $\sigma_{+-}(\omega)$. The low energy peaks become sharper at high temperature, $T=2\Delta_{0,1}$, and there is basically a single peak at $\omega=\omega_{c}$ in $\sigma_{-+}(\omega)$ and at $\omega=\omega_{f}$ in $\sigma_{-+}(\omega)$. These two peaks at high temperature simply correspond to the unhybridized conduction electrons and $f$-electrons, which are directly seen in Eq. (12); contributions from high energy states with large Landau level indices $n$ become dominant at very high temperature since their momenta $\pi_{\pm}\sim\sqrt{n}/l_{B}$ are large, and hence one can neglect hybridization matrix elements $v_{0},v_{1}a\sqrt{n}/l_{B}\ll\omega_{c}n,\omega_{f}n$ in the Hamiltonian ${\mathcal{H}}_{n}$. Then a straightforward calculation leads to $\sigma_{-+}(\omega\geq 0)\propto\omega_{c}/(m_{c}^{2}T)\delta(\omega-\omega_{c})$ and $\sigma_{+-}(\omega\geq 0)\propto\omega_{f}/(m_{f}^{2}T)\delta(\omega-\omega_{f})$ in the limit $\gamma\rightarrow 0$. The conduction and $f$-electrons form a hybridized state at low temperature for which energy levels are non-linear in the magnetic field $B$ and located in between the unhybridized conduction electron energy and $f$-electron energy. This evolution of the system is a (non-interacting variant of) Kondo effect and it would be useful for studying evolution of temperature dependent electronic structures under magnetic fields where photoemission experiments Denlinger et al. ; Okawa et al. (2015) are generally difficult.

The temperature dependence is well characterized by low energy spectral weight of the conductivity,

$\displaystyle W_{-+}=\int_{\Omega_{1}}^{\Omega_{2}}d\omega\textrm{Re}\sigma_{-+}(\omega).$

(20)

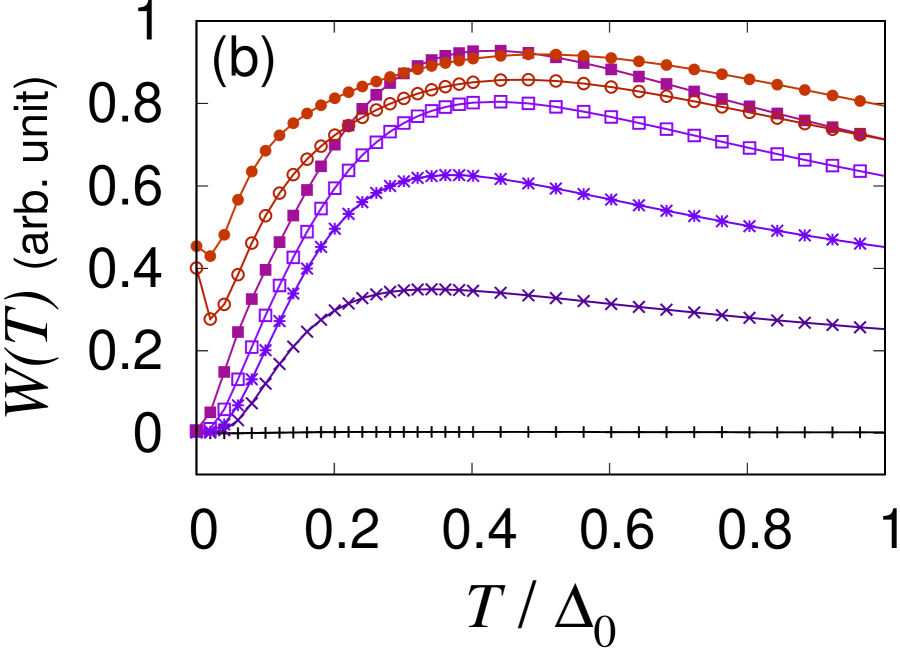
We choose the cut off energy scales $\Omega_{1,2}$ so that only the anomalous low energy peaks are taken into account; $\Omega_{1}=0$ and $\Omega_{2}=\omega_{c}-10\gamma$ for a given magnetic field. Although the precise value of $W_{-+}$ depends on a choice of $\Omega_{1,2}$, contributions from unhybridized conduction and $f$-electrons are suppressed with the present $\Omega_{1,2}$. Besides, only the transitions between states at Landau levels $n\leftrightarrow n+1$ with energies $\Omega_{1}\lesssim|\varepsilon_{n+1,m}-\varepsilon_{nm^{\prime}}\pm\gamma|\lesssim\Omega_{2}$ contribute to $W_{-+}$. Figure 5 shows $W_{-+}$ for several values of magnetic fields $b$. We see that $W_{-+}$ develops as temperature is reduced via the Kondo effect and it becomes maximum roughly around $T\sim 0.3\Delta_{0,1}\textrm{ - }0.4\Delta_{0,1}$. At low temperature, the weight behaves as $W_{-+}(T)\sim\exp(-\Delta_{-+}/T)$ with a gap $\Delta_{-+}$ in the insulating regime. $\Delta_{-+}$ corresponds to the minimum value of $|\varepsilon_{nm}-\mu|$ for the given magnetic field, because the temperature factor of $W_{-+}$ behaves as $|f(\varepsilon_{n+1,m})-f(\varepsilon_{nm^{\prime}})|\simeq e^{-|\varepsilon_{n+1,m}-\mu|/T}(1-e^{-|\varepsilon_{n+1,m}-\varepsilon_{nm^{\prime}}|/T})$ e.g. for $|\varepsilon_{n+1,m}-\mu|<|\varepsilon_{nm^{\prime}}-\mu|$. $W_{-+}$ is enhanced as the magnetic field increases in both non-topological and topological Kondo insulators in a similar fashion, which again means that the enhancement is a universal property of the Kondo insulators with band inversion. In this way, the low energy peaks can become pronounced even in the insulating regime when the system is close to the insulator-metal transition point. The gap $\Delta_{-+}$ becomes zero at the critical point $b=b_{c}\simeq 0.058$. For larger magnetic fields $b=0.06,0.07>b_{c}$ where the system is metallic, there exist resonance peaks in $\sigma_{-+}(\omega)$ in between $\omega_{f}\leq\omega\leq\omega_{c}$ corresponding to heavy fermions and $W_{-+}$ remains non-zero at $T=0$.

Our results for the clean non-interacting model imply that the anomalous low energy peaks corresponding to the characteristic Landau level structure are most clearly visible around an intermediate temperature regime ($T\sim 0.3\Delta_{0,1}\textrm{ - }0.4\Delta_{0,1}$ in the above calculation). In real materials, however, sharp peaks will be smeared by disorder and interactions especially at temperature above Kondo temperature which is roughly $T_{K}\sim\Delta_{0,1}$  Appel and Overhauser (1978); Takada and Ando (1978); Ando et al. (1982); Asano and Ando (1998); Kanki and Yamada (1997), and sufficiently low temperature would be required for an experiment. At the same time, signal amplitudes would be reduced at low temperature, which is a common subtle issue also for observables where only states near the chemical potential contribute Pal et al. (2016); Knolle and Cooper (2017b). Nevertheless, quantum oscillations in static longitudinal transport have indeed been observed not only in YbB₁₂ but also in band inverted insulating quantum wells at low temperature Xiang et al. (2018); Xiao et al. (2019); Han et al. (2019), and discussed theoretically Peters et al. (2019). Since cyclotron resonance can be observed at relatively high temperature in general, anomalous cyclotron resonance can be seen in some intermediate temperature range below Kondo temperature and provide a useful insight for the observed quantum oscillations.

Finally, we qualitatively discuss effects of three dimensionality for which the response function is $\sigma(\omega,q_{z})$ for a light perpendicular to the $xy$-plane with an in-plane polarization. Since we are interested in the frequency range below the activation gap $\Delta_{0,1}=O$(meV) or even smaller due to the renormalization effect, wavelength of the light used in a cyclotron resonance experiment will be much longer than a quasi-particle mean free path. Such a long wavelength may be regarded as the $q_{z}\rightarrow 0$ limit and a resonance peak position at $\omega=(\varepsilon_{n+1,m}(k_{z}+q_{z})-\varepsilon_{nm^{\prime}}(k_{z}))$ remains almost unchanged from that for a two-dimensional system. Therefore, the qualitative behaviors discussed in the present study will still hold for three dimensions. In case of a topological Kondo insulator, there are Zeeman split surface states and they may give additional contributions to cyclotron resonance, but they would be subdominant for a thick sample. In a thin film, however, the surface mode contribution could be significant. A cyclotron resonance experiment with tilted field angles may provide useful information about the dimensionality of the carriers for the quantum oscillations. There is another additional contribution even in two-dimensions arising from electron spins, but it could be separated from cyclotron resonance because its magnitude is usually small and the characteristic energy scale is Zeeman energy which differs from a cyclotron frequency especially in an $f$-electron system. The spin response under a magnetic field itself will contain important information on elecronic structures similarly to those at zero magnetic field  Fuhrman et al. (2015); Singh and Lee (2018).