CsV₃Sb₅: a $\mathbb{Z}_{2}$ topological kagome metal with a superconducting ground state

Kagome metals are a rich frontier for the stabilization of novel correlated and topological electronic states. Depending on the degree of electron filling within the kagome lattice, a wide array of instabilities are possible, ranging from bond density wave order Wang et al. (2013); Isakov et al. (2006), charge fractionalization O’Brien et al. (2010); Rüegg and Fiete (2011), spin liquid states Yan et al. (2011), charge density waves Guo and Franz (2009), and superconductivity Wang et al. (2013); Ko et al. (2009). Additionally, the kagome structural motif imparts the possibility of topologically nontrivial electronic structures, where the coexistence of Dirac cones and flatbands promoting strong correlation effects may engender correlated topological states. For instance, the presence of magnetic order Kang et al. (2020); Ye et al. (2018); Morali et al. (2019) in kagome compounds has been noted to stabilize novel quantum anomalous Hall behaviors, and electron-electron interactions in certain scenarios are proposed to drive the formation of topological insulating phases Wen et al. (2010).

One widely sought electronic instability on a two-dimensional kagome lattice is the formation of a superconducting ground state. Layered kagome metals that superconduct are rare, and the interplay between the nontrivial topology accessible via their electronic band structures and the formation of an intrinsic superconducting state makes this a particularly appealing space for realizing exotic ground states and quasiparticles. Unconventional superconductivity is predicted to emerge via nesting-driven interactions in heavily doped kagome lattices Yu and Li (2012). This mechanism, first pointed out in theories for doped graphene (which shares the hexagonal symmetry of the kagome lattice)Nandkishore and Chubukov (2012); Nandkishore et al. (2012), relies upon scattering between saddle points of a band at the M points of the 2d Brillouin zone, which are relevant when the system possesses a nearly hexagonal Fermi surface proximate to a topological transition. Superconductivity potentially competes with a variety of other electronic instabilities at different fillings Kiesel et al. (2013); Wen et al. (2010). Realizing superconductivity in a two-dimensional kagome material that avoids these competing instabilities remains an open challenge.

Recently a new family of layered kagome metals that crystallize in the AV₃Sb₅ structure (A: K, Rb, Cs) was reported Ortiz et al. (2019). These materials crystallize into the $P$6/$mmm$ space group, with a kagome network of vanadium cations coordinated by octahedra of Sb. The compounds are layered, with the kagome sheets separated by layers of the A-site alkali metal ions (Fig. 1). Compounds across the series are high mobility, two-dimensional metals with signatures of correlation effects and potential electronically-driven symmetry breaking. Recent studies have further shown that one variant, KV₃Sb₅, is a Dirac semimetal with an extraordinarily large anomalous Hall effect in the absence of long-range magnetic order Yang et al. (2020). Remarkably little however remains known about this new class of kagome metals, particularly with regards to their capacity for hosting correlated topological states.

Here we identify that CsV₃Sb₅, the heaviest member of the new kagome compounds, is a $\mathbb{Z}_{2}$ topological metal with a superconducting ground state. Angle-resolved photoemission spectroscopy (ARPES) measurements combined with density-functional theory (DFT) calculations reveal the presence of multiple Dirac points near the Fermi level and predict topologically protected surfaces states only 0.05 eV above the Fermi level at the $M$-points. Furthermore, both ARPES and DFT observe hexagonal Fermi surfaces, consistent with close proximity of saddle points at $M$. Magnetization, heat capacity, and electrical resistivity measurements reveal the onset of superconductivity at $T_{c}=2.5$ K and further identify a higher temperature $T^{*}=94$ K transition suggestive of charge density wave order. Our work establishes CsV₃Sb₅ as a novel exfoliable, kagome metal with a superconducting ground state and protected Dirac crossings close to $E_{F}$.

Single crystals of CsV₃Sb₅ were synthesized via a self-flux growth method sup . Magnetization measurements were performed using a Quantum Design SQUID Magnetometer (MPMS3) in vibrating-sample measurement mode (VSM), and resistivity and heat capacity measurements were performed using a Quantum Design Dynacool Physical Properties Measurement System (PPMS). Angle-resolved photoemission (ARPES) measurements were obtained at the Stanford Synchrotron Radiation Lightsource (SSRL, beamline 5-2), a division of the SLAC National Accelerator Laboratory using 120 eV photons with an energy resolution better than 20 meV. Temperature-dependent X-ray diffraction data was collected at Brookhaven National Laboratory (beamline 28-ID-1) and at the Advanced Photon Source at Argonne National Laboratory (Sector 6-ID-D). Rietveld refinements of temperature-dependent diffraction were performed using TOPAS Academic V6.Coelho (2018) Structure visualization was performed with the VESTA software package Momma and Izumi (2011), and the electronic structure of CsV₃Sb₅ was calculated in VASP $v$5.4.4 Kresse and Hafner (1994); Kresse and Furthmüller (1996a, b) using projector-augmented wave (PAW) potentials Blöchl (1994); Kresse and Joubert (1999) with details described in the supplemental materials sup .

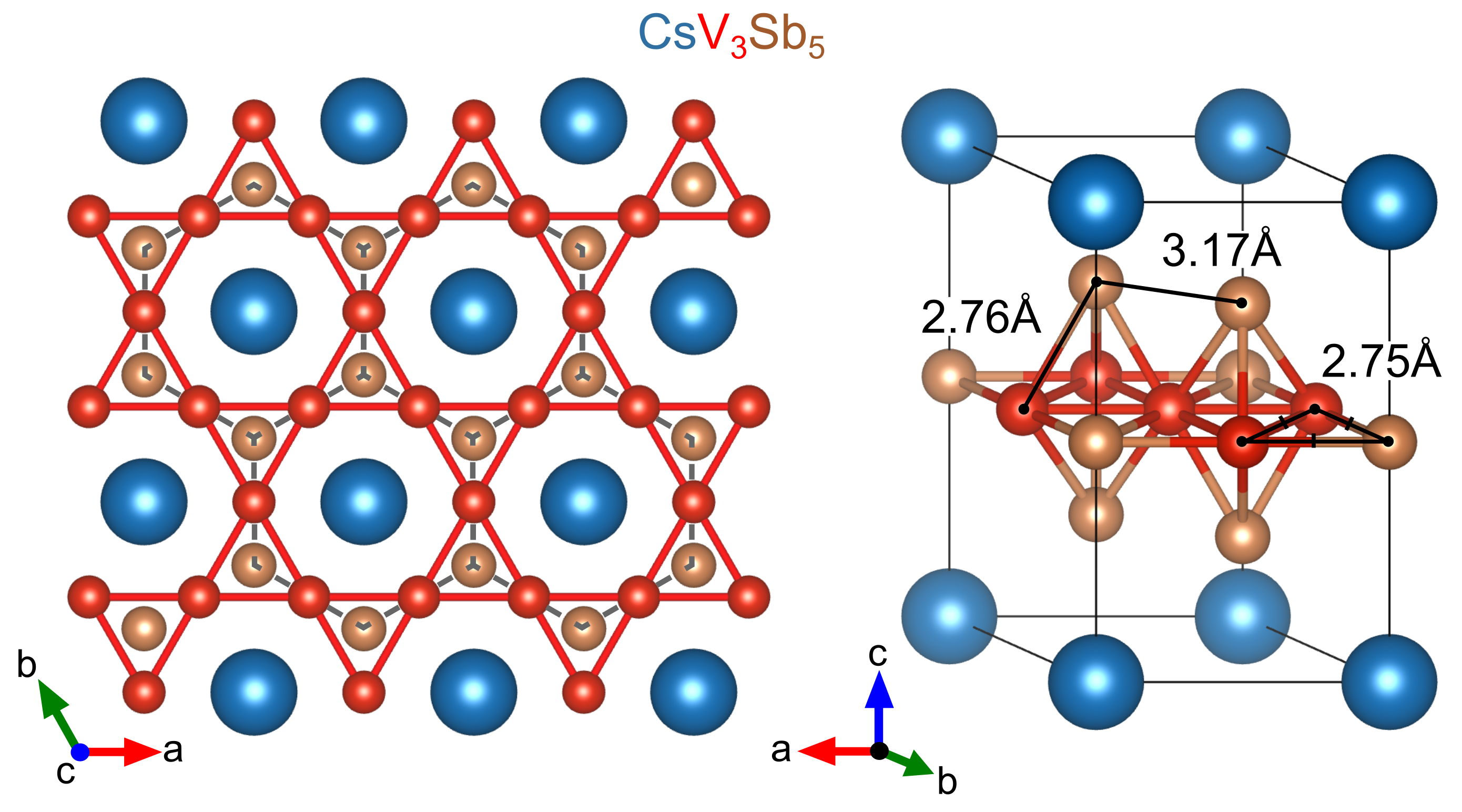
For an intuitive understanding of the CsV₃Sb₅ structure, we first consider the constituent sublattices. The hallmark two-dimensional kagome network is formed by the V1 sublattice, and is interpenetrated by a simple hexagonal net of Sb1 antimony. All interatomic distances within the kagome layer are equal (2.75Å), as required by the high symmetry of the V1 (Wyckoff 3g) and Sb1 (Wyckoff 1b) sites. The Sb2 sublattice creates graphite-like layers of Sb (antimonene) that encapsulate the kagome sheets. The Cs1 sublattice naturally fills the space between the graphite-like sheets, and the nearest Cs-Sb distance is nearly 4Å.

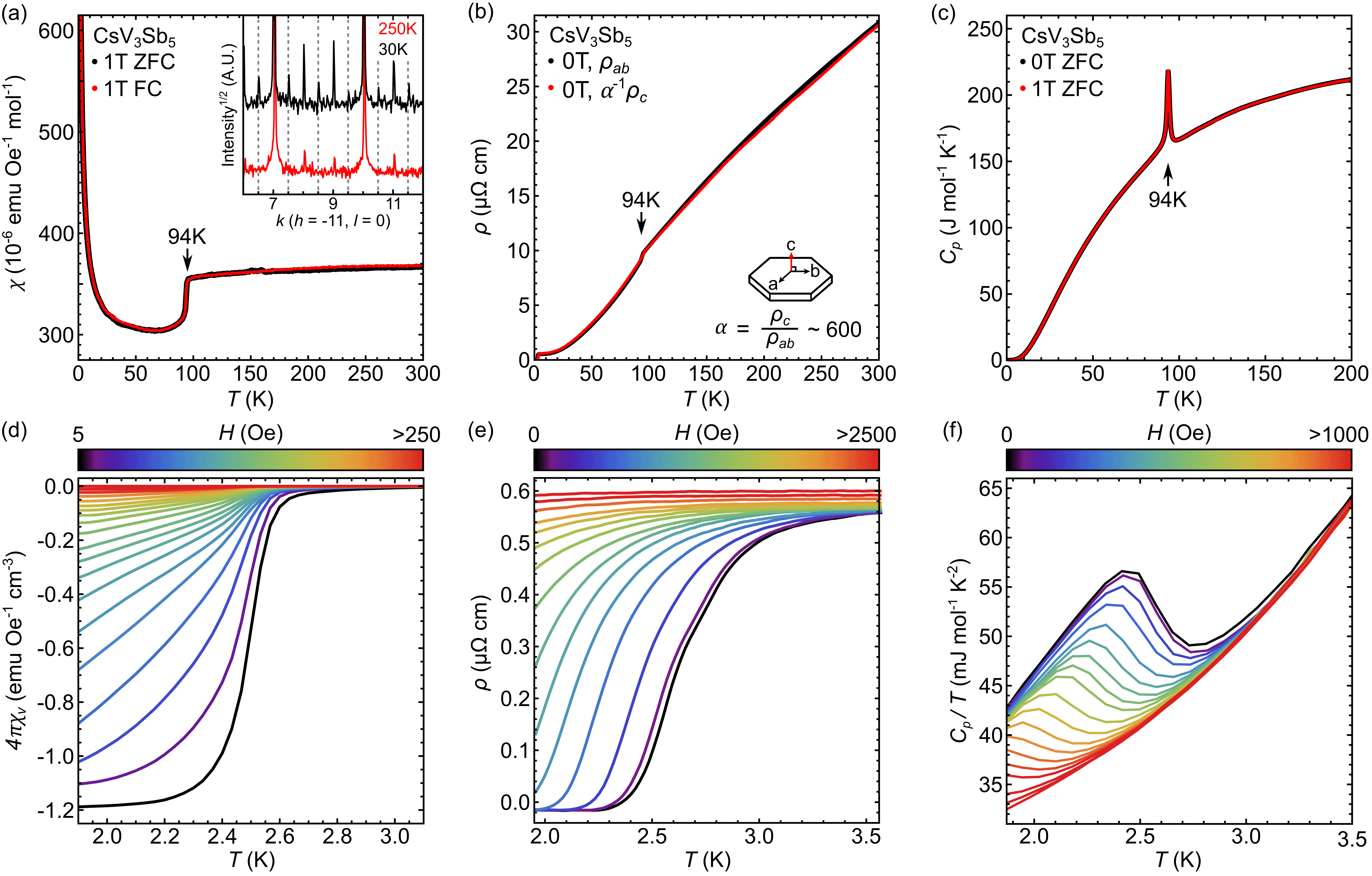
Bulk electronic properties of CsV₃Sb₅ were studied via electron transport, magnetization, and heat capacity measurements. Figures 2(a, b, c) show characterization data collected across a broad range of temperatures. Magnetization data collected under $\mu_{0}H=1$ T are plotted as susceptibility $\chi=\frac{M}{H}$ in Fig. 2 (a) and show a high temperature response ($T>100$ K) consistent with Pauli paramagnetism. As a rough estimate, DFT calculations of the density of states at the Fermi level $g(E_{F})\approx 10$ eV^-1cell^-1 estimate $\chi\approx 200\times 10^{-6}$ emu Oe^-1mol^-1, which agrees reasonably well with the experimental data.

At temperatures below 94 K, a sharp drop in the magnetization data denotes the onset of a phase transition, noted as $T^{*}$. This transition also appears as an inflection point in the resistivity data shown in Figure 2(b), where temperature-dependent resistivity data with current flowing both in the kagome planes ($\rho_{a}b$) and between the planes ($\rho_{c}$) are plotted. The out-of-plane resistivity is nearly 600 times larger than in-plane, emphasizing the two-dimensional nature of the Fermi surface. Heat capacity data plotted in Fig. 2 (c) also illustrate a strong entropy anomaly at $T^{*}=94$ K. The integrated entropy released through the $T^{*}$ transition is approximately $\Delta S=1.6$ J mol^-1K^-1, and is naively too small to account for collective spin freezing of free V-moments. Instead, it likely arises from freezing within the charge sector Wen et al. (2010), suggesting a potential charge/bond density wave anomaly that will be discussed later in this manuscript.

Figures 2(d-f) show the onset of superconductivity in magnetization, resistivity, and heat capacity, respectively. In all cases, the onset of superconductivity occurs at approximately $T_{c}=2.5$ K. Magnetization data reveal bulk superconductivity and a well-defined Meissner state, and heat capacity measurements show a sharp entropy anomaly at the superconducting transition, although, due to a limited temperature regime, we are unable to fully characterize the gapped behavior far below $T_{c}$. The slight offset in the onset of $T_{c}$ in electrical resistivity (Figure 2(e)) measurements is due to the high probe currents (8 mA) used in the DC measurement. Reduced currents show $T_{c}$ return to nominal values, although the data quality suffers significantly due to the low resistivity of CsV₃Sb₅ single crystals.

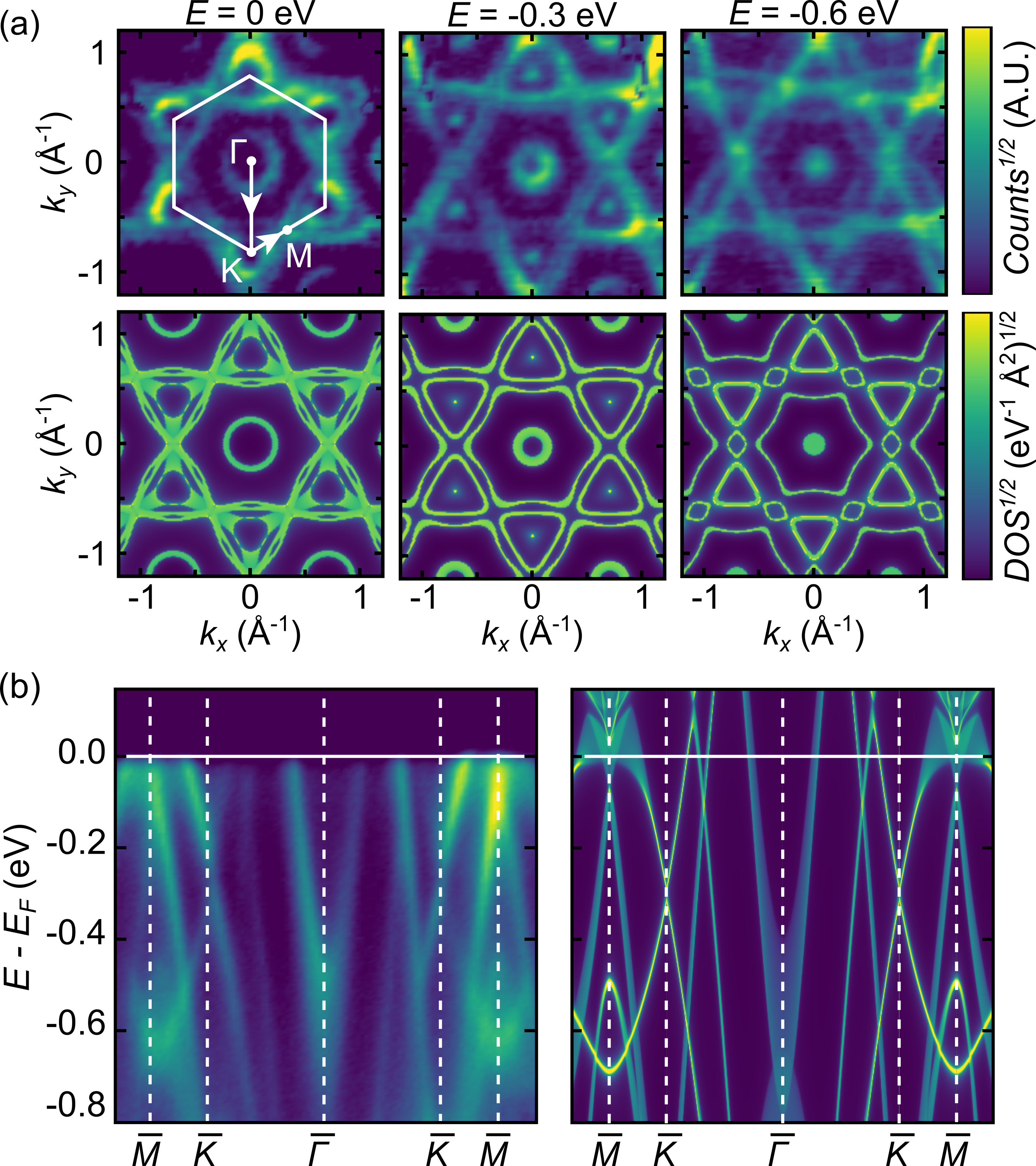
Having determined that CsV₃Sb₅ is a bulk kagome superconductor with a transition temperature $T_{c}=2.5$ K, we next examine the normal state metal via a combination of ARPES measurements and DFT modeling. Figure 3(a) shows both ARPES and DFT modeling data with the hexagonal Brillouin zone superimposed on the $E=0$ eV constant energy contour and high symmetry points $K$, $M$, and $\Gamma$ labeled. Data collected with differing photon energies did not reveal any appreciable dispersion along $k_{z}$, consistent with a quasi-2D band structure. ARPES data were collected at 50 K, 80 K, 100 K, and 120 K, and no resolvable changes were observed in the band structure when transitioning through the $T^{*}$ transition. The DFT model shows remarkable agreement with the ARPES data, recovering all experimental observed crossings below the Fermi level. Figure 3(b) shows both the measured and calculated electronic structure hosts multiple Dirac points at finite binding energies.

While inaccessible in the present ARPES data, the DFT model further reveals multiple topological band features slightly above the Fermi energy. The $\overline{M}$-point is of particular interest, as $M$ is a time-reversal invariant momentum (TRIM) point. Figure 4 shows the results of a tight binding calculation of surface states in CsV₃Sb₅, where bright spots slightly above the Fermi energy indicate surface states.

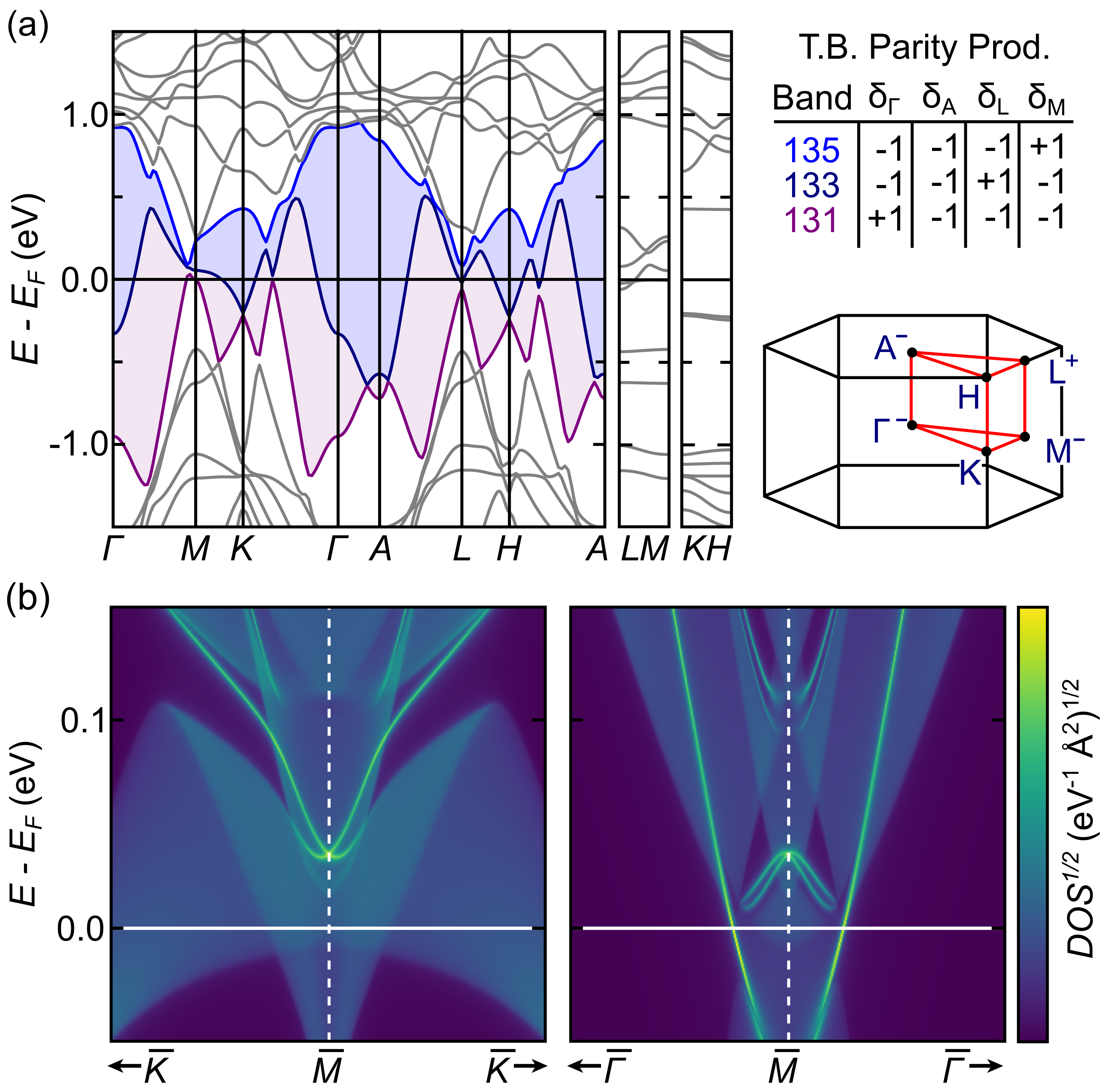
Unlike many heavily studied kagome lattices (e.g. ZnCu₃(OH)₆Cl₂,Braithwaite et al. (2004); Freedman et al. (2010); Han et al. (2012) Fe₃Sn₂,Ye et al. (2018); Wang et al. (2020) Mn₃Ge,Nayak et al. (2016); Kiyohara et al. (2016) Co₃Sn₂S₂Vaqueiro and Sobany (2009); Xu et al. (2018); Morali et al. (2019)), CsV₃Sb₅ does not exhibit resolvable magnetic order. Given that CsV₃Sb₅ possesses both time-reversal and inversion symmetry as well as a continuous, symmetry-enforced, direct gap at every k-point, one can calculate the $\mathbb{Z}_{2}$ topological invariant between each pair of bands near the Fermi level by simply analyzing the parity of the wave function at the TRIM (time-reversal invariant momentum) points Fu and Kane (2007). This analysis reveals a number of topologically nontrivial crossings between adjacent bands in the region $\pm$ 1 eV from the Fermi level. For clarity, we will focus on the surface states crossing at the $\overline{M}$-point here with further analysis presented in the supplemental material sup . Fig. 4(b) presents a close-up of the calculated surface states near the $\overline{M}$ point. The surface states at the $\overline{M}$-point manifest approximately 0.05 eV above the Fermi energy. The apparent anisotropy in the calculated surface state dispersions ($\overline{M}$-$\overline{K}$ versus $\overline{M}$-$\overline{\Gamma}$) derives from the direct “gap” moving up or down in energy depending on direction away from the $\overline{M}$ point. This is not uncommon amongst topological metals Singh et al. (2018); Cucchi et al. (2020); Yu et al. (2015).

Topologically nontrivial surface states close to $E_{F}$ and the continuous direct gap throughout the Brillouin zone allow the identification of the normal state as a $\mathbb{Z}_{2}$ topological metal Schoop et al. (2015); Nayak et al. (2017). The $T^{*}$ transition in this compound also suggests that electronic interactions are appreciable in this material. This transition is accompanied by a subtle change in the derivative of the lattice parameters, cell volume, and associated crystallographic parameters upon crossing $T^{*}$ sup . Single crystal x-ray diffraction further shows the formation of a weak superlattice of charge scattering at half-integer reflections (an example shown in the inset of Fig. 2 (a)) sup .

The presence of a weak, structural superlattice is suggestive of a secondary structural response to a primary electronic order parameter such as a charge or bond density wave instability. Theoretical studies of partially filled kagome lattices predict a wide array of electronic order parameters Wen et al. (2010). The metallic nature of CsV₃Sb₅ and its high degree of covalency makes formal charge assignment imprecise; however, in the ionic limit, the kagome lattice of V-sites would possess one electron per triangle (1/6 filling). Charge density wave (CDW) order with a ($\pi$, $0$) in-plane wave vector consistent with our single crystal x-ray diffraction data is predicted in spinful models and spinless fermion models of interacting electrons in a partially filled kagome lattice.Wen et al. (2010)

Nesting across a two-dimensional Fermi surface with an underlying hexagonal motif is also thought to promote the formation of a superconducting state Nandkishore et al. (2012). Competing density wave instabilities may also arise, and in the present case, scattering along the ($\pi$, $0$) wave vector would connect an enhanced density of states at saddle points near the Fermi energy at the M-points in CsV₃Sb₅’s band structure. To our knowledge, this is the first material example hosting the band structure, Fermi energy, and ground state requisite for this theoretical mechanism. Given the CDW-like instability observed at $T^{*}$ in this compound, interactions along this wave vector are likely enhanced and may promote a competition between CDW and superconducting instabilities. Although a structural superlattice exists, ARPES data do not resolve spectral broadening of the Fermi surface across the nested M-points, consistent with the long-range, weak nature of the high temperature density wave order. Unconventional superconductivity with chiral $d$-wave pairing may emerge in this scenario Wang et al. (2013); Nandkishore and Chubukov (2012).

Superconductivity manifest within an electronically two-dimensional kagome lattice is rare unto itself. While other materials with kagome networks embedded within their lattice structures are known to superconduct (e.g. in certain silicides and borides Rauchschwalbe et al. (1984); Lu et al. (2015)), all of these examples are inherently three-dimensional both structurally and electronically. CsV₃Sb₅ seemingly opens a unique opportunity for mapping to models of nesting-driven instabilities emergent within a two-dimensional kagome metal. Isostructural variants KV₃Sb₅ and RbV₃Sb₅ host similar $T^{*}$ transitions at $80$ K and $104$ K respectively, likely indicative of a similar high-temperature density wave order Ortiz et al. (2019); however superconductivity has only been observed in CsV₃Sb₅ to date. Understanding the interplay between the potentially competing $T^{*}$ order parameter and the formation of superconductivity across the AV₃Sb₅ family is an interesting topic for future study.

The $\mathbb{Z}_{2}$ topological band structure of CsV₃Sb₅ may also be of interest for stabilizing the formation of Majorana modes within the vortex cores of a natively proximitized, superconducting surface state. Materials hosting both topologically nontrivial surface states and a native superconducting ground state are uncommon, with relatively few promising candidates identified in FeSe_(1-x)Te_x,Wang et al. (2015); Xu et al. (2016); Wu et al. (2016); Zhang et al. (2018); Machida et al. (2019) doped-Bi₂Se₃,Fu and Berg (2010); Kriener et al. (2011); Sasaki et al. (2011); Liu et al. (2015); Du et al. (2017) and Sn_(1-x)In_xTeSato et al. (2013); Novak et al. (2013); Polley et al. (2016). With relatively light electron-doping (such as Ba substitution), CsV₃Sb₅ can likely be driven into a regime where such a proximitized topological surface state could be tested.

In summary, our results demonstrate that kagome metals can serve as a rich arena for exploring the interplay between correlated electron effects and superconductivity within a topologically nontrivial band structure. Our results demonstrate bulk superconductivity with $T_{c}=2.5$ K in single crystals of CsV₃Sb₅ and classify its normal state as a $\mathbb{Z}_{2}$ topological metal with multiple topologically nontrivial band crossings in close proximity to the Fermi level. An anomalous CDW-like transition in the normal state suggests strong correlation effects and an electronic instability that weakly couples to the lattice. Future studies exploring the relation between this instability and the potential emergence of nesting-driven, unconventional superconductivity on the kagome lattice is motivated by our present results.