Cross-View Consistency Regularisation for
Knowledge Distillation

Weijia Zhang Shanghai Jiao Tong UniversityShanghaiChina [email protected] , Dongnan Liu University of SydneySydneyAustralia [email protected] , Weidong Cai University of SydneySydneyAustralia [email protected] and Chao Ma Shanghai Jiao Tong UniversityShanghaiChina [email protected]

(2024)

Abstract.

Knowledge distillation (KD) is an established paradigm for transferring privileged knowledge from a cumbersome model to a lightweight and efficient one. In recent years, logit-based KD methods are quickly catching up in performance with their feature-based counterparts. However, previous research has pointed out that logit-based methods are still fundamentally limited by two major issues in their training process, namely overconfident teacher and confirmation bias. Inspired by the success of cross-view learning in fields such as semi-supervised learning, in this work we introduce within-view and cross-view regularisations to standard logit-based distillation frameworks to combat the above cruxes. We also perform confidence-based soft label mining to improve the quality of distilling signals from the teacher, which further mitigates the confirmation bias problem. Despite its apparent simplicity, the proposed Consistency-Regularisation-based Logit Distillation (CRLD) significantly boosts student learning, setting new state-of-the-art results on the standard CIFAR-100, Tiny-ImageNet, and ImageNet datasets across a diversity of teacher and student architectures, whilst introducing no extra network parameters. Orthogonal to on-going logit-based distillation research, our method enjoys excellent generalisation properties and, without bells and whistles, boosts the performance of various existing approaches by considerable margins. Our code and models are available at https://github.com/arcaninez/crld.

Knowledge Distillation, Consistency Regularisation, Image Classification

^†^†journalyear: 2024^†^†copyright: acmlicensed^†^†conference: Proceedings of the 32nd ACM International Conference on Multimedia; October 28-November 1, 2024; Melbourne, VIC, Australia^†^†booktitle: Proceedings of the 32nd ACM International Conference on Multimedia (MM ’24), October 28-November 1, 2024, Melbourne, VIC, Australia^†^†doi: 10.1145/3664647.3681206^†^†isbn: 979-8-4007-0686-8/24/10^†^†ccs: Computing Methodologies Machine Learning

Refer to caption — Figure 1. A schematic comparison of logit-based distillation methods from a cross-view learning perspective: (a) Methods mimicking logits in an unitary view (Hinton et al., 2015; Mirzadeh et al., 2020; Li et al., 2023; Zhao et al., 2022; Yang et al., 2023b; Jin et al., 2023; Chi et al., 2023). (b) Methods optimising and mimicking contrastive relations (Xu et al., 2020). (c) The proposed CRLD which involves within-view and cross-view logit transfer.

1. Introduction

Deep neural networks (DNNs) have achieved tremendous success across a plethora of computer vision, natural language processing, and multimedia tasks (Simonyan and Zisserman, 2015; He et al., 2016; Dosovitskiy et al., 2021). Behind their widespread applications, high-performance DNNs are often associated with larger if not prohibitive model sizes and computational overheads, which render them hard to implement on resource-constrained devices and platforms. Towards computation-efficient, storage-friendly, and real-time deployment of DNNs, a viable solution is knowledge distillation (KD), which was first proposed by Hinton et al. (Hinton et al., 2015) for model compression. KD works by transferring the advanced capability of a larger, cumbersome teacher model to a more lightweight and efficient student model. Since its proposal, KD has witnessed significant advancements in the past decade as a range of feature-based (Romero et al., 2015; Heo et al., 2019; Tian et al., 2020; Zagoruyko and Komodakis, 2017; Guo et al., 2023; Park et al., 2019; Chen et al., 2021a, b; Yang et al., 2022b; Liu et al., 2021; Yim et al., 2017; Tung and Mori, 2019) and response-based (logit-based) (Hinton et al., 2015; Xu et al., 2020; Mirzadeh et al., 2020; Zhao et al., 2022; Jin et al., 2023; Yang et al., 2023b; Chi et al., 2023) KD algorithms are proposed for diverse tasks and applications (Hinton et al., 2015; Yang et al., 2022a; Wang et al., 2019; Hong et al., 2022; Zhou et al., 2023; Liu et al., 2019). State-of-the-art KD methods have largely reduced the teacher-student performance gap. For instance, top-performing methods (Zhao et al., 2022; Chi et al., 2023; Jin et al., 2023) are capable of training students that are on par with or even surpass their corresponding teacher models on smaller datasets such as CIFAR-100 (see Table LABEL:tab:cifar100_homo), and are not far behind on larger datasets (Deng et al., 2009) (Tables LABEL:tab:timagenet and LABEL:tab:imagenet).

In this paper, our goal is to further advance the capability of knowledge distillation by addressing two long-standing problems in existing KD methods. Previous research has reported that stronger teacher models and more accurate teacher predictions do not necessarily lead to better distilled students (Hinton et al., 2015; Cho and Hariharan, 2019; Mirzadeh et al., 2020; Yuan et al., 2020). This counter-intuitive observation points to a prominent and fundamental problem in knowledge distillation — overconfident teacher. In the pioneering work of KD (Hinton et al., 2015), Hinton et al. argued that valuable information is hidden in teacher’s predictions of the non-target classes. These predictions, known as the “dark information”, are however largely suppressed when the teacher make predictions with an overly-high confidence. Hence, regularisation of teacher predictions is essential to distilling knowledge with greater generalisation capabilities to the student (Guo et al., 2017; Müller et al., 2019; Hinton et al., 2015).

In their work (Hinton et al., 2015), Hinton et al. propose to mitigate the overconfidence problem by softening the predicted probabilities after Softmax using the temperature hyperparameter. This practice is inherited by many later works (Li et al., 2023; Zhao et al., 2022; Chi et al., 2023; Yang et al., 2023b; Jin et al., 2023; Sun et al., 2024). Some methods (Mirzadeh et al., 2020) produce smoothed teacher predictions by introducing auxiliary teacher networks with smaller capacity. More straightforward techniques have also been investigated, including label smoothing (Müller et al., 2019) and early stopping (Cho and Hariharan, 2019). These works also highlighted overfitting as another detrimental phenomenon closely related to overconfident teacher. These efforts motivate us to look at consistency regularisation via view transformation — another viable solution to combat overconfidence and overfitting. Although widely explored in the semi-supervised learning (SSL) literature (Xie et al., 2020; Sohn et al., 2020), consistency regularisation and view transformation have received little attention in knowledge distillation research. According to (Yang et al., 2023a), strong augmentation amplifies the dark information that is insignificant in the weak view. As such, in this paper we reframe these techniques for KD by designing a novel set of within-view and cross-view consistency regularisation objectives and achieve state-of-the-art KD performance.

On the other hand, teacher’s predictions are not always correct. Confirmation bias (Arazo et al., 2020) arises when erroneous pseudo-labels predicted by the teacher is used to teach the student. In existing logit-based methods (Hinton et al., 2015; Li et al., 2023; Zhao et al., 2022; Yang et al., 2023b; Chi et al., 2023), the student is designated to faithfully learn whatever supervision the teacher has to provide. Such blind mimicking neglects a key fact that the teacher’s predictions may be erroneous and misleading, thereby exacerbating the confirmation bias phenomenon. It has been pointed out in recent research (Yang et al., 2023a) that strong perturbation helps mitigate such confirmation bias, which also supports our introduction of a strongly-augmented view of the input image. To further mitigate confirmation bias, we draw inspiration from state-of-the-art SSL frameworks whose success is partially attributed to their confidence-aware pseudo-labelling (Sohn et al., 2020; Xie et al., 2020; Yang et al., 2023a). As such, we propose to selectively pick the more reliable predictions made by the teacher for the student to learn, which is proven beneficial in our experiments.

The considerations and designs described above altogether lead to a novel Consistency-Regularisation-based Logit Distillation framework, dubbed “CRLD”. By drawing inspiration and reaping the fruits from orthogonal research on semi-supervised learning (SSL), CRLD presents a simple yet highly effective and versatile solution to knowledge distillation. Besides reporting state-of-the-art results across different datasets and distillation pairs, CRLD also easily boosts advanced logit-based methods (Zhao et al., 2022; Yang et al., 2023b; Jin et al., 2023; Chi et al., 2023) by considerable margins without introducing extra network parameters. A schematic comparison of CRLD against prior logit-based approaches from a cross-view learning perspective is depicted in Figure 1.

In summary, the contributions of this paper include:

(1)

We introduce extensive within-view and cross-view consistency regularisations to combat the overconfident teacher and over-fitting problems common in KD.
(2)

We design a reliable pseudo-label mining module to sidestep the negative impact of unreliable and erroneous supervisory signals from the teacher, thereby mitigating confirmation bias in KD.
(3)

We present the simple, versatile, and highly effective CRLD framework. CRLD achieves new state-of-the-art results on multiple benchmarks across diverse network architectures and readily boosts existing logit-based methods by considerable margins.

2. Related Work

2.1. Knowledge Distillation

Knowledge distribution (KD) is first proposed in (Hinton et al., 2015) as a model compression technique. It transfers advanced knowledge from a larger, cumbersome “teacher” model to a smaller, lightweight “student” model. Following its nascent success in image classification (Hinton et al., 2015; Romero et al., 2015) and object detection (Wang et al., 2019; Yang et al., 2022a; Zheng et al., 2022), KD quickly has its effectiveness proven in more challenging downstream tasks (Guo et al., 2021; Hong et al., 2022; Zhang et al., 2024; Zhou et al., 2023; Zhang et al., 2023; Huang et al., 2022a; Kim et al., 2021; Cui et al., 2023; Gu et al., 2024). Existing KD methods are primarily divided into feature-based and logit-based distillation according to where in the network knowledge transfer takes place — the feature space or the logit space.

Feature-based Distillation. As its name suggests, feature-based distillation transfers knowledge in the intermediate feature space of the teacher and student models. A most straightforward way is to simply let the student mimic the features of the teacher, as is done in many early works (Romero et al., 2015; Heo et al., 2019; Ahn et al., 2019; Tian et al., 2020). Some methods also mine and transfer higher-order information from the teacher’s feature maps to the student, including inter-channel (Liu et al., 2021), inter-layer (Yim et al., 2017), inter-class (Huang et al., 2022b), intra-class (Huang et al., 2022b), and inter-sample (Passalis and Tefas, 2018; Peng et al., 2019; Park et al., 2019; Tung and Mori, 2019) correlations, as well as the teacher network’s attention (Zagoruyko and Komodakis, 2017; Guo et al., 2023). Generative modelling has also been leveraged for feature-based distillation (Yang et al., 2022b), where randomly masked student features are required to re-generate full teacher features. In addition, cross-stage distillation paths (Chen et al., 2021a, b) and one-to-all pixel paths (Lin et al., 2022) are also proposed for improved feature-based distillation.

Logit-based Distillation. Logits are the prediction output by a neural network before its final Softmax layer. Distillation methods that perform knowledge transfer in the prediction space are referred to as logit-based or response-based distillation. Pioneering methods such as KD (Hinton et al., 2015) and DML (Zhang et al., 2018b) directly transfer the teacher’s predictions to the student by minimising the Kullback-Leibler (KL) divergence between their predictions. Akin to advances in feature-based distillation, intra-sample and inter-sample relations are also exploited for transfer within the logit space in several works (Xu et al., 2020; Jin et al., 2023). Instead of treating all logits indiscriminately, DKD (Zhao et al., 2022) and NKD (Yang et al., 2023b) decompose all logits into target-class and non-target class logits and treat them separately, demonstrating stronger knowledge transfer performance. More recent methods such as CTKD (Li et al., 2023), NormKD (Chi et al., 2023), LSKD (Sun et al., 2024), and TTM (Zheng and Yang, 2024) dynamically adjust the logit distribution, as opposed to fixed ones in previous works (Hinton et al., 2015; Zhang et al., 2018b; Mirzadeh et al., 2020; Zhao et al., 2022), and have reported state-of-the-art performance. Another branch of methods (Mirzadeh et al., 2020; Son et al., 2021) introduce assistant networks between the teacher and the student to aid the imparting of logit-space knowledge to the latter.

2.2. Consistency Regularisation

Consistency regularisation is at the core of the success of recent state-of-the-art semi-supervised learning algorithms (Laine and Aila, 2017; Sajjadi et al., 2016; Xie et al., 2020; Tarvainen and Valpola, 2017; Berthelot et al., 2019, 2020; Sohn et al., 2020). It involves enforcing invariant representations across different views of the same unlabelled input image to improve the generalisation of learnt representations on unseen data and distribution. The different views of an input image are generated by semantic-preserving transformations, from simple operations such as random crop, horizontal flip, and MixUp (Zhang et al., 2018a) as weak transformations, to more sophisticated (Cubuk et al., 2020; Hendrycks et al., 2020) or even adaptive (Cubuk et al., 2019; Berthelot et al., 2020) augmentation strategies for producing strongly-augmented views. Given these artificially generated views, representation consistency can be enforced across two stochastical weak views as is done in (Berthelot et al., 2019; Xie et al., 2020), or a pair of strong and weak views as in (Sohn et al., 2020; Berthelot et al., 2020). To our best knowledge, beyond SSL, the idea of cross-view consistency regularisation has not been explored within the context of knowledge distillation.

2.3. Data Augmentation for KD

Data augmentation has been a pillar of deep learning’s decade-long triumph. By transforming training samples into augmented versions whilst preserving their semantic connotation, data augmentation conveniently produces an abundant if not unlimited amount of extra training data to improve the generalisation of deep neural networks. In the context of knowledge distillation, data augmentation is yet to receive considerable attention, with only a handful of preliminary studies conducted (Wang et al., 2022; Beyer et al., 2022; Das et al., 2020; Cui and Yan, 2021). Specifically, Das et al. (Das et al., 2020) study the effect of data augmentation in training the teacher model. Wang et al. (Wang et al., 2022) and IDA (Cui and Yan, 2021) design data augmentation strategies tailored to the KD task. SSKD (Xu et al., 2020) and HSAKD (Yang et al., 2021a) incorporate elements of contrastive learning. They apply simple rotation to establish a self-supervised pretext task for improved student learning. Our focus in this work is not the design of a data augmentation strategy itself but to leverage the idea of consistency regularisation to improve student’s learning. In other words, data augmentation is simply our tool, which makes the formulation of consistency regularisation objectives possible, as is done in advanced SSL methods.

3. Methodology

3.1. Knowledge Distillation

Knowledge distillation (KD) involves the student model learning from both ground-truth (GT) labels and distillation signals from a pre-trained teacher. For the image classification task, GT supervisions are widely enforced via a cross-entropy minimisation objective $\mathcal{L}_{CE}$ ; the distillation objective $\mathcal{L}_{KD}$ is enforced by minimising the distance between either the intermediate features or the final predictions of the teacher and the student. Thus, KD in its simplest form has $\mathcal{L}=\mathcal{L}_{CE}+\lambda_{KD}\mathcal{L}_{KD}$ as its objective, where $\lambda_{KD}$ is a balancing scalar. In this paper, we investigate logit-based distillation, where $\mathcal{L}_{KD}$ minimises the discrepancy between predicted probabilities by the teacher and the student, and is commonly implemented as the Kullback-Leibler divergence (KLD) loss.

Input : A batch of training samples

\mathbf{x}

& their labels

\mathbf{y}

; weak augmentation

T_{w}(\cdot)

& strong augmentation

T_{s}(\cdot)

; teacher network

\mathcal{F}^{T}

with parameters

\theta^{T}

& student network

\mathcal{F}^{S}

with parameters

\theta^{S}

while model $\mathcal{F}^{S}$ not converged do

for i=1 to step do

\mathbf{p}^{T}_{w}=\mathcal{F}^{T}(T_{w}(\mathbf{x});\theta^{T})\quad\quad\mathbf{p}^{T}_{s}=\mathcal{F}^{T}(T_{s}(\mathbf{x});\theta^{T})

\mathbf{p}^{S}_{w}=\mathcal{F}^{S}(T_{w}(\mathbf{x});\theta^{S})\quad\quad\mathbf{p}^{S}_{s}=\mathcal{F}^{S}(T_{s}(\mathbf{x});\theta^{S})

\mathbf{M}_{w}=\text{SLS}(\mathbf{p}^{T}_{w},\tau_{w})\quad\quad\quad\mathbf{M}_{s}=\text{SLS}(\mathbf{p}^{T}_{s},\tau_{s})

\mathcal{L}_{CE}=\text{CE}(\mathbf{p}^{S}_{w},\mathbf{y})+\text{CE}(\mathbf{p}^{S}_{s},\mathbf{y})

\mathcal{L}^{WV}_{KD}=\text{KLD}(\mathbf{p}^{S}_{w},\mathbf{p}^{T}_{w})\mathbf{M}_{w}+\text{KLD}(\mathbf{p}^{S}_{s},\mathbf{p}^{T}_{s})\mathbf{M}_{s}

\mathcal{L}^{CV}_{KD}=\text{KLD}(\mathbf{p}^{S}_{s},\mathbf{p}^{T}_{w})\mathbf{M}_{w}+\text{KLD}(\mathbf{p}^{S}_{w},\mathbf{p}^{T}_{s})\mathbf{M}_{s}

\mathcal{L}_{KD}=\mathcal{L}^{WV}_{KD}+\mathcal{L}^{CV}_{KD}

\mathcal{L}_{Overall}=\mathcal{L}_{CE}+\lambda_{KD}\mathcal{L}_{KD}

Update

\theta^{S}

acc. to

\mathcal{L}_{Overall}

end for

end while

Output : Well-trained model

\mathcal{F}^{S}

with parameters

\theta^{S}

Algorithm 1 The CRLD algorithm

Table 1. Top-1 accuracy (%) on CIFAR-100 with homogeneous-architecture teacher-student pairs.

Method	Teacher	ResNet56	ResNet110	ResNet32 $\times$ 4	WRN-40-2	WRN-40-2	VGG13	Avg.
	Teacher	72.34	74.31	79.42	75.61	75.61	74.64
	Student	ResNet20	ResNet32	ResNet8 $\times$ 4	WRN-16-2	WRN-40-1	VGG8
	Student	69.06	71.14	72.50	73.26	71.98	70.36
Feature KD	RKD (Park et al., 2019)	69.61	71.82	71.90	73.35	72.22	71.48	71.73
	FitNets (Romero et al., 2015)	69.21	71.06	73.50	73.58	72.24	71.02	71.77
	AT (Zagoruyko and Komodakis, 2017)	70.55	72.31	73.44	74.08	72.77	71.43	72.43
	OFD (Heo et al., 2019)	70.98	73.23	74.95	75.24	74.33	73.95	73.78
	CRD (Tian et al., 2020)	71.16	73.48	75.51	75.48	74.14	73.94	73.95
	SRRL (Yang et al., 2021b)	71.13	73.48	75.33	75.59	74.18	73.44	73.86
	ICKD (Liu et al., 2021)	71.76	73.89	75.25	75.64	74.33	73.42	74.05
	PEFD (Chen et al., 2022b)	70.07	73.26	76.08	76.02	74.92	74.35	74.12
	CAT-KD (Guo et al., 2023)	71.05	73.62	76.91	75.60	74.82	74.65	74.44
	TaT (Lin et al., 2022)	71.59	74.05	75.89	76.06	74.97	74.39	74.49
	ReviewKD (Chen et al., 2021a)	71.89	73.89	75.63	76.12	75.09	74.84	74.58
	SimKD (Chen et al., 2022a)	71.05	73.92	78.08	75.53	74.53	74.89	74.67
Logit KD	KD (Hinton et al., 2015)	70.66	73.08	73.33	74.92	73.54	72.98	73.09
	TAKD (Mirzadeh et al., 2020)	70.83	73.37	73.81	75.12	73.78	73.23	73.36
	CTKD (Li et al., 2023)	71.19	73.52	73.79	75.45	73.93	73.52	73.57
	NKD (Yang et al., 2023b)	70.40	72.77	76.35	75.24	74.07	74.86	73.95
	TTM (Zheng and Yang, 2024)	71.83	73.97	76.17	76.23	74.32	74.33	74.48
	LSKD (Sun et al., 2024)	71.43	74.17	76.62	76.11	74.37	74.36	74.51
	NormKD (Chi et al., 2023)	71.40	73.91	76.57	76.40	74.84	74.45	74.60
	DKD (Zhao et al., 2022)	71.97	74.11	76.32	76.24	74.81	74.68	74.69
	CRLD	72.10	74.42	77.60	76.45	75.58	75.27	75.24
	CRLD-NormKD	72.08	74.59	78.22	76.49	75.71	75.48	75.43
	MLLD $\dagger$ (Jin et al., 2023)	72.19	74.11	77.08	76.63	75.35	75.18	75.09
	CRLD $\dagger$	72.42	74.87	78.28	76.94	76.02	75.45	75.66
	CRLD-NormKD $\dagger$	72.57	75.08	78.53	76.91	76.20	75.59	75.81

Table 2. Top-1 accuracy (%) on CIFAR-100 with heterogeneous-architecture teacher-student pairs.

Method	Teacher	ResNet32 $\times$ 4	ResNet32 $\times$ 4	WRN-40-2	WRN-40-2	VGG13	ResNet50	Avg.
	Teacher	79.42	79.42	75.61	75.61	74.64	79.34
	Student	ShuffleNetV2	WRN-16-2	ResNet8 $\times$ 4	MobileNetV2	MobileNetV2	MobileNetV2
	Student	71.82	73.26	72.50	64.60	64.60	64.60
Feature KD	AT (Zagoruyko and Komodakis, 2017)	72.73	73.91	74.11	60.78	59.40	58.58	66.59
	RKD (Park et al., 2019)	73.21	74.86	75.26	69.27	64.52	64.43	70.26
	FitNets (Romero et al., 2015)	73.54	74.70	77.69	68.64	64.16	63.16	70.32
	CRD (Tian et al., 2020)	75.65	75.65	75.24	70.28	69.63	69.11	72.59
	OFD (Heo et al., 2019)	76.82	76.17	74.36	69.92	69.48	69.04	72.63
	ReviewKD (Chen et al., 2021a)	77.78	76.11	74.34	71.28	70.37	69.89	73.30
	SimKD (Chen et al., 2022a)	78.39	77.17	75.29	70.10	69.44	69.97	73.39
	CAT-KD (Guo et al., 2023)	78.41	76.97	75.38	70.24	69.13	71.36	73.58
Logit KD	KD (Hinton et al., 2015)	74.45	74.90	73.97	68.36	67.37	67.35	71.07
	CTKD (Li et al., 2023)	75.37	74.57	74.61	68.34	68.50	68.67	71.68
	LSKD (Sun et al., 2024)	75.56	75.26	77.11	69.23	68.61	69.02	72.47
	NormKD (Chi et al., 2023)	76.01	75.17	76.80	69.14	69.53	69.57	72.70
	DKD (Zhao et al., 2022)	77.07	75.70	75.56	69.28	69.71	70.35	72.95
	CRLD	78.27	76.92	77.28	70.37	70.39	71.36	74.10
	CRLD-NormKD	78.35	77.28	77.51	70.55	70.34	71.47	74.25
	MLLD $\dagger$ (Jin et al., 2023)	78.44	76.52	77.33	70.78	70.57	71.04	74.11
	CRLD $\dagger$	78.50	77.04	77.75	71.26	70.70	71.43	74.45
	CRLD-NormKD $\dagger$	78.52	77.39	77.98	71.36	70.81	71.49	74.59

Table 3. Top-1 and Top-5 accuracy (%) on Tiny-ImageNet.

Method	Teacher	ResNet32 $\times$ 4
	Teacher	64.30/85.07
	Student	ResNet8 $\times$ 4
	Student	55.25/79.62
Feature KD	FCFD (Liu et al., 2023)	60.15/82.80
Logit KD	KD (Hinton et al., 2015)	56.00/79.64
	DKD (Zhao et al., 2022)	57.79/81.57
	NKD (Yang et al., 2023b)	58.63/82.12
	NormKD (Chi et al., 2023)	62.05/83.98
	CRLD	63.39/84.20
	CRLD-NormKD	63.77/84.57
	MLLD $\dagger$ (Jin et al., 2023)	61.91/83.77
	CRLD $\dagger$	63.65/84.74
	CRLD-NormKD $\dagger$	63.84/85.52

3.2. Logit-Space Consistency Regularisation

Consistency regularisation has been widely employed in SSL research (Sajjadi et al., 2016; Tarvainen and Valpola, 2017; Sohn et al., 2020; Berthelot et al., 2019, 2020). It involves creating different views of the same unlabelled image, which are separately fed into a neural network to obtain a pair of network predictions. Consistency regularisation is enforced between the pair of predictions given the prior knowledge that both views fundamentally represent the same high-level information such as the object category.

In CRLD, we employ one weak and one strong view to set the stage for our set of within-view and cross-view consistency criteria. Specifically, we adopt RandAugment (Cubuk et al., 2020) with random magnitude alongside random crop, random horizontal flip, and Cutout (DeVries and Taylor, 2017) as our strong data augmentation policy. A full list of RandAugment’s transformation operations is provided in the Supplementary Materials. For the weak augmentation, we simply apply random crop and random horizontal flip, which is the standard data augmentation in previous logit-based KD methods (Hinton et al., 2015; Zhao et al., 2022; Chi et al., 2023; Yang et al., 2023b; Sun et al., 2024). We denote our weak and strong view transformation functions by $T_{w}(\cdot)$ and $T_{s}(\cdot)$ , respectively.

Concretely, given a batch of $B$ training samples $\mathbf{x}=\{x_{b}:b\in(1,...,B)\}$ , we separately apply $T_{w}(\cdot)$ and $T_{s}(\cdot)$ to each sample to obtain a weakly-augmented and a strongly-augmented view of $x_{b}$ , denoted as $x^{w}_{b}$ and $x^{s}_{b}$ , respectively. Next, we feed both views of the input image individually to the teacher and the student, obtaining four network predictions, namely $\mathbf{p}_{w}^{T}$ , $\mathbf{p}_{s}^{T}$ , $\mathbf{p}_{w}^{S}$ , and $\mathbf{p}_{s}^{S}$ , where we drop subscript $b$ for brevity.

We define within-view consistency regularisation as the consistency criterion between teacher’s and student’s predictions of the same weak or strong view. The within-view consistency objective is therefore computed as:

(1)

\mathcal{L}^{WV}_{KD}=\text{KLD}(\mathbf{p}^{S}_{w},\mathbf{p}^{T}_{w})+\text{KLD}(\mathbf{p}^{S}_{s},\mathbf{p}^{T}_{s})

Next, we design a novel cross-view consistency regularisation. It demands the teacher and student to receive differently augmented views of an image and yet produce logit predictions as similar as possible. Formally, this cross-view objective is given by:

(2)

\mathcal{L}^{CV}_{KD}=\text{KLD}(\mathbf{p}^{S}_{w},\mathbf{p}^{T}_{s})+\text{KLD}(\mathbf{p}^{S}_{s},\mathbf{p}^{T}_{w})

The overall KD objective is a weighted sum of the within-view and cross-view consistency losses: $\mathcal{L}_{KD}=\lambda^{WV}_{KD}\mathcal{L}^{WV}_{KD}+\lambda^{CV}_{KD}\mathcal{L}^{CV}_{KD}$ . A schematic diagram of the pipeline is provided in Figure 2 .

Furthermore, a previous work (Beyer et al., 2022) reported that teacher and student shall receive an identical view of the same input using the same image transformation for maximal knowledge distillation performance. With our specific design, however, we will demonstrate that the teacher and student receiving different views of an input using different view transformations leads to optimal performance. In Section 4.4, we conduct extensive ablation experiments to examine whether and when the proposed cross-view learning really works. As will be shown, cross-view consistency regularisation using different views of the same input image is key to the strong performance of the proposed CRLD framework.

3.3. Confidence-based Soft Label Mining

Confirmation bias harms distillation when the student learns from erroneous soft labels provided by the teacher. By introducing the more challenging strongly-augmented views, we are also increasing the likelihood that the well-trained teacher produces misleading predictions that undermine student learning. We experimentally observe that strongly-augmented samples generated by our strong view transformation policy can sometimes be almost unintelligible (refer to Supplementary Materials for examples), with false predictions made by the teacher. Therefore, we are motivated to refrain unreliable teacher predictions from forming the consistency regularisation pairs. To this end, we propose a simple thresholding mechanism by considering the highest class probability in teacher’s per-instance prediction as an indicator of teacher’s uncertainty about this prediction. Teacher predictions whose highest class probability is below a given threshold are discarded.

In practice, we apply two thresholds $\tau_{w}$ and $\tau_{s}$ for teacher’s predictions of the weak and strong views, respectively. Different from the common practice in SSL (Xie et al., 2020; Sohn et al., 2020), we do not convert the preserved predictions into hard, one-hot pseudo-labels. This is due to the nature of the KD task, whose success hinges on the dark knowledge carried within the non-target class predictions (Hinton et al., 2015; Zhao et al., 2022; Yang et al., 2023b). Instead, we keep teacher’s soft predictions as they are as supervision. As an example, $\text{KLD}(\mathbf{p}^{S}_{w},\mathbf{p}^{T}_{s})$ in Equation 2 becomes $\mathbbm{1}(\max\mathbf{p}^{T}_{s}>\tau_{s})\text{KLD}(\mathbf{p}^{S}_{w},\mathbf{p}^{T}_{s})$ , where $\mathbbm{1}(\cdot)$ is the indicator function. Other objectives are defined like-wise and are omitted for brevity.

Table 4. Top-1 and Top-5 accuracy (%) on ImageNet.

Method	Teacher	ResNet34	ResNet50
	Teacher	73.31/91.42	76.16/92.86
	Student	ResNet18	MobileNetV1
	Student	69.75/89.07	68.87/88.76
Feature KD	AT (Zagoruyko and Komodakis, 2017)	70.69/90.01	69.56/89.33
	OFD (Heo et al., 2019)	70.81/89.98	71.25/90.34
	CRD (Tian et al., 2020)	71.17/90.13	71.37/90.41
	RKD (Park et al., 2019)	71.34/90.37	71.32/90.62
	CAT-KD (Guo et al., 2023)	71.26/90.45	72.24/91.13
	SimKD (Chen et al., 2022a)	71.59/90.48	72.25/90.86
	ReviewKD (Chen et al., 2021a)	71.61/90.51	72.56/91.00
	SRRL (Yang et al., 2021b)	71.73/90.60	72.49/90.92
Logit KD	KD (Hinton et al., 2015)	70.66/89.88	68.58/88.98
	TAKD (Mirzadeh et al., 2020)	70.78/90.16	70.82/90.01
	CTKD (Li et al., 2023)	71.51/-	90.47/-
	NormKD (Chi et al., 2023)	71.56/90.47	72.12/90.86
	DKD (Zhao et al., 2022)	71.70/90.41	72.05/91.05
	NKD (Yang et al., 2023b)	71.96/-	72.58/-
	MLLD (Jin et al., 2023)	71.90/90.55	73.01/91.42
	TTM (Zheng and Yang, 2024)	72.19/-	73.09/-
	LSKD (Sun et al., 2024)	72.08/90.74	73.22/91.59
	CRLD	72.37/90.76	73.53/91.43
	CRLD-NormKD	72.39/90.87	73.74/91.61

3.4. Training Objective

The overall training objective for CRLD is a weighted combination of previously described loss terms, namely a ground-truth supervision loss $\mathcal{L}_{CE}$ and a teacher supervision KD loss $\mathcal{L}_{KD}$ .

(3)

\mathcal{L}=\mathcal{L}_{CE}+\lambda_{KD}\mathcal{L}_{KD}=\mathcal{L}_{CE}+\lambda^{WV}_{KD}\mathcal{L}^{WV}_{KD}+\lambda^{CV}_{KD}\mathcal{L}^{CV}_{KD}

where $\lambda_{KD}$ is a balancing weight. $\mathcal{L}_{CE}$ is computed between student’s predictions of both the weakly- and strong-augmented inputs and the GT label using the cross-entropy loss.

The pseudo-code for the training of CRLD is provided in Algorithm 1, where $\text{SLS}(\cdot)$ denotes the confidence-based soft label mining operation with $\tau_{w}$ or $\tau_{s}$ as its parameter. $\text{SLS}(\cdot)$ produces binary mask $\mathbf{M}$ which indicates the selected instance-wise predictions.

4. Experiments

4.1. Datasets

CIFAR-100 (Krizhevsky, 2009): a classic image classification benchmark with 50,000 training and 10,000 validation (or test) RGB images of 100 classes.

Tiny-ImageNet: a subset of ImageNet (Deng et al., 2009) which consists of 100,000 training and 50,000 validation RGB images over 200 classes, with image resolution downsized from ImageNet’s $256\times 256$ to $64\times 64$ .

ImageNet (Deng et al., 2009): a widely used large-scale image classification dataset, comprising 1.28 million training and 50,000 validation RGB images annotated in 100 classes.

4.2. Implementation Details

We evaluate our method across various teacher-student pairs of common DNN architecture families: ResNet (He et al., 2016), WRN (Zagorukyo and Komodakis, 2016), VGG (Simonyan and Zisserman, 2015), MobileNet (Howard et al., 2017; Sandler et al., 2018), and ShuffleNet (Zhang et al., 2018c). In all experiments, we strictly adhere to standardised training configurations of previous knowledge distillation methods (Hinton et al., 2015; Zagoruyko and Komodakis, 2017; Romero et al., 2015; Heo et al., 2019; Tung and Mori, 2019; Peng et al., 2019; Passalis and Tefas, 2018; Chen et al., 2021b; Tian et al., 2020; Park et al., 2019; Chen et al., 2021a, 2022b; Yang et al., 2021b, a; Chi et al., 2023; Yang et al., 2023b; Li et al., 2023; Guo et al., 2023). All reported experimental results are averaged over 3 independent runs.

Specifically, for CIFAR-100 and Tiny-ImageNet, we train our method for a total of 240 epochs, with an initial learning rate of 0.025 for MobileNet (Sandler et al., 2018) and ShuffleNet (Zhang et al., 2018c) students and 0.05 for others. The learning rate decays by a factor of 10 after the 150th, 180th, and 210th epochs; the SGD optimiser is used, with a momentum of 0.9, a weight decay of $5\times 10^{-4}$ , and a batch size of 64. For ImageNet, we conduct 100-epoch training with a batch size of 512 and an initial learning rate of 0.2 that decays by a factor of 10 at the 30th, 60th, and 90th epochs. Other parameters, unless otherwise stated, follow CIFAR-100 and Tiny-ImageNet experiments. Our method is implemented in the mdistiller codebase.

Table 5. Ablation experiments on different consistency regularisation designs using CIFAR-100.

Expt.	$\mathbf{p}^{S}_{w}$ - $\mathbf{p}^{T}_{w}$	$\mathbf{p}^{S}_{s}$ - $\mathbf{p}^{T}_{s}$	$\mathbf{p}^{S}_{w}$ - $\mathbf{p}^{T}_{s}$	$\mathbf{p}^{S}_{s}$ - $\mathbf{p}^{T}_{w}$	ResNet32 $\times$ 4
Expt.	$\mathbf{p}^{S}_{w}$ - $\mathbf{p}^{T}_{w}$	$\mathbf{p}^{S}_{s}$ - $\mathbf{p}^{T}_{s}$	$\mathbf{p}^{S}_{w}$ - $\mathbf{p}^{T}_{s}$	$\mathbf{p}^{S}_{s}$ - $\mathbf{p}^{T}_{w}$	ResNet8 $\times$ 4
A	✔				76.26
B		✔			76.75
C			✔		74.10
D				✔	75.38
E	✔		✔		76.60
F	✔			✔	77.36
G	✔	✔			77.39
H	✔	✔	✔		77.71
I	✔	✔		✔	78.11
J	✔	✔	✔	✔	78.18

Table 6. Generalisation to existing logit-based methods on CIFAR-100.

Teacher	ResNet56	ResNet110	ResNet32 $\times$ 4	WRN-40-2	WRN-40-2	VGG13	Avg.
Teacher	72.34	74.31	79.42	75.61	75.61	74.64
Student	ResNet20	ResNet32	ResNet8 $\times$ 4	WRN-16-2	WRN-40-1	VGG8
Student	69.06	71.14	72.50	73.26	71.98	70.36
KD (Hinton et al., 2015)	70.69	73.57	73.53	75.22	73.74	73.43	73.36
+CRLD	72.10	74.42	77.60	76.45	75.58	75.27	75.24
NKD (Yang et al., 2023b)	70.40	72.77	76.21	75.24	74.07	74.40	73.85
+CRLD	71.95	74.40	78.16	76.60	74.87	75.16	75.19
MLLD (Jin et al., 2023)	71.24	73.96	74.64	75.57	73.97	73.80	73.86
+CRLD	72.07	74.64	77.00	76.75	75.46	74.87	75.13
DKD (Zhao et al., 2022)	71.49	73.95	75.96	75.67	74.47	74.67	74.37
+CRLD	70.70	73.45	77.90	76.27	75.16	75.57	74.84
NormKD (Chi et al., 2023)	71.43	73.95	76.26	76.01	74.55	74.45	74.44
+CRLD	72.08	74.59	78.22	76.49	75.71	75.48	75.43
MLLD $\dagger$ (Jin et al., 2023)	72.19	74.11	77.08	76.63	75.35	75.18	75.09
+CRLD $\dagger$	72.42	74.87	78.28	76.94	76.02	75.45	75.66

4.3. Main Results

Distillation performance. We present extensive experimental results on CIFAR-100, Tiny-ImageNet, and ImageNet datasets using a diversity of teacher-student pairs in Tables LABEL:tab:cifar100_homo to LABEL:tab:imagenet. Specifically, the proposed CRLD outperforms all existing methods on all evaluated datasets across teacher-student pairs of both homogeneous (Tables LABEL:tab:cifar100_homo, LABEL:tab:timagenet, and LABEL:tab:imagenet) and heterogeneous (Tables LABEL:tab:cifar100_het and LABEL:tab:imagenet) architectures. When using MLLD’s (Jin et al., 2023) training configurations (marked with “ $\dagger$ ”), our method achieves further performance gains and leads MLLD by a considerable margin.

Generalisation capabilities In addition to NormKD (Chi et al., 2023), we also apply the proposed CRLD to state-of-the-art logit-based knowledge distillation frameworks (Hinton et al., 2015; Yang et al., 2023b; Jin et al., 2023; Zhao et al., 2022) and report the results in Table 6. Note that for a fair comparison, we report our reproduced results for compared methods, using official implementations and specifications. The experimental results cogently validate the generalisation capability of our method. The proposed CRLD works orthogonally with existing knowledge distillation methods and can be easily incorporated to significantly boost knowledge transfer performance without introducing any extra network parameter or any additional inference overhead.

4.4. Ablation Studies

Design of consistency regularisation. We break down our full training objective and investigate the play of each individual term in CRLD’s overall effectiveness. A set of ablation experiments are conducted with results presented in Table 5. First, we observe that within-view losses are individually effective and consistency within the strong view alone is more effective compared to weak view alone (Expt. A-B). Intriguingly, cross-view consistencies are harmful when used individually (Expt. B-C), but are rather beneficial when applied in concert with within-view consistencies (Expt. E-J). Finally, our ablation experiments (Expt. G-J) demonstrate that each individual consistency objective in our full objective plays a non-negligible part and their joint play leads to the optimal performance. Note that our experiments also highlight that the effectiveness of CRLD does not stem from a mere increase in the diversity of training samples, as a notable $+1.56\%$ accuracy gain is achieved compared to when the exact same set of strong view augmentation policies are applied in a naive manner (i.e., Expt. B $\rightarrow$ J).

Strengths of view transformations. Table 7 probes how the absolute and relative strengths of CRLD’s view transformations impact its performance. “w/o CVL” denotes “without cross-view learning”. Apparently, CVL is beneficial regardless of the transformation strengths, but the “strong-weak” duo produces the best results. See Supplementary Materials for more discussions.

Sensitivity to $\mathbf{\tau_{w}}$ and $\mathbf{\tau_{s}}$ . Figure 6 plots the performance of CRLD across different $\tau_{w}$ & $\tau_{s}$ values. According to the empirical results, CRLD demonstrates limited sensitivity to these thresholding hyperparameters over the entire hyperaprameter space, despite peak performance within specific intervals.

Sensitivity to strength of strong view transformations. To see how the strength of strong view transformations may influence the performance of CRLD, we conveniently tweak hyperparameter $n$ , the number of view transformation operations randomly sampled and applied from all RandAugment operations. Moreover, we also apply a probability multiplier, $p_{s}$ , to modulate the parameter values of sampled operations. Varying $n$ and $p_{s}$ allows an intuitive understanding of the impact of view transformation strength, plotted in Figure 7, and the selection of these hyperparameters. More details can be found in the Supplementary Materials.

Table 7. Effect of different view transformation strengths.

Method	CIFAR-100	Tiny-ImageNet
w/o CVL	76.26	60.83 /83.08
Weak-Weak	76.66	62.83 /84.10
Strong-Strong	76.73	61.67 /83.94
Strong-Weak	78.22	63.77 /84.57

4.5. Further Analyses

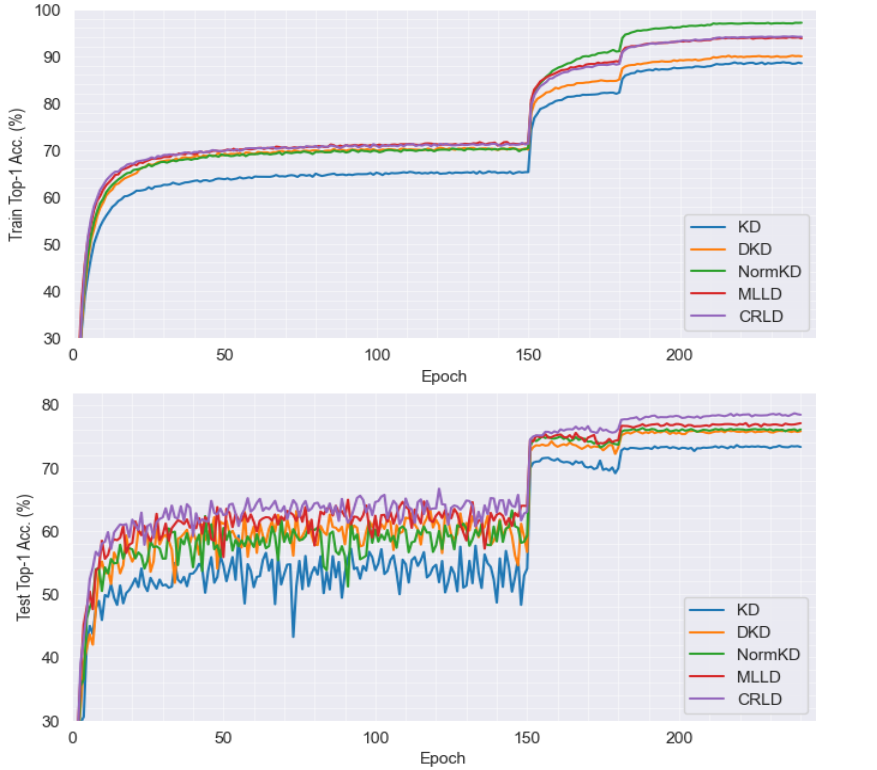
Training dynamics. For further insights into the training profile of different methods, in Table 3 we plot the evolution of training and test accuracies at each epoch throughout the training process. We observe that NormKD demonstrates much higher training accuracy than other methods but has only comparable or even lower test accuracy with respect to MLLD and DKD, which implies overfitting on training data. When the proposed CRLD is applied to NormKD, training accuracy lowers while test accuracy notably increases, suggesting alleviated overfitting and improved generalisation brought about by CRLD. In addition, we also notice less oscillatory test accuracy curves of CRLD, which is likely due to improved generalisation and mitigated confirmation bias of our method.

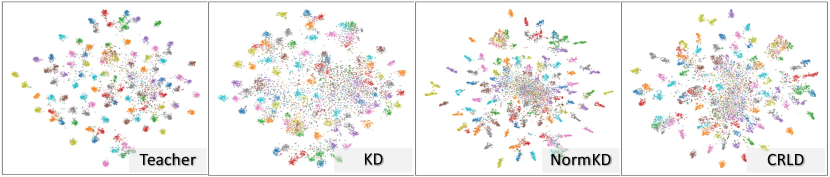
t-SNE visualisation. We visualise the feature space learnt by the student using different logit-based distillation methods. As seen in Figure 4, features learnt using the proposed CRLD are significantly more seperable in the feature space, with more tightly clustered class-wise features and greater inter-class feature variations. These observations imply greater generalisation of the learnt model and substantiate the superiority of the proposed distillation method.

Teacher-student output correlations. To understand how well a trained student is able to mimic its teacher’s predictions from a different perspective, we compute and visualise the correlations between student’s and teacher’s predictions in the Euclidean space in Figure 5. The left map corresponds to NormKD (Chi et al., 2023) and the right CRLD applied to NormKD. It is clear that with CRLD, the average distance between teacher and student predictions are significantly reduced for all categories on the test data — a compelling evidence of better distilled teacher knowledge and greater generalisation capabilities of the trained student.

Distillation without ground-truths. We assess the performance of different methods under the “label-free knowledge distillation” set-up, a more practical scenario where GT labels used to train the teacher are no longer available when performing KD. As shown in Table LABEL:tab:lfkd, GT labels are indispensable to feature-based methods, and the proposed CRLD is the most resilient to missing GT labels amongst logit-based methods.

Application to ViT. To verify the effectiveness of our method on transformer-based models, we further consider the scenario where we distill from a ViT-L (Dosovitskiy et al., 2021) teacher to a ResNet-18 student. Table 9 presents the performance of different methods compared to CRLD on Tiny-ImageNet, where a 100-epoch training policy is employed. As observed, CRLD substantially outperforms all other methods, which suggests that our method generalises well to models with significantly distinctive underlying architectures.

Implication on Beyer et al. (Beyer et al., 2022). Finally, we revisit the “seemingly contradictory” conclusions made in (Beyer et al., 2022) which we have raised earlier on. It turned out our conclusions do not contradict: The consistent matching in (Beyer et al., 2022) is exactly our within-view consistency regularsation. (Beyer et al., 2022) argues consistent matching alone outperforms inconsistent matching alone, which aligns with our observations (Table 5 A & B v.s. C & D). Our work takes a step further by suggesting that consistent and inconsistent (i.e., cross-view) matchings are compatible, and can lead to state-of-the-art results when used in tandem.

Table 8. Top-1 accuracy (%) under the label-free knowledge distillation (LFKD) set-up on CIFAR-100.

Method	Teacher	ResNet32 $\times$ 4	VGG13
Method	Student	ResNet8 $\times$ 4	VGG8
Feature KD	FitNets (Romero et al., 2015)	1.39	1.09
Feature KD	OFD (Heo et al., 2019)	1.43	1.71
Logit KD	KD (Hinton et al., 2015)	73.76	73.49
	MLLD (Jin et al., 2023)	74.10	73.03
	NormKD (Chi et al., 2023)	76.49	74.39
	CRLD	77.82	75.36

Table 9. Top-1 accuracy (%) on Tiny-ImageNet for ViT-L-to-ResNet18 distillation.

Teacher	Student	DKD	NKD	KD	NormKD	LSKD	MLLD	CRLD
86.43	56.90	59.41	60.41	60.50	61.83	62.07	62.44	63.41

More discussions. More analyses and discussions are provided in the Supplementary Materials.

5. Conclusion

In this paper, we presented a novel logit-based knowledge distillation framework named CRLD. The motivation of CRLD lies in revamping popular ideas found in the semi-supervised learning literature, such as consistency regularisation and pseudo-labelling, to combat the overconfident teacher and confirmation bias problems in knowledge distillation. Our design of within-view and cross-view consistency regularsations, enabled by weak and strong image transformations and coupled with a confidence-based soft label selection scheme, leads to a highly effective and versatile knowledge distillation framework. Extensive experiments demonstrate that CRLD can boost existing logit-based methods by considerable margins and sets new records on different image classification datasets and under different configurations.

Acknowledgements.

This work was supported in part by NSFC (62322113, 62376156), Shanghai Municipal Science and Technology Major Project (2021SH
ZDZX0102), and the Fundamental Research Funds for the Central Universities.

References

(1)
Ahn et al. (2019) Sungsoo Ahn, Shell Xu Hu, Andreas Damianou, Neil D. Lawrence, and Zhenwen Dai. 2019. Variational Information Distillation for Knowledge Transfer. In CVPR.
Arazo et al. (2020) Eric Arazo, Diego Ortego, Paul Albert, Noel E. O’Connor, and Kevin McGuinness. 2020. Pseudo-Labeling and Confirmation Bias in Deep Semi-Supervised Learning.
Berthelot et al. (2020) David Berthelot, Nicholas Carlini, Ekin D. Cubuk, Alex Kurakin, Kihyuk Sohn, Han Zhang, and Colin Raffel. 2020. ReMixMatch: Semi-Supervised Learning with Distribution Alignment and Augmentation Anchoring. In ICLR.
Berthelot et al. (2019) David Berthelot, Nicholas Carlini, Ian Goodfellow, Nicolas Papernot, Avital Oliver, and Colin A. Raffel. 2019. MixMatch: A Holistic Approach to Semi-Supervised Learning. In NIPS.
Beyer et al. (2022) Lucas Beyer, Xiaohua Zhai, Amelie Royer, Larisa Markeeva, Rohan Anil, and Alexander Kolesnikov. 2022. Knowledge Distillation: A Good Teacher is Patient and Consistent. In CVPR.
Chen et al. (2022a) Defang Chen, Jian-Ping Mei, Hailin Zhang, Can Wang, Yan Feng, and Chun Chen. 2022a. Knowledge Distillation with the Reused Teacher Classifier. In CVPR.
Chen et al. (2021b) Defang Chen, Jian-Ping Mei, Yuan Zhang, Can Wang, Zhe Wang, Yan Feng, and Chun Chen. 2021b. Cross-Layer Distillation with Semantic Calibration. In AAAI.
Chen et al. (2021a) Pengguang Chen, Shu Liu, Hengshuang Zhao, and Jiaya Jia. 2021a. Distilling Knowledge via Knowledge Review. In CVPR.
Chen et al. (2022b) Yudong Chen, Sen Wang, Jiajun Liu, Xuwei Xu, Frank de Hoog, and Zi Huang. 2022b. Improved Feature Distillation via Projector Ensemble. In NeurIPS.
Chi et al. (2023) Zhihao Chi, Tu Zheng, Hengjia Li, Zheng Yang, Boxi Wu, Binbin Lin, and Deng Cai. 2023. NormKD: Normalized Logits for Knowledge Distillation. In arXiv:2308.00520.
Cho and Hariharan (2019) Jang Hyun Cho and Bharath Hariharan. 2019. On the Efficacy of Knowledge Distillation. In ICCV.
Cubuk et al. (2019) Ekin D. Cubuk, Barret Zoph, Dandelion Mane, Vijay Vasudevan, and Quoc V. Le. 2019. AutoAugment: Learning Augmentation Strategies from Data. In CVPR.
Cubuk et al. (2020) Ekin Dogus Cubuk, Barret Zoph, Jon Shlens, and Quoc Le. 2020. RandAugment: Practical Automated Data Augmentation with a Reduced Search Space. In NIPS.
Cui et al. (2023) Kaiwen Cui, Yingchen Yu, Fangneng Zhan, Shengcai Liao, Shijian Lu, and Eric P Xing. 2023. KD-DLGAN: Data limited image generation via knowledge distillation. In CVPR.
Cui and Yan (2021) Wanyun Cui and Sen Yan. 2021. Isotonic Data Augmentation for Knowledge Distillation. In IJCAI.
Das et al. (2020) Deepan Das, Haley Massa, Abhimanyu Kulkarni, and Theodoros Rekatsinas. 2020. An Empirical Analysis of the Impact of Data Augmentation on Knowledge Distillation. In ICML Workshop.
Deng et al. (2009) Jia Deng, Wei Dong, Richard Socher, Li-Jia Li, Kai Li, and Li Fei-Fei. 2009. ImageNet: A Large-Scale Hierarchical Image Database. In CVPR.
DeVries and Taylor (2017) Terrance DeVries and Graham W. Taylor. 2017. Improved Regularization of Convolutional Neural Networks with Cutout. In arXiv:1708.04552.
Dosovitskiy et al. (2021) Alexey Dosovitskiy, Lucas Beyer, Alexander Kolesnikov, Dirk Weissenborn, Xiaohua Zhai, Thomas Unterthiner, Mostafa Dehghani, Matthias Minderer, Georg Heigold, Sylvain Gelly, Jakob Uszkoreit, and Neil Houlsby. 2021. An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale. In ICLR.
Gu et al. (2024) Yuxian Gu, Li Dong, Furu Wei, and Minlie Huang. 2024. MiniLLM: Knowledge distillation of large language models. In ICLR.
Guo et al. (2017) Chuan Guo, Geoff Pleiss, Yu Sun, and Kilian Q. Weinberger. 2017. On Calibration of Modern Neural Networks. In ICML.
Guo et al. (2021) Xiaoyang Guo, Shaoshuai Shi, Xiaogang Wang, and Hongsheng Li. 2021. LIGA-Stereo: Learning LiDAR Geometry Aware Representations for Stereo-based 3D Detector. In ICCV.
Guo et al. (2023) Ziyao Guo, Haonan Yan, Hui Li, and Xiaodong Lin. 2023. Class Attention Transfer Based Knowledge Distillation. In CVPR.
He et al. (2016) Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. 2016. Deep Residual Learning for Image Recognition. In CVPR.
Hendrycks et al. (2020) Dan Hendrycks, Norman Mu, Ekin D. Cubuk, Barret Zoph, Justin Gilmer, and Balaji Lakshminarayanan. 2020. AugMix: A Simple Data Processing Method to Improve Robustness and Uncertainty. In ICLR.
Heo et al. (2019) Byeongho Heo, Jeesoo Kim, Sangdoo Yun, Hyojin Park, Nojun Kwak, and Jin Young Choi. 2019. A Comprehensive Overhaul of Feature Distillation. In ICCV.
Hinton et al. (2015) Geoffrey Hinton, Oriol Vinyals, and Jeff Dean. 2015. Distilling the Knowlegde in a Neural Network. In arXiv:1503.02531.
Hong et al. (2022) Yu Hong, Hang Dai, and Yong Ding. 2022. Cross-modality Knowledge Distillation Network for Monocular 3D Object Detection. In ECCV.
Howard et al. (2017) Andrew G. Howard, Menglong Zhu, Bo Chen, Dmitry Kalenichenko, Weijun Wang, Tobias Weyand, Marco Andreetto, and Hartwig Adam. 2017. MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications. In arXiv:1704.04861.
Huang et al. (2022b) Tao Huang, Shan You, Fei Wang, Chen Qian, and Chang Xu. 2022b. Knowledge Distillation from a Stronger Teacher. In NeurIPS.
Huang et al. (2022a) Yuge Huang, Jiaxiang Wu, Xingkun Xu, and Shouhong Ding. 2022a. Evaluation-oriented knowledge distillation for deep face recognition. In CVPR.
Jin et al. (2023) Ying Jin, Jiaqi Wang, and Dahua Lin. 2023. Multi-level Logit Distillation. In CVPR.
Kim et al. (2021) Minha Kim, Shahroz Tariq, and Simon S Woo. 2021. Fretal: Generalizing deepfake detection using knowledge distillation and representation learning. In CVPR.
Krizhevsky (2009) Alex Krizhevsky. 2009. Learning Multiple Layers of Features from Tiny Images.
Laine and Aila (2017) Samuli Laine and Timo Aila. 2017. Temporal Ensembling for Semi-Supervised Learning. In ICLR.
Li et al. (2023) Zheng Li, Xiang Li, Lingfeng Yang, Borui Zhao, Renjie Song, Lei Luo, Jun Li, and Jian Yang. 2023. Curriculum Temperature for Knowledge Distillation. In AAAI.
Lin et al. (2022) Sihao Lin, Hongwei Xie, Bing Wang, Kaicheng Yu, Xiaojun Chang, Xiaodan Liang, and Gang Wang. 2022. Knowledge Distillation via the Target-aware Transformer. In CVPR.
Liu et al. (2023) Dongyang Liu, Meina Kan, Shiguang Shan, and Xilin Chen. 2023. Function-Consistent Feature Distillation. In ICLR.
Liu et al. (2021) Li Liu, Qingle Huang, Sihao Lin, Hongwei Xie, Bing Wang, Xiaojun Chang, and Xiaodan Liang. 2021. Exploring Inter-Channel Correlation for Diversity-preserved Knowledge Distillation. In ICCV.
Liu et al. (2019) Yifan Liu, Ke Chen, Chris Liu, Zengchang Qin, Zhenbo Luo, and Jingdong Wang. 2019. Structured Knowledge Distillation for Semantic Segmentation. In CVPR.
Mirzadeh et al. (2020) Seyed-Iman Mirzadeh, Mehrdad Farajtabar, Ang Li, Nir Levine, Akihiro Matsukawa, and Hassan Ghasemzadeh. 2020. Improved Knowledge Distillation via Teacher Assistant. In AAAI.
Müller et al. (2019) Rafael Müller, Simon Kornblith, and Geoffrey Hinton. 2019. When Does Label Smoothing Help?. In NIPS.
Park et al. (2019) Wonpyo Park, Dongju Kim, Yan Lu, and Minsu Cho. 2019. Relational Knowledge Distillation. In CVPR.
Passalis and Tefas (2018) Nikolaos Passalis and Anastasios Tefas. 2018. Learning Deep Representations with Probabilistic Knowledge Transfer. In ECCV.
Peng et al. (2019) Baoyun Peng, Xiao Jin, Jiaheng Liu, Shunfeng Zhou, Yichao Wu, Yu Liu, Dongsheng Li, and Zhaoning Zhang. 2019. Correlation Congruence for Knowledge Distillation. In CVPR.
Romero et al. (2015) Adriana Romero, Nicolas Ballas, Samira Ebrahimi Kahou, Antoine Chassang, Carlo Gatta, and Yoshua Bengio. 2015. FitNets: Hints for Thin Deep Nets. In ICLR.
Sajjadi et al. (2016) Mehdi Sajjadi, Mehran Javanmardi, and Tolga Tasdizen. 2016. Regularization with Stochastic Transformations and Perturbations for Deep Semi-Supervised Learning. In NIPS.
Sandler et al. (2018) Mark Sandler, Andrew Howard, Menglong Zhu, Andrey Zhmoginov, and Liang-Chieh Chen. 2018. MobileNetV2: Inverted Residuals and Linear Bottlenecks. In CVPR.
Simonyan and Zisserman (2015) Karen Simonyan and Andrew Zisserman. 2015. Very Deep Convolutional Networks for Large-Scale Image Recognition. In ICLR.
Sohn et al. (2020) Kihyuk Sohn, David Berthelot, Chun-Liang Li, Zizhao Zhang, Nicholas Carlini, Ekin D. Cubuk, Alex Kurakin, Han Zhang, and Colin Raffel. 2020. FixMatch: Simplifying Semi-Supervised Learning with Consistency and Confidence. In NIPS.
Son et al. (2021) Wonchul Son, Jaemin Na, Junyong Choi, and Wonjun Hwang. 2021. Densely Guided Knowledge Distillation using Multiple Teacher Assistants. In ICCV.
Sun et al. (2024) Shangquan Sun, Wenqi Ren, Jingzhi Li, Rui Wang, Rui Wang, and Xiaochun Cao. 2024. Logit Standardization in Knowledge Distillation. In CVPR.
Tarvainen and Valpola (2017) Antti Tarvainen and Harri Valpola. 2017. Mean Teachers Are Better Role Models: Weight-Averaged Consistency Targets Improve Semi-Supervised Deep Learning Results. In NIPS.
Tian et al. (2020) Yonglong Tian, Dilip Krishnan, and Phillip Isola. 2020. Contrastive Representation Distillation. In ICLR.
Tung and Mori (2019) Frederick Tung and Greg Mori. 2019. Similarity-Preserving Knowledge Distillation. In ICCV.
Wang et al. (2022) Huan Wang, Suhas Lohit, Mike Jones, and Yun Fu. 2022. What Makes A ”Good” Data Augmentation in Knowledge Distillation - A Statistical Perspective. In NIPS.
Wang et al. (2019) Tao Wang, Li Yuan, Xiaopeng Zhang, and Jiashi Feng. 2019. Distilling object detectors with fine-grained feature imitation. In CVPR.
Xie et al. (2020) Qizhe Xie, Zihang Dai, Eduard Hovy, Minh-Thang Luong, and Quoc V. Le. 2020. Unsupervised Data Augmentation for Consistency Training. In NIPS.
Xu et al. (2020) Guodong Xu, Ziwei Liu, Xiaoxiao Li, and Chen Change Loy. 2020. Knowledge Distillation Meets Self-Supervision. In ECCV.
Yang et al. (2021a) Chuanguang Yang, Zhulin An, Linhang Cai, and Yongjun Xu. 2021a. Hierarchical Self-Supervised Augmented Knowledge Distillation. In IJCAI.
Yang et al. (2021b) Jing Yang, Brais Martinez, Adrian Bulat, and Georgios Tzimiropoulos. 2021b. Knowledge Distillation via Softmax Regression Representation Learning. In ICLR.
Yang et al. (2023a) Lihe Yang, Lei Qi, litong Feng, Wayne Zhang, and Yinghuan Shi. 2023a. Revisiting Weak-to-Strong Consistency in Semi-Supervised Semantic Segmentation. In CVPR.
Yang et al. (2022a) Zhendong Yang, Zhe Li, Xiaohu Jiang, Yuan Gong, Zehuan Yuan, Danpei Zhao, and Chun Yuan. 2022a. Focal and Global Knowledge Distillation for Detectors. In CVPR.
Yang et al. (2022b) Zhendong Yang, Zhe Li, Mingqi Shao, Dachuan Shi, Zehuan Yuan, and Chun Yuan. 2022b. Masked Generative Distillation. In ECCV.
Yang et al. (2023b) Zhendong Yang, Ailing Zeng, Zhe Li, Tianke Zhang, Chun Yuan, and Yu Li. 2023b. From Knowledge Distillation to Self-Knowledge Distillation: A Unified Approach with Normalized Loss and Customized Soft Labels. In ICCV.
Yim et al. (2017) Junho Yim, Donggyu Joo, Jihoon Bae, and Junmo Km. 2017. A Gift from Knowledge Distillation: Fast Optimization, Network Minimization and Transfer Learning. In CVPR.
Yuan et al. (2020) Li Yuan, Francis EH Tay, Guilin Li, Tao Wang, and Jiashi Feng. 2020. Revisiting Knowledge Distillation via Label Smoothing Regularization. In CVPR.
Zagorukyo and Komodakis (2016) Sergey Zagorukyo and Nikos Komodakis. 2016. Wide Residual Networks. In BMVC.
Zagoruyko and Komodakis (2017) Sergey Zagoruyko and Nikos Komodakis. 2017. Paying More Attention to Attention: Improving the Performance of Convolutional Neural Networks via Attention Transfer. In ICLR.
Zhang et al. (2023) Bo Zhang, Jiacheng Sui, and Li Niu. 2023. Foreground Object Search by Distilling Composite Image Feature. In ICCV.
Zhang et al. (2018a) Hongyi Zhang, Moustapha Cisse, Yann N. Dauphin, and David Lopez-Paz. 2018a. mixup: Beyond Empirical Risk Minimization. In ICLR.
Zhang et al. (2024) Weijia Zhang, Dongnan Liu, Chao Ma, and Weidong Cai. 2024. Alleviating Foreground Sparsity for Semi-Supervised Monocular 3D Object Detection. In WACV.
Zhang et al. (2018c) Xiangyu Zhang, Xinyu Zhou, Mengxiao Lin, and Jian Sun. 2018c. ShuffleNet: An Extremely Efficient Convolutional Neural Network for Mobile Devices. In CVPR.
Zhang et al. (2018b) Ying Zhang, Tao Xiang, Timothy M. Hospedales, and Huchuan Lu. 2018b. Deep Mutual Learning. In CVPR.
Zhao et al. (2022) Borui Zhao, Quan Cui, Renjie Song, Yiyu Qiu, and Jiajun Liang. 2022. Decoupled Knowledge Distillation. In CVPR.
Zheng and Yang (2024) Kaixiang Zheng and En-Hui Yang. 2024. Knowledge Distillation based on Transformed Teaching Matching. In ICLR.
Zheng et al. (2022) Zhaohui Zheng, Rongguang Ye, Ping Wang, Dongwei Ren, Wangmeng Zuo, Qibin Hou, and Ming-Ming Cheng. 2022. Localization Distillation for Dense Object Detection. In CVPR.
Zhou et al. (2023) Shengchao Zhou, Weizhou Liu, Chen Hu, Shuchang Zhou, and Chao Ma. 2023. UniDistill: A Universal Cross-Modality Knowledge Distillation Framework for 3D Object Detection in Bird’s-Eye View. In CVPR.

Cross-View Consistency Regularisation for Knowledge Distillation

Abstract.

1. Introduction

2. Related Work

2.1. Knowledge Distillation

2.2. Consistency Regularisation

2.3. Data Augmentation for KD

3. Methodology

3.1. Knowledge Distillation

3.2. Logit-Space Consistency Regularisation

3.3. Confidence-based Soft Label Mining

3.4. Training Objective

4. Experiments

4.1. Datasets

4.2. Implementation Details

4.3. Main Results

4.4. Ablation Studies

4.5. Further Analyses

5. Conclusion

Acknowledgements.

References

Cross-View Consistency Regularisation for
Knowledge Distillation