Critical non-Hermitian Skin Effect

Linhu Li [email protected] Department of Physics, National University of Singapore, Singapore 117542 Ching Hua Lee [email protected] Department of Physics, National University of Singapore, Singapore 117542 Institute of High Performance Computing, A*STAR, Singapore 138632 Sen Mu [email protected] Department of Physics, National University of Singapore, Singapore 117542 Jiangbin Gong [email protected] Department of Physics, National University of Singapore, Singapore 117542

Abstract

This work uncovers a new class of criticality where eigenenergies and eigenstates of non-Hermitian lattice systems jump discontinuously across a critical point in the thermodynamic limit, unlike established Hermitian and non-Hermitian critical scenarios where spectrum remains continuous across a transition. Such critical behavior, dubbed the “critical skin effect”, is rather generic, occuring whenever subsystems with dissimilar non-Hermitian skin localization lengths are coupled, however weakly. Due to the existence of this criticality, the thermodynamical limit and the zero-coupling limit cannot be exchanged, thus challenging the celebrated generalized Brillouin zone (GBZ) approach when applied to finite-size systems. As manifestations of the critical skin effect in finite-size systems, we present stimulating examples with anomalous scaling behavior regarding spectrum, correlation functions, entanglement entropy, and scale-free wavefunctions that decay exponentially rather than power-law. More spectacularly, topological in-gap modes can even be induced by changing the system size.

Introduction.– Lying at the boundary between distinct phases, critical systems exhibit a wide range of interesting universal properties from divergent susceptibilities to anomalous scaling behavior. They have broad ramifications in conformal and statistical field theory Coniglio and Klein (1980); Hu (1984); Aizenman et al. (1987); Boulatov and Kazakov (1987); Zamolodchikov (1987, 1989); Cardy (1992); Oshikawa and Affleck (1996); Dziarmaga (2005), Schramm-Loewner evolution Gruzberg (2006); Kozdron (2009); Stevenson and Weigel (2011); Werner (2007), entanglement entropy (EE) Vidal et al. (2003); Korepin (2004); Larsson and Johannesson (2005); Ryu and Takayanagi (2006); Barthel et al. (2006); Laflorencie et al. (2006); Swingle (2010); Swingle and Senthil (2013); Lee et al. (2015); Swingle and McGreevy (2016); Chang et al. (2019) and many other contexts. Recently, concepts crucial to criticality - like band gaps and localization - have been challenged by studies of non-Hermitian systems Bender and Boettcher (1998); Bender (2007); Moiseyev (2011); Gong et al. (2018); Kawabata et al. (2019a) exhibiting exceptional points Berry (2004); Dembowski et al. (2004); Rotter (2009); Jin and Song (2009); Longhi (2010); Heiss and Harney (2001); Heiss (2012); Xu et al. (2016); Hassan et al. (2017); Hu et al. (2017); Shen et al. (2018); Wang et al. (2019); Ghatak and Das (2019); Miri and Alù (2019); Zhang and Gong (2020); Yuce (2020); Jin et al. (2019); Kawabata et al. (2019b) or the non-Hermitian skin effect (NHSE), which are characterized by enigmatic bulk-boundary correspondence (BBC) violations, robust directed amplifications, discontinuous Berry curvature and anomalous transport behavior Lee (2016); Xiong (2018); Kunst et al. (2018); Yao and Wang (2018); Yokomizo and Murakami (2019); Lee et al. (2018); Lee and Thomale (2019); Song et al. (2019a, b); Li et al. (2019); Borgnia et al. (2020); Zhang et al. (2019); Yoshida et al. ; Yang et al. ; Lee et al. ; Longhi (2019); Luo (2020).

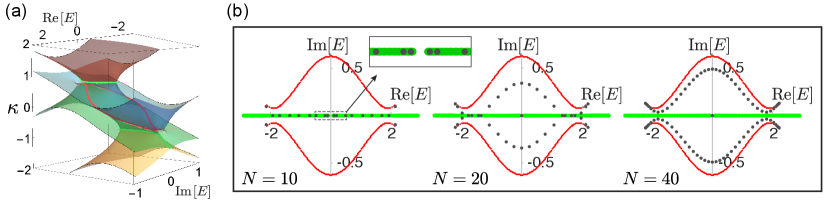
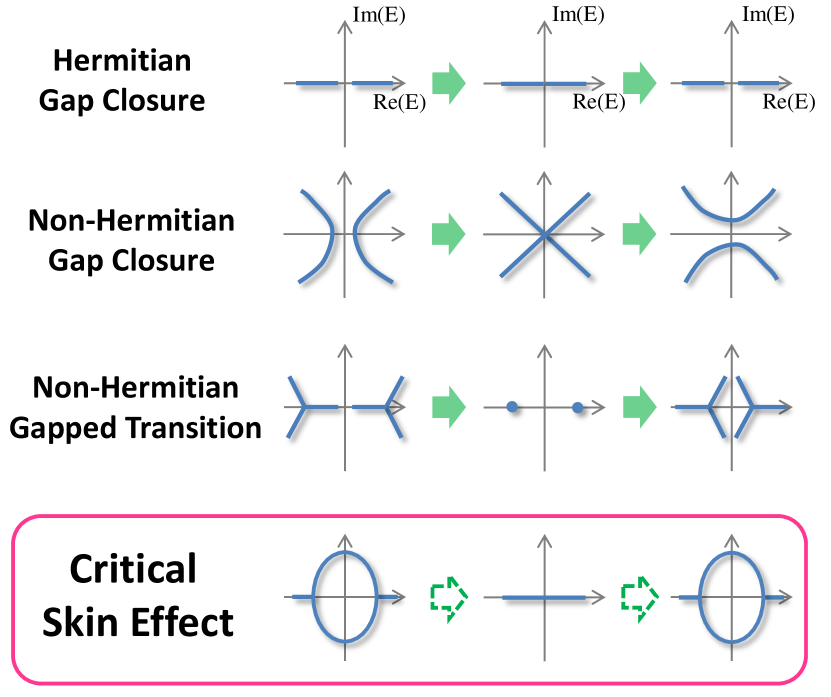
We uncover here a new class of criticality, dubbed the “critical skin effect” (CSE), where the eigenenergies and eigenstates in the thermodynamic limit “jump” discontinuously across the critical point. This is distinct from previously known phase transitions (Hermitian and non-Hermitian) [Fig. 1], where the eigenenergy spectrum can be continuously interpolated across the two bordering phases. A CSE transition, by contrast, is characterized by a discontinuous jump between two different complex spectra along with two different sets of eigenstates. As elaborated below, this behavior appears generically whenever systems of dissimilar NHSE localization lengths are coupled, no matter how weakly ¹¹1Not all subsystems need to be non-Hermitian; indeed, the CSE even occurs if a Hermitian chain is coupled a chain with NHSE. Importantly, at experimentally accessible finite system sizes ²²2Non-Hermitian system, particularly those exhibiting the NHSE, exhibit divergences in local density of states in the thermodynamic limit., the jump smooths out into an interpolation between the two phases in a strongly size-dependent manner, such that the system may exhibit qualitatively different properties i.e. real vs. complex spectrum or presence/absence of topological modes at different system sizes. Being strongly affected by minute perturbations around the critical point, such behavior may prove useful in sensing applications Brandenbourger et al. (2019); Schomerus (2020).

CSE as a limitation of the GBZ.– In non-Hermitian systems with unbalanced gain and loss, spectra under periodic boundary conditions (PBCs) and open boundary conditions (OBCs) can be very different Lee (2016); Xiong (2018); Yao and Wang (2018); Longhi (2020); Lee and Thomale (2019). Indeed, under OBC, eigenstates due to NHSE can exponentially localize at a boundary, in contrast to Bloch states under PBCs. This also explains the possible violation of the BBC, taken for granted in Hermitian settings.

The celebrated GBZ formalism aims to restore the BBC through a complex momentum deformation Yao and Wang (2018); Yokomizo and Murakami (2019); Lee and Thomale (2019); Yang et al. ; Okuma et al. (2020); Lee et al. . Rigorously applicable for bounded but infinitely large systems, it has however been an open question whether the GBZ can still accurately describe finite-size systems. The GBZ of a momentum-space Hamiltonian $H(z)$ , $z=e^{ik}$ can be derived from its characteristic Laurent polynomial (energy eigenequation)

\displaystyle f(z,E):=\det[H(z)-E]=0,

(1)

where $E$ is the eigenenergy. While the ordinary BZ is given by the span of allowed real quasimomenta $k$ , the GBZ is defined by the complex analytically-continued momentum $k\rightarrow k+i\kappa(k)$ , with the NHSE inverse decay length $\kappa(k)=-\log|z|$ determined by the smallest complex deformation $z\rightarrow e^{ik}e^{-\kappa(k)}$ such that $f(z,E)$ possesses a pair of zeros $z_{\mu}$ , $z_{\nu}$ satisfying $|z_{\mu}|=|z_{\nu}|$ for the same $E$ Yao and Wang (2018); Lee and Thomale (2019); Lee et al. . Due to the double degeneracy of states with equal asymptotic decay rate at these $E$ , there exist a pair of eigenstates $\psi_{\mu},\psi_{\nu}$ that can superpose to satisfy OBCs i.e. zero net amplitude at both boundaries. As such, provided that the characteristic polynomial cannot be made reducible by adding a small perturbation, the OBC spectrum in the thermodynamic limit (denoted as $E_{\infty}$ ) can be obtained from the PBC spectrum via $E(e^{ik})\rightarrow E(e^{ik}e^{-\kappa(k)})$ , apart from isolated topological modes. Thus it is often claimed that the BBC is “restored” in the GBZ defined by $k\rightarrow k+i\kappa(k)$ or, at the operator level, with the surrogate Hamiltonian $H(e^{ik})\rightarrow H(e^{ik}e^{-\kappa(k)})$ Lee et al. . In general, different $E$ (energy band) solutions can admit different functional forms of $\kappa(k)$ , leading to band-dependent GBZs that have recently also been described with the auxiliary GBZ formalism Yang et al. . Since $e^{ik}e^{-\kappa(k)}$ is generically non-analytic, it represents effectively non-local hopping terms Lee et al. . As such, the GBZ description challenges the very notion of locality, which is central to critical systems, by effectively “unraveling” the real-space eigenstate accumulation through replacing local hoppings with effectively non-local ones.

Refer to caption — Figure 1: Four different types of critical transitions. Hermitian phase transitions (Top) are marked by gap closures along the real line. In non-Hermitian cases (2nd to 4th rows, axis labels omitted), spectral phase transitions can take more sophisticated possibilities in the 2D complex energy plane. For instance, the spectral topology can change under line gap closures (2nd Row) or shrink to a point and re-emerge in a different topological configuration (3rd row), without the gap ever closing Lee *et al.* . The spectrum continuously passes through a gapless or point-like regime in the first three cases. The CSE (bottom row), however, is special in that OBC spectrum the thermodynamic limit, denoted $E_{\infty}$ , jumps discontinuously from one configuration (left), to a different one (middle), and to another (right) as certain parameter changes from $-\epsilon$ to $0$ (critical border), and to $\epsilon$ , for an arbitrarily small $\epsilon$ .

Due to the robustness of the NHSE, eigenspectra predicted from the GBZ typically converge rapidly to the exact numerically obtained OBC spectra even for small system sizes( $\mathcal{O}(10^{1})$ sites) ³³3In principle, the convergence should be exact in the thermodynamic limit. But in practical computations, floating point errors $\epsilon$ are continuously amplified as they propagate across the system, and we expect accurate numerical spectra only when $L<-\log(\epsilon)/\text{max}(\kappa)$ . . However, this numerical agreement fails spectacularly near a critical point where $f(z,E)$ changes from being reducible to irreducible. To understand the significance of this algebraic property of reducibility, consider a set of coupled irreducible subsystems described by the characteristic polynomial

f(z,E)=f_{0}+\prod_{i}f_{i}(z,E),

(2)

where $f_{i}(z,E)$ is the characteristic polynomial of the $i$ -th subsystem, and $f_{0}$ is a constant that represents the simplest possible form for the subsystem coupling. When $f_{0}=0$ , $f(z,E)$ completely factorizes into irreducible polynomials, as expected from a Hamiltonian $H(z)$ that block-diagonalizes into irreducible sectors associated with the individual $f_{i}(z,E)$ ’s. In particular, the OBC spectrum of this completely decoupled scenario is derived from the independent $\kappa_{i}(k)$ ’s of each subsystem, each determined by $z_{\mu},z_{\nu}$ from the same subsystem.

Yet, a nonzero coupling $f_{0}$ , no matter how small, can have dramatic physical consequences. For arbitrarily small $f_{0}\neq 0$ , the different sectors can hybridize significantly if the $f_{i}$ ’s are different ⁴⁴4If two $f_{i}$ ’s are equivalent, $f_{0}+f_{i}^{2}=(f_{i}+i\sqrt{f_{0}})(f_{i}-i\sqrt{f_{0}})$ is still reducible.. Indeed, such hybridization is inevitable in the thermodynamic limit, with OBC eigenstates formed from superpositions of eigenstates $\psi_{\mu},\psi_{\nu}$ from dissimilar subsystems, each corresponding non-Bloch momenta $-i\log z_{\mu/\nu}$ . Hence the GBZs i.e. $\kappa(k)$ ’s of the coupled system, which are defined in the thermodynamic limit, are thus determined by all pairs of $|z_{\mu}|=|z_{\nu}|$ not necessarily from the same subsystem. Therefore, the GBZs in the coupled case, no matter how small is $f_{0}$ , can differ from the decoupled GBZs at $f_{0}=0$ . That is, the thermodynamic limit and the $f_{0}\rightarrow 0$ limit are not exchangeable. However, since an actual finite physical system cannot possibly possess very different spectrum and band structure upon an arbitrarily small variation in its system parameter, the GBZ picture must be inapplicable in describing such finite-size systems in the presence of CSE.

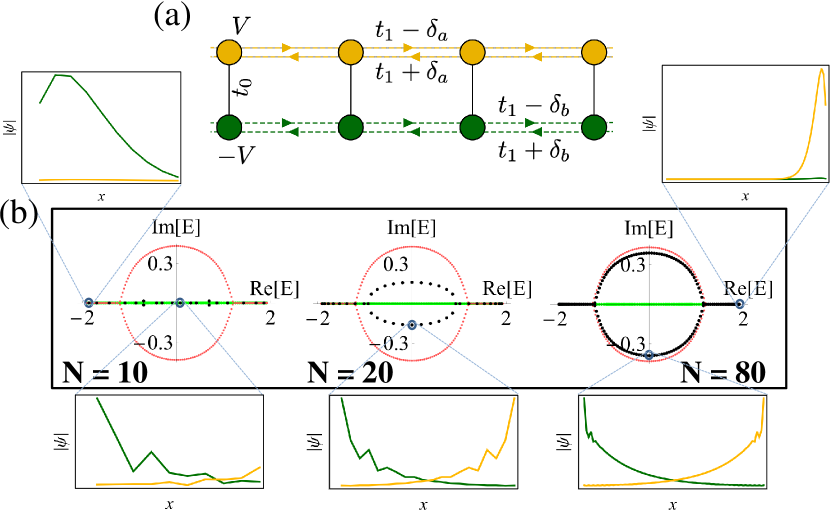
Anomalous finite-size scaling from CSE.– For illustration, we turn to a minimal example of two coupled non-Hermitian 1D Hatano-Nelson chains Hatano and Nelson (1996, 1997, 1998) each containing only non-reciprocal (unbalanced) nearest neighbor (NN) hoppings [Fig. 2(a)]. Its Hamiltonian reads

\displaystyle H_{\text{2-chain}}(z)=\left(\begin{matrix}g_{a}(z)&t_{0}\\ t_{0}&g_{b}(z)\\ \end{matrix}\right)

(3)

with $g_{a}(z)=t_{a}^{+}z+t_{a}^{-}/z+V$ and $g_{b}(z)=t_{b}^{+}z+t_{b}^{-}/z-V$ , $t_{a/b}^{\pm}=t_{1}\pm\delta_{a/b}$ being the forward/backward hopping of chains $a$ and $b$ . This model can be also realized with a reciprocal system with skin effect in a certain parameter regime Sup . When $t_{0}=0$ , the two chains are decoupled, and the characteristic polynomial is reducible as $f(z,E)=[g_{a}(z)-E][g_{b}(z)-E]$ . Each factor $f_{a/b}(z,E)=g_{a/b}(z)-E$ determines the skin eigensolutions of its respective chain. However, even an infinitesimal coupling $t_{0}\neq 0$ generically makes $f(z,E)$ irreducible. Specifically, consider the simple case of $t^{+}_{a}=t^{-}_{b}=1$ and $t_{a}^{-}=t_{b}^{+}=0$ . Without couplings ( $t_{0}=0$ ), the two chains under OBC respectively yields a Jordan-block Hamiltonian matrix in real space, with the spectrum given by $E=\pm V$ . Because the eigenstates of the decoupled chains are exclusively localized at the first or the last site, their GBZs collapse Longhi (2020). By contrast, for any $t_{0}\neq 0$ , $f(z,E)=E^{2}-E(z+z^{-1})+(z+V)(z^{-1}-V)-t_{0}^{2}$ is irreducible (here $-t_{0}^{2}=f_{0}$ from Eq. 2), insofar as the eigenenergy roots $E=\cos k\pm\sqrt{t_{0}^{2}+(V+i\sin k)^{2}}$ are no longer Laurent polynomials in $z=e^{ik}$ that can be separately interpreted as de facto subsystems with local hoppings ⁵⁵5In higher degree polynomials, an algebriac expression for $z$ may not even exist as implied by the Abel-Ruffini theorem.. Importantly, the corresponding OBC $E_{\infty}$ spectrum and the GBZ for $t_{0}\neq 0$ are now qualitatively different. As derived in the Supplementary Material Sup , setting $|z_{a}|=|z_{b}|$ gives OBC spectrum (in the thermodynamic limit): $E_{\infty}^{2}=\frac{1-\eta^{2}}{1+\eta^{2}}+V^{2}+t_{0}^{2}\pm 2\sqrt{t_{0}^{2}-\eta^{2}+\eta^{2}t_{0}^{2}}/(1+\eta^{2})$ , with $\eta\in\mathbb{R}$ . Clearly, even one now takes the $t_{0}\rightarrow 0$ limit, $E_{\infty}^{2}$ only simplifies to $E_{\infty}^{2}\rightarrow V^{2}+\frac{1\pm i\eta}{1\mp i\eta}$ , which is not the above-mentioned OBC spectrum of the two decoupled chains. Likewise, the $t_{0}\rightarrow 0$ limit of the coupled GBZ, which can be shown to be the locus of $z=\pm\sqrt{V^{2}+e^{i\theta}}-V$ , $\theta\in[0,2\pi]$ , has nothing in common with the collapsed GBZs of the decoupled case.

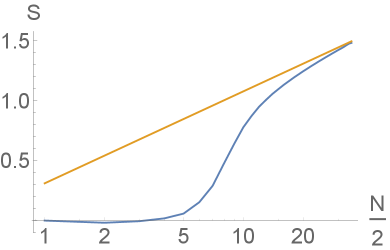
This paradoxical singular behavior is manifested as anomalous scaling behavior in finite-size systems that are more relevant to experimental setups. The discontinuous critical transition illustrated above becomes a smooth crossover between the different OBC $E_{\infty}$ solutions. As the size $N$ of a coupled system is varied, its physical OBC spectrum interpolates between the decoupled and coupled OBC $E_{\infty}$ solutions. As illustrated in Fig. 2(b) for the 2-chain model Eq. 3 at small coupling $t_{0}=0.01$ (with $t_{1}=0.75$ and $\delta_{a}=-\delta_{b}=0.25$ for well-defined skin modes), the OBC spectrum (black dots) changes dramatically from $N=10$ to $80$ unit cells. For small $N=10$ , it approximates the OBC $E_{\infty}$ (green) for $t_{0}=0$ lying on the real line, while at large $N=80$ , it converges towards the true OBC $E_{\infty}$ (red curve) with nonzero coupling. Indeed, the eigenstates for $N=10$ are almost entirely decoupled across the two chains, while those for $N=80$ are maximally coupled/decoupled depending on whether they approach the red/green $E_{\infty}$ curves. In the intermediate $N=20$ case, the OBC spectrum lies far between the two $E_{\infty}$ ’s, and cannot be characterized by their associated GBZs.

Let us now explain the above-observed dramatic size-dependent spectrum via the competition between dissimilarly accumulated skin modes and the couplings across them. The general conditions for such are unveiled in Sec. I.a of Sup . In our model [Eq. 3], the inverse decay lengths in chains $a,b$ are given by $\kappa_{a/b}=\frac{1}{2}\log(t^{+}_{a/b}/t^{-}_{a/b})$ , which will be dissimilar as long as $\delta_{a}\neq\delta_{b}$ . After performing a similarity transform that rescales each site $j$ by a factor of $e^{j\kappa_{b}}$ , chain $b$ becomes reciprocal with $\kappa^{\prime}_{b}=0$ while chain $a$ has a rescaled inverse decay length $\kappa^{\prime}_{a}=\kappa_{a}-\kappa_{b}$ . If $\kappa^{\prime}_{a}\neq 0$ , chain $a$ always possesses exponentially growing skin modes scaling like $~{}e^{\kappa^{\prime}_{a}N}$ at one end. As such, the coupling $t_{0}$ , even if extremely small, still affects the spectrum and eigenstates dramatically as the system size $N$ increases.

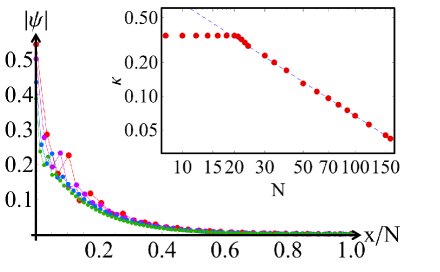
Scale-free exponential wavefunctions.– A hallmark of conventional critical systems is scale-free power-law behavior, particularly in the wavefunctions. Interestingly, such scale-free behavior can also be found in the exponentially decaying wavefunctions i.e. skin modes. Shown in Fig. 3(a) are the profiles of the slowest decaying eigenstates $\psi(x)$ of $H_{\text{2-chain}}$ at different system sizes $N=20,40,60$ and $80$ , with the horizontal axis normalized by $N$ . These featured eigenstates belong to the top of the central black ring in Fig. 2(b), with their distance from the coupled OBC $E_{\infty}$ ring (red) decreasing as $\sim N^{-1}$ . Unlike usual exponentially decaying wavefunctions with fixed spatial decay length, here $|\psi(x)|\sim e^{-\kappa x}$ with $\kappa\sim N^{-1}$ [Fig. 3(b)], such that the overall profile $\psi(x)$ has no fixed length scale. Such unique scale-free eigenmodes result from the slow critical migration of the eigenstates between $E_{\infty}$ solutions [Fig. 2(a) inset].

Anomalous correlations and entanglement entropy.– The CSE can also violate the usual logarithmic scaling of the EE Calabrese and Cardy (2004, 2009); Gioev and Klich (2006); Eisert et al. (2010), since the OBC spectrum can be gapped at some system sizes, and gapless at others. Consider for instance the OBC $H_{\text{2-chain}}$ [Eq. 3] with parameters chosen to gap out the OBC spectrum at small system sizes $N$ Sup . With all $\text{Re}[E]<0$ states occupied by spinless free Fermions, the real-space entanglement entropy $S$ (blue curve in [Fig. 3(c)]) exhibits a crossover from the decoupled gapped regime at $N\leq 5$ to the gapless regime $N>20$ , where it approaches the usual $\frac{1}{3}\log N$ behavior (yellow line). In generic CSE scenarios with multiple competing OBC $E_{\infty}$ loci, $S$ can scale differently at different system size regimes, choices of fillings and entanglement cuts, challenging the notion of a single well-defined scaling behavior. As shown in the Supplementary Material Sup , The two-Fermion correlator $\langle\psi(1)\psi(x)\rangle$ characterizing the EE also crossovers from rapid exponential decay at small $N$ to $1/x$ power-law decay at large $N$ . Remarkably, the probability of finding another Fermion nearby generally increases drastically when the system is enlarged (with filling fraction maintained).

Size-dependent topological modes.– Topological modes are usually associated with bulk invariants in the thermodynamic limit, with finite-size effects playing a diminishing role in the face of topological robustness. The CSE here can cause topological edge modes to appear only at certain system size regimes. Consider replacing the non-reciprocal intra-chain couplings of our $H_{\text{2-chain}}$ model with inter-chain couplings with non-reciprocity $\pm\delta_{ab}$ between adjacent unit cells [Fig. 4(a)], as described by the following CSE Su-Schrieffer-Heeger (SSH) model:

\displaystyle H_{\text{CSE-SSH}}(z)

\displaystyle=

\displaystyle h_{y}(z)\sigma_{y}+h_{z}(z)\sigma_{z}+h_{0}(z)\mathbb{I}

(4)

where $h_{y}(z)=i\delta_{ab}(z+1/z)$ , $h_{z}(z)=V+\delta_{-}(z-1/z)$ , and $h_{0}(z)=t_{1}(z+1/z)+\delta_{+}(z-1/z)$ , with $\delta_{\pm}=(\delta_{a}\pm\delta_{b})/2$ . $H_{\text{CSE-SSH}}$ is so named because interestingly, at $\delta_{-}=\delta_{ab}$ , it can be transformed via a basis rotation $\sigma_{z}\rightarrow\sigma_{x}$ into an extended (SSH) model Su et al. (1979) with non-reciprocal inter-cell couplings given by $\pm 2\delta_{-}$ and a uniform next-nearest neighbor hopping given by $t_{1}\pm\delta_{+}$ Sup , which is known to possess a topologically nontrivial phase.

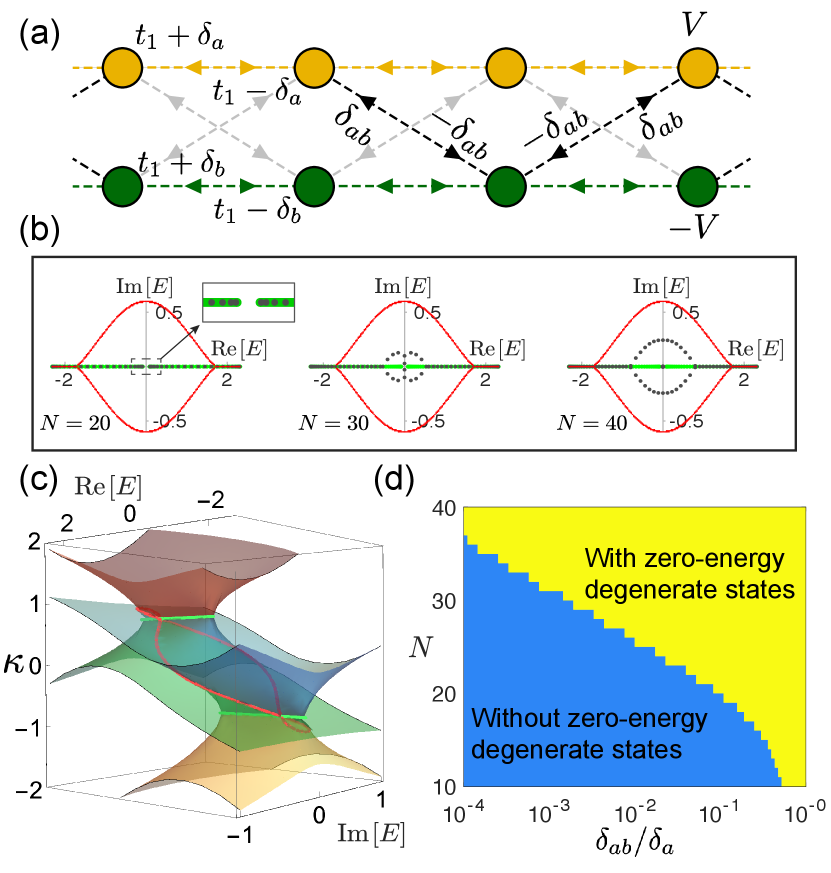
When $\delta_{ab}=0$ , the system is decoupled into two Hatano-Nelson chains which must be topologically trivial. The OBC spectrum $E_{\infty}$ in the decoupled case and the associated inverse decay length $\kappa$ are shown in Figs. 4(b) and (c)(green curves), with positive/negative $\kappa$ corresponding to skin modes accumulating population at opposite boundaries. Also shown in in Figs. 4(b) and (c)(red curves) are $E_{\infty}$ in the coupled case and the corresponding $\kappa$ for the hybridized skin modes. With small $N=20$ unit cells in Fig. 4(b), the finite-size OBC spectrum (gray dots) qualitatively agrees with the decoupled $E_{\infty}$ (green), with a real-valued gap at $E=0$ along the $\text{Im}[E]=0$ axis (inset). Upon the size increase to $N=30$ and then to $N=40$ , such a gap first closes on the complex plane and then develops into a point gap with two zero-energy degenerate modes lying in its center. The topological origin of such in-gap modes is also verified in Supplementary Material. The gap closure and then the emergence of in-gap topological modes resemble the typical behavior of a topological phase transition. Yet, here it is an intriguing size-induced effect. Further, the emergence of in-gap modes only requires exponentially weaker inter-chain coupling (i.e. smaller $\delta_{ab}/\delta_{a}$ ) for larger $N$ , as shown in the “phase” diagram shown in Fig. 4(d).

Discussion.- In mathematical terms, the CSE arises when the energy eigenequation exhibits an algebraic singularity that leads to inequivalent auxiliary GBZs across the transition. The CSE heralds a whole new class of discontinuous critical phase transitions with rich anomalous scaling behavior, challenging traditional associations of criticality with scale-free behavior. Even a vanishingly small coupling between dissimilar skin modes can be consequential as the system size increases. This insight is much relevant to sensing and switching applications. Beyond our two-chain models, there are other scenarios that can engineer coupling between subsystems of dissimilar NHSE length scales and hence yield CSE Sup . In particular, we anticipate fruitful investigations in various experimentally feasible settings such as electric circuits Helbig et al. ; Hofmann et al. ; Hofmann et al. (2019); Ezawa (2019), cold atom systems Li et al. ; Gou et al. (2020), photonic quantum walks Xiao et al. and metamaterials Ghatak et al. ; Brandenbourger et al. (2019).

Acknowledgements.- J.G. acknowledges support from Singapore NRF Grant No. NRF-NRFI2017-04 (WBS No. R-144-000-378-281).

C.H.L. and L.L. contributed equally to this work.

References

Coniglio and Klein (1980) A Coniglio and W Klein, “Clusters and ising critical droplets: a renormalisation group approach,” Journal of Physics A: Mathematical and General 13, 2775 (1980).
Hu (1984) Chin-Kun Hu, “Percolation, clusters, and phase transitions in spin models,” Physical Review B 29, 5103 (1984).
Aizenman et al. (1987) Michael Aizenman, David J Barsky, and Roberto Fernández, “The phase transition in a general class of ising-type models is sharp,” Journal of Statistical Physics 47, 343–374 (1987).
Boulatov and Kazakov (1987) DV Boulatov and VA Kazakov, “The ising model on a random planar lattice: the structure of the phase transition and the exact critical exponents,” Physics Letters B 186, 379–384 (1987).
Zamolodchikov (1987) Al B Zamolodchikov, “Conformal scalar field on the hyperelliptic curve and critical ashkin-teller multipoint correlation functions,” Nuclear Physics B 285, 481–503 (1987).
Zamolodchikov (1989) AB Zamolodchikov, “Exact solutions of conformal field theory in two dimensions and critical phenomena,” Reviews in Mathematical Physics 1, 197–234 (1989).
Cardy (1992) John L Cardy, “Critical percolation in finite geometries,” Journal of Physics A: Mathematical and General 25, L201 (1992).
Oshikawa and Affleck (1996) Masaki Oshikawa and Ian Affleck, “Boundary conformal field theory approach to the two-dimensional critical ising model with a defect line,” arXiv preprint cond-mat/9612187 (1996).
Dziarmaga (2005) Jacek Dziarmaga, “Dynamics of a quantum phase transition: Exact solution of the quantum ising model,” Physical review letters 95, 245701 (2005).
Gruzberg (2006) Ilya A Gruzberg, “Stochastic geometry of critical curves, schramm–loewner evolutions and conformal field theory,” Journal of Physics A: Mathematical and General 39, 12601 (2006).
Kozdron (2009) Michael J Kozdron, “Using the schramm–loewner evolution to explain certain non-local observables in the 2d critical ising model,” Journal of Physics A: Mathematical and Theoretical 42, 265003 (2009).
Stevenson and Weigel (2011) Jacob D Stevenson and Martin Weigel, “Domain walls and schramm-loewner evolution in the random-field ising model,” EPL (Europhysics Letters) 95, 40001 (2011).
Werner (2007) Wendelin Werner, “Lectures on two-dimensional critical percolation,” arXiv preprint arXiv:0710.0856 (2007).
Vidal et al. (2003) Guifre Vidal, José Ignacio Latorre, Enrique Rico, and Alexei Kitaev, “Entanglement in quantum critical phenomena,” Physical review letters 90, 227902 (2003).
Korepin (2004) VE Korepin, “Universality of entropy scaling in one dimensional gapless models,” Physical review letters 92, 096402 (2004).
Larsson and Johannesson (2005) Daniel Larsson and Henrik Johannesson, “Entanglement scaling in the one-dimensional hubbard model at criticality,” Physical review letters 95, 196406 (2005).
Ryu and Takayanagi (2006) Shinsei Ryu and Tadashi Takayanagi, “Aspects of holographic entanglement entropy,” Journal of High Energy Physics 2006, 045 (2006).
Barthel et al. (2006) Thomas Barthel, M-C Chung, and Ulrich Schollwoeck, “Entanglement scaling in critical two-dimensional fermionic and bosonic systems,” Physical Review A 74, 022329 (2006).
Laflorencie et al. (2006) Nicolas Laflorencie, Erik S Sørensen, Ming-Shyang Chang, and Ian Affleck, “Boundary effects in the critical scaling of entanglement entropy in 1d systems,” Physical review letters 96, 100603 (2006).
Swingle (2010) Brian Swingle, “Entanglement entropy and the fermi surface,” Physical review letters 105, 050502 (2010).
Swingle and Senthil (2013) Brian Swingle and T Senthil, “Universal crossovers between entanglement entropy and thermal entropy,” Physical Review B 87, 045123 (2013).
Lee et al. (2015) Ching Hua Lee, Yuki Yamada, Tatsuya Kumamoto, and Hiroaki Matsueda, “Exact mapping from singular-value spectrum of fractal images to entanglement spectrum of one-dimensional quantum systems,” Journal of the Physical Society of Japan 84, 013001 (2015).
Swingle and McGreevy (2016) Brian Swingle and John McGreevy, “Area law for gapless states from local entanglement thermodynamics,” Physical Review B 93, 205120 (2016).
Chang et al. (2019) Po-Yao Chang, Jhih-Shih You, Xueda Wen, and Shinsei Ryu, “Entanglement spectrum and entropy in topological non-hermitian systems and non-unitary conformal field theories,” arXiv preprint arXiv:1909.01346 (2019).
Bender and Boettcher (1998) Carl M. Bender and Stefan Boettcher, “Real spectra in non-hermitian hamiltonians having $pt$ symmetry,” Phys. Rev. Lett. 80, 5243–5246 (1998).
Bender (2007) Carl M Bender, “Making sense of non-hermitian hamiltonians,” Reports on Progress in Physics 70, 947 (2007).
Moiseyev (2011) N. Moiseyev, “Non-hermitian quantum mechanics,” Cambridge University Press (2011).
Gong et al. (2018) Zongping Gong, Yuto Ashida, Kohei Kawabata, Kazuaki Takasan, Sho Higashikawa, and Masahito Ueda, “Topological phases of non-hermitian systems,” Physical Review X 8, 031079 (2018).
Kawabata et al. (2019a) Kohei Kawabata, Ken Shiozaki, Masahito Ueda, and Masatoshi Sato, “Symmetry and topology in non-hermitian physics,” Physical Review X 9, 041015 (2019a).
Berry (2004) Michael V Berry, “Physics of nonhermitian degeneracies,” Czechoslovak journal of physics 54, 1039–1047 (2004).
Dembowski et al. (2004) C Dembowski, B Dietz, H-D Gräf, HL Harney, A Heine, WD Heiss, and A Richter, “Encircling an exceptional point,” Physical Review E 69, 056216 (2004).
Rotter (2009) Ingrid Rotter, “A non-hermitian hamilton operator and the physics of open quantum systems,” Journal of Physics A: Mathematical and Theoretical 42, 153001 (2009).
Jin and Song (2009) L Jin and Z Song, “Solutions of p t-symmetric tight-binding chain and its equivalent hermitian counterpart,” Physical Review A 80, 052107 (2009).
Longhi (2010) Stefano Longhi, “Pt-symmetric laser absorber,” Physical Review A 82, 031801 (2010).
Heiss and Harney (2001) WD Heiss and HL Harney, “The chirality of exceptional points,” The European Physical Journal D-Atomic, Molecular, Optical and Plasma Physics 17, 149–151 (2001).
Heiss (2012) WD Heiss, “The physics of exceptional points,” Journal of Physics A: Mathematical and Theoretical 45, 444016 (2012).
Xu et al. (2016) Haitan Xu, David Mason, Luyao Jiang, and JGE Harris, “Topological energy transfer in an optomechanical system with exceptional points,” Nature 537, 80 (2016).
Hassan et al. (2017) Absar U. Hassan, Bo Zhen, Marin Soljačić, Mercedeh Khajavikhan, and Demetrios N. Christodoulides, “Dynamically encircling exceptional points: Exact evolution and polarization state conversion,” Phys. Rev. Lett. 118, 093002 (2017).
Hu et al. (2017) Wenchao Hu, Hailong Wang, Perry Ping Shum, and Y. D. Chong, “Exceptional points in a non-hermitian topological pump,” Phys. Rev. B 95, 184306 (2017).
Shen et al. (2018) Huitao Shen, Bo Zhen, and Liang Fu, “Topological band theory for non-hermitian hamiltonians,” Phys. Rev. Lett. 120, 146402 (2018).
Wang et al. (2019) Shubo Wang, Bo Hou, Weixin Lu, Yuntian Chen, ZQ Zhang, and CT Chan, “Arbitrary order exceptional point induced by photonic spin–orbit interaction in coupled resonators,” Nature communications 10, 1–9 (2019).
Ghatak and Das (2019) Ananya Ghatak and Tanmoy Das, “New topological invariants in non-hermitian systems,” Journal of Physics: Condensed Matter 31, 263001 (2019).
Miri and Alù (2019) Mohammad-Ali Miri and Andrea Alù, “Exceptional points in optics and photonics,” Science 363, eaar7709 (2019).
Zhang and Gong (2020) Xizheng Zhang and Jiangbin Gong, “Non-hermitian floquet topological phases: Exceptional points, coalescent edge modes, and the skin effect,” Physical Review B 101, 045415 (2020).
Yuce (2020) C Yuce, “Non-hermitian anomalous skin effect,” Physics Letters A 384, 126094 (2020).
Jin et al. (2019) L Jin, HC Wu, Bo-Bo Wei, and Z Song, “Hybrid exceptional point created from type iii dirac point,” arXiv preprint arXiv:1908.10512 (2019).
Kawabata et al. (2019b) Kohei Kawabata, Takumi Bessho, and Masatoshi Sato, “Classification of exceptional points and non-hermitian topological semimetals,” Physical review letters 123, 066405 (2019b).
Lee (2016) Tony E. Lee, “Anomalous edge state in a non-hermitian lattice,” Phys. Rev. Lett. 116, 133903 (2016).
Xiong (2018) Ye Xiong, “Why does bulk boundary correspondence fail in some non-hermitian topological models,” Journal of Physics Communications 2, 035043 (2018).
Kunst et al. (2018) Flore K. Kunst, Elisabet Edvardsson, Jan Carl Budich, and Emil J. Bergholtz, “Biorthogonal bulk-boundary correspondence in non-hermitian systems,” Phys. Rev. Lett. 121, 026808 (2018).
Yao and Wang (2018) Shunyu Yao and Zhong Wang, “Edge states and topological invariants of non-hermitian systems,” Phys. Rev. Lett. 121, 086803 (2018).
Yokomizo and Murakami (2019) Kazuki Yokomizo and Shuichi Murakami, “Non-bloch band theory of non-hermitian systems,” Physical review letters 123, 066404 (2019).
Lee et al. (2018) Ching Hua Lee, Guangjie Li, Yuhan Liu, Tommy Tai, Ronny Thomale, and Xiao Zhang, “Tidal surface states as fingerprints of non-hermitian nodal knot metals,” arXiv preprint arXiv:1812.02011 (2018).
Lee and Thomale (2019) Ching Hua Lee and Ronny Thomale, “Anatomy of skin modes and topology in non-hermitian systems,” Phys. Rev. B 99, 201103 (2019).
Song et al. (2019a) Fei Song, Shunyu Yao, and Zhong Wang, “Non-hermitian skin effect and chiral damping in open quantum systems,” Physical review letters 123, 170401 (2019a).
Song et al. (2019b) Fei Song, Shunyu Yao, and Zhong Wang, “Non-hermitian topological invariants in real space,” Physical Review Letters 123, 246801 (2019b).
Li et al. (2019) Linhu Li, Ching Hua Lee, and Jiangbin Gong, “Geometric characterization of non-hermitian topological systems through the singularity ring in pseudospin vector space,” Physical Review B 100, 075403 (2019).
Borgnia et al. (2020) Dan S. Borgnia, Alex Jura Kruchkov, and Robert-Jan Slager, “Non-hermitian boundary modes and topology,” Phys. Rev. Lett. 124, 056802 (2020).
Zhang et al. (2019) Kai Zhang, Zhesen Yang, and Chen Fang, “Correspondence between winding numbers and skin modes in non-hermitian systems,” arXiv preprint arXiv:1910.01131 (2019).
(60) Tsuneya Yoshida, Tomonari Mizoguchi, and Yasuhiro Hatsugai, “Mirror skin effect and its electric circuit simulation,” 1912.12022v1 .
(61) Zhesen Yang, Kai Zhang, Chen Fang, and Jiangping Hu, “Auxiliary generalized brillouin zone method in non-hermitian band theory,” 1912.05499v1 .
(62) Ching Hua Lee, Linhu Li, Ronny Thomale, and Jiangbin Gong, “Unraveling non-hermitian pumping: emergent spectral singularities and anomalous responses,” 1912.06974v2 .
Longhi (2019) Stefano Longhi, “Probing non-hermitian skin effect and non-bloch phase transitions,” Physical Review Research 1, 023013 (2019).
Luo (2020) Ma Luo, “Skin effect and excitation spectral of interacting non-hermitian system,” arXiv preprint arXiv:2001.00697 (2020).
Note (1) Not all subsystems need to be non-Hermitian; indeed, the CSE even occurs if a Hermitian chain is coupled a chain with NHSE.
Note (2) Non-Hermitian system, particularly those exhibiting the NHSE, exhibit divergences in local density of states in the thermodynamic limit.
Brandenbourger et al. (2019) Martin Brandenbourger, Xander Locsin, Edan Lerner, and Corentin Coulais, “Non-reciprocal robotic metamaterials,” Nature communications 10, 1–8 (2019).
Schomerus (2020) Henning Schomerus, “Nonreciprocal response theory of non-hermitian mechanical metamaterials: Response phase transition from the skin effect of zero modes,” Physical Review Research 2, 013058 (2020).
Longhi (2020) S. Longhi, “Non-bloch-band collapse and chiral zener tunneling,” Phys. Rev. Lett. 124, 066602 (2020).
Okuma et al. (2020) Nobuyuki Okuma, Kohei Kawabata, Ken Shiozaki, and Masatoshi Sato, “Topological origin of non-hermitian skin effects,” Phys. Rev. Lett. 124, 086801 (2020).
Note (3) In principle, the convergence should be exact in the thermodynamic limit. But in practical computations, floating point errors $\epsilon$ are continuously amplified as they propagate across the system, and we expect accurate numerical spectra only when $L<-\mathop{log}\nolimits(\epsilon)/\text{max}(\kappa)$ .
Note (4) If two $f_{i}$ ’s are equivalent, $f_{0}+f_{i}^{2}=(f_{i}+i\sqrt{f_{0}})(f_{i}-i\sqrt{f_{0}})$ is still reducible.
Hatano and Nelson (1996) Naomichi Hatano and David R. Nelson, “Localization transitions in non-hermitian quantum mechanics,” Phys. Rev. Lett. 77, 570–573 (1996).
Hatano and Nelson (1997) Naomichi Hatano and David R. Nelson, “Vortex pinning and non-hermitian quantum mechanics,” Phys. Rev. B 56, 8651–8673 (1997).
Hatano and Nelson (1998) Naomichi Hatano and David R. Nelson, “Non-hermitian delocalization and eigenfunctions,” Phys. Rev. B 58, 8384–8390 (1998).
(76) “Supplemental materials,” Supplemental Materials .
Note (5) In higher degree polynomials, an algebriac expression for $z$ may not even exist as implied by the Abel-Ruffini theorem.
Calabrese and Cardy (2004) Pasquale Calabrese and John Cardy, “Entanglement entropy and quantum field theory,” Journal of Statistical Mechanics: Theory and Experiment 2004, P06002 (2004).
Calabrese and Cardy (2009) Pasquale Calabrese and John Cardy, “Entanglement entropy and conformal field theory,” Journal of Physics A: Mathematical and Theoretical 42, 504005 (2009).
Gioev and Klich (2006) Dimitri Gioev and Israel Klich, “Entanglement entropy of fermions in any dimension and the widom conjecture,” Phys. Rev. Lett. 96, 100503 (2006).
Eisert et al. (2010) J. Eisert, M. Cramer, and M. B. Plenio, “Colloquium: Area laws for the entanglement entropy,” Rev. Mod. Phys. 82, 277–306 (2010).
Su et al. (1979) W. P. Su, J. R. Schrieffer, and A. J. Heeger, “Solitons in polyacetylene,” Phys. Rev. Lett. 42, 1698–1701 (1979).
(83) Tobias Helbig, Tobias Hofmann, Stefan Imhof, Mohamed Abdelghany, Tobias Kiessling, Laurens W. Molenkamp, Ching Hua Lee, Alexander Szameit, Martin Greiter, and Ronny Thomale, “Observation of bulk boundary correspondence breakdown in topolectrical circuits,” 1907.11562v1 .
(84) Tobias Hofmann, Tobias Helbig, Frank Schindler, Nora Salgo, Marta Brzezińska, Martin Greiter, Tobias Kiessling, David Wolf, Achim Vollhardt, Anton Kabaši, et al., “Reciprocal skin effect and its realization in a topolectrical circuit,” 1908.02759v1 .
Hofmann et al. (2019) Tobias Hofmann, Tobias Helbig, Ching Hua Lee, Martin Greiter, and Ronny Thomale, “Chiral voltage propagation and calibration in a topolectrical chern circuit,” Physical review letters 122, 247702 (2019).
Ezawa (2019) Motohiko Ezawa, “Electric circuits for non-hermitian chern insulators,” Physical Review B 100, 081401 (2019).
(87) Linhu Li, Ching Hua Lee, and Jiangbin Gong, “Topology-induced spontaneous non-reciprocal pumping in cold-atom systems with loss,” 1910.03229v1 .
Gou et al. (2020) Wei Gou, Tao Chen, Dizhou Xie, Teng Xiao, Tian-Shu Deng, Bryce Gadway, Wei Yi, and Bo Yan, “Tunable non-reciprocal quantum transport through a dissipative aharonov-bohm ring in ultracold atoms,” Phys. Rev. Lett. 124, 070402 (2020).
(89) Lei Xiao, Tianshu Deng, Kunkun Wang, Gaoyan Zhu, Zhong Wang, Wei Yi, and Peng Xue, “Observation of non-hermitian bulk-boundary correspondence in quantum dynamics,” 1907.12566v1 .
(90) Ananya Ghatak, Martin Brandenbourger, Jasper van Wezel, and Corentin Coulais, “Observation of non-hermitian topology and its bulk-edge correspondence,” 1907.11619v1 .
Herviou et al. (2019) Loïc Herviou, Nicolas Regnault, and Jens H Bardarson, “Entanglement spectrum and symmetries in non-hermitian fermionic non-interacting models,” arXiv preprint arXiv:1908.09852 (2019).
Mu et al. (2019) Sen Mu, Ching Hua Lee, Linhu Li, and Jiangbin Gong, “Emergent fermi surface in a many-body non-hermitian fermionic chain,” arXiv preprint arXiv:1911.00023 (2019).
Peschel (2003) Ingo Peschel, “Calculation of reduced density matrices from correlation functions,” Journal of Physics A: Mathematical and General 36, L205 (2003).
Alexandradinata et al. (2011) Aris Alexandradinata, Taylor L Hughes, and B Andrei Bernevig, “Trace index and spectral flow in the entanglement spectrum of topological insulators,” Phys. Rev. B 84, 195103 (2011).
Lee and Ye (2015) Ching Hua Lee and Peng Ye, “Free-fermion entanglement spectrum through wannier interpolation,” Physical Review B 91, 085119 (2015).
Yin et al. (2018) Chuanhao Yin, Hui Jiang, Linhu Li, Rong Lü, and Shu Chen, “Geometrical meaning of winding number and its characterization of topological phases in one-dimensional chiral non-hermitian systems,” Phys. Rev. A 97, 052115 (2018).

Supplementary Materials

I I. Conditions for having discontinuous transition of GBZ solutions $E_{\infty}$ for the Critical Skin Effect

I.1 a. Two-chain models

The discontinuous transition induced by an infinitesimal transverse coupling in thermodynamic limit, and also the crossover in a finite system, exist only when the two decoupled chains have different $\kappa$ of their OBC skin solutions. To see this, we consider a general two-chain model described by Hamiltonian

\displaystyle h(z)=\left(\begin{matrix}g_{a}(z)+V_{a}&t_{0}\\ t_{0}&g_{b}(z)+V_{b}\\ \end{matrix}\right),

(S1)

where $g_{a,b}(z)$ only contain terms with nonzero order of $z$ . When decoupled, the two chains correspond to the polynomials $g_{a,b}(z)+V_{a,b}$ respectively, and possess the same $\kappa$ solutions when and only when $g_{b}(z)=cg_{a}(z)$ , with $c$ a nonzero coefficient. When a nonzero transverse coupling $t_{0}$ is introduced, the characteristic polynomial of the two-chain system takes the form of

$\displaystyle P_{c}(z)$	$\displaystyle=$	$\displaystyle(g_{a}(z)+V_{a}-E)(g_{b}(z)+V_{b}-E)-r^{2}$	(S2)
	$\displaystyle=$	$\displaystyle cg_{a}^{2}(z)+\left[(V_{b}-E)+c(V_{a}-E)\right]g_{a}+V_{a}V_{b}+E^{2}-r^{2}$
	$\displaystyle=$	$\displaystyle(cg_{a}(z)-A)(g_{a}(z)-B),$

where $A,B$ are two coefficients determined by $V_{a,b}$ , $r=t_{0}$ , and $E$ . Therefore for two chains with the same $\kappa$ solutions, a transverse coupling $t_{0}$ only modifies the energy offset between them, without inducing a transition of skin solutions.

Nevertheless, the above factorization does not hold when the coupling term $r$ is $z$ -dependent, corresponding to inter-chain couplings between different unit cells. Under this condition, $P_{c}(z)$ cannot be factorized into two sub-polynomials of $g_{a}(z)$ and $g_{b}(z)=cg_{z}(a)$ , meaning that the skin solution is changed for the system.

I.2 b. Dissimilar skin modes in general two-band models

In a more general picture, the critical skin effect and the size-dependent variation may exist when different parts of the system have dissimilar skin accumulation of eigenmodes. In the two-chain model, we mainly consider regime with small inter-chain couplings, thus the two energy bands (overlapped or connected in most cases) with dissimilar skin modes are mostly given by one of the two chains respectively. To unveil the condition of having dissimilar skin modes in a general two-band system, we consider an arbitrary two-band system described by a non-Bloch Hamiltonian $H(z)=h_{0}(z)\mathbb{I}+\sum_{n=1,2,3}h_{n}(z)\sigma_{n}$ , with $z=e^{ik}e^{-\kappa(k)}$ , and $\kappa(k)$ a complex deformation of momentum $k$ describing the NHSE. Its characteristic polynomial is given by

\displaystyle f(z,E)=[E-h_{0}(z)]^{2}-P(z)=0

(S3)

with $P(z)=\sum_{n=1,2,3}h_{n}^{2}(z)$ .NHSE can be described by a GBZ where the solutions of $f(z,E)=0$ satisfy $E_{\alpha}(z_{\mu})=E_{\alpha}(z_{\nu})$ with $|z_{\mu}|=|z_{\nu}|$ and $\alpha=\pm$ the band index, and $\kappa(k)=-\log|z|$ gives the inverse decay length. Conventionally, NHSE is studied mostly for system with only nonzero $h_{0}(z)$ (i.e. a one-band model) or $P(z)$ (e.g. the non-reciprocal SSH model), where the zeros of $f(z,E)$ lead to $E_{\pm}=h_{0}(z)$ and $E_{\pm}^{2}=P(z)$ respectively. In either case, we can see that the two bands of $E_{\pm}$ must have the same inverse skin localization depth $\kappa(k)$ , as $E_{\alpha}(z_{\mu})=E_{\alpha}(z_{\nu})$ must be satisfied for $\alpha=\pm$ with the same $z_{\mu,\nu}$ . To have dissimilar skin modes for the two bands, $h_{0}(z)$ and $P(z)$ must both be non-vanishing, and possess different skin solutions. That is, although $h_{0}(z_{\mu})=h_{0}(z_{\nu})$ and $P(z_{\mu^{\prime}})=h_{0}(z_{\nu^{\prime}})$ can still be satisfied with $|z_{\mu}|=|z_{\nu}|$ and $|z_{\mu^{\prime}}|=|z_{\nu^{\prime}}|$ , we cannot have $z_{\mu}=z_{\mu}^{\prime}$ and $z_{\nu}=z_{\nu}^{\prime}$ at the same time, otherwise the same $\kappa(k)$ can be obtained for the two bands.

I.3 c. Non-monotonicity of convergence towards $E_{\infty}$

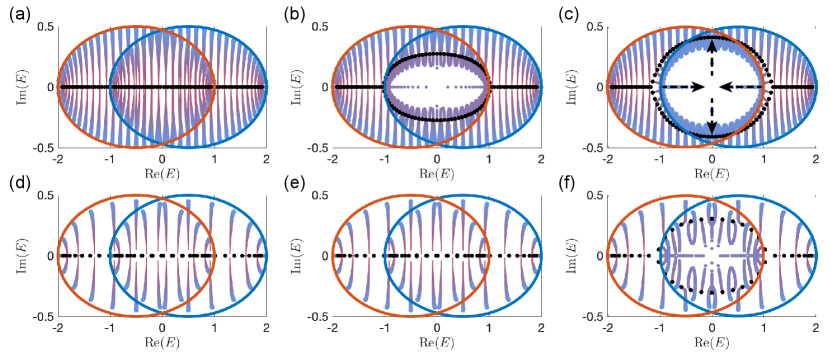
In Fig. S1, we illustrate the PBC-OBC spectral flow Lee and Thomale (2019) of the two-chain model with different parameters, by rescaling the amplitudes of the hopping across the boundary as $t_{1}\pm\delta_{a,b}\rightarrow c(t_{1}\pm\delta_{a,b})$ , and tuning $c$ from $1$ (PBC) to $0$ (OBC). We can see that in the decoupled limit, each of the two PBC bands (red or blue) merges with itself along the real axis when approaching OBC limit [Fig. S1(a,d,e)]. On the other hand, in the coupled regime of Fig. S1(b,c,f), each band first flows toward the real axis, but then ”turns back” and merges with the other band, forming a central-loop structure. In this process, the PBC bands do not necessarily go monotonically closer to OBC spectrum that reflects the GBZ solutions. A systematic study of the interplay between the switching off of boundary couplings (PBC-OBC interpolation) and subsystem coupling ( $t_{0}$ ) is deferred to future work.

I.4 d. Reciprocal realization of the two-chain model

Here, we discuss how the CSE, which requires subsystems of different NHSE decay lengths, can in fact be realized with reciprocal models that are more easily realizable in experiment. In the two-chain model, the Hamiltonian can be rewritten in the form of Pauli matrices as

	$\displaystyle h(z)$	$\displaystyle=$	$\displaystyle[t(z+1/z)+\delta_{+}\sin k(z-1/z)]\sigma_{0}$		(S4)
			$\displaystyle+t_{0}\sigma_{x}+[V+\delta_{-}(z-1/z)]\sigma_{z},$		(S4)

with $\delta_{\pm}=(\delta_{a}\pm\delta_{b})/2$ . Here $\delta_{+}$ describes the equivalent part of non-Hermiticity acting on the two chains, which shall induce the same NHSE to them. The critical behavior and transition of NHSE occurs only with nonzero $\delta_{-}$ , which induces band-dependent NHSE along the two chains. As shown in Fig. S2, $\delta_{\pm}$ can be divided into different couplings with a rotation of pseudospin $\sigma_{z}\rightarrow\sigma_{y}$ , and the rotated Bloch Hamiltonian $h_{r}(k)$ satisfies $h_{r}^{T}(k)=h_{r}(-k)$ at $\delta_{+}=V=0$ . Under this condition, the rotated system is reciprocal, and thus provides convenience for experimental realization such as RLC circuit lattices.

II II. Anomalous scaling behavior

II.1 a. Competition between skin localization and inter-chain coupling

As mentioned in the main text, if two coupling chains have inverse NHSE decay lengths (non-Hermitian localization length scales) $\kappa_{a},\kappa_{b}$ , a change of basis will bring their coupling to be effectively between a chain with no skin effect, and another with an effective skin depth $\kappa_{a}-\kappa_{b}$ . Since that entails exponentially growing skin modes scaling like $e^{(\kappa_{a}-\kappa_{b})N}$ at one end, we expect the effect of even an infinitesimally small inter-chain coupling $t_{0}$ to scale exponentially with $N$ , and eventually change the OBC spectrum substantially.

Consider increasing the inter-chain coupling $t_{0}$ in our two-chain model (Eq. 3 of main text) from zero. At sufficiently small $t_{0}$ , we have two practically independent OBC Hatano-Nelson chains with real spectra. Their infinitesimal coupling only shifts their eigenenergies slightly along the real line. But at a critical $t_{0}=t_{c}$ , the OBC spectrum is rendered complex as one or more pairs of eigenenergies coalesece and repel along in the imaginary direction. Shown in Fig. S3(a) is the inverse exponential scaling of the critical $t_{0}=t_{c}$ with $N$ . We observe that $t_{c}^{2}e^{(\kappa_{a}-\kappa_{b})N}\sim\mathcal{O}(1)$ , in agreement with the intuitive expectation that $t_{c}$ should scale inverse exponentially with $N$ because the effect of $t_{0}$ scales exponentially with $N$ . Yet, the fact that $t_{c}^{2}\sim e^{-(\kappa_{a}-\kappa_{b})N}$ signifies that the Critical Skin Effect is fundamentally a non-perturbative effect, since it differs from $t_{c}\sim e^{-(\kappa_{a}-\kappa_{b})N}$ as expected from first-order perturbation theory with left and right eigenstates that are oppositely exponentially localized spatially.

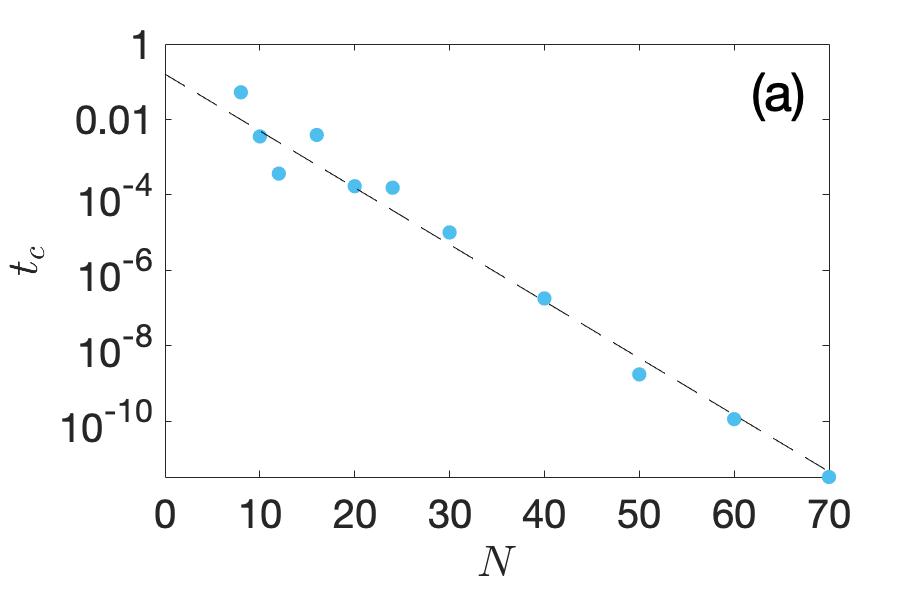
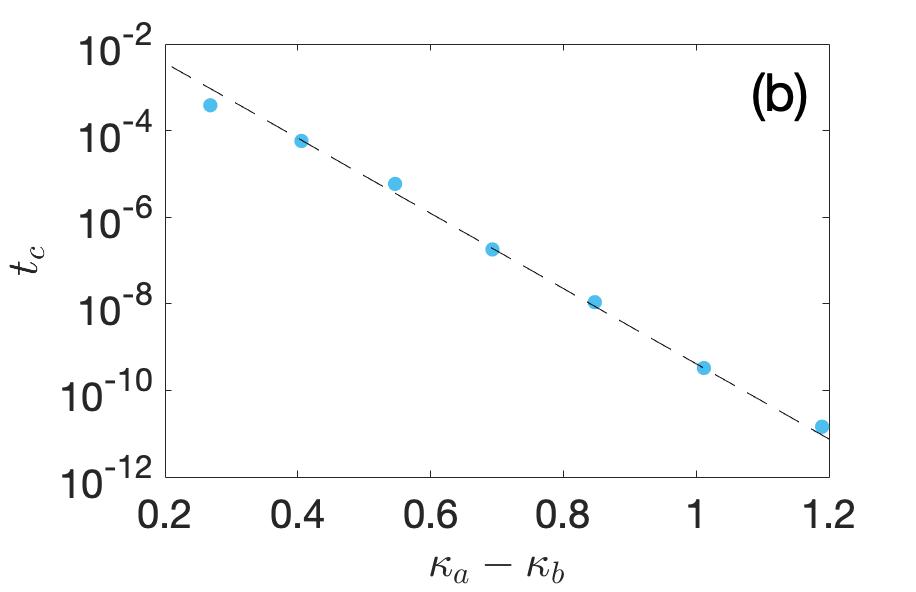
The scaling behavior of $e^{(\kappa_{a}-\kappa_{b})N}$ also suggests that increasing $N$ has similar consequences as increasing the non-reciprocity in the system, the strength of which is reflected by the absolute value of $(\kappa_{a}-\kappa_{b})$ . Therefore it is also expected that the critical skin effect shall emerge when we enhance the non-reciprocity but fix $N$ . In Fig. S3(b) we show the inverse exponential scaling of the critical $t_{0}=t_{c}$ with $\kappa_{a}-\kappa_{b}$ , where the inverse NHSE decay lengths are given by

\displaystyle e^{\kappa_{a,b}}=\sqrt{\frac{t_{1}+\delta_{a,b}}{t_{1}-\delta_{a,b}}}

(S5)

for the two decoupled chains. The scaling behavior versus $\kappa_{a}-\kappa_{b}$ further confirms that $t_{c}^{2}\sim e^{-(\kappa_{a}-\kappa_{b})N}$ .

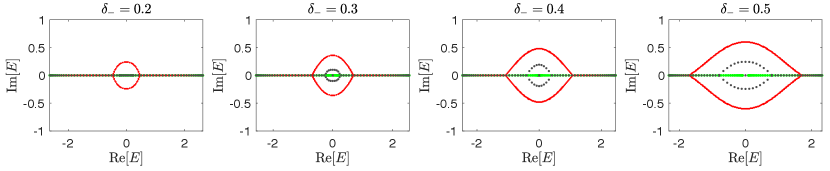
In Fig. S4, we illustrate another example of our two-chain model with non-Hermitian cross inter-chain coupling $\delta_{ab}$ , i.e. $H_{\rm CS-SSH}$ in the main text. By increasing $\delta_{-}$ , the non-reciprocity is strengthened along each chain, but toward opposite directions. Thus the effective inverse skin depth $\kappa_{a}-\kappa_{b}$ is enhanced, and we observe a transition of OBC spectrum from a line to a central-loop structure, accompanied with a topological transition reflected by the emergence of zero-energy degenerate edge states. This behavior is similar to the transition with enlarging $N$ as discussed in the main text.

II.2 b. Anomalous scaling of entanglement entropy

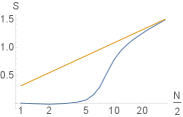
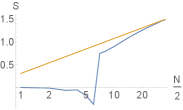
The Fermionic entanglement entropy (EE) $S$ scaling behavior depends qualitatively on the nature of the phase, increasing as $~{}\frac{1}{3}\log N$ at an ordinary critical point, decreasing possibly as a negative multiple of $\log N$ at a critical exceptional point Chang et al. (2019), and saturating at a gapped or decoupled scenario. Since $N$ itself can drive phase transitions in our case of the Critical Skin Effect, we expect the scaling of $S$ to interpolate and transition through distinct behaviors.

For free Fermions in a many-body state $|\Psi\rangle$ , the (biorthogonal) EE Herviou et al. (2019); Mu et al. (2019) for a chosen entanglement cut can be computed via

S=-\sum_{j}[c_{j}\log c_{j}+(1-c_{j})\log(1-c_{j})],

(S6)

where the $c_{j}$ ’s are the eigenvalues of the 2-particle correlator $C=PQP$ Peschel (2003); Alexandradinata et al. (2011); Lee and Ye (2015). Here $P$ is the projector implementing the entanglement cut and $Q=\sum_{\mu\in occ.}|\psi_{\mu}\rangle\langle\psi_{\mu}|$ is the single-body biorthogonal projector onto the set of basis states $|\psi_{\mu}\rangle$ occupied by the many-body state $|\Psi\rangle$ . In a perfectly unentangled case, $c_{j}=0$ or $1$ only, giving rise to a vanishing EE. With increased entanglement, the $c_{j}$ ’s encroach closer to $1/2$ , attaining the latter when the sector $j$ is fully entangled. In the biorthogonal setting, it is possible for $c_{j}$ to take values outside of $[0,1]$ since $|\psi_{\mu}\rangle$ is not the complex conjugate of $\langle\psi_{\mu}|$ , leading to negative or even imaginary contributions to $S$ Chang et al. (2019).

In Fig. S5, we observe a crossover from a decoupled regime to a critical regime when $N$ increases. $S$ also exhibits non-universal negative values for certain even $N$ [Fig. S5(b)], a behavior resulting from $c_{j}\notin[0,1]$ for a few of these $N$ . In real space, the two-Fermion correlator $C$ decays rapidly for small $N$ , but interesting decays more slowly like $x^{-1}$ for larger $N$ when the system becomes gapless. As such, correlators generally become enhanced in larger systems where the effects of coupling become amplified by the CSE.

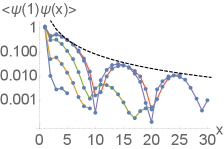
III III. GBZ solutions $E_{\infty}$ for the 2-chain model

For analytic tractability, we consider the case of Eq. 3 of the main text with $t^{+}_{a}=t_{b}^{-}=1$ and $t^{-}_{a}=t^{+}_{b}=0$ (i.e. $t_{1}=\delta_{a}=-\delta_{b}=0.5$ ), but nonzero $b$ and $V$ . We obtain

H_{\text{2-chain}}(z)=\left(\begin{matrix}z+V&t_{0}\\ t_{0}&1/z-V\end{matrix}\right)

(S7)

with characteristic polynomial given by

	$\displaystyle f(z,E)$	$\displaystyle=$	$\displaystyle E^{2}-E(z^{-1}+z)+[(z+V)(z^{-1}-V)-t_{0}^{2}]$		(S8)
		$\displaystyle=$	$\displaystyle\frac{V-E}{z}-z(V+E)+[E^{2}-V^{2}-t_{0}^{2}+1]$		(S8)

To find the GBZ solutions $E_{\infty}$ for comparison with the actual OBC solutions, we solve for roots $|z_{+}|=|z_{-}|$ of $f(z,E)=0$ (with $\Sigma=E^{2}-V^{2}-t_{0}^{2}+1$ ):

	$\displaystyle z_{\pm}$	$\displaystyle=$	$\displaystyle\frac{\left(\Sigma\pm\sqrt{\Sigma^{2}+4(V^{2}-E^{2})}\right)}{2(V+E)}$		(S9)
		$\displaystyle=$	$\displaystyle\frac{\Sigma\pm\sqrt{(\Sigma-2)^{2}-4t_{0}^{2}}}{2(V+E)}$		(S9)

For $|z_{+}|=|z_{-}|$ to hold, the square root quantity must differ from $\Sigma$ by a complex argument of $\pi/2$ Lee et al. i.e.

\sqrt{(\Sigma-2)^{2}-4t_{0}^{2}}=i{\color[rgb]{0,0,0}\eta}\Sigma

(S10)

where $\eta\in\mathbb{R}$ . Simplifying, we obtain $\Sigma=\frac{2}{1+\eta^{2}}\left(1\pm\sqrt{t_{0}^{2}+\eta^{2}(t_{0}^{2}-1)}\right)$ or, in terms of $E^{2}\rightarrow E_{\infty}^{2}$ ,

E_{\infty}^{2}=\frac{1-\eta^{2}\pm 2\sqrt{t_{0}^{2}-\eta^{2}+\eta^{2}t_{0}^{2}}}{1+\eta^{2}}+V^{2}+t_{0}^{2}

(S11)

as in the main text, with $\eta$ tracing out a one-parameter continuous spectrum. The GBZ can be numerically obtained by substituting Eq. S11 into the expression for $z_{\pm}$ in Eq. S9 with $E=E_{\infty}$ . From that, we obtain two momentum values $k_{\pm}=\text{Re}[-i\log z_{\pm}]$ with $\kappa(k_{+})=\kappa(k_{-})=-\log|z_{+}|=-\log|z_{-}|$ inverse length scales. Note however that because of the proximity to the $t_{0}=0$ critical point, this value of $\kappa(k_{\pm})$ is significantly different from the actual inverse OBC skin depth for a large range of finite system sizes.

IV IV. Mapping between the SSH model and two non-reciprocal 1D chains

In the main text we have considered a two-chain model with both intra-chain and inter-chain couplings being non-reciprocal, described by the Hamiltonian

\displaystyle H_{\text{CS-SSH}}(z)

\displaystyle=

\displaystyle[i\delta_{ab}(z+1/z)]\sigma_{y}+[V+\delta_{-}(z-1/z)]\sigma_{z}+[t_{1}(z+1/z)+\delta_{+}(z-1/z)]\mathbb{I}

(S12)

with $\delta_{\pm}=(\delta_{a}\pm\delta_{b})/2$ . In the parameter regime with $\delta_{ab}=\delta_{-}$ , through a rotation of basis $\sigma_{z}\rightarrow\sigma_{x}$ , this Hamiltonian becomes

\displaystyle H_{r}(z)=\left(\begin{matrix}t_{1}(z+1/z)+\delta_{+}(z-1/z)&V+2\delta_{-}z\\ V-2\delta_{-}/z&t_{1}(z+1/z)+\delta_{+}(z-1/z)\end{matrix}\right).

(S13)

This Hamiltonian describes a SSH model with non-reciprocal inter-cell couplings and second-nearest-neighbor couplings, as illustrated in Fig. S6. In the main text we have chosen $\delta_{a}=-\delta_{b}$ , so that $\delta_{+}=0$ and the second-nearest-neighbor couplings are Hermitian. In this parameter regime, by redefining the unit cell as the red dashed line in Fig. S6 (shifting one lattice site), we can see that the rotated model is equivalent to the non-reciprocal SSH model studied in Refs. Yao and Wang (2018); Yin et al. (2018) etc. with a uniform second-nearest-neighbor couplings, described by the Hamiltonian

\displaystyle H^{\prime}_{r}(z)=\left(\begin{matrix}t_{1}(z+1/z)&V/z+2\delta_{-}\\ Vz-2\delta_{-}&t_{1}(z+1/z)\end{matrix}\right).

(S14)

Finally, by applying another rotation of basis $\sigma_{y}\rightarrow\sigma_{z}$ , the system can be further transformed into a ladder model with non-Hermiticity being only on-site gain and loss Song et al. (2019a); Li et al. .

Note that in the main text we have considered the case with $\delta_{ab}\ll\delta_{-}$ . In the SSH model, this inequality corresponds to some extra longer-range couplings. Also note that the redefinition of unit cells also corresponds to a different lattice structure where the first and last lattice sites are coupled by $V$ instead of $\pm\delta_{-}$ . Under OBCs, these two choices of unit cells will result in different behaviors of topological edge states.

V V. Topological edge states in a line gap

Here we consider the two-chain model with cross inter-chain couplings discussed in the main text, but with a stronger inter-chain coupling strength $\delta_{ab}=0.15$ . We can see in Fig. S7 that the system has a narrow real line-gap at small $N=10$ , a point-gap at $N=20$ , and an imaginary line-gap at $N=40$ . Degenerate zero-energy edge states emerge in the later two cases. As the two OBC bands are fully separated from each others in the last case, a Berry phase can be well-defined for each non-Bloch band to characterize the topological properties in this system.