Creation and annihilation of mobile fractional solitons in atomic chains

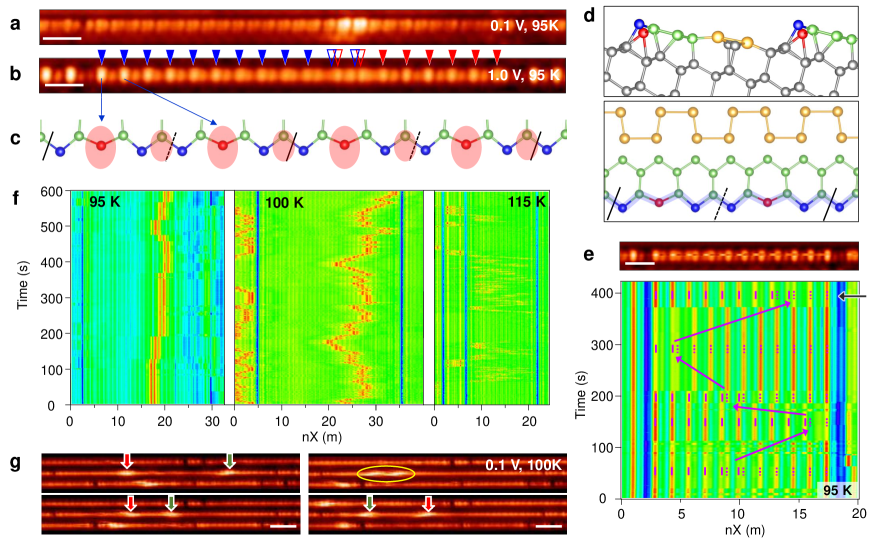
The surface of a vicinal Si(553) crystal with an optimized coverage of Au adatoms form a well ordered array of Si and Au atomic chains with very narrow (1.3 nm in width) terraces (Fig. 1g) erwi10 ; aulb13 ; brau18 . Each terrace consists basically of double Au chains and a Si honeycomb chain on its topmost layer (Fig. 1d) erwi10 ; aulb13 ; brau18 (more detailed atomic structure in Supplementary Fig. 6). What concern the present work are step-edge Si atoms with dangling bonds, which correspond to one side of the Si honeycomb chain (blue and red balls in Fig. 1c) and to the rows of bright protrusions in the STM topographs (Fig. 1b). Its low-temperature atomic structure has long been intrigued with contradictory suggestions of a CDW insulator with a periodic lattice distortion ahn05 ; snij06 and an antiferromagnetic insulator with a spin ordering erwi10 . Very recent DFT calculations successfully found a distorted CDW structure explaining most of the experimental data brau18 . Below the transition temperature of 200 K, the STM images exhibit a structural distortion in a high empty-state bias, namely, the alternation of bright and dim protrusions in a 3a₀ (a₀, silicon surface unit cell of 0.384 nm) periodicity (Fig. 1b), which represent a monomer and a dimer in each trimer unit cell, respectively. As detailed below, this distorted structure is a 1D CDW state as driven by the quasi 1D metallic band of unsaturated dangling bonds of step-edge Si atoms (Fig. 2a).

The silicon trimer chains are well known to contain extrinsic defects, which appear as missing bright protrusions in high bias STM images snij06 ; shin12 . However, extra local features appear with bright contrast when we lower the bias closer to the Fermi energy where the 3a₀ periodic modulation in STM becomes weak (Fig. 1a). A careful inspection of this extra feature back in the high bias image reveals the presence of a phase mismatch of the 3a₀ periodicity such as a $\times$4 (4a₀) or a $\times$5 (5a₀) ($\times$2 (2a₀)) unit with gradually decreasing amplitude of the 3a₀ protrusions (Fig. 1b and Supplementary Fig. 2). Moreover, the hopping of the phase defect is frequently noticed by the sudden a₀ shift of the 3a₀ modulations (Figs. 1e and 1f) and its motion is even directly imaged in sequential STM images (Fig. 1g and Supplementary Movie 1). The enhanced contrast of the phase defects in the low bias suggests the existence of a localized in-gap state. These observations indicate that the trimer Si chains have mobile topological solitons emerging from its 1D CDW states as revealed unambiguously below. Note that the previous observations of the phase defects snij06 ; shin12 ; hafk20 had no means to reveal their intrinsic soliton nature.

The undistorted Si step-edge chain has a strongly-1D and partially-filled electronic band due to its dangling bond electrons (Supplementary Fig. 8a). In the present structure model, fully relaxed within the DFT calculations (Fig. 1d) brau18 , every third Si atom along the step edge is distorted downward to split the band with an energy gap of 0.6 eV at the Fermi level (Fig. 2a). The band gap is due to the rehybridization of $sp{{}^{3}}$ dangling bonds into $sp{{}^{2}}$ and $p$ orbitals; the unoccupied $p$ bands around 0.2 eV from distorted Si atoms (red balls in Fig. 1d) and the occupied $sp{{}^{2}}$ bands around -0.4 and -0.7 eV from undistorted Si atoms (blue balls). This electronic structure is consistent with the spectroscopy observation shown in Fig. 3d.

This band structure can be described well with a much simpler 1D tight-binding model considering only the single Si zigzag chain at the step edge (yellow lines in Fig. 2a). The neighboring Au chains (the bands of dashed lines) affect only the fine structures of the valence bands around -0.4 $\sim$ -0.7 eV, which do not affect the following discussion (Supplementary Fig. 11). This 1D tight binding model is straightforwardly transformed into a trimer Su-Schrieffer-Heeger (SSH) Hamiltonian as described by three hopping amplitudes (Fig. 2b); t₁ of 0.57 eV, as enhanced by the shorter Si-Si bond length due to the trimer distortion, and the t₂ and t₃ of 0.47 and 0.43 eV, respectively.

Breaking translational symmetry by the trimer structure immediately leads to three degenerated ground states with fractionalized phase shifts of 0, 2$\pi$/3, and 4$\pi$/3 (Fig. 2b). These ground states can be connected with a few different types of phase defects (or domain walls) as shown in Fig. 2c and Supplementary Fig. 7. Only four of them are distinct, which we label with the distance between the neighboring Si atoms distorted. Namely, a defect with a phase shift of 2$\pi$/3 (4$\pi$/3) corresponds to the $\times$2 (2a₀) or $\times$5 ($\times$1 or $\times$4) defects. In order to identify detailed atomic and electronic structures of them, we performed DFT calculations with huge supercells (Supplementary Fig. 3). The results reveal that the $\times$4 structure is most stable in energetics [the formation energy of 0.092 ($\times$4), 0.124 ($\times$5), and 0.177 ($\times$2) eV/unit cell] (Supplementary Table I). The simulated STM image for the $\times$4 structure reproduces fairly well the experimental ones discussed above, that is, the enhanced contrast at 0.1 V and the shifted protrusions at 1.0 V (Fig. 3a). We also examined the other structure model proposed for the present system, the antiferromagnetic chain model erwi10 , but the phase defects could not be reproduced consistently (Supplementary Fig. 5).

The DFT (and also the tight-binding) calculations predict that the $\times$4 phase defect has its own electronic states within the band gap of the trimer chain as shown in Fig 3c. The empty and filled states of the pristine 3a₀ Si chain are located at about +0.3 and -0.5 eV but the phase defect has its localized electronic state at around -0.2 eV. The localized in-gap state is clearly visualized in the STS map on a $\times$4 phase defect (Fig. 3c). The phase shifts, atomic structures, and the in-gap electronic states detailed above converge convincingly to the topological soliton picture of the phase defects observed.

Among four different types of phase defects (Fig. 2c), the $\times$4 defect was found to be most popular (Supplementary Fig. 1) in accord to the energetics calculated. The $\times$1 defect is unstable to relax spontaneously into the $\times$4 defect. The $\times$2 defect can also easily relax into the $\times$5 defect by simply recovering one distorted Si atom as shown in Fig. 2c. The energy barrier of this process is as small as 0.01 eV (Supplementary Fig. 15). Even the $\times$5 defect can transform into a more energetically favorable structure of two $\times$4 defects combined (called as $\times$4$\times$4) as shown in Fig. 2d. The energy barrier is 0.06 eV being smaller than the hopping barrier of about 0.1 eV (Supplementary Fig. 15).

Indeed, we find quite a few $\times$4$\times$4 defect but rarely a $\times$5 defect (Supplementary Fig. 1). Note that the phase shifts themselves are preserved in these relaxation processes of the phase defects. The simulated STM image (Fig. 2f) of a $\times$4$\times$4 defect or a two soliton bound state is in good agreement with the experiment. Its electronic structure is similar to the isolated $\times$4 defect in both experiments and calculations (Supplementary Fig. 4) except for a small bonding-antibonding splitting (Supplementary Fig. 3). The merging and splitting of two $\times$4 defects are hinted in the real time imaging (Fig. 1g and the supplementary movie1).

As any other topological system, the topological nature of the present system is revealed by analyzing its band structure and edge states. The topological invariant of a trimer chain can be related to an effective higher dimensional (2D) bulk system theoretically krau12 . We construct such a 2D model by putting an adiabatic dimension and obtain the Chern numbers of (-1, 2, -1) for the three lowest energy bands (Supplementary Fig. 10) as predicted in previous theoretical studies mart19 ; ke16 . The band gaps of the system contain five different edge states dictated by the topology (Fig. 2e), which match well the DFT calculations (Supplementary Fig. 9). The major edge state of the C phase around 0.2 eV corresponds to the in-gap state observed in the experiment. A 2$\pi$/3 or 4$\pi$/3 fractional phase shift for an 1D electronic system guarantees fractionalized charges on corresponding solitons, while measuring the charge itself is a tremendous technical challenge - the tunneling occurs through not solitons themselves but electrons. In theoretical aspects, we found that the 4$\pi$/3 phase-shift soliton has the fractionalized charges of +2e/3 (occupied) and -e/3 (empty) per spin and the 2$\pi$/3 phase-shift soliton has +e/3 (occupied) and -2e/3 (empty) per spin (Supplementary Fig. 12 and 13) conz20 . The fractional charge is insensitive to detailed domain wall structures but depends only on the phase shift due to its topological origin. For example, the fractional charge on a $\times$5 and a $\times$4$\times$4 defects is consistent (Supplementary Fig. 13).

We observe that the phase defects propagate at a higher temperature. At a 90 K, one seldom see the hopping of solitons, but, at 95 K, they exhibit several hoppings (by one 3a₀ unit cell of 1.16 nm) within a time window of 600 sec (Fig. 1e and 1f). The hopping becomes more and more frequent with only a small change of the temperature as shown in Fig. 1f (Supplementary Movie1) and solitons become highly mobile already at 115 K. The drift velocity of the soliton at 100 K is measured as 0.10 nm/sec, which increase to 0.65 nm/sec at 115 K (Supplementary Fig. 14). An estimation of Arrhenius-type diffusion velocity, D=D₀exp(-E_b/$k_{B}$T), gives the expectation of the velocity enhancement of 4.28 from 100 to 115 K (Supplementary Fig. 15a), which is roughly consistent with the observation. The turn-on of the soliton motion at around 100 K, related to the hopping barrier of a soliton 0.1 eV (Supplementary Fig. 15), seems consistent with the thermally induced disordering of the 3a₀ lattice, which was attributed to the generation of phase defects hafk20 . The real time images also clearly indicate that the soliton is immune to the defect scattering (it bounces back or jumps over the extrinsic defects, Fig. 1f) and the soliton-soliton scattering (they are reflected but prohibited to pass through, Fig. 1g, and Supplementary Movie1, and Supplementary Fig. 16). Of course, when the ground state structure of the Si chain is destroyed, for example, by impurity adsorption and increase of temperature, its edge modes, solitons, cannot be sustained.

A soliton is found to be reproducibly generated under the probe tip by the tunneling bias application at very low temperature. Figure 4a shows an atomically resolved atomic force microscopy (AFM) image of the surface at 4.4 K. In the AFM image, two undistorted Si atoms (blue atoms in the model of Fig. 2) of a trimer appear as dark contrast due to their closer distance to the tip. After the application of a single tunneling pulse at the location of the distorted Si atom (yellow circled in Fig. 4a), one can observe one trimer destroyed (Fig. 4b). This transiently forms a $\times$6 chain in our structure model (Fig. 2) and relaxes into a $\times$5 soliton (Fig. 4c) and the phase shift of the neighboring trimers. This indicates the pair creation of $\times$1 and $\times$5 solitons with the former quickly moving out of the view frame to induce the phase shift. The soliton can also be erased by applying the same bias in a nearby site as shown in Figs. 4d-4f. That is, the second soliton generated annihilates the first one. This switches back-and-forth the topological phase shift of a given trimer chain as shown in Figs. 4d-4f. That is, one can manipulate a single soliton and decode the topological phase information on each chain.