22institutetext: Instituto Nacional de Investigaciones Nucleares (ININ), Estado de México, México,
33institutetext: Universidad Iberoamericana, Ciudad de México, México, 44institutetext: Área de Física de Procesos Irreversibles, Departamento de Ciencias Básicas, Universidad Autónoma Metropolitana-Azcapotzalco (UAM-A), Ciudad de México, México.
44email: [email protected], 44email: [email protected], 44email: [email protected], 44email: [email protected], 44email: [email protected], 44email: [email protected] 44email: [email protected]
Creating and using large grids of pre-calculated model atmospheres for rapid analysis of stellar spectra
Abstract
We present a database of 45,000 atmospheric models (which will become 80,000 models by the end of the project) with stellar masses between 9 and 120 M⊙, covering the region of the OB main sequence and W-R stars in the H–R diagram. The models were calculated using the ABACUS I supercomputer and the stellar atmosphere code CMFGEN. The parameter space has 6 dimensions: the effective temperature , the luminosity , the metallicity , and three stellar wind parameters, namely the exponent , the terminal velocity , and the volume filling factor . For each model, we also calculate synthetic spectra in the UV (900-2000 Å), optical (3500-7000 Å), and near IR (10000-30000 Å) regions. To facilitate comparison with observations, the synthetic spectra were rotationally broaden using ROTIN3, by covering v sin i velocities between 10 and 350 km/s with steps of 10 km/s, resulting in a library of 1 575 000 synthetic spectra. In order to demonstrate the benefits of employing the databases of pre-calculated models, we also present the results of the re-analysis of Ori by using our grid.
Keywords:
astronomical databases: miscellaneous — methods: data analysis — stars: atmospheres1 Introduction
Thanks to the fertile combination of the large amount of public data and the availability of sophisticated stellar atmosphere codes such as CMFGEN [14], TLUSTY [15], FASTWIND [20, 19], and the Potsdam Wolf-Rayet code (PoWR) [9, 10] self-consistent analysis of spectral regions from the UV to the IR is now possible. As a result of this we have made significant advances in the understanding of the physical conditions in the atmospheres and winds of massive stars.
For example, early far-UV observations showed that there were inconsistencies between the optical effective temperature scale and that implied by the observed wind ionization [8]. Studies by Martins et al. [16], and others, have shown that the neglect of line blanketing in the models leads to a systematic overestimate of the effective temperature when derived from optical H and He lines. On the other hand, Crowther et al. [4], Bouret at al. [2], and Hillier et al. [13] simultaneously analyzed the , the , and the optical spectra of O stars and were able to derive consistent effective temperatures using a wide variety of diagnostics.
Another crucial result was the recognition of the important effect of wind inhomogeneities (clumping) on the spectral analyses of O stars. For instance, Crowther et al. [4] and Hillier et al. [13] could not reproduce the observed V 1118-1128 profiles when using mass-loss rates derived from the analysis of H lines. The only ways the V and the H profile discrepancies could be resolved were either by assuming substantial clumping or using unrealistically low phosphorus abundances. As a consequence of clumping, the mass-loss rates have been lowered by significant factors (i.e., from 3 to 10). However, the possibility of optically thick clumping was raised recently which would change this conclusion (see, e.g., Ref. [21] and references therein).
Unfortunately, performing such investigations by using any of the above mentioned stellar atmosphere codes is not an easy task! To run these codes and perform a reliable analysis requires a lot of experience; something that many investigators do not have the time to gain. Therefore, it is useful to develop databases of pre-calculated models. Such databases will free up valuable time for astronomers, who could study stellar atmospheres with reasonable accuracy but without the need of running time consuming simulations. Furthermore, these databases will also accelerate the studies of large numbers of observed spectra that are in line for analysis.
The basic parameters of such databases of pre-calculated models are: the surface temperature (), the stellar mass (), and the surface chemical composition. An adequate analysis of massive stars also has to take into account the parameters associated with the stellar wind, such as the terminal velocity (), the mass-loss rate (Ṁ), and the clumping. If one takes into account the variations of all necessary parameters the number of pre-calculated models that are needed increases exponentially. Therefore, production of such databases is only possible by using supercomputing facilities.
There are already a few databases of synthetic stellar spectra available, but only with a few tens or hundreds of stellar models (see, for example, the atlas of CMFGEN models for OB massive stars by Fierro et al. [6], the grid of W-R stars by Hamann and Gräfener [10], and the POLLUX database by Palacios et al. [17]). On the other hand, we are generating a database with tens of thousands of models [22], which will be publicly available in a year or so. Obviously, it will be impossible to manually compare an observed spectrum with such an amount of model calculations. Therefore, it is imperative to develop tools that allow the automation of this process but without compromising the quality of the fit. In particular, in Ref. [7] we have presented FITspec, a program that searches our database for a model that better fits the observed spectrum in the optical region. It uses the Balmer lines to measure the surface gravity () and the equivalent width ratios of II and I lines to estimate .
In this article we describe the state of our grid of pre-calculated models and the results of a test analysis to verify the usefulness of the grid. In § 2 and § 2.1, we briefly describe the stellar atmosphere code (CMFGEN) which we use to produce our models. In § 3, we describe our model grid and in § 4 we describe a simple test analysis to demonstrate the benefits of using our grid. Finally, in § 5 we summarize the relevant conclusions.
2 CMFGEN
CMFGEN is a sophisticated and widely-used non-LTE stellar atmosphere code [13, 14]. It models the full spectrum and has been used successfully to model O & B stars, W-R stars, luminous blue variables, and even supernovae. The code determines the temperature, ionization structure, and level populations for all elements in the stellar atmosphere and wind. It solves the spherical radiative transfer equation in the co-moving frame in conjunction with the statistical equilibrium equations and radiative equilibrium equation. The hydrostatic structure can be computed below the sonic point, thereby allowing the simultaneous treatment of spectral lines formed in the atmosphere, the stellar wind, and the transition region between the two. Such features make it particularly well suited for the study of massive OB stars with winds. However, there is a price for such sophistication, a CMFGEN simulation takes anywhere between 24 and 36 hours of microprocessor time to be completed.
For atomic models, CMFGEN utilizes the concept of “super levels” by which levels of similar energies are grouped together and treated as a single level in the statistical equilibrium equations (see, Ref. [14] and references therein for more details). The stellar models in this project include 28 explicit ions of the different elements as function of their . Table 1 summarizes the levels and super levels included in the models. The atomic data references are given by Herald and Bianchi [11].
| Element | I | II | III | IV | V | VI | VII | VIII |
|---|---|---|---|---|---|---|---|---|
| H | 20/30 | 1/1 | ||||||
| He | 45/69 | 22/30 | 1/1 | |||||
| C | 40/92 | 51/84 | 59/64 | 1/1 | ||||
| N | 45/85 | 41/82 | 44/76 | 41/49 | 1/1 | |||
| O | 54/123 | 88/170 | 38/78 | 32/56 | 25/31 | 1/1 | ||
| Si | 33/33 | 22/33 | 1/1 | |||||
| P | 30/90 | 16/62 | 1/1 | |||||
| S | 24/44 | 51/142 | 31/98 | 28/58 | 1/1 | |||
| Fe | 104/1433 | 74/540 | 50/220 | 44/433 | 29/153 | 1/1 |
To model the stellar wind, CMFGEN requires values for the mass loss rate (Ṁ), terminal velocity (), parameter, and the volume filling factor of the wind (). The profile of wind speed is modeled by a beta-type law [3]
| (1) |
The parameter controls how the stellar wind is accelerated to reach the terminal velocity (see Fig. 1), while the volume filling factor is used to introduce the effects of optically thin clumping in the wind (see Ref. [21] and references therein).

2.1 Synthetic spectra
The auxiliary program CMF_FLUX of the CMFGEN package computes the synthetic observed spectrum in the observer’s frame which is one of the most important output of our models [12]. To simulate the effects of rotation on the spectral lines, the synthetic spectra are also rotationally broadened using the program ROTIN3, which is part of the TLUSTY package [15].
For each model in the grid, we calculate the normalized spectra in the UV (900-3500 Å ), optical (3500-7000 Å ), and IR (7000-40 000 Å ) range; then, we apply rotation by sampling the range between 10 and 350 km/s-1 with steps of 10 km/s-1. This process results in a library with a total of 1 575 000 synthetic spectra.
3 The model grid
The main parameters of a model atmosphere are the luminosity (L) and the effective temperature (), whose values allow to place the star in the H-R diagram. In order to constrain appropriately the input parameters, we use the evolutionary tracks of Ekström et al. [5] calculated with solar metallicity (Z=0.014) at the zero age main sequence (ZAMS). For any track, each point corresponds to a star with specific values of , luminosity (), and stellar mass (). We calculated several models along each track with the approximate steps of 2 500 K in , while the stellar radius and the surface gravity were calculated to get the luminosity and the stellar mass corresponding to the track.
The elements included in our models are H, He, C, N, O, Si, P, S, and Fe. The values of H, He, C, N, and O were taken from the tables of Ekström et al. [5]. For consistency, we assumed solar metallicity as reported by Asplund et al. [1] for Si, P, S, and Fe in all models.
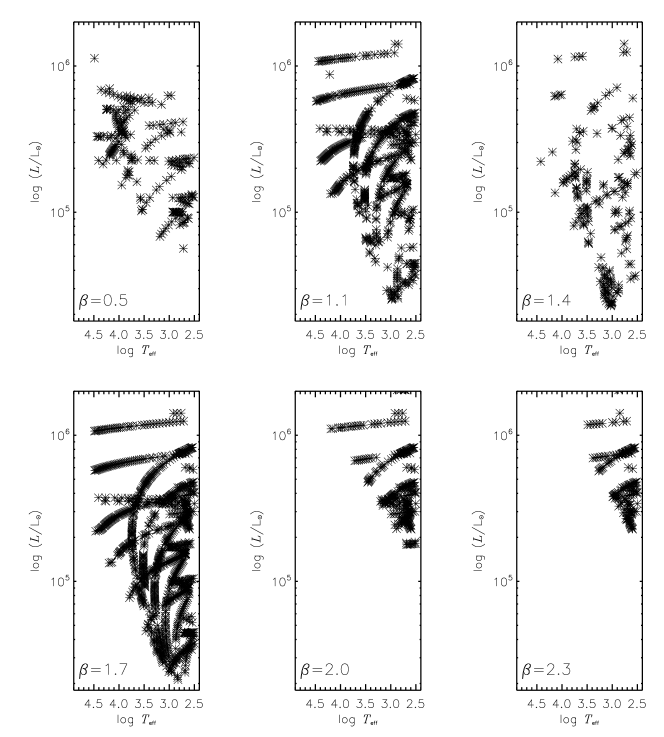


The grid is organized as a hypercube data in dimensions which correspond to , , , , , and the metallicity. The plane generated by and is the H-R diagram (see upper part of Figure 2); the values of these variables are restricted by evolutionary tracks. For we use two values, a low () and a high () velocity model, where the escape velocity () has the usual meaning. The fourth dimension is the parameter of the stellar wind for which we use the values of , 0.8, 1.1, 1.4, 1.7, 2.0, and 2.3 (see bottom left of Figure 2). Models with different values of , , and populate a data cube. Each value of , 0.30, 0.60, and 1.0 generates a similar cube, all of which are aligned one after another in a fifth dimension. Finally, we have two values of metallicity: solar and solar enhanced by rotation. This 6-dimensional arrangement generates a plane populated with data cubes (see bottom right of Figure 2).
This arrangement only populates regions of the H-R diagram where nature forms stars, and does not produce non-physical models. If needed, we can interpolate between models to achieve better fits to the observed spectra.
4 A simple test to demonstrate the usefulness of our grid
We demonstrate the benefits of having a mega-grid by a re-analysis of Ori. This O9/B0 supergiant was studied by Puebla et al. [18] by using CMFGEN in the traditional way (i.e., by producing every model that was needed). They reported 27,000 K, log g = 3, a mass-loss rate Ṁ yr-1, and a highly clumped and slowly accelerating wind (, ) for this star. Figure 3 shows a comparison of selected models from the grid with the optical I and II lines observed for Ori. We tried to select models which only differ in the effective temperature and have a low mass-loss rate to avoid complications. Obviously, our grid is still not fine enough to be able to do that.
The He lines are normally used to estimate the effective temperature of O stars. Although, the II lines are very weak for Ori since this star is on the borderline between type O and B, the comparison still shows that has to be around 25,000 K.

Moreover, Figure 4 shows models from the grid which vary in log g in comparison with the observed H Balmer series. Unfortunately, the H Balmer lines are also affected by mass-loss, namely the absorption is filled in by the emission in the base of the wind. For example, Fig. 4 shows that H and H are basically useless as log g indicator even at relatively low Ṁ. Neverheless, the higher order members of the Balmer series are not affected by mass-loss and they support the published value of log g 3.

The most useful spectral region to estimate the mass-loss rate (Ṁ) and terminal velocity () is the ultraviolet one. Here, we encounter strong resonance lines of the dominant ionization states of various elements in the winds of massive stars. These lines normally show P-Cygnii profiles which are particularly useful to measure Ṁ and ; see e.g., the IV doublet around 1550Å or the IV doublet around 1400Å in Fig. 5. However, these lines are not useful to estimate and, if saturated, they are also useless to measure . The comparison of models with the observations in Fig. 5 shows a somewhat contradictory situation, while the IV 1400 doublet suggests a low Ṁ. To fit the IV 1552 profile we would need much higher mass-loss rates. However, Ṁ yr-1 would result in H emission which is not observed. Therefore, we conclude that Ṁ yr-1 is the best estimate we can have.

Estimations of and are very difficult because we do not have many diagnostics and those that we have, like H, are affected by a combination of parameters. Nevertheless, the comparison of selected models with the observed H lines in Fig. 6 indicates that the values reported in Ref. [18] are plausible.

As expected, the re-analysis of Ori supported the values that were published in Ref. [18]. Obviously, the analysis by using the grid is much cruder, but also much faster. We needed only an afternoon to perform the analysis presented here, while several months of work was necessary to achieve the results presented by Puebla et al. [18].
5 Summary
We present a mega grid of 45,000 (which will soon becomes more than 80,000) stellar atmospheric models calculated by the CMFGEN package. These models cover the region of the H-R diagram populated by OB main sequence and W-R stars with masses between 9 and 120 . The grid provides UV, visual, and IR spectra for each model.
We use and luminosity values that correspond to the evolutionary tracks of Ekström et al. [5]. Furthermore, we sample seven values of , five values of the clumping factor, and two different metallicities and terminal velocities. This generates a 6-dimensional hypercube of stellar atmospheric models, which we intend to release to the general astronomical community as a free tool for analyzing OB stars.
We have also demonstrated the usefulness of our mega-grid by the re-analysis of Ori. Our somewhat crude but very rapid analysis supported the stellar an wind parameters reported by Puebla et al. [18]. The re-analysis has demonstrated the benefits of having a large grid of pre-calculated models. This way we can perform rapid and reliable estimates of the stellar and wind parameters for a star; and if needed, a more detailed study can be performed but by starting with good initial values. This significantly shortens the time that is needed to complete the spectral analysis.
Acknowledgments
The authors acknowledge the use of the ABACUS-I supercomputer at the Laboratory of Applied Mathematics and High-Performance Computing of the Mathematics Department of CINVESTAV-IPN, where this work was performed. J. Zsargo acknowledges CONACyT CB-2011-01 No. 168632 grant for support. The research leading to these results has received funding from the European Union’s Horizon 2020 Programme under the ENERXICO Project, grant agreement no 828947 and under the Mexican CONACYT-SENER-Hidrocarburos grant agreement B-S-69926. J. K. acknowledges financial support by the Consejo Nacional de Ciencia y Tecnología (CONACyT), México, under grant 283151.
References
- [1] Asplund, M., Grevesse, N., Sauval, A.J., Scott, P.: The chemical composition of the sun. ARA&A 47, 481–522 (2009).
- [2] Bouret, J.C., Lanz, T., Hillier, D.J., Heap, S.R., Hubeny, I., Lennon, D.J., Smith, L.J., Evans, C.J.: Quantitative spectroscopy of O stars at low metallicity: O dwarfs in NGC 346. ApJ 595, 1182–1205 (2003).
- [3] Castor, J.I., Abbott, D.C., Klein, R.I.: Radiation-driven winds in Of stars. ApJ 195, 157–174 (1975).
- [4] Crowther, P.A., Hillier, D.J., Evans, C.J., Fullerton, A.W., De Marco, O., Willis, A.J.: Revised stellar temperatures of Magellanic cloud O supergiants from far ultraviolet spectroscopic explorer and Very Large Telescope UV-Visual Echelle Spectrograph spectroscopy. ApJ 579, 774–799 (2002).
- [5] Ekström, S., Georgy, C., Eggenberger, P., Meynet, G., Mowlavi, N., Wyttenbach, A., Granada, A., Decressin, T., Hirschi, R., Frischknecht, U., Charbonnel, C., Maeder, A.: Grids of stellar models with rotation. I. Models from 0.8 to 120 at solar metallicity (). A&A 537, A146 (2012).
- [6] Fierro, C.R., Borissova, J., Zsargó, J., Díaz-Azuara, A., Kurtev, R., Georgiev, L., Ramírez Alegría, S., Peñaloza, F.: Atlas of CMFGEN Models for OB Massive Stars. PASP 127, 428–436 (2015).
- [7] Fierro-Santillán, C.R., Zsargó, J., Klapp, J., Díaz-Azuara, S.A., Arrieta, A., Arias, L., Sigalotti, L. Di G.: FITspec: A new algorithm for the automated fit of synthetic stellar spectra for OB stars. ApJS 236, 38 (2018).
- [8] Fullerton, A.W., Crowther, P.A., De Marco, O., Hutchings, J.B., Bianchi, L., Brownsberger, K.R., Massa, D.L., Morton, D.C., Rachford, B.L., Snow, T.P., Sonneborn, G., Tumlinson, J., Willis, A.J.: Far ultraviolet spectroscopic explorer observations of the stellar winds of two O7 supergiants in the Magellanic clouds. ApJL 538, L43–L46 (2000).
- [9] Gräfener, G., Koesterke, L., Hamann, W.R.: Line-blanketed model atmospheres for WR stars. A&A 387, 244–257 (2002).
- [10] Hamann, W.R., Gräfener, G.: Grids of model spectra for WN stars, ready for use. A&A 427, 697–704 (2004).
- [11] Herald, J.E., Bianchi, L.: A far-ultraviolet spectroscopic analysis of the central star of the planetary nebula Longmore 1. PASP 116, 391–396 (2004).
- [12] Hillier, D.J.: CMFGEN Manual. (2013).
- [13] Hillier, D.J., Lanz, T., Heap, S.R., Hubeny, I., Smith, L.J., Evans, C.J., Lennon, D.J., Bouret, J.C.: A tale of two stars: The extreme O7 lafsupergiant AV 83 and the OC7.5III((f)) star AV 69. ApJ 588, 1039–1063 (2003).
- [14] Hillier, D.J., Miller, D.L.: The treatment of non-LTE line blanketing in spherically expanding outflows. ApJ 496, 407–427 (1998).
- [15] Lanz, T., Hubeny, I.: Non-LTE line-blanketed model atmospheres of hot stars. II. Hot, metal-rich white dwarfs. ApJ 439, 905–916 (1995).
- [16] Martins, F., Schaerer, D., Hillier, D.J.: On the effective temperature of O stars. A&A 382, 999–1004 (2002).
- [17] Palacios, A., Gebran, M., Josselin, E., Martins, F., Plez, B., Belmas, M., Lèbre, A.: POLLUX: a database of synthetic stellar spectra. A&A 516, A13 (2010).
- [18] Puebla, R.E., Hillier, D.J., Zsargó, J., Cohen, D.H., Leutenegger, M.A.: X-ray, UV and optical analysis of supergiants: Ori. MNRAS 456, 2907–2936 (2016).
- [19] Puls, J., Urbaneja, M.A., Venero, R., Repolust, T., Springmann, U., Jokuthy, A., Mokiem, M.R.: Atmospheric NLTE-models for the spectroscopic analysis of blue stars with winds. II. Line-blanketed models. A&A 435, 669–698 (2005).
- [20] Santolaya-Rey, A.E., Puls, J., Herrero, A.: Atmospheric NLTE-models for the spectroscopic analysis of luminous blue stars with winds. A&A 323, 488–512 (1997).
- [21] Sundqvist, J.O., Puls, J., Owocki, S.P.: Mass loss from inhomogeneous hot star winds. III. An effective-opacity formalism for line radiative transfer in accelerating, clumped two-component media, and first results on theory and diagnostics. A&A 568, A59 (2014).
- [22] Zsargo, J., Arrieta, A., Fierro, C., Klapp, J., Hillier, D.J., Arias, L., Mendoza, J., Georgiev, L.N.: A Mega-Grid of CMFGEN Model Atmospheres for Rapid Analysis of Stellar Spectra. In: Miroshnichenko, A., Zharikov, S., Korčáková, D., Wolf, M. (eds.) The B[e] Phenomenon: Forty Years of Studies. Astronomical Society of the Pacific Conference Series, vol. 508, p. 407 (Feb 2017).