CRA-PCN: Point Cloud Completion with Intra- and Inter-level Cross-Resolution Transformers
Abstract
Point cloud completion is an indispensable task for recovering complete point clouds due to incompleteness caused by occlusion, limited sensor resolution, etc. The family of coarse-to-fine generation architectures has recently exhibited great success in point cloud completion and gradually became mainstream. In this work, we unveil one of the key ingredients behind these methods: meticulously devised feature extraction operations with explicit cross-resolution aggregation. We present Cross-Resolution Transformer that efficiently performs cross-resolution aggregation with local attention mechanisms. With the help of our recursive designs, the proposed operation can capture more scales of features than common aggregation operations, which is beneficial for capturing fine geometric characteristics. While prior methodologies have ventured into various manifestations of inter-level cross-resolution aggregation, the effectiveness of intra-level one and their combination has not been analyzed. With unified designs, Cross-Resolution Transformer can perform intra- or inter-level cross-resolution aggregation by switching inputs. We integrate two forms of Cross-Resolution Transformers into one up-sampling block for point generation, and following the coarse-to-fine manner, we construct CRA-PCN to incrementally predict complete shapes with stacked up-sampling blocks. Extensive experiments demonstrate that our method outperforms state-of-the-art methods by a large margin on several widely used benchmarks. Codes are available at https://github.com/EasyRy/CRA-PCN.
Introduction
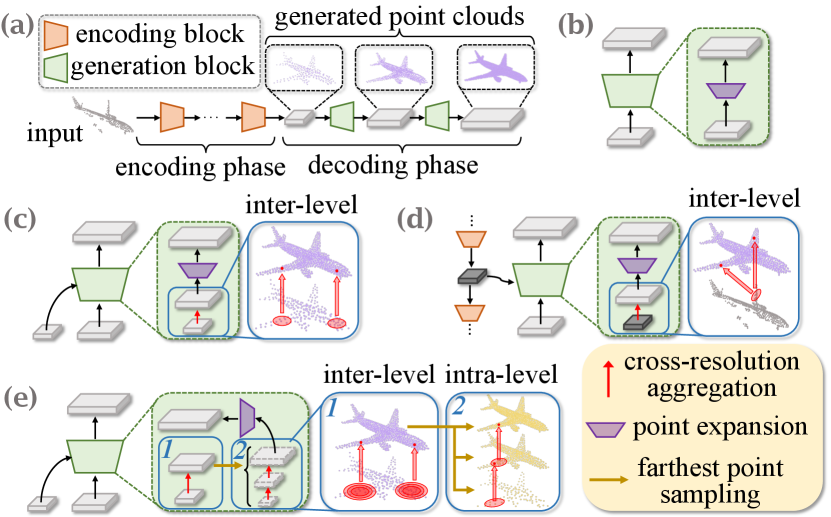
Driven by the rapid development of 3D acquisition technologies, 3D vision is in great demand for research. Among various types of 3D data, point cloud is the most popular description and commonly used in real-world applications (Cadena et al. 2016; Reddy, Vo, and Narasimhan 2018; Rusu et al. 2008). However, due to self-occlusion and limited sensor resolution, acquired point clouds are usually highly sparse and incomplete, which impedes further applications. Therefore, recovering complete point clouds is an indispensable task, whose major purposes are to preserve details of partial observations, infer missing parts, and densify sparse surfaces.
In the realm of deep learning, various approaches have been proposed to tackle this problem (Yang et al. 2018; Choy et al. 2016; Girdhar et al. 2016; Xie et al. 2020). Especially with the success of PointNet (Qi et al. 2017a) and its successors (Qi et al. 2017b; Wang et al. 2019; Zhao et al. 2021), most approaches recover complete point clouds directly based on 3D coordinates (Yuan et al. 2018; Wen et al. 2020, 2021; Tchapmi et al. 2019; Yu et al. 2021; Wang, Ang Jr, and Lee 2020). Due to the unordered and unstructured nature of point cloud data, learning fine geometric characteristics and structural features is essential for predicting reasonable shapes. To accomplish this aim, mainstreams of the recent methods (Xiang et al. 2021; Zhou et al. 2022; Huang et al. 2020; Yan et al. 2022; Huang et al. 2020; Tang et al. 2022; Wang et al. 2022) formulate the point cloud completion task as a tree-like generation process where an encoder-decoder architecture is adopted to extract shape representation (e.g., a latent vector representing a complete shape) and subsequently recover the complete point cloud from low-resolution to high-resolution, as shown in Fig. 1(a).
As illustrated in Fig. 1, we select several representative methods and conduct an analysis from the perspective of cross-resolution aggregation (CRA), which is a crucial component of these hierarchical methods. Prior to generating the points, it is crucial to extract semantic information from the current point cloud. The plain methods (Yuan et al. 2018; Huang et al. 2020) adopt common feature extraction operations without considering aggregating features from point clouds with different resolutions, namely cross-resolution aggregation. Based on skip connections (or dense connections) among different generation stages, the methods showed in Fig. 1(c) realize cross-resolution aggregation via interpolation followed by multi-layer perceptrons (Yifan et al. 2019) or transformers (Yan et al. 2022; Zhou et al. 2022). As illustrated in Fig. 1(d), U-Net-like methods (Wen et al. 2020; Yu et al. 2021) aggregate features of partial inputs for current point clouds, commonly based on global attention mechanisms due to the mismatching of shapes, yet another form of cross-resolution aggregation. While plain methods can extract multi-scale representations in the generation phase, the success of the latter two methods suggests that explicit cross-resolution aggregation is beneficial for efficiently capturing multi-scale features and promoting the completion performance.
Although prior approaches accomplished cross-resolution aggregation with inter-layer connections (i.e., inter-level CRA), they overlooked cross-resolution aggregation inside layers (i.e., intra-level CRA). In the process of point cloud completion, missing points are not generated all at once but are gradually completed through layer-by-layer generation, which indicates that the details of the intermediate point clouds are not exactly the same, making it hard for inter-level CRA-based methods to find generation patterns that fit local regions best. In other words, it is crucial to combine inter-level and intra-level CRA, as shown in Fig. 1(e), to overcome the flaws of previous methods.
To this end, we propose Cross-Resolution Transformer that performs multiple scales of cross-resolution aggregation with recursive designs and local attention mechanisms. Cross-Resolution Transformer has several favorable properties: (1) Explicit cross-resolution aggregation: Point cloud directly aggregates features from ones with different resolutions without intermediate aids; (2) Multi-scale aggregation: Unlike previous methods, which only realized CRA on a few scales, our method can extract more scales of features with recursive designs, even taking two resolutions of point clouds as input; (3) Unified design: Intra- and inter-level CRA share the same implementation, and different forms of CRA can be achieved by switching inputs; (4) Plug-and-play: Without introducing significant computation, Cross-resolution Transformer can serve as a plug-and-play module to extract local features in the decoder or encoder with large receptive fields.
We integrate two forms of Cross-Resolution Transformers in one up-sampling block for intra- and inter-level cross-resolution aggregation, respectively. Thanks to this combination, the decoding block can precisely capture multi-scale geometric characteristics and generate points that best fit local regions. Mainly based on the up-sampling block, we propose CRA-PCN for point cloud completion. CRA-PCN has an encode-decoder architecture, and its decoder consists of three consecutive up-sampling blocks. With the help of this effective decoder, our method outperforms state-of-the-art completion networks on several widely used benchmarks. The contributions in this work can be summarized as follows:
-
•
We show that one of the key ingredients behind the success of prior methods is explicit cross-resolution aggregation (CRA) and propose the combination of inter- and intra-level CRA to extract fine local features.
-
•
We devise an effective local aggregation operation named Cross-Resolution Transformer, which can adaptively summarize multi-scale geometric characteristics in the manner of cross-resolution aggregation.
-
•
We propose a novel CRA-PCN for point cloud completion, which precisely captures multi-scale local properties and predicts rich details.

Related Work
Point Cloud Learning
Early works usually adopt multi-view projection (Li, Zhang, and Xia 2016; Chen et al. 2017; Lang et al. 2019) or 3D voxelization (Maturana and Scherer 2015; Song et al. 2017; Riegler, Osman Ulusoy, and Geiger 2017; Choy, Gwak, and Savarese 2019) to transform the irregular point clouds into regular representations, followed by 2D/3D CNNs. However, the converting costs are expensive, and geometric details will inevitably be lost in the transforming process. Therefore, researchers have designed deep networks which can directly process 3D coordinates based on permutation-invariant operators. PointNet (Qi et al. 2017a) and PointNet++ (Qi et al. 2017b) are the pioneering point-based networks which adopt MLPs and max pooling to extract and aggregate features across the whole set or around local regions. Based on them, a number of point-based methods have been proposed. Some methods (Wang et al. 2019; Zhao et al. 2019; Simonovsky and Komodakis 2017) convert the local region to a graph, followed by graph convolution layers. Other methods (Xu et al. 2018; Wu, Qi, and Fuxin 2019; Thomas et al. 2019) define novel convolutional operators that apply directly to the 3D coordinates without quantization. Recently, attention-based methods, especially the family of transformers (Vaswani et al. 2017; Zhao et al. 2021; Guo et al. 2021; Park et al. 2022), have achieved impressive success thanks to the inherent permutation-invariant, where the whole point set or local region is converted to a sequence and the aggregation weights are adaptively determined by data. Among them, we exploit vector attention mechanisms (Zhao et al. 2021) to construct our Cross-Resolution Transformer.
Point Cloud Completion
Like traditional methods for point cloud learning, early attempts (Choy et al. 2016; Girdhar et al. 2016; Han et al. 2017) at 3D shape completion usually adopt intermediate aids (i.e., voxel grids). However, these methods usually suffer from heavy computational costs and geometric information loss. Boosted by the point-based learning mechanisms discussed above, researchers pay more attention to designing point-based completion methods. PCN (Yuan et al. 2018) is the first learning-based work that adopts an encoder-decoder architecture. It recovers point cloud in a two-stage process where a coarse result is predicted by MLP and then the fine result is predicted with folding operation (Yang et al. 2018) from the coarse one. Along this line, more methods (Xiang et al. 2021; Zhou et al. 2022; Yan et al. 2022; Tang et al. 2022; Wang et al. 2022; Li et al. 2023; Chen et al. 2023) spring up and yield impressive results with the help of more generation stages, better feature extraction, or structured generation process. As discussed before, explicit cross-resolution aggregation is another key ingredient behind their success. Following the coarse-to-fine manner, we propose CRA-PCN, and our insight into promoting point cloud completion is to introduce well-designed cross-resolution aggregation mechanisms.
Method
In this section, we will first elaborate on the details of Cross-Resolution Transformer. Then, we will illustrate the architecture of CRA-PCN in detail. Lastly, we will introduce the loss function used for training.

Inter-level Cross-Resolution Transformer
As shown in Fig. 2(a), the purpose of Cross-Resolution Transformer (CRT for short) is to aggregate features of the support point cloud (green) for the query point cloud (blue) on multiple scales. The query point cloud is the current point cloud to be up-sampled, and the support one was generated in the early generation stage; therefore, the query one has a higher resolution than the support one. We design CRT in a recursive manner, which means it can work on arbitrary-number scales and the computational complexity is bounded.
Given coordinates and the corresponding features of the query point cloud with and of the support one, we first adopt hierarchical down-sampling to obtain their subsets, respectively. The number of subsets, namely number of scales, is . The subsets of original coordinates and features are denoted as , , , and , like shown in Fig. 2(a). Note that the index corresponds to the original point cloud. Then, we exploit the local attention mechanism (Zhao et al. 2021) to achieve cross-resolution aggregation on the -th scale. The attention relations in the neighborhood of each query point can be calculated as follows:
| (1) |
where is a non-linear projection function implemented with multi-layer perceptron (MLP). Let be the -th coordinate of , we use algorithm to search the indexes of its neighborhood in the support point cloud, which is denoted as . is the position encoding generated by subtraction between and followed by a MLP. is the query vector projected from the -th feature vector of via linear projection, and is projected from the corresponding feature vector of (i.e., ). For all , we normalize for with channel-wise function and aggregate local features:
| (2) |
Here, indicates the -th feature of , as shown in Fig. 2(a), and is projected from via linear projection, like . Next, we adopt feature interpolation (Qi et al. 2017b) to map onto the coordinates and , and the two interpolated features are concatenated with and followed by MLPs for feature fusion, respectively. The two enhanced features are passed through the aforementioned attention mechanism for . The process is iterated until we obtain , which is the output of CRT.
The common cross-resolution aggregation operations only work on the -th scale, i.e., the bottom scale shown in Fig. 2. We argue that these single-scale designs restrict the modeling power, leading to unreasonable predictions. While several methods (Qian et al. 2021; He et al. 2023) adopt stacked feature extraction layers with dense connections among these layers to capture multi-scale features, the computational complexities of them are not bounded as the number of layers grows, and the receptive fields grow slowly without explicit hierarchical down-sampling.
Intra-level Cross-Resolution Transformer
With the help of unified implementation, let the query point cloud and support one be the same, inter-level CRT degrades to the intra-level one. In this case, the cross-resolution aggregation is decomposed into self-attention, interpolation, and feature fusion, as illustrated in Fig. 2(b).
Inter-level CRT plays an important role in preserving learned features and capturing multi-scale features. However, the generated point cloud with lower resolution is not necessarily a subset of the current one, and the local details of them are sometimes different due to irregular outliers or shrinkages caused by unreasonable coordinate predictions. Therefore, only using inter-level CRTs is not sufficient for finding fine generation patterns that fit local regions best. To alleviate this problem, we introduce intra-level CRT and integrate both into an up-sampling block, like shown in Fig. 3(b). Note that the combination of inter- and intra-level CRT is not an incremental improvement. The experiments demonstrate that their combination outperforms the variants only using two consecutive intra- or inter-level CRTs by a large margin with the same number of parameters.
| Methods | Average | Plane | Cabinet | Car | Chair | Lamp | Couch | Table | Boat |
| FoldingNet (Yang et al. 2018) | 14.31 | 9.49 | 15.80 | 12.61 | 15.55 | 16.41 | 15.97 | 13.65 | 14.99 |
| TopNet (Tchapmi et al. 2019) | 12.15 | 7.61 | 13.31 | 10.90 | 13.82 | 14.44 | 14.78 | 11.22 | 11.12 |
| PCN (Yuan et al. 2018) | 9.64 | 5.50 | 22.70 | 10.63 | 8.70 | 11.00 | 11.34 | 11.68 | 8.59 |
| GRNet (Xie et al. 2020) | 8.83 | 6.45 | 10.37 | 9.45 | 9.41 | 7.96 | 10.51 | 8.44 | 8.04 |
| PoinTr (Yu et al. 2021) | 8.38 | 4.75 | 10.47 | 8.68 | 9.39 | 7.75 | 10.93 | 7.78 | 7.29 |
| SnowflakeNet (Xiang et al. 2021) | 7.21 | 4.29 | 9.16 | 8.08 | 7.89 | 6.07 | 9.23 | 6.55 | 6.40 |
| FBNet (Yan et al. 2022) | 6.94 | 3.99 | 9.05 | 7.90 | 7.38 | 5.82 | 8.85 | 6.35 | 6.18 |
| ProxyFormer (Li et al. 2023) | 6.77 | 4.01 | 9.01 | 7.88 | 7.11 | 5.35 | 8.77 | 6.03 | 5.98 |
| SeedFormer (Zhou et al. 2022) | 6.74 | 3.85 | 9.05 | 8.06 | 7.06 | 5.21 | 8.85 | 6.05 | 5.85 |
| AnchorFormer (Chen et al. 2023) | 6.59 | 3.70 | 8.94 | 7.57 | 7.05 | 5.21 | 8.40 | 6.03 | 5.81 |
| Ours | 6.39 | 3.59 | 8.70 | 7.50 | 6.70 | 5.06 | 8.24 | 5.72 | 5.64 |

CRA-PCN
The overall architecture of CRA-PCN is illustrated in Fig. 3(a), which consists of encoder, seed generator, and decoder. The decoder consists of three up-sampling blocks.
Encoder and seed generator.
The purpose of the encoder is to extract a shape vector and per-point features of pooled partial input. The input of the encoder is the partial point cloud . With hierarchical aggregation and down-sampling followed by a max-pooling operation, we can obtain the shape vector and down-sampled partial points and corresponding features . Specifically, we adopt three layers of set abstraction (Qi et al. 2017b) (SA layer) to down-sample point set and aggregate local features; moreover, we insert an intra-level CRT between two consecutive SA layers to enrich semantic contexts.
The seed generator aims to produce a representation with coordinates and features representing a sketch point cloud with low resolution yet complete shape, which is named seed. To leverage the impressive detail-preserving ability of Upsample Transformer (Zhou et al. 2022) for seed generation, we feed and into Upsample Transformer without activation. The seed generation phase can be formulated as follows:
| (3) |
where is the set of seed features that carry the local properties of seed points, and indicates Upsample Transformer. We concatenate with and then feed the concatenated features into a MLP for seed coordinates . For better optimization, following prior methods (Xiang et al. 2021; Wang, Ang Jr, and Lee 2020), we merge partial input with and down-sample the merged set to obtain the starting points .
Decoder.
The objective of the decoder is to gradually recover the complete shape from starting points . Our decoder consists of three up-sampling blocks. Given starting coordinates , the decoder will gradually produce , , and , where is the input of the -th block and for each .
Up-sampling block.
As illustrated in Fig 3(b), each block is mainly composed of a mini-PointNet (Qi et al. 2017a), inter-level CRT, intra-level CRT, and deconvolution (Xiang et al. 2021). The -th block can upsample current point set at the rate of . With shape vector , we first adopt a mini-PointNet (Qi et al. 2017a) to learn per-point features . Then, let be the coordinates of the support point cloud with corresponding features and be the coordinates of the query one with corresponding features , we employ inter-level CRT to extract features (i.e., ) in the cross-resolution manner. Note that, in the case of , and . Next, and are fed into intra-level CRT to capture internal multi-scale geometric features and obtain feature . Finally, with , we use deconvolution to predict offsets for each point and subsequently obtain up-sampled coordinates . Note that, and are sent to the next up-sampling block via skip connection.
| Methods | Table | Chair | Air plane | Car | Sofa | Bird house | Bag | Remote | Key board | Rocket | CD-S | CD-M | CD-H | CD-Avg |
| FoldingNet | 2.53 | 2.81 | 1.43 | 1.98 | 2.48 | 4.71 | 2.79 | 1.44 | 1.24 | 1.48 | 2.67 | 2.66 | 4.05 | 3.12 |
| PCN | 2.13 | 2.29 | 1.02 | 1.85 | 2.06 | 4.50 | 2.86 | 1.33 | 0.89 | 1.32 | 1.94 | 1.96 | 4.08 | 2.66 |
| TopNet | 2.21 | 2.53 | 1.14 | 2.28 | 2.36 | 4.83 | 2.93 | 1.49 | 0.95 | 1.32 | 2.26 | 2.16 | 4.30 | 2.91 |
| PFNet | 3.95 | 4.24 | 1.81 | 2.53 | 3.34 | 6.21 | 4.96 | 2.91 | 1.29 | 2.36 | 3.83 | 3.87 | 7.97 | 5.22 |
| GRNet | 1.63 | 1.88 | 1.02 | 1.64 | 1.72 | 2.97 | 2.06 | 1.09 | 0.89 | 1.03 | 1.35 | 1.71 | 2.85 | 1.97 |
| PoinTr | 0.81 | 0.95 | 0.44 | 0.91 | 0.79 | 1.86 | 0.93 | 0.53 | 0.38 | 0.57 | 0.58 | 0.88 | 1.79 | 1.09 |
| SeedFormer | 0.72 | 0.81 | 0.40 | 0.89 | 0.71 | 1.51 | 0.79 | 0.46 | 0.36 | 0.50 | 0.50 | 0.77 | 1.49 | 0.92 |
| Ours | 0.66 | 0.74 | 0.37 | 0.85 | 0.66 | 1.36 | 0.73 | 0.43 | 0.35 | 0.50 | 0.48 | 0.71 | 1.37 | 0.85 |
Loss Function
We use Chamfer Distance (CD) (Fan, Su, and Guibas 2017) of the L1-norm as the primary component of our loss function. We supervise all predicted point sets with ground truth , and the loss function can be written as:
| (4) |
Here, we use FPS algorithm (Qi et al. 2017b) to down-sample to the same density (i.e., ) as with .
Experiments
In this section, we first conduct extensive experiments to demonstrate the effectiveness of our model on three widely used benchmark datasets including PCN (Yuan et al. 2018), ShapeNet-55/34 (Yu et al. 2021) and MVP (Pan et al. 2021b). Then, we conduct the ablation studies on PCN dataset to analyze different designs of our model.
Training Setup
We implement CRA-PCN with Pytorch (Paszke et al. 2019). All models are trained on two NVIDIA Tesla V100 graphic cards with a batch size of 72. We use Adam optimizer (Kingma and Ba 2014) with and . We set the feature dim in the decoder to 128. The initial learning rate is set to 0.001 with continuous decay of 0.1 for every 100 epochs. We train our model for 300 epochs on PCN dataset (Yuan et al. 2018) and ShapeNet-55/34 (Yu et al. 2021) while 50 epochs on MVP dataset (Pan et al. 2021b).
Evaluation on PCN Dataset
Dataset and metric.
The PCN dataset (Yuan et al. 2018) is the subset of ShapeNet dataset (Chang et al. 2015) and it consists of 30,974 shapes from 8 categories. Each ground truth point cloud is generated by evenly sampling 16,384 points on the mesh surface. The partial inputs of 2,048 points are generated by back-projecting 2.5D depth images into 3D. For a fair comparison, we follow the standard evaluation metric in (Yuan et al. 2018), and all results on PCN dataset are evaluated in terms of L1 Chamfer Distance (CD-1).
Quantitative results.
In Tab. 1, we report the quantitative results of our CRA-PCN and other methods on PCN dataset. We see that CRA-PCN achieves the best performance over all previous methods in all categories. Compared to the second-ranked AnchorFormer, our method reduces the average CD-1 by , which is lower than AnchorFormer. While several previous methods (Xiang et al. 2021; Zhou et al. 2022; Yan et al. 2022) in Tab. 1 also use a similar coarse-to-fine architecture, CRA-PCN outperforms them by a large margin with the help of several novel designs.
Qualitative results.
In Fig. 4, we visually compare CRA-PCN with previous state-of-the-art methods in four selected categories (Plane, Table, Lamp, and Chair). The visual results show that CRA-PCN can predict smoother surfaces and produce less noise. Specifically, in Table category in the second row, the visible seat predicted by CRA-PCN has smooth details, while other methods generate many noise points. As for Lamp category in the third row, all other methods fail to reconstruct the missing spherical surface.
| 34 seen catagories | 21 unseen categories | |||||||
| Methods | CD-S | CD-M | CD-H | CD-Avg | CD-S | CD-M | CD-H | CD-Avg |
| FoldingNet (Yang et al. 2018) | 1.86 | 1.81 | 3.38 | 2.35 | 2.76 | 2.74 | 5.36 | 3.62 |
| PCN (Yuan et al. 2018) | 1.87 | 1.81 | 2.97 | 2.22 | 3.17 | 3.08 | 5.29 | 3.85 |
| TopNet (Tchapmi et al. 2019) | 1.77 | 1.61 | 3.54 | 2.31 | 2.62 | 2.43 | 5.44 | 3.50 |
| PFNet (Huang et al. 2020) | 3.16 | 3.19 | 7.71 | 4.68 | 5.29 | 5.87 | 13.33 | 8.16 |
| GRNet (Xie et al. 2020) | 1.26 | 1.39 | 2.57 | 1.74 | 1.85 | 2.25 | 4.87 | 2.99 |
| PoinTr (Yu et al. 2021) | 0.76 | 1.05 | 1.88 | 1.23 | 1.04 | 1.67 | 3.44 | 2.05 |
| SeedFormer (Zhou et al. 2022) | 0.48 | 0.70 | 1.30 | 0.83 | 0.61 | 1.07 | 2.35 | 1.34 |
| Ours | 0.45 | 0.65 | 1.18 | 0.76 | 0.55 | 0.97 | 2.19 | 1.24 |
Evaluation on ShapeNet-55/34
Dataset and metric.
To further evaluate the generalization ability of our model, we conduct experiments on ShapeNet-55 and ShapeNet-34 (Yu et al. 2021). Like PCN dataset, ShapeNet-55 and ShapeNet-34 are derived from ShapeNet, but contain all the objects in ShapeNet from 55 categories. Specifically, ShapeNet-55 contains 41,952 models for training and 10,518 models for testing, while the training set of ShapeNet-34 contains 46,765 objects from 34 categories and its testing set consists of 3,400 objects from 34 seen categories and 2,305 objects from the remaining 21 novel categories. Using the training and evaluation protocol proposed in (Yu et al. 2021), partial inputs are generated online. Specifically, partial point clouds are generated by selecting certain viewpoints and removing percentage farthest points of complete shapes, where viewpoints are randomly selected during training and fixed during evaluation. During the evaluation, is set to 25%, 50%, and 75%, respectively, corresponding to three difficulty degrees, namely simple, moderate and hard. Following (Yu et al. 2021), we evaluate the performance of the methods (Yang et al. 2018; Yuan et al. 2018; Tchapmi et al. 2019; Huang et al. 2020; Xie et al. 2020; Yu et al. 2021; Zhou et al. 2022) in terms of CD-2 under the above three difficulties, and we also report the average CD.
| Methods | CD-2 | F-Score% |
| PCN (Yuan et al. 2018) | 9.77 | 0.320 |
| TopNet (Tchapmi et al. 2019) | 10.11 | 0.308 |
| MSN (Liu et al. 2020) | 7.90 | 0.432 |
| CDN (Wang, Ang Jr, and Lee 2020) | 7.25 | 0.434 |
| ECG (Pan 2020) | 6.64 | 0.476 |
| VRCNet (Pan et al. 2021a) | 5.96 | 0.499 |
| Ours | 5.33 | 0.529 |
Results on ShapeNet-55.
The last four columns of Tab. 2 show the superior performance of CRA-PCN under various situations with diverse viewpoints and diverse incomplete patterns. Besides, we sample 10 categories and report CD-2 of them. Categories in the columns from 2 to 6 contain sufficient samples, while the quantities of the following five categories are insufficient. According to the results, we can clearly see the powerful generalization ability of our model.
Results on ShapeNet-34.
As shown in Tab. 3, our method achieves the best CD-2 in the 34 seen categories of ShapeNet-34. Moreover, as for the 21 unseen categories that do not appear in training phase, our method outperforms other competitors. Especially, we achieve improvement compared with the second-ranked SeedFormer under hard setting in 21 unseen categories, which justifies the effectiveness of our method.
| Methods | Latency | Memory | CD |
| FBNet | 0.905 s | 3421 MB | 6.94 |
| SeedFormer | 0.297 s | 10701 MB | 6.74 |
| AnchorFormer | 0.608 s | 3735 MB | 6.59 |
| Ours | 0.469 s | 4459 MB | 6.39 |
| Variations | Inter-level | Intra-level | CD-1 |
| A | 7.85 | ||
| B | ✓ | 6.92 | |
| C | ✓ | 6.80 | |
| D | 6.74 | ||
| E | 6.61 | ||
| F | second | first | 6.54 |
| G | ✓ | ✓ | 6.39 |
| Variations | inter-level | intra-level | CD-1 |
| A | 6.75 | ||
| B | 6.50 | ||
| C | 6.51 | ||
| D | 6.39 |
Evaluation on MVP Dataset
Dataset and metric.
The MVP dataset (Pan et al. 2021b) is a multi-view partial point cloud dataset which consists of 16 categories of high-quality partial/complete point clouds. For each complete shape, 26 partial point clouds are generated by selecting 26 camera poses which are uniformly distributed on a unit sphere. MVP dataset provides various resolutions of ground truth, and we choose 2,048 among them. In training phase, we follow the way of data splitting in (Pan et al. 2021a). In evaluation phase, we evaluate performances in terms of CD-2 and F-Score (Tatarchenko et al. 2019).
Results.
Accuracy-Complexity Trade-Offs
We report the run-time memory usage and latency in Tab. 5. All methods were evaluated on a single Nvidia GeForce GTX 1080Ti graphic card with a batch size of 32. For fair comparisons, we disable gradient calculation and use point clouds with a resolution of 2,048. From the results, we see CRA-PCN can achieve better trade-offs than prior methods.
Ablation Studies
Here, we present ablation studies demonstrating the effectiveness of several proposed operations. All experiments are conducted under unified settings on the PCN dataset.
Analysis of Cross-Resolution Transformers.
Tab. 6 summarizes the evaluation results of inter- and intra-level Cross-Resolution Transformers, where model G is our CRA-PCN. We remove both inter- and intra-level CRT (model A), and we find the performance drops a lot, which justifies the effectiveness of cross-resolution aggregation. Then we remove inter-level CRT (model B) or intra-level CRT (model C), respectively. To keep the number of parameters the same with CRA-PCN, we double the number of intra-level CRT (model D) or inter-level CRT (model E). However, the aforementioned four variations exhibit poor performances compared to model G, and the results highlight the importance of the combination of intra- and inter-level cross-resolution aggregation. Moreover, we switch the order of inter- and intra-level CRT (model F), and we can find the performance drops a little. The empirical results here justify the effectiveness of Cross-Resolution Transformer and the combination of inter- and intra-level CRA.
Analysis of recursive/multi-scale designs.
To justify the advantages of our recursive designs on multiple scales for point cloud completion, we conduct ablation study and report the results in Tab. 7. Model D is our CRA-PCN, and we set the number of scales to 3. Note that, if we set to 1, Cross-Resolution Transformer will degrade to point transformer (Zhao et al. 2021) which can only achieve single-scale cross-resolution aggregation. We replace all multi-scale CRTs with single-scale ones (model A) by setting both to 1, and we can clearly find the performance drops a lot. We separately set of inter-level CRT and intra-level CRT to 1 (model B and C), they increase CD-1 by and , respectively. The results of these three variations confirm the effectiveness of our recursive and multi-scale designs.
Conclusion
In this paper, focusing on explicit cross-resolution aggregation, we present Cross-Resolution Transformer that efficiently performs cross-resolution and multi-scale feature aggregation. Moreover, we propose a combination of intra- and inter-level cross-resolution aggregation with the unified designs of Cross-Resolution Transformer. Based on the aforementioned techniques, we propose a novel deep network for point cloud completion, named CRA-PCN, which adopts an encoder-decoder architecture. Extensive experiments demonstrate the superiority of our method. It will be an interesting future direction to extend our work to similar tasks such as point cloud reconstruction and up-sampling.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (Grant No. 62372223).
References
- Cadena et al. (2016) Cadena, C.; Carlone, L.; Carrillo, H.; Latif, Y.; Scaramuzza, D.; Neira, J.; Reid, I.; and Leonard, J. J. 2016. Past, present, and future of simultaneous localization and mapping: Toward the robust-perception age. IEEE Transactions on robotics, 32(6): 1309–1332.
- Chang et al. (2015) Chang, A. X.; Funkhouser, T.; Guibas, L.; Hanrahan, P.; Huang, Q.; Li, Z.; Savarese, S.; Savva, M.; Song, S.; Su, H.; et al. 2015. Shapenet: An information-rich 3d model repository. arXiv preprint arXiv:1512.03012.
- Chen et al. (2017) Chen, X.; Ma, H.; Wan, J.; Li, B.; and Xia, T. 2017. Multi-view 3d object detection network for autonomous driving. In Proceedings of the IEEE conference on Computer Vision and Pattern Recognition, 1907–1915.
- Chen et al. (2023) Chen, Z.; Long, F.; Qiu, Z.; Yao, T.; Zhou, W.; Luo, J.; and Mei, T. 2023. AnchorFormer: Point Cloud Completion From Discriminative Nodes. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 13581–13590.
- Choy, Gwak, and Savarese (2019) Choy, C.; Gwak, J.; and Savarese, S. 2019. 4d spatio-temporal convnets: Minkowski convolutional neural networks. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 3075–3084.
- Choy et al. (2016) Choy, C. B.; Xu, D.; Gwak, J.; Chen, K.; and Savarese, S. 2016. 3d-r2n2: A unified approach for single and multi-view 3d object reconstruction. In Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, October 11-14, 2016, Proceedings, Part VIII 14, 628–644. Springer.
- Fan, Su, and Guibas (2017) Fan, H.; Su, H.; and Guibas, L. J. 2017. A point set generation network for 3d object reconstruction from a single image. In Proceedings of the IEEE conference on computer vision and pattern recognition, 605–613.
- Girdhar et al. (2016) Girdhar, R.; Fouhey, D. F.; Rodriguez, M.; and Gupta, A. 2016. Learning a predictable and generative vector representation for objects. In Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, October 11-14, 2016, Proceedings, Part VI 14, 484–499. Springer.
- Guo et al. (2021) Guo, M.-H.; Cai, J.-X.; Liu, Z.-N.; Mu, T.-J.; Martin, R. R.; and Hu, S.-M. 2021. Pct: Point cloud transformer. Computational Visual Media, 7: 187–199.
- Han et al. (2017) Han, X.; Li, Z.; Huang, H.; Kalogerakis, E.; and Yu, Y. 2017. High-resolution shape completion using deep neural networks for global structure and local geometry inference. In Proceedings of the IEEE international conference on computer vision, 85–93.
- He et al. (2023) He, Y.; Tang, D.; Zhang, Y.; Xue, X.; and Fu, Y. 2023. Grad-PU: Arbitrary-Scale Point Cloud Upsampling via Gradient Descent with Learned Distance Functions. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 5354–5363.
- Huang et al. (2020) Huang, Z.; Yu, Y.; Xu, J.; Ni, F.; and Le, X. 2020. Pf-net: Point fractal network for 3d point cloud completion. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 7662–7670.
- Kingma and Ba (2014) Kingma, D. P.; and Ba, J. 2014. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980.
- Lang et al. (2019) Lang, A. H.; Vora, S.; Caesar, H.; Zhou, L.; Yang, J.; and Beijbom, O. 2019. Pointpillars: Fast encoders for object detection from point clouds. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 12697–12705.
- Li, Zhang, and Xia (2016) Li, B.; Zhang, T.; and Xia, T. 2016. Vehicle detection from 3d lidar using fully convolutional network. arXiv preprint arXiv:1608.07916.
- Li et al. (2023) Li, S.; Gao, P.; Tan, X.; and Wei, M. 2023. ProxyFormer: Proxy Alignment Assisted Point Cloud Completion with Missing Part Sensitive Transformer. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 9466–9475.
- Liu et al. (2020) Liu, M.; Sheng, L.; Yang, S.; Shao, J.; and Hu, S.-M. 2020. Morphing and sampling network for dense point cloud completion. In Proceedings of the AAAI conference on artificial intelligence, volume 34, 11596–11603.
- Maturana and Scherer (2015) Maturana, D.; and Scherer, S. 2015. Voxnet: A 3d convolutional neural network for real-time object recognition. In 2015 IEEE/RSJ international conference on intelligent robots and systems (IROS), 922–928. IEEE.
- Pan (2020) Pan, L. 2020. ECG: Edge-aware point cloud completion with graph convolution. IEEE Robotics and Automation Letters, 5(3): 4392–4398.
- Pan et al. (2021a) Pan, L.; Chen, X.; Cai, Z.; Zhang, J.; Zhao, H.; Yi, S.; and Liu, Z. 2021a. Variational relational point completion network. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 8524–8533.
- Pan et al. (2021b) Pan, L.; Wu, T.; Cai, Z.; Liu, Z.; Yu, X.; Rao, Y.; Lu, J.; Zhou, J.; Xu, M.; Luo, X.; et al. 2021b. Multi-view partial (mvp) point cloud challenge 2021 on completion and registration: Methods and results. arXiv preprint arXiv:2112.12053.
- Park et al. (2022) Park, C.; Jeong, Y.; Cho, M.; and Park, J. 2022. Fast point transformer. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 16949–16958.
- Paszke et al. (2019) Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. 2019. Pytorch: An imperative style, high-performance deep learning library. Advances in neural information processing systems, 32.
- Qi et al. (2017a) Qi, C. R.; Su, H.; Mo, K.; and Guibas, L. J. 2017a. Pointnet: Deep learning on point sets for 3d classification and segmentation. In Proceedings of the IEEE conference on computer vision and pattern recognition, 652–660.
- Qi et al. (2017b) Qi, C. R.; Yi, L.; Su, H.; and Guibas, L. J. 2017b. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. Advances in neural information processing systems, 30.
- Qian et al. (2021) Qian, G.; Abualshour, A.; Li, G.; Thabet, A.; and Ghanem, B. 2021. Pu-gcn: Point cloud upsampling using graph convolutional networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 11683–11692.
- Reddy, Vo, and Narasimhan (2018) Reddy, N. D.; Vo, M.; and Narasimhan, S. G. 2018. Carfusion: Combining point tracking and part detection for dynamic 3d reconstruction of vehicles. In Proceedings of the IEEE conference on computer vision and pattern recognition, 1906–1915.
- Riegler, Osman Ulusoy, and Geiger (2017) Riegler, G.; Osman Ulusoy, A.; and Geiger, A. 2017. Octnet: Learning deep 3d representations at high resolutions. In Proceedings of the IEEE conference on computer vision and pattern recognition, 3577–3586.
- Rusu et al. (2008) Rusu, R. B.; Marton, Z. C.; Blodow, N.; Dolha, M.; and Beetz, M. 2008. Towards 3D point cloud based object maps for household environments. Robotics and Autonomous Systems, 56(11): 927–941.
- Simonovsky and Komodakis (2017) Simonovsky, M.; and Komodakis, N. 2017. Dynamic edge-conditioned filters in convolutional neural networks on graphs. In Proceedings of the IEEE conference on computer vision and pattern recognition, 3693–3702.
- Song et al. (2017) Song, S.; Yu, F.; Zeng, A.; Chang, A. X.; Savva, M.; and Funkhouser, T. 2017. Semantic scene completion from a single depth image. In Proceedings of the IEEE conference on computer vision and pattern recognition, 1746–1754.
- Tang et al. (2022) Tang, J.; Gong, Z.; Yi, R.; Xie, Y.; and Ma, L. 2022. LAKe-Net: topology-aware point cloud completion by localizing aligned keypoints. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 1726–1735.
- Tatarchenko et al. (2019) Tatarchenko, M.; Richter, S. R.; Ranftl, R.; Li, Z.; Koltun, V.; and Brox, T. 2019. What do single-view 3d reconstruction networks learn? In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 3405–3414.
- Tchapmi et al. (2019) Tchapmi, L. P.; Kosaraju, V.; Rezatofighi, H.; Reid, I.; and Savarese, S. 2019. Topnet: Structural point cloud decoder. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 383–392.
- Thomas et al. (2019) Thomas, H.; Qi, C. R.; Deschaud, J.-E.; Marcotegui, B.; Goulette, F.; and Guibas, L. J. 2019. Kpconv: Flexible and deformable convolution for point clouds. In Proceedings of the IEEE/CVF international conference on computer vision, 6411–6420.
- Vaswani et al. (2017) Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A. N.; Kaiser, Ł.; and Polosukhin, I. 2017. Attention is all you need. Advances in neural information processing systems, 30.
- Wang, Ang Jr, and Lee (2020) Wang, X.; Ang Jr, M. H.; and Lee, G. H. 2020. Cascaded refinement network for point cloud completion. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 790–799.
- Wang et al. (2019) Wang, Y.; Sun, Y.; Liu, Z.; Sarma, S. E.; Bronstein, M. M.; and Solomon, J. M. 2019. Dynamic graph cnn for learning on point clouds. Acm Transactions On Graphics (tog), 38(5): 1–12.
- Wang et al. (2022) Wang, Y.; Tan, D. J.; Navab, N.; and Tombari, F. 2022. Learning local displacements for point cloud completion. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 1568–1577.
- Wen et al. (2020) Wen, X.; Li, T.; Han, Z.; and Liu, Y.-S. 2020. Point cloud completion by skip-attention network with hierarchical folding. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 1939–1948.
- Wen et al. (2021) Wen, X.; Xiang, P.; Han, Z.; Cao, Y.-P.; Wan, P.; Zheng, W.; and Liu, Y.-S. 2021. Pmp-net: Point cloud completion by learning multi-step point moving paths. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 7443–7452.
- Wu, Qi, and Fuxin (2019) Wu, W.; Qi, Z.; and Fuxin, L. 2019. Pointconv: Deep convolutional networks on 3d point clouds. In Proceedings of the IEEE/CVF Conference on computer vision and pattern recognition, 9621–9630.
- Xiang et al. (2021) Xiang, P.; Wen, X.; Liu, Y.-S.; Cao, Y.-P.; Wan, P.; Zheng, W.; and Han, Z. 2021. Snowflakenet: Point cloud completion by snowflake point deconvolution with skip-transformer. In Proceedings of the IEEE/CVF international conference on computer vision, 5499–5509.
- Xie et al. (2020) Xie, H.; Yao, H.; Zhou, S.; Mao, J.; Zhang, S.; and Sun, W. 2020. Grnet: Gridding residual network for dense point cloud completion. In Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, August 23–28, 2020, Proceedings, Part IX, 365–381. Springer.
- Xu et al. (2018) Xu, Y.; Fan, T.; Xu, M.; Zeng, L.; and Qiao, Y. 2018. Spidercnn: Deep learning on point sets with parameterized convolutional filters. In Proceedings of the European conference on computer vision (ECCV), 87–102.
- Yan et al. (2022) Yan, X.; Yan, H.; Wang, J.; Du, H.; Wu, Z.; Xie, D.; Pu, S.; and Lu, L. 2022. Fbnet: Feedback network for point cloud completion. In Computer Vision–ECCV 2022: 17th European Conference, Tel Aviv, Israel, October 23–27, 2022, Proceedings, Part II, 676–693. Springer.
- Yang et al. (2018) Yang, Y.; Feng, C.; Shen, Y.; and Tian, D. 2018. Foldingnet: Point cloud auto-encoder via deep grid deformation. In Proceedings of the IEEE conference on computer vision and pattern recognition, 206–215.
- Yifan et al. (2019) Yifan, W.; Wu, S.; Huang, H.; Cohen-Or, D.; and Sorkine-Hornung, O. 2019. Patch-based progressive 3d point set upsampling. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 5958–5967.
- Yu et al. (2021) Yu, X.; Rao, Y.; Wang, Z.; Liu, Z.; Lu, J.; and Zhou, J. 2021. Pointr: Diverse point cloud completion with geometry-aware transformers. In Proceedings of the IEEE/CVF international conference on computer vision, 12498–12507.
- Yuan et al. (2018) Yuan, W.; Khot, T.; Held, D.; Mertz, C.; and Hebert, M. 2018. Pcn: Point completion network. In 2018 international conference on 3D vision (3DV), 728–737. IEEE.
- Zhao et al. (2019) Zhao, H.; Jiang, L.; Fu, C.-W.; and Jia, J. 2019. Pointweb: Enhancing local neighborhood features for point cloud processing. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 5565–5573.
- Zhao et al. (2021) Zhao, H.; Jiang, L.; Jia, J.; Torr, P. H.; and Koltun, V. 2021. Point transformer. In Proceedings of the IEEE/CVF international conference on computer vision, 16259–16268.
- Zhou et al. (2022) Zhou, H.; Cao, Y.; Chu, W.; Zhu, J.; Lu, T.; Tai, Y.; and Wang, C. 2022. Seedformer: Patch seeds based point cloud completion with upsample transformer. In Computer Vision–ECCV 2022: 17th European Conference, Tel Aviv, Israel, October 23–27, 2022, Proceedings, Part III, 416–432. Springer.