CP Violation in Rare Lepton-Number-Violating $W$ Decays at the LHC

It is useful to make some preliminary remarks. For the decay $W^{-}\to F$, where $F$ is the final state, the signal of CP violation will be a nonzero value of

$$A_{\rm CP}=\frac{BR(W^{-}\to F)-BR(W^{+}\to{\bar{F}})}{BR(W^{-}\to F)+BR(W^{+}\to{\bar{F}})}~{}.$$

(3)

Suppose this decay has two contributing amplitudes, $A$ and $B$. The total amplitude is then

$\displaystyle A_{\rm tot}=A+B=|A|e^{i\phi_{A}}e^{i\delta_{A}}+|B|e^{i\phi_{B}}e^{i\delta_{B}}~{},$

(4)

where $\phi_{A,B}$ and $\delta_{A,B}$ are CP-odd and CP-even phases, respectively. With this,

$$A_{\rm CP}=\frac{2|A||B|\sin(\phi_{A}-\phi_{B})\sin(\delta_{A}-\delta_{B})}{|A|^{2}+|B|^{2}+2|A||B|\cos(\phi_{A}-\phi_{B})\cos(\delta_{A}-\delta_{B})}~{}.$$

(5)

The point is that, in order to produce a nonzero $A_{\rm CP}$, the two interfering amplitudes must have different CP-odd and CP-even phases. In $W^{-}\to\ell_{1}^{-}\ell_{2}^{-}(q^{\prime}{\bar{q}})^{+}$, the two amplitudes are $W^{-}\to\ell_{1}^{-}{\bar{N}}_{1,2}$, with ${\bar{N}}_{1,2}$ each subsequently decaying to $\ell_{2}^{-}(q^{\prime}{\bar{q}})^{+}$. The two CP-odd phases are $\arg[B_{\ell_{1}N_{1}}B_{\ell_{2}N_{1}}]$ and $\arg[B_{\ell_{1}N_{2}}B_{\ell_{2}N_{2}}]$, which can clearly be different.

For the CP-even phases, things are a bit more complicated. The usual way such phases are generated is via gluon exchange (which is why they are often referred to as “strong phases”). However, since this decay involves the $W^{\pm}$, $\ell_{i}^{\pm}$ and $N_{i}$, which are all colourless, this is not possible. Instead, the CP-even phases can be generated in one of two ways. First, the propagator for the $N_{i}$ is proportional to

	$\displaystyle\frac{1}{(p_{N}^{2}-M_{N_{i}}^{2})+iM_{N_{i}}\Gamma_{N_{i}}}$	$\displaystyle=$	$\displaystyle\frac{1}{\sqrt{(p_{N}^{2}-M_{N_{i}}^{2})^{2}+M_{N_{i}}^{2}\Gamma_{N_{i}}^{2}}}\,e^{i\eta_{i}}~{},$
	$\displaystyle{\rm with}~{}~{}~{}~{}~{}\tan\eta_{i}$	$\displaystyle=$	$\displaystyle\frac{-M_{N_{i}}\Gamma_{N_{i}}}{(p_{N}^{2}-M_{N_{i}}^{2})}~{}.$		(6)

Thus, $\eta_{i}$ is the CP-even phase associated with the propagator. Since $N_{1}$ and $N_{2}$ do not have the same mass – they are nearly, but not exactly, degenerate – if one of the $N_{i}$ is on shell ($p_{N}^{2}=M_{N_{i}}^{2}$), the other is not. This creates a nonzero CP-even phase difference: the on-shell $N_{i}$ has $\eta_{i}=-\pi/2$, while the CP-even phase of the other $N_{i}$ obeys $|\eta_{i}|<\pi/2$. This leads to what is known as resonant CP violation¹¹1Note that it is important that the $N_{i}$ be nearly degenerate. From Eq. (5) we see that $A_{\rm CP}$ is sizeable only when the two contributing amplitudes are of similar size ($|A|\sim|B|$). But if the masses of $N_{1}$ and $N_{2}$ were very different, the size of their contributions to the decay would also be very different, leading to a small $A_{\rm CP}$..

A second way of generating a CP-even phase difference is through oscillations of the heavy neutrinos. As we will see below, the time evolution of a heavy $N_{i}$ mass eigenstate involves $e^{-iE_{i}t}$ (in addition to the exponential decay factor). Since $N_{1}$ and $N_{2}$ do not have tne same mass, their energies are different, leading to different $e^{-iE_{i}t}$ factors. This is another type of CP-even phase difference, and can also lead to CP violation.

Below we derive the amplitudes for $W^{-}\to\ell_{1}^{-}{\bar{N}}_{i}$, with each ${\bar{N}}_{i}$ subsequently decaying to $\ell_{2}^{-}(q^{\prime}{\bar{q}})^{+}$, including both types of CP-even phases.

Consider the diagram of Fig. 1, with $N_{i}=N_{1}$. If this were the only contribution, its amplitude could be written simply as the product of two amplitudes, one for $W^{-}\to\ell_{1}^{-}{\bar{N}}_{i}$, the other for ${\bar{N}}_{1}\to\ell_{2}^{-}(q^{\prime}{\bar{q}})^{+}$. However, because there are contributions from $N_{1}$ and $N_{2}$, and because $N_{1}$ and $N_{2}$ cannot be on shell simultaneously, we must include the heavy neutrino propagator.

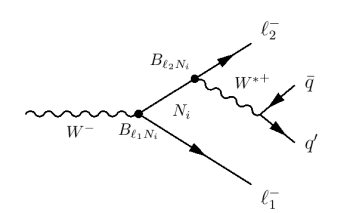
Furthermore, although the neutrino is produced as ${\bar{N}}_{i}$, it actually decays as $N_{i}$, leading to the fermion-number-violating and LNV process $W^{-}\to\ell_{1}^{-}\ell_{2}^{-}(q^{\prime}{\bar{q}})^{+}$. This implies that (i) conjugate fields will be involved in the amplitudes, and (ii) the amplitudes will be proportional to the neutrino mass.

We can now construct the amplitudes ${\cal M}_{i}^{--}\equiv{\cal M}(W^{-}\to\ell_{1}^{-}{\bar{N}}_{i},N_{i}\to\ell_{2}^{-}W^{*+}(\to(q^{\prime}{\bar{q}})^{+})$. Writing ${\cal M}_{i}^{--}={\cal M}_{i}^{\mu\nu}\epsilon_{\mu}j_{\nu}$, where $\epsilon_{\mu}$ is the polarization of the initial $W^{-}$ and $j_{\nu}=\frac{g}{\sqrt{2}}{\bar{q}}\gamma_{\nu}P_{L}q^{\prime}$ is the current of final-state particles to which $W^{*+}$ decays, we have

	$\displaystyle{\cal M}_{i}^{\mu\nu}$	$\displaystyle=$	$\displaystyle\bar{\ell}_{1}\gamma^{\mu}P_{L}\left(\frac{g}{\sqrt{2}}B_{\ell_{1}N_{i}}\right)N_{i}\times e^{-\Gamma_{i}t/2}e^{-iE_{i}t}\times\bar{\ell}_{2}\gamma^{\nu}P_{L}\left(\frac{g}{\sqrt{2}}B_{\ell_{2}N_{i}}\right)N_{i}$		(7)
		$\displaystyle=$	$\displaystyle\frac{g^{2}}{2}B_{\ell_{1}N_{i}}B_{\ell_{2}N_{i}}\,\bar{\ell}_{1}\gamma^{\mu}P_{L}N_{i}\,\overline{N_{i}^{c}}\gamma^{\nu}P_{R}\ell_{2}^{c}\times e^{-\Gamma_{i}t/2}e^{-iE_{i}t}$
		$\displaystyle\to$	$\displaystyle\frac{g^{2}}{2}B_{\ell_{1}N_{i}}B_{\ell_{2}N_{i}}\,\bar{\ell}_{1}\gamma^{\mu}P_{L}\frac{\raise 0.6458pt\hbox{$/$}\kern-5.70007ptp+M_{i}}{p_{N}^{2}-M^{2}_{i}+i\Gamma_{i}M_{i}}\,\gamma^{\nu}P_{R}\ell_{2}^{c}\times e^{-\Gamma_{i}t/2}e^{-iE_{i}t}$
		$\displaystyle=$	$\displaystyle\frac{\frac{g^{2}}{2}B_{\ell_{1}N_{i}}B_{\ell_{2}N_{i}}\,M_{i}\,e^{-\Gamma_{i}t/2}e^{-iE_{i}t}}{p_{N}^{2}-M^{2}_{i}+i\Gamma_{i}M_{i}}\,L^{\mu\nu}~{},$

where $L^{\mu\nu}=\bar{\ell}_{1}\gamma^{\mu}\gamma^{\nu}P_{R}\ell_{2}^{c}$. In the first line, the first term is the amplitude for $W^{-}\to\ell_{1}^{-}{\bar{N}}_{i}$, the second term is the time dependence of the $N_{i}$ state, and the third term is the amplitude for $N_{i}\to\ell_{2}^{-}W^{*+}$. The $e^{-iE_{i}t}$ factor is due to the quantum-mechanical evolution of the $N_{i}$ state; its energy $E_{i}$ is evaluated in the rest frame of the decaying $W$. In the second line, we have taken the transpose of the third term, writing the current in terms of conjugate fields, $\psi^{c}=C{\bar{\psi}}^{T}$. And in the third line, we have replaced $N_{i}\,\overline{N_{i}^{c}}$ by the neutrino propagator.

Another contribution to this process comes from a diagram like that of Fig. 1, but with $\ell_{1}\leftrightarrow\ell_{2}$. The amplitude for this diagram is the same as that above, but with (i) $p_{N}\to p^{\prime}_{N}$ and (ii) $\bar{\ell}_{1}\gamma^{\mu}\gamma^{\nu}P_{R}\ell_{2}^{c}\to\bar{\ell}_{2}\gamma^{\mu}\gamma^{\nu}P_{R}\ell_{1}^{c}=-\bar{\ell}_{1}\gamma^{\nu}\gamma^{\mu}P_{R}\ell_{2}^{c}$. Now, if $\ell_{1}\neq\ell_{2}$, one simply adds the diagrams, while if $\ell_{1}=\ell_{2}$, there is an additional minus sign. Thus, the amplitude for this second diagram is

$\displaystyle{\cal M}_{i}^{\prime\mu\nu}$

$\displaystyle=$

$\displaystyle\pm\frac{\frac{g^{2}}{2}B_{\ell_{1}N_{i}}B_{\ell_{2}N_{i}}\,M_{i}\,e^{-\Gamma_{i}t/2}e^{-iE_{i}t}}{{p^{\prime}_{N}}^{2}-M^{2}_{i}+i\Gamma_{i}M_{i}}\,L^{\mu\nu}~{},$

(8)

and the total amplitude is ${\cal M}_{i}^{\mu\nu}+{\cal M}_{i}^{\prime\mu\nu}$. Now, the dominant contributions to these amplitudes come from (almost) on-shell $N_{i}$s. This means that, while both diagrams lead to $W^{-}\to\ell_{1}^{-}\ell_{2}^{-}(q^{\prime}{\bar{q}})^{+}$, the final-state particles do not have the same momenta in the two cases. As a result, when the total amplitude is squared, ${\cal M}_{i}^{\mu\nu}$ and ${\cal M}_{i}^{\prime\mu\nu}$ will not interfere. Thus, we can consider only the ${\cal M}_{i}^{\mu\nu}$; the contribution from the ${\cal M}_{i}^{\prime\mu\nu}$ will be identical.

We can now compute ${\cal M}^{\mu\nu}={\cal M}_{1}^{\mu\nu}+{\cal M}_{2}^{\mu\nu}$. Writing

$$B_{\ell_{1}N_{1}}B_{\ell_{2}N_{1}}=B_{1}e^{i\phi_{1}}~{}~{},~{}~{}~{}~{}B_{\ell_{1}N_{2}}B_{\ell_{2}N_{2}}=B_{2}e^{i\phi_{2}}~{},$$

(9)

we have

$${\cal M}^{\mu\nu}=\frac{g^{2}}{2}\left(\frac{M_{1}B_{1}e^{i\phi_{1}}e^{-\Gamma_{1}t/2}e^{-iE_{1}t}}{p_{N}^{2}-M_{1}^{2}+i\Gamma_{1}M_{1}}+\frac{M_{2}B_{2}e^{i\phi_{2}}e^{-\Gamma_{2}t/2}e^{-iE_{2}t}}{p_{N}^{2}-M_{2}^{2}+i\Gamma_{2}M_{2}}\right)L^{\mu\nu}~{}.$$

(10)

The complete amplitude is ${\cal M}_{\rm tot}^{--}={\cal M}^{\mu\nu}\epsilon_{\mu}j_{\nu}=(g^{2}/2)\,{\cal A}_{--}(t)\,L^{\mu\nu}\,\epsilon_{\mu}j_{\nu}$, where ${\cal A}_{--}(t)$ is the piece in parentheses in Eq. (10). The next step is to compute $|{\cal M}_{\rm tot}^{--}|^{2}$.

From the point of view of studying CP violation in the decay $W^{-}\to\ell_{1}^{-}\ell_{2}^{-}(q^{\prime}{\bar{q}})^{+}$, the most important term in ${\cal M}_{\rm tot}^{--}$ is ${\cal A}_{--}(t)$. It is instructive to compare this quantity with Eq. (4) above. In the first term of ${\cal A}_{--}(t)$, we can identify the CP-odd phase ($\phi_{1}$) and the CP-even phase associated with neutrino oscillations ($-E_{1}t$). There is also a (different) CP-even phase $\eta_{i}$ associated with the propagator [see Eq. (6)]. The phases of the second term can be similarly identified.

Consider now $|{\cal A}_{--}(t)|^{2}$. We have

	$\displaystyle|{\cal A}_{--}(t)|^{2}$	$\displaystyle=$	$\displaystyle\frac{M_{1}^{2}B_{1}^{2}e^{-\Gamma_{1}t}}{(p_{N}^{2}-M_{1}^{2})^{2}+\Gamma_{1}^{2}M_{1}^{2}}+\frac{M_{2}^{2}B_{2}^{2}e^{-\Gamma_{2}t}}{(p_{N}^{2}-M_{2}^{2})^{2}+\Gamma_{2}^{2}M_{2}^{2}}$		(11)
			$\displaystyle\hskip 14.22636pt+~{}2{\rm Re}\left(\frac{M_{1}M_{2}B_{1}B_{2}\,e^{-i\delta\phi}\,e^{-\Gamma_{\rm avg}t}\,e^{-i\Delta Et}}{(p_{N}^{2}-M_{1}^{2}+i\Gamma_{1}M_{1})(p_{N}^{2}-M_{2}^{2}-i\Gamma_{2}M_{2})}\right)~{},$

where

$$\Gamma_{\rm avg}=\frac{1}{2}(\Gamma_{1}+\Gamma_{2})~{},~{}~{}\Delta E\equiv E_{1}-E_{2}=\frac{M_{1}^{2}-M_{2}^{2}}{2M_{W}}~{},~{}~{}\delta\phi\equiv\phi_{2}-\phi_{1}~{}.$$

(12)

There are two simplifications that can be made. First, in order to compute the rate for the decay, it will be necessary to integrate over the phase space of the final-state particles. Due to energy-momentum conservation, this will involve an integral over $p_{N}$. Since the $N_{i}$ can go on shell, we can use the narrow-width approximation to replace

$$\frac{1}{(p_{N}^{2}-M_{i}^{2})^{2}+\Gamma_{i}^{2}M_{i}^{2}}~{}~{}\to~{}~{}\frac{\pi}{\Gamma_{i}M_{i}}\,\delta(p_{N}^{2}-M_{i}^{2})~{}.$$

(13)

Second, although it is important to take neutrino oscillations into account in considerations of CP violation, we do not focus on actually measuring such oscillations. (This is examined in Refs. Antusch:2017ebe ; Cvetic:2018elt ; Cvetic:2019rms .) That is, we can integrate over time: $\int_{0}^{\infty}{dt}|{\cal A}_{--}(t)|^{2}=|{\cal A}_{--}|^{2}$. Note that, in integrating to $\infty$, we assume that the $N_{i}$ are heavy enough that their lifetimes are sufficiently small that most $N_{i}$s decay in the detector. We will quantify this in the next Section.

Now consider the interference term. Using the narrow-width approximation, the product of propagators can be written

	$\displaystyle\frac{1}{(p_{N}^{2}-M_{1}^{2}+i\Gamma_{1}M_{1})(p_{N}^{2}-M_{2}^{2}-i\Gamma_{2}M_{2})}=$
	$\displaystyle\hskip 85.35826pt\frac{\Gamma_{1}M_{1}\pi\delta(p_{N}^{2}-M_{2}^{2})}{(\Delta M^{2})^{2}+\Gamma_{1}^{2}M_{1}^{2}}+\frac{\Gamma_{2}M_{2}\pi\delta(p_{N}^{2}-M_{1}^{2})}{(\Delta M^{2})^{2}+\Gamma_{2}^{2}M_{2}^{2}}$
	$\displaystyle\hskip 85.35826pt-~{}\frac{i\Delta M^{2}\pi\delta(p_{N}^{2}-M_{2}^{2})}{(\Delta M^{2})^{2}+\Gamma_{1}^{2}M_{1}^{2}}-\frac{i\Delta M^{2}\pi\delta(p_{N}^{2}-M_{1}^{2})}{(\Delta M^{2})^{2}+\Gamma_{2}^{2}M_{2}^{2}}~{},$		(14)

where $\Delta M^{2}\equiv M_{1}^{2}-M_{2}^{2}$. Note that the imaginary part is proportional to $\Delta M^{2}=(M_{1}-M_{2})(M_{1}+M_{2})\equiv\Delta M(M_{1}+M_{2})$. Referring to Eq. (6), we see that the CP-even phase difference $\eta_{1}-\eta_{2}$ is proportional to $\Delta M$.

Putting all the pieces together, we obtain

	$\displaystyle|{\cal A}_{--}|^{2}$	$\displaystyle=$	$\displaystyle\frac{\pi M_{1}B_{1}^{2}}{\Gamma_{1}^{2}}\delta(p_{N}^{2}-M_{1}^{2})+\frac{\pi M_{2}B_{2}^{2}}{\Gamma_{2}^{2}}\delta(p_{N}^{2}-M_{2}^{2})$
			$\displaystyle\hskip-42.67912pt+~{}\frac{2M_{1}M_{2}B_{1}B_{2}}{\Gamma^{2}_{\rm avg}+(\Delta E)^{2}}\,\ \left(\frac{\Gamma_{1}M_{1}\pi\delta(p_{N}^{2}-M_{2}^{2})}{(\Delta M^{2})^{2}+\Gamma_{1}^{2}M_{1}^{2}}+\frac{\Gamma_{2}M_{2}\pi\delta(p_{N}^{2}-M_{1}^{2})}{(\Delta M^{2})^{2}+\Gamma_{2}^{2}M_{2}^{2}}\right)(\cos(\delta\phi)\Gamma_{\rm avg}-\Delta E\sin(\delta\phi))$
			$\displaystyle\hskip-42.67912pt+~{}\frac{2M_{1}M_{2}B_{1}B_{2}}{\Gamma^{2}_{\rm avg}+(\Delta E)^{2}}\,\ \left(\frac{\Delta M^{2}\pi\delta(p_{N}^{2}-M_{2}^{2})}{(\Delta M^{2})^{2}+\Gamma_{1}^{2}M_{1}^{2}}+\frac{\Delta M^{2}\pi\delta(p_{N}^{2}-M_{1}^{2})}{(\Delta M^{2})^{2}+\Gamma_{2}^{2}M_{2}^{2}}\right)(\cos(\delta\phi)\Delta E+\sin(\delta\phi)\Gamma_{\rm avg})~{}.$

The time-integrated square of the amplitude for $W^{-}\to\ell_{1}^{-}\ell_{2}^{-}(q^{\prime}{\bar{q}})^{+}$ is therefore $|{\cal M}_{--}|^{2}=(g^{2}/2)^{2}\,|{\cal A}_{--}|^{2}\,|L^{\mu\nu}\,\epsilon_{\mu}j_{\nu}|^{2}$. The CP asymmetry is defined as [see Eq. (3)]

$$A_{\rm CP}=\frac{\int{d\rho}\,(|{\cal M}_{--}|^{2}-|{\cal M}_{++}|^{2})}{\int{d\rho}\,(|{\cal M}_{--}|^{2}+|{\cal M}_{++}|^{2})}=\frac{\int{d\rho}\,(|{\cal A}_{--}|^{2}-|{\cal A}_{++}|^{2})|L^{\mu\nu}\,\epsilon_{\mu}j_{\nu}|^{2}}{\int{d\rho}\,(|{\cal A}_{--}|^{2}+|{\cal A}_{++}|^{2})|L^{\mu\nu}\,\epsilon_{\mu}j_{\nu}|^{2}}~{},$$

(16)

where $|{\cal A}_{++}|^{2}$ is obtained from $|{\cal A}_{--}|^{2}$ [Eq. (2.3)] by changing the sign of the CP-odd phase, and $\int d\rho$ indicates integration over the phase space.

For the phase-space integration, the only pieces that depend on the integration variables are the delta function $\delta(p_{N}^{2}-M_{i}^{2})$ in Eq. (2.3) and $|L^{\mu\nu}\,\epsilon_{\mu}j_{\nu}|^{2}$. The phase-space integrals are therefore

$${\cal I}(M_{i})=\int{d\rho}\,\pi\delta(p_{N}^{2}-M_{i}^{2})|L^{\mu\nu}\,\epsilon_{\mu}j_{\nu}|^{2}~{}.$$

(17)

In Ref. Dib:2014pga , it was shown that, since $M_{1}\simeq M_{2}$, ${\cal I}(M_{1})\simeq{\cal I}(M_{2})$. Thus, to a very good approximation, these terms cancel in Eq. (16), so that

$$A_{\rm CP}=\frac{|{\tilde{\cal A}}_{--}|^{2}-|{\tilde{\cal A}}_{++}|^{2}}{|{\tilde{\cal A}}_{--}|^{2}+|{\tilde{\cal A}}_{++}|^{2}}~{},$$

(18)

where ${\tilde{\cal A}}_{--}$ (${\tilde{\cal A}}_{++}$ ) is the same as ${\cal A}_{--}$ (${\cal A}_{++}$), but with the $\pi\delta(p_{N}^{2}-M_{i}^{2})$ factors removed.

In the numerator we have

	$\displaystyle|{\tilde{\cal A}}_{--}|^{2}-|{\tilde{\cal A}}_{++}|^{2}=$		(19)
	$\displaystyle\hskip 14.22636pt-~{}\frac{2M_{1}M_{2}B_{1}B_{2}}{\Gamma^{2}_{\rm avg}+(\Delta E)^{2}}\,\ \left(\frac{\Gamma_{1}M_{1}}{(\Delta M^{2})^{2}+\Gamma_{1}^{2}M_{1}^{2}}+\frac{\Gamma_{2}M_{2}}{(\Delta M^{2})^{2}+\Gamma_{2}^{2}M_{2}^{2}}\right)(2\Delta E\sin(\delta\phi))$
	$\displaystyle\hskip 14.22636pt+~{}\frac{2M_{1}M_{2}B_{1}B_{2}}{\Gamma^{2}_{\rm avg}+(\Delta E)^{2}}\,\ \left(\frac{\Delta M^{2}}{(\Delta M^{2})^{2}+\Gamma_{1}^{2}M_{1}^{2}}+\frac{\Delta M^{2}}{(\Delta M^{2})^{2}+\Gamma_{2}^{2}M_{2}^{2}}\right)(2\sin(\delta\phi)\Gamma_{\rm avg})~{}.$

In Eq. (5), we see that $A_{\rm CP}$ is proportional to $\sin(\phi_{A}-\phi_{B})\sin(\delta_{A}-\delta_{B})$, i.e., a nonzero $A_{\rm CP}$ requires that the two interfering amplitudes have different CP-odd and CP-even phases. This is also true in the present case. Above, both terms are proportional to $\sin(\delta\phi)$ ($\delta\phi$ is the CP-odd phase difference). In the first term, the CP-even phase arises due to neutrino oscillations: $\sin(\delta_{A}-\delta_{B})$ is proportional to $\Delta E$. And in the second term, the CP-even phase difference comes from the propagators [see Eq. (14)]: it is proportional to $\Delta M$. In the denominator,

	$\displaystyle|{\tilde{\cal A}}_{--}|^{2}+|{\tilde{\cal A}}_{++}|^{2}=\frac{2M_{1}B_{1}^{2}}{\Gamma_{1}^{2}}+\frac{2M_{2}B_{2}^{2}}{\Gamma_{2}^{2}}$		(20)
	$\displaystyle\hskip 14.22636pt+~{}\frac{2M_{1}M_{2}B_{1}B_{2}}{\Gamma^{2}_{\rm avg}+(\Delta E)^{2}}\,\ \left(\frac{\Gamma_{1}M_{1}}{(\Delta M^{2})^{2}+\Gamma_{1}^{2}M_{1}^{2}}+\frac{\Gamma_{2}M_{2}}{(\Delta M^{2})^{2}+\Gamma_{2}^{2}M_{2}^{2}}\right)(2\cos(\delta\phi)\Gamma_{\rm avg})$
	$\displaystyle\hskip 14.22636pt-~{}\frac{2M_{1}M_{2}B_{1}B_{2}}{\Gamma^{2}_{\rm avg}+(\Delta E)^{2}}\,\ \left(\frac{\Delta M^{2}}{(\Delta M^{2})^{2}+\Gamma_{1}^{2}M_{1}^{2}}+\frac{\Delta M^{2}}{(\Delta M^{2})^{2}+\Gamma_{2}^{2}M_{2}^{2}}\right)(2\cos(\delta\phi)\Delta E)~{}.$

We now make the (reasonable) approximations that $\Gamma_{1}\simeq\Gamma_{2}\equiv\Gamma$ and $M_{1}\simeq M_{2}\equiv M_{N}$ (but $\Delta M\neq 0$ and is $\ll M_{N}$). With the assumption that $B_{1}=B_{2}$, $A_{\rm CP}$ takes a simple form:

$$A_{\rm CP}=\frac{2(2y-x)\sin\delta\phi}{(1+x^{2})(1+4y^{2})+2(1-2xy)\cos\delta\phi}~{},$$

(21)

where

$$x\equiv\frac{\Delta E}{\Gamma}~{}~{},~{}~{}~{}~{}y\equiv\frac{\Delta M}{\Gamma}~{}.$$

(22)

Once again comparing to Eq. (5), we see that $x$ and $y$ each play the role of the CP-even phase-difference term $\sin(\delta_{A}-\delta_{B})$. Now, $x$ and $y$ reflect CP-even phases arising from neutrino oscillations and the neutrino propagator, respectively. However, they are not, in fact, independent. From Eq. (12), we have

$$\Delta E=\frac{M_{1}^{2}-M_{2}^{2}}{2M_{W}}=\frac{2\,\Delta M\,M_{N}}{2M_{W}}~{}~{}~{}~{}\Longrightarrow~{}~{}~{}~{}x=y\,\frac{M_{N}}{M_{W}}~{}.$$

(23)

Thus, $y$ is always present; $x$ is generally subdominant, except for large values of $M_{N}$.

Furthermore, we note that $x$ and $y$ have the same sign, and that $|x|<|y|$. Thus, $|2y-x|\leq|2y|$. That is, as $|x|$ increases, $A_{\rm CP}$ decreases. We therefore expect to see smaller CP-violating effects for larger values of $M_{N}$. The reason this occurs is as follows. Above, we said that $x$ and $y$ each play the role of $\sin(\delta_{A}-\delta_{B})$. However, in this system, their contributions have the opposite sign, hence the factor $2y-x$ in Eq. (21).

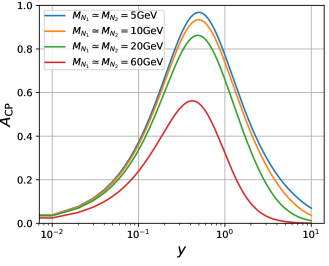
In order to get an estimate of the potential size of $A_{\rm CP}$, we set $\delta\phi=\pi/2$. In Fig. 2, we show $A_{\rm CP}$ as a function of $y$, for various values of $M_{N}$. We see that large values ($\geq 0.9$) of $|A_{\rm CP}|$ can be produced for light $M_{N}$. The maximal values of $|A_{\rm CP}|$ are found when $y\simeq\pm\frac{1}{2}$, with $|A_{\rm CP}|$ decreasing for larger values of $|y|$. As expected, the size of $|A_{\rm CP}|$ decreases as $M_{N}$ increases, with $|A_{\rm CP}|_{\rm max}<0.6$ for larger values of $M_{N}$.