Covers of surfaces
Abstract.
We study the homeomorphism types of certain covers of (always orientable) surfaces, usually of infinite-type. We show that every surface with non-abelian fundamental group is covered by every noncompact surface, we identify the universal abelian covers and the -homology covers of surfaces, and we show that non-locally finite characteristic covers of surfaces have four possible homeomorphism types.
1. Introduction
We are interested in the question of when a given surface covers another given surface, either in general or with constraints on the type of covering. Our first theorem is as follows.
Theorem 1.1 (Everything covers everything).
Suppose that is an orientable, borderless surface with non-abelian fundamental group. Then is covered by any noncompact borderless orientable surface.
A borderless surface is a topological -manifold with empty boundary. We stick with orientable surfaces for simplicity. The only orientable surfaces not covered by the theorem are the disk, the annulus, and the torus, each of which is only covered by itself and the former surface. A version of Theorem 1.1 also appears in [8] in which the author shows that any infinite-type surface covers any compact surface with negative euler characteristic. Moreover, they also allow for non-orientable surfaces.
If is any surface, there are certain natural covers coming from homology. The universal abelian cover of is the cover corresponding to the commutator subgroup of . We prove:
Theorem 1.2 (Universal abelian covers).
Let be an orientable, borderless surface, and let be its universal abelian cover. Then
-
(1)
if is , the annulus, or the torus then ,
-
(2)
if is the sphere, so is ,
-
(3)
if is the once-punctured torus, then is a flute surface,
-
(4)
if is a finite-type surface with one puncture and genus at least , then is the spotted Loch Ness monster surface,
-
(5)
otherwise, is the Loch Ness monster surface.
Note that the commutator subgroup of is the kernel of the map so the universal abelian cover could also be called the “-homology cover” of . We also consider the -homology cover corresponding to the kernel of the map
When has finite-type, the -homology cover is a finite cover, and one can figure out the topological type of via an Euler characteristic argument and by analyzing how boundary components lift. On the other hand, when has infinite-type, its -homology covers all have infinite degree, and it turns out their topology is quite constrained.
Theorem 1.3 (-homology covers).
Suppose that is an infinite-type orientable borderless surface, , and is the -homology cover. If has no isolated planar ends, then is homeomorphic to the Loch Ness monster surface. Otherwise, is homeomorphic to the spotted Loch Ness monster surface.
Suppose that a cover corresponds to the subgroup . We say that the cover is characteristic if is characteristic, i.e., if is invariant under every automorphism of . The and -homology covers above are all characteristic. Motivated by Theorems 1.2 and 1.3, we ask:
Question 1.4.
Are all infinite-degree characteristic covers of orientable borderless surfaces homeomorphic to either the disk, the flute surface, the Loch Ness monster surface, or the spotted Loch Ness monster surface?
Note that it is important to say ‘infinite degree’ above. Indeed, if has finite type it has many finite-degree characteristic covers , all of which also have finite type. (For these , in practice one can usually figure out the topological type of by analyzing how boundary components lift and using an Euler characteristic argument.) When has infinite type, the ‘infinite degree’ hypothesis just prohibits the cover from being trivial (which is obviously necessary), since , the free group on a countably infinite alphabet, does not have any proper finite-index characteristic subgroups.
Here is some evidence that the answer to Question 1.4 could be yes.
Theorem 1.5 (Characteristic covers of finite-type surfaces).
Suppose that is an orientable borderless surface of finite type and is an infinite-degree, geometrically characteristic cover. Then is homeomorphic to either a disc, the flute surface, the Loch Ness monster surface, or the spotted Loch Ness monster surface.
Above, an automorphism of is called geometric if it is induced by a homeomorphism that preserves the basepoint . We call a subgroup geometrically characteristic if is invariant under all geometric automorphisms of . So, ‘geometrically characteristic’ is a weaker condition than ‘characteristic’. A cover is geometrically characteristic if it corresponds to a geometrically characterstic subgroup of .
It follows quickly from Theorem 1.5 that any non-universal characteristic cover of a closed surface is homeomorphic to the Loch Ness monster surface. This was proved earlier by Atarihuana–García–Hidalgo–Quispe–Maluendas [2, Prop 6.1], using the fact that is also a characteristic cover of a triangle orbifold. However, their argument does not extend to the finite-type setting.
Infinite-type surfaces can be exhausted by finite-type surfaces, and characteristic subgroups of the infinite-type surface group intersect the finite-type surface groups in characteristic subgroups (see §3.2 for details) which suggests that the theorem above can be promoted to apply to infinite-type . However, there is a problem: there are infinite-degree characteristic covers of infinite-type surfaces that restrict to finite-degree covers on all finite-type subsurfaces, and Theorem 1.5 does not apply to finite covers. To deal with this, we make the following definition.
Definition 1.6.
If is a group, a subgroup is locally finite index if intersects every finitely generated subgroup in a finite-index subgroup of . A cover is locally finite if it corresponds to a locally finite index subgroup of . Equivalently, is locally finite if for every compact subsurface , each component of is compact.
When has finite-type, a locally finite cover is just a finite cover. When has infinite-type, the -homology covers discussed above are locally finite, but not finite. Locally finite index subgroups have been studied previously in [3, 9], for instance, but we are not aware of any previous discussion of locally finite covering maps. We prove:
Theorem 1.7 (Characteristic covers that are not locally finite).
Suppose that is an orientable, infinite-type borderless surface and is a characteristic cover that is not locally finite. Then is homeomorphic to either a disc, the flute surface, the Loch Ness monster surface, or the spotted Loch Ness monster surface.
So, to answer Question 1.4, it only remains to understand locally finite characteristic covers of infinite-type surfaces. One can check that the -homology covers discussed above are the only such covers that are abelian, and we have answered Question 1.4 positively for those covers. An example of a non-abelian, locally finite, characteristic cover of a surface is the cover corresponding to the subgroup generated by all third powers of elements of . This cover is obviously characteristic, and it is locally finite because Burnside [6] proved that the group is finite for all . It is not clear to us what is in this case.
Our interest in Theorem 1.7 is partly inspired by work on big mapping class groups of surfaces. In particular, Aramayona–Leininger–McLeay [1, Proposition 3.3] show that the homology cover of the Loch Ness monster surface is the Loch Ness monster surface. They use this to show that the mapping class group of the once-punctured Loch Ness monster surface admits a continuous injective homomorphism that is not surjective. We note that there is a gap in the published version of their proof of the covering statement, but they were able to fix it quickly when we notified them about it. Alternatively, their Proposition 3.3 follows from Theorem 1.3, or even from Theorem 1.5 or [2, Proposition 6.1], since the Loch Ness monster surface is itself a characteristic cover of a genus two surface.
Surprisingly, to our knowledge there are not many previous results in which the homeomorphism types of infinite covers of surfaces are studied. In particular, we were surprised that a result like Theorem 1.1 does not currently exist in the literature. However, there are a few results out there that are related to ours. First, a classification of the possible homeomorphism types of infinite-degree regular covers of a closed surface is readily deduced from the fact that the cover and the deck group are quasi-isometric (for instance, see [4, Proposition 5.2]). Then there are older papers of Maskit [10] and Papakyriakopoulos [11] on identifying when certain covers of surfaces are planar; their motivation was some interesting applications to -manifolds, including a new proof of the Loop Theorem. There are the papers of Aramayona–Leininger–McLeay [1] and Atarihuana et al [2] referenced above, and there is also a forthcoming paper of Ghaswala–McLeay in which (among other things) the authors construct finite-degree covers from certain maps between potential end spaces of surfaces.
1.1. Ideas of the proofs
The proofs of our theorems above have distinct flavors. We will sketch each of them here for the convenience of the reader.
Theorem 1.1, in which we show that every noncompact surface covers every surface with non-abelian fundamental group, is very hands-on. Every surface with non-abelian fundamental group has an essential pair of pants and so is covered by an open pair of pants. The universal abelian cover of an open pair of pants is the Loch Ness monster surface, which is covered by the blooming Cantor tree surface, and every noncompact surface can be -injectively embedded in the blooming Cantor tree surface, and hence covers the blooming Cantor tree surface. (Here the embedding is as a component of the complement of a set of closed curves and bi-infinite arcs.) Composing, we get a covering map .
Theorem 1.2, in which we identify the universal abelian covers of surfaces , is proved as follows. When has finite-type, one can identify using the fact that the deck group is free abelian, along with the knowledge of whether the peripheral curves of lift or not. We deal with infinite-type by exhausting them with finite-type subsurfaces and saying that is exhausted by the universal abelian covers of the subsurfaces.
Theorem 1.3, in which we show that the -homology cover of any infinite-type surface is either the Loch Ness monster surface or its spotted version, uses the fact that the cover is abelian, together with the fact that it unwraps curves that appear basically everywhere in . Assuming for simplicity that has no cusps, we show that has one end as follows: take two points that are far away from some chosen basepoint, and a path between them. This may pass close to the basepoint of , but we can construct a new path between them that stays far from the basepoint, by using abelianness of the cover to form a path-quadrilateral in where are a pair of opposite sides. See also the beginning of §3.4.1 for a more detailed sketch of the most important part of the argument.
Theorem 1.5, in which we identify all infinite-degree characteristic covers of finite-type surfaces , has the most complicated proof. The argument is inspired by Proposition 3.3 in [1], which we discussed above.
Say for simplicity that is closed. We want to prove that has one end. Here, is quasiisometric to the deck group . If has more than one end, it admits an action on a tree with finite edge stabilizers and no global fixed point, by Stallings’s Theorem. We then construct a -equivariant map that is transverse to the union of edge midpoints, and let be the preimage of the set of edge midpoints, which is then a properly embedded -submanifold invariant under . Since edge stabilizers are finite, each component of is a simple closed curve. Using similar methods and an inductive argument, we can enlarge until every component of is one-ended.
If is the projection of , and is an essential curve in , then is ‘at most one ended’, meaning that all lifts of to are either compact or are bi-infinite arcs both of whose ends go out the same end of . Any at most one-ended projects to an element of that acts elliptically on . Since the cover is characteristic, any homeomorphism of lifts to a homeomorphism of , and hence the image of under any homeomorphism of also is at most one-ended, and therefore acts elliptically on . The point is then that this gives a lot of elements of that act elliptically, enough so that Serre’s criterion (see 2.5) implies that the action of on has a global fixed point, a contradiction.
There are some complications in extending this argument to the setting of noncompact finite-type surfaces. For instance, one needs a version of Stallings’s Theorem that works relative to the peripheral groups, in a certain sense. Luckily, there is indeed a relative version of Stallings’s theorem due to Swarup [16], but it is phrased in terms of group cohomology. In order to apply Swarup’s theorem in our context, we wrote an Appendix (see §A) translating between the group cohomological interpretation of ends and the version that is natural for our paper. We could not find a readable treatment of this in the existing literature, and we hope this can be a useful reference for others.
1.2. Outline of the Paper
In §2 we review the necessary background. We define the surfaces mentioned in the introduction, set conventions, and review actions on trees, ends, Stallings’s Theorem, and the classification of infinite-type surfaces. In §3 we study characteristic covers of surfaces, proving Theorems 1.5, 1.7, 1.2 and 1.3 in subsections 3.1, 3.2, 3.3 and 3.4, respectively. In §4 we prove Theorem 1.1, and then §A is our appendix on ends via group cohomology.
1.3. Acknowledgements
IB was partially supported by NSF CAREER award 1654114. TC was partially supported by MSCA grant 101107744–DefHyp. NGV was partially supported by NSF award 2212922 and PSC-CUNY awards 66435-00 54 and 67380-00 55. JT was partially supported by NSF award 2304920.
2. Background
2.1. Conventions
All surfaces within this work are assumed to be connected, second countable, orientable, and possibly with boundary. We say the surface is borderless if it has no boundary, and remind the reader that some of the surfaces which appear in our proofs may have non-empty boundary with possibly non-compact boundary components. All borderless surfaces, whether finite or infinite type, are classified by their genus and the topology of their space of ends, see Theorem 2.2. We let denote the finite-type surface with boundary components, genus, and punctures.
There are a handful of special infinite-type surfaces that occur in our main theorem statements:
-
(1)
The flute surface is homeomorphic to .
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/bd3c2ffc-5e97-447c-8a12-0042bb06270a/x1.png)
-
(2)
The Loch Ness monster surface is the unique borderless orientable infinite-type surface with one end.
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/bd3c2ffc-5e97-447c-8a12-0042bb06270a/x2.png)
-
(3)
The spotted Loch Ness monster surface is obtained from the Loch Ness monster surface by removing an infinite, discrete set of points.
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/bd3c2ffc-5e97-447c-8a12-0042bb06270a/x3.png)
-
(4)
The Cantor tree surface is homeomorphic to , where is an embedding of a Cantor set.
-
(5)
The blooming Cantor tree surface is the surface with infinitely many genus whose ends space, , and ends space accumulated by genus, , satisfy .
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/bd3c2ffc-5e97-447c-8a12-0042bb06270a/x4.png)
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/bd3c2ffc-5e97-447c-8a12-0042bb06270a/x5.png)
2.2. Ends of a topological space
Given a topological space , its space of ends is defined to be
where the inverse limit is taken over all compact subsets .
For a finitely generated group , consider its Cayley graph with respect to a finite generating set . We define the space of ends of by . The following proposition shows that is independent of the choice of a finite generating set of .
Proposition 2.1.
[5, Prop. 8.29] Given two proper geodesic metric spaces and , then any quasi-isometry induces a homeomorphism .
2.3. Classification of surfaces
Let be an orientable surface with genus and end space . Recall that is always compact, totally disconnected, and metrizable. We may take a neighborhood of an end to be an open subset of containing the end. An end is planar if it has a neighborhood that embeds into the plane, and accumulated by genus otherwise. Let be the closed subset consisting of all ends that are accumulated by genus. The following classification theorem was first proved by Kérekjarto, and the proof was later simplified by Richards, see [12].
Theorem 2.2.
Two borderless, orientable surfaces and are homeomorphic if and only if and there is a homeomorphism of pairs
Moreover, for every and for every compact, totally disconnected metrizable space , and closed subset , there is an orientable surface such that and is homeomorphic to .
Below, we’ll call the pair the genus-marked end space of .
2.4. Preliminaries on covers
By a cover of , we mean a space equipped with a surjective map so that every point has a neighborhood so that for each component of , the restriction is a homeomorphism. We will occasionally use the word “cover” just to refer to the covering surface . The Galois correspondence associates subgroups of with (equivalence classes of) connected covers of .
Remark 2.3.
Suppose is a surface with non-abelian , and is a nontrivial, infinite-index, normal subgroup. Then the cover corresponding to is an infinite-type surface.
We record a general proof that the cover of a surface corresponding to the fundamental group of an essential subsurface is homeomorphic to the interior of the subsurface. For us, a subsurface of a surface is always a properly embedded, closed submanifold of . Given a -injective subsurface of a surface and a point , we identify with its image under the monomorphism induced by the inclusion . When necessary, we will keep track of base points, otherwise we omit them and simply write and view it as a subgroup of .
Lemma 2.4.
Let be a –injective subsurface of a borderless surface . Then the cover of corresponding to is homeomorphic to the interior of .
Proof.
Let be the cover corresponding to and observe that the inclusion lifts to an embedding , which induces an isomorphism . Therefore, any loop in is a homotopic to one in the interior of . This implies that each boundary component of is separating—otherwise, there is an essential loop of which essentially intersects a component of . Further, each component of is topologically a product. This shows . ∎
2.5. Group actions on trees
Let be a simplicial tree, and let be a group acting on . By convention, we assume all such group actions are by simplicial isomorphisms and without edge inversions. Here, an edge inversion is a tree automorphism that leaves invariant some edge but reverses its orientation. An element acts elliptically on if fixes a vertex of , and hyperbolically otherwise, in which case it translates along a geodesic axis. We direct the reader to Serre’s book on Trees [13] for more information about group actions on trees.
2.5.1. Stallings’s Theorem and its relative version
Theorem 2.5 (Stallings’s Theorem, [15]).
Suppose is a finitely generated group with more than one end. Then admits an action on a simplicial tree with finite edge stablizers, no edge inversions, and no global fixed point.
We also need the following relative version of Stallings’s Theorem.
Theorem 2.6 (Relative Stallings’s Theorem).
Let be a finitely generated group and let be finitely generated subgroups of . Suppose there is a nonconstant, continuous function that is constant on the boundary of each right coset , where and . Then admits an action on a simplicial tree with finite edge stabilizers, no inversions, no global fixed point, and where for each , the action of on has a global fixed point.
This is really a result of Swarup [16], but Swarup’s result is stated in terms of group cohomology with group ring coefficients. In Appendix A, we give a gentle introduction to ends via group cohomology and show how the formulation above follows from Swarup’s result.
The intuition behind the relative version is as follows. Let be the smallest equivalence relation on such that
-
(1)
for every right coset , all points in are equivalent,
-
(2)
–equivalence classes are closed in .
Taking the quotient , we are continuously collapsing the ends of all these cosets. The hypothesis in Theorem 2.6 is that has more than one element, which intuitively means that has more than one end even up to collapsing cosets of the . So, there should be an action of on a tree , as in Stallings’s Theorem, in which the are not really used.
In this paper, we use Theorem 2.6 in the following rather explicit context. The group acting will be the deck group of a regular cover , where is a compact surface with boundary satifying . The subgroups will be stabilizers of noncompact boundary components of . Deleting these boundary components creates a new surface , in which the two ends of each such boundary component become a single end of . So, the end space is the same as the quotient discussed in the previous paragraph, and the hypothesis in Theorem 2.6 is that has more than one end. In the paper, we phrase all of this in a way that appeals directly to the statement of Theorem 2.6, though, rather than talking about the relation above.
In addition to Stalling’s Theorem and our formulation of its relative version, our main arguments in Section 3.1 uses Serre’s criterion to cook up a proof by contradiction to ensure the surface is one-ended.
Lemma 2.7 (Serre’s Criterion, see Corollary 2 in §6.5 of [13]).
Let be a group acting on a tree . If admits a generating set such that and act elliptically on for each distinct and , then the -action has a global fixed point.
3. Characteristic covers
In this section we study characteristic covers of surface, proving Theorems 1.5, 1.7, 1.2 and 1.3 in sections 3.1, 3.2, 3.3 and 3.4, respectively.
3.1. Finite-type surfaces
Here, we prove the following theorem from the introduction.
Theorem 1.5.
Any infinite-degree, geometrically characteristic cover of an orientable, borderless, finite-type surface is either a disc, the flute surface, the Loch Ness monster surface, or the spotted Loch Ness monster surface.
Throughout the section, we use the following notation: Given a surface , we let denote the surface obtained by removing every non-compact boundary component of . We’ll prove the following statement.
Proposition 3.1.
Let be a compact, orientable surface. If is a geometrically characteristic cover of infinite degree, then has one end.
Proof of Theorem 1.5.
Note that any finite-type surface can be identified as the interior of some compact surface . Further, a geometrically characteristic cover of the interior of is the interior of a geometrically characteristic cover . Thus, the goal is to show that the interior of is one of the four surfaces listed.
Let be the associated deck group of . First assume that has no compact boundary components, so . As is infinite and acts cocompactly on , the genus of is either or infinity, so the classification of surfaces (Theorem 2.2) implies that it is either the disc or the Loch Ness monster surface. Now, suppose that has a compact boundary component. As is infinite, has infinitely many compact boundary components. Gluing discs to each compact boundary component, we obtain a surface without boundary, call it . By Proposition 3.1, has a single end, and again the classification of surfaces (Theorem 2.2) implies that is either the disc or the Loch Ness monster surface. To finish, observe that is obtained from by puncturing all the infinitely many discs, so then is either the flute surface or the spotted Loch Ness monster surface. ∎
In the proof of Proposition 3.1, we will start by assuming has more than one end. We then use a relative version of Stallings’ Theorem to produce an action on a tree , and decompose equivariantly into subsurfaces essentially corresponding to the vertices of . We use the induced decomposition of to construct elements of that act elliptically on , then use the fact that the cover is characteristic to construct many more elements that act elliptically, in fact so many that the action on must have a global fixed point, a contradiction.
For clarity of exposition, though, before starting the proof properly in §3.1.1, we isolate some of its components into a series of preliminary results. First, the following will allow us to construct the action on the tree referenced above.
Lemma 3.2 (A peripherally elliptic action).
Let be a regular cover of a compact surface . If has more than one end, then there is an action of the deck group on a tree with no edge inversions and no global fixed point, such that the projection to of every peripheral element of acts elliptically on .
Proof.
Let be defined as follows: given , take a sequence of points with , and define to be the limit in . It is readily verified that is a well-defined continuous surjection.
As the action of on is co-compact and proper, the end space of , denoted , is homeomorphic to . If has more than one end, then there is a non-constant continuous function . Consider the composition
Pick cyclic subgroups of representing the boundary components, and let denote their projections to . For any right coset , the intersection is either empty (if is finite, which happens when that boundary component lifts to a closed curve in ) or projects to the endpoints in of some non-compact boundary component of , both of which (if they are distinct) map to the same element of .
We have established that is non-constant but that it is constant on for each and each right coset . Therefore, by Theorem 2.6 there exists an action of on a tree , with no edge inversions and finite edge stabilizers, and no global fixed point, such that all the subgroups act elliptically. Every peripheral element of projects to an element of that is conjugate into one of the ’s and hence acts elliptically on as desired. ∎
Given a peripherally elliptic action of on a tree , the following proposition constructs a -equivariant collection of simple closed curves in corresponding (perhaps multiple-to-one) to the edges of . Cutting along these curves decomposes into subsurfaces corresponding to the vertices of .
Proposition 3.3.
Let be a regular cover of a compact surface with deck group . Suppose acts on a tree with finite edge stabilizers, no edge inversions, no global fixed point, and such that the projection to of every peripheral element of acts elliptically on . Then there exists a -equivariant map such that each component of maps to a vertex under . Moreover, if is the set of edge midpoints in , then the preimage is a properly embedded -submanifold of , each component of which is a simple closed curve, and its projection is a compact -submanifold of each component of which is non-peripheral and essential.
Above, there may be components of that are parallel, which is why we call a -submanifold and not a multicurve.
Proof.
We begin by constructing a prototype for the map , which we call . Following Shalen [14], we construct the -equivariant map as follows. Fix a triangulation of , and consider its associated -invariant triangulation of . Let contain a single representative for each orbit equivalence class of , and pick a map
that is arbitrary, except that for every component , we require that takes to a single vertex of that is fixed by the stabilizer ; this can be done as is the projection to of a peripheral -subgroup of , so acts with a global fixed point on by assumption. (Note that must fix a vertex, since it acts simplicially without edge inversions.)

There is a unique -equivariant extension of to a map
The map is readily extended to a piecewise linear map (see Figure 1). Observe that, under this piecewise linear extension, each boundary component of is mapped to a point by , as its vertices are all mapped to the same point by construction.
Let be the set of all edge midpoints of , let , and let . We claim that each component (resp., ) is a simple closed curve. By the construction of , we know that the components of form a locally finite family of pairwise-disjoint 1-submanifolds of . As is a local homeomorphism and is invariant under the action of , we have that is a compact 1-submanifold of ; in particular, each component of is a simple closed curve. Now, let be a component of . Then is compact, and as the action of on has finite edge stabilizers, the stabilizer of is finite, implying that is compact. Therefore, is a union of simple closed curves. We now need to edit so that no component of nor is peripheral or bounds a disk.
First, suppose that there is a component of that bounds a disk. Let be the outermost disks bounded by components of , so that if is a component of bounding a disk, then there exists a unique such that . Choose a lift in for each of the , and for , let . Let be the edge with vertices whose midpoint is . By the construction of , all the -cells in that intersect are mapped to segments in that all contain the edge . If the -cells in are mapped into the side of , we can define a new map
that maps the 0-cells in to , but agrees with otherwise. We can now extend to a -invariant piecewise linear map in such a way that for any . Setting and , we have that and no component of bounds a disk.
Now, suppose that contains a peripheral component. Then each peripheral component of bounds an annulus with a component of . Let be the outermost annuli, so that if is a component of bounding an annulus with a component of , then there exists a unique such that . Each lift of an is again an annulus in as the component of are compact. We now proceed identically as we did above with the disks replaced with the annuli . The result is a -equivariant map so that and have neither peripheral nor inessential components. ∎
Corollary 3.4.
Let be a regular cover of a compact surface. If has more than one end, then there is a non-peripheral, essential, simple closed curve on such that every component of is compact.
Proof.
Given a properly embedded -submanifold on a surface , we write to refer to the surface obtained by cutting along , that is, the surface obtained by removing an open regular neighborhood of from .
Lemma 3.5 (Cutting covers into one-ended pieces).
If is a regular cover of a compact surface and is a compact -submanifold such that every component of is compact. Then there exists a compact -submanifold containing such that
-
•
every component of is compact, and
-
•
every component of has at most one end.
Proof.
It suffices to show that if some component of has more than one end, then there is an essential, nonperipheral simple closed curve such that every component of is compact. For then we can add such curves recursively to to produce as required. Since the number of isotopy classes in a collection of pairwise disjoint curves on is bounded, this process terminates.
So, let be a component of , and assume that we have a component such that has more than one end. We claim that the restriction of to is a regular covering map Indeed, if two points have the same projection to , then there is a deck transformation of with , and since is invariant under the deck group, we have , implying restricts to a deck transformation of taking to .
Corollary 3.4 then says that there is some essential, non-peripheral curve in such that every component of is compact. But since the cover is regular, this implies that every component of is compact, so we are done. ∎
3.1.1. Proof of Proposition 3.1
We argue by way of contradiction: assume that has more than one end. Let be the deck group associated to the covering . Apply Proposition 3.3 to obtain a tree , a peripherally elliptic action of on with no global fixed point, and the 1-submanifolds and of and , respectively, and apply Lemma 3.5 to get the -submanifold on . Recall that the action of on has finite edge stabilizers, no edge inversions, no global fixed point, and every element of that is the image of a peripheral element in acts elliptically on . The contradiction will arise by showing that the action of has a global fixed point.
We say that a closed curve is at most one ended in if for some (equivalently, any) component of , we have that is either compact or it is non-compact and its two ends go out the same end of . In particular, any closed curve disjoint from is at most one ended in .
We say two closed curves and in have the same homeomorphism type if there exists a homeomorphism such . As is geometrically characteristic, every homeomorphism lifts to a homeomorphism . Also note that the restriction of any homeomorphism to induces a homeomorphism . Therefore, if is a closed curve that has the same homeomorphism type as a closed curve disjoint from , then is at most one ended in .
Now, we claim that if is an essential closed curve on that is at most one ended, then acts elliptically on , i.e., any element of in the free homotopy class of acts elliptically on , where we let act on via the action factoring through .
To see this, pick some that is the projection of an element of in the free homotopy class of , and hoping for a contradiction, suppose that acts hyperbolically on . Now stabilizes some component . Since acts hyperbolically on , the image is a proper bi-infinite path in , whose ends go out distinct ends of . Pick some edge midpoint that separates those two ends, and let Then is a union of components of .
We claim that has finitely many components. If not, then since the projection has only finitely many components, there are infinitely many elements of that send a component of to a component of , and hence has infinite stabilizer, contradicting our assumption that acts with finite edge stabilizers. Hence, has finitely many components.
The two ends of the path lie in different components of , since they map to different components of . Since is compact, this means that the two ends of converge to distinct ends of , a contradiction. This establishes the claim that acts elliptically on .
Thus far, we have established that any essential closed curve on that has the same homeomorphism type as a curve disjoint from acts elliptically on . In the rest of the proof, using this plethora of elliptic elements, we apply Serre’s Criterion (Lemma 2.7) to show that the action has a global fixed point.
First, let us assume that there is no non-separating simple closed curve on that is disjoint from . Then the components of are all planar and are connected together in the pattern of a tree, since if there is a cycle in the component graph, you can realize it as a simple closed curve on intersecting some component of once, and then that component of is non-separating, contradicting that there are no non-separating curves disjoint from . It follows that is planar, and hence its fundamental group can be generated by a set of elements representing all but one of the boundary components of . By the construction of the action of on , all such curves act elliptically on .
A boundary product is a simple closed curve on that bounds a pair of pants with two boundary components of . Note that all boundary products in differ by homeomorphisms of . If we choose orientations for the generators above correctly, all products of pairs of distinct generators are homotopic to boundary products. Looking within a component of that is a leaf of the associated component tree, we can find a boundary product disjoint from , so it follows from the above that all boundary products act elliptically on , and hence the action has a global fixed point by Serre’s Criterion (Lemma 2.7), a contradiction.
Now assume there is a non-separating simple closed curve disjoint from . Then all non-separating curves on act elliptically on . Consider a ‘standard’ generating set for consisting of two non-separating curves intersecting once for each genus, plus generators for all but one peripheral curve (see Figure 2). All these generators act elliptically on . A product of a pair of generators is freely homotopic to either a boundary product or a non-separating simple closed curve. To use Serre’s Criterion again to get a contradiction, it suffices to prove that all boundary products on act elliptically on .

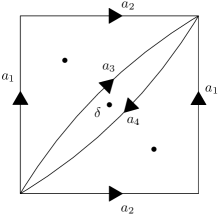
Fix a boundary product . Recall that this means that bounds a pair of pants in . Call and the two peripheral curves of this pair of pants. Since has a non-separating curve, it has positive genus. It follows that there is an essential genus one subsurface containing that has either two or three boundary components. Indeed, if has genus one and only two boundary components, then set . Otherwise, we can find a separating curve in that cuts off a subsurface of genus one containing , and only has three boundary components. In either case, both and are peripheral curves of .
Given such an , we can find a generating set for consisting of non-separating curves, such that every product of distinct pairs of generators is either non-separating or is freely homotopic to . See Figure 3. Since non-separating curves and peripheral curves in act elliptically on , by Serre’s criterion we have that the action has a global fixed point. In particular, acts elliptically on . Since was an arbitrary boundary product, all boundary products act elliptically on .
We have now established that the action of on has a global fixed point, a contradiction. This finishes the proof of Proposition 3.1.
3.2. Non-locally finite covers of infinite-type surfaces
Recall that a subgroup of a group is locally finite index if is finite index in whenever is finitely generated; a cover is locally finite if is locally finite index in . In this section we prove:
Theorem 1.7.
Let be an orientable, infinite-type borderless surface. If is a characteristic cover that is not locally finite, then is homeomorphic to either a disc, the flute surface, the Loch Ness monster surface, or the spotted Loch Ness monster surface.
We first start with some terminology and three lemmas. Recall that a subgroup of a group is a free factor if there exists another subgroup of such that is the internal free product of and . The three lemmas below tell us the following: given a non-locally finite characteristic cover and a “large” compact subsurface of , the restriction of to a component of is an infinite-sheeted characteristic cover .
Lemma 3.6.
Let be a noncompact surface, and let be a compact subsurface of . If each component of is a separating curve and each component of is noncompact, then is a free factor of .
Proof.
We observe that if is a separating curve in , such that both sides of and of are not precompact, then can be extended to a free basis for and . By Van Kampen’s theorem, . It is not hard to see from this that any basis for can be extended to a basis for . ∎
Lemma 3.7.
Let be a noncompact surface, and let be a non-locally finite characteristic cover. Then there exists such that if is an -injective subsurface whose fundamental group contains a free factor of of rank , then each component of is not compact.
Proof.
Let . As fails to be locally finite index in , there exists a finitely generated group such that is infinite. Using the fact that is finitely generated, we can find a free factor of containing ; let denote the rank of . Let be a -injective subsurface so that contains a free factor of of rank . Then there exists an automorphism of such that . As is characteristic, , implying that
In particular, as , we have that the index of in is infinite. Given a component of , the restriction of to is a covering with corresponding subgroup , and hence is an infinite-sheeted cover of , implying it is noncompact. ∎
Lemma 3.8.
Let be a noncompact surface, and let be a compact subsurface such that each component of is a separating curve and each component of is noncompact. If is characteristic, then is a characteristic subgroup of .
Proof.
Let . By Lemma 3.6, is a free factor of , and so there exists such that is isomorphic to . We can therefore extend to an automorphism of by declaring for all and . So,
Hence, is characteristic in . ∎
We are now ready to prove Theorem 1.7.
Proof of Theorem 1.7.
Let be an infinite-type surface, and let denote the surface obtained by removing an open annular neighborhood of each isolated planar end of . That is, is obtained by replacing the isolated planar ends of with compact boundary components.
Let be an infinite-sheeted characteristic cover. We will prove that is one ended (recall that is obtained by deleting the non-compact boundary components of ). Note that we are actually interested in the topology of ; however, if is one ended, then the result is a consequence of the classification of surfaces.
Let be a compact subset. By possibly enlarging , we can assume that no component of is precompact. Our goal is to show is connected.
Let be the constant of Lemma 3.7. We can exhaust by compact subsurfaces whose boundary components are separating and whose complementary components are not precompact. Thus, we may find two nested compact subsurfaces with the following properties.
-
•
The interior of contains .
-
•
Each boundary component of is separating, and each component of is noncompact,
-
•
Each component of has a fundamental group containing a free factor of rank .
Now let be the component of containing , and let be the associated component of . By Lemma 3.8, the restriction to gives a characteristic cover , so it follows from Proposition 3.1 that is one ended. In particular, has only one component which is not precompact. On the other hand, by Lemma 3.7, no component of is precompact, so the same is true of . This shows the complement of in , and hence in , is connected. ∎
3.3. The universal abelian cover
If is an orientable borderless surface with fundamental group , one example of a characteristic cover of is the universal abelian cover , which is defined to be the cover corresponding to the commutator subgroup . Unless is a disk or sphere, the universal abelian cover has infinite degree and is not locally finite, so Theorem 1.7 implies that is homeomorphic to either the disk, the flute surface, the Loch Ness monster surface, or the spotted Loch Ness monster surface. Given a surface , the next theorem tells you which of these surfaces is its universal abelian cover.
Theorem 1.2 (Universal abelian covers).
For a surface , let be its universal abelian cover. Then
-
(1)
if is , the annulus, or the torus, then ,
-
(2)
if is the sphere, then so is ,
-
(3)
if is the once-punctured torus, then is the flute surface,
-
(4)
if is a finite-type surface with one puncture and genus at least two, then is the spotted Loch Ness monster surface,
-
(5)
otherwise, is the Loch Ness monster surface.
Proof.
Cases (1) and (2) are trivial, so let us assume from now on that has non-abelian fundamental group.
First, assume that is a finite-type genus surface with punctures. We can then realize as the interior of a compact surface with boundary components. The abelianization of is , so acts properly and cocompactly on ; hence, the end space of and the end space of are homeomorphic. As we are assuming that is not abelian, we have that , so that , and hence , is one ended.
If , then , and the classification of surfaces implies that is the Loch Ness monster surface. If , then the preimage of in is a collection of properly embedded lines. Deleting these lines cannot increase the number of ends, so is also one-ended. Hence, is the Loch Ness monster surface.
Now, suppose , which implies that . The single boundary component of lifts homeomorphically, and so is an infinite collection of circles. Gluing on a disk to each of these circles results in a borderless one-ended surface and a covering with deck group , where is the closed surface obtained by gluing on a disk to . By the classification of surfaces, is either the plane or the Loch Ness monster surface. If it is the plane, then this covering map is the universal covering map and the fundamental group of the surface is free abelian; hence, is a torus, so is the once-punctured torus and its universal abelian cover is obtained by puncturing the plane in an infinite discrete set of points, implying is the flute surface. Otherwise, is the Loch Ness monster surface, and is obtained by puncturing the Loch Ness monster surface in an infinite discrete set of points, implying that is the spotted Loch Ness monster surface.
Finally, assume that is an infinite-type surface. The universal abelian cover is not locally finite, as the deck group is free abelian and hence not a torsion group. By Theorem 1.7 and the fact that is nontrivial, the only options are the flute surface, the Loch Ness monster surface, or the spotted Loch Ness monster surface. We claim there are no isolated planar ends in . Indeed, regularity of the cover implies that any such end covers an isolated planar end of . But any peripheral curve in is part of a free basis for , and hence no power of it lies in the commutator subgroup, so the preimage of any annular neighborhood of an isolated planar end of has simply connected components in . Hence, is the Loch Ness monster surface. ∎
3.4. -homology covers
Recall from the introduction that the -homology cover of a surface is the cover corresponding to the kernel of the map .
Theorem 1.3 (-homology covers).
Say is an infinite-type orientable surface and is its -homology cover, where . If has no isolated planar ends, then is homeomorphic to the Loch Ness monster surface. Otherwise, is homeomorphic to the spotted Loch Ness monster surface.
The main point is to show the following lemma:
Lemma 3.9.
With as above, the cover has at most one end that is not an isolated planar end.
Proof Theorem 1.3.
The first step is to prove:
Claim 3.10.
has infinite genus.
Proof.
Since is a regular cover of infinite degree, it suffices to prove that has positive genus.
If has positive genus, we can pick an embedded once punctured torus . Since has infinite-type, is noncompact, so Mayer-Vietoris implies that . Hence, picking a component
the cover is the -homology cover of . As , we have
so the cover has degree , so . However, since is trivial in homology, it lifts homeomorphically to , and hence has boundary components, implying is a -punctured torus111One can also just visualize the cover directly by unwrapping the meridian and longitude direction -times., so has positive genus.
If has genus zero, take some essential -punctured sphere . Then has four components. Moreover, all four components of are noncompact: any compact component is a planar surface with one boundary component, and hence is a disk, contradicting that is essential. It follows that . Hence, if is a component, then is the -homology covering of , which has degree , so . Each component of is primitive in , so unwraps times in , and hence there are lifts of each, for a total of boundary components. A quick computation shows that has genus , which is never zero for . ∎
By Lemma 3.9 and Claim 3.10, is either the Loch Ness monster surface or its spotted version. If has isolated planar ends, these ends lift to isolated planar ends in , so is the spotted Loch Ness monster surface. Conversely, since the cover is regular, any isolated planar end in covers an isolated planar end in . So if has no isolated planar ends, is the Loch Ness monster surface. ∎
3.4.1. The proof of Lemma 3.9
Before formally proving the Lemma 3.9, we give a brief heuristic of the proof.
The rough idea here is to use the fact that the cover is abelian, and the fact that homologically essential curves are ubiquitous in , and such curves do not lift homeomorphically to . Slightly more precisely, and assuming for simplicity that neither nor has isolated planar ends, we take a compact set that projects to , a path in with endpoints outside of , and we claim that there exists another path with the same endpoints that does not enter (this will show that is one-ended). To construct such a we work as follows. Writing and , it may be that there is not really another way to travel within between the endpoints of without roughly following , which might take us through . So, we try to construct so that at some point its projection follows , but when it does so, still avoids going through . To do this, we first make loop around some homologically essential curve , so that when tracks the lift is actually tracking a translate of rather than itself. We then loop backwards around at the end, and use that the cover is abelian to say that this cancels out the first loop around , so that terminates at an endpoint of rather than at some translate of that endpoint.
We now prove Lemma 3.9 by contradiction. Suppose that has more than one end that is not isolated and planar. We first show:
Claim 3.11.
There exists a connected, finite-type subsurface such that
-
(1)
every component of has infinite type, and
-
(2)
there is a finite-type connected component of such that the complement contains two distinct infinite-type connected components and .
Proof.
Since has more than one end that is not isolated and planar, there is a compact subsurface that has two distinct infinite-type connected components. The projection is compact, so there is a finite-type subsurface containing the projection. We can assume that all components of have infinite type, by adding any finite type components into . Since is locally finite (see §1.6), all components of have finite type, and the component containing has at least two infinite-type complementary components. ∎
Pick an oriented path in that starts at a point and ends at a point and let be the projections to . Then lies in and is adjacent to a component . As has infinite type, there is a nonseparating bi-infinite arc in . If , we can choose the arcs so that the union is nonseparating in . Let be an oriented loop in that starts and ends at , and that intersects exactly once. If , we can assume that is disjoint from .
Consider now the path in , which starts at and ends at , see Figure 4 for a configuration.
Then is a loop that starts and ends at , and since
this loop is trivial in homology and therefore lifts to . Choose the lift such that the terminal lifts to the already defined path , which starts at and ends at . If we do this, then the resulting lift of starts at and ends at .
Claim 3.12.
is disjoint from .
This claim will finish the proof of Lemma 3.9, as it contradicts the fact that and lie on the boundaries of distinct connected components of . So, all that is left is to prove the claim.
Proof of Claim 3.12.
Below, when we talk about ‘the lift of’ a path like or or , etc., we mean the lift that appears as the associated subpath of . Since there are two traversals of in , we refer to the two lifts as the ‘first lift’ of and the ‘second lift’ of , using the order they appear in the word. In this terminology, orientations matter: the ‘lift of ’ may not be obtained by traversing the ‘lift of ’ backwards.
First, observe that all the lifts of are disjoint from , as their projections are disjoint from by construction. Now, suppose the first lift of intersects . Then we can create a loop in by concatenating the lift of , part of the lift of , and a path in . The projection of this loop to intersects exactly once, as the latter two parts project into . This is impossible, since the projection must be trivial in -homology. The same argument shows that the lift of is disjoint from : if not, one can construct a loop that is trivial in -homology and intersects once.
A similar argument shows that the second lift of is disjoint from : if not, one can construct a loop that is trivial in -homology and intersects once. Note that above, we could have used or , but here we need to use , as both and appear before the second occurrence of in the word defining . ∎
4. Arbitrary covers
In this section we prove the following theorem.
Theorem 1.1 (Everything covers everything).
Suppose that is an orientable, borderless surface with non-abelian fundamental group. Then is covered by any noncompact borderless orientable surface.
The idea for the proof of Theorem 1.1 is to show that any surface with non-abelian fundamental group is covered by the blooming Cantor tree surface and that any infinite-type surface admits a -injective embedding into , see Proposition 4.2. Then, Lemma 2.4 gives us Theorem 1.1.
Before starting the proof of Theorem 1.1 we show that the blooming Cantor tree surface regularly covers the Loch Ness monster surface.
Lemma 4.1.
The blooming Cantor tree surface regularly covers the Loch Ness monster surface.
Proof.
Let be the Cayley graph of . Note that if we replace every vertex of by a four-punctured torus and we glue them according to the edges relation we obtain a surface that, by classification, is homeomorphic to the Loch Ness monster surface. Let be the universal cover of , i.e., is a complete 4-valent tree. Then, if we replace each vertex of by a four punctured torus we obtain a surface that, again by classification, is homeomorphic to the blooming Cantor tree surface. Then the induced covering map from the graphs induces the required covering map from to .∎
We now show that any infinite-type surface can be embedded in the blooming Cantor tree surface as a connected component of the complement of a collection of simple closed curves and bi-infinite arcs.
Proposition 4.2.
For any borderless non-compact orientable surface , there is a -injective embedding of into the blooming Cantor tree .
Proof.
We assume throughout the proof that has either zero or infinite genus, since an arbitrary surface can be written as the connected sum of such an and a closed orientable surface , and a -injective embedding induces a -injective embedding of .
Let be the genus-marked end space of , which is nonempty since is non-compact. Since the end space is a Cantor set, we can fix an embedding , and we let and . We will construct an open, connected -injective subsurface such that
-
(a)
the inclusion induces a homeomorphism ,
-
(b)
the genus of is the same as the genus of .
By classification of surfaces, see Theorem 2.2, such a surface will be homeomorphic to , proving the proposition.
As a first step, we construct a -injective closed subsurface (with boundary) that has properties (a) and (b). Let be a union of simple closed curves that cuts into a collection of thrice-punctured tori, connected together in the pattern of a trivalent tree. For each of the thrice-punctured tori , cut along some simple closed curve into a punctured torus , and a four-punctured sphere . See Figure 5 for such a configuration.

Fixing some component as the ‘root’, we then define to be the union of:
-
(1)
all such that separates from some point of ,
-
(2)
all such that separates from some point of ,
here and are just the closures of the open subsurfaces mentioned above. Observe that is connected, it -injects into , there is a homeomorphism as above and the genus of is the same as that of . The boundary consists of countably many circles. Our goal now is to remove the compact boundary components of so that they are replaced by half-planes.
We claim that for any orientable surface such that is a union of simple closed curves, there is a -injective borderless subsurface , with the same genus, such that the inclusion induces a homeomorphism of genus-marked end spaces. Let be the collection of boundary components of and let be a locally finite collection of pairwise disjoint properly embedded rays on such that starts on , and let be a closed regular neighborhood of in . If we take these regular neighborhoods small enough, they are all disjoint and we obtain a surface . Observe that the end space of agrees with that of , so it also satisfies the required properties.
Composing the inclusions gives an open, -injective subsurface of satisfying (a) and (b) above, which proves the proposition. ∎

Proof of Theorem 1.1.
By Proposition 4.2 and Lemma 2.4 it suffices to show that given there exists a covering space homeomorphic to a blooming Cantor tree surface. Since has non-abelian we can find a -injective pair of pants . Then, by Lemma 2.4 we get a cover where is an open pair of pants. By Theorem 1.2 is covered by a Loch Ness monster surface and we conclude by Lemma 4.1. ∎
Appendix A Appendix
The goal of this appendix is to show how Theorem 2.6 is a restatement of the main result in Swarup’s paper [16]. To do so, we relate three ways of looking at ends of a group . In the background, we have the space of ends as defined in §2.2. We want to relate this to , which is the definition of the space of ends in Swarup’s paper [16]. To do so, we relate both to a combinatorial description of ends that is similar to a description in Stallings’s paper [15]. All of this material is likely well known to experts, but we did not readily find a reference for the portions relevant to the goals of this article, and so we present it here in hopes of providing a useful reference to others.
A.1. Group cohomology
Let be a group. A -module is an abelian group that comes equipped with an action of by automorphisms. For instance, any abelian group with the trivial action is a -module. On the other end of the spectrum, let
which we consider as an abelian group under addition of functions. We realize as a -module by defining the (left) -action . So, the action of precomposes with left translation by . From this definition we observe the following equality, which will be used several times: if and , then
| (1) |
The group ring of , denoted by , is the submodule of given by
where the support of is the set of all with . We can express the elements of as formal -linear combinations
where and—abusing notation—we view as the indicator function that assigns to and to all other group elements. The elements of can then be realized as the formal sums in which for all but finitely many g. We will switch back and forth between formal -linear combinations and functions as convenient.
Suppose that is a -module. We will now define the cohomology groups with coefficients in . An -cochain with coefficients in is a function , where , and by convention . Let denote the set of -cochains. We then define the coboundary maps as follows: for , set
and for , set
| (2) |
The cohomology groups are now defined to be
This definition relies on the fact that , a fact we have not checked; we will verify this for below, which is the only case we will use in this appendix.
Now, -chains are functions , or in other words, a choice of an element of . By (2), exactly when the element is invariant under the action of , and hence we get
Here are some examples for different -modules .
-
(1)
If is an abelian group with the trivial -action, then .
-
(2)
If , then since the -invariant elements of are exactly those where all the coefficients are the same.
-
(3)
If , then
Indeed, if , then the support of is finite and for all .
To compute , we need to understand the image of (i.e., the set of coboundaries) and the kernel of (i.e., the set of cocycles). Given , define the 1-cochain by
In (2), we computed the image of , establishing that the set of 1-coboundaries is .
To understand -cocycles, first note that if is a -cochain, then
Setting the right-hand side to zero, we see that is a -cocycle if and only if
i.e., satisfies the cocycle condition. Let us verify that every 1-coboundary is a 1-cocycle, i.e., . Fix a 1-cobounday , where . Then
| (3) |
implying that satisfies the cocycle condition and is therefore a 1-cocycle.
Let us work out two example computations of .
-
(A)
Suppose that is an abelian group with a trivial -action. In this case, the cocycle condition becomes , i.e. is a homomorphism. Given a coboundary , there exists such that . It follows that , and hence . As all coboundaries vanish,
In the case , we have that is isomorphic to the free part of the abelianization of .
-
(B)
Suppose that . We claim that . To see this, suppose is a 1-cocycle. Define by
We claim that , and hence is a coboundary. Indeed, if , then:
where the third equality uses (1) and the second-to-last equality uses the cocycle condition. Therefore, , implying that is a coboundary. It follows that .
A.2. Ends via group cohomology
In this section we describe how the set of ends of is encoded in the cohomology group . It is well known that the number of ends of an infinite finitely generated group is equal to , where rank denotes the cardinality of a maximal -linearly independent subset (see for example [7, Theorem 13.5.5]). However, we require a more transparent proof of this fact that will allow us to more easily generalize to the relative setting discussed in Theorem 2.6.
Suppose is generated by a finite set that is symmetric under inversion. Let be the associated left Cayley graph for , that is, the graph whose vertex set is and where and are adjacent if for some . Note that this is opposite the usual construction of Cayley graphs; however, we need to use left Cayley graphs here since we chose to consider as a left -module.
Given , the boundary of is the subset consisting of all such that for some . For example, if , , and
then
Recall that, given , we defined by
The next two lemmas tell us that if has finite boundary, then is a 1-cocycle with coefficients and that these account for all 1-cocycles with coefficients. The third lemma characterizes the 1-coboundaries with coefficients.
Lemma A.1.
If , then is a 1-cochain with coefficients if and only if is finite.
Proof.
If , then there exists such that . By (1), it follows that and hence , which says that is an element in the support of . It follows that is contained in the union of the supports of the elements for . If we assume that is a 1-cochain with coefficients, then for all ; it follows that is finite, establishing the forwards direction.
Now, assume is finite. Fix . If , where , we claim that is supported within the -neighborhood of , with respect to the word metric. Indeed, if lies outside this neighborhood, then for each , the elements does not lie in , so , and inductively we get . Using (1), we have that , so implying that . As was arbitrary, we conclude that is a 1-cochain with coefficients. ∎
Lemma A.2 (-cocycles with -coefficients).
A 1-cochain with coefficients is a 1-cocycle if and only if there exists with finite boundary such that .
Proof.
Let with finite boundary. Lemma A.1 tells us that is a 1-cochain with coefficients, and then (2) tells us that is a 1-cocycle with coefficients. Conversely, if is a 1-cocycle with coefficients, then the computation in (B) above tells us that with defined by . It is left to check that has finite boundary: as , we have that for all ; hence, by Lemma A.1, has finite boundary. ∎
Lemma A.3.
Let . If is a 1-cocycle with coefficients, then is a 1-coboundary with coefficients if and only if is constant outside a finite set of .
Proof.
By definition, is a 1-coboundary if and only if there exists such that . For the forwards direction, suppose that is a 1-coboundary. Then there exists such that for every . In particular, for each , implying that is constant. Hence, is constant off the finite support of . Conversely, suppose that is constant outside a finite subset of . Let such that for all . Define by if and if . Then is constant, and by repeating the computation above in reverse, , implying that is a 1-coboundary ∎
Now, suppose that is an infinite finitely generated group. Let be the space of ends of , and equip with the usual topology. Identifying with the vertex set of , we can view as a topological space. It is an exercise to show that is either a singleton, doubleton, or a perfect set; we define to be one, two, or , respectively.
If has finite boundary, then any end of has a neighborhood in on which is constant, so there is a unique function such that is continuous.
Let be the set of all continuous functions , which is an abelian group under addition. Let be the constant functions. As mentioned above, the rank of an abelian group , denoted , is the cardinality of a maximal -linearly independent subset of .
Theorem A.4.
Let be an infinite finitely generated group. The map
defined by is an isomorphism, where satisfies . Consequently, we have
Note that we are supposing is infinite above, so that is nonempty. If is finite, then and, by Lemma A.2, .
Proof of Theorem A.4.
First, we claim the map is well defined: suppose . Then there exists such that , , and, by Lemma A.3, is constant, implying , as desired. The map is a homomorphism as
and the map is linear.
Next, we show the map is injective: suppose with finite boundary such that . As , there exists such that for all . It follows that for every that lies in an infinite component of . As is finite, Lemma A.3 implies that . Now, we turn to surjectivity. If , then the continuity of and the compactness of imply that the image of is finite; let be the image of . The preimages are clopen sets that partition ; therefore, there exists a finite subset of such that each of the are the accumulation points in of a component of . Define such that for all and otherwise. The boundary is contained in the -neighborhood of , so is finite, and . By Lemma A.2, is a 1-cocycle, and by construction, the image of is , establishing the surjectivity of the map.
We have established that the given map is an isomorphism, so it is left to check the that . First suppose that . Let and define by and if . Then is generated by , and it is clear that this set of generators is -linearly independent; in particular, . Therefore, the quotient , yielding the desired result. Now, suppose that is infinite. For any , there exists pairwise-disjoint clopen sets of such that . Arguing as in the finite end case, the functions defined to be 1 on and 0 on the complement of generate a copy of in , and therefore their equivalence classes generate a copy of in . It follows that the rank of is infinite, yielding the desired result. ∎
It not relevant to the work that follows, but we note that as is a free abelian group (see [7, Theorem 13.5.3]), if is infinite, then is isomorphic to a countably infinite direct sum of copies of .
We can now state Stallings’s theorem in terms of group cohomology.
Theorem A.5.
If is a finitely generated group such that is nontrivial, then admits an action on a simplicial tree with finite edge stabilizers, no edge inversions and no global fixed point. ∎
A.3. Swarup’s Theorem
Swarup [16] has proved a relative version of Stallings’s Theorem, which we now describe. Let be a finitely generated group, and let be a subgroup. There is a natural restriction map given by
| (4) |
Here, is the quotient of the set of all functions satisfying by the subset of such that are of the form for some .
Theorem A.6 (Swarup [16]).
Let be a finitely generated group, and let be subgroups of . For each , let
denote the restriction map. If the intersection , then there is an action of on a simplicial tree , with finite edge stabilizers, no edge inversions, no global fixed point, and such that each is contained in the stabilizer of some vertex .
Equivalently, as stated in [16], the conclusion is that or in such a way that each is conjugate into or . The following proposition interprets Swarup’s theorem in terms of end spaces, at least when the subgroups are finitely generated.
Proposition A.7.
Here, is the closure of in . Given multiple subgroups as in Swarup’s theorem, the intersection of the kernels is the set of all that are constant on for each and each right coset .
Proof of Proposition A.7.
By Lemma A.2, any -cocycle with -coefficients is of the form , where has finite boundary. The map takes to the class in of the restriction given by
which is trivial in exactly when there is an element such that for all . This last equality is equivalent to saying that for all , or saying that is invariant under the left action of . So, we have that if and only if the function is left -invariant outside of a finite subset of .
If is left -invariant outside a finite subset of , then on each right coset , the function is constant outside of a finite subset, and hence the boundary map is constant on .
Conversely, suppose is constant on for each . Fix a finite generating set for . As is finitely generated, we can pick large enough so that is generated by elements of with word length at most in the generating set of . Note that any two points in a coset can then be joined in by a path that stays in the -neighborhood of . Call a coset relevant if it intersects the -neighborhood of , and call it irrevelant otherwise. As is finite, there are only finitely many relevant cosets; moreover, each irrelevant coset lies in a single component of . Let be the union of and all intersections that are finite sets, where is any relevant coset and is any component of . Since there are only finitely many and finitely many relevant , the set is finite.
We claim that is left -invariant on the complement of , meaning that for every right coset , the function is constant on . If is irrelevant, then it lies in a single component of , and hence any two points in can be joined by a path avoiding , implying that is constant on as desired. If is relevant, then since is constant on , it follows that on all components of that intersects in an infinite set, the value of is the same constant. Hence is constant on as desired. ∎
References
- [1] Javier Aramayona, Christopher J Leininger, and Alan McLeay, Big mapping class groups and the co-hopfian property, Michigan Mathematical Journal 1 (2023), no. 1, 1–29.
- [2] Yasmina Atarihuana, Juan García, Rubén A Hidalgo, Saúl Quispe, and Camilo Ramírez Maluendas, Dessins d’enfants and some holomorphic structures on the Loch Ness monster, The Quarterly Journal of Mathematics 73 (2022), no. 1, 349–369.
- [3] Taras Banakh, J Higes, and Ihor Zarichnyi, The coarse classification of countable abelian groups, Transactions of the American Mathematical Society 362 (2010), no. 9, 4755–4780.
- [4] Ara Basmajian and Nicholas G. Vlamis, There are no exotic ladder surfaces, Ann. Fenn. Math. 47 (2022), no. 2, 1007–1023. MR 4453410
- [5] Martin R. Bridson and André Haefliger, Metric spaces of non-positive curvature, Springer-Verlag Berlin Heidelberg, 1999.
- [6] William Burnside, On an unsettled question in the theory of discontinuous groups, Quart. J. Pure and Appl. Math. 33 (1902), 230–238.
- [7] Ross Geoghegan, Topological methods in group theory, vol. 243, Springer Science & Business Media, 2007.
- [8] Martin E. Goldman, An algebraic classification of noncompact -manifolds, Transactions of the American Mathematical Society 156 (1971), 241–258.
- [9] CR Hampton and Dl S Passman, On the semisimplicity of group rings of solvable groups, Transactions of the American Mathematical Society 173 (1972), 289–301.
- [10] Bernard Maskit, A theorem on planar covering surfaces with applications to 3-manifolds, Annals of Mathematics 81 (1965), no. 2, 341–355.
- [11] CD Papakyriakopoulos, Planar regular coverings of orientable closed surfaces, Ann. of Math. Stud 84 (1975), 261–292.
- [12] Ian Richards, On the classification of noncompact surfaces, Transactions of the American Mathematical Society 106 (1963), no. 2, 259–269.
- [13] Jean-Pierre Serre, Trees, Springer Monographs in Mathematics, Springer-Verlag, Berlin, 2003, Translated from the French original by John Stillwell, Corrected 2nd printing of the 1980 English translation. MR 1954121
- [14] Peter B Shalen et al., Representations of 3-manifold groups, Handbook of geometric topology (2002), 955–1044.
- [15] John Stallings, Group theory and three-dimensional manifolds, Yale Mathematical Monographs, vol. 4, Yale University Press, New Haven, Conn.-London, 1971, A James K. Whittemore Lecture in Mathematics given at Yale University, 1969. MR 415622
- [16] G Ananda Swarup, Relative version of a theorem of stallings, Journal of Pure and Applied Algebra 11 (1977), no. 1-3, 75–82.