Countering detector manipulation attacks in quantum communication through detector self-testing

Introduction – Quantum key distribution (QKD) is a communication method that uses quantum states of light as a trusted courier such that any eavesdropping attempt in this information transmission is revealed as part of the underlying quantum physics of the measurement process on the states Bennett and Brassard (1984); Ekert (1991); Gisin et al. (2002). While the basic protocols are secure within their set of assumptions, practical QKD systems can exhibit vulnerabilities through imperfect implementation of the original protocol scenarios, through imperfect preparation and detection devices, or through side channels that leak information out of the supposedly safe perimeter of the two communication partners Scarani et al. (2009); Scarani and Kurtsiefer (2014); Xu et al. (2020). Families of such vulnerabilities have been identified and addressed through technical measures and advanced protocols. Examples are the photon number splitting attacks where single photons were approximated by faint coherent pulses Brassard et al. (2000); Lütkenhaus (2000), Trojan horse attacks Vakhitov et al. (2001); Gisin et al. (2002), various timing attacks Qi et al. (2007); Lamas-Linares and Kurtsiefer (2007); Zhao et al. (2008) and classes of information leakage into parasitic degrees of freedom.

Perhaps the most critical vulnerability of QKD sys- tems is the detector blinding / fake state attack fam- ily on single-photon detectors Makarov (2009). This attack has been experimentally demonstrated to work for detectors based on avalanche photodiodes and superconducting nanowires Lydersen et al. (2010, 2011); Goltsman et al. (2019), and allowed to completely recover a key generated by QKD without being noticed by the error detection step in a QKD implementation Gerhardt et al. (2011). The attack is based on the fact that these single photon detectors can be blinded by a macroscopic light level into not giving any response, while an even stronger light pulse or a recovery event from a blinded state could create an output signal from the blinded detector that emulates a photon detection event Makarov (2009) (see Fig. 1). This vulnerability can be exploited by carrying out an undetected man-in-the-middle attack, where an eavesdropper intercepts photon states carrying the information, measures the quantum state in a basis of his/her choice, and copies the measurement results into the photon detector of the legitimate receiver with macroscopic powers of light.

Various countermeasures against the detector control attack have been suggested and implemented. One class of countermeasures addresses technical aspects of the detectors. Examples are using more than one detector or a multi-pixel detector for one measurement basis Honjo et al. (2013); Ferreira Da Silva et al. (2015); Wang et al. (2016); Gras et al. (2021), including a watchdog detector for the blinding light Lydersen et al. (2010); Dixon et al. (2017), effectively varying the detector efficiency at random timings Lim et al. (2015); Qian et al. (2019), and carefully monitoring the photocurrent or breakdown status of the detector Yuan et al. (2010, 2011) to identify a detector manipulation. However, most of these countermeasures have operational drawbacks. For example, additional single photon detectors significantly increase the overall cost and complexity, and beam splitters in the receiver for watchdog detectors introduce additional optical losses. Varying the efficiency frequently to get enough statistics to identify the blinding attack could significantly affect the QKD bit rate, and changing the detector operation condition or monitoring its state increases the complexity of the electronic circuitry around the single photon detectors. Such countermeasures may also introduce additional vulnerabilities that may be exploited in an arms race style Huang et al. (2016).

An elegant countermeasure on the protocol level is provided by the so-called measurement-device independent quantum key distribution (MDI-QKD) Lo et al. (2012), which further developed the idea of device-independent QKD where a photon pair source can be made public or even controlled by an eavesdropper Pironio et al. (2009) to a scenario where the detectors receiving single photons (or approximations thereof) can be public, or controlled by an eavesdropper. The scheme has been demonstrated experimentally several times by now Liu et al. (2013); Tang et al. (2014); Yin et al. (2016); Liu et al. (2019). It requires a pair of single photons (or weak coherent pulses) from two communication partners without a phase correlation to arrive within a coherence time on a Bell state analyzer, where single photon detection is carried out, and the result is published. This requires a matching of emission times and wavelengths of two spatially separated light sources with both communication partners.

The MDI-QKD approach counteracts any active or passive attack on single photon detectors, as their result need not to be private anymore. The communication partners can simply test if the detectors were performing single photon detection through a error detection process similar to the original QKD protocols.

In this work, we present a method of testing the proper operation of single photon detectors in a QKD scenario that does not require the synchronization of light sources like in the MDI-QKD approach, while also not touching the specific detector mechanism. It brings the idea of self-testing of quantum systems Mayers and Yao (1998); van Dam et al. (2000); Šupić and Bowles (2020) to single photon detectors that can remain black boxes. We use a light emitter (LE) under control of a legitimate communication partner that is weakly coupled to its single photon detector for this self-testing. When the single photon detector is under a blinding attack, it is insensitive to low-intensity light fields used for quantum key distribution. Thus, by turning on the LE at times not predictable by an eavesdropper, “salt” optical detection events are generated in the detector when it operates normal, while it does not react to the test light when blinded. Complementary, the test light intensity can be raised to blinding levels of the photodetector, which thereby is desensitized to legitimate single photons. Registration of any detector events under self-blinding then suggests the presence of fake state events.

Self-testing strategy – In a generic QKD system, a transmitter generates photons containing quantum information in either polarization or time encoding, and sends them through an optical path (“quantum channel”) to a receiver. Therein, a measurement basis choice is made either through passive or active optical components, and the light arriving from the quantum channel is directed to single photon detectors. In a blinding/fake state attack, an eavesdropper measures a photon in the quantum channel, and copies the result into the corresponding photon detector of the legitimate receiver using blinding and fake state light levels. For detector testing, a light emitter (LE) in the receiver is controlled by a random number generator and weakly coupled to the single photon detectors.

An unblinded single-photon detector generates events due to photons from the legitimate source or the background (labeled “N” in Fig. 2(a)). The brightness of the legitimate source, the transmission of the quantum channel, the efficiency of the single photon detectors, and the detector dark count rate determine the average number $\bar{n}$ of the photon-detection events registered in a time interval $T$. An eavesdropper would choose a rate of “fake” detection events (labeled “F” in Fig. 2(a)) similar to normal QKD operation to prevent detecting the attack by monitoring photon detection statistics.

We illustrate three different examples of detector self-testing to detect detector manipulation attacks.

In the first one, the legitimate receiver switches occasionally the light emitter LE to a low light level for a test time interval $T$ at a random timing unpredictable by an eavesdropper, while it is off for the rest of the time. In the test interval, an unblinded detector would see an increase of detector events above $\bar{n}$ due to additional salt events (“S” in Fig. 2(b)). The legitimate receiver has complete control of the light emitter to make excess photon detection events statistically detectable in the probe interval $T$. A single photon detector under blinding attack would be insensitive to the low light levels of LE, so only detector events generated by positive detector manipulations like fake states would be registered (labeled “F” in Fig. 2(b)). A statistically significant presence of salt events in a time interval $T$ would therefore allow to sense a negative detector manipulation e.g. through blinding. Note that the test interval $T$ does not need to be distributed contiguously in time.

This leads to a second self-testing example, which turns on the light emitter for a short pulse time interval $\delta t$ at a random timing and with a high enough energy (a few photons) to cause a detection event with almost unit probability in an unblinded single-photon detector. A blinded detector is again insensitive to such a short optical pulse as long as the light level is way below the fake state threshold. In this situation, detecting a single flag event can witness a non-blinded detector (see Fig. 2(c)).

The third self-testing example uses the light emitter in the receiver to locally blind the detector. The typical power necessary to blind an APD is on the order of a few nW, which can easily be accomplished by weakly coupling even faint light sources like LEDs. Detection events caused by single photons from the legitimate source will be suppressed by the local blinding light. In absence of a negative detector manipulation (e.g. detector blinding), the intense light at the onset of the self-blinding period will almost deterministically create a flag event in the detector, which then remains silent during the rest of the self-blinding interval (see Fig. 2(d)). However, any positive detector manipulation will overrule the local blinding, and cause a false detection event. Both the initial flag event and any possible later event can be easily checked. This method only requires a small number of registered events in a time interval $T$ to discover both a negative and positive detector manipulation attack.

A detector event could also be triggered when the detector recovers from a (remote) blinding exposure Tanner et al. (2014). Local blinding will suppress such “fake” detector events, so they may not get noticed by looking for signals under local blinding. However, in such a case, the flag event will also be suppressed. Therefore, a combination of checking for detection events during self-blinding and looking for a flag event is necessary to identify such an attack.

Experimental results – We demonstrate our countermeasure with a single-photon detector commonly used in quantum key distribution which is susceptible to manipulation attacks (see Fig. 3(a)). Light that simulates legitimate quantum signals and provides the larger power levels required for detector manipulation is generated by combining the output of a continuous wave (cw) laser diode (LD1) with light from a pulsed laser diode (LD2) on a fiber beam splitter (BS). The 2 ns long bright fake states from LD2 can be emitted upon detection events from an auxiliary avalanche photodetector (APD1) to emulate a credible (Poissonian) event distribution. On the receiver side, the light from the quantum channel passes through an interference filter (IF) before it is focused onto the main photodetector (APD2), a passively quenched InGaAs device (S-Fifteen Instruments IRSPD1) with a maximal count rate of $5\times 10^{5}\,\text{s}^{-1}$ and a dark count rate of $7\times 10^{3}\,\text{s}^{-1}$. The light emitter (LE) for detector self-testing is a light emitting diode with a center wavelength of 940 nm (Vishay VSLY5940), which is reflected off the IF (acting as a dichroic beam splitter) onto APD2.

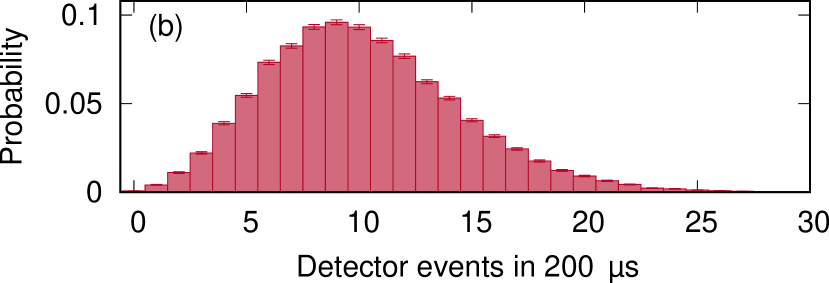
For the demonstration, we consider an event rate of $\approx 5\times 10^{4}\,\text{s}^{-1}$ at APD2, which is about an order of magnitude below the maximal detection rate to not reduce the detector efficiency significantly. Figure 3(b) shows a histogram of detection events in a time interval of $T=200\,\mu\text{s}$ generated by choosing an appropriate light level of LD1. The result with a mean photodetection number $\bar{n}\approx 10$ differs slightly from a Poisson distribution since the detector has an after-pulse possibility of about 40 %. To implement a detector manipulation with the same event characteristic, we elevate the optical output power of LD1 to 500 pW, the minimal power to completely blind detector APD2. Fake states that emulate photodetection events in APD2 are generated with optical pulses through LD2 with a peak power of 3 $\mu$W.

To demonstrate the first example of detector self-testing, we turn on the light emitter LE in the test interval $T$ both for a normally operating and a manipulated detector. The resulting detection event distributions are shown in Fig. 4. For a normally operating detector, the observed APD2 events in the test interval increase significantly to a mean of about $\bar{n}_{T1}\approx 100$, while for a manipulated detector, the distribution is similar to the “normal” distribution with $\bar{n}_{N}\approx 10$ in Fig. 3(b). With a threshold at $n=50$, the two distributions can be easily distinguished, and a detector manipulation attempt (specifically: the presence of a blinding light level) easily identified in a single measurement interval $T$; in the experiment, the unmanipulated detector never showed less than 78 events, while the manipulated showed never more than 30 events.

The necessary time to detect a manipulated detector can be shortened even further with the second example of self-testing. We demonstrate this by driving the light emitter LE to emit $\delta t=25$ ns long pulses, and increasing the coupling to the detector APD2 compared to the previous example. Figure 5 shows the probability of registering a signal from APD2 as a function of the time $\Delta t$ after the start of the self-testing pulse. A non-manipulated detector shows an overall detector response probability $p_{1}=93.4\%$ within 60 ns (11720 photon detection events out of 12542 optical pulse). This number does not reach 100%, as the detector may have been in a recovery state from a previous detection event. For a manipulated detector, i.e., in presence of both detector blinding and fake states, we find an integral detector event probability $p_{2}=0.3\%$ (36 out of 12380 test pulses). These events were caused by fake states, not by light from the LE. Detector manipulation (specifically, the detector blinding) can therefore be identified with a few short test pulses to a very high statistical significance.

To demonstrate the third example of detector self-testing, we increased the optical power of LE on detector APD2 to a level that it could reliably blind the detector. Figure 6 shows both a distribution of detection events in a test interval $T=200\,\mu\text{s}$, taken 60 ns after the onset of light emission by LE. The un-manipulated detector is insensitive to single photons in this interval; we observed only 8 events in 7608 test runs (likely due to electrical noise), while a manipulated detector still reported events due to fake states present at the input; we observed 7655 out of 7658 events (with the missing events compatible with statistics). The onset of the test light emission triggered a detector reaction within the first 60 ns with a probability $p_{1}=97.6\%$ (7426 detector events out of 7608 test runs, see inset of Fig. 6) for a non-manipulated detector, while the probability of an onset event was $p_{2}=0.2\%$ (17 out of 7658 runs) for a manipulated detector caused by fake states. A local light emitter that is able to self-blind the detector is thus able to reveal the presence of both blinding and the fake state in a detector manipulation attempt.

Conclusion – We demonstrated self-testing of single photon detectors that can reliably reveal manipulation attacks. The self-testing strategy relies on a light source near the detector under possible external manipulation, and is able to detect both negative manipulations (i.e. suppression of single photon detections) and positive manipulations (i.e., generating detector events that are not caused by single photon detections) in a relatively short time with a high statistical significance. The detector self-testing makes no assumptions on the nature of the manipulation attack of the detector, and thus also covers manipulations that are not of the known nature like detector blinding and fake states. As the self-testing can be accomplished by a relatively simple light source (as long as this is outside the control and knowledge of an adversary), this scheme can address one of the most significant hardware vulnerabilities of QKD systems in a significantly simpler way as compared to device-independent or measurement-device independent approaches, and may even be a suitable to retrofit existing QKD systems to make them resilient against detector manipulation attacks.