Counterexamples to Gerbner’s Conjecture on Stability of Maximal $F$ -free Graphs

Jian Wang Shipeng Wang Weihua Yang Department of Mathematics, Taiyuan University of Technology, Taiyuan 030024, P. R. China. E-mail: [email protected]. Research supported by NSFC No.11701407.Department of Mathematics, Jiangsu University, Zhenjiang, Jiangsu 212013, P. R. China. E-mail: [email protected]. Research supported by NSFC No.12001242.Department of Mathematics, Taiyuan University of Technology, Taiyuan 030024, P. R. China. E-mail: [email protected]. Research supported by NSFC No.11671296.

Abstract

Let $F$ be an $(r+1)$ -color critical graph with $r\geq 2$ , that is, $\chi(F)=r+1$ and there is an edge $e$ in $F$ such that $\chi(F-e)=r$ . Gerbner recently conjectured that every $n$ -vertex maximal $F$ -free graph with at least $(1-\frac{1}{r})\frac{n^{2}}{2}-o(n^{\frac{r+1}{r}})$ edges contains an induced complete $r$ -partite graph on $n-o(n)$ vertices. Let $F_{s,k}$ be a graph obtained from $s$ copies of $C_{2k+1}$ by sharing a common edge. In this paper, we show that for all $k\geq 2$ if $G$ is an $n$ -vertex maximal $F_{s,k}$ -free graph with at least $n^{2}/4-o(n^{\frac{s+2}{s+1}})$ edges, then $G$ contains an induced complete bipartite graph on $n-o(n)$ vertices. We also show that it is best possible. This disproves Gerbner’s conjecture for $r=2$ .

1 Introduction

A graph is called $F$ -free if it does not contain $F$ as a subgraph. The extremal number $ex(n,F)$ is defined as the maximum number of edges in an $F$ -free $n$ -vertex graph. Let $T_{r}(n)$ be the complete $r$ -partite graph on $n$ vertices with partition classes of size $\lfloor\frac{n}{r}\rfloor$ or $\lceil\frac{n}{r}\rceil$ and let $t_{r}(n)$ be the number of edges in $T_{r}(n)$ . The classical Turán Theorem [7] shows that $ex(n,K_{r+1})=t_{r}(n)$ and $T_{r}(n)$ is the unique graph attaining it. Since then the problem of determining $ex(n,F)$ becomes a central topic in extremal graph theory, which has been extensively studied.

In the past decades, many stability extensions to extremal problems were also well-studied. The stability phenomenon is that if an $F$ -free graph is “close” to extremal in the number of edges, then it must be “close” to the extremal graph in its structure. The famous stability theorem of Erdős and Simonovits [2, 5] implies the following: if $G$ is a $K_{r+1}$ -free graph with $t_{r}(n)-o(n^{2})$ edges, then $G$ can be made into a copy of $T_{r}(n)$ by adding or deleting $o(n^{2})$ edges.

A graph $G$ is called maximal $F$ -free if it is $F$ -free and the addition of any edge in the complement $\overline{G}$ creates a copy of $F$ . Tyomkyn and Uzzel [8] considered a different kind of stability problems: when can one guarantee an ‘almost spanning’ complete $r$ -partite subgraph in a maximal $K_{r+1}$ -free graph $G$ with $t_{r}(n)-o(n^{2})$ edges? They showed that every maximal $K_{4}$ -free graph $G$ with $t_{3}(n)-cn$ edges contains a complete $3$ -partite subgraph on $(1-o(1))n$ vertices. Popielarz, Sahasrabudhe and Snyder [4] completely answered this question.

Theorem 1.1 ([4]).

Let $r\geq 2$ be an integer. Every maximal $K_{r+1}$ -free on $n$ vertices with at least $t_{r}(n)-o(n^{\frac{r+1}{r}})$ edges contains an induced complete $r$ -partite subgraph on $(1-o(1))n$ vertices.

Let $f(F,n,m)$ be the maximum integer $t$ such that every maximal $F$ -free graph with at least $ex(n,F)-t$ edges contains an induced complete $(\chi(F)-1)$ -partite subgraph on $n-m$ vertices. Popielarz, Sahasrabudhe and Snyder [4] give constructions to show that $f(K_{r+1},n,o(n))=o(n^{\frac{r+1}{r}})$ . In [9], Theorem 1.1 was extended to maximal $C_{2k+1}$ -free graphs.

Theorem 1.2 ([9]).

For every $k\geq 1$ , $f(C_{2k+1},n,o(n))=o(n^{\frac{3}{2}})$ .

We say that a graph $F$ is $(r+1)$ -color-critical, if $\chi(F)=r+1$ but there is an edge $e$ in it such that $\chi(F-e)=r$ . Recently, Gerbner proposed the following conjecture.

Conjecture 1.3 ([1]).

Let $r\geq 2$ be an integer and $F$ be an $(r+1)$ -color critical graph. Then $f(F,n,o(n))\geq o(n^{\frac{r+1}{r}})$ .

He verified Conjecture 1.3 for some special 3-color-critical graphs.

Theorem 1.4 ([1]).

Let $F$ be a 3-color-critical graph in which every edge has a vertex that is contained in a triangle. Then $f(F,n,o(n))\geq o(n^{\frac{3}{2}})$ .

Let $F_{s,k}$ be a graph obtained from $s$ copies of $C_{2k+1}$ by sharing a common edge. It is easy to see that $F_{s,k}$ is 3-color-critical. Note that each vertex of $F_{s,1}$ is contained in a triangle, and so $f(F_{s,1},n,o(n))\geq o(n^{\frac{3}{2}})$ by Theorem 1.4. Actually, one can show that $f(F_{s,1},n,o(n))=o(n^{\frac{3}{2}})$ by a similar construction in [4]. Since $F_{1,k}=C_{2k+1}$ , $f(F_{1,k},n,o(n))$ has been determined in Theorem 1.2.

In this paper, we extend the two results above and determine $f(F_{s,k},n,o(n))$ for all $k\geq 2$ and $s\geq 2$ , and this disproves Conjecture 1.3 for $r=2$ .

Theorem 1.5.

For $k\geq 2$ and $s\geq 2$ ,

f(F_{s,k},n,o(n))=o(n^{\frac{s+2}{s+1}}).

We prove Theorem 1.5 by the following two lemmas.

Lemma 1.6.

For $k,s\geq 2$ , $0\leq\alpha\leq\frac{1}{2}$ and $n\geq\frac{8k^{2}s^{2}}{\alpha}$ , there is a maximal $F_{s,k}$ -free graph $G$ with $e(G)\geq\frac{n^{2}}{4}-2ks\alpha n^{\frac{s+2}{s+1}}$ such that any induced complete bipartite subgraph of $G$ has at most $(1-\alpha^{s})n$ vertices.

Lemma 1.7.

Let $k,s\geq 2$ . For sufficiently large $n$ and $0<\alpha<1$ , if $G$ is an $n$ -vertex maximal $F_{s,k}$ -free graph with at least $n^{2}/4-\alpha n^{\frac{s+2}{s+1}}$ edges, then $G$ contains an induced complete bipartite graph on $n-4\cdot(12sk)^{s+3}\alpha n$ vertices.

In the rest of the paper, we prove Lemma 1.6 in Section 2 and prove Lemma 1.7 in Section 3. We follow standard notation throughout. Let $G$ be a graph. Denote by $\bar{G}$ the complement of $G$ . For $v\in V(G)$ , we use $N_{G}(v)$ to denote the set of neighbors of $v$ in $G$ and let $\deg_{G}(v)=|N_{G}(v)|$ . Denote by $\delta(G)$ the minimum degree of $G$ . Let $S$ be a subset of $V(G)$ . We use $N_{G}(v,S)$ to denote the set of neighbors of $v$ in $S$ and let $\deg_{G}(v,S)=|N_{G}(v,S)|$ . Denote by $G[S]$ and $G-S$ the subgraphs of $G$ induced by $S$ and $V(G)\setminus S$ , respectively. When $S=\{v\}$ , we simply write $G-v$ for $G-\{v\}$ . Denote by $e_{G}(S)$ the number of edges of $G$ with both ends in $S$ . For $xy\in E(\bar{G})$ , let $G+xy$ be the graph obtained from $G$ by adding $xy$ . For $xy\in E(G)$ , let $G-xy$ be the graph obtained from $G$ by deleting $xy$ . For any two disjoint subsets $X,Y$ of $V(G)$ , let $G[X,Y]$ denote the bipartite subgraph of $G$ with the partite sets $X,Y$ and the edge set

\{xy\in E(G)\colon x\in X\mbox{ and }y\in Y\}.

Denote by $e_{G}(X,Y)$ the number of edges in $G[X,Y]$ . We also use $E[X,Y]$ and $\bar{E}[X,Y]$ to denote the edge set of $G[X,Y]$ and $\bar{G}[X,Y]$ , respectively. We often omit the subscript when the underlying graph is clear. We also omit the floor and ceiling signs where they do not affect the arguments.

2 Proof of Lemma 1.6

In this section, we give a construction to show that for every small $\varepsilon>0$ , there is a maximal $F_{s,k}$ -free graph with at least $\frac{n^{2}}{4}-\varepsilon n^{\frac{s+2}{s+1}}$ edges, from which a positive fraction of vertices has to be deleted to obtain an induced complete bipartite subgraph. First we introduce a function about the $t$ -ary representations of positive integers, which will be used in our construction.

Definition 2.1.

For every integer $s,t\geq 2$ and $x\in[0,t^{s}-1]$ , $x$ can be expressed uniquely as follows:

x=q_{s-1}t^{s-1}+q_{s-2}t^{s-2}+\ldots+q_{1}t+q_{0},

where $q_{0},q_{1},\ldots,q_{s-1}\in[0,t-1]$ . We define the function $b_{t,s}(x,p)=q_{p}$ for $p=0,1,\ldots,s-1$ .

We construct a class of graphs, which contains the desired graph.

Definition 2.2.

Given $k\geq 2$ , $s\geq 2$ , $0<\alpha<\frac{1}{2}$ and $n\geq\frac{8k^{2}s^{2}}{\alpha}$ . Let $t=\alpha n^{\frac{1}{s+1}}$ and let $\mathcal{G}_{s,k,\alpha}(n)$ be a class of graphs as follows. A graph $G$ on $n$ vertices is in $\mathcal{G}_{s,k,\alpha}(n)$ if $V(G)$ can be partitioned into subsets

X_{0},\ldots,X_{t^{s}-1},X_{t^{s}},Y_{0},\ldots,Y_{t^{s}-1},Y_{t^{s}}

and

Z_{0,0},\ldots,Z_{0,t-1},Z_{1,0},\ldots,Z_{1,t-1},\ldots,Z_{s-1,0},\ldots,Z_{s-1,t-1}

such that:

(i)

For each $p=0,\ldots,s-1$ and $q=0,\ldots,t-1$ , $|Z_{p,q}|=2k-1$ and $G[Z_{p,q}]$ contains a path of length $2k-2$ , say $z_{p,q}^{1}z_{p,q}^{2}\ldots z_{p,q}^{2k-1}$ .

(ii)

For each $i=0,1,\ldots,t^{s}-1$ ,

|X_{i}|=|Y_{i}|=n^{\frac{1}{s+1}}.

and $X_{t^{s}},Y_{t^{s}}$ is a balanced partition of

V(G)\setminus\bigcup_{0\leq i\leq t^{s}-1}(X_{i}\cup Y_{i})\setminus\bigcup_{\begin{subarray}{c}0\leq p\leq s-1\\[2.0pt] 0\leq q\leq t-1\end{subarray}}Z_{p,q}.

(iii)

For each $i=0,\ldots,t^{s}-1$ , $G[X_{i},Y_{i}]$ is empty and $G[X_{t^{s}},Y_{t^{s}}]$ is complete. For each $i,j\in\{0,\ldots,t^{s}\}$ with $i\neq j$ , $G[X_{i},Y_{j}]$ is complete.
(iv)

Let $I(t,s,p,q)=\{i\in[0,t^{s}-1]:b_{t,s}(i,p)=q\}$ . For each $p=0,\ldots,s-1$ and each $q=0,\ldots,t-1$ , $z_{p,q}^{1}$ is adjacent to every vertex in

$\bigcup_{i\in I(t,s,p,q)}X_{i},$

and $z_{p,q}^{2k-1}$ is adjacent to every vertex in

$\bigcup_{i\in I(t,s,p,q)}Y_{i}.$

When refer to vertex classes of a graph in $\mathcal{G}_{s,k,\alpha}$ , we use $X,Y,Z_{p}$ and $Z$ to denote

\bigcup_{0\leq i\leq t^{s}}X_{i},\ \bigcup_{0\leq i\leq t^{s}}Y_{i},\ \bigcup_{0\leq q\leq t-1}Z_{p,q}\mbox{ and }\bigcup_{\begin{subarray}{c}0\leq p\leq s-1\\[2.0pt] 0\leq q\leq t-1\end{subarray}}Z_{p,q},

respectively.

Proposition 2.3.

If $G$ is the graph in $\mathcal{G}_{s,k,\alpha}(n)$ with minimum number of edges, then $G$ is $F_{s,k}$ -free.

Proof.

Suppose not, let $H$ be a copy of $F_{s,k}$ in $G$ . By Definition 2.2 (i), $G[Z_{p,q}]$ is a path of length $2k-2$ for $p=0,1,\ldots,s-1$ and $q=0,1,\ldots,t-1$ . Note that $z_{p,q}^{k}$ is the middle vertex on the path $G[Z_{p,q}]$ . Let

\left\{\begin{array}[]{l}Z_{p,q}^{1}=\{z_{p,q}^{r}\colon r<k\mbox{ and $r$ is odd}\}\cup\{z_{p,q}^{r}\colon r>k\mbox{ and $r$ is even}\},\\[6.0pt] Z_{p,q}^{2}=\{z_{p,q}^{r}\colon r<k\mbox{ and $r$ is even}\}\cup\{z_{p,q}^{r}\colon r>k\mbox{ and $r$ is odd}\}.\end{array}\right.

Clearly, $Z_{p,q}=Z_{p,q}^{1}\cup Z_{p,q}^{2}\cup\{z_{p,q}^{k}\}$ . By Definition 2.2 (iv), $z_{p,q}^{1}$ is not adjacent to any vertex in $Y$ and $z_{p,q}^{2k-1}$ is not adjacent to any vertex in $X$ . It follows that both $X\cup Z_{p,q}^{2}$ and $Y\cup Z_{p,q}^{1}$ are independent sets of $G$ . Let

Z^{0}=\{z_{p,q}^{k}\colon 0\leq p\leq s-1,0\leq q\leq t-1\},\ Z^{1}=\bigcup_{\begin{subarray}{c}0\leq p\leq s-1\\[2.0pt] 0\leq q\leq t-1\end{subarray}}Z_{p,q}^{1}\mbox{ and }Z^{2}=\bigcup_{\begin{subarray}{c}0\leq p\leq s-1\\[2.0pt] 0\leq q\leq t-1\end{subarray}}Z_{p,q}^{2}.

Then $Z^{0}$ , $X\cup Z^{2}$ and $Y\cup Z^{1}$ are all independent sets of $G$ . Let $xy$ be the common edge of $s$ cycles in $H$ , and let $P^{0},P^{1},\ldots,P^{s-1}$ be $s$ paths of $H-xy$ . Since $\deg_{H}(x)=s+1>2$ , $\deg_{H}(y)=s+1>2$ and $\deg_{G}(z_{p,q}^{k})=2$ for every $p\in[0,s-1]$ and $q\in[0,t-1]$ , we have $\{x,y\}\cap Z^{0}=\emptyset$ . Since $G-Z_{0}$ is bipartite and $P^{i}+xy$ is an odd cycle for $i=0,1,\ldots,s-1$ , we see that $|V(P^{i})\cap Z^{0}|\geq 1$ , and let $z_{p_{i},q_{i}}^{k}\in V(P^{i})\cap Z^{0}$ . By Definition 2.2 (i), $G[Z_{p_{i},q_{i}}]=z_{p_{i},q_{i}}^{1}z_{p_{i},q_{i}}^{2}\ldots z_{p_{i},q_{i}}^{2k-1}$ is a subpath of $P^{i}$ . Then there are exactly two vertices on $P^{i}+xy$ that are not in $Z_{p_{i},q_{i}}$ . By Definition 2.2 (iv), all the neighbors of $z_{p_{i},q_{i}}^{1}$ except $z_{p_{i},q_{i}}^{2}$ are in $X\setminus X_{t^{s}}$ and all the neighbors of $z_{p_{i},q_{i}}^{2k-1}$ except $z_{p_{i},q_{i}}^{2k-2}$ are in $Y\setminus Y_{t^{s}}$ . Hence $V(P^{i}+xy)$ has one vertex in $X\setminus X_{t^{s}}$ , one vertex in $Y\setminus Y_{t^{s}}$ and all the other vertices in $Z_{p_{i},q_{i}}$ for each $i=0,1,\ldots,s-1$ .

For distinct $i,j\in\{0,1,\ldots,s-1\}$ , we claim that $p_{i}\neq p_{j}$ or $q_{i}\neq q_{j}$ . Otherwise, we have $V(P^{i}+xy)\cap V(P^{j}+xy)\supset Z_{p_{i},q_{i}}$ , implying that $|V(P^{i}+xy)\cap V(P^{j}+xy)|\geq 2k-1\geq 3$ , a contradiction. (Note that here is the only place we use $k\geq 2$ in the proof and explain that the construction fails for $k=1$ .) Thus $Z_{p_{i},q_{i}}$ and $Z_{p_{j},q_{j}}$ are disjoint, implying that $Z_{p_{i},q_{i}},Z_{p_{j},q_{j}}\subset V(H)\setminus\{x,y\}$ . Moreover, one of $x,y$ is the common neighbor of $z_{p_{i},q_{i}}^{1}$ and $z_{p_{j},q_{j}}^{1}$ and the other is the common neighbor of $z_{p_{i},q_{i}}^{2k-1}$ and $z_{p_{j},q_{j}}^{2k-1}$ . By Definition 2.2 (iv), $\{x,y\}\subset(X\setminus X_{t^{s}})\cup(Y\setminus Y_{t^{s}})$ . Without loss of generality, we may assume that $x\in X_{a}$ and $y\in Y_{b}$ with $a,b\in[0,t^{s}-1]$ . Since $xy$ is an edge in $H$ , we have $a\neq b$ .

Then $x$ is the common neighbor of $z^{1}_{p_{0},q_{0}},z^{1}_{p_{1},q_{1}},\ldots,z^{1}_{p_{s-1},q_{s-1}}$ and $y$ is the common neighbor of $z^{2k-1}_{p_{0},q_{0}},z^{2k-1}_{p_{1},q_{1}},\ldots,z^{2k-1}_{p_{s-1},q_{s-1}}$ . By Definition 2.2 (iv), we have $a\in I(t,s,p_{i},q_{i})$ and $b\in I(t,s,p_{i},q_{i})$ , implying that $b_{t,s}(a,p_{i})=q_{i}$ and $b_{t,s}(b,p_{i})=q_{i}$ for $i=0,1,\ldots,s-1$ . If $p_{i}=p_{j}$ for some $i\neq j$ , then $q_{i}=b_{t,s}(a,p_{i})=b_{t,s}(a,p_{j})=q_{j}$ , contradicting the fact that $p_{i}\neq p_{j}$ or $q_{i}\neq q_{j}$ . Thus $p_{0},p_{1},\ldots,p_{s-1}$ is a permutation of $\{0,1,\ldots,s-1\}$ . Without loss of generality, we assume that $p_{i}=i$ for $i=0,1,\ldots,s-1$ , then

a=q_{s-1}t^{s-1}+q_{s-2}t^{s-2}+\ldots+q_{1}t+q_{0}=b,

a contradiction. Therefore, $G$ is $F_{s,k}$ -free. ∎

Now we are in a position to prove Lemma 1.6.

Proof of Lemma 1.6..

By Proposition 2.3, we may choose a maximal $F_{s,k}$ -free graph $G$ in $\mathcal{G}_{s,k,\alpha}(n)$ .

Claim 1.

Both $X$ and $Y$ are independent sets in $G$ .

Proof.

By Definition 2.2 (iii), $G[X,Y_{t^{s}}]$ is complete bipartite. Note that

	$\displaystyle\|X\|>\|Y_{t^{s}}\|$	$\displaystyle=\frac{n-\|Z\|-\|X\setminus X_{t^{s}}\|-\|Y\setminus Y_{t^{s}}\|}{2}$
		$\displaystyle=\frac{n-st(2k-1)-2t^{s}n^{\frac{1}{s+1}}}{2}$
		$\displaystyle=\frac{n-s\alpha n^{\frac{1}{s+1}}(2k-1)-2(\alpha n^{\frac{1}{s+1}})^{s}n^{\frac{1}{s+1}}}{2}$
		$\displaystyle>\frac{n}{2}-ks\alpha n^{\frac{1}{s+1}}-\alpha^{s}n.$

Note that $s\geq 2,\alpha<\frac{1}{2}$ and $n\geq\frac{8k^{2}s^{2}}{\alpha}$ . Then

\displaystyle|X|>|Y_{t^{s}}|>\frac{n}{2}-\frac{ksn^{\frac{1}{3}}}{2}-\frac{n}{4}\geq\frac{n^{\frac{1}{3}}}{4}(n^{\frac{2}{3}}-2ks)\geq 2sk>|V(F_{s,k})|.

If there is an edge $e$ in $G[X]$ , then it is easy to find a copy of $F_{s,k}$ in $G[X\cup Y_{t^{s}}]$ because $F_{s,k}$ is 3-color-critical. Thus $X$ is an independent set of $G$ . Similarly, $Y$ is an independent set of $G$ . ∎

Claim 2.

For $i=0,1,\ldots,t^{s}-1$ , $G[X_{i},Y_{i}]$ is empty.

Proof.

Suppose not, and let $xy$ be an edge with $x\in X_{i}$ and $y\in Y_{i}$ . Assume that

i=q_{s-1}t^{s-1}+q_{s-2}t^{s-2}+\ldots+q_{1}t+q_{0}.

By Definition 2.2 (iv), $z^{1}_{0,q_{0}},\ldots,z^{1}_{s-1,q_{s-1}}$ have a common neighbor $x$ , and $z^{2k-1}_{0,q_{0}},\ldots,z^{2k-1}_{s-1,q_{s-1}}$ have a common neighbor $y$ . It follows that $G[Z_{0,q_{0}}\cup\ldots\cup Z_{s-1,q_{s-1}}\cup\{x,y\}]$ contains a copy of $F_{s,k}$ , contradicting the fact that $G$ is $F_{s,k}$ -free. ∎

By Claims 1 and 2, we have

$\displaystyle e(G[X\cup Y])$	$\displaystyle=\|X\|\|Y\|-\sum_{i=0}^{t^{s}-1}\|X_{i}\|\|Y_{i}\|$
	$\displaystyle\geq\left(\frac{n-(2k-1)st}{2}\right)^{2}-t^{s}\left(n^{\frac{1}{s+1}}\right)^{2}$
	$\displaystyle=\left(\frac{n-(2k-1)s\alpha n^{\frac{1}{s+1}}}{2}\right)^{2}-\alpha^{s}n^{\frac{s}{s+1}}n^{\frac{2}{s+1}}$
	$\displaystyle>\left(\frac{n}{2}-ks\alpha n^{\frac{1}{s+1}}\right)^{2}-\alpha^{s}n^{\frac{s+2}{s+1}}$
	$\displaystyle>\frac{n^{2}}{4}-ks\alpha n^{\frac{s+2}{s+1}}-\alpha^{s}n^{\frac{s+2}{s+1}}$
	$\displaystyle>\frac{n^{2}}{4}-2ks\alpha n^{\frac{s+2}{s+1}}.$	(2.1)

In the following, we shall show that any induced complete bipartite subgraph of $G$ has at most $(1-\frac{\alpha}{4})n$ vertices. Assume that $H$ is a largest induced complete bipartite subgraph of $G$ with vertex classes $A$ and $B$ . Note that each vertex of $X_{i}$ (or $Y_{i}$ ) plays the same role in $G$ . If there is a vertex in $X_{i}$ (or $Y_{i}$ ) belongs to $V(H)$ , then by the maximality of $H$ , every vertex of $X_{i}$ (or $Y_{i}$ ) belongs to $V(H)$ .

Suppose first that $X_{t^{s}}\cap(A\cup B)=\emptyset$ or $Y_{t^{s}}\cap(A\cup B)=\emptyset$ . Then

$\displaystyle\|A\|+\|B\|$	$\displaystyle\leq n-\min\{\|X_{t^{s}}\|,\|Y_{t^{s}}\|\}$
	$\displaystyle=n-\frac{n-\|Z\|-\|X\setminus X_{t^{s}}\|-\|Y\setminus Y_{t^{s}}\|}{2}$
	$\displaystyle=\frac{n+\|Z\|+\|X\setminus X_{t^{s}}\|+\|Y\setminus Y_{t^{s}}\|}{2}$
	$\displaystyle=\frac{n+s\alpha n^{\frac{1}{s+1}}(2k-1)+2(\alpha n^{\frac{1}{s+1}})^{s}n^{\frac{1}{s+1}}}{2}$
	$\displaystyle<\frac{n}{2}+ks\alpha n^{\frac{1}{s+1}}+\alpha^{s}n$
	$\displaystyle\leq\left(1-\alpha^{s}\right)n.$	(2.2)

Now suppose that $X_{t^{s}}\cap(A\cup B)\neq\emptyset$ and $Y_{t^{s}}\cap(A\cup B)\neq\emptyset$ . Then $X_{t^{s}},Y_{t^{s}}\subset A\cup B$ . Without loss of generality, we assume that $X_{t^{s}}\subset A$ and $Y_{t^{s}}\subset B$ . Since $G[X_{i},Y_{i}]$ ( $0\leq i\leq t^{s}-1$ ) is empty, and both $G[X_{i},Y_{t^{s}}]$ and $G[X_{t^{s}},Y_{i}]$ are complete bipartite, it follows that at most one of $X_{i}$ and $Y_{i}$ is in $A\cup B$ . Hence $H$ is missing at least $t^{s}$ of $X_{0},\ldots,X_{t^{s}-1},Y_{0},\ldots,Y_{t^{s}-1}$ and so

\displaystyle|A\cup B|

\displaystyle\leq n-t^{s}n^{\frac{1}{s+1}}=n-\alpha^{s}n=\left(1-\alpha^{s}\right)n.

(2.3)

This completes the proof. ∎

3 Proof of Lemma 1.7

In this section, we prove a stability theorem for maximal $F_{s,k}$ -free graphs. We say that a vertex of a graph $G$ is color-critical, if deleting that vertex results in $G$ with smaller chromatic number. The following two results are needed.

Lemma 3.1 ([1]).

Let $F$ be a 3-chromatic graph with a color-critical vertex and $n$ be sufficiently large. Let $\frac{20|V(F)|}{n}<\varepsilon<\frac{1}{11|V(F)|^{2}}$ . If $G$ is an $n$ -vertex $F$ -free graph with $|E(G)|\geq ex(n,F)-\varepsilon n^{2}$ , then there is a bipartite subgraph $G^{\prime}$ of $G$ with at least $(1-12|V(F)|\varepsilon)n$ vertices, at least $ex(n,F)-13|V(F)|\varepsilon n^{2}$ edges and minimum degree at least $\left(\frac{1}{2}-\frac{1}{11|V(F)|}\right)n$ such that every vertex of $G^{\prime}$ is adjacent in $G$ to at most $|V(F)|$ vertices in the same partite set of $G^{\prime}$ .

Theorem 3.2 ([6]).

Let $F$ be an $(r+1)$ -color-critical graph. There exists an $n_{0}$ such that if $n>n_{0}$ , then $ex(n,F)=t_{r}(n)$ .

We find a large induced bipartite subgraphs with useful structures in maximal $F_{s,k}$ -free graphs by the following lemma.

Lemma 3.3.

Let $G$ be an $n$ -vertex maximal $F_{s,k}$ -free graph with at least $\frac{n^{2}}{4}-\varepsilon n^{2}$ edges and let $h=|V(F_{s,k})|$ . Then there is a partition $(U,V,T)$ of $V(G)$ such that

(i)

$\left(\frac{1}{2}-\frac{1}{10h}\right)n\leq|U|,|V|\leq\left(\frac{1}{2}+\frac{1}{10h}\right)n$ and $|T|\leq 30h^{2}\varepsilon n$ ;
(ii)

$G[U\cup V]$ is an induced bipartite subgraph of $G$ with partite sets $U,V$ , minimum degree $\left(\frac{1}{2}-\frac{1}{10h}\right)n$ and at least $\frac{n^{2}}{4}-25h^{2}\varepsilon n^{2}$ edges;
(iii)

for every $x\in T$ , if $x$ has neighbors in $U$ (or $V$ ), then it has at least $h+1$ neighbors in $U$ (or $V$ ).

Proof.

Since $F_{s,k}$ is 3-color-critical, by Theorem 3.2 we have $ex(n,F_{s,k})=\lfloor\frac{n^{2}}{4}\rfloor$ . Since $F_{s,k}$ has two critical vertices, by Lemma 3.1 there is a bipartite subgraph $G^{\prime}$ of $G$ with at least $(1-12h\varepsilon)n$ vertices, at least $\frac{n^{2}}{4}-13h\varepsilon n^{2}$ edges and minimum degree at least $\left(\frac{1}{2}-\frac{1}{11h}\right)n$ . Let $U_{0},V_{0}$ be two partite sets of $G^{\prime}$ and let $T_{0}=V(G)\setminus V(G^{\prime})$ . Clearly, $\left(\frac{1}{2}-\frac{1}{11h}\right)n\leq|U_{0}|,|V_{0}|\leq\left(\frac{1}{2}+\frac{1}{11h}\right)n$ and $|T_{0}|\leq 12h\varepsilon n$ .

Claim 3.

Both $U_{0}$ and $V_{0}$ are independent sets in $G$ , that is, $G^{\prime}$ is induced.

Proof.

By contradiction, we may assume, without loss of generality, that $U_{0}$ is not an independent set. Then there is an edge $u_{1}u_{2}$ in $G[U_{0}]$ . Since $\delta(G^{\prime})\geq\left(\frac{1}{2}-\frac{1}{11h}\right)n$ and $|V_{0}|\leq\left(\frac{1}{2}+\frac{1}{11h}\right)n$ , each $u_{i}(i=1,2$ ) has at most $\frac{2n}{11h}$ non-neighbors in $V_{0}$ . It follows that $u_{1},u_{2}$ have at least $\left(\frac{1}{2}-\frac{5}{11h}\right)n$ common neighbors in $V_{0}$ . Let $V_{0}^{\prime}$ be the set of the common neighbors of $u_{1},u_{2}$ and $U_{0}^{\prime}=U_{0}\setminus\{u_{1},u_{2}\}$ . By $\delta(G^{\prime})\geq\left(\frac{1}{2}-\frac{1}{11h}\right)n$ and since $n$ is sufficiently large, we have

e(U_{0}^{\prime},V_{0}^{\prime})\geq|V_{0}^{\prime}|\left(\left(\frac{1}{2}-\frac{1}{11h}\right)n-2\right)>\left(\frac{1}{2}-\frac{5}{11h}\right)n\left(\frac{1}{2}-\frac{2}{11h}\right)n>\frac{n^{2}}{6}\geq\frac{(h+s-3)n}{2}.

By Erdős-Gallai theorem [3], there is a path $P$ on $h+s-1$ vertices in $G[U_{0}^{\prime},V_{0}^{\prime}]$ . We truncate $P$ into $s$ vertex-disjoint paths with endpoints in $V_{0}^{\prime}$ and each of length $2k-2$ . These paths together with $u_{1},u_{2}$ form a copy of $F_{s,k}$ , a contradiction. ∎

Let $T=T_{0}$ , $U=U_{0}$ and $V=V_{0}$ . Now we remove a small amount of vertices from $U$ to $T$ by a greedy algorithm. In each step, if there is a vertex $x\in T$ with $1\leq\deg(x,U)\leq h$ , then we remove all the neighbors of $x$ from $U$ to $T$ . If every vertex in $T$ either has at least $h+1$ neighbors or no neighbors in $U$ , then we stop. By Claim 3, $U_{0}$ is an independent set, then each vertex added in $T$ has no neighbors in $U$ . Moveover, if all the neighbors of $x\in T_{0}$ have been removed from $U$ to $T$ , then $x$ has no neighbors in the updated $U$ . Hence the algorithm will stop in at most $|T_{0}|$ steps. Let $U^{\prime}$ be the vertices removed from $U$ to $T$ by the algorithm. It follows that

|U^{\prime}|\leq h|T_{0}|\leq 12h^{2}\varepsilon n.

Then we remove a small amount of vertices from $V$ to $T$ similarly. In each step, if there is a vertex $x\in T$ with $1\leq\deg(x,V)\leq h$ , then we remove all the neighbors of $x$ from $V$ to $T$ . Similarly, the algorithm will stop in at most $|T_{0}|+|U^{\prime}|$ steps. Since $\delta(G^{\prime})\geq\left(\frac{1}{2}-\frac{1}{11h}\right)n$ , each $x\in U^{\prime}$ has at least $\left(\frac{1}{2}-\frac{1}{11h}\right)n$ neighbors in $V_{0}$ . It follows that each $x\in U^{\prime}$ has at least $\left(\frac{1}{2}-\frac{1}{11h}\right)n-(|T_{0}|+|U^{\prime}|)h\geq h+1$ neighbors in $V$ in the executing of the algorithm. That is, the neighbors of vertices in $U^{\prime}$ will not be removed in the algorithm. Hence, the algorithm will stop in at most $|T_{0}|$ steps. Let $V^{\prime}$ be the vertices removed from $V$ to $T$ by the algorithm. It follows that

|V^{\prime}|\leq h|T_{0}|\leq 12h^{2}\varepsilon n.

Let $U,V,T$ be the resulting sets at the end of the algorithm. By Claim 3 and since $U\subset U_{0},V\subset V_{0}$ , both $U$ and $V$ are independent sets. Let $G^{\prime\prime}$ be the bipartite subgraph induced by $U$ and $V$ . Since both $|U^{\prime}|$ and $|V^{\prime}|$ have size at most $12h^{2}\varepsilon n$ , we have

|T|\leq|T_{0}|+|U^{\prime}|+|V^{\prime}|\leq 12h\varepsilon n+24h^{2}\varepsilon n\leq 30h^{2}\varepsilon n,

and

	$\displaystyle e(G^{\prime\prime})$	$\displaystyle\geq e(G^{\prime})-(\|U^{\prime}\|+\|V^{\prime}\|)\cdot\max\{\|U_{0}\|,\|V_{0}\|\}$
		$\displaystyle\geq\frac{n^{2}}{4}-13h\varepsilon n^{2}-24h^{2}\varepsilon n\left(\frac{1}{2}+\frac{1}{11h}\right)n$
		$\displaystyle\geq\frac{n^{2}}{4}-25h^{2}\varepsilon n^{2},$

and

\delta(G^{\prime\prime})\geq\delta(G^{\prime})-\max\{|U^{\prime}|,|V^{\prime}|\}\geq\left(\frac{1}{2}-\frac{1}{11h}\right)n-12h^{2}\varepsilon n\geq\left(\frac{1}{2}-\frac{1}{10h}\right)n.

It follows that

\left(\frac{1}{2}-\frac{1}{10h}\right)n\leq|U|,|V|\leq\left(\frac{1}{2}+\frac{1}{10h}\right)n.

Moreover, for each $x\in T$ , $x$ either has at least $h+1$ neighbors or no neighbors in $U$ , and $x$ either has at least $h+1$ neighbors or no neighbors in $V$ . Thus the lemma holds. ∎

Lemma 3.4.

Let $G$ be a bipartite graph with partite sets $U,V$ and let $W$ be a subset of $U\cup V$ with $|W|=h$ . If $\left(\frac{1}{2}-\frac{1}{10h}\right)n\leq|U|,|V|\leq\left(\frac{1}{2}+\frac{1}{10h}\right)n$ , $\delta(G)\geq\left(\frac{1}{2}-\frac{1}{10h}\right)n$ and $n\geq 10h$ , then the following holds.

(i)

For every $u\in U,v\in V$ and every odd integer $l$ with $3\leq l\leq h$ , there is a $uv$ -path $P$ of length $l$ such that $(V(P)\setminus\{u,v\})\cap W=\emptyset$ .
(ii)

For every $u,v\in U$ and every even integer $l$ with $2\leq l\leq h$ , there is a $uv$ -path $P$ of length $l$ such that $(V(P)\setminus\{u,v\})\cap W=\emptyset$ .

Proof.

For any $u\in U,v\in V$ , let $A=N(v)\setminus(W\cup\{u\})$ and $B=N(u)\setminus(W\cup\{v\})$ . Then

\left(\frac{1}{2}-\frac{1}{10h}\right)n-h-1\leq|A|,|B|\leq\left(\frac{1}{2}+\frac{1}{10h}\right)n

and the minimum degree of $G[A,B]$ is at least

	$\displaystyle\delta(G)-\max\left\{\|U\|-\|A\|,\|V\|-\|B\|\right\}$	$\displaystyle\geq\left(\frac{1}{2}-\frac{1}{10h}\right)n-\left(\frac{n}{5h}+h+1\right)$
		$\displaystyle\geq\left(\frac{1}{2}-\frac{3}{10h}\right)n-h-1.$

It follows that

	$\displaystyle e(A,B)=\frac{1}{2}$	$\displaystyle\sum_{x\in A\cup B}\deg_{G[A,B]}(x)$
		$\displaystyle\geq\frac{1}{2}\left(\left(\frac{1}{2}-\frac{3}{10h}\right)n-h-1\right)(\|A\|+\|B\|)$
		$\displaystyle\geq\frac{1}{2}\left(\left(\frac{1}{2}-\frac{3}{10h}\right)10h-h-1\right)(\|A\|+\|B\|)$
		$\displaystyle>\frac{h}{2}(\|A\|+\|B\|)$
		$\displaystyle>\frac{(l-2)-1}{2}(\|A\|+\|B\|).$

For any odd integer $l$ with $3\leq l\leq h$ , there is a path of length $l-2$ in $G[A,B]$ by Erdős-Gallai Theorem [3], which together with $u,v$ is our desired path.

If $u,v\in U$ , then let $A=U\setminus(W\cup\{u,v\})$ and $B=N(u)\cap N(v)\setminus W$ . Clearly,

|A|\geq\left(\frac{1}{2}-\frac{1}{10h}\right)n-h-2

and

	$\displaystyle\|B\|$	$\displaystyle\geq\|N(u)\cap N(v)\|-h$
		$\displaystyle\geq\|N(u)\|+\|N(v)\|-\|V\|-h$
		$\displaystyle\geq 2\left(\frac{1}{2}-\frac{1}{10h}\right)n-\left(\frac{1}{2}+\frac{1}{10h}\right)n-h$
		$\displaystyle=\left(\frac{1}{2}-\frac{3}{10h}\right)n-h.$

The minimum degree of $G[A,B]$ is at least

	$\displaystyle\delta(G)-\max\left\{\|U\|-\|A\|,\|V\|-\|B\|\right\}$	$\displaystyle\geq\left(\frac{1}{2}-\frac{1}{10h}\right)n-\left(\frac{2n}{5h}+h\right)$
		$\displaystyle\geq\left(\frac{1}{2}-\frac{1}{2h}\right)n-h.$

It follows that

	$\displaystyle e(A,B)=\frac{1}{2}$	$\displaystyle\sum_{x\in A\cup B}\deg_{G[A,B]}(x)$
		$\displaystyle\geq\frac{1}{2}\left(\left(\frac{1}{2}-\frac{1}{2h}\right)n-h\right)(\|A\|+\|B\|)$
		$\displaystyle\geq\frac{1}{2}\left(\left(\frac{1}{2}-\frac{1}{2h}\right)10h-h\right)(\|A\|+\|B\|)$
		$\displaystyle>\frac{h}{2}(\|A\|+\|B\|)$
		$\displaystyle>\frac{l-1}{2}(\|A\|+\|B\|).$

For any even integer $l$ with $2\leq l\leq h$ , there is a path of length $l$ in $G[A,B]$ by Erdős-Gallai Theorem [3], say $x_{1}x_{2}\ldots x_{l+1}$ . If $x_{1},x_{l+1}\in A$ , then $ux_{2}\ldots x_{l}v$ is the desired path. If $x_{1},x_{l+1}\in B$ , then $ux_{3}\ldots x_{l+1}v$ is the desired path. This completes the proof. ∎

We need some definitions in the proof of Lemma 1.7. Let $F,G$ be two graphs. A homomorphism from $F$ to $G$ is a mapping $\phi:V(F)\rightarrow V(G)$ with the property that $\{\phi(u),\phi(v)\}\in E(G)$ whenever $\{u,v\}\in E(F)$ . A homomorphism from $F$ to $G$ is also called an $F$ -homomorphism in $G$ . If $\phi$ is injective, then $\phi$ is called an injective homomorphism. If $\phi$ is both injective and surjective, then $\phi$ is called an isomorphism. Now we prove Lemma 1.7 by a delicate vertex-deletion process.

Proof of Lemma 1.7..

Let $G$ be an $n$ -vertex maximal $F_{s,k}$ -free graph with at least $\frac{n^{2}}{4}-\varepsilon n^{2}$ edges and let $h=|V(F_{s,k})|$ . By Lemma 3.3, there is a partition $(U,V,T)$ of $V(G)$ satisfying conditions (i), (ii) and (iii) of Lemma 3.3. Let $G^{\prime}=G[U,V]$ . We are left to delete vertices in $G^{\prime}$ until the resulting graph is complete bipartite.

We write $F$ instead of $F_{s,k}$ for simplicity. For any non-edge $xy$ of $G^{\prime}$ with $x\in U$ and $y\in V$ , $G+xy$ contains at least one copy of $F$ since $G$ is maximal $F$ -free. Let $F_{xy}$ be one of such copies and let $\phi_{xy}$ be the isomorphism from $F$ to $F_{xy}$ . Let

\Omega=\{xy\colon x\in U,\ y\in V\mbox{ and }xy\notin E(G^{\prime})\}.

Claim 4.

For each $xy\in\Omega$ , $N_{F_{xy}}(x)\cap T\neq\emptyset$ and $N_{F_{xy}}(y)\cap T\neq\emptyset$ .

Proof.

By contradiction, we may suppose that $N_{F_{xy}}(x)\cap T=\emptyset$ without loss of generality. Let $y_{0}=y,y_{1},\ldots,y_{p}$ be the neighbors of $x$ in $F_{xy}$ . Then $y_{1},\ldots,y_{p}$ are all in $V$ because $U$ is an independent set. Since the maximum degree of $F_{xy}$ is $s+1$ , it follows that $p\leq s$ . By Lemma 3.3 (ii), we have $\delta(G^{\prime})\geq\left(\frac{1}{2}-\frac{1}{10h}\right)n$ and $\left(\frac{1}{2}-\frac{1}{10h}\right)n\leq|U|\leq\left(\frac{1}{2}+\frac{1}{10h}\right)n$ , then each $y_{i}$ ( $i=0,1,\ldots,p$ ) has at most $\frac{n}{5h}$ non-neighbors in $U$ . Note that

h=s(2k-1)+2\geq 3s+2>2s+3\geq 2p+3

as $k\geq 2$ and $s\geq p$ . Therefore, the number of common neighbors of $y_{0},y_{1},\ldots,y_{p}$ in $U$ is at least

	$\displaystyle\left(\frac{1}{2}-\frac{1}{10h}\right)n-(p+1)\frac{n}{5h}$	$\displaystyle\geq\left(\frac{1}{2}-\frac{2p+3}{10h}\right)n$
		$\displaystyle>\left(\frac{1}{2}-\frac{1}{10}\right)n$
		$\displaystyle\geq\frac{2n}{5}$
		$\displaystyle>h.$

Thus, there is a vertex $x^{\prime}\in U$ such that $x^{\prime}\notin V(F_{xy})$ and $x^{\prime}y_{i}\in E(G)$ for $i=0,1,\ldots,p$ . Then by replacing $x$ with $x^{\prime}$ in $F_{xy}$ we obtain a copy of $F$ in $G$ , contradicting the fact that $G$ is $F$ -free. ∎

Let $a,b$ be the vertices of degree $s+1$ in $F$ and let $ac_{1}^{i}\ldots c_{2k-1}^{i}b$ ( $i=1,\ldots,s$ ) be those paths in $F-ab$ . Now we partition $\Omega$ into three classes as follows:

\left\{\begin{array}[]{l}\Omega_{1}=\left\{xy\in\Omega\colon\phi_{xy}^{-1}(x),\phi_{xy}^{-1}(y)\in V(F)\setminus\{a,b\}\right\},\\[6.0pt] \Omega_{2}=\left\{xy\in\Omega\colon\{\phi_{xy}^{-1}(x),\phi_{xy}^{-1}(y)\}=\{a,b\}\right\},\\[6.0pt] \Omega_{3}=\left\{xy\in\Omega\colon|\{\phi_{xy}^{-1}(x),\phi_{xy}^{-1}(y)\}\cap\{a,b\}|=1\right\}.\end{array}\right.

We delete a small amount of vertices from $U\cup V$ to destroy all non-edges in $\Omega$ in the following three steps.

Step 1. We can find $U_{1}\subset U$ and $V_{1}\subset V$ such that $|U\setminus U_{1}|+|V\setminus V_{1}|\leq 160h^{3}\varepsilon n^{\frac{3}{2}}$ and $\bar{E}[U_{1},V_{1}]\cap\Omega_{1}=\emptyset$ . That is, by deleting at most $160h^{3}\varepsilon n^{\frac{3}{2}}$ vertices from $U\cup V$ we destroy all non-edges in $\Omega_{1}$ .

Proof.

If $\Omega_{1}=\emptyset$ , we have nothing to do. So assume that $\Omega_{1}\neq\emptyset$ , then there is a non-edge $xy$ in $\Omega_{1}$ with $x\in U$ and $y\in V$ . By definition of $\Omega_{1}$ , we see that both $x$ and $y$ have degree two in $F_{xy}$ . By Claim 4, $N_{F_{xy}}(x)\cap T\neq\emptyset$ and $N_{F_{xy}}(y)\cap T\neq\emptyset$ . Let $x^{*}\in N_{F_{xy}}(x)\cap T$ and $y^{*}\in N_{F_{xy}}(y)\cap T$ . Then $x^{*}\neq y^{*}$ since $F_{xy}$ is triangle-free. Let $X=N_{G}(x^{*},U)$ , $Y=N_{G}(y^{*},V)$ and let $S$ be one of $X$ and $Y$ with smaller size.

For any edge $x^{\prime}y^{\prime}$ in $G$ with $x^{\prime}\in X$ and $y^{\prime}\in Y$ , if $\{x^{\prime},y^{\prime}\}\cap V(F_{xy})=\emptyset$ , then by replacing $x,y$ with $x^{\prime},y^{\prime}$ in $F_{xy}$ we obtain a copy of $F$ in $G$ , a contradiction. Thus, every edge in $G[X,Y]$ intersects $V(F_{xy})$ , implying that $e(X,Y)\leq h(|X|+|Y|)$ . Then

e_{\bar{G}}(X,Y)=|X||Y|-e(X,Y)\geq|X||Y|-h(|X|+|Y|).

Without loss of generality, we assume that $|X|\leq|Y|$ , then $S=X$ . If $|S|\geq 4h$ , then

	$\displaystyle e_{\bar{G}}(X,Y)$	$\displaystyle\geq\|S\|\|Y\|-h(\|S\|+\|Y\|)$
		$\displaystyle=\|Y\|(\|S\|-h)-h\|S\|$
		$\displaystyle\geq\|S\|^{2}-2h\|S\|$
		$\displaystyle\geq\frac{\|S\|^{2}}{2}>\frac{\|S\|^{2}}{16h^{2}}.$

If $|S|<4h$ , then since $xy$ is a non-edge of $G$ between $X$ and $Y$ , we have

e_{\bar{G}}(X,Y)\geq 1>\frac{|S|^{2}}{16h^{2}}.

Thus, there are at least $\frac{|S|^{2}}{16h^{2}}$ non-edges between $X$ and $Y$ . We delete vertices in $S$ from $U\cup V$ and let $U^{\prime}=U\setminus S$ and $V^{\prime}=V\setminus S$ . If $\bar{E}[U^{\prime},V^{\prime}]\cap\Omega_{1}=\emptyset$ , then we are done. Otherwise, there is another non-edge $xy$ in $\Omega_{1}$ with $x\in U^{\prime},y\in V^{\prime}$ , and we delete another $S^{\prime}$ from $U^{\prime}\cup V^{\prime}$ incidents with at least $\frac{|S^{\prime}|^{2}}{16h^{2}}$ non-edges between $U^{\prime}$ and $V^{\prime}$ . By deleting vertices greedily, we shall obtain a sequence of disjoint sets $S_{1},S_{2},\ldots,S_{l}$ in $U\cup V$ such that $\bar{E}[U\setminus(S_{1}\cup\ldots\cup S_{l}),V\setminus(S_{1}\cup\ldots\cup S_{l})]\cap\Omega_{1}=\emptyset$ . In each step of the greedy algorithm, there is a $u\in T$ such that either $N(u)\cap U$ or $N(u)\cap V$ is deleted, implying that $l\leq 2|T|$ .

By Lemma 3.3 (ii), $G[U,V]$ has at least $\frac{n^{2}}{4}-25h^{2}\varepsilon n^{2}$ edges. It follows that the number of non-edges between $U$ and $V$ is at most

|U||V|-\left(\frac{n^{2}}{4}-25h^{2}\varepsilon n^{2}\right)\leq 25h^{2}\varepsilon n^{2}.

Thus,

\displaystyle\sum_{i=1}^{l}\frac{|S_{i}|^{2}}{16h^{2}}\leq 25h^{2}\varepsilon n^{2}.

(3.1)

By Cauchy-Schwarz inequality, we have

\displaystyle\left(\sum_{i=1}^{l}|S_{i}|\right)^{2}\leq\left(\sum_{i=1}^{l}|S_{i}|^{2}\right)l.

(3.2)

Note that $|T|\leq 30h^{2}\varepsilon n$ from Lemma 3.3 (i). By (3.1), (3.2) and $l\leq 2|T|$ , we arrive at

\left(\sum_{i=1}^{l}|S_{i}|\right)^{2}\leq 16h^{2}\cdot 25h^{2}\varepsilon n^{2}l\leq 20^{2}h^{4}\varepsilon n^{2}\cdot 2|T|\leq 20^{2}h^{4}\varepsilon n^{2}\cdot 60h^{2}\varepsilon n.

Let $U_{1}=U\setminus(S_{1}\cup\ldots\cup S_{l})$ and $V_{1}=V\setminus(S_{1}\cup\ldots\cup S_{l})$ . Then

|U\setminus U_{1}|+|V\setminus V_{1}|\leq\sum_{i=1}^{l}|S_{i}|\leq 160h^{3}\varepsilon n^{\frac{3}{2}}

and Step 1 is finished. ∎

Step 2. We can find $U_{2}\subset U_{1}$ and $V_{2}\subset V_{1}$ such that $|U_{1}\setminus U_{2}|+|V_{1}\setminus V_{2}|\leq(6h)^{s+3}\varepsilon^{\frac{s+1}{2}}n^{\frac{s+2}{2}}$ and $\bar{E}[U_{2},V_{2}]\cap(\Omega_{1}\cup\Omega_{2})=\emptyset$ . That is, by deleting at most $(6h)^{s+2}\varepsilon^{\frac{s+1}{2}}n^{\frac{s+2}{2}}$ vertices from $U_{1}\cup V_{1}$ we destroy all non-edges in $\Omega_{2}$ .

Proof.

By Step 1, we see that $E[U_{1},V_{1}]\cap\Omega_{1}=\emptyset$ . Thus, we are left to delete vertices from $U_{1}\cup V_{1}$ to destroy all non-edges in $\Omega_{2}\cap\bar{E}[U_{1},V_{1}]$ . If $\Omega_{2}\cap\bar{E}[U_{1},V_{1}]=\emptyset$ , we have nothing to do. So assume that $\Omega_{2}\cap\bar{E}[U_{1},V_{1}]\neq\emptyset$ , then there is a non-edge $xy$ in $\Omega_{2}$ with $x\in U_{1}$ and $y\in V_{1}$ . For $xy\in\Omega_{2}$ , let

\mathcal{F}_{xy}=\left\{F_{xy}\colon F_{xy}\mbox{ is a copy of }F\mbox{ in }G+xy\mbox{ with }\deg_{F_{xy}}(x)=\deg_{F_{xy}}(y)=s+1\right\}.

Clearly, $\mathcal{F}_{xy}\neq\emptyset$ .

Claim 5.

There is an $F_{xy}\in\mathcal{F}_{xy}$ such that

(i)

for every $u\in V(F_{xy})\setminus\left(T\cup\{x,y\}\right)$ , $\deg_{F_{xy}}(u,T)\leq 1$ ;
(ii)

for every $uv\in E(F_{xy}-T-\{x,y\})$ , $\deg_{F_{xy}}(u,T)+\deg_{F_{xy}}(v,T)\leq 1$ .

Proof.

For any $F_{xy}\in\mathcal{F}_{xy}$ , let

\theta_{1}(F_{xy})=\left|\left\{u\in V(F_{xy})\setminus\left(T\cup\{x,y\}\right)\colon\deg_{F_{xy}}(u,T)=2\right\}\right|

and

\theta_{2}(F_{xy})=\left|\left\{uv\in E(F_{xy}-T-\{x,y\})\colon\deg_{F_{xy}}(u,T)+\deg_{F_{xy}}(v,T)\geq 2\right\}\right|.

We choose $F_{xy}$ from $\mathcal{F}_{xy}$ such that $\theta_{1}(F_{xy})+\theta_{2}(F_{xy})$ is minimized, and show that $\theta_{1}(F_{xy})=\theta_{2}(F_{xy})=0$ to finish the proof. Suppose first that $\theta_{1}(F_{xy})\geq 1$ . Then there is a $u\in V(F_{xy})\setminus\left(T\cup\{x,y\}\right)$ such that $\deg_{F_{xy}}(u,T)=2$ . Let $C=xy\ldots u_{1}^{*}uu_{2}^{*}\ldots x$ be the cycle in $F_{xy}$ with $u_{1}^{*},u_{2}^{*}\in T$ . Clearly, $C$ has length $2k+1$ . Without loss of generality, we assume that $u\in U$ . If the path $uu_{2}^{*}\ldots x$ has even length $l$ , then by Lemma 3.4 (ii) with $W=V(F_{xy})$ there is a $ux$ -path $P$ of length $l$ in $G[U,V]$ such that $V(P)\cap V(F_{xy})=\{u,x\}$ . By replacing $uu_{2}^{*}\ldots x$ from $F_{xy}$ with $P$ , we obtain a new copy $F_{xy}^{\prime}$ of $F$ with $F_{xy}^{\prime}\in\mathcal{F}$ and $\theta_{1}(F_{xy}^{\prime})<\theta_{1}(F_{xy})$ , contradicting the choice of $F_{xy}$ . If the path $uu_{2}^{*}\ldots x$ has odd length $l$ , then by Lemma 3.4 (i) with $W=V(F_{xy})$ there is a $uy$ -path $Q$ of length $2k-l$ in $G[U,V]$ such that $V(Q)\cap V(F_{xy})=\{u,y\}$ . By replacing $y\ldots u_{1}^{*}u$ from $F_{xy}$ with $Q$ , we obtain a new copy $F_{xy}^{\prime}$ of $F$ with $F_{xy}^{\prime}\in\mathcal{F}$ and $\theta_{1}(F_{xy}^{\prime})<\theta_{1}(F_{xy})$ , contradicting the choice of $F_{xy}$ .

Suppose next that $\theta_{2}(F_{xy})\geq 1$ . Then there is an edge $uv\in E(F_{xy}-x-y)$ with $u\in U$ and $v\in V$ such that $\deg_{F_{xy}}(u,T)=\deg_{F_{xy}}(v,T)=1$ , say $N_{F_{xy}}(u,T)=\{u^{*}\}$ and $N_{F_{xy}}(v,T)=\{v^{*}\}$ . Let $C$ be the cycle in $F_{xy}$ containing $u,v,u^{*},v^{*},x,y$ . Assume that $C=xy\ldots u^{*}uvv^{*}\ldots x$ or $C=yx\ldots u^{*}uvv^{*}\ldots y$ . We now distinguish the following two cases.

Case 1. $C=xy\ldots u^{*}uvv^{*}\ldots x$ .

If $y\ldots u^{*}u$ has odd length $l$ , then by Lemma 3.4 (i) with $W=V(F_{xy})$ there is a $yu$ -path $P$ of length $l$ in $G[U,V]$ such that $V(P)\cap V(F_{xy})=\{y,u\}$ . By replacing $y\ldots u^{*}u$ from $F_{xy}$ with $P$ , we obtain a new copy $F_{xy}^{\prime}$ of $F$ with $F_{xy}^{\prime}\in\mathcal{F}_{xy}$ and $\theta_{2}(F_{xy}^{\prime})<\theta_{2}(F_{xy})$ , contradicting the choice of $F_{xy}$ . If $y\ldots u^{*}u$ has even length $l$ , then the path $vv^{*}\ldots x$ has odd length $2k-1-l$ . By Lemma 3.4 (i) with $W=V(F_{xy})$ there is a $vx$ -path $Q$ of length $2k-1-l$ in $G[U,V]$ such that $V(Q)\cap V(F_{xy})=\{v,x\}$ . By replacing $vv^{*}\ldots x$ from $F_{xy}$ with $Q$ , we obtain a new copy $F_{xy}^{\prime}$ of $F$ with $F_{xy}^{\prime}\in\mathcal{F}_{xy}$ and $\theta_{2}(F_{xy}^{\prime})<\theta_{2}(F_{xy})$ , contradicting the choice of $F_{xy}$ .

Case 2. $C=yx\ldots u^{*}uvv^{*}\ldots y$ .

If $x\ldots u^{*}u$ has even length $l$ , then by Lemma 3.4 (ii) with $W=V(F_{xy})$ there is a $xu$ -path $P$ of length $l$ in $G[U,V]$ such that $V(P)\cap V(F_{xy})=\{x,u\}$ . By replacing $x\ldots u^{*}u$ from $F_{xy}$ with $P$ , we obtain a new copy $F_{xy}^{\prime}$ of $F$ with $F_{xy}^{\prime}\in\mathcal{F}_{xy}$ and $\theta_{2}(F_{xy}^{\prime})<\theta_{2}(F_{xy})$ , contradicting the choice of $F_{xy}$ . If $x\ldots u^{*}u$ has odd length $l$ , then the path $vv^{*}\ldots y$ has even length $2k-1-l$ . By Lemma 3.4 (ii) with $W=V(F_{xy})$ there is a $vy$ -path $Q$ of length $2k-1-l$ in $G[U,V]$ such that $V(Q)\cap V(F_{xy})=\{v,y\}$ . By replacing $vv^{*}\ldots y$ from $F_{xy}$ with $Q$ , we obtain a new copy $F_{xy}^{\prime}$ of $F$ with $F_{xy}^{\prime}\in\mathcal{F}_{xy}$ and $\theta_{2}(F_{xy}^{\prime})<\theta_{2}(F_{xy})$ , contradicting the choice of $F_{xy}$ .

Thus $\theta_{1}(F_{xy})=\theta_{2}(F_{xy})=0$ and the claim follows. ∎

By Claim 4, both $N_{F_{xy}}(x)\cap T$ and $N_{F_{xy}}(y)\cap T$ are not empty, and let $N_{F_{xy}}(x)\cap T=\{x_{1}^{*},x_{2}^{*},\ldots,x_{p}^{*}\}$ , $N_{F_{xy}}(y)\cap T=\{y_{1}^{*},y_{2}^{*},\ldots,y_{q}^{*}\}$ . Then $\{x_{1}^{*},x_{2}^{*},\ldots,x_{p}^{*}\}\cap\{y_{1}^{*},y_{2}^{*},\ldots,y_{q}^{*}\}=\emptyset$ since $F$ is $K_{3}$ -free. Let $N_{F_{xy}}(x)\cap V=\{z_{1},z_{2},\ldots,z_{f},z_{f+1},\ldots,z_{s-p}\}$ such that $N_{F_{xy}}(z_{\ell})\cap T\neq\emptyset$ for $\ell\leq f$ and $N_{F_{xy}}(z_{\ell})\cap T=\emptyset$ for $f+1\leq\ell\leq s-p$ . In $F_{xy}$ , each $z_{\ell}$ ( $\ell=1,\ldots,f$ ) has one neighbor being $x$ and the other one $z_{\ell}^{*}$ in $T$ , and each $z_{\ell}$ ( $\ell=f+1,\ldots,s-p$ ) has one neighbor being $x$ and the other one $u_{\ell}$ in $U$ . Let $X$ be the set of common neighbors of $x_{1}^{*},x_{2}^{*},\ldots,x_{p}^{*}$ in $U_{1}$ and let $Z_{\ell}$ be the set of neighbors of $z_{\ell}^{*}$ in $V$ for each $\ell=1,\ldots,f$ . Similarly, $N_{F_{xy}}(y)\cap U=\{w_{1},w_{2},\ldots,w_{g},w_{g+1},\ldots,w_{s-q}\}$ such that $N_{F_{xy}}(w_{\ell})\cap T\neq\emptyset$ for $\ell\leq g$ and $N_{F_{xy}}(w_{\ell})\cap T=\emptyset$ for $g+1\leq\ell\leq s-q$ . In $F_{xy}$ , each $w_{\ell}$ ( $\ell=1,\ldots,g$ ) has one neighbor being $y$ and the other one $w_{\ell}^{*}$ in $T$ , and each $w_{\ell}$ ( $\ell=g+1,\ldots,s-q$ ) has one neighbor being $y$ and the other one $v_{\ell}$ in $V$ . Let $Y$ be the set of common neighbors of $y_{1}^{*},y_{2}^{*},\ldots,y_{q}^{*}$ in $V_{1}$ and let $W_{\ell}$ be the set of neighbors of $w_{\ell}^{*}$ in $U$ for each $\ell=1,\ldots,g$ as shown in Figure 1.

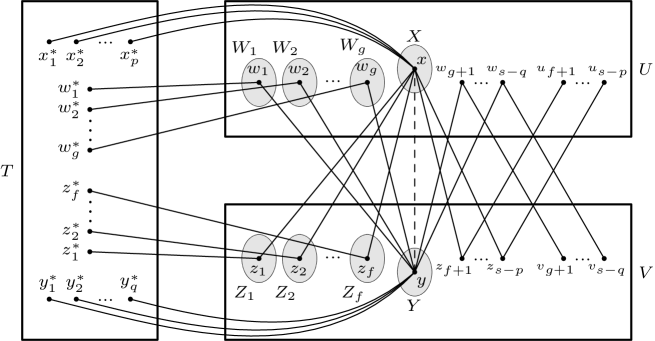
Refer to caption — Figure 1: The local structure of $F_{xy}$ with $xy\in\Omega_{2}$ .

For distinct vertices $x^{\prime}\in X,z_{1}^{\prime}\in Z_{1},\ldots,z_{f}^{\prime}\in Z_{f}$ , if $x^{\prime}z_{1}^{\prime},x^{\prime}z_{2}^{\prime},\ldots,x^{\prime}z_{f}^{\prime}$ are edges in $G$ then we say that $G[x^{\prime};z_{1}^{\prime},\ldots,z_{f}^{\prime}]$ is an $(X,Z_{1},\ldots,Z_{f})$ -star with center $x^{\prime}$ . Let

X_{0}=\left\{x^{\prime}\in X\colon\mbox{there exists }\mbox{an }(X,Z_{1},\ldots,Z_{f})\mbox{-star with center }x^{\prime}\right\}.

Clearly, $G[x;z_{1},\ldots,z_{f}]$ is an $(X,Z_{1},\ldots,Z_{f})$ -star, implying that $x\in X_{0}$ . Similarly, let

Y_{0}=\left\{y^{\prime}\in Y\colon\mbox{there exists }\mbox{a }(Y,W_{1},\ldots,W_{g})\mbox{-star with center }y^{\prime}\right\}

and clearly $y\in Y_{0}$ .

For any pair $(x^{\prime},y^{\prime})$ with $x^{\prime}\in X_{0}$ and $y^{\prime}\in Y_{0}$ , if there exist $z_{1}^{\prime},\ldots,z_{f}^{\prime}$ such that $G[x^{\prime};z_{1}^{\prime},\ldots,z_{f}^{\prime}]$ is an $(X,Z_{1},\ldots,Z_{f})$ -star and $y^{\prime}\notin\{z_{1}^{\prime},\ldots,z_{f}^{\prime}\}$ , then we say that $y^{\prime}$ is good to $x^{\prime}$ ; otherwise $y^{\prime}$ is bad to $x^{\prime}$ . Similarly, if there exist $w_{1}^{\prime},\ldots,w_{g}^{\prime}$ such that $G[y^{\prime};w_{1}^{\prime},\ldots,w_{g}^{\prime}]$ is a $(Y,W_{1},\ldots,W_{g})$ -star and $x^{\prime}\notin\{w_{1}^{\prime},\ldots,w_{g}^{\prime}\}$ , then we say that $x^{\prime}$ is good to $y^{\prime}$ , otherwise $x^{\prime}$ is bad to $y^{\prime}$ . We call $(x^{\prime},y^{\prime})$ a compatible pair if $y^{\prime}$ is good to $x^{\prime}$ and $x^{\prime}$ is good to $y^{\prime}$ ; otherwise we say that $(x^{\prime},y^{\prime})$ is incompatible. For each $x^{\prime}\in X_{0}$ , there exist $z_{1}^{\prime},\ldots,z_{f}^{\prime}$ such that $G[x^{\prime};z_{1}^{\prime},\ldots,z_{f}^{\prime}]$ is an $(X,Z_{1},\ldots,Z_{f})$ -star, implying that the number of vertices in $Y_{0}$ that are bad to $x^{\prime}$ is at most $f$ . Similarly, for each $y^{\prime}\in Y_{0}$ the number of vertices in $X_{0}$ that are bad to $y^{\prime}$ is at most $g$ . Then the number of incompatible pairs between $X_{0}$ and $Y_{0}$ is at most $f|X_{0}|+g|Y_{0}|$ . Thus, the number of compatible pairs between $X_{0}$ and $Y_{0}$ is at least $|X_{0}||Y_{0}|-f|X_{0}|-g|Y_{0}|$ .

Claim 6.

Every compatible pair $(x^{\prime},y^{\prime})$ with $x^{\prime}\in X_{0}$ and $y^{\prime}\in Y_{0}$ is a non-edge of $G[U_{1},V_{1}]$ .

Proof.

Suppose not, let $(x^{\prime},y^{\prime})$ with $x^{\prime}\in X_{0}$ , $y^{\prime}\in Y_{0}$ be a compatible pair and $x^{\prime}y^{\prime}\in E(G)$ . Then there exist $z_{1}^{\prime},\ldots,z_{f}^{\prime}$ and $w_{1}^{\prime},\ldots,w_{g}^{\prime}$ such that $G[x^{\prime},z_{1}^{\prime},\ldots,z_{f}^{\prime}]$ is an $(X,Z_{1},\ldots,Z_{f})$ -star and $G[y^{\prime};w_{1}^{\prime},\ldots,w_{g}^{\prime}]$ is a $(Y,W_{1},\ldots,W_{g})$ -star. We shall find a copy of $F$ in $G$ , which leads to a contradiction.

Let

R_{1}^{\prime}=\{x^{\prime},y^{\prime},z_{1}^{\prime},\ldots,z_{f}^{\prime},w_{1}^{\prime},\ldots,w_{g}^{\prime}\}.

Since $u_{\ell}$ $(f+1\leq\ell\leq s-p)$ and $x^{\prime}$ have at least $\left(\frac{1}{2}-\frac{1}{10h}\right)n$ common neighbors in $V$ and $n$ is sufficiently large, we may choose distinct $z_{f+1}^{\prime},\ldots,z_{s-p}^{\prime}$ from $V\setminus(V(F_{xy})\cup R_{1}^{\prime})$ such that $z_{\ell}^{\prime}\in N(x^{\prime},V)\cap N(u_{\ell},V)$ for each $\ell=f+1,\ldots,s-p$ . Similarly, we may choose distinct $w_{g+1}^{\prime},\ldots,w_{s-q}^{\prime}$ from $U\setminus(V(F_{xy})\cup R_{1}^{\prime})$ such that $w_{\ell}^{\prime}\in N(y^{\prime},U)\cap N(v_{\ell},U)$ for each $\ell=g+1,\ldots,s-q$ . Let

R_{1}=\{x,y,z_{1},\ldots,z_{f},w_{1},\ldots,w_{g}\},\ R_{2}=\{z_{f+1},\ldots,z_{s-p},w_{g+1},\ldots,w_{s-q}\}

and

R_{2}^{\prime}=\{z_{f+1}^{\prime},\ldots,z_{s-p}^{\prime},w_{g+1}^{\prime},\ldots,w_{s-q}^{\prime}\}.

Clearly, $R_{2}^{\prime}\cap(R_{1}^{\prime}\cup V(F_{xy}))=\emptyset$ . Let $F^{0}$ be a graph obtained from $F_{xy}$ by replacing vertices in $R_{1}\cup R_{2}$ with vertices in $R_{1}^{\prime}\cup R_{2}^{\prime}$ . If $R_{1}^{\prime}\cap(V(F_{xy})\setminus(R_{1}\cup R_{2}))=\emptyset$ , then $F^{0}$ is a copy of $F$ in $G$ , a contradiction. Hence $R_{1}^{\prime}\cap(V(F_{xy})\setminus(R_{1}\cup R_{2}))\neq\emptyset$ , that is, $F^{0}$ is the image of an $F$ -homomorphism but not a copy of $F$ .

Now we replace the overlapped vertices in $F^{0}$ to get a copy of $F$ by a greedy algorithm. Let $\phi_{0}$ be the homomorphism from $F$ to $F_{0}$ and let $\phi_{xy}$ be the isomorphism from $F$ to $F_{xy}$ . Then $\phi_{0}$ is not an isomorphism and $\phi_{xy}$ is an isomorphism. Let $R_{1}^{*}=\phi_{xy}^{-1}(R_{1})$ and $R_{2}^{*}=\phi_{xy}^{-1}(R_{2})$ . By the labeling of $F$ , we see that

\displaystyle R_{1}^{*}\cup R_{2}^{*}=\left\{a,b\right\}\cup\left\{c_{1}^{i}\colon\phi_{xy}(c_{1}^{i})\in U\cup V\right\}\cup\left\{c_{2k-1}^{i}\colon\phi_{xy}(c_{2k-1}^{i})\in U\cup V\right\}.

Let

\displaystyle R_{3}^{*}=\left\{u\in V(F)\colon\phi_{xy}(u)\in T\right\}\mbox{ and }R_{4}^{*}=\left(\cup_{i=1}^{s}\left\{c_{2}^{i},\ldots,c_{2k-2}^{i}\right\}\right)\setminus R_{3}^{*}.

(3.3)

Clearly, $(R_{1}^{*},R_{2}^{*},R_{3}^{*},R_{4}^{*})$ is a partition of $V(F)$ and $\phi_{xy}(R_{4}^{*})\subset U\cup V$ . Since for any edge $uv$ of $F$ with $u\in R_{1}^{*}$ we have $\phi_{xy}(v)\in T\cup R_{1}\cup R_{2}$ , it follows that $v\in R_{1}^{*}\cup R_{2}^{*}\cup R_{3}^{*}$ . Thus there is no edge between $R_{1}^{*}$ and $R_{4}^{*}$ in $F$ . Note that $\phi_{0}$ can be expressed explicitly as follows:

(i)

$\phi_{0}(\phi_{xy}^{-1}(x))=x^{\prime}$ and $\phi_{0}(\phi_{xy}^{-1}(y))=y^{\prime}$ ;
(ii)

for each $\ell=1,\ldots,s-p$ , $\phi_{0}(\phi_{xy}^{-1}(z_{\ell}))=z_{\ell}^{\prime}$ and for each $\ell=1,\ldots,s-q$ , $\phi_{0}(\phi_{xy}^{-1}(w_{\ell}))=w_{\ell}^{\prime}$ ;
(iii)

$\phi_{0}(c)=\phi_{xy}(c)$ for $c\in R_{3}^{*}\cup R_{4}^{*}$ .

Since vertices in $R_{2}^{\prime}$ are chosen disjoint from $V(F_{xy})\cup R_{1}^{\prime}$ , we have $\phi_{0}(R_{2}^{*})\cap\phi_{0}(R_{1}^{*}\cup R_{3}^{*}\cup R_{4}^{*})=\emptyset$ . Then $\phi_{0}(R_{1}^{*})\cap\phi_{0}(R_{4}^{*})\neq\emptyset$ because $\phi_{0}$ is not an isomorphism and $\phi_{xy}$ is an isomorphism.

For any $a\in R_{1}^{*}$ and $c\in R_{4}^{*}$ with $\phi_{0}(a)=\phi_{0}(c)$ , $\phi_{0}(c)=\phi_{0}(a)\in\phi_{0}(R_{1}^{*})=R_{1}^{\prime}\subset U\cup V$ . By (3.3) we have $c\in\cup_{i=1}^{s}\{c_{2}^{i},\ldots,c_{2k-2}^{i}\}$ . Let $d_{1},d_{2}$ be two neighbors of $c$ in $F$ . Clearly, $d_{i}$ has degree two in $F$ for $i=1,2$ . Since $c\in R_{4}^{*}$ and there is no edge between $R_{1}^{*}$ and $R_{4}^{*}$ in $F$ , it follows that $d_{1},d_{2}\notin R_{1}^{*}$ . Since $\phi_{0}(c)=\phi_{xy}(c)\in V(F_{xy})\setminus(T\cap\{x,y\})$ , at most one of $\phi_{xy}(d_{1}),\phi_{xy}(d_{2})$ is in $T$ by Claim 5 (i). Recall that $F^{0}$ is obtained from $F_{xy}$ by replacing vertices in $R_{1}\cup R_{2}$ with vertices in $R_{1}^{\prime}\cup R_{2}^{\prime}$ and never changing vertices in $T$ . Thus $|\{\phi_{0}(d_{1}),\phi_{0}(d_{2})\}\cap T|=|\{\phi_{xy}(d_{1}),\phi_{xy}(d_{2})\}\cap T|\leq 1$ . We shall find an $F$ -homomorphism $\phi_{1}$ such that $|\phi_{1}(V(F))|>|\phi_{0}(V(F))|$ by distinguishing two cases.

Case 1. $|\{\phi_{0}(d_{1}),\phi_{0}(d_{2})\}\cap T|=0$ .

Without loss of generality, we assume that $\phi_{0}(c)\in U$ and $\phi_{0}(d_{1}),\phi_{0}(d_{2})\in V$ . Since $\phi_{0}(d_{1}),\phi_{0}(d_{2})$ have at least $\left(\frac{1}{2}-\frac{1}{10h}\right)n$ common neighbors in $U$ , we may choose $u^{\prime}$ from $N(\phi_{0}(d_{1}))\cap N(\phi_{0}(d_{2}))\setminus\phi_{0}(V(F))$ . Define $\phi_{1}(c)=u^{\prime}$ and $\phi_{1}(a)=\phi_{0}(a)$ for all $a\in V(F)\setminus\{c\}$ . It is easy to see that $\phi_{1}$ is an $F$ -homomorphism with $|\phi_{1}(V(F))|=|\phi_{0}(V(F))|+1$ .

Case 2. $|\{\phi_{0}(d_{1}),\phi_{0}(d_{2})\}\cap T|=1$ .

Without loss of generality, we assume that $\phi_{0}(c)\in U$ , $\phi_{0}(d_{1})\in V$ and $\phi_{0}(d_{2})\in T$ . Recall that $d_{1}$ has exactly two neighbors in $F$ and one of them is $c$ , and let $d_{3}$ be the other one. Since $\phi_{xy}(cd_{1})$ is an edge of $F_{xy}-T-\{x,y\}$ , by Claim 5 (ii) $\deg_{F_{xy}}(\phi_{xy}(c),T)+\deg_{F_{xy}}(\phi_{xy}(d_{1}),T)\leq 1$ , that is, $|\phi_{xy}(\{d_{1},d_{2}\})\cap T|+|\phi_{xy}(\{c,d_{3}\})\cap T|\leq 1$ . Because $F^{0}$ is obtained from $F_{xy}$ by replacing vertices in $R_{1}\cup R_{2}$ with vertices in $R_{1}^{\prime}\cup R_{2}^{\prime}$ and never changing vertices in $T$ , we have $|\phi_{0}(\{d_{1},d_{2}\})\cap T|+|\phi_{0}(\{c,d_{3}\})\cap T|=|\phi_{xy}(\{d_{1},d_{2}\})\cap T|+|\phi_{xy}(\{c,d_{3}\})\cap T|\leq 1$ . Then $|\phi_{0}(\{c,d_{3}\})\cap T|=0$ by $|\phi_{0}(\{d_{1},d_{2}\})\cap T|=1$ , implying that $\phi_{0}(d_{3})\in U$ . Since $\phi_{0}(d_{2})$ has one neighbor $\phi_{0}(c)$ in $U$ , by Lemma 3.3 (iii) we know that $\phi_{0}(d_{2})$ has at least $h+1$ neighbors in $U$ , and let $u^{\prime}\in N(\phi_{0}(d_{2}),U)\setminus\phi_{0}(V(F))$ . Moreover, since $u^{\prime}$ and $\phi_{0}(d_{3})$ have at least $\left(\frac{1}{2}-\frac{1}{10h}\right)n>h$ common neighbors in $V$ , we may choose $v^{\prime}\in N(u^{\prime},V)\cap N(\phi_{0}(d_{3}),V)\setminus\phi_{0}(V(F))$ . Define $\phi_{1}(c)=u^{\prime}$ , $\phi_{1}(d_{1})=v^{\prime}$ and $\phi_{1}(a)=\phi_{0}(a)$ for all $a\in V(F)\setminus\{c,d_{1}\}$ . It is easy to see that $\phi_{1}$ is an $F$ -homomorphism with $|\phi_{1}(V(F))|\geq|\phi_{0}(V(F))|+1$ .

If $\phi_{1}$ is not an $F$ -isomorphism, then there exist $a^{\prime}\in R_{1}^{*}$ and $c^{\prime}\in R_{4}^{*}$ with $\phi_{1}(a^{\prime})=\phi_{1}(c^{\prime})$ . By the same argument above, we shall find an $F$ -homomorphism $\phi_{2}$ such that $|\phi_{2}(V(F))|>|\phi_{1}(V(F))|$ . Do this repeatedly, we get $F$ -homomorphisms $\phi_{1},\phi_{2},\ldots,\phi_{l},\ldots$ with $h-|R_{1}^{\prime}|\leq|\phi_{0}(V(F))|<|\phi_{1}(V(F))|<\cdots<|\phi_{l}(V(F))|<\cdots$ . Since $|\phi_{i}(V(F))|\leq h$ for all $i$ , we shall obtain an $F$ -isomorphism in at most $|R_{1}^{\prime}|$ steps, contradicting the fact that $G$ is $F$ -free. Thus, every compatible pair $(x^{\prime},y^{\prime})$ with $x^{\prime}\in X_{0}$ and $y^{\prime}\in Y_{0}$ is not an edge in $G[U_{1},V_{1}]$ . ∎

Recall that the number of compatible pairs between $X_{0}$ and $Y_{0}$ is at least $|X_{0}||Y_{0}|-f|X_{0}|-g|Y_{0}|$ . Since $f,g\leq h$ , it follows that

e_{\bar{G}}(X_{0},Y_{0})\geq|X_{0}||Y_{0}|-f|X_{0}|-g|Y_{0}|\geq|X_{0}||Y_{0}|-h(|X_{0}|+|Y_{0}|).

Let $S$ be one of $X_{0}$ and $Y_{0}$ with smaller size. By the same argument as in the proof of Step 1, we have

e_{\bar{G}}(X_{0},Y_{0})\geq\frac{|S|^{2}}{16h^{2}}.

We delete vertices in $S$ from $U_{1}\cup V_{1}$ and let $U_{1}^{\prime}=U_{1}\setminus S$ and $V_{1}^{\prime}=V_{1}\setminus S$ . If $\bar{E}[U_{1}^{\prime},V_{1}^{\prime}]\cap\Omega_{2}=\emptyset$ , then we are done. Otherwise, there is another non-edge $xy$ in $\Omega_{2}$ with $x\in U_{1}^{\prime}$ , $y\in V_{1}^{\prime}$ , and we delete another $S^{\prime}$ from $U_{1}^{\prime}\cup V_{1}^{\prime}$ incidents with at least $\frac{|S^{\prime}|^{2}}{16h^{2}}$ non-edges between $U_{1}^{\prime}$ and $V_{1}^{\prime}$ . By deleting vertices greedily, we shall obtain a sequence of disjoint sets $S_{1},S_{2},\ldots,S_{l}$ in $U_{1}\cup V_{1}$ such that $\bar{E}[U_{1}\setminus(S_{1}\cup\ldots\cup S_{l}),V_{1}\setminus(S_{1}\cup\ldots\cup S_{l})]\cap\Omega_{2}=\emptyset$ .

In each step of the greedy algorithm, there are vertices $x_{1}^{*},\ldots,x_{p}^{*},z_{1}^{*},\ldots z_{f}^{*}\in T$ and $y_{1}^{*},\ldots,y_{q}^{*},w_{1}^{*},\ldots w_{g}^{*}\in T$ such that either $X_{0}$ or $Y_{0}$ is deleted. If $X_{0}$ is deleted, then since $X$ is the set of common neighbors of $x_{1}^{*},\ldots,x_{p}^{*}$ in the $U_{1}\setminus X_{0}$ , there are no $(X,Z_{1},\ldots,Z_{f})$ -stars in the future steps. It follows that the tuple $(x_{1}^{*},\ldots,x_{p}^{*},z_{1}^{*},\ldots z_{f}^{*})$ will not appear in the future steps of the algorithm. Similarly, if $Y_{0}$ is deleted, then the tuple $(y_{1}^{*},\ldots,y_{q}^{*},w_{1}^{*},\ldots w_{g}^{*})$ will not appear in the future steps of the algorithm. Since $p+f\leq s$ and $q+g\leq s$ , it follows that

	$\displaystyle l$	$\displaystyle\leq\sum_{p+f\leq s}\binom{\|T\|}{p}\binom{\|T\|-p}{f}+\sum_{q+g\leq s}\binom{\|T\|}{q}\binom{\|T\|-q}{g}$
		$\displaystyle=2\sum_{p+f\leq s}\binom{\|T\|}{p}\binom{\|T\|-p}{f}$
		$\displaystyle\leq 2\sum_{p+f\leq s}\|T\|^{s}\leq 2s^{2}\|T\|^{s}.$

Similarly, by (3.1) and (3.2) we arrive at

\left(\sum_{i=1}^{l}|S_{i}|\right)^{2}\leq 16h^{2}\cdot 25h^{2}\varepsilon n^{2}l\leq 20^{2}h^{4}\varepsilon n^{2}\cdot 2s^{2}|T|^{s}\leq 20^{2}h^{4}\varepsilon n^{2}\cdot 2s^{2}(30h^{2}\varepsilon n)^{s}.

Let $U_{2}=U_{1}\setminus(S_{1}\cup\ldots\cup S_{l})$ and $V_{2}=V_{1}\setminus(S_{1}\cup\ldots\cup S_{l})$ . Then

|U_{1}\setminus U_{2}|+|V_{1}\setminus V_{2}|\leq\sum_{i=1}^{l}|S_{i}|\leq 20\sqrt{2}\cdot 30^{\frac{s}{2}}h^{s+2}s\varepsilon^{\frac{s+1}{2}}n^{\frac{s+2}{2}}\leq(6h)^{s+2}\varepsilon^{\frac{s+1}{2}}n^{\frac{s+2}{2}}

and Step 2 is finished. ∎

By Step 2, we see that $\bar{E}[U_{2},V_{2}]\cap(\Omega_{1}\cup\Omega_{2})=\emptyset$ . Thus, we are left to delete vertices from $U_{2}\cup V_{2}$ to destroy all non-edges in $\Omega_{3}\cap\bar{E}[U_{2},V_{2}]$ . If $\Omega_{3}\cap\bar{E}[U_{2},V_{2}]=\emptyset$ , we have nothing to do. Hence we assume that $\Omega_{3}\cap\bar{E}[U_{2},V_{2}]\neq\emptyset$ and let $xy$ be a non-edge in $\Omega_{3}$ with $x\in U_{2}$ and $y\in V_{2}$ . By definition of $\Omega_{3}$ , there is at least one copy $F_{xy}$ of $F$ such that $\deg_{F_{xy}}(x)=s+1$ and $\deg_{F_{xy}}(y)=2$ or $\deg_{F_{xy}}(x)=2$ and $\deg_{F_{xy}}(y)=s+1$ . We partition $\Omega_{3}$ into four classes as follows:

\left\{\begin{array}[]{l}\Omega_{31}=\left\{xy\in\Omega_{3}\colon\deg_{F_{xy}}(x)=s+1,\ \deg_{F_{xy}}(y)=2,\ \deg_{F_{xy}}(x,T)=s\right\},\\[6.0pt] \Omega_{32}=\left\{xy\in\Omega_{3}\colon\deg_{F_{xy}}(x)=2,\ \deg_{F_{xy}}(y)=s+1,\ \deg_{F_{xy}}(y,T)=s\right\},\\[6.0pt] \Omega_{33}=\left\{xy\in\Omega_{3}\colon\deg_{F_{xy}}(x)=s+1,\ \deg_{F_{xy}}(y)=2,\ \deg_{F_{xy}}(x,T)\leq s-1\right\},\\[6.0pt] \Omega_{34}=\left\{xy\in\Omega_{3}\colon\deg_{F_{xy}}(x)=2,\ \deg_{F_{xy}}(y)=s+1,\ \deg_{F_{xy}}(y,T)\leq s-1\right\}.\end{array}\right.

We complete the proof by the following two steps.

Step 3.1. We can find $U_{3}\subset U_{2}$ and $V_{3}\subset V_{2}$ such that $|U_{2}\setminus U_{3}|+|V_{2}\setminus V_{3}|\leq(6h)^{s+3}\varepsilon^{\frac{s+1}{2}}n^{\frac{s+2}{2}}$ and $\bar{E}[U_{3},V_{3}]\cap(\Omega_{31}\cup\Omega_{32})=\emptyset$ . That is, by deleting at most $(6h)^{s+3}\varepsilon^{\frac{s+1}{2}}n^{\frac{s+2}{2}}$ vertices from $U_{2}\cup V_{2}$ we destroy all non-edges in $\Omega_{31}\cup\Omega_{32}$ .

Proof.

If $\bar{E}[U_{2},V_{2}]\cap(\Omega_{31}\cup\Omega_{32})=\emptyset$ , we have nothing to do. So assume that $\bar{E}[U_{2},V_{2}]\cap(\Omega_{31}\cup\Omega_{32})\neq\emptyset$ , then there is a non-edge $xy$ in $\Omega_{31}\cup\Omega_{32}$ with $x\in U_{2}$ and $y\in V_{2}$ . Without loss of generality, we assume that $xy\in\Omega_{31}$ . By Claim 4, $\deg_{F_{xy}}(y,T)=1$ and let $N_{F_{xy}}(y,T)=\{y^{*}\}$ . Assume that

N_{F_{xy}}(x)\cap T=\{x_{1}^{*},x_{2}^{*},\ldots,x_{s}^{*}\}.

Let $X$ be the set of common neighbors of $x_{1}^{*},\ldots,x_{s}^{*}$ in $U_{2}$ of $G$ and let $Y=N_{G}(y^{*},V_{2})$ . For any edge $x^{\prime}y^{\prime}$ in $G[X,Y]$ , if $\{x^{\prime},y^{\prime}\}\cap V(F_{xy})=\emptyset$ , then by replacing $x,y$ with $x^{\prime},y^{\prime}$ in $F_{xy}$ we obtain a copy of $F$ in $G$ , a contradiction. Thus, every edge in $G[X,Y]$ intersects $V(F_{xy})$ , implying that $e(X,Y)\leq h(|X|+|Y|)$ . Then

e_{\bar{G}}(X,Y)=|X||Y|-e(X,Y)\geq|X||Y|-h(|X|+|Y|).

Let $S$ be one of $X$ and $Y$ with the smaller size. By the same argument as in Step 1, we have

e_{\bar{G}}(X,Y)\geq\frac{|S|^{2}}{16h^{2}}.

We delete vertices in $S$ from $U_{2}\cup V_{2}$ and let $U_{2}^{\prime}=U_{2}\setminus S$ and $V_{2}^{\prime}=V_{2}\setminus S$ . If $\bar{E}[U_{2}^{\prime},V_{2}^{\prime}]\cap(\Omega_{31}\cup\Omega_{32})=\emptyset$ , then we are done. Otherwise, there is another non-edge $xy$ in $\Omega_{31}\cup\Omega_{32}$ with $x\in U_{2}^{\prime}$ , $y\in V_{2}^{\prime}$ , and we delete another $S^{\prime}$ from $U_{2}^{\prime}\cup V_{2}^{\prime}$ incidents with at least $\frac{|S^{\prime}|^{2}}{16h^{2}}$ non-edges between $U_{2}^{\prime}$ and $V_{2}^{\prime}$ . By deleting vertices greedily, we shall obtain a sequence of disjoint sets $S_{1},S_{2},\ldots,S_{l}$ in $U_{2}\cup V_{2}$ such that $\bar{E}[U_{2}\setminus(S_{1}\cup\ldots\cup S_{l}),V_{2}\setminus(S_{1}\cup\ldots\cup S_{l})]\cap(\Omega_{31}\cup\Omega_{32})=\emptyset$ .

In each step of the greedy algorithm, if there is a non-edge $xy\in\Omega_{31}$ between $U_{2}$ and $V_{2}$ , then there exist vertices $x_{1}^{*},\ldots,x_{s}^{*},y^{*}\in T$ such that either $X=\cap_{i=1}^{s}N(x_{i}^{*},U_{2})$ or $Y=N(y^{*},V_{2})$ is deleted. If there is a non-edge $xy\in\Omega_{32}$ between $U_{2}$ and $V_{2}$ , then there exist vertices $y_{1}^{*},\ldots,y_{s}^{*},x^{*}\in T$ such that either $X=N(x^{*},U_{2})$ or $Y=\cap_{i=1}^{s}N(y_{i}^{*},V_{2})$ is deleted. It follows that

l\leq 2\left(\binom{|T|}{s}+|T|\right)<2(|T|^{s}+|T|)\leq 4|T|^{s}\leq 4(30h^{2}\varepsilon n)^{s}.

By (3.1) and (3.2), we arrive at

\left(\sum_{i=1}^{l}|S_{i}|\right)^{2}\leq 16h^{2}\cdot 25h^{2}\varepsilon n^{2}l\leq 20^{2}h^{4}\varepsilon n^{2}\cdot 4(30h^{2}\varepsilon n)^{s}=40^{2}\cdot 30^{s}h^{2s+4}\varepsilon^{s+1}n^{s+2}.

Let $U_{3}=U_{2}\setminus(S_{1}\cup\ldots\cup S_{l})$ and $V_{3}=V_{2}\setminus(S_{1}\cup\ldots\cup S_{l})$ . Then

|U_{2}\setminus U_{3}|+|V_{2}\setminus V_{3}|\leq\sum_{i=1}^{l}|S_{i}|\leq 40\cdot 30^{\frac{s}{2}}h^{s+2}\varepsilon^{\frac{s+1}{2}}n^{\frac{s+2}{2}}\leq(6h)^{s+3}\varepsilon^{\frac{s+1}{2}}n^{\frac{s+2}{2}}

and Step 3.1 is finished. ∎

Step 3.2. We can find $U_{4}\subset U_{3}$ and $V_{4}\subset V_{3}$ such that $|U_{3}\setminus U_{4}|+|V_{3}\setminus V_{4}|\leq(6h)^{s+3}\varepsilon^{\frac{s+1}{2}}n^{\frac{s+2}{2}}$ and $G[U_{4},V_{4}]$ is complete bipartite, i.e., by deleting at most $(6h)^{s+3}\varepsilon^{\frac{s+1}{2}}n^{\frac{s+2}{2}}$ vertices from $U_{3}\cup V_{3}$ we obtain an induced complete bipartite subgraph of $G$ .

Proof.

If $\bar{E}[U_{3},V_{3}]\cap(\Omega_{33}\cup\Omega_{34})=\emptyset$ , we have nothing to do. So assume that $\bar{E}[U_{3},V_{3}]\cap(\Omega_{33}\cup\Omega_{34})\neq\emptyset$ , then there is a non-edge $xy$ in $\Omega_{33}\cup\Omega_{34}$ with $x\in U_{3}$ and $y\in V_{3}$ . Without loss of generality, we assume that $\deg_{F_{xy}}(x)=s+1$ and $\deg_{F_{xy}}(y)=2$ . By Claim 4, $\deg_{F_{xy}}(y,T)=1$ and let $N_{F_{xy}}(y,T)=\{y^{*}\}$ . Let $N_{F_{xy}}(x)\cap T=\{x_{1}^{*},x_{2}^{*},\ldots,x_{p}^{*}\}$ and $N_{F_{xy}}(x)\cap V=\{z_{p+1},\ldots,z_{s},y\}$ with $p\leq s-1$ . By Claim 4, we have $p\geq 1$ . Let $X$ be the set of common neighbors of $x_{1}^{*},\ldots,x_{p}^{*}$ in $U_{3}$ of $G$ and let $Y=N_{G}(y^{*},V_{3})$ .

Let $\phi_{xy}$ be the isomorphism from $F$ to $F_{xy}$ . Without loss of generality, assume that $\phi_{xy}(a)=x$ and $\phi_{xy}(c_{1}^{1})=y$ . If $\psi$ is an injective homomorphism from $F-c_{1}^{1}$ to $G$ with

\psi(\phi_{xy}^{-1}(x_{1}^{*}))=x_{1}^{*},\ \ldots,\ \psi(\phi_{xy}^{-1}(x_{p}^{*}))=x_{p}^{*},\ \psi(\phi_{xy}^{-1}(y^{*}))=y^{*}

and

\psi(\phi_{xy}^{-1}(z_{p+1}))\in V,\ \ldots,\ \psi(\phi_{xy}^{-1}(z_{s}))\in V,\ \psi(a)\in X,

then we say that $\psi$ is agree with $\phi_{xy}$ . Define

\Psi_{xy}=\{\psi\colon\psi\mbox{ is an injective homomorphism from $F-c_{1}^{1}$ to $G$ that is agree with }\phi_{xy}\}.

Let

X_{0}=\{x^{\prime}\in X\colon\exists\psi_{x^{\prime}}\in\Psi_{xy}\mbox{ such that }\psi_{x^{\prime}}(a)=x^{\prime}\}.

For any $x^{\prime}\in X_{0}$ , let $H_{x^{\prime}}$ be a copy of $F-c_{1}^{1}$ in $G$ corresponding to $\psi_{x^{\prime}}$ . If there is $y^{\prime}\in Y\setminus V(H_{x^{\prime}})$ such that $x^{\prime}y^{\prime}\in E(G)$ , then we define a homomorphism $\phi$ from $F$ to $G$ as follows:

\phi(u)=\psi_{x^{\prime}}(u)\mbox{ for all }u\in V(F-c_{1}^{1})\mbox{ and }\phi(c_{1}^{1})=y^{\prime}.

Then $\phi$ is an injective homomorphism from $F$ to $G$ , contradicting the fact that $G$ is $F$ -free. Hence each $x^{\prime}\in X_{0}$ has at most $V(H_{x^{\prime}})$ neighbors in $Y$ , implying that

e_{\bar{G}}(X_{0},Y)\geq|X_{0}||Y|-|X_{0}|h\geq|X_{0}||Y|-h(|X_{0}|+|Y|).

Let $S$ be one of $X_{0}$ and $Y$ with the smaller size. By the same argument as in Step 1, we have

e_{\bar{G}}(X_{0},Y)\geq\frac{|S|^{2}}{16h^{2}}.

We delete vertices in $S$ from $U_{3}\cup V_{3}$ and let $U_{3}^{\prime}=U_{3}\setminus S$ and $V_{3}^{\prime}=V_{3}\setminus S$ . If $\bar{E}[U_{3}^{\prime},V_{3}^{\prime}]\cap(\Omega_{33}\cup\Omega_{34})=\emptyset$ , then we are done. Otherwise, there is another non-edge $xy$ in $(\Omega_{33}\cup\Omega_{34})$ with $x\in U_{3}^{\prime}$ , $y\in V_{3}^{\prime}$ , and we delete another $S^{\prime}$ from $U_{3}^{\prime}\cup V_{3}^{\prime}$ incident with at least $\frac{|S^{\prime}|^{2}}{16h^{2}}$ non-edges between $U_{3}^{\prime}$ and $V_{3}^{\prime}$ . By deleting vertices greedily, we shall obtain a sequence of disjoint sets $S_{1},S_{2},\ldots,S_{l}$ in $U_{3}\cup V_{3}$ such that $\bar{E}[U_{3}\setminus(S_{1}\cup\ldots\cup S_{l}),V_{3}\setminus(S_{1}\cup\ldots\cup S_{l})]\cap(\Omega_{33}\cup\Omega_{34})=\emptyset$ .

In each step of the greedy algorithm, if there is a non-edges $xy\in\Omega_{33}$ between $U_{3}$ and $V_{3}$ , then there exist vertices $x_{1}^{*},\ldots,x_{p}^{*},y^{*}\in T$ such that either $X_{0}$ or $Y$ is deleted. If $Y$ is deleted, then $y^{*}$ has no neighbor in $V_{3}\setminus Y$ . If $X_{0}$ is deleted, then there is no non-edge $x^{\prime}y^{\prime}\in\Omega_{33}$ between $U_{3}\setminus X_{0}$ and $V_{3}$ such that $N_{F_{x^{\prime}y^{\prime}}}(x^{\prime})\cap T=\{x_{1}^{*},x_{2}^{*},\ldots,x_{p}^{*}\}$ and $N_{F_{x^{\prime}y^{\prime}}}(y^{\prime})\cap T=\{y^{*}\}$ . For otherwise, $F_{x^{\prime}y^{\prime}}-y^{\prime}$ is a copy of $F-\phi_{x^{\prime}y^{\prime}}^{-1}(y^{\prime})$ , which is also a copy of $F-c_{1}^{1}$ , contradicting the assumption that $x^{\prime}\notin U_{3}\setminus X_{0}$ . It follows that the tuple $(x_{1}^{*},\ldots,x_{p}^{*},y^{*})$ will not appear in the future steps of the algorithm. If there is a non-edges $xy\in\Omega_{34}$ between $U_{3}$ and $V_{3}$ , then there exist vertices $y_{1}^{*},\ldots,y_{q}^{*},x^{*}\in T$ such that either $X=N(x^{*},U_{2})$ or $Y_{0}$ (which can be defined similarly) is deleted. By the same argument, we see that the tuple $(y_{1}^{*},\ldots,y_{q}^{*},x^{*})$ will not appear in the future steps of the algorithm. Therefore,

l\leq\sum_{p=1}^{s-1}\binom{|T|}{p}|T|+\sum_{q=1}^{s-1}\binom{|T|}{q}|T|<\sum_{p=1}^{s-1}|T|^{p+1}+\sum_{q=1}^{s-1}|T|^{q+1}<2s|T|^{s}\leq 2s(30h^{2}\varepsilon n)^{s}.

By (3.1) and (3.2), we arrive at

\left(\sum_{i=1}^{l}|S_{i}|\right)^{2}\leq 16h^{2}\cdot 25h^{2}\varepsilon n^{2}l\leq 20^{2}h^{4}\varepsilon n^{2}\cdot 2s(30h^{2}\varepsilon n)^{s}=2\cdot 20^{2}\cdot 30^{s}sh^{2s+4}\varepsilon^{s+1}n^{s+2}.

Let $U_{4}=U_{3}\setminus(S_{1}\cup\ldots\cup S_{l})$ and $V_{4}=V_{3}\setminus(S_{1}\cup\ldots\cup S_{l})$ . Since $\bar{E}[U_{4},V_{4}]\cap(\Omega_{1}\cup\Omega_{2}\cup\Omega_{3})=\emptyset$ , $G[U_{4},V_{4}]$ is complete bipartite. Moreover,

|U_{3}\setminus U_{4}|+|V_{3}\setminus V_{4}|\leq\sum_{i=1}^{l}|S_{i}|\leq 20\sqrt{2}\cdot 30^{\frac{s}{2}}\sqrt{s}h^{s+2}\varepsilon^{\frac{s+1}{2}}n^{\frac{s+2}{2}}\leq(6h)^{s+3}\varepsilon^{\frac{s+1}{2}}n^{\frac{s+2}{2}}.

Thus Step 3.2 is finished. ∎

Let $n^{\prime}$ be the total number of vertices we deleted from $G$ to obtain an induced complete bipartite graph. By Lemma 3.3 (i) and Steps 1, 2, 3.1, 3.2, we have

\displaystyle n^{\prime}=|T|+|(U\cup V)\setminus(U_{4}\cup V_{4})|

\displaystyle\leq 30h^{2}\varepsilon n+160h^{3}\varepsilon n^{\frac{3}{2}}+3\cdot(6h)^{s+3}\varepsilon^{\frac{s+1}{2}}n^{\frac{s+2}{2}}.

Let $\varepsilon=\alpha n^{-\frac{s}{s+1}}$ . Then for $s\geq 2$ , $\alpha<1$ and $h\leq 2sk$ , we have

	$\displaystyle n^{\prime}$	$\displaystyle=30h^{2}\alpha n^{\frac{1}{s+1}}+160h^{3}\alpha n^{\frac{3}{2}-\frac{s}{s+1}}+3\cdot(6h)^{s+3}\alpha^{\frac{s+1}{2}}n$
		$\displaystyle\leq\left(30h^{2}+160h^{3}+3\cdot(6h)^{s+3}\alpha^{\frac{s-1}{2}}\right)\alpha n$
		$\displaystyle\leq 4\cdot(6h)^{s+3}\alpha n$
		$\displaystyle\leq 4\cdot(12sk)^{s+3}\alpha n.$

This completes the proof. ∎

References

[1] D. Gerbner, A note on stability for maximal $F$ -free graphs, Graphs Combin. (2021), https://doi.org/10.1007/s00373-021-02372-z.
[2] P. Erdős, Some recent results on extremal problems in graph theory (Results), Theory of Graphs (Internl. Symp. Rome) (1966), 118–123.
[3] P. Erdős and T. Gallai, On maximal paths and circuits of graphs, Acta Math. Hungar. 10 (1959), 337–356.
[4] K. Popielarz, J. Sahasrabudhe and R. Snyder, A stability theorem for maximal $K_{r+1}$ -free graphs, J. Combin. Theory Ser. B 132 (2018), 236–257.
[5] M. Simonovits, A method for solving extremal problems in graph theory, stability problems, in: Theory of Graphs (Proc. Colloq. Tihany, 1966), Academic Press, New York (1968), 279–319.
[6] M. Simonovits, Extremal graph problems with symmetrical extremal graphs. Additional chromatic conditions, Discrete Math. 7 (1974), 349–376.
[7] P. Turán, On an extremal problem in graph theory (in Hungarian), Math. Fiz. Lapok 48 (1941), 436–452.
[8] M. Tyomkyn and A.J. Uzzel, Strong Turán stability, Electron. J. Combin. 22 (2015), P3.9, 24pp.
[9] J. Wang, S. Wang, W. Yang and X. Yuan, A stability theorem for maximal $C_{2k+1}$ -free graphs, J. Graph Theory. (2022), 1-14. https://doi.org/10.1002/jgt.22824.

	$\displaystyle e(A,B)=\frac{1}{2}$	$\displaystyle\sum_{x\in A\cup B}\deg_{G[A,B]}(x)$
		$\displaystyle\geq\frac{1}{2}\left(\left(\frac{1}{2}-\frac{3}{10h}\right)n-h-1\right)(\|A\|+\|B\|)$
		$\displaystyle\geq\frac{1}{2}\left(\left(\frac{1}{2}-\frac{3}{10h}\right)10h-h-1\right)(\|A\|+\|B\|)$
		$\displaystyle>\frac{h}{2}(\|A\|+\|B\|)$
		$\displaystyle>\frac{(l-2)-1}{2}(\|A\|+\|B\|).$

	$\displaystyle\|B\|$	$\displaystyle\geq\|N(u)\cap N(v)\|-h$
		$\displaystyle\geq\|N(u)\|+\|N(v)\|-\|V\|-h$
		$\displaystyle\geq 2\left(\frac{1}{2}-\frac{1}{10h}\right)n-\left(\frac{1}{2}+\frac{1}{10h}\right)n-h$
		$\displaystyle=\left(\frac{1}{2}-\frac{3}{10h}\right)n-h.$

	$\displaystyle e(A,B)=\frac{1}{2}$	$\displaystyle\sum_{x\in A\cup B}\deg_{G[A,B]}(x)$
		$\displaystyle\geq\frac{1}{2}\left(\left(\frac{1}{2}-\frac{1}{2h}\right)n-h\right)(\|A\|+\|B\|)$
		$\displaystyle\geq\frac{1}{2}\left(\left(\frac{1}{2}-\frac{1}{2h}\right)10h-h\right)(\|A\|+\|B\|)$
		$\displaystyle>\frac{h}{2}(\|A\|+\|B\|)$
		$\displaystyle>\frac{l-1}{2}(\|A\|+\|B\|).$

	$\displaystyle e_{\bar{G}}(X,Y)$	$\displaystyle\geq\|S\|\|Y\|-h(\|S\|+\|Y\|)$
		$\displaystyle=\|Y\|(\|S\|-h)-h\|S\|$
		$\displaystyle\geq\|S\|^{2}-2h\|S\|$
		$\displaystyle\geq\frac{\|S\|^{2}}{2}>\frac{\|S\|^{2}}{16h^{2}}.$

	$\displaystyle l$	$\displaystyle\leq\sum_{p+f\leq s}\binom{\|T\|}{p}\binom{\|T\|-p}{f}+\sum_{q+g\leq s}\binom{\|T\|}{q}\binom{\|T\|-q}{g}$
		$\displaystyle=2\sum_{p+f\leq s}\binom{\|T\|}{p}\binom{\|T\|-p}{f}$
		$\displaystyle\leq 2\sum_{p+f\leq s}\|T\|^{s}\leq 2s^{2}\|T\|^{s}.$

Counterexamples to Gerbner’s Conjecture on Stability of Maximal FF-free Graphs

Abstract

1 Introduction

Theorem 1.1 ([4]).

Theorem 1.2 ([9]).

Conjecture 1.3 ([1]).

Theorem 1.4 ([1]).

Theorem 1.5.

Lemma 1.6.

Lemma 1.7.

2 Proof of Lemma 1.6

Definition 2.1.

Definition 2.2.

Proposition 2.3.

Proof.

Proof of Lemma 1.6..

Claim 1.

Proof.

Claim 2.

Proof.

3 Proof of Lemma 1.7

Lemma 3.1 ([1]).

Theorem 3.2 ([6]).

Lemma 3.3.

Proof.

Claim 3.

Proof.

Lemma 3.4.

Proof.

Proof of Lemma 1.7..

Claim 4.

Proof.

Proof.

Proof.

Claim 5.

Proof.

Claim 6.

Proof.

Proof.

Proof.

References

Counterexamples to Gerbner’s Conjecture on Stability of Maximal $F$ -free Graphs