CoT: Decentralized Elastic Caches for Cloud Environments

Victor Zakhary Lawrence Lim Divyakant Agrawal Amr El Abbadi
Department of Computer Science
UC Santa Barbara
Santa Barbara, California, 93106
victorzakhary,lawrenceklim,divyagrawal,[email protected]

Abstract

Distributed caches are widely deployed to serve social networks and web applications at billion-user scales. However, typical workload skew results in load-imbalance among caching servers. This load-imbalance decreases the request throughput and increases the request latency reducing the benefit of caching. Recent work has theoretically shown that a small perfect cache at the front-end has a big positive effect on distributed caches load-balance. However, determining the cache size and the replacement policy that achieve near perfect caching at front-end servers is challenging especially for dynamically changing and evolving workloads. This paper presents Cache-on-Track (CoT), a decentralized, elastic, and predictive caching framework for cloud environments. CoT is the answer to the following question: What is the necessary front-end cache size that achieves load-balancing at the caching server side? CoT proposes a new cache replacement policy specifically tailored for small front-end caches that serve skewed workloads. Front-end servers use a heavy hitter tracking algorithm to continuously track the top-k hot keys. CoT dynamically caches the hottest C keys out of the tracked keys. In addition, each front-end server independently monitors its effect on caching servers load-imbalance and adjusts its tracker and cache sizes accordingly. Our experiments show that CoT’s replacement policy consistently outperforms the hit-rates of LRU, LFU, and ARC for the same cache size on different skewed workloads. Also, CoT slightly outperforms the hit-rate of LRU-2 when both policies are configured with the same tracking (history) size. CoT achieves server size load-balance with 50% to 93.75% less front-end cache in comparison to other replacement policies. Finally, our experiments show that CoT’s resizing algorithm successfully auto-configures the tracker and cache sizes to achieve back-end load-balance in the presence of workload distribution changes.

1 Introduction

Social networks, the web, and mobile applications have attracted hundreds of millions of users [3, 7]. These users share their relationships and exchange images and videos in timely personalized experiences [13]. To enable this real-time experience, the underlying storage systems have to provide efficient, scalable, and highly available access to big data. Social network users consume several orders of magnitude more data than they produce [10]. In addition, a single page load requires hundreds of object lookups that need to be served in a fraction of a second [13]. Therefore, traditional disk-based storage systems are not suitable to handle requests at this scale due to the high access latency of disks and I/O throughput bounds [50].

To overcome these limitations, distributed caching services have been widely deployed on top of persistent storage in order to efficiently serve user requests at scale [49]. Distributed caching systems such as Memcached [4] and Redis [5] are widely adopted by cloud service providers such as Amazon ElastiCache [1] and Azure Redis Cache [2]. These caching services offer significant latency and throughput improvements to systems that directly access the persistent storage layer. Redis and Memcached use consistent hashing [35] to distribute keys among several caching servers. Although consistent hashing ensures a fair distribution of the number of keys assigned to each caching shard, it does not consider the workload per key in the assignment process. Real-world workloads are typically skewed with few keys being significantly hotter than other keys [30]. This skew causes load-imbalance among caching servers.

Load imbalance in the caching layer can have significant impact on the overall application performance. In particular, it may cause drastic increases in the latency of operations at the tail end of the access frequency distribution [29]. In addition, the average throughput decreases and the average latency increases when the workload skew increases [15]. This increase in the average and tail latency is amplified for real workloads when operations are executed in chains of dependent data objects [41]. A single Facebook page-load results in retrieving hundreds of objects in multiple rounds of data fetching operations [44, 13]. Finally, solutions that equally overprovision the caching layer resources to handle the most loaded caching server suffer from resource under-utilization in the least loaded caching servers.

Various approaches have been proposed to solve the load-imbalance problem using centralized load monitoring [9, 48], server side load monitoring [29], or front-end load monitoring [24]. Adya et al. [9] propose Slicer that separates the data serving plane from the control plane. The control plane is a centralized system component that collects metadata about shard accesses and server workload. It periodically runs an optimization algorithm that decides to redistribute, repartition, or replicate slices of the key space to achieve better back-end load-balance. Hong et al. [29] use a distributed server side load monitoring to solve the load-imbalance problem. Each back-end server independently tracks its hot keys and decides to distribute the workload of its hot keys among other back-end servers. Solutions in [9, 48] and [29] require the back-end to change the key-to-caching-server mapping and announce the new mapping to all the front-end servers. Fan et al. [24] use a distributed front-end load-monitoring approach. This approach shows that adding a small cache in the front-end servers has significant impact on solving the back-end load-imbalance. Caching the heavy hitters at front-end servers reduces the skew among the keys served from the caching servers and hence achieves better back-end load-balance. Fan et al. theoretically show through analysis and simulation that a small perfect cache at each front-end solves the back-end load-imbalance problem. However, perfect caching is practically hard to achieve. Determining the cache size and the replacement policy that achieve near perfect caching at the front-end for dynamically changing and evolving workloads is challenging.

In this paper, we propose Cache-on-Track (CoT); a decentralized, elastic, and predictive heavy hitter caching at front-end servers. CoT proposes a new cache replacement policy specifically tailored for small front-end caches that serve skewed workloads. CoT uses a small front-end cache to solve back-end load-imbalance as introduced in [24]. However, CoT does not assume perfect caching at the front-end. CoT uses the space saving algorithm [43] to track the top-k heavy hitters. The tracking information allows CoT to cache the exact top C hot-most keys out of the approximate top-k tracked keys preventing cold and noisy keys from the long tail to replace hot keys in the cache. CoT is decentralized in the sense that each front-end independently determines its hot key set based on the key access distribution served at this specific front-end. This allows CoT to address back-end load-imbalance without introducing single points of failure or bottlenecks that typically come with centralized solutions. In addition, this allows CoT to scale to thousands of front-end servers, a common requirement of social network and modern web applications. CoT is elastic in that each front-end uses its local load information to monitor its contribution to the back-end load-imbalance. Each front-end elastically adjusts its tracker and cache sizes to reduce the load-imbalance caused by this front-end. In the presence of workload changes, CoT dynamically adjusts front-end tracker to cache ratio in addition to both the tracker and cache sizes to eliminate any back-end load-imbalance.

In traditional architectures, memory sizes are static and caching algorithms strive to achieve the best usage of all the available resources. However, in a cloud setting where there are theoretically infinite memory and processing resources and cloud instance migration is the norm, cloud end-users aim to achieve their SLOs while reducing the required cloud resources and thus decreasing their monetary deployment costs. CoT’s main goal is to reduce the necessary front-end cache size at each front-end to eliminate server-side load-imbalance. Reducing front-end cache size is crucial for the following reasons: 1) it reduces the monetary cost of deploying front-end caches. For this, we quote David Lomet in his recent works [40, 39, 38] where he shows that cost/performance is usually more important than sheer performance: ”the argument here is not that there is insufficient main memory to hold the data, but that there is a less costly way to manage data.”. 2) In the presence of data updates and when data consistency is a requirement, increasing front-end cache sizes significantly increases the cost of the data consistency management technique. Note that social networks and modern web applications run on thousands of front-end servers. Increasing front-end cache size not only multiplies the cost of deploying bigger cache by the number of front-end servers, but also increases several costs in the consistency management pipeline including a) the cost of tracking key incarnations in different front-end servers and b) the network and processing costs to propagate updates to front-end servers. 3) Since the workload is skewed, our experiments clearly demonstrate that the relative benefit of adding more front-end cache-lines, measured by the average cache-hits per cache-line and back-end load-imbalance reduction, drastically decreases as front-end cache sizes increase.

CoT’s resizing algorithm dynamically increases or decreases front-end allocated memory in response to dynamic workload changes. CoT’s dynamic resizing algorithm is valuable in different cloud settings where 1) all front-end servers are deployed in the same datacenter and obtain the same dynamically evolving workload distribution, 2) all front-end servers are deployed in the same datacenter but obtain different dynamically evolving workload distributions, and finally 3) front-end servers are deployed at different edge-datacenters and obtain different dynamically evolving workload distributions. In particular, CoT aims to capture local trends from each individual front-end server perspective. In social network applications, front-end servers that serve different geographical regions might experience different key access distributions and different local trends (e.g., #miami vs. #ny). Similarly, in large scale data processing pipelines, several applications are deployed on top of a shared caching layer. Each application might be interested in different partitions of the data and hence experience different key access distributions and local trends. While CoT operates on a fine-grain key level at front-end servers, solutions like Slicer [9] operate on coarser grain slices or shards at the caching servers. Server side solutions are complementary to CoT. Although capturing local trends alleviates the load and reduces load-imbalance among caching servers, other factors can result in load-imbalance and hence using server-side load-balancing, e.g., Slicer, might still be beneficial.

We summarize our contributions in this paper as follows.

•

Cache-on-Track (CoT) is a decentralized, elastic, and predictive front-end caching framework that reduces back-end load-imbalance and improves overall performance.
•

CoT dynamically minimizes the required front-end cache size to achieve back-end load-balance. CoT’s built-in elasticity is a key novel advantage over other replacement policies.
•

Extensive experimental studies that compare CoT’s replacement policy to both traditional as well as state-of-the-art replacement policies, namely, LFU, LRU, ARC, and LRU-2. The experiments demonstrate that CoT achieves server size load-balance for different workload with 50% to 93.75% less front-end cache in comparison to other replacement policies.
•

The experimental study demonstrates that CoT successfully auto-configures its tracker and cache sizes to achieve back-end load-balance.
•

In our experiments, we found a bug in YCSB’s [19] ScrambledZipfian workload generator. This generator generates workloads that are significantly less-skewed than the promised Zipfian distribution.

The rest of the paper is organized as follows. In Section 2, the system and data models are explained. In Section 3, we motivate CoT by presenting the main advantages and limitations of using LRU, LFU, ARC, and LRU-k caches at the front-end. We present the details of CoT in Section 4. In Section 5, we evaluate the performance and the overhead of CoT. The related work is discussed in Section 6 and the paper is concluded in Section 7.

2 System and Data Models

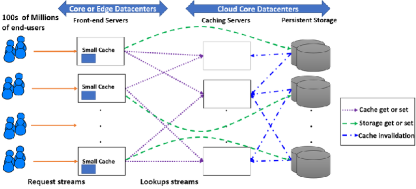
Refer to caption — Figure 1: Overview of the system architecture.

This section introduces the system and data access models. Figure 1 presents the system architecture where user-data is stored in a distributed back-end storage layer in the cloud. The back-end storage layer consists of a distributed in-memory caching layer deployed on top of a distributed persistent storage layer. The caching layer aims to improve the request latency and system throughput and to alleviate the load on the persistent storage layer. As shown in Figure 1, hundreds of millions of end-users send streams of page-load and page-update requests to thousands of stateless front-end servers. These front-end servers are either deployed in the same core datacenter as the back-end storage layer or distributed among other core and edge datacenters near end-users. Each end-user request results in hundreds of data object lookups and updates served from the back-end storage layer. According to Facebook Tao [13], 99.8% of the accesses are reads and 0.2% of them are writes. Therefore, the storage system has to be read optimized to efficiently handle end-user requests at scale.

The front-end servers can be viewed as the clients of the back-end storage layer. We assume a typical key/value store interface between the front-end servers and the storage layer. The API consists of the following calls:

•

v = get(k) retrieves value v corresponding to key k.
•

set(k, v) assigns value v to key k.
•

delete(k) deletes the entry corresponding key k.

Front-end servers use consistent hashing [35] to locate keys in the caching layer. Consistent hashing solves the key discovery problem and reduces key churn when a caching server is added to or removed from the caching layer. We extend this model by adding an additional layer in the cache hierarchy. As shown in Figure 1, each front-end server maintains a small cache of its hot keys. This cache is populated according to the accesses that are served by this front-end server.

We assume a client driven caching protocol similar to the protocol implemented by Memcached [4]. A cache client library is deployed in the front-end servers. Get requests are initially attempted to be served from the local cache. If the requested key is in the local cache, the value is returned and the request is marked as served. Otherwise, a null value is returned and the front-end has to request this key from the caching layer at the back-end storage layer. If the key is cached in the caching layer, its value is returned to the front-end. Otherwise, a null value is returned and the front-end has to request this key from the persistent storage layer and upon receiving the corresponding value, the front-end inserts the value in its front-end local cache and in the server-side caching layer as well. As in [44], a set, or an update, request invalidates the key in both the local cache and the caching layer. Updates are directly sent to the persistent storage, local values are set to null, and delete requests are sent to the caching layer to invalidate the updated keys. The Memcached client driven approach allows the deployment of a stateless caching layer. As requests are driven by the client, a caching server does not need to maintain the state of any request. This simplifies scaling and tolerating failures at the caching layer. Although, we adopt the Memcached client driven request handling protocol, our model works as well with write-through request handling protocols.

Our model is not tied to any replica consistency model. Each key can have multiple incarnations in the storage layer and the caching layer. Updates can be synchronously propagated if strong consistency guarantees are needed or asynchronously propagated if weak consistency guarantees suffice. Achieving strong consistency guarantees among replicas of the same object has been widely studied in [15, 29]. Ghandeharizadeh et al. [26, 27] propose several complementary techniques to CoT to deal with consistency in the presence of updates and configuration changes. These techniques can easily be adopted in our model according to the application requirements. We understand that deploying an additional vertical layer of cache increases potential data inconsistencies and hence increases update propagation and synchronization overheads. Therefore, our goal in this paper is to reduce the front-end cache size in order to limit the inconsistencies and the synchronization overheads that result from deploying front-end caches, while maximizing their benefits.

3 Front-end Cache Alternatives

Fan et al. [24] show that a small cache in the front-end servers has big impact on the caching layer load-balance. Their analysis assumes perfect caching in front-end servers for the hottest keys. A perfect cache of $C$ cache-lines is defined such that accesses for the $C$ hot-most keys always hit the cache while other accesses always miss the cache. However, the perfect caching assumption is impractical especially for dynamically changing and evolving workloads. Different replacement policies have been developed to approximate perfect caching for different workloads. In this section, we discuss the workload assumptions and various client caching objectives. This is followed by a discussion of the advantages and limitations of common caching replacement policies such as Least Recently Used (LRU), Least Frequently Used (LFU), Adaptive Replacement Cache (ARC [42]) and LRU-k [45].

Workload assumptions: Real-world workloads are typically skewed with few keys being significantly hotter than other keys [30]. Zipfian distribution is a common example of a key hotness distribution. However, key hotness can follow different distributions such as Gaussian or different variations of Zipfian [12, 28]. In this paper, we assume skewed workloads with periods of stability (where hot keys remain hot during these periods).

Client caching objectives: Front-end servers construct their perspective of the key hotness distribution based on the requests they serve. Front-end servers aim to achieve the following caching objectives:

•

The cache replacement policy should prevent cold keys from replacing hotter keys in the cache.
•

Front-end caches should adapt to the changes in the workload. In particular, front-end servers should have a way to retire hot keys that are no longer accessed. In addition, front-end caches should have a mechanism to expand or shrink their local caches in response to changes in workload distribution. For example, front-end servers that serve uniform access distributions should dynamically shrink their cache size to zero since caching is of no value in this situation. On the other hand, front-end servers that serve highly skewed Zipfian (e.g., s = 1.5) should dynamically expand their cache size to capture all the hot keys that cause load-imbalance among the back-end caching servers.

A popular policy for implementing client caching is the LRU replacement policy. Least Recently Used (LRU) costs O(1) per access and caches keys based on their recency of access. This may allow cold keys that are recently accessed to replace hotter cached keys. Also, LRU cannot distinguish well between frequently and infrequently accessed keys [36]. For example, this access sequence (A, B, C, D, A, B, C, E, A, B, C, F, …) would always have a cache miss for an LRU cache of size 3. Alternatively, Least Frequently Used (LFU) can be used as a replacement policy. LFU costs $O(log(C))$ per access where $C$ is the cache size. LFU is typically implemented using a min-heap and allows cold keys to replace hotter keys at the root of the heap. Also, LFU cannot distinguish between old references and recent ones. For example, this access sequence (A, A, B, B, C, D, E, C, D, E, C, D, E ….) would always have a cache miss for an LFU cache of size 3 except for the $2^{nd}$ and $4^{th}$ accesses. This means that LFU cannot adapt to changes in workload. Both LRU and LFU are limited in their knowledge to the content of the cache and cannot develop a wider perspective about the hotness distribution outside of their static cache size. Our experiments in Section 5 show that replacement policies that track more keys beyond their cache sizes (e.g., ARC, LRU-k, and CoT) beat the hit-rates of replacement policies that have no access information of keys beyond their cache size especially for periodically stable skewed workloads.

Adaptive Replacement Cache (ARC) [42] tries to realize the benefits of both LRU and LFU policies by maintaining two caching lists: one for recency and one for frequency. ARC dynamically changes the number of cache-lines allocated for each list to either favor recency or frequency of access in response to workload changes. In addition, ARC uses shadow queues to track more keys beyond the cache size. This helps ARC to maintain a broader perspective of the access distribution beyond the cache size. ARC is designed to find the fine balance between recent and frequent accesses. As a result, ARC pays the cost of caching every new cold key in the recency list evicting a hot key from the frequency list. This cost is significant especially when the cache size is much smaller than the key space and the workload is skewed favoring frequency over recency.

LRU-k tracks the last k accesses for each key in the cache, in addition to a pre-configured fixed size history that include the access information of the recently evicted keys from the cache. New keys replace the key with the least recently $k^{th}$ access in the cache. The evicted key is moved to the history, which is typically implemented using a LRU like queue. LRU-k is a suitable strategy to mock perfect caching of periodically stable skewed workloads when its cache and history sizes are perfectly pre-configured for this specific workload. However, due to the lack of LRU-k’s dynamic resizing and elasticity of both its cache and history sizes, we choose to introduce CoT that is designed with native resizing and elasticity functionality. This functionality allows CoT to adapt its cache and tracker sizes in response to workload changes.

4 Cache on Track (CoT)

Front-end caches serve two main purposes: 1) decrease the load on the back-end caching layer and 2) reduce the load-imbalance among the back-end caching servers. CoT focuses on the latter goal and considers back-end load reduction a complementary side effect. CoT’s design philosophy is to track more keys beyond the cache size. This tracking serves as a filter that prevents cold keys from populating the small cache and therefore, only hot keys can populate the cache. In addition, the tracker and the cache are dynamically and adaptively resized to ensure that the load served by the back-end layer follows a load-balance target.

The idea of tracking more keys beyond the cache size has been widely used in replacement policies such as 2Q [34], MQ [51], LRU-k [45, 46], ARC [42], and in other works like Cliffhanger [17] to solve other cache problems. Both 2Q and MQ use multiple LRU queues to overcome the weaknesses of LRU of allowing cold keys to replace warmer keys in the cache. Cliffhanger uses shadow queues to solve a different problem of memory allocation among cache blobs. All these policies are desgined for fixed memory size environments. However, in a cloud environment where elastic resources can be requested on-demand, a new cache replacement policy is needed to take advantage of this elasticity.

CoT presents a new cache replacement policy that uses a shadow heap to track more keys beyond the cache size. Previous works have established the efficiency of heaps in tracking frequent items [43]. In this section, we explain how CoT uses tracking beyond the cache size to achieve the caching objectives listed in Section 3. In particular, CoT answers the following questions: 1) how to prevent cold keys from replacing hotter keys in the cache?, 2) how to reduce the required front-end cache size that achieves lookup load-balance?, 3) how to adaptively resize the cache in response to changes in the workload distribution? and finally 4) how to dynamically retire old heavy hitters?.

First, we develop the notation in Section 4.1. Then, we explain the space saving tracking algorithm [43] in Section 4.2. CoT uses the space saving algorithm to track the approximate top-k keys in the lookup stream. In Section 4.3, we extend the space saving algorithm to capture the exact top C keys out of the approximately tracked top-k keys. CoT’s cache replacement policy dynamically captures and caches the exact top C keys thus preventing cold keys from replacing hotter keys in the cache. CoT’s adaptive cache resizing algorithm is presented in Section 4.4. CoT’s resizing algorithm exploits the elasticity and the migration flexibility of the cloud and minimizes the required front-end memory size to achieve back-end load-balance. Section 4.4.2 explains how CoT expands and shrinks front-end tracker and cache sizes in response to changes in workload.

4.1 Notation

$S$	key space
$K$	number of tracked keys at the front-end
$C$	number of cached keys at the front-end
$h_{k}$	hotness of a key k
$k.r_{c}$	read count of a key k
$k.u_{c}$	update count of a key k
$r_{w}$	the weight of a read operation
$u_{w}$	the weight of an update operation
$h_{min}$	the minimum key hotness in the cache
$S_{k}$	the set of all tracked keys
$S_{c}$	the set of tracked and cached keys
$S_{k-c}$	the set of tracked but not cached keys
$I_{c}$	the current local lookup load-imbalance
$I_{t}$	the target lookup load-imbalance
$\alpha$	the average hit-rate per cache-line

Table 1: Summary of notation.

The key space, denoted by $S$ , is assumed to be large in the scale of trillions of keys. Each front-end server maintains a cache of size $C<<<S$ . The set of cached keys is denoted by $S_{c}$ . To capture the hot-most $C$ keys, each front-end server tracks $K>C$ keys. The set of tracked key is denoted by $S_{k}$ . Front-end servers cache the hot-most $C$ keys where $S_{c}\subset S_{k}$ . A key hotness $h_{k}$ is determined using the dual cost model introduced in [22]. In this model, read accesses increase a key hotness by a read weight $r_{w}$ while update accesses decrease it by an update weight $u_{w}$ . As update accesses cause cache invalidations, frequently updated keys should not be cached and thus an update access decreases key hotness. For each tracked key, the read count $k.r_{c}$ and the update count $k.u_{c}$ are maintained to capture the number of read and update accesses of this key. Equation 1 shows how the hotness of key $k$ is calculated.

h_{k}=k.r_{c}\times r_{w}-k.u_{c}\times u_{w}

(1)

$h_{min}$ refers to the minimum key hotness in the cache. $h_{min}$ splits the tracked keys into two subsets: 1) the set of tracked and cached keys $S_{c}$ of size $C$ and 2) the set of tracked but not cached keys $S_{k-c}$ of size $K-C$ . The current local load-imbalance among caching servers lookup load is denoted by $I_{c}$ . $I_{c}$ is a local variable at each front-end that determines the current contribution of this front-end to the back-end load-imbalance. $I_{c}$ is defined as the workload ratio between the most loaded back-end server and the least loaded back-end server as observed at a front-end server. For example, if a front-end server sends, during an epoch, a maximum of 5K key lookups to some back-end server and, during the same epoch, a minimum of 1K key lookups to another back-end server then $I_{c}$ , at this front-end, equals $5$ . $I_{t}$ is the target load-imbalance among the caching servers. $I_{t}$ is the only input parameter set by the system administrator and is used by front-end servers to dynamically adjust their cache and tracker sizes. Ideally $I_{t}$ should be set close to 1. $I_{t}=1.1$ means that back-end load-balance is achieved if the most loaded server observe at most 10% more key lookups that the least loaded server. Finally, we define another local auto-adjusted variable $\alpha$ . $\alpha$ is the average hits per cache-line and it determines the quality of the cached keys. $\alpha$ helps detect changes in workload and adjust the cache size accordingly. Note that CoT automatically infers the value of $\alpha$ based on the observed workload. Hence, the system administrator does not need to set the value of $\alpha$ . Table 1 summarizes the notation.

4.2 Space-Saving Hotness Tracking Algorithm

We use the space-saving algorithm introduced in [43] to track the key hotness at front-end servers. Space-saving uses a min-heap to order keys based on their hotness and a hashmap to lookup keys in the tracker in O(1). The space-saving algorithm is shown in Algorithm 1. If the accessed key $k$ is not in the tracker (Line 1), it replaces the key with minimum hotness at the root of the min-heap (Lines 2, 3, and 4). The algorithm gives the newly added key the benefit of doubt and assigns it the hotness of the replaced key. As a result, the newly added key gets the opportunity to survive immediate replacement in the tracker. Whether the accessed key $k$ was in the tracker or is newly added to the tracker, the hotness of the key is updated based on the access type according to Equation 1 (Line 6) and the heap is accordingly adjusted (Line 7).

Algorithm 1 The space-saving algorithm: track_key( key k, access_type t).

State: $S_{k}$ : keys in the tracker.
Input: (key k, access_type t)

1:if

k\notin S_{k}

then

2: let

k^{{}^{\prime}}

be the root of the min-heap

3: replace

k^{{}^{\prime}}

with

k

h_{k}

h_{k^{{}^{\prime}}}

5:end if

h_{k}

:= update_hotness(k, t)

7:adjust_heap(k)

8:return

h_{k}

4.3 CoT: Cache Replacement Policy

CoT’s tracker captures the approximate top $K$ hot keys. Each front-end server should cache the exact top $C$ keys out of the tracked $K$ keys where $C<K$ . The exactness of the top $C$ cached keys is considered with respect to the approximation of the top $K$ tracked keys. Caching the exact top $C$ keys prevents cold and noisy keys from replacing hotter keys in the cache and achieves the first caching objective. To determine the exact top $C$ keys, CoT maintains a cache of size C in a min-heap structure. Cached keys are partially ordered in the min-heap based on their hotness. The root of the cache min-heap gives the minimum hotness, $h_{min}$ , among the cached keys. $h_{min}$ splits the tracked keys into two unordered subsets $S_{c}$ and $S_{k-c}$ such that:

•

$|S_{c}|=C$ and $\forall_{x\in S_{c}}h_{x}\geq h_{min}$
•

$|S_{k-c}|=K-C$ and $\forall_{x\in S_{k-c}}h_{x}<h_{min}$

For every key access, the hotness information of the accessed key is updated in the tracker. If the accessed key is cached, its hotness information is updated in the cache as well. However, if the accessed key is not cached, its hotness is compared against $h_{min}$ . As shown in Figure 2, the accessed key is inserted into the cache only if its hotness exceeds $h_{min}$ . Algorithm 2 explains the details of CoT’s cache replacement algorithm.

Algorithm 2 CoT’s caching algorithm

State: $S_{k}$ : keys in the tracker and $S_{c}$ : keys in the cache.
Input: (key k, access_type t)

h_{k}

= track_key(k, t) as in Algorithm 1

2:if

k\in S_{c}

then

3: let v = access(

S_{c}

, k) // local cache access

4:else

5: let v = server_access(k) // caching server access

6: if

h_{k}>h_{min}

then

7: insert(

S_{c}

, k, v) // local cache insert

8: end if

9:end if

10:return v

For every key access, the track_key function of Algorithm 1 is called (Line 1) to update the tracking information and the hotness of the accessed key. Then, a key access is served from the local cache only if the key is in the cache (Lines 3). Otherwise, the access is served from the caching server (Line 5). Serving an access from the local cache implicitly updates the accessed key hotness and location in the cache min-heap. If the accessed key is not cached, its hotness is compared against $h_{min}$ (Line 6). The accessed key is inserted to the local cache if its hotness exceeds $h_{min}$ (Line 7). This happens only if there is a tracked but not cached key that is hotter than one of the cached keys. Keys are inserted to the cache together with their tracked hotness information. Inserting keys into the cache follows the LFU replacement policy. This implies that a local cache insert (Line 7) would result in the replacement of the coldest key in the cache (the root of the cache heap) if the local cache is full.

4.4 CoT: Adaptive Cache Resizing

This section answers the following questions: how to reduce the necessary front-end cache size that achieves front-end lookup load-balance? How to shrink the cache size when the workload’s skew decreases? and How to detect changes in the set of hot keys? As explained in Section 1, Reducing the front-end cache size decreases the front-end cache monetary cost, limits the overheads of data consistency management techniques, and maximizes the benefit of front-end caches measured by the average cache-hits per cache-line and back-end load-imbalance reduction.

4.4.1 The Need for Cache Resizing:

Figure 3 experimentally shows the effect of increasing the front-end cache size on both back-end load-imbalance reduction and decreasing the workload at the back-end. In this experiment, 8 memcached shards are deployed to serve back-end lookups and 20 clients send lookup requests following a significantly skewed Zipfian distribution (s = 1.5). The size of the key space is 1 million and the total number of lookups is 10 millions. The front-end cache size at each client is varied from 0 cachelines (no cache) to 2048 cachelines ( $\approx$ 0.2% of the key space). Front-end caches use CoT’s replacement policy and a ratio of 4:1 is maintained between CoT’s tracker size and CoT’s cache size. We define back-end load-imbalance as the workload ratio between the most loaded server and the least loaded server. The target load-imbalance $I_{t}$ is set to 1.5. As shown in Figure 3, processing all the lookups from the back-end caching servers (front-end cache size = 0) leads to a significant load-imbalance of 16.26 among the caching servers. This means that the most loaded caching server receives 16.26 times the number of lookup requests received by the least loaded caching server. As the front-end cache size increases, the server size load-imbalance drastically decreases. As shown, a front-end cache of size 64 cache lines at each client reduces the load-imbalance to 1.44 (an order of magnitude less load-imbalance across the caching servers) achieving the target load-imbalance $I_{t}=1.5$ . Increasing the front-end cache size beyond 64 cache lines only reduces the back-end aggregated load but not the back-end load-imbalance. The relative server load is calculated by comparing the server load for a given front-end cache size to the server load when there is no front-end caching (cache size = 0). Figure 3 demonstrates the reduction in the relative server load as the front-end cache size increases. However, the benefit of doubling the cache size proportionally decays with the key hotness distribution. As shown in Figure 3, the first 64 cachelines reduce the relative server load by 91% while the second 64 cachelines reduce the relative server load by only 2% more.

The failure of the ”one size fits all” design strategy suggests that statically allocating fixed cache and tracker sizes to all front-end servers is not ideal. Each front-end server should independently and adaptively be configured according to the key access distribution it serves. Also, changes in workloads can alter the key access distribution, the skew level, or the set of hot keys. For example, social networks and web front-end servers that serve different geographical regions might experience different key access distributions and different local trends (e.g., #miami vs. #ny). Similarly, in large scale data processing pipelines, several applications are deployed on top of a shared caching layer. Front-end servers of different applications serve accesses that might be interested in different partitions of the data and hence experience different key access distributions and local trends. Therefore, CoT’s cache resizing algorithm learns the key access distribution independently at each front-end and dynamically resizes the cache and the tracker to achieve lookup load-imbalance target $I_{t}$ . CoT is designed to reduce the front-end cache size that achieves $I_{t}$ . Any increase in the front-end cache size beyond CoT’s recommendation mainly decreases back-end load and should consider other conflicting parameters such as the additional cost of the memory cost, the cost of updates and maintaining the additional cached keys, and the percentage of back-end load reduction that results from allocating additional front-end caches.

4.4.2 CoT: Cache Resizing Algorithm:

Front-end servers use CoT to minimize the cache size that achieves a target load-imbalance $I_{t}$ . Initially, front-end servers are configured with no front-end caches. The system administrator configures CoT by an input target load-imbalance parameter $I_{t}$ that determines the maximum tolerable imbalance between the most loaded and least loaded back-end caching servers. Afterwards, CoT expands both tracker and cache sizes until the current load-imbalance achieves the inequality $I_{c}\leq I_{t}$ .

Algorithm 3 describes CoT’s cache resizing algorithm. CoT divides the timeline into epochs and each epoch consists of $E$ accesses. Algorithm 3 is executed at the end of each epoch. The epoch size $E$ is proportional to the tracker size $K$ and is dynamically updated to guarantee that $E\geq K$ (Line 4). This inequality is required to guarantee that CoT does not trigger consecutive resizes before the cache and the tracker are filled with keys. During each epoch, CoT tracks the number of lookups sent to every back-end caching server. In addition, CoT tracks the total number of cache hits and tracker hits during this epoch. At the end of each epoch, CoT calculates the current load-imbalance $I_{c}$ as the ratio between the highest and the lowest load on back-end servers during this epoch. Also, CoT calculates the current average hit per cached key $\alpha_{c}$ . $\alpha_{c}$ equals the total cache hits in the current epoch divided by the cache size. Similarly, CoT calculates the current average hit per tracked but not cache key $\alpha_{k-c}$ . CoT compares $I_{c}$ to $I_{t}$ and decides on a resizing action as follows.

1.

$I_{c}>I_{t}$ (Line 1), this means that the target load-imbalance is not achieved. CoT follows the binary search algorithm in searching for the front-end cache size that achieves $I_{t}$ . Therefore, CoT decides to double the front-end cache size (Line 2). As a result, CoT doubles the tracker size as well to maintain a tracker to cache size ratio of at least 2, $K\geq 2\cdot C$ (Line 3). In addition, CoT uses a local variable $\alpha_{t}$ to capture the quality of the cached keys when $I_{t}$ is first achieved. Initially, $\alpha_{t}=0$ . CoT then sets $\alpha_{t}$ to the average hits per cache-line $\alpha_{c}$ during the current epoch (Line 5). In subsequent epochs, $\alpha_{t}$ is used to detect changes in workload.
2.

$I_{c}\leq I_{t}$ (Line 6), this means that the target load-imbalance has been achieved. However, changes in workload could alter the quality of the cached keys. Therefore, CoT uses $\alpha_{t}$ to detect and handle changes in workload in future epochs as explained below.

Algorithm 3 CoT’s elastic resizing algorithm.

State: $S_{c}$ : keys in the cache, $S_{k}$ : keys in the tracker, C: cache capacity, K: tracker capacity, $\alpha_{c}$ : average hits per key in $S_{c}$ in the current epoch, $\alpha_{k-c}$ : average hits per key in $S_{k-c}$ in the current epoch, $I_{c}$ : current load-imbalance, and $\alpha_{t}$ : target average hit per key
Input: $I_{t}$

1:if

I_{c}>I_{t}

then

2: resize(

S_{c}

2\times C

)

3: resize(

S_{k}

2\times K

)

4: E := max (E,

K

)

5: Let

\alpha_{t}

\alpha_{c}

6:else

7: if

\alpha_{c}<(1-\epsilon).\alpha_{t}

and

\alpha_{k-c}<(1-\epsilon).\alpha_{t}

then

8: resize(

S_{c}

\frac{C}{2}

)

9: resize(

S_{k}

\frac{K}{2}

)

10: else if

\alpha_{c}<(1-\epsilon).\alpha_{t}

and

\alpha_{k-c}>(1-\epsilon).\alpha_{t}

then

11: half_life_time_decay()

12: else

13: do_nothing()

14: end if

15:end if

$\alpha_{t}$ is reset whenever the inequality $I_{c}\leq I_{t}$ is violated and Algorithm 3 expands cache and tracker sizes. Ideally, when the inequality $I_{c}\leq I_{t}$ holds, keys in the cache (the set $S_{c}$ ) achieve $\alpha_{t}$ hits per cache-line during every epoch while keys in the tracker but not in the cache (the set $S_{k-c}$ ) do not achieve $\alpha_{t}$ . This happens because keys in the set $S_{k-c}$ are less hot than keys in the set $S_{c}$ . $\alpha_{t}$ represents a target hit-rate per cache-line for future epochs. Therefore, if keys in the cache do not meet the target $\alpha_{t}$ in a following epoch, this indicates that the quality of the cached keys has changed and an action needs to be taken as follows.

1.

Case 1: keys in $S_{c}$ , on the average, do not achieve $\alpha_{t}$ hits per cacheline and keys in $S_{k-c}$ do not achieve $\alpha_{t}$ hits as well (Line 7). This indicates that the quality of the cached keys decreased. In response. CoT shrinks both the cache and the tracker sizes (Lines 8 and 9). If shrinking both cache and tracker sizes results in a violation of the inequality $I_{c}<I_{t}$ , Algorithm 3 doubles both tracker and cache sizes in the following epoch and $\alpha_{t}$ is reset as a result. In Line 7, we compare the average hits per key in both $S_{c}$ and $S_{k-c}$ to $(1-\epsilon)\cdot\alpha_{t}$ instead of $\alpha_{t}$ . Note that $\epsilon$ is a small constant $<<<1$ that is used to avoid unnecessary resizing actions due to insignificant statistical variations.
2.

Case 2: keys in $S_{c}$ do not achieve $\alpha_{t}$ while keys in $S_{k-c}$ achieve $\alpha_{t}$ (Line 10). This signals that the set of hot keys is changing and keys in $S_{k-c}$ are becoming hotter than keys in $S_{c}$ . For this, CoT triggers a half-life time decaying algorithm that halves the hotness of all cached and tracked keys (Line 11). This decaying algorithm aims to forget old trends that are no longer hot to be cached (e.g., Gangnam style song). Different decaying algorithms have been developed in the literature [20, 21, 18]. Therefore, this paper only focuses on the resizing algorithm details without implementing a decaying algorithm.
3.

Case 3: keys in $S_{c}$ achieve $\alpha_{t}$ while keys in $S_{k-c}$ do not achieve $\alpha_{t}$ . This means that the quality of the cached keys has not changed and therefore, CoT does not take any action. Similarly, if keys in both sets $S_{c}$ and $S_{k-c}$ achieve $\alpha_{t}$ , CoT does not take any action as long as the inequality $I_{c}<I_{t}$ holds (Line 13).

5 Experimental Evaluation

In this section, we evaluate CoT’s caching algorithm and CoT’s adaptive resizing algorithm. We choose to compare CoT to traditional and widely used replacement policies like LRU and LFU. In addition, we compare CoT to both ARC [42] and LRU-k [45]. As stated in [42], ARC, in its online auto-configuration setting, achieves comparable performance to LRU-2 (which is the most responsive LRU-k ) [45, 46], 2Q [34], LRFU [36], and LIRS [32] even when these policies are perfectly tuned offline. Also, ARC outperforms the online adaptive replacement policy MQ [51]. Therefore, we compare with ARC and LRU-2 as representatives of these different polices. The experimental setup is explained in Section 5.1. First, we compare the hit rates of CoT’s cache algorithm to LRU, LFU, ARC, and LRU-2 hit rates for different front-end cache sizes in Section 5.2. Then, we compare the required front-end cache size for each replacement policy to achieve a target back-end load-imbalance $I_{t}$ in Section 5.3. In Section 5.4, we provide an end-to-end evaluation of front-end caches comparing the end-to-end performance of CoT, LRU, LFU, ARC, and LRU-2 on different workloads with the configuration where no front-end cache is deployed. Finally, CoT’s resizing algorithm is evaluated in Section 5.5.

5.1 Experiment Setup

We deploy 8 instances of memcached [4] on a small cluster of 4 caching servers (2 memcached instance per server). Each caching server has an Intel(R) Xeon(R) CPU E31235 with 4GB RAM dedicated to each memcached instance.

Dedicated client machines are used to generate client workloads. Each client machine executes multiple client threads to submit workloads to caching servers. Client threads use Spymemcached 2.11.4 [6], a Java-based memcached client, to communicate with memcached cluster. Spymemcached provides communication abstractions that distribute workload among caching servers using consistent hashing [35]. We slightly modified Spymemcached to monitor the workload per back-end server at each front-end. Client threads use Yahoo! Cloud Serving Benchmark (YCSB) [19] to generate workloads for the experiments. YCSB is a standard key/value store benchmarking framework. YCSB is used to generate key/value store requests such as Get, Set, and Insert. YCSB enables configuring the ratio between read (Get) and write (Set) accesses. Also, YCSB allows the generation of accesses that follow different access distributions. As YCSB is CPU-intensive, client machines run at most 20 client threads per machine to avoid contention among client threads. During our experiments, we realized that YCSB’s ScrambledZipfian workload generator has a bug as it generates Zipfian workload distributions with significantly less skew than the skew level it is configured with. Therefore, we use YCSB’s ZipfianGenerator instead of YCSB’s ScrambledZipfian.

Our experiments use different variations of YCSB core workloads. Workloads consist of 1 million key/value pairs. Each key consists of a common prefix ”usertable:” and a unique ID. We use a value size of 750 KB making a dataset of size 715GB. Experiments use read intensive workloads that follow Tao’s [13] read-to-write ratio of 99.8% reads and 0.2% updates. Unless otherwise specified, experiments consist of 10 million key accesses sampled from different access distributions such as Zipfian (s = 0.90, 0.99, or 1.2) and uniform. Client threads submit access requests back-to-back. Each client thread can have only one outgoing request. Clients submit a new request as soon as they receive an acknowledgement for their outgoing request.

5.2 Hit Rate

The first experiment compares CoT’s hit rate to LRU, LFU, ARC, and LRU-2 hit rates using equal cache sizes for all replacement policies. 20 client threads are provisioned on one client machine and each cache client maintains its own cache. The cache size is varied from a very small cache of 2 cache-lines to 1024 cache-lines. The hit rate is compared using different Zipfian access distributions with skew parameter values s = 0.90, 0.99, and 1.2 as shown in Figures 4(a), 4(b), and 4(c) respectively. CoT’s tracker to cache size ratio determines how many tracking nodes are used for every cache-line. CoT automatically detects the ideal tracker to cache ratio for any workload by fixing the cache size and doubling the tracker size until the observed hit-rate gains from increasing the tracker size are insignificant i.e., the observed hit-rate saturates. The tracker to cache size ratio decreases as the workload skew increases. A workload with high skew simplifies the task of distinguishing hot keys from cold keys and hence, CoT requires a smaller tracker size to successfully filter hot keys from cold keys. Note that LRU-2 is also configured with the same history to cache size as CoT’s tracker to cache size. In this experiment, for each skew level, CoT’s tracker to cache size ratio is varied as follows: 16:1 for Zipfian 0.9, 8:1 for Zipfian 0.99, and 4:1 for Zipfian 1.2. Note that CoT’s tracker maintains only the meta-data of tracked keys. Each tracker node consists of a read counter and a write counter with 8 bytes of memory overhead per tracking node. In real-world workloads, value sizes vary from few hundreds KBs to few MBs. For example, Google’s Bigtable [14] uses a value size of 64 MB. Therefore, a memory overhead of at most $\frac{1}{8}$ KB (16 tracker nodes * 8 bytes) per cache-line is negligible.

In Figures 4, the x-axis represents the cache size expressed as the number of cache-lines. The y-axis represents the front-end cache hit rate (%) as a percentage of the total workload size. At each cache size, the cache hit rates are reported for LRU, LFU, ARC, LRU-2, and CoT cache replacement policies. In addition, TPC represents the theoretically calculated hit-rate from the Zipfian distribution CDF if a perfect cache with the same cache size is deployed. For example, a perfect cache of size 2 cache-lines stores the hot most 2 keys and hence any access to these 2 keys results in a cache hit while accesses to other keys result in cache misses.

As shown in Figure 4(a), CoT surpasses LRU, LFU, ARC, and LRU-2 hit rates at all cache sizes. In fact, CoT achieves almost similar hit-rate to the TPC hit-rate. In Figure 4(a), CoT outperforms TPC for some cache size which is counter intuitive. This happens as TPC is theoretically calculated using the Zipfian CDF while CoT’s hit-rate is calculate out of YCSB’s sampled distributions which are approximate distributions. In addition, CoT achieves higher hit-rates than both LRU and LFU with 75% less cache-lines. As shown, CoT with 512 cache-lines achieves 10% more hits than both LRU and LFU with 2048 cache-lines. Also, CoT achieves higher hit rate than ARC using 50% less cache-lines. In fact, CoT configured with 512 cache-lines achieves 2% more hits than ARC with 1024 cache-lines. Taking tracking memory overhead into account, CoT maintains a tracker to cache size ratio of 16:1 for this workload (Zipfian 0.9). This means that CoT adds an overhead of 128 bytes (16 tracking nodes * 8 bytes each) per cache-line. The percentage of CoT’s tracking memory overhead decreases as the cache-line size increases. For example, CoT introduces a tracking overhead of 0.02% when the cache-line size is 750KB. Finally, CoT consistently achieves 8-10% higher hit-rate than LRU-2 configured with the same history and cache sizes as CoT’s tracker and cache sizes.

Similarly, as illustrated in Figures 4(b) and 4(c), CoT outpaces LRU, LFU, ARC, and LRU-2 hit rates at all different cache sizes. Figure 4(b) shows that a configuration of CoT using 512 cache-lines achieves 3% more hits than both configurations of LRU and LFU with 2048 cache-lines. Also, CoT consistently outperforms ARC’s hit rate with 50% less cache-lines. Finally, CoT achieves 3-7% higher hit-rate than LRU-2 configured with the same history and cache sizes. Figures 4(b) and 4(c) highlight that increasing workload skew decreases the advantage of CoT. As workload skew increases, the ability of LRU, LFU, ARC, LRU-2 to distinguish between hot and cold keys increases and hence CoT’s preeminence decreases.

5.3 Back-End Load-Imbalance

In this section, we compare the required front-end cache sizes for different replacement policies to achieve a back-end load-imbalance target $I_{t}$ . Different skewed workloads are used, namely, Zipfian s = 0.9, s = 0.99, and s = 1.2. For each distribution, we first measure the back-end load-imbalance when no front-end cache is used. A back-end load-imbalance target $I_{t}$ is set to $I_{t}=1.1$ . This means that the back-end is load balanced if the most loaded back-end server processes at most 10% more lookups than the least loaded back-end server. We evaluate the back-end load-imbalance while increasing the front-end cache size using different cache replacement policies, namely, LRU, LFU, ARC, LRU-2, and CoT. In this experiment, CoT uses the same tracker-to-cache size ratio as in Section 5.2. For each replacement policy, we report the minimum required number of cache-lines to achieve $I_{t}$ .

Dist.

Load- imbalance No cache

Number of cache-lines

to achieve

I_{t}=1.1

LRU

LFU

ARC

LRU-2

CoT

Zipf 0.9

1.35

Zipf 0.99

1.73

128

Zipf 1.20

4.18

2048

1024

512

Table 2: The minimum required number of cache-lines for different replacement policies to achieve a back-end load-imbalance target

I_{t}=1.1

for different workload distributions.

Table 2 summarizes the reported results for different distributions using LRU, LFU, ARC, LRU-2, and CoT replacement policies. For each distribution, the initial back-end load-imbalance is measured using no front-end cache. As shown, the initial load-imbalances for Zipf 0.9, Zipf 0.99, and Zipf 1.20 are 1.35, 1.73, and 4.18 respectively. For each distribution, the minimum required number of cache-lines for LRU, LFU, ARC, and CoT to achieve a target load-imbalance of $I_{t}=1.1$ is reported. As shown, CoT requires 50% to 93.75% less cache-lines than other replacement policies to achieve $I_{t}$ . Since LRU-2 is configured with a history size equals to CoT’s tracker size, LRU-2 requires the second least number of cache-lines to achieve $I_{t}$ .

5.4 End-to-End Evaluation

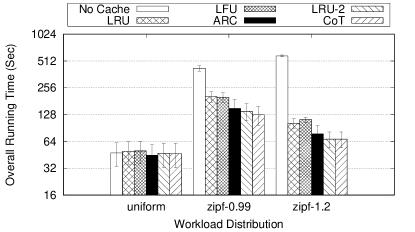
In this section, we evaluate the effect of front-end caches using LRU, LFU, ARC, LRU-2, and CoT replacement policies on the overall running time of different workloads. This experiment also demonstrates the overhead of front-end caches on the overall running time. In this experiment, we use 3 different workload distributions, namely, uniform, Zipfian (s = 0.99), and Zipfian (s = 1.2) distributions as shown in Figure 5. For all the three workloads, each replacement policy is configured with 512 cache-lines. Also, CoT and LRU-2 maintains a tracker (history) to cache size ratio of 8:1 for Zipfian 0.99 and 4:1 for both Zipfian 1.2 and uniform distributions. In this experiment, a total of 1M accesses are sent to the caching servers by 20 client threads running on one client machine. Each experiment is executed 10 times and the average overall running time with 95% confidence intervals are reported in Figure 5.

In this experiment, the front-end servers are allocated in the same cluster as the back-end servers. The average Round-Trip Time (RTT) between front-end machines and back-end machines is 244 $\mu$ s. This small RTT allows us to fairly measure the overhead of front-end caches by minimizing the performance advantages achieved by front-end cache hits. In real-world deployments where front-end servers are deployed in edge-datacenters and the RTT between front-end servers and back-end servers is in order of 10s of ms, front-end caches achieve more significant performance gains.

The uniform workload is used to measure the overhead of front-end caches. In a uniform workload, all keys in the key space are equally hot and front-end caches cannot take any advantage of workload skew to benefit some keys over others. Therefore, front-end caches only introduce the overhead of maintaining the cache without achieving any significant performance gains. As shown in Figure 5, there is no significant statistical difference between the overall running time when there is no front-end cache and when there is a small front-end cache with different replacement policies. Adding a small front-end cache does not incur running time overhead even for replacement policies that use a heap (e.g., LFU, LRU-2, and CoT).

The workloads Zipfian 0.99 and Zipfian 1.2 are used to show the advantage of front-end caches even when the network delays between front-end servers and back-end servers are minimal. As shown in Figure 5, workload skew results in significant overall running time overhead in the absence of front-end caches. This happens because the most loaded server introduces a performance bottleneck especially under thrashing (managing 20 connections, one from each client thread). As the load-imbalance increases, the effect of this bottleneck is worsen. Specifically, in Figure 5, the overall running time of Zipfian 0.99 and Zipfian 1.2 workloads are respectively 8.9x and 12.27x of the uniform workload when no front-end cache is deployed. Deploying a small front-end cache of 512 cachelines significantly reduces the effect of back-end bottlenecks. Deploying a CoT small cache in the front-end results in 70% running time reduction for Zipfian 0.99 and 88% running time reduction for Zipfian 1.2 in comparison to having no front-end cache. Other replacement policies achieve running time reductions of 52% to 67% for Zipfian 0.99 and 80% to 88% for Zipfian 1.2. LRU-2 achieves the second best average overall running time after CoT with no significant statistical difference between the two policies. Since both policies use the same tracker (history) size, this again suggests that having a bigger tracker helps separate cold and noisy keys from hot keys. Since the ideal tracker to cache size ratio differs from one workload to another, having an automatic and dynamic way to configure this ratio at run-time while serving workload gives CoT a big leap over statically configured replacement policies.

To isolate the effect of both front-end and back-end thrashing on the overall running time, we run the same experiment with only one client thread that executes 50K lookups (1M/20) and we report the results of this experiment in Figure 6. The first interesting observation of this experiment is that the overall running time of Zipfian 0.99 and Zipfian 1.2 workloads are respectively 3.2x and 4.5x of the uniform workload when no front-end cache is deployed. These numbers are proportional to the load-imbalance factors of these two distributions (1.73 for Zipfian 0.99 and 4.18 for Zipfian 1.2). These factors are significantly worsen under thrashing as shown in the previous experiment. The second interesting observation is that deploying a small front-end cache in a non-thrashing environment results in a lower overall running time for skewed workload (e.g., Zipfian 0.99 and Zipfian 1.2) than for a uniform workload. This occurs because front-end caches eliminate back-end load-imbalance and locally serve lookups as well.

5.5 Adaptive Resizing

This section evaluates CoT’s auto-configure and resizing algorithms. First, we configure a front-end client that serves a Zipfian 1.2 workload with a tiny cache of size two cachelines and a tracker of size of four tracking entries. This experiment aims to show how CoT expands cache and tracker sizes to achieve a target load-imbalance $I_{t}$ as shown in Figure 7. After CoT reaches the cache size that achieves $I_{t}$ , the average hit per cache-line $\alpha_{t}$ is recorded as explained in Algorithm 3. Second, we alter the workload distribution to uniform and monitors how CoT shrinks tracker and cache sizes in response to workload changes without violating the load-imbalance target $I_{t}$ in Figure 8. In both experiments, $I_{t}$ is set to 1.1 and the epoch size is 5000 accesses. In both Figures 7(a) and 8(a), the x-axis represents the epoch number, the left y-axis represents the number of tracker and cache lines, and the right y-axis represents the load-imbalance. The black and red lines represent cache and tracker sizes respectively with respect to the left y-axis. The blue and green lines represent the current load-imbalance and the target load-imbalance respectively with respect to the right y-axis. Same axis description applies for both Figures 7(b) and 8(b) except that the right y-axis represents the average hit per cache-line during each epoch. Also, the light blue and the dark blue lines represent the current average hit per cache-line and the target hit per cache-line at each epoch with respect to the right y-axis.

In Figure 7(a), CoT is initially configured with a cache of size 2 and a tracker of size 4. CoT’s resizing algorithm runs in 2 phases. In the first phase, CoT discovers the ideal tracker-to-cache size ratio that maximizes the hit rate for a fixed cache size for the current workload. For this, CoT fixes the cache size and doubles the tracker size until doubling the tracker size achieves no significant benefit on the hit rate. This is shown in Figure 7(b) in the first 15 epochs. CoT allows a warm up period of 5 epochs after each tracker or cache resizing decision. Notice that increasing the tracker size while fixing the cache size reduces the current load-imbalance $I_{c}$ (shown in Figure 7(a)) and increases the current observed hit per cache-line $\alpha_{c}$ (shown in Figure 7(b)). Figure 7(b) shows that CoT first expands the tracker size to 16 and during the warm up epochs (epochs 10-15), CoT observes no significant benefit in terms of $\alpha_{c}$ when compared to a tracker size of 8. In response, CoT therefore shrinks the tracker size to 8 as shown in the dip in the red line in Figure 7(b) at epoch 16. Afterwards, CoT starts phase 2 searching for the smallest cache size that achieves $I_{t}$ . For this, CoT doubles the tracker and caches sizes until the target load-imbalance is achieved and the inequality $I_{c}\leq I_{t}$ holds as shown in Figure 7(a). CoT captures $\alpha_{t}$ when $I_{t}$ is first achieved. $\alpha_{t}$ determines the quality of the cached keys when $I_{t}$ is reached for the first time. In this experiment, CoT does not trigger resizing if $I_{c}$ is within 2% of $I_{t}$ . Also, as the cache size increases, $\alpha_{c}$ decreases as the skew of the additionally cached keys decreases. For a Zipfian 1.2 workload and to achieve $I_{t}=1.1$ , CoT requires 512 cache-lines and 2048 tracker lines and achieves an average hit per cache-line of $\alpha_{t}=7.8$ per epoch.

Figure 8 shows how CoT successfully shrinks tracker and cache sizes in response to workload skew drop without violating $I_{t}$ . After running the experiment in Figure 7, we alter the workload to uniform. Therefore, CoT detects a drop in the current average hit per cache-line as shown in Figure 8(b). At the same time, CoT observe that the current load-imbalance $I_{c}$ achieves the inequality $I_{c}\leq I_{t}=1.1$ . Therefore, CoT decides to shrink both the tracker and cache sizes until either $\alpha_{c}\approx\alpha_{t}=7.8$ or $I_{t}$ is violated or until cache and tracker sizes are negligible. First, CoT resets the tracker to cache size ratio to 2:1 and then searches for the right tracker to cache size ratio for the current workload. Since the workload is uniform, expanding the tracker size beyond double the cache size achieves no hit-rate gains as shown in Figure 8(b). Therefore, CoT moves to the second phase of shrinking both tracker and cache sizes as long $\alpha_{t}$ is not achieved and $I_{t}$ is not violated. As shown, in Figure 8, CoT shrinks both the tracker and the cache sizes until front-end cache size becomes negligible. As shown in Figure 8(a), CoT shrinks cache and tracker sizes while ensuring that the target load-imbalance is not violated.

6 Related Work

Distributed caches are widely deployed to serve social networks and the web at scale [13, 44, 49]. Real-world workloads are typically skewed with few keys that are significantly hotter than other keys [30]. This skew can cause load-imbalance among the caching servers. Load-imbalancing negatively affects the overall performance of the caching layer. Therefore, many works in the literature have addressed the load-imbalacing problem from different angles. Solutions use different load-monitoring techniques (e.g., centralized tracking [9, 31, 8, 48], server-side tracking [29, 15], and client-side tracking [24, 33]). Based on the load-monitoring, different solutions redistribute keys among caching servers at different granularities. The following paragraphs summarize the related works under different categories.

Centralized load-monitoring: Slicer [9] separates the data serving plane from the control plane. The key space is divided into slices where each slice is assigned to one or more servers. The control plane is a centralized system component that collects the access information of each slice and the workload per server. The control plane periodically runs an optimization that generates a new slice assignment. This assignment might result in redistributing, repartitioning, or replicating slices among servers to achieve better load-balancing. Unlike in Centrifuge [8], Slicer does not use consistent hashing to map keys to servers. Instead, Slicer distributes the generated assignments to the front-end servers to allow them to locate keys. Also, Slicer highly replicates the centralized control plane to achieve high availability and to solve the fault-tolerance problem in both Centrifuge [8] and in [15]. CoT is complementary to systems like Slicer. Our goal is to cache heavy hitters at front-end servers to reduce key skew at back-end caching servers and hence, reduce Slicer’s initiated re-configurations. Our focus is on developing a replacement policy and an adaptive cache resizing algorithm to enhance the performance of front-end caches. Also, our approach is distributed and front-end driven that does not require any system component to develop a global view of the workload. This allows CoT to scale to thousands of front-end servers without introducing any centralized bottlenecks.

Server side load-monitoring: Another approach to load-monitoring is to distribute the load-monitoring among the caching shard servers. In [29], each caching server tracks its own hot-spots. When the hotness of a key surpasses a certain threshold, this key is replicated to $\gamma$ caching servers and the replication decision is broadcast to all the front-end servers. Any further accesses on this hot key shall be equally distributed among these $\gamma$ servers. This approach aims to distribute the workload of the hot keys among multiple caching servers to achieve better load balancing. Cheng et al. [15] extend the work in [29] to allow moving coarse-grain key cachelets (shards) among threads and caching servers. Our approach reduces the need for server side load-monitoring. Instead, load-monitoring happens at the edge. This allows individual front-end servers to independently identify their local trends.

Client side load-monitoring: Fan et al. [24] theoretically show through analysis and simulation that a small cache in the client side can provide load balancing to n caching servers by caching only O(n log(n)) entries. Their result provides the theoretical foundations for our work. Unlike in [24], our approach does not assume perfect caching nor a priori knowledge of the workload access distribution. Gavrielatos et al. [25] propose symmetric caching to track and cache the hot-most items at every front-end server. Symmetric caching assumes that all front-end servers obtain the same access distribution and hence allocates the same cache size to all front-end servers. However, different front-end servers might serve different geographical regions and therefore observe different access distributions. CoT discovers the workload access distribution independently at each front-end server and adjusts the cache size to achieve a target load-imbalance $I_{t}$ . NetCache [33] uses programmable switches to implement heavy hitter tracking and caching at the network level. Like symmetric caching, NetCache assumes a fixed cache size for different access distributions. To the best of our knowledge, CoT is the first front-end caching algorithm that exploits the cloud elasticity allowing each front-end server to independently reduce the necessary required front-end cache memory to achieve back-end load-balance.

Other works in the literature focus on maximizing cache hit rates for fixed memory sizes. Cidon et al. [16, 17] redistribute available memory among memory slabs to maximize memory utilization and reduce cache miss rates. Fan et al. [23] use cuckoo hashing [47] to increase memory utilization. Lim et al. [37] increase memory locality by assigning requests that access the same data item to the same CPU. Bechmann et al. [11] propose Least Hit Density (LHD), a new cache replacement policy. LHD predicts the expected hit density of each object and evicts the object with the lowest hit density. LHD aims to evict objects that contribute low hit rates with respect to the cache space they occupy. Unlike these works, CoT does not assume a static cache size. In contrast, CoT maximizes the hit rate of the available cache and exploits the cloud elasticity allowing front-end servers to independently expand or shrink their cache memory sizes as needed.

7 Conclusion

In this paper, we present Cache on Track (CoT), a decentralized, elastic, and predictive cache at the edge of a distributed cloud-based caching infrastructure. CoT proposes a new cache replacement policy specifically tailored for small front-end caches that serve skewed workloads. Using CoT, system administrators do not need to statically specify cache size at each front-end in-advance. Instead, they specify a target back-end load-imbalance $I_{t}$ and CoT dynamically adjusts front-end cache sizes to achieve $I_{t}$ . Our experiments show that CoT’s replacement policy outperforms the hit-rates of LRU, LFU, ARC, and LRU-2 for the same cache size on different skewed workloads. CoT achieves a target server size load-imbalance with 50% to 93.75% less front-end cache in comparison to other replacement policies. Finally, our experiments show that CoT’s resizing algorithm successfully auto-configures front-end tracker and cache sizes to achieve the back-end target load-imbalance $I_{t}$ in the presence of workload distribution changes.

References

[1] Amazon elasticache in-memory data store and cache. https://aws.amazon.com/elasticache/, 2018.
[2] Azure redis cache. https://azure.microsoft.com/en-us/services/cache/, 2018.
[3] Facebook company info. http://newsroom.fb.com/company-info/, 2018.
[4] Memcached. a distributed memory object caching system. https://memcached.org/, 2018.
[5] Redis. http://redis.io/, 2018.
[6] A simple, asynchronous, single-threaded memcached client written in java. http://code.google.com/p/spymemcached/, 2018.
[7] Twitter: number of active users 2010-2018. https://www.statista.com/statistics/282087/number-of-monthly-active-twitter-users/, 2018.
[8] A. Adya, J. Dunagan, and A. Wolman. Centrifuge: Integrated lease management and partitioning for cloud services. In Proceedings of the 7th USENIX conference on Networked systems design and implementation, pages 1–1. USENIX Association, 2010.
[9] A. Adya, D. Myers, J. Howell, J. Elson, C. Meek, V. Khemani, S. Fulger, P. Gu, L. Bhuvanagiri, J. Hunter, et al. Slicer: Auto-sharding for datacenter applications. In OSDI, pages 739–753, 2016.
[10] B. Atikoglu, Y. Xu, E. Frachtenberg, S. Jiang, and M. Paleczny. Workload analysis of a large-scale key-value store. In ACM SIGMETRICS Performance Evaluation Review, volume 40, pages 53–64. ACM, 2012.
[11] N. Beckmann, H. Chen, and A. Cidon. LHD: Improving cache hit rate by maximizing hit density. In 15th USENIX Symposium on Networked Systems Design and Implementation (NSDI 18), pages 389–403, Renton, WA, 2018. USENIX Association.
[12] L. Breslau, P. Cao, L. Fan, G. Phillips, and S. Shenker. Web caching and zipf-like distributions: Evidence and implications. In INFOCOM’99. Eighteenth Annual Joint Conference of the IEEE Computer and Communications Societies. Proceedings. IEEE, volume 1, pages 126–134. IEEE, 1999.
[13] N. Bronson, Z. Amsden, G. Cabrera, P. Chakka, P. Dimov, H. Ding, J. Ferris, A. Giardullo, S. Kulkarni, H. Li, et al. Tao: Facebook’s distributed data store for the social graph. In Presented as part of the 2013 USENIX Annual Technical Conference (USENIX ATC 13), pages 49–60, 2013.
[14] F. Chang, J. Dean, S. Ghemawat, W. C. Hsieh, D. A. Wallach, M. Burrows, T. Chandra, A. Fikes, and R. E. Gruber. Bigtable: A distributed storage system for structured data. ACM Transactions on Computer Systems (TOCS), 26(2):4, 2008.
[15] Y. Cheng, A. Gupta, and A. R. Butt. An in-memory object caching framework with adaptive load balancing. In Proceedings of the Tenth European Conference on Computer Systems, page 4. ACM, 2015.
[16] A. Cidon, A. Eisenman, M. Alizadeh, and S. Katti. Dynacache: Dynamic cloud caching. In 7th USENIX Workshop on Hot Topics in Cloud Computing (HotCloud 15), 2015.
[17] A. Cidon, A. Eisenman, M. Alizadeh, and S. Katti. Cliffhanger: Scaling performance cliffs in web memory caches. In NSDI, pages 379–392, 2016.
[18] E. Cohen and M. Strauss. Maintaining time-decaying stream aggregates. In Proceedings of the twenty-second ACM SIGMOD-SIGACT-SIGART symposium on Principles of database systems, pages 223–233. ACM, 2003.
[19] B. F. Cooper, A. Silberstein, E. Tam, R. Ramakrishnan, and R. Sears. Benchmarking cloud serving systems with ycsb. In Proceedings of the 1st ACM symposium on Cloud computing, pages 143–154. ACM, 2010.
[20] G. Cormode, F. Korn, and S. Tirthapura. Exponentially decayed aggregates on data streams. In Data Engineering, 2008. ICDE 2008. IEEE 24th International Conference on, pages 1379–1381. IEEE, 2008.
[21] G. Cormode, V. Shkapenyuk, D. Srivastava, and B. Xu. Forward decay: A practical time decay model for streaming systems. In Data Engineering, 2009. ICDE’09. IEEE 25th International Conference on, pages 138–149. IEEE, 2009.
[22] A. Dasgupta, R. Kumar, and T. Sarlós. Caching with dual costs. In Proceedings of the 26th International Conference on World Wide Web Companion, pages 643–652. International World Wide Web Conferences Steering Committee, 2017.
[23] B. Fan, D. G. Andersen, and M. Kaminsky. Memc3: Compact and concurrent memcache with dumber caching and smarter hashing. In Presented as part of the 10th USENIX Symposium on Networked Systems Design and Implementation (NSDI 13), pages 371–384, 2013.
[24] B. Fan, H. Lim, D. G. Andersen, and M. Kaminsky. Small cache, big effect: Provable load balancing for randomly partitioned cluster services. In Proceedings of the 2nd ACM Symposium on Cloud Computing, page 23. ACM, 2011.
[25] V. Gavrielatos, A. Katsarakis, A. Joshi, N. Oswald, B. Grot, and V. Nagarajan. Scale-out ccNUMA: exploiting skew with strongly consistent caching. In Proceedings of the Thirteenth EuroSys Conference, page 21. ACM, 2018.
[26] S. Ghandeharizadeh, M. Almaymoni, and H. Huang. Rejig: a scalable online algorithm for cache server configuration changes. In Transactions on Large-Scale Data-and Knowledge-Centered Systems XLII, pages 111–134. Springer, 2019.
[27] S. Ghandeharizadeh and H. Nguyen. Design, implementation, and evaluation of write-back policy with cache augmented data stores. Proceedings of the VLDB Endowment, 12(8):836–849, 2019.
[28] L. Guo, E. Tan, S. Chen, Z. Xiao, and X. Zhang. The stretched exponential distribution of internet media access patterns. In Proceedings of the twenty-seventh ACM symposium on Principles of distributed computing, pages 283–294. ACM, 2008.
[29] Y.-J. Hong and M. Thottethodi. Understanding and mitigating the impact of load imbalance in the memory caching tier. In Proceedings of the 4th annual Symposium on Cloud Computing, page 13. ACM, 2013.
[30] Q. Huang, H. Gudmundsdottir, Y. Vigfusson, D. A. Freedman, K. Birman, and R. van Renesse. Characterizing load imbalance in real-world networked caches. In Proceedings of the 13th ACM Workshop on Hot Topics in Networks, page 8. ACM, 2014.
[31] J. Hwang and T. Wood. Adaptive performance-aware distributed memory caching. In ICAC, volume 13, pages 33–43, 2013.
[32] S. Jiang and X. Zhang. Lirs: an efficient low inter-reference recency set replacement policy to improve buffer cache performance. ACM SIGMETRICS Performance Evaluation Review, 30(1):31–42, 2002.
[33] X. Jin, X. Li, H. Zhang, R. Soulé, J. Lee, N. Foster, C. Kim, and I. Stoica. Netcache: Balancing key-value stores with fast in-network caching. In Proceedings of the 26th Symposium on Operating Systems Principles, pages 121–136. ACM, 2017.
[34] T. Johnson and D. Shasha. X3: A low overhead high performance buffer management replacement algorithm. In Proceedings of the 20th VLDB Conference, 1994.
[35] D. Karger, E. Lehman, T. Leighton, R. Panigrahy, M. Levine, and D. Lewin. Consistent hashing and random trees: Distributed caching protocols for relieving hot spots on the world wide web. In Proceedings of the twenty-ninth annual ACM symposium on Theory of computing, pages 654–663. ACM, 1997.
[36] D. Lee, J. Choi, J.-H. Kim, S. H. Noh, S. L. Min, Y. Cho, and C. S. Kim. Lrfu: A spectrum of policies that subsumes the least recently used and least frequently used policies. IEEE transactions on Computers, 50(12):1352–1361, 2001.
[37] H. Lim, D. Han, D. G. Andersen, and M. Kaminsky. Mica: a holistic approach to fast in-memory key-value storage. In 11th USENIX Symposium on Networked Systems Design and Implementation (NSDI 14), pages 429–444, 2014.
[38] D. Lomet. Caching data stores: High performance at low cost. In 2018 IEEE 34th International Conference on Data Engineering (ICDE), pages 1661–1661. IEEE, 2018.
[39] D. Lomet. Cost/performance in modern data stores: how data caching systems succeed. In Proceedings of the 14th International Workshop on Data Management on New Hardware, page 9. ACM, 2018.
[40] D. B. Lomet. Data caching systems win the cost/performance game. IEEE Data Eng. Bull., 42(1):3–5, 2019.
[41] H. Lu, C. Hodsdon, K. Ngo, S. Mu, and W. Lloyd. The snow theorem and latency-optimal read-only transactions. In OSDI, pages 135–150, 2016.
[42] N. Megiddo and D. S. Modha. Arc: A self-tuning, low overhead replacement cache. In FAST, volume 3, pages 115–130, 2003.
[43] A. Metwally, D. Agrawal, and A. El Abbadi. Efficient computation of frequent and top-k elements in data streams. In International Conference on Database Theory, pages 398–412. Springer, 2005.
[44] R. Nishtala, H. Fugal, S. Grimm, M. Kwiatkowski, H. Lee, H. C. Li, R. McElroy, M. Paleczny, D. Peek, P. Saab, et al. Scaling memcache at facebook. In Presented as part of the 10th USENIX Symposium on Networked Systems Design and Implementation (NSDI 13), pages 385–398, 2013.
[45] E. J. O’neil, P. E. O’neil, and G. Weikum. The lru-k page replacement algorithm for database disk buffering. Acm Sigmod Record, 22(2):297–306, 1993.
[46] E. J. O’neil, P. E. O’Neil, and G. Weikum. An optimality proof of the lru-k page replacement algorithm. Journal of the ACM (JACM), 46(1):92–112, 1999.
[47] R. Pagh and F. F. Rodler. Cuckoo hashing. Journal of Algorithms, 51(2):122–144, 2004.
[48] C. Wu, V. Sreekanti, and J. M. Hellerstein. Autoscaling tiered cloud storage in anna. Proceedings of the VLDB Endowment, 12(6):624–638, 2019.
[49] V. Zakhary, D. Agrawal, and A. E. Abbadi. Caching at the web scale. Proceedings of the VLDB Endowment, 10(12):2002–2005, 2017.
[50] H. Zhang, G. Chen, B. C. Ooi, K.-L. Tan, and M. Zhang. In-memory big data management and processing: A survey. IEEE Transactions on Knowledge and Data Engineering, 27(7):1920–1948, 2015.
[51] Y. Zhou, J. Philbin, and K. Li. The multi-queue replacement algorithm for second level buffer caches. In USENIX Annual Technical Conference, General Track, pages 91–104, 2001.