Coronal Properties of Low-Accreting AGNs using Swift, XMM-Newton and NuSTAR Observations

The primary aim of this work is to investigate the coronal properties of low-accreting AGNs. We chose our sample from the all-sky Swift/BAT hard X-ray survey¹¹1https://swift.gsfc.nasa.gov/results/bs105mon/ (Oh et al., 2018). The BAT survey was compiled for 105 months, and the spectra are stacked together. The survey has a sensitivity of $8.4\times 10^{-12}$ erg cm^-2 s^-1  in $14-195$ keV range, and is almost unbiased by obscuration up to $N_{\rm H}\sim 10^{24}\rm\,cm^{-2}$ (Ricci et al., 2015). Initially, we chose a sample of AGNs within the range of $14-195$ keV, where the luminosity is less than $10^{45}$ erg s^-1. Our main goal is to select sources with an Eddington ratio $<10^{-3}$.

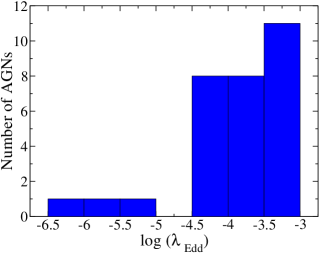
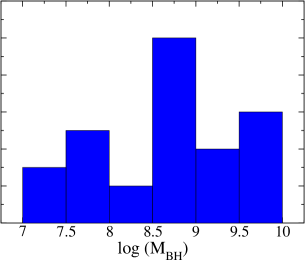
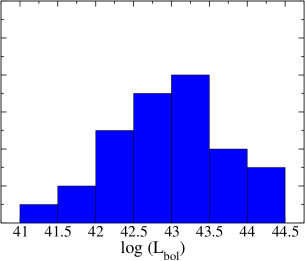
We selected all BAT AGNs with publicly available NuSTAR  observations. We also added XMM-Newton  or Swift/XRT observations for the soft X-ray band ($0.5-10$ keV) to construct the spectra in a broad energy range of $0.5-150$ keV²²2Check Appendix A for details.. From the combined spectra, we performed spectral analysis to calculate the bolometric luminosity ($L_{\rm bol}$) and Eddington ratio ($\lambda_{\rm Edd}$; see Section 3 for details). We selected sources with $\lambda_{\rm Edd}<10^{-3}$ for our sample. We excluded several sources from our sample (with $\lambda_{\rm Edd}<10^{-3}$) due to low signal-to-noise ratio (SNR), e.g., NCG 660, NGC 3486, NGC 678, or the presence of other sources in the field of view, e.g., NGC 5194. In the case of NGC 5194, several ULXs have been detected in the NuSTAR  field. As NuSTAR  does not resolve them, the emission is not purely from the AGN (Brightman et al., 2018). Hence, we did not include NGC 5194 in our sample. The final sample consists of 30 sources and are tabulated in Table 1. In Figure 1, we show the distribution of Eddington ratio ($\lambda_{\rm Edd}$), black hole mass ($M_{\rm BH}$), and bolometric luminosity ($L_{\rm bol}$) of our sample, in the left, middle, and right panels, respectively. Our sample extends over three orders of magnitude for all three parameters.

The $0.5-8$ keV Swift/XRT spectra were generated using the standard online tools provided by the UK Swift Science Data Centre (Evans et al., 2009)⁶⁶6https://www.swift.ac.uk/user_objects/. We utilized the Swift/XRT spectra for 17 objects when the simultaneous observations were available with NuSTAR. For five objects, we stacked several XRT spectra together to achieve a good SNR.

The $14-150$ keV Swift/BAT spectra and response matrices were obtained from the 105-month Swift-BAT All-sky Hard X-Ray Survey⁷⁷7https://swift.gsfc.nasa.gov/results/bs105mon/.

The spectral analysis of combined spectra in the $0.5-150$ keV range was performed in xspec v12.10 (Arnaud, 1996). For our analysis, we adopted the cross-section from Verner et al. (1996), and angr abundances (Anders & Grevesse, 1989). We used cross-normalization constants between the FPMA, FPMB, and BAT (Madsen et al., 2015; Madsen et al., 2017) instruments while carrying out simultaneous spectral fitting.

We started X-ray spectral modelling using an absorbed power law model with a cutoff at high energy. In xspec, the model reads as zphabs*zcutoff. We also added another component in the model for the absorption due to the Compton scattering, modelled with cabs. A component for the scattered primary emission, modelled with constant*zcutoff was added (e.g., Gupta et al., 2021). For the reprocessed emission, we used the convolution model reflect⁸⁸8https://heasarc.gsfc.nasa.gov/xanadu/xspec/manual/node297.html (Magdziarz & Zdziarski, 1995). Reflect is a generalization of the widely used pexrav model. It describes the reflection from a cold, neutral semi-infinite slab. The model parameters are reflection fraction ($R$), inclination angle ($i$), iron abundance ($A_{\rm Fe}$), and metal abundances ($A_{\rm M}$). We also added a Gaussian function at $\sim 6.4$ keV to incorporate the iron K-line emission. For the soft-excess emission, we added a blackbody model. However, one can also use the powerlaw to approximate the soft-excess (e.g., Nandi et al., 2021). The model setup (hereafter Model-1a) reads in XSPEC as,

Const1*phabs1*(zphabs2*cabs*reflect*zcutoffpl1 + Gauss + const2*cutoffpl2 + blackbody).

where, phabs1 represents the Galactic absorption and is calculated using NH⁹⁹9https://heasarc.gsfc.nasa.gov/cgi-bin/Tools/w3nh/w3nh.pl tools of FTOOLs (HI4PI Collaboration et al., 2016). Const1 represents the cross-normalization factor between the FPMA, FPMB, and BAT. The zphabs2*cabs*zcutoffpl1 represents the absorbed direct primary emission. const2*cutoffpl represents the scattered primary emission, while const2 is the scattering fraction ($f_{\rm Scat}$). The photon index ($\Gamma$), cutoff energy ($E_{\rm cut}$), normalization of cutoffpl1 and zcutoffpl2 are linked together. The column densities of the cabs and zphabs2 models are tied together and represent the line-of-sight obscuration towards the AGN. We fixed the $A_{\rm Fe}$ and $A_{\rm M}$ at the Solar values, i.e., 1 and the inclination angle at 60°  in our analysis. We allowed the Gaussian parameters to vary freely. However, when we could not constrain, we fixed the line energy at 6.4 keV and line width at 0.01, 0.05, or 0.1 keV, depending on the initial fitting.

We obtained good fits for all the sources using Model-1a. We noticed that the soft-excess is present in seven sources, namely, NGC 2655, NGC 4102, NGC 4258, NGC 5033, NGC 5290, NGC 7213, and HE 1136–2304. The spectra of the rest 23 sources can be fitted without the blackbody component in Model-1a. The scattered emission is present in 15 sources in our sample. The photon index ($\Gamma$) and cutoff energy ($E_{\rm cut}$) were obtained from the fitting. The hot electron temperature of the corona ($kT_{\rm e}$) can be calculated from the cutoff energy, using the empirical relation $E_{\rm cut}=2kT_{\rm e}$ (for $\tau_{\rm e}<1$) or $E_{\rm cut}=3kT_{\rm e}$ (for $\tau_{\rm e}>>1$) (Petrucci et al., 2001). Instead of this, one may also use Comptonization models such as compTT (Titarchuk, 1994) or nthcomp (Zdziarski et al., 1996, 1999) to obtain the hot electron temperature. To use the Comptonization model to probe the corona, we replaced cutoffpl with the nthcomp in the Model-1a. The spectral model reads in XSPEC as (hereafter Model-1b),

Const1*phabs1*(zphabs2*cabs*reflect*nthcomp + Gaussian + const2*nthcomp + blackbody).

During the spectral fitting, we froze the seed photon temperature of nthcomp component at 10 eV, which is a reasonable assumption for the SMBH with $M_{\rm BH}>10^{7}$ $M_{\odot}$(e.g., Shakura & Sunyaev, 1973; Makishima et al., 2000). We verified that the variations of the seed photon temperature from 5 eV to 20 eV did not affect the spectral fitting. We obtained good fits for all the sources with Model-1b. Table 5 shows the results obtained by applying Model-1a and Model-1b in our spectral fitting.

Next, we replaced reflect with a torus-based physically motivated model borus¹⁰¹⁰10https://sites.astro.caltech.edu/~mislavb/download/ (Baloković et al., 2018) in Model-1a. The borus02  model consists of a spherical homogeneous torus with two polar cutouts in a conical shape. The torus covering factor and the inclination angle are the free parameters in the model. The borus02  model also allows us to separate the line of sight column density ($N_{\rm H}^{\rm los}$) from the torus/obscuring material column density ($N_{\rm H}^{\rm tor}$). We did not require the Gaussian function while fitting with the borus02  model, as borus02  self-consistently calculates the Fe k$\alpha$ and Fe K$\beta$ lines. In our fitting, we also fixed the torus covering factor at 0.5 and the inclination angle at 60°. The spectral model reads in XSPEC as (hereafter Model-2a),

Const1*phabs1*(zphabs2*cabs*zcutoffpl1 + borus02 + const2*cutoffpl2 + blackbody).

The Model-2a gave us a good fit for all the sources in our sample. We obtained $N_{\rm H}^{\rm los}$, $N_{\rm H}^{\rm tor}$, $\Gamma$ and $E_{\rm cut}$ from the spectral modelling with Model-2a. As in the case of Model-1, to probe the corona with the Comptonized model, we replaced cutoffpl and borus02, with nthcomp and borus12 models, respectively, in Model-2a. In the borus12 model, the primary emission is described by nthcomp, replacing the cutoffpl model. The torus structure and geometry remain the same. This spectral model reads as (hereafter Model-2b),

Const1*phabs1*(zphabs2*cabs*nthcomp + borus12 + const2*nthcomp + blackbody).

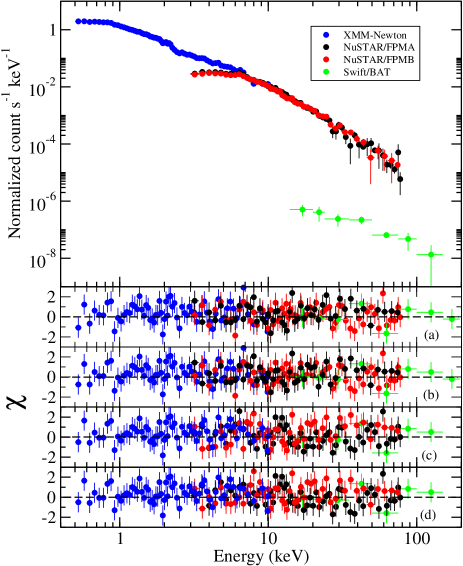
During fitting with the borus02  model, we linked $\Gamma$, $E_{\rm cut}$ and normalization of cutoffpl1, cutoffpl2, and borus02  together. The spectral analysis with the borus12 model returned with a good fit for all the sources. Table 7 shows the results obtained from our spectral fitting by applying Model-2a and Model-2b. Figure 2 shows the representative spectrum of NGC 4507 in the top panel. In the middle and bottom panels, the $\chi$ distributions are shown while using Model-1 and Model-2, respectively.

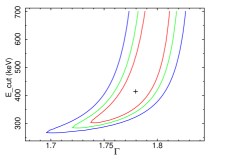
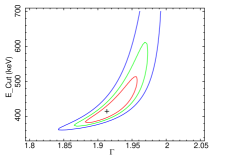
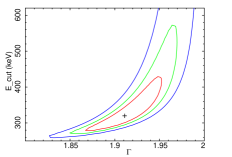
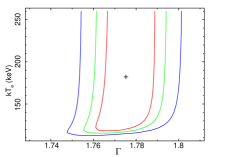
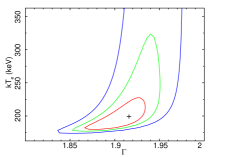
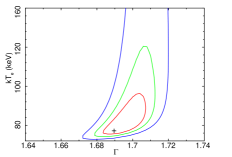
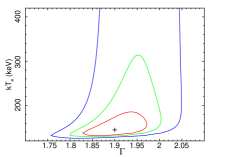
To estimate the uncertainties in the parameters, we ran the steppar command in XSPEC. The uncertainties are estimated at 68%, 90%, and 99% confidence levels. We quoted uncertainties at 90% confidence level throughout the paper unless mentioned otherwise. We show confidence contours between the $\Gamma$ and the $E_{\rm cut}$ in Figure 3 for NGC 454E, NGC 3147, NGC 3998, NGC 4102, NGC 7213, and HE 1136–2304 obtained from the fitting with Model-2a. Figure 4 shows the confidence contours between the $\Gamma$ and the $kT_{\rm e}$, obtained from the spectral analysis of data with Model-2b for NGC 454E, NGC 3147, NGC 3998, NGC 4102, NGC 7213, and HE 1136–2304. In Figure 3 (Figure 4), we selected six sources randomly to show that $E_{\rm cut}$ ($kT_{\rm e}$) could not be constrained in all sources. Detailed spectral analysis result is tabulated in Table 7.

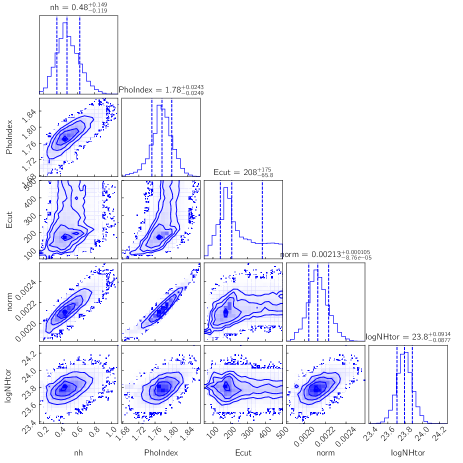
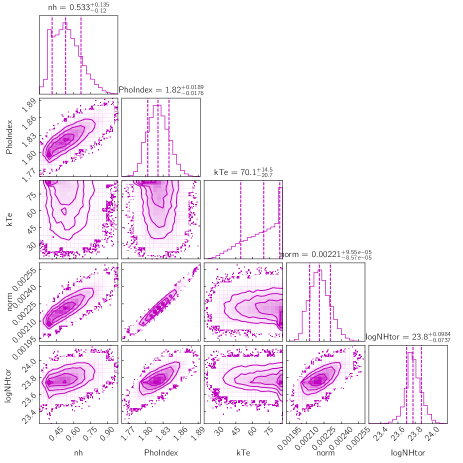
We also ran Markov Chain Monte Carlo (MCMC) in XSPEC¹¹¹¹11https://heasarc.gsfc.nasa.gov/xanadu/xspec/manual/node43.html to calculate the uncertainty. Using the Goodman–Weare algorithm, the chains were run with eight walkers for a total of $10^{6}$ steps. We discarded first 10000 steps of the chains, assuming them to be in the “burn-in” phase. Figure 14 shows the posterior distribution of the spectral parameters and errors obtained with the Model-2a and Model-2b in the left and right panels, respectively, for NGC 5033.

The spectral analysis is carried out with four different models, with the differences in the choice of the primary continuum (cutoffpl or nthcomp), and reprocessed emission (reflect or borus). We obtained similar results with all four models. The common parameters in all four models are $\Gamma$ and $N_{\rm H}^{\rm los}$. The mean value of $\Gamma$ is obtained to be $1.73\pm 0.05$, $1.73\pm 0.06$, $1.74\pm 0.04$, and $1.75\pm 0.04$, from Model-1a, Model-1b, Model-2a, and Model-2b, respectively. The mean value of $N_{\rm H}^{\rm los}$  is found to be $\log$ $N_{\rm H}^{\rm los}$  $23.39\pm 0.08$, $23.38\pm 0.10$, $23.40\pm 0.09$, and $23.40\pm 0.10$ from the spectral fitting with the Model-1a, Model-1b, Model-2a, and Model-2b, respectively. The mean values of $E_{\rm cut}$ and $kT_{\rm e}$ are also similar within uncertainties from different models. As Model-1 and Model-2 returned similar values of the spectral parameters, we used the spectral results from Model-2 in the rest of the paper or mentioned otherwise.

For 24 sources, we used black hole mass from the BAT AGN Spectroscopic Survey (BASS; Koss et al., 2017, 2022; Ricci et al., 2017a). For the remaining six sources, we searched for the black hole mass in the literature (see Table 1). From the spectral fitting, we estimated the intrinsic luminosity ($L_{\rm int}$) of the sources in the $2-10$ keV energy range. The bolometric luminosity is obtained by using the bolometric correction factor 10 (Vasudevan & Fabian, 2009). We calculated the Eddington ratio as $\lambda_{\rm Edd}=L_{\rm bol}/L_{\rm Edd}$, where $L_{\rm Edd}$ is the Eddington luminosity and given by, $L_{\rm Edd}=1.3\times 10^{38}~{}(M_{\rm BH}/M_{\odot})$ erg s^-1.

The $\Gamma$, $kT_{\rm e}$ and $E_{\rm cut}$ were obtained from the spectral fitting. The optical depth of the corona is estimated by using the following relation (Zdziarski et al., 1996),

where, $\theta=kT_{\rm e}/m_{e}c^{2}$ is the dimensionless temperature.

The dimensionless compactness parameter is calculated using the following equation (e.g., Fabian et al., 2015, 2017),

where, $R_{\rm X}$ is coronal size, and $L_{\rm X}$ is the coronal luminosity in the $0.1-200$ keV energy range. The $0.1-200$ keV luminosity is calculated from the extrapolation of the best-fitted model. In this work, we used $R_{\rm X}=10~{}R_{\rm g}$ (e.g., Fabian et al., 2015).

In the Compton cloud, the seed photons are up-scattered by the hot electrons and gain energy (e.g., Sunyaev & Titarchuk, 1980, 1985). The mean of the energy gained by photons per scattering can be estimated by the Compton-y parameter, $y=4\theta~{}{\rm max}(\tau_{\rm e},\tau_{\rm e}^{2})$ (e.g., Rybicki & Lightman, 1979). On the other hand, the total energy gain also depends on the number of scattering of the photons before escaping the medium. The average number of scattering ($N_{\rm S}$) is given by, $N_{\rm S}=y/\theta$.

A strong jet is expected in a low-accreting regime (Fender & Belloni, 2004). In general, the radio luminosity ($L_{\rm R}$) is considered a good proxy of the jet luminosity ($L_{\rm jet}$; e.g., Fender & Belloni, 2004). We collected jet luminosity ($L_{\rm jet}$ or $L_{\rm R}$ at $1.4$ GHz) of sources from the NASA Extragalactic Database (NED) archive¹²¹²12https://ned.ipac.caltech.edu/.

We estimated several spectral parameters of our sample. The detailed results are presented in Table 9.

Correlations among several coronal parameters have been extensively studied in the past (e.g., Ricci et al., 2017a; Kamraj et al., 2018). Here, we explored such co-dependencies among various spectral parameters. We employed Pearson, Spearman, and Kendall rank correlations to understand the relations among numerous parameters vis-á-vis the accretion mechanism around the LAC-AGNs. The results of our correlation study are tabulated in Table 3. Overall, all three correlation studies yield similar results. In total, we examined 30 correlations from our study. We considered the correlation is significant if the p-value is less than $0.01$. For nine pairs of parameters, we found the corresponding p-value as $<0.01$. We found a strong anti-correlation between $kT_{\rm e}$ and $E_{\rm cut}$. The $N_{\rm S}$ is observed to be strongly correlated with $kT_{\rm e}$ and $E_{\rm cut}$. We found moderate anti-correlations and correlations for three pairs of parameters each.

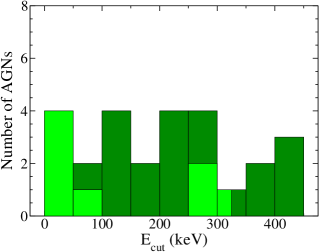
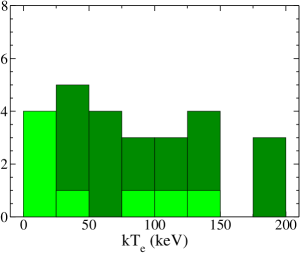
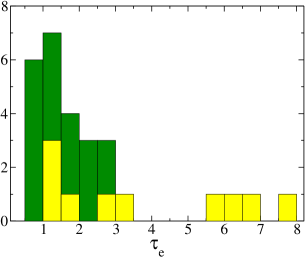
The corona is characterized by several parameters, namely the photon index ($\Gamma$), hot electron temperature ($kT_{\rm e}$), cutoff energy ($E_{\rm cut}$), and optical depth ($\tau_{\rm e}$). We obtained $\Gamma$, $kT_{\rm e}$ and $E_{\rm cut}$ from the spectral analysis, while $\tau_{\rm e}$ is obtained using Equation 1. Figure 5 shows the distribution of $E_{\rm cut}$, $kT_{\rm e}$ and $\tau_{\rm e}$ in our sample.

We are able to constrain $E_{\rm cut}$ in 22 sources out of a total of 30 sources considered in our sample. The $E_{\rm cut}$ is distributed in a wide range of $\sim 50-500$ keV in our sample. The broad parameter space of $E_{\rm cut}$ is consistent with the other recent studies (e.g., Ricci et al., 2018; Baloković et al., 2020; Hinkle & Mushotzky, 2021). We found that the lower limit of $E_{\rm cut}$ is below 50 keV for two sources when $E_{\rm cut}$ is not constrained. The median value of $E_{\rm cut}$ for our sample is found to be $238\pm 93$ keV with mean $<E_{\rm cut}>=241\pm 84$ keV, when $E_{\rm cut}$ is constrained. However, these values do not represent the whole sample, as the sources with the unconstrained $E_{\rm cut}$ are not considered.

To constrain the mean and median of the whole sample, we performed 1000 Monte Carlo simulations for each value of $E_{\rm cut}$. For each simulation, the values of $E_{\rm cut}$ are substituted with the values selected randomly from a Gaussian distribution with the standard deviation given by the uncertainty. The lower limits (L) are substituted with the values randomly selected from a uniform distribution in the interval of [L, $E_{\rm C,max}$], where $E_{\rm C,max}=1000$ keV. For each run, we calculated the median of all values and used the mean of 1000 simulations (see, Ricci et al., 2017a, 2018, for details). We find that the mean of $E_{\rm cut}$ is $284\pm 102$ KeV, while the median is $267\pm 110$ keV. Our results are consistent with the results of Ricci et al. (2017a, 2018) and the studies of the cosmic X-ray background, which suggest that the mean cutoff energy of AGNs should be $\lesssim 300$ keV (e.g., Gilli et al., 2007; Ueda et al., 2014; Ananna et al., 2020).

Using Model-2, we additionally constrained $kT_{\rm e}$ for those 22 sources. We found a lower limit for the other eight sources. Analogous to $E_{\rm cut}$, $kT_{\rm e}$ was also obtained in a broad range between $\sim 10-300$ keV which was found in other studies (e.g., Tortosa et al., 2018; Akylas & Georgantopoulos, 2021). We obtained the lower limit of $kT_{\rm e}$ as $15$ keV for IC 4518A, which is the lowest value among the sources in our samples. We calculated the mean and median of $kT_{\rm e}$ by running 1000 Monte Carlo simulations, as mentioned in the previous paragraph. We considered the maximum value of $kT_{\rm e}$ as 500 keV for the sources with the lower limit in the simulation. We found the mean value of our samples as $<kT_{\rm e}>=126\pm 54$ keV with a median at $110\pm 45$ keV.

As $\tau_{\rm e}$ is calculated using $kT_{\rm e}$, we also derived upper limits on $\tau_{\rm e}$ for six observations. Excluding the upper limits, $\tau_{\rm e}$ is observed to vary within the range of $\sim 0.5-3$. The mean of the optical depth is estimated to be $<\tau_{\rm e}>=1.77\pm 0.76$ with median $\tau_{\rm e}=1.47\pm 0.58$ in our sample.

The corona remains hot for low mass accretion rate AGNs as the cooling is inefficient. The hot corona also leads to high $E_{\rm cut}$ and optically thin medium ($\tau_{\rm e}<1$). Ricci et al. (2018) found the median of cutoff energy, $E_{\rm cut}=160\pm 41$ keV for $\lambda_{\rm Edd}>0.1$, and $E_{\rm cut}=370\pm 51$ keV for $L/L_{\rm Edd}<0.1$. As we explored an even lower Eddington ratio ($\lambda_{\rm Edd}<0.001$) regime, the median of the cutoff energy is expected to be higher. However, this was not observed for our sample of low Eddington ratio AGN.

In the current work, we studied a sample of AGNs with low $\lambda_{\rm Edd}$ to understand the coronal properties in the low accretion regime. The $\Gamma-\lambda_{\rm Edd}$ relation has been studied widely in the past (e.g., Gu & Cao, 2009; Yang et al., 2015). A positive correlation is observed in HAC-AGN (e.g., Brightman et al., 2013; Risaliti et al., 2009; Shemmer et al., 2006, 2008; Jana et al., 2020; Jana et al., 2021) while a negative correlation is found in the LLAGNs (e.g., Gu & Cao, 2009; Younes et al., 2011; Hernández-García et al., 2013). The accretion mechanism differs in the low accretion state from the high accretion state. The opposite correlation indicates that the accretion mechanisms in different luminosity states are distinct.

The thin disc-corona model naturally explains the positive correlation in the high accretion state (e.g., Yang et al., 2015). In the high accreting regime ($\lambda_{\rm Edd}>10^{-3}$), as the accretion rate increases, the number of seed photons increases, which cools the corona efficiently, producing the soft spectra. Contrary to that, the negative correlation in the low accretion state ($\lambda_{\rm Edd}<10^{-3}$) could be explained with a hybrid truncated thin disc associated with hot accretion flow/corona and jet models (e.g., Gardner & Done, 2013; Qiao & Liu, 2013; Yang et al., 2015). In this scenario, due to the lack of matter supply, the inner disc evaporates into a hot accretion flow or corona (e.g., Esin et al., 1997; Yuan & Narayan, 2014; Yang et al., 2015). As the mass accretion rate (or $\lambda_{\rm Edd}$) increases, the electron density and magnetic field strength increase, which in turn increases the synchrotron self-absorption depth. The self-absorbed synchrotron emission provides the seed photons for Comptonization. In this case, the hard X-ray flux ($L_{\rm X}$) increases more rapidly than the seed photon flux ($L_{\rm seed}$), which implies a negative correlation of $L_{\rm seed}/L_{\rm X}$ with $L_{\rm X}$. This leads to the negative correlation of the $\Gamma$ and $L_{X}$ or $\lambda_{\rm Edd}$ (e.g., Yang et al., 2015). If the accretion rate further reduces ($\lambda_{\rm Edd}<10^{-6.5}$), the synchrotron emission from the jet dominates, leading to a saturation of the photon index at $\Gamma\sim 2$ (e.g., Plotkin et al., 2013; Yang et al., 2015).

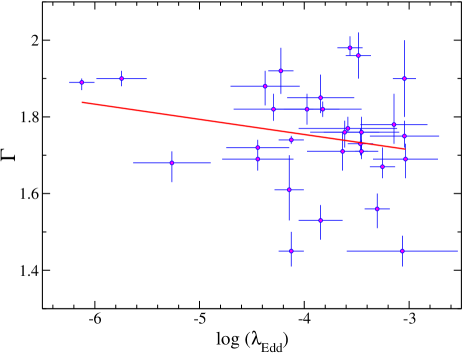
In our sample, $\lambda_{\rm Edd}$ spans the range $10^{-6.5}<\lambda_{\rm Edd}<10^{-3}$, where a negative correlation of $\Gamma-\lambda_{\rm Edd}$ is expected. However, we did not find a significant correlation between $\Gamma$ and $\lambda_{\rm Edd}$. The Pearson correlation coefficient between $\Gamma-\lambda_{\rm Edd}$ is $-0.22$ with p-value 0.24. Figure 6 shows the variation of $\Gamma$ with the $\lambda_{\rm Edd}$. The solid red line represents the best linear fit. Using the linear regression method, we obtained $\Gamma=(-0.04\pm 0.03)\log\lambda_{\rm Edd}+(1.59\pm 0.13)$. The observed relation is weaker than the one found in previous studies. For examples, Gu & Cao (2009) found $\Gamma=(-0.09\pm 0.03)\log\lambda_{\rm Edd}+(1.55\pm 0.07)$, Younes et al. (2011) observed $\Gamma=(-0.31\pm 0.06)\log\lambda_{\rm Edd}+(0.11\pm 0.40)$, Jang et al. (2014) pointed $\Gamma=(-0.18\pm 0.04)\log\lambda_{\rm Edd}+(0.66\pm 0.25)$, and She et al. (2018) obtained $\Gamma=(-0.15\pm 0.05)\log\lambda_{\rm Edd}+(1.0\pm 0.03)$. Most of the previous studies were conducted using Chandra  or XMM-Newton  observations, which have a limited band-pass. Trakhtenbrot et al. (2017) found a shallower slope of the $\Gamma-\lambda_{\rm Edd}$ correlation with respect to previous studies, when considering the results obtained by broad-band X-ray spectroscopy. In the current work, we used high-quality broad-band spectra, though our sample is limited to 30 sources. Thus, we are unable to make a firm conclusion on the correlation/anti-correlation of $\lambda_{\rm Edd}-\Gamma$. Recently, Diaz et al. (2023) studied a sample of LLAGNs and found similar results. They argued that due to the small number of sources, they did not find a statistically significant correlation of $\Gamma-\lambda_{\rm Edd}$. We also inspected whether other spectral parameters are correlated with the $\lambda_{\rm Edd}$ and did not observe any correlation between $\lambda_{\rm Edd}$ and $kT_{\rm e}$, $\tau_{\rm e}$ or $E_{\rm cut}$.

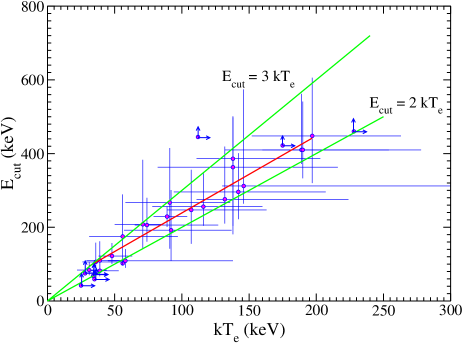
We found that $kT_{\rm e}$ and $E_{\rm cut}$ are strongly correlated (see Table 3) in our sample. The linear fitting yields $E_{\rm cut}=(2.10\pm 0.12)kT_{\rm e}+(29.4\pm 12.1)$. Figure 7 shows that all the 22 sources with constrained $E_{\rm cut}$ and $kT_{\rm e}$ lie within the $E_{\rm cut}=2kT_{\rm e}$ and $E_{\rm cut}=3kT_{\rm e}$ lines. This agrees with the empirical approximation of $E_{\rm cut}\approx 2-3~{}kT_{\rm e}$ (Petrucci et al., 2001). However, Middei et al. (2019) argued that the empirical relation only holds for low $\tau_{\rm e}$ and low $kT_{\rm e}$. They suggested that if the origin of X-rays is other than the thermal Comptonization, for example, synchrotron self Comptonization, the relation $E_{\rm cut}\sim 2-3~{}kT_{\rm e}$ may not hold. The deviation from this relation has been observed in a few sources (e.g., Pal et al., 2022). We tested this relation from the spectral modelling with the reflect model (Model-1a & Model-1b). We obtained $E_{\rm cut}=(2.18\pm 0.16)kT_{\rm e}+(25.\pm 17.2)$, which is similar to the findings with the borus model (Model-2a & Model-2b). Nonetheless, our study found $E_{\rm cut}\approx 2~{}kT_{\rm e}$ is an acceptable approximation for the LAC-AGNs.

We obtained a weak positive correlation between $kT_{\rm e}$ and $\Gamma$, with the Pearson correlation coefficient of $0.34$ with a p-value of $0.01$. For purely thermal Comptonization, a negative correlation between $kT_{\rm e}$ and $\Gamma$ is expected. However, if there are non-thermal seed photons, e.g., synchrotron emission from a jet, a negative correlation may not hold (e.g., Yang et al., 2015). Nonetheless, the observed relation indicates a complex process for the X-ray emission other than thermal Comptonization.

We calculated the average number of scatterings the photons suffered before escaping the Compton cloud (see § 3.2). We find that $N_{\rm s}$ is anti-correlated with $\Gamma$ having a Pearson correlation coefficient of $-0.65$ with $p<0.01$, as presented in the earlier works (e.g., Sunyaev & Titarchuk, 1980; Pozdnyakov et al., 1983). $N_{\rm S}$ is also found to be strongly anti-correlated with $kT_{\rm e}$ and $E_{\rm cut}$. The Pearson correlation index is obtained to be $-0.85$ with the p-value of $<0.01$ for $kT_{\rm e}$, and $-0.85$ with the p-value of $<0.01$ for $E_{\rm cut}$, respectively. This is expected as a high $kT_{\rm e}$ would lead the corona to be optically thin, hence, the lower value of $N_{\rm S}$. The anti-correlation between $N_{\rm S}$ and $kT_{\rm e}$ is also consistent with the previous simulations (e.g., Chatterjee et al., 2017a, b). Compton scattering could induce X-ray polarization. The variation in the polarization caused by repeated scatterings could be detected above the minimum detectable polarization with the ongoing Imaging X-ray Polarimetry Explorer (Weisskopf et al., 2016) or future X-ray polarimetry missions, such as XPoSat.

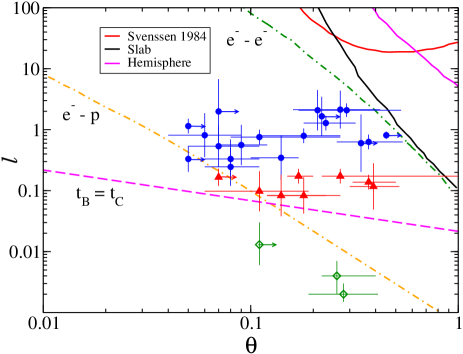
We constructed the compactness-temperature ($l-\theta$) diagram in Figure 8. Solid black and red lines correspond to the pair production lines for slab and hemispherical geometries from Stern et al. (1995). The solid magenta line represents the pair production line from Svensson (1984). The compactness ($l$) is calculated using Equation 2.

The pair production is thought to be a fundamental process in AGN coronae due to photon-photon collisions (e.g., Svensson, 1982a, b; Guilbert et al., 1983). This process could, in fact, lead to a runway pair production, which might act as a thermostat for the corona (e.g., Bisnovatyi-Kogan et al., 1971; Svensson, 1984; Zdziarski, 1985; Fabian et al., 2015, 2017). If that were the case, then the AGN would be expected to lie below the pair line. We found that all the sources are located below the theoretical pair lines for slab and hemispherical geometry. The sources in our sample are located around the electron-electron ($e^{-}-e^{-}$) and electron-proton ($e^{-}-p$) coupling lines, which could indicate the processes responsible for the cooling. We also found that three sources lie below the bremsstrahlung cooling line ($t_{\rm B}=t_{\rm C}$). All three sources, namely NGC 3718, NGC 3998, and UGC 12282, have $\lambda_{\rm Edd}<10^{-5}$ and, as the Eddington ratio is directly proportional to the compactness, which leads to the low compactness (Ricci et al., 2018).

The covering factor of the circumnuclear obscuring materials has been found to decrease with increasing accretion rates (e.g., Ueda et al., 2003; Treister et al., 2008). However, recent work has shown that the obscuring material in nearby AGN is regulated by the Eddington ratio (Ricci et al., 2017b). It has been found that the covering factor is $\sim 85\%$ for $\lambda_{\rm Edd}\sim 10^{-4}-10^{-1.5}$, and sharply decreases at $\lambda_{\rm Edd}>10^{-1.5}$ (Ricci et al., 2017b). The obscuring material is expected to disappear at very low accretion rates (e.g., Elitzur, 2008) due to the lack of outflowing material (e.g., Elitzur, 2008). Ricci et al. (2022) suggested that an inactive AGN ($\lambda_{\rm Edd}<<10^{-4}$) starts accreting following an inflow of gas and dust (see also Ricci et al., 2017b). This increases both $N_{\rm H}$ and $\lambda_{\rm Edd}$. When $\lambda_{\rm Edd}$ reaches a critical value ($\lambda_{\rm Edd}\sim 10^{-1.5}$), the radiation pressure blows away the obscuring material. The AGN spends some time as unobscured ($N_{\rm H}<10^{22}$ cm^-2) before moving back to the low $\lambda_{\rm Edd}$ state with low $N_{\rm H}$.

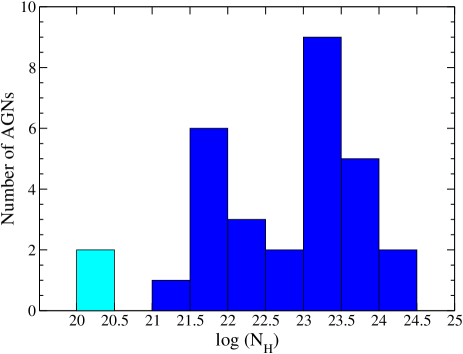
Figure 9 shows the histogram of our sample’s line of sight column density. In our sample, we found that nine sources are unobscured ($N_{\rm H}^{\rm los}$$<10^{22}$ cm^-2) and 21 sources are obscured ($N_{\rm H}^{\rm los}$$>10^{22}$ cm^-2). Among the 21 obscured sources, two sources are Compton-thick ($N_{\rm H}^{\rm los}$$>10^{24}$ cm^-2) and 19 sources are Compton-thin ($N_{\rm H}^{\rm los}$$=10^{22-24}$ cm^-2). We found two unobscured sources and one obscured source (one of them in CT) in an extremely low accretion region ($\lambda_{\rm Edd}<10^{-5}$). On the other hand, at $10^{-5}<\lambda_{\rm Edd}<10^{-3}$, we observed that seven sources are unobscured, and 20 sources are obscured. If we move towards the low accretion region ($\lambda_{\rm Edd}<-5$), the fraction of obscured sources drops from $\sim 73^{+8}_{-9}$% to $\sim 39^{+23}_{-20}\%$¹³¹³13The fractions are computed following Cameron (2011), and the reported uncertainties represent the 16th and 84th quantiles of a binomial distribution.. The increasing fraction of unobscured sources towards the low-accretion regime supports the Eddington ratio regulated unification model (e.g., Ricci et al., 2017b, 2022).

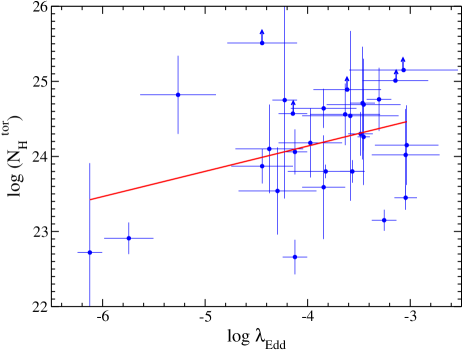
We obtained the average density of the obscuring material ($N_{\rm H}^{\rm tor}$), which is responsible for the reprocessing emission. The median of $N_{\rm H}^{\rm tor}$ is found to be $\log N_{\rm H}^{\rm tor}=24.22\pm 0.45$, which is higher than the $N_{\rm H}^{\rm los}$. The median of the line of sight column density is $\log N_{\rm H}^{\rm los}=23.02\pm 0.08$. We plot the variation of $N_{\rm H}^{\rm tor}$ as a function of $\lambda_{\rm Edd}$ in Figure 10. The linear regression analysis found that $\log N_{\rm H}^{\rm tor}=(0.34\pm 0.04)\log{\lambda_{\rm Edd}}+(25.5\pm 0.5)$, suggesting a positive relation between $\lambda_{\rm Edd}$ and $N_{\rm H}^{\rm tor}$. This suggests that at low Eddington ratio, the average column density decreases. Diaz et al. (2023) also found a similar relation between $N_{\rm H}^{\rm tor}$ and $\lambda_{\rm Edd}$. The relation between $N_{\rm H}^{\rm tor}$ and $\lambda_{\rm Edd}$ also supports the Eddington ratio regulated unification and growth model (e.g., Ricci et al., 2022).

We obtained the reflection parameter ($R$) from Model-1a and Model-1b. From our analysis, it is found that $R$ could be constrained only in 7 sources out of a total of 30 sources. As in case of $E_{\rm cut}$ and $kT_{\rm e}$, we calculated the mean of $R$ by running 1000 Monte Carlo simulations, with the range of $R$ between 0 to 10. We found the mean $<R>=0.25\pm 0.08$ with a median of $0.26\pm 0.09$. Ricci et al. (2017a) found a higher value of median of $R$ as $0.53\pm 0.09$ with a sample of 838 BAT AGNs. Our finding is consistent with the fact that the low-accreting AGNs show weak reflection (e.g., Younes et al., 2011; Ptak et al., 2004).

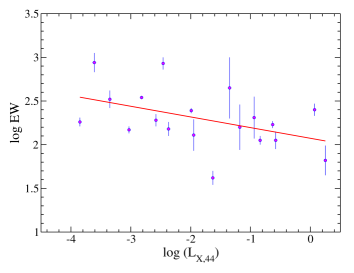
We modelled the Fe K-emission line with a Gaussian function while fitting the data with Model-1. Out of total of 30 sources, a Gaussian line is required in 28 objects. We did not find the iron K$\alpha$ line for two sources: NGC 3147 and NGC 3998. We could constrain the equivalent width (EW) for 19 sources. We tested the so-called ‘X-ray Baldwin effect’, i.e., the correlation of EW with the X-ray luminosity in our sample (Iwasawa & Taniguchi, 1993). Figure 11 shows the EW of Fe K$\alpha$ line as a function of X-ray luminosity ($L_{\rm X,44}$). The linear regression analysis returned as $\log{\rm EW}=(-0.12\pm 0.09)\log L_{\rm X,44}+(2.1\pm 0.1)$, where EW and $L_{X,44}$ are in the unit of eV, and $10^{44}$ erg s^-1, respectively. This relation is consistent with the previous studies of the X-ray Baldwin effect (e.g., Bianchi et al., 2007; Ricci et al., 2013). We also checked the relation of EW with $\lambda_{\rm Edd}$. The linear best-fit result returned with $\log{\rm EW}=(-0.15\pm 0.10)\log\lambda_{\rm Edd}+(1.74\pm 0.52).$ Our result is consistent with the previous studies (e.g., Ricci et al., 2013). The observed relation suggests that the reprocessing mechanism of LAC-AGNs is similar to the HAC-AGNs.

We did not find any correlation or anti-correlation of EW with the $L_{\rm 2-10}$ keV, $L_{\rm X,44}$, and $\lambda_{\rm Edd}$. The small sample size could be the reason for not observing any correlation/anti-correlation of EW with other parameters.

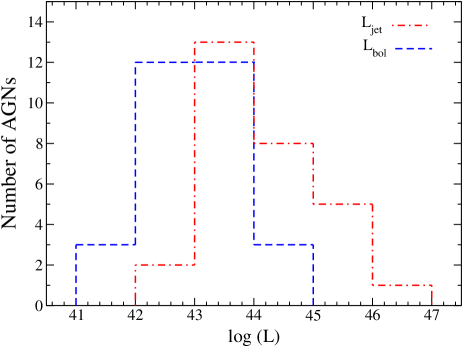
In LAC-AGNs X-ray radiation is believed to be produced in a radiatively inefficient flow (e.g., Narayan & Yi, 1994; Quataert, 2001; Nemmen et al., 2014), or from the base of the jet (e.g., Markoff et al., 2001; Falcke et al., 2004). The observed jet luminosity ($L_{\rm jet}$)¹⁴¹⁴14$L_{\rm jet}$ is calculated from the $L_{\rm R}$. is tabulated in Table 3. Figure 12 shows the histogram plots for the $L_{\rm bol}$ and the $L_{\rm jet}$ of our sample. The red dashed, and solid blue lines represent the $L_{\rm jet}$ and $L_{\rm bol}$, respectively. We observed that the $L_{\rm jet}$ is higher than the $L_{\rm bol}$¹⁵¹⁵15The $L_{\rm bol}$ is calculated from the $2-10$ keV X-ray luminosity (see § 3) for every source in our sample. The $L_{\rm jet}$ is found to be $\sim 0-3$ orders of magnitude higher than the $L_{\rm bol}$. If we consider $\sim 5\%$ power of the jet is radiated away (e.g., Blandford & Königl, 1979; Fender, 2001), the total jet power ($Q_{\rm jet}$) would be $\sim 0-4$ orders of magnitude higher than the bolometric luminosity ($L_{\rm bol}$). This is not uncommon for LLAGNs: Nagar et al. (2005) studied a sample of LLAGNs and found $Q_{\rm jet}$ (also $L_{\rm jet}$) exceeds the $L_{\rm bol}$ by $0-4.5$ magnitude with a mean around three orders in their sample. This study suggests that the jet luminosity greatly surpasses the accretion power in the LAC-AGNs.

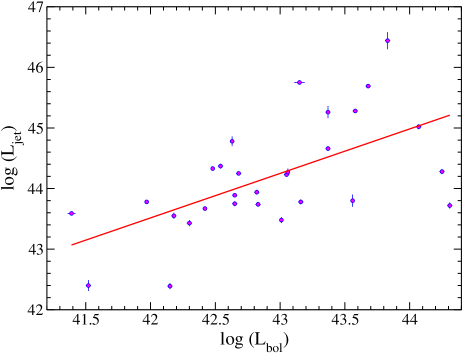
Figure 13 shows the variation of the jet luminosity ($L_{\rm jet}$) with the bolometric luminosity ($L_{\rm bol}$). The solid red line represents the best linear fit $\log(L_{\rm jet})=(0.68\pm 0.12)\log(L_{\rm bol})+(12.7\pm 8.1)$ from the linear regression analysis. This relation is consistent with the standard radio-X-ray correlation of coefficient of $\sim 0.6-0.7$ (e.g., Corbel et al., 2000, 2003; Merloni et al., 2003; Gallo et al., 2003, 2014; Körding et al., 2006). The standard correlation is the relation between the radio and X-ray flux in the low hard state of black holes. Thus, the similar relation of $L_{\rm jet}-L_{\rm bol}$ for the present sample indicates a radiatively inefficient accretion flow in the LAC-AGNs.