Copula bounds for circular data
Abstract
We propose the extension of Fréchet-Hoeffding copula bounds for circular data. The copula is a powerful tool for describing the dependency of random variables. In two dimensions, the Fréchet-Hoeffding upper (lower) bound indicates the perfect positive (negative) dependence between two random variables. However, for circular random variables, the usual concept of dependency is not accepted because of their periodicity. In this work, we redefine Fréchet-Hoeffding bounds and consider modified Fréchet and Mardia families of copulas for modelling the dependency of two circular random variables. Simulation studies are also given to demonstrate the behavior of the model.
keywords : Circular statistics ; copulas ; Fréchet-Hoeffding bounds
1 Introduction
Circular statistics deals with observations that are represented as points on a unit circle. Directional data is a typical example of this, because a direction is represented as an angle from a certain zero direction. Common examples often cited are: wind direction, river flow direction, and the direction of migrating birds in flight. For a comprehensive explanation of circular statistics, we refer to Fisher (1995), Mardia and Jupp (1999), Jammalamadaka and SenGupta (2001), to name a few.
If the observation is a pair of circular data, usually denoted by , it is represented as a point on a torus. When we have bivariate data, we can investigate the relationship between them. Although the Pearson correlation coefficient is the representative measure of a relationship between two random variables, it does not work for circular data because of its periodic structure. Many measures of association for circular data have been proposed so far. Section 11.2.2. of Mardia and Jupp (1999) provides a summary of circular-circular correlations.
Another powerful tool for describing the dependency between two random variables is a copula. It is a function rather than a single value and provides much more information regarding dependency. Mathematically speaking, the copula is a joint distribution function on whose margins are uniform. For a circular version, Jones et al. (2015) introduced a circular analogue of copula density, called “circulas,” assuming the existence of density function. In this paper, we consider a copula function—not a copula density—for circular data. Because we do not assume the existence of the density function, we can deal with singular copulas. We give special consideration to circular analogues of Fréchet-Hoeffding copula bounds, which are examples of singular copulas. Due to the arbitrary nature of the origin in the circular variable, they are not uniquely specified.
The remainder of the paper is organized as follows: Section 2 provides the definition of the equivalence class of circular copula functions from the aspect of the arbitrariness of the origin point. Section 3 introduces circular analogues of Fréchet-Hoeffding copula bounds. We prove that the following (i) and (ii) are equivalent.
-
(i)
The bivariate circular random variables have the circular Fréchet-Hoeffding upper (lower) copula bounds.
-
(ii)
Support of the bivariate circular random variables is nondecreasing (nonincreasing) in the sense of .
Section 4 gives a Monte Carlo simulation. We generate observations from the circular version of the Mardia copula family, and investigate their behavior. Section 5 provides our summary and conclusion.
2 Equivalence Class of Circular Copula Functions
A copula is the joint distribution function on whose margins are uniform. Sklar’s theorem insists any joint distribution function is written by the copula function and their marginal distribution function , , like
In the case of circular random variables, marginal and joint distribution functions depend on the choice of the zero direction. However, we should not consider the difference caused solely by the difference of the zero direction. This section gives the concept of the equivalence class of circular copula functions in the sense of the arbitrariness of the choice of the zero direction.
First, let us give the definitions of circular distribution functions, quasi-inverses of circular distribution functions and circular joint distribution functions following the style of Definitions 2.3.1, 2.3.6, and 2.3.2. in Nelsen (2006).
Definition 1.
A circular distribution function is a function with domain such that
-
1.
is nondecreasing,
-
2.
and .
Definition 2.
Let be a circular distribution function. Then a quasi-inverse of is any function with domain such that
Definition 3.
A circular joint distribution function is a function with domain such that
-
1.
for any rectangle ,
-
2.
and .
Now let us extend the domain of to in the following way
If we change the zero direction to , its distribution function becomes
The choice of should be arbitrary, so we can define the equivalence class of circular distribution functions .
Similarly, we extend the domain of to in the following way
If we change the zero directions to , its joint distribution function becomes
The choice of should be arbitrary, so we can define the equivalence class of circular joint distribution functions .
From Sklar’s theorem, the circular copula function is defined by
| (1) |
The choice of zero directions should be arbitrary, so we can define the equivalence class of circular copula functions .
3 Circular Fréchet-Hoeffding copula bounds
A copula is known to have both upper and lower bounds. That is, for every ,
The bounds and are themselves copulas and are called Fréchet-Hoeffding upper bounds and Fréchet-Hoeffding lower bounds, respectively.
Here, we introduce the concept of a nondecreasing (nonincreasing) set in .
Definition 4 (Definition 2.5.1 in Nelsen (2006)).
A subset of is nondecreasing if for any and in , implies . Similarly, a subset of is nonincreasing if for any and is , implies .
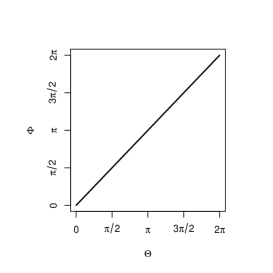
The example of a nondecreasing set is given in Figure 1.
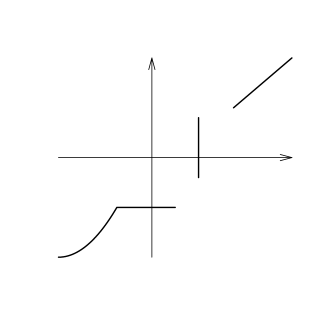
If the pair of random variables have a Fréchet-Hoeffding upper (lower) bound, then the support of is nondecreasing (nonincreasing). See Theorems 2.5.4 and 2.5.5 of Nelsen (2006). In this sense, a Fréchet-Hoeffding upper (lower) bound indicates the perfect positive (negative) dependence between and .
Now let us consider the pair of circular (angular) random variables . When has perfect positive dependence, its support should be like the examples shown in the left column of Figure 2. The upper figures are for a continuous circular random variable and the lower figures are for a discrete variable. The figures in the middle and right columns are redrawings of those in the left column when we regard and as zero directions (indicated by cross marks in the figures in the left column), respectively. Due to the arbitrary nature of the zero directions, the all support plots in Figure 2 should indicate perfect positive dependence.
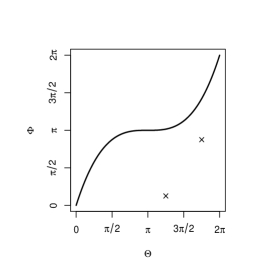
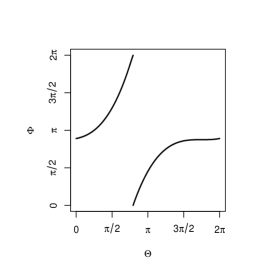
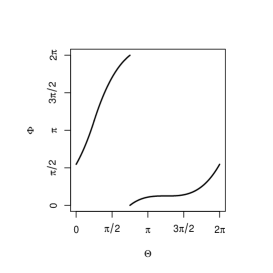
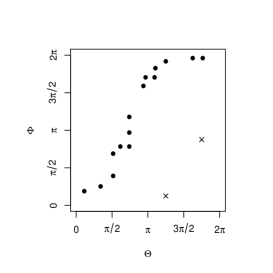
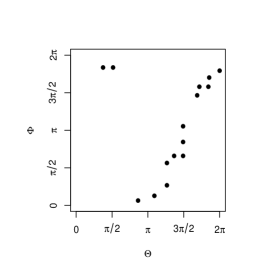
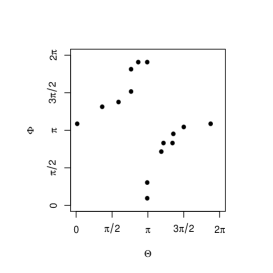
Now, we give the equivalence class of the circular Fréchet-Hoeffding copula upper bound in the following theorem.
Theorem 1 (Circular Fréchet-Hoeffding copula upper bound).
Let . The equivalence class of the circular Fréchet-Hoeffding copula upper bound is given by
Proof is given in the Appendix.
The copula is introduced in Exercise 3.9 of Nelsen (2006). It is the joint distribution function when the probability mass is uniformly distributed on two line segments, one joining to with mass , and the other joining to with mass . Theorem 1 clarifies this corresponds to the circular Fréchet-Hoeffding copula upper bound.
We can also find the equivalence class of the circular Fréchet-Hoeffding copula lower bound in the following theorem.
Theorem 2 (Circular Fréchet-Hoeffding copula lower bound).
Let . The equivalence class of the circular Fréchet-Hoeffding copula lower bound is given by
Proof is omitted because it is similar to that of Theorem 1.
The copula is introduced in Example 3.4 of Nelsen (2006). It is the joint distribution function when the probability mass is uniformly distributed on two line segments, one joining to with mass , and the other joining to with mass .
When describing the dependency between and , their periodic structure must be considered. Fisher and Lee (1983) proposed the complete dependence between and as
| (2) | |||
| (3) |
where is an arbitrary fixed direction. If we use display, the supports of (2) are expressed as in Figure 3.
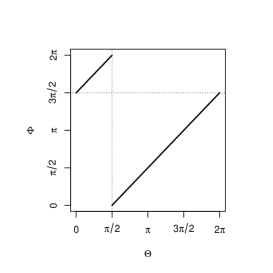
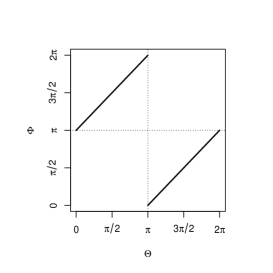
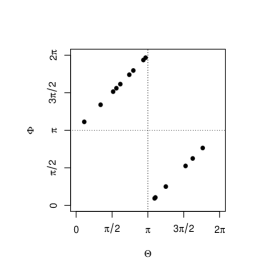
Because of arbitrary nature of , not only the left column but also the middle and right columns indicate complete positive dependence. Figure 3 is the special case of Figure 2. Therefore, the circular perfect dependence with the concept of nondecreasing (nonincreasing) set can be considered as the generalization of complete dependence in the sense of Fisher and Lee (1983).
4 Monte Carlo Simulations
In this section, we consider the copula
| (4) | |||
Here, , are the copulas introduced in Theorems 1, 2, and is an independent copula. This is a linear combination of these three copulas and an analog to the model in Mardia (1970). The parameter controls the weights of these three copulas, and correspond (perfect positive dependence), (independent), (perfect negative dependence), respectively.
Now we generate a random circular bivariate sample from (4). Both marginals are set to a Cardioid distribution, whose distribution function is given by
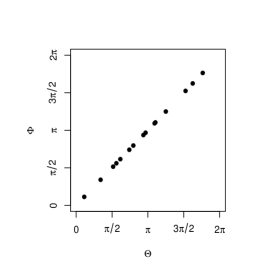
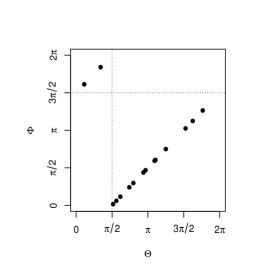
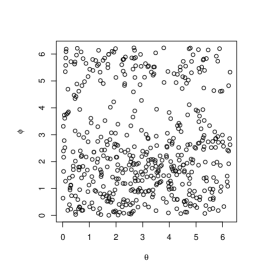
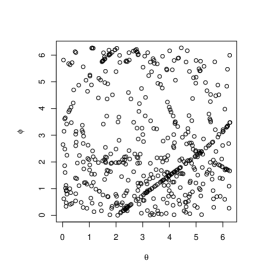
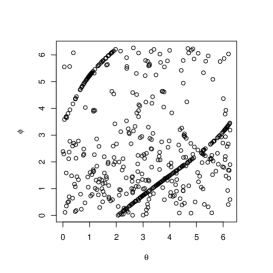
The parameters for marginals are set to , for and , for . Figure 4 shows the simulated circular bivariate plots with (upper left), (upper middle), (upper right), (lower left), (lower middle), (lower right). When is close to and , (4) is close to and , which are singular copulas. When , we can clearly see the singular components in the plots.
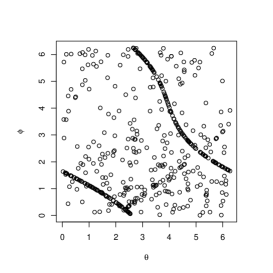
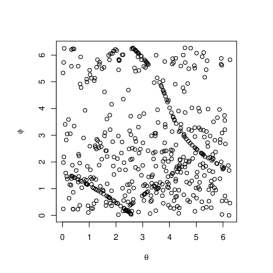
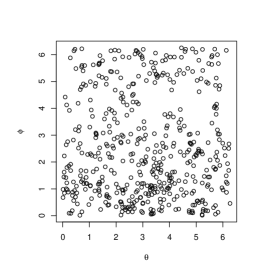
5 Summary and Conclusions
We considered the equivalence class of univariate and bivariate circular distribution functions ascribed to the arbitrary nature of the origin point. Then, we introduced the equivalence class of circular copula functions with Sklar’s theorem. Using the concept of the equivalence class of circular copula functions, we introduced circular analogues of Fréchet-Hoeffding copula upper and lower bounds. We explained they are the generalizations of complete positive and negative dependence in the sense of Fisher and Lee (1983). We also introduced the circular analogue of Mardia’s copula model and simulated a dataset following this model. When the model is close to its extremes, we can find the singular components in the plots.
Appendix
Proof of Theorem 1
Let
Fix arbitrary zero directions . From the discussion in Section 2, the circular Fréchet-Hoeffding copula upper bound is
When is discrete, is restricted on . Now, let us divide into the following four regions:
First, for ,
Here,
Therefore,
When , we divide into
When , we divide into
Then,
| (5) | ||||
Second, for ,
Here,
Therefore,
When , we divide into
When , we do not divide further and rename it as . Then,
| (6) | ||||
Third, for ,
Here,
Therefore,
When , we do not divide further and rename it . When , we divide into
Then,
| (7) | ||||
Lastly, for ,
Here,
Therefore,
When , we divide into
When , we divide into
Then,
| (8) | ||||
Acknowledgements
Financial support for this research was received from JSPS KAKENHI in the form of grant 18K11193. We would like to thank Editage (www.editage.jp) for English language editing.
References
- Fisher (1995) Fisher NI (1995) Statistical Analysis of Circular Data. Cambridge University Press.
- Fisher and Lee (1983) Fisher NI, Lee AJ (1983) A correlation coefficient for circular data. BIOMETRIKA 70:327-332
- Jammalamadaka and SenGupta (2001) Jammalamadaka SA, SenGupta AS (2001) Topics in circular statistics. World Scientific Publishing Co. New York
- Jones et al. (2015) Jones MC, Pewsey A, Kato S (2015) On a class of circulas: copulas for circular distributions, ANN I STAT MATH 67:843-862
- Mardia (1970) Mardia KV (1970). Families of Bivariate Distributions. Hafner Publishing Company, Darien, Connecticut.
- Mardia and Jupp (1999) Mardia KV, Jupp PE (1999) Directional Statistics. Wiley, Chichester
- Nelsen (2006) Nelsen, RB (2006) An Introduction to Copulas. Springer.