Coordination on Time-Varying Antagonistic Networks

The utilized notation in this paper is standard. The nonnegative integer set, real number set and complex number set are described by the triple $(\mathbb{Z},\mathbb{R},\mathbb{C})$. Superscript $``\prime"$ represents the transpose with respect to a vector or a matrix, and ${\rm sgn}(\cdot)$ is the sign function. Moreover, subscript (resp. superscript) $(\cdot)_{n^{2}}$ (resp. $(\cdot)^{n^{2}}$) is the abbreviation of $(\cdot)_{nn}$ (resp. $(\cdot)^{nn}$). Cardinality or module is measured by $|\cdot|$. $\|x\|$ denotes the Euclidean norm of a vector $x$, and $\|Q\|$ is the spectral norm of a matrix $Q$. $\lambda(Q)$ is the eigenvalue for a square matrix $Q$. In addition, $Q^{-1}$ is the inverse of a nonsingular matrix $Q$. $\|Q\|_{\mathscr{H}}$ refers to the spectral norm restricted in the pre-defined space $\mathscr{H}$. $\mathcal{C}_{\mathscr{F}}(\mathscr{H})$ stands for the complementary space of $\mathscr{H}$ restricted on set $\mathscr{F}$, and $\overline{\mathscr{H}}$ is the closure of space $\mathscr{H}$. Denote $\{1,...,M,M+1,...,N\}$ by $\mathbbm{I}_{N}$.

A graph $\mathcal{G}=\{\mathbb{V},\mathbb{E},\mathbb{A}\}$ is usually specified by a node set $\mathbb{V}$, and an edge set $\mathbb{E}$ with an adjacency matrix $\mathbb{A}=[a_{ij}]_{N^{2}}$ satisfying $a_{ij}>0$ if $(j,i)\in\mathbb{E}$ and $a_{ij}=0$ otherwise. Self-loops are forbidden in this paper and hence $a_{ii}=0$. Laplacian matrix $\mathcal{L}=[l_{ij}]_{N^{2}}$ associated with $\mathcal{G}$ is defined by $l_{ii}=\sum^{N}_{j=1,j\neq i}a_{ij}$ and $l_{ij,j\neq i}=-a_{ij,j\neq i}$. If $(i,j)\in\mathbb{E}$, $i$ is the parent node and $j$ is the child node. A directed path connecting nodes $v_{p_{j}}$ and $v_{p_{i}}$ is a non-repetitive sequence of edges $(v_{p_{j}},v_{p_{j}+1}),(v_{p_{j}+1},v_{p_{j}+2}),...,(v_{p_{i}-1},v_{p_{i}})$, where $v_{p_{j}+i}\in\mathbb{V}$. A node is said to be a root in $\mathcal{G}$ if it has directed paths to every other node. A digraph is said to be strongly connected if for any two distinct nodes, there always exists a directed path connecting these two nodes. A digraph is said to be a directed tree if it has merely a root, and each of the remaining nodes owns exactly a parent. A directed spanning tree is a directed tree preserving all nodes in $\mathcal{G}$. A directed spanning forest is comprised of several directed trees preserving all nodes in $\mathcal{G}$.

Consider a family of participating agents, each of which updates its state according to

where $\xi_{i}(k)\in\mathbb{R}$ is the state variable with respect to the $i$th agent, and $\epsilon>0$ is a constant. $u_{i}(k)$ represents the coordination algorithm, and features form

where $\hat{\mathbbm{I}}_{N}\triangleq\{1,...,M\}$ is the set of rooted agents and $\hat{\mathbbm{I}}^{c}_{N}=\mathbbm{I}_{N}-\hat{\mathbbm{I}}_{N}$ is the set of non-rooted agents. $a_{ij}(k)$ denotes the $(i,j)$th element in adjacent matrix $\mathbb{A}(k)$ at $k$th instant, and $\mathcal{N}^{r}_{i}(k)$ represents rooted agent $i$’s neighboring set that are also rooted agents. In addition, $\mathcal{N}^{1}_{i}(k)$ and $\mathcal{N}^{2}_{i}(k)$ are, respectively, agent $i$’s neighboring sets that are non-rooted agents and that are rooted agents satisfying $\mathcal{N}^{1}_{i}(k)\bigcap\mathcal{N}^{2}_{i}(k)=\emptyset$. Evidently, the neighboring set for non-rooted agent $i$ meets $\mathcal{N}^{1}_{i}(k)\bigcup\mathcal{N}^{2}_{i}(k)$. Scaling constant parameter $\delta_{j}\neq 0$, characterizing the antagonistic ($\delta_{j}<0$) or rewarding ($\delta_{j}>0$) information sent by the $j$th agent, is bounded for $j\in\hat{\mathbbm{I}}_{N}$.

It is worthwhile to illustrate that merely two generic of agents are involved for multi-agent systems, i.e., rooted and non-rooted agents. It is also known that the former entirely affects the later, not vice versa. Therefore, we specify that the interactions among rooted agents preserve both cooperative and hostile information, while these among non-rooted agents are cooperative, completely in the context of conventional multi-agent systems. This thoroughly coincides with configurations $(\ref{eqlua})$ and $(\ref{eqlub})$, respectively.

Before proceeding further, a definition regarding to the coordination problem for system $(\ref{eq1})$ is given in advance.

In view of Definition 1, it preserves the mutually utilized definition for consensus [1, 2], bipartite consensus [12], or with respect to scaled consensus [21] for some nonzero constants $\delta_{i}$ as particular cases.

As a matter of fact, the objective of this paper is to study the coordination problem for time-varying antagonistic networks in the context of usual algebraic theory (that is, $a_{ij}\geq 0$ is always permitted), which differs from the formulations in the existing literature, such as $l_{ii}=\sum^{N}_{j=1,j\neq i}|a_{ij}|$ in [12, 13, 22, 14], or $\sum^{N}_{j=1}|a_{ij}|=1$ in [23]. Therefore, the proposed coordination algorithm in $(\ref{eq1})$ preserves the potential to be extended to the second-order case [1], and the high-order case [24] with minor modifications, where the communication among a family of reciprocal individuals could be adversarial.

Unlike most of the existing efforts on consensus/coordination problems with antagonistic interactions, as an instance singed graph based formulation [12], directed spanning tree condition suffices to assure the consensus/stability of the participating agents. By leverage of $u_{i}(k)$ in $(\ref{eqlu0})$, antagonistic information would result in the collapse of the underlying system. More precisely, let’s start with a simple example.

Example 1 essentially indicates that 1) antagonistic information would be harmful for coordination of the agents; 2) directed spanning tree requirement acts merely a necessary condition for coordination of multi-agent systems, even for first-order scenario. In a nutshell, to the best of authors’ knowledge, the proposed coordination algorithm in $(\ref{eqlu0})$ actually brings in something new phenomena that have not been fully discussed in the literature.

In connection with Example 1, for the purpose of coordination for the considered system, $u_{i}(k)$ in $(\ref{eqlu0})$ is modified by

where $\varrho_{i}$ is a weighted gain whose existence shall be elaborated later.

In view of coordination algorithm $(\ref{eq1u})$, it essentially features that the interacting manner among agents and the description of antagonistic information are quantified in a fully decouple perspective.

Stacking the state variables and reformulating $(\ref{eq1})$ with $u_{i}(k)$ in $(\ref{eq1u})$ into a compact form yields

with $\xi(k)=[\xi_{1}(k),...,\xi_{M}(k),\xi_{M+1}(k),...,\xi_{N}(k)]^{\prime}$, $\mathscr{L}(k)=I-\epsilon\mathcal{M}(k)$ and

where $I$ and $\mathcal{O}$ are, respectively, identity and zero matrices with appropriate dimensions. $\mathbb{D}={\rm diag}(\varrho_{1},...,\varrho_{M})$ is the weighted gain matrix, and $\mathcal{D}={\rm diag}(\delta_{1},...,\delta_{M})$ stands for the scaling parameter matrix. $\mathcal{L}(k)$ is the Laplacian matrix, at which matrix $\mathcal{L}_{1}(k)\in\mathbb{R}^{M^{2}}$ characterizes the interactions among rooted agents, while matrix $\mathcal{L}_{2}(k)\in\mathbb{R}^{(N-M)M}$ describes the information flows from rooted agents to associated non-rooted agents.

It is noted that matrix $\mathcal{L}_{3}(k)\in\mathbb{R}^{(N-M)^{2}}$ in $\mathcal{M}(k)$ corresponds to the non-rooted nodes contained in communication graph $\mathcal{G}(k)$. In other words, we cannot find a directed path whose root is associated with $\mathcal{L}_{3}(k)$ connecting some of the remaining nodes in $\mathcal{G}$. Furthermore, it is known that the aggregated common quantity is irrelevant to the initial states of the agents associated with $\mathcal{L}_{3}(k)$. In fact, matrix $\mathcal{L}_{3}(k)$ quantifies the information flow among non-rooted agents, apart from in addition to the influence of rooted agents characterized by $\mathcal{L}_{2}(k)\mathcal{D}$ in matrix $\mathcal{M}(k)$.

It should be emphasized that hypothesis of the directed spanning tree is only the necessary condition to guarantee that $\mathbb{L}(k)=\mathbb{D}\mathcal{L}_{1}(k)\mathcal{D}$ has a simple zero eigenvalue. Note that even if communication graph $\mathcal{G}(k)$ attains a directed spanning tree, we still cannot declare that $\mathbb{L}(k)=\mathbb{D}\mathcal{L}_{1}(k)\mathcal{D}$ preserves a simple zero eigenvalue in general. As a matter of fact, we cannot even declare that zero eigenvalues in $\mathbb{D}\mathcal{L}_{1}(k)$ and $\mathcal{L}_{1}\mathcal{D}(k)$ is simple whenever merely directed spanning tree hypothesis in $\mathcal{G}(k)$ is assured. This is a distinguished difference in contrast to the conventional consensus problem with single dynamics (cf. [25]).

Fortunately, we can still establish a simple connection among the considered matrices.

Incorporating equation $(\ref{eq2})$ with directed spanning tree condition, it is not difficult to access that the eigenvalues of $\mathcal{L}_{3}(k)$ are in the open right half plane. Hence, the following work is to demonstrate that $\mathbb{L}(k)$ possesses a simple zero eigenvalue and the remaining eigenvalues are located in the open right half plane. This, however, is completely determined by the weighted gain matrix $\mathbb{D}$ and the scaling parameter matrix $\mathcal{D}$. To this end, the result of multiplicative inverse eigenvalue problem should be consulted in advance.

Moreover, one also has following proposition.

We point out here that for a general digraph with respect to $\mathcal{L}_{1}(k)$, which merely contains a directed spanning tree, the conclusion drawn by Proposition 2 may be not true.

By using the above preparations, we will give an affirmative answer to the existence of the weighted gain $\varrho_{i}$ in updating equation $(\ref{eq1})$ with $(\ref{eq1ua})$ for $i\in\hat{\mathbbm{I}}_{N}$.

Actually, the existence of the weighted gain $\varrho_{i}$ can always be fulfilled. As an example, let $\varrho_{i}={\rm sgn}(\delta_{i})$ and $\delta_{j}\neq 0$ be similar to that in [21], $\varrho_{i}=1$ and $\delta_{i}=1$ with $\delta_{j}={\rm sgn}(a_{ij})$ in [12, 22, 14], $\varrho_{i}={\rm sgn}(a_{ij})=\delta_{i}$ with $\delta_{j}=1$ in [13] (notice that $a_{ij}\geq 0$ in $(\ref{eq1})$), or $\varrho_{i}=\mu_{i}{\rm sgn}(\delta_{i})$ for some positive constant $\mu_{i}$, etc. Moreover, the choice of the weighted gain is far from unique according to Proposition 2. Furthermore, $\varrho_{i}\neq 0$, where the $i$th eigenvalue in $\mathcal{L}_{1}(k)$ is zero, should be desirable since the subgraph associated with matrix $\mathcal{L}_{1}(k)$ is strongly connected. Evidently, $\varrho_{i}=0$ is straightforward if the graph $\mathcal{G}(k)$ has exactly a root $i$, since agent $i$ has no neighbors in such a circumstance.

Although we have shown the existence of the weighted gains, it is still insufficient to thoroughly deal with the considered coordination problem. As is hinted by Example 1, $\mathcal{L}_{1}(k)$ has a simple zero eigenvalue with directed spanning tree condition, while the matrix $\mathcal{L}_{1}(k)\mathcal{D}$ may contain multiple zero eigenvalues in addition to the nonzero eigenvalues. This is the directed consequence of multiply factor $\mathcal{D}$. However, matrix $\mathbb{L}(k)$ should merely preserve a simple zero eigenvalue and the remaining eigenvalues have positive real parts if we want to solve coordination problem depicted in $(\ref{eq1})$, which may be tightly determined by some connections among $\varrho_{i}$, $\delta_{i}$ and the principle minors of $\mathcal{L}_{1}(k)$.

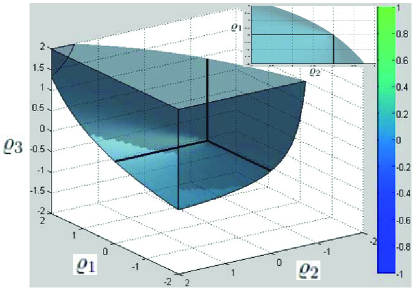
Let’s first examine a simple example as below.

The following theorem describes the relationship among the signs for pairwise $(\varrho_{i},\delta_{i})$, the principle minors of $\mathcal{L}_{1}(k)$ and the configuration of the eigenvalues in the matrix $\mathbb{L}(k)$.

To prove Theorem 2, it necessitates an auxiliary lemma.

The proof for Lemma 2 is depicted in Appendix 6.1 for the sake of neatness.

We now dedicate to proving Theorem 2.

It is ready to give some comparisons in contrast to the existing literature. Since there may exist some pairs of $(\varrho_{i},\delta_{i})$ equipping with ${\rm sgn}(\varrho_{i})\neq{\rm sgn}(\delta_{i})$. Therefore, the conventional consensus problem (e.g., [1, 2]) cannot be immediately applicable to setup $(\ref{eq1})$. For instance, denoted by $z(k)=\Gamma^{\star}\xi(k)$ with $\Gamma^{\star}={\rm diag}(\mathcal{D},I)$, it yields

with $\Gamma^{\ast}={\rm diag}(\mathbb{D},I)$. Unfortunately, the fact that $\Gamma^{\star}\Gamma^{\ast}$ is not positive definite leads to that $\Gamma^{\star}\Gamma^{\ast}\mathcal{L}(k)$ is not a Laplacian matrix in the context of usual algebraic graph theory. More importantly, $I-\epsilon\Gamma^{\star}\Gamma^{\ast}\mathcal{L}(k)$ will not be a stochastic matrix in general. Thereby, the classical tool of the infinite product of stochastic matrices fails to deal with formulated problem in this paper. For the scaled consensus [21], there needed $\varrho_{i}={\rm sgn}(\delta_{i})$ for all $i$. Obviously, this requirement can sometimes be relaxed according to Theorem 2.

From Theorems 1 and 2, we are dedicated to showing that control law $(\ref{eq1u})$ is capable for coordination problem with directed spanning tree requirement. Recalling a statement suggested by Ref. [25], left eigenvector with respect to the zero eigenvalue of Laplacian matrix is paramount for solving the coordination problem. The result derived below indicates that if the final aggregated viewpoint for a collection of reciprocal agents is thoroughly decided by the initial conditions of $s$ $(s>1)$ agents, there exist exactly $s$ rooted nodes in the graph $\mathcal{G}(k)$. The converse argument is also true.

In terms of Lemma 3, it is plausible to deal with coordination problem in $(\ref{eq1})$ by virtue of some conventional tools, such as the algebraic-based methods (continuous-time case) [25, 21], the infinite product of stochastic matrices (discrete-time case)[3, 25, 5] in terms of the coordinate transformation on condition that both weighted gains, scaling parameters and their relationships are deterministic in advance [21], and the Lyapunov-based approaches [6], just to name a few. Unfortunately, an apparent drawback in the aforementioned references is that the final consensus interest should be previously known [3, 25, 21], or the reference variable related to a convex combination of agents’ current states should be mutually computed [6]. Nevertheless, both consensus interest and reference variable are the global information for distributed systems, and they may be unavailable in general [30].

To overcome foregoing downside triggered by utilization of global information, a linear transformation related to coordination error is devised by

By leverage of linear transformation $(\ref{eq8})$, state variable $\xi(k)$ and coordination error $\zeta(k)$ enjoy a connection by

where elements in matrix $P=[\mathbbm{p}_{ij}]\in\mathbb{R}^{(N-1)N}$ feature the following properties

For such a transformation matrix $P$, we have the following result, which eliminates the conservative concern of solving coordination problem relying on global information, explicitly described by the induced matrix $A$.

The proof for Lemma 4 is presented in Appendix 6.2.

In the sequel, the characteristics of the elements in the matrix $A(k)=[\mathbbm{a}_{ij}(k)]\in\mathbb{R}^{(N-1)^{2}}$ could be detailed by