Coordinates are messy
— not only in General Relativity

In Newtonian Gravity, we can think of an “isolated system at a given instant of time” as given by a matter density function $\rho\colon\mathbb{R}^{3}\to[0,\infty)$ which has compact support or at least decays suitably fast towards infinity. For example, one could ask that $\rho=O(r^{-3-\varepsilon})$ as $r\to\infty$ for some (small) $\varepsilon>0$, that is, $\rho$ decays to zero at least as fast as $r^{-3+\varepsilon}$, where $r$ denotes the radial coordinate on $\mathbb{R}^{3}$. Alternatively but not equivalently, one could ask that $\rho\in L^{1}(\mathbb{R}^{3})$. Both assumptions are independent of the chosen Cartesian coordinates because any two systems of Cartesian coordinates on $\mathbb{R}^{3}$ differ only by a rigid motion. Either of these decay assumptions is sufficient for the total mass

to be well-defined and finite. Anticipating the discussion below, let us point out that the $O$-assumption suggests computing the integral in (2.1) as an improper Riemann integral in polar coordinates, while the $L^{1}$-assumption suggests treating it as a Lebesgue integral. Of course, the resulting mass $m$ will be the same whatever notion of integral one refers to, as long as it converges. However, taking the former viewpoint, we can take advantage of cancellations in the spherical integrals. Also note that the decay assumptions are of course not independent of arbitrary coordinate changes.

In General Relativity, an “isolated system at a given instant of time” is modelled as an asymptotically Euclidean (or asymptotically flat) relativistic initial data set (or time-slice): As usual, an initial data set $(M,g,K)$ consists of a $3$-dimensional Riemannian manifold $(M,g)$ carrying a symmetric $(0,2)$-tensor field $K$ playing the role of second fundamental form (or extrinsic curvature) of the initial data set in the spacetime modelling the system.

In addition, a relativistic initial data set carries an energy density $\mu\colon M\to\mathbb{R}$ and a momentum density one-form $J$ related to $g$ and $K$ via the well-known Einstein constraint equations

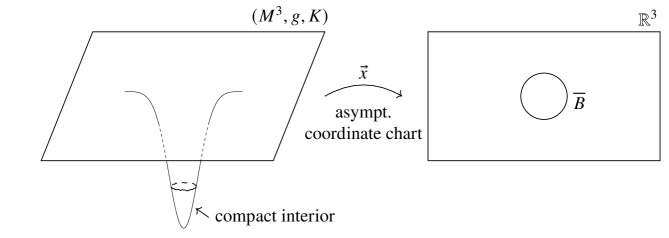
and derived from the energy-momentum tensor $T$ of the spacetime. Here, $\operatorname{R}$ denotes the scalar curvature of $(M,g)$, and $|\cdot|$, $\operatorname{tr}$, and $\operatorname{div}$ denote the tensor norm, trace, and divergence with respect to $g$, respectively. We will adopt the following standard definition, see also Figure 1.

The (total) mass $m_{\text{ADM}}$ of an asymptotically Euclidean relativistic initial data set $(M,g,K)$ was defined by Arnowitt, Deser, and Misner in [1] via the (total) energy $E_{\text{ADM}}$ and (total) linear momentum $\vec{P}_{\text{ADM}}$ and has become the standard definition, satisfying many desirable properties such as for example positivity ([12, 13]):

where $dA_{\delta}$ denotes the Euclidean area measure on $S_{R}(0)$. In [2], Bartnik uses harmonic asymptotically Euclidean coordinate charts to prove that $E_{\text{ADM}}$ is well-defined and independent of the choice of asymptotically Euclidean coordinate charts, see Section 3. Note that Bartnik uses the weaker $L^{1}$-decay condition on $\mu$. From this, (2.8), (2.5) and (2.6), it follows directly that $m_{\text{ADM}}$ is also well-defined and independent of the choice of asymptotically Euclidean coordinate chart via the Divergence Theorem. Again, this argument only uses the weaker $L^{1}$-condition on $J$.

You may wonder why one asks for such general decay rates in (2.4)–(2.6), and not just for, say,

etc.. This has two reasons: First, the theory of asymptotically Euclidean relativistic initial data sets does not become more complicated if one does so. Second, it actually becomes richer, i.e., allows for more examples, see [4] and the references cited therein.

Next, let us discuss how a single relativistic initial data set can carry different asymptotic coordinate charts and discuss the relationship between different such charts.

At this point, it is instructive to recall that the decay condition (2.4) cannot be relaxed as was shown by a counter-example by Denissov and Solovyev [7]: Inspired by their example, let us consider the Euclidean relativistic initial data set $(M=\mathbb{R}^{3},g=\delta,K=0)$ in the coordinates

for some non-zero $a\in\mathbb{R}$ which leads to (2.4) with $\varepsilon=0$ and the unphysical result $m_{\text{ADM}}=\frac{a^{2}}{8}$. One can argue similarly for (2.5) as we will discuss elsewhere; alternatively, one can compute in a lengthy but straightforward way that the decay conditions (2.4) and (2.5) transform equivariantly under coordinate boosts in the ambient spacetime. From this and the example by Denissov and Solovyev, one can conclude that (2.5) is necessary for physicality of the definition of $m_{\text{ADM}}$.

In summary, (convergence and coordinate independence of) mass is very well understood in both Newtonian Gravity and General Relativity and depends crucially on the decay of the matter variables, as well as, in General Relativity, on the asymptotics of the relativistic initial data set itself.

One of the main tools introduced by Bartnik for the study of mass and energy are the “harmonic asymptotically Euclidean coordinates” we will now explain.

Provided $m\neq 0$, the center of mass in Newtonian Gravity is naturally defined as the averaged weighted integral of the position vector $\vec{x}$,

Looking at (5.1) as a Lebesgue integral, it suggests itself that one should ask that $\rho r\in L^{1}(\mathbb{R}^{3})$. Instead, for this to be well-defined and finite as an improper Riemann integral,

it suggests itself to assume $\rho=O_{0}(r^{-4-\varepsilon})$ for some $\varepsilon>0$, in analogy with the choice of decay rate used for ensuring that the mass is well-defined; this of course settles the convergence issue for Newtonian gravitating systems.

However, let us — ahistorically — take a different approach in analogy with the standard approach taken to resolve the corresponding issue in General Relativity. To this end, let us instead make a further parity-based decay assumption, namely

where

is the odd part of $\rho$. This approach relies on the insight that the contribution to (5.2) of the even part

vanishes by parity on each sphere $S_{r}(0)$.

In view of the analogous approach taken in General Relativity, let us take the time to consider the parity condition

and its properties in more detail. Importantly, we would like to bring to the reader’s attention that the parity condition is not independent of the choice of Cartesian coordinate systems because the reflection $\vec{x}\mapsto-\vec{x}$ involved in the definition of $\rho^{\mathrm{odd}}$ does not interact well with translations. However, the desirable invariance under choice of Cartesian coordinate systems can be restored if one assumes that in some, and hence all, Cartesian coordinate systems, one has $\rho=O_{1}(r^{-3-\varepsilon})$, by appealing to the Mean Value Theorem.

In General Relativity, a (total) notion of center of mass $\vec{C}_{\text{B\'{O}RT}}$ of an isolated system at a given instant of time was put forward by Beig and Ó Murchadha in [3], based on previous work by Regge and Teitelboim [11] and similar in spirit and derivation to the ADM-quantities. For an asymptotically Euclidean relativistic initial data set $(M,g,K)$ with $E_{\text{ADM}}\neq 0$, its components are formally defined by

with respect to the given asymptotically Euclidean coordinate chart $\vec{x}$. Just as in the Newtonian case, this is a formal definition in the sense that it need not and does not always converge.

One instance where it diverges²²2For further examples of divergence of the center of mass, see [5] and the references cited therein. is the canonical Schwarzschild relativistic initial data set $(\mathbb{R}^{3}\setminus\overline{B_{2m}(0)},\frac{1}{1-\frac{2m}{r}}dr^{2}+r^{2}d\Omega^{2},K=0)$ of mass $m\neq 0$, when considered with respect to the asymptotic coordinate chart $\vec{y}$ arising from the Cartesian coordinates $\vec{x}$ computed from the spherical polar Schwarzschild coordinates via (3.1). As in the Newtonian Gravity case discussed above, one finds via a lengthy computation that $\left(\vec{C}_{\text{B\'{O}RT}}\right)_{\vec{y}}$ diverges like $\sin(\ln s)\vec{a}$ for $s=|\vec{y}|\to\infty$, while of course $\left(\vec{C}_{\text{B\'{O}RT}}\right)_{\vec{x}}$=0 and $E_{\text{ADM}}=m$. We would like to draw the reader’s attention to the fact that this initial data set has $\mu=0$, $J=0$, so the divergence problem clearly does not arise from poor decay of the matter.

A first idea one might have to remedy the divergence problem of $\vec{C}_{\text{B\'{O}RT}}$ could be to assume the stronger decay condition $g_{ij}-\delta_{ij}=O_{1}(r^{-2-\varepsilon})$, thereby enforcing convergence in a way similar to remedying the convergence issue of $E_{\text{ADM}}$ discovered by Denissov and Solovyev, see Section 3.1. However, this implies $E_{\text{ADM}}=0$ which is undesirable when interested in the center of mass.

Instead, one usually resorts to parity assumptions. Before we do so in Section 5.2.2, let us briefly take a look at the transformation behavior of the center of mass under changes of asymptotic coordinates.

All examples discussed in this section originate from our joint work with Jan Metzger [4]. Following ideas by Cederbaum and Nerz [5], we focus on relativistic initial data sets in the Schwarzschild spacetime of mass $m\in\mathbb{R}$ in the Cartesian coordinates $\vec{x}$ associated with the Schwarzschild coordinates. These can and will be described as graphs over the canonical relativistic initial data set $\{t=0\}$ of suitable graph functions $T\colon\mathbb{R}^{3}\setminus C\to\mathbb{R}$ for a suitable compact set $C\subset\mathbb{R}^{3}$. Writing the Schwarzschild spacetime as

on $\mathbb{R}\times(r_{m},\infty)\times\mathbb{S}^{2}$ with $d\Omega^{2}$ denoting the canonical metric on the sphere $\mathbb{S}^{2}$, one finds

on the graph $M_{T}=\{t=T(\vec{x}):\vec{x}\in\mathbb{R}^{3}\setminus C\}$, see Figure 2.

Choosing

as in [5] for non-trivial $\vec{u}\in\mathbb{R}^{3}$, one obtains a relativistic initial data set $(M_{T_{1}},g^{T_{1}},K^{T_{1}})$ which satisfies neither the weak nor the strong Regge–Teitelboim conditions with respect to $\vec{x}$; in fact, $\vec{C}_{\text{B\'{O}RT}}$ diverges like $\sin(\ln r)\vec{u}$ in this example, see [5, 4]. It is worth noting that the metric $g^{T_{1}}$ in fact does satisfy the weak (but not the strong) Regge–Teitelboim conditions with respect to $\vec{x}$ (see [5]); they fail to hold only for $K^{T_{1}}$.

Suitably exploiting Theorems 6.1 and 6.2 and the decay of $T_{1}$, $N$, and $h$, one can assert that $(M_{T_{1}},g^{T_{1}},K^{T_{1}})$ does not satisfy the weak nor the strong Regge–Teitelboim conditions in any asymptotically Euclidean coordinate chart.

Similarly, choosing

for $0<\beta<\frac{1}{2}$, one finds that $(M_{T_{2}},g^{T_{2}},K^{T_{2}})$ does satisfy the weak Regge–Teitelboim conditions (for $\varepsilon<\frac{1}{2}$) but does not possess any asymptotically Euclidean coordinate chart in which the strong Regge–Teitelboim conditions hold. Again, the problematic (non-)decay occurs in $K^{T_{2}}$.

Finally, we still owe the reader a justification of why the weak Regge–Teitelboim conditions are relevant for the study of the center of mass $\vec{C}_{\text{B\'{O}RT}}$: Indeed, Huisken and Yau in [8] developed an alternative definition of center of mass, called $\vec{C}_{\text{CMC}}$, via asymptotic Constant Mean Curvature (CMC) foliations. In a series of works culminating in a paper by Nerz [10], it was shown that, for asymptotically Euclidean relativistic initial data sets satisfying the weak Regge–Teitelboim conditions, one has

in the sense that either both centers diverge or both converge to the same limit.

Roughly, Huisken and Yau in [8] and Nerz in [10] prove existence and uniqueness of a foliation (that is, a smoothly parametrized partition into smooth $2$-spheres parametrized by $\sigma\in(0,\sigma_{0})$) of the asymptotic end of an asymptotically Euclidean relativistic initial data set, such that the leaves have constant mean (i.e., average extrinsic) curvature $H(\Sigma_{\sigma})=\sigma$. The leaves (i.e., the $2$-spheres) $\Sigma_{\sigma}$ of this foliation are indicated as colored curves in Figure 3. Pushing forward the leaves via the asymptotic coordinates $\vec{x}$, $\vec{x}(\Sigma_{\sigma})$, gives rise to a foliation of a neighborhood of infinity in $\mathbb{R}^{3}$ and one computes the average position of a point on $\vec{x}(\Sigma_{\sigma})$ in $\mathbb{R}^{3}$ as

where $|\vec{x}(\Sigma_{\sigma})|$ denotes the surface area of $\vec{x}(\Sigma_{\sigma})$ in $\mathbb{R}^{3}$ with respect to the Euclidean metric $\delta$, see Figure 3. The center $\vec{C}_{\text{CMC}}$ then arises as the limit

outward along this foliation, provided this limit exists. We refer the interested reader to [5] for more information on this construction and its dependence on the choice of asymptotic coordinates.