Cooperative Multi-Modal Localization in Connected and Autonomous Vehicles

Localization is one of the main pillars of Intelligent Transportation Systems (ITS). Although, Global Navigation Satellite System (GNSS), e.g GPS, provide absolute position information, their accuracy is limited and deviations up to 10 m or higher may arise [8], [10], especially in harsh environments such as urban canyons and tunnels. Since the localization error in autonomous driving should be no greater than 5 m in the worst case, accurate localization methods must be developed. In recent years, there is a growing interest in Cooperative Localization (CL) as a means to improve GPS accuracy. CL is based on the 5G communication technology V2X, allowing the vehicles of a Vehicular-Ad-hoc-NETwork (VANET) to share information among them, in order to improve the position accuracy. Useful information could be absolute position, relative distance and azimuth angle to neighbouring and connected vehicles.

Multi-modal CL in VANET’s is a research area closely related to CL in Wireless Sensor Networks (WSN). An overview of multi-modal CL in WSN is provided in [1]. Recent approaches of CL on VANETs, include [2] where an objective function is formulated by the Maximum Likelihood Estimation criterion and is minimized by employing Distributed Alternating Direction Method of Multipliers. In [3], vehicles share absolute position, relative position and motion state measurements and Distributed CL is performed by a Covariance Intersection Filter (CIF), integrating those informations. The VANET of [4], fuses absolute position and range measurements, using Extended Kalman Filter (EKF) and CIF, in a Distributed manner. In [5], a Distributed CL method in tunnels, that fuses V2X measurements using Particle Filtering, is presented. In [6], a Distributed CL method in urban canyons, that fuses absolute position and range measurements using EKF is proposed. In [7], a Centralized CL method based on Generalized Approximate Message Passing and Kalman Filter (KF) is developed. It exploits navigation measurements from Inertial Navigation Unit, GPS, signals of opportunity, ground stations and inter-vehicular measurements. In [8], a Distributed method is developed, where GPS and vehicles dynamics measurements are fed into a KF and combined with any information available about surrounding features. In [9], a Distributed Bayesian approach that fuses GPS and inter-vehicle distance measurements, is employed in order to perform CL. Finally, [10] provide an overview for cooperative and non-cooperative localization techniques in VANETs.

The previously discussed methods, focus only on the pair-wise measurements of the interconnected vehicles. To the best of our knowledge, the method proposed here is the first one which treats the VANET as a graph and uses graph regulizers to fuse different measurement modalities. Moreover, high-dimensional location trajectories often lie in a low-dimensional subspace and can be recovered more accurately when using exact low-rank matrix recovery approaches methods. We exploit this property of motion patterns using low-rank modelling and optimization tools.

Our main contributions can be summarized as follows:

• •

  A novel method for efficient CL is proposed. Our method performs cooperative multi-modal fusion and uses different graph and low-rank modelling tools for exploiting spatial and temporal coherences of moving vehicles.

• •

  The new method is implemented in a centralized fashion, assuming the existence of a fusion center.

• •

  As shown via extensive experiments, the reduction of Mean Square Localization Error with respect to GPS, can reach 94%.

The rest of the paper is organized as follows: Section II presents the graph regulizer used for exploiting spatial coherences; Section III presents the batch sequential solution that exploits the low-dimensional subspace of the high-dimensional location data; Section IV is dedicated to the experimental setup and simulation results while Section V concludes our work.

The approach that will be derived in this Section, is based on a proper extension of the Laplacian Processing technique [11]. The motivation was related to estimating vehicles' locations through their differential properties, using LIDAR or RADAR. These differential properties are also derived from certain linear operators defined on the graph that represents the VANET. These two observations motivated us to design graph regulizers that are used for fusing different modalities and exploit spatial coherences in a centralized manner.

Consider a 2-D region where N connected vehicles collect measurements while moving. An example of such a VANET, is shown in Fig. 1.

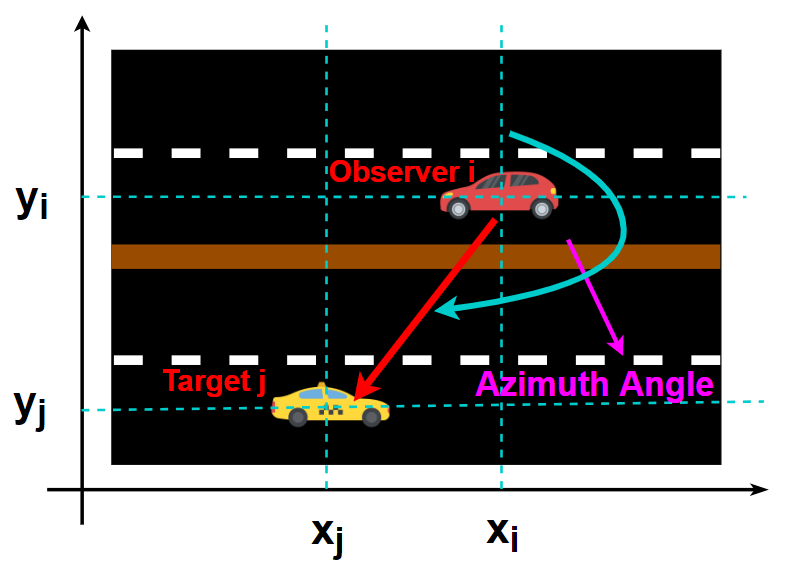
The location of the $i$-th vehicle at $k$-th time instant is given by $\bm{x_{i}^{(k)}}=\begin{bmatrix}x_{i}^{(k)}&y_{i}^{(k)}\end{bmatrix}$. Each vehicle knows its absolute position from GPS and measures its relative distances and azimuth angles with respect to neighbouring and connected vehicles using LIDAR or RADAR. The true relative distance between connected vehicles $i$ and $j$ is given by: $z_{d,ij}^{(k)}=\left\lVert{\bm{x_{j}^{(k)}}-\bm{x_{i}^{(k)}}}\right\rVert_{2}$ , where $\left\lVert\cdot\right\rVert_{2}$ is the $l_{2}$ norm. The true azimuth angle (shown in Fig. 2) between connected vehicles $i$ (observer) and $j$ (target) is given by: $z_{az,ij}^{(k)}=\begin{cases}\lambda\pi+\arctan{\frac{|x_{j}^{(k)}-x_{i}^{(k)}|}{|y_{j}^{(k)}-y_{i}^{(k)}|}},\ \lambda=0,1\\ \lambda\pi+\arctan{\frac{|y_{j}^{(k)}-y_{i}^{(k)}|}{|x_{j}^{(k)}-x_{i}^{(k)}|}},\ \lambda=\frac{1}{2},\frac{3}{2}\end{cases}$. For example, in Fig. 2, $\lambda=1$. The acquired measurements are assumed to be described by the following models:

• •

  Distance measurement:

  $\displaystyle\begin{split}\tilde{z}_{d,ij}^{(k)}=z_{d,ij}^{(k)}+w_{d}^{(k)},\ w_{d}^{(k)}\sim\mathcal{N}(0,\sigma{{}_{d}^{2}})\end{split}$

  (1)

• •

  Azimuth Angle measurement:

  $\displaystyle\begin{split}\tilde{z}_{az,ij}^{(k)}=z{{}_{az,ij}^{(k)}}+w_{az}^{(k)},\ w_{az}^{(k)}\sim\mathcal{N}(0,\sigma{{}_{az}^{2}})\end{split}$

  (2)

• •

  Absolute position measurement:

  $\displaystyle\begin{split}\bm{\tilde{z}_{p,i}^{(k)}}=\bm{x_{i}^{(k)}}+\bm{w_{p}^{(k)}},\ \bm{w_{p}^{(k)}}\sim\mathcal{N}(0,\bm{\Sigma{{}_{p}}})\end{split}$

  (3)

  Covariance matrix $\bm{\Sigma{{}_{p}}}$ is a diagonal matrix equal to $diag(\sigma_{x}^{2},\sigma_{y}^{2})$.

The noise introduced in the measurements is assumed to be Gaussian, as commonly done in relevant literature [2], [3], [4], [5].

Let $G^{(k)}=(\mathcal{V}^{(k)},\mathcal{E}^{(k)})$ be an undirected graph, which changes over time, where $\mathcal{V}^{(k)}$ is the set of vertices and $\mathcal{E}^{(k)}$ the set of edges. Each vertex $\bm{v_{i}^{(k)}}$ is represented by absolute cartesian coordinates as $\bm{v_{i}^{(k)}}=\begin{bmatrix}x_{i}^{(k)}&y_{i}^{(k)}\end{bmatrix}$. The differential coordinates $\bm{\delta{{}_{i}^{(k)}}}$ for each vertex $\bm{v_{i}^{(k)}}$ are defined as:

, where $d_{i}^{(k)}$ is the number of neighbours of vertex $\bm{v_{i}^{(k)}}$ and $N(i)$ denotes the set of neighbours of $\bm{v_{i}^{(k)}}$. Obviously, $\bm{\delta^{(k),(x)}},\bm{\delta^{(k),(y)}}\in\mathbb{R}^{N\times 1}$. We also define the diagonal degree matrix $\bm{D^{(k)}}\in\mathbb{R}^{N\times N}$ (with $D^{(k)}[i,i]=d_{i}^{(k)}$ and $D^{(k)}[i,j]=0$, if $i\neq j$) and adjacency matrix $\bm{A^{(k)}}\in\mathbb{R}^{N\times N}$ (with $A^{(k)}[i,j]$ = 1, if $(i,j)\in{\mathcal{E}^{(k)}}$ and $A^{(k)}[i,j]=0$, otherwise). Finally, the Laplacian Matrix $\bm{L^{(k)}}\in\mathbb{R}^{N\times N}$ of graph is equal to $\bm{L^{(k)}}=\bm{D^{(k)}}-\bm{A^{(k)}}$. Relying on the previously defined $\bm{\delta^{(k)}}$ coordinates, one can recover the true absolute coordinates of the vertices, represented by the vectors $\bm{x^{(k)}}\in\mathbb{R}^{N\times 1}$ and $\bm{y^{(k)}}\in\mathbb{R}^{N\times 1}$, by solving the systems:

We can also notice from Fig. 2 that:

As such, by considering the vehicles of the network as vertices of a graph and the communication links between the neighbours as its edges, we can create matrices $\bm{D^{(k)}},\bm{A^{(k)}},\bm{L^{(k)}}$. The graph that represents the VANET of Fig. 1, is shown in Fig. 3. Moreover, each vehicle utilizing measurement models (1) and (2), can define the $\bm{\delta_{i}^{(k)}}$ coordinates and send them to a fusion center, which will try to solve the systems in (4). However, $\bm{L^{(k)}}$ is a singular matrix, which implies that systems in (4) are not solvable. Thus, we need to add into the systems some anchor points $\bm{c_{i}^{(k)}}=\begin{bmatrix}c_{i}^{(k),(x)}&c_{i}^{(k),(y)}\end{bmatrix}$ with known absolute coordinates.

Furthermore, if we assume as anchors the vertices $\bm{v_{1}^{(k)}}$ and $\bm{v_{5}^{(k)}}$, then we define the extended $\bm{\tilde{L}^{(k)}}$ which is equal to: $\bm{\tilde{L}^{(k)}}=\left(\IEEEeqnarraybox*[][c]{c/c/c}&\bm{L^{(k)}}\\ \bm{e_{1}}\\ \bm{e_{5}}\right)$ , where $\bm{e_{i}}\in\mathbb{R}^{1\times N}$ is a vector with zeros and $e_{i}[i]=1$. If the number of available anchors is $\alpha$, then $\bm{\tilde{L}^{(k)}}\in\mathbb{R}^{(N+\alpha)\times N}$. After adding the anchor points, the system in (4) for $x$-coordinates, can be re-written as:

Apparently $\bm{b^{(k),(x)}}\in\mathbb{R}^{(N+\alpha)\times 1}$. The required location vector $\bm{x^{(k)}}$ can be computed in the least-squares sense as follows:

The same approach of (7) and (8) is followed for estimating the true $y$-coordinates. In practice, as anchor points the noisy GPS positions of the vehicles of the network (measurement model (3)) can be used. Furthermore, each $\bm{\delta{{}_{i}^{(k)}}}$ must be multiplied with $d_{i}^{(k)}$, so as to remain in accordance with (4). We named our CL approach, Graph Regularization for CL or GR-CL. The main steps of GR-CL are summarized on Algorithm 1.

Note that this scheme, can be potentially useful for the self-localization task, where only visually detected road landmarks (e.g. poles, facades) and their relative distance, angle and position to the ego vehicle are exploited.

Kinematic models of vehicles (e.g. bicycle model of [13]) but also data extracted by open source autonomous driving simulators (e.g. CARLA) exhibit low-rank properties that are attributed to the fact that for various time periods clusters of vehicles move in parallel directions. Motivated by that, we generated the trajectories of N vehicles for a certain time period and we stored the locations of each time instant to the columns of a matrix. Due to the fact that the columns were correlated and not independent from each other, the matrix proved to be a low-rank. However, if we stored the noisy positions provided by GPS, the matrix will no longer be a low-rank. Based on that facts, we claim that if we were able to recover a low-rank matrix from a batch of continuous but noisy locations, then the true locations would be estimated with high accuracy.

The method of this Section, uses as input the output of the spatial graph regularization of Section II. At each $k$-th time instant, GR-CL is implemented and assuming that the fusion center can store the current and the previous $\tau-1$ $\bm{\delta_{i}}$ coordinates and the GR-CL estimations, then matrix $\bm{B^{(x)}}\in\mathbb{R}^{2N\times\tau}$ can be formulated, where:

That matrix contains the concatenated vectors $\bm{b^{(x)}}$ from $(k-\tau)$-th up to $\tau$-th time instant. The GR-CL estimations now act as the anchors. We consider also that the VANET graph does not change while the vehicles are moving, which means that $\bm{\tilde{L}}$ remains the same. Thus, a least-squares minimization problem with rank constraints can be formulated:

, where $\bm{X^{(k)}}\in\mathbb{R}^{N\times\tau}$, $\left\lVert\cdot\right\rVert_{F}$ is the Frobenius norm and $s\in[1,min(N,\tau)]$. Matrix $\bm{X^{(k)}}$ is in fact the low-rank matrix that correspond to the true $x$-coordinates of the vehicles of the current estimation window of range $\tau$.

In order to solve (10), first perform Singular Value Decomposition (SVD) on $\bm{\tilde{L}}$, as $\bm{\tilde{L}}$ = $\bm{USV^{T}}$. Then, create the matrix $\bm{W^{(k),(x)}}$ = $\bm{U^{T}B^{(k),(x)}}$. According to [12], matrix $\bm{X^{(k)}}$ is equal to:

Operation $SVT(\cdot)_{s}$ stands for Singular Value Thresholding, which means that only the $s$ largest singular values are used. Apparently, only the last column of $\bm{X^{(k)}}$ is of interest, since it refers to the locations estimation of the current $k$-th time instant. Solving (10) requires cubic time complexity, caused by SVD. Therefore a rather small range of estimation window is needed, in order to reduce the computational time. The same approach of (9), (10), (11) is followed for estimating the true $y$-coordinates.

As a consequence, a batch sequential method has been developed. It exploits not only the spatially, but also the temporal coherences of moving vehicles. As long as the motion of vehicles is correlated, the temporal coherences are exploited in the sense of determining a low-rank matrix that corresponds to the true location of vehicles. We named this method Graph and Low-Rank Regularization for CL or GLRR-CL, which is summarized on Algorithm 2.

In this paper, a two-stage method for CL has been developed. In the first stage, we modeled the vehicles of a VANET as vertices of an undirected graph and the communication links between them as its edges. A graph regulizer has been developed, which exploits only spatially coherences, by creating the Laplacian Matrix and defining the $\bm{\delta}$ coordinates. During the second stage, a graph and low-rank regulizer uses the temporal coherence of vehicles in order to recover a low-rank matrix. An optimization problem with rank and Laplacian constraints has been formulated for the recovery. Different experimental scenarios have proven that the reduction of GPS MSLE with our method can reach 94%.

This paper has received funding from the European Union’s H2020 research and innovation programme CPSoSaware under grant agreement No 871738.