Convex polygons and separation of convex sets††thanks: Partially supported by Conacyt, México.
Abstract
We prove that for any collection of pairwise disjoint compact convex sets in the plane there is a pair of sets and in such that any line that separates from separates either or from a subcollection of with at least sets.
Keywords.- Convex polygon. Plane Compact Convex Set. Separating line.
1 Introduction
H. Tverberg [5] proved that for each positive integer , there is a minimum integer such that for every collection of or more plane compact convex sets with pairwise disjoint interiors, there is a line that separates one set in from a subcollection of with at least sets. R. Hope and M. Katchalski [3] showed that .
Later E. Rivera-Campo and J. Töröcsik [4] proved that in any collection of pairwise disjoint compact convex sets in the plane, there is a pair of sets and such that any line that separates from separates either or from at least sets in . In this paper we give a higher lower bound of sets in for any collection of sets.
2 Preliminary results
Theorem 1.
Any collection of compact, convex and pairwise disjoint sets in the plane may be covered with non-overlapping convex polygons with a total of not more than sides. Furthermore no more than distinct slopes are required.
We adapt part of the proof given in [1] to obtain the following result.
Lemma 1.
Let be a collection of pairwise disjoint convex polygons in the plane. There exists a collection of pairwise non-overlapping convex polygons such that:
-
1.
For , is contained in .
-
2.
For , each side of supports a side of .
-
3.
The total number of sides among polygons is at most .
Proof.
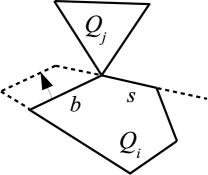
A side of a polygon is reducible with respect to if the triangle (not containing ), bounded by and the lines supporting the sides of incident to , does not intersect the interior of any another polygon . Equivalently, a side of a polygon is reducible with respect to if it vanishes before reaching the interior of a polygon when it is translated in the direction orthogonal to and away from (see Fig. 1).
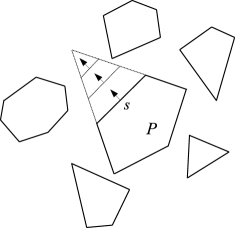
We modify by growing, one at a time, polygons in as follows: if some polygon has a reducible side with respect to substitute in with polygon . Repeat this until no polygon in has a reducible side. Denote by the family of polygons thus obtained.
Its is clear that satisfies conditions 1) and 2), we claim it also satisfies condition 3. To prove this consider a third family of convex polygons obtained from by further growing polygons in the following way.
A side of a polygon in is free with respect to if the open polygonal region, not containing , which is determined by and the lines supporting the two sides of adjacent to contains no points of polygons in .
Let be a circle containing all polygons in . Starting with the non free sides of polygons , translate one at a time a side of a polygon (also in the direction orthogonal to and away from ) as far as possible without intersecting the interior of another (possibly already grown) polygon or the exterior of (see Fig. 2).

Stop when no side can be translated as indicated and let where, for , is the polygon obtained from in this manner. We claim that if is chosen large enough, then each polygon in contains at most 3 free sides and all non free sides of a polygon in are in contact with a polygon with .
By the choice of no side of a polygon vanishes, therefore for the number of sides of is equal to the number of sides of .
We define a plane graph with one vertex placed in the interior of each polygon and a vertex placed outside circle . The edge set of consists of 6 types of edges as follows:
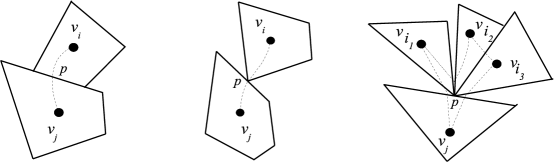
a) If a side of a polygon and a side of a polygon have a segment in common choose an arbitrary point in and draw an edge through as in Fig. 3 (left).
b) If a vertex of a polygon lies in the interior of a side of a polygon and is not a vertex of a polygon in other than , then draw an edge through as in Fig. 3 (center).
c) If two or more polygons share a vertex which lies in the interior of a side of a polygon and is not a point of any polygon other than , then there is a neighbourhood of containing no points of polygons with . In this case draw a cycle with edges as in Fig. 3 (right).
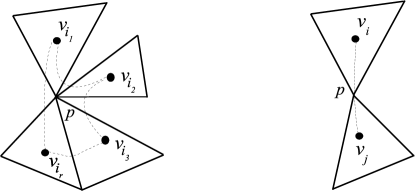
d) If three or more polygons share a vertex and is not a point of any polygon other than , then there is a neighbourhood of containing no points of any polygon with . In this case draw a cycle with edges as in Fig. 4 (left).
e) If two polygons and share a vertex and is not a point of any polygon in other than and , then draw an edge through as in Fig. 4 (right).
f) For each free side of a polygon add an edge drawn through an interior of point in .
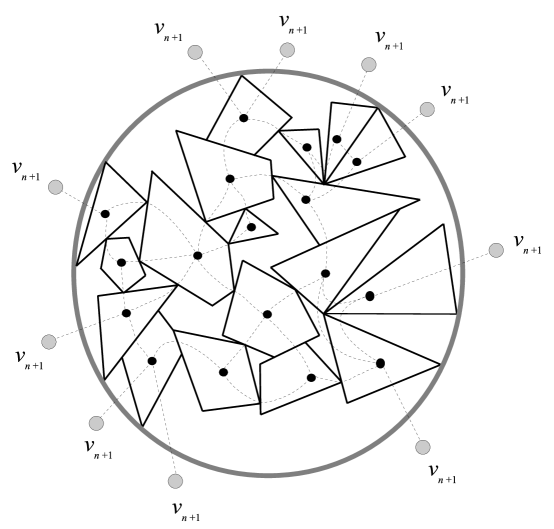
Notice that edges of type f) are the only possible multiple edges of . Therefore is a plane multigraph with vertices and edges, where for , denotes the number of polygons in with free sides.
We say that an edge of intersects a side of a polygon in if is drawn through either an interior point of or through a vertex of . Each non free side among polygons in is intersected by at least one edge of of type a), b), c), d) or e) and each free side is intersected by an edge of type f). We claim that if an edge of is of type e) then two of the 4 sides intersected by are intersected by at least another edge of .
Proof of Claim. Let be an edge of of type e). Then either two sides of (of or one side of and one side of are such that the lines supporting and separate and (see Fig. 6).

Without loss of generality we assume the line supporting a side of separates and . Let be the other side of incident in the common vertex of and . Then side must contain a point of a polygon other than and , otherwise could be translated away from in the direction orthogonal to which is not possible by the properties of (see Fig. 7). This means that side is intersected by an edge of other than edge .
Analogously a side , incident with , is intersected by an edge of other than .
Let denote the total number of sides among polygons in . Also let , and denote the number of edges of , the number of edges of of type e) and the number of edges of of type f), respectively. Since polygons in contain at most 3 free edges, , where for is the number of polygons in containing free edges.
In order to bound the number of sides among polygons in we add the number of sides intersected by edges of and subtract the number of sides intersected by at least two edges of (2 sides for each edge of type e)). Considering that edges of types a), b), c), and d), intersect at most 3 sides; edges of type e) intersect 4 sides and edges of type f) intersect one side, we have:
∎
Consider the following familly of plane geometric graphs , given by Edelsbrunner et al [1] where it is used to show that the bounds in the number of sides and slopes on Theorem 1 are tight.
is the graph with vertices shown on Fig. 8 (left); for , is the graph obtained from as in Fig. 8 (right). For the graph is a plane geometric graph with internal faces. The three inner-most faces are quadrilaterals while all other faces are hexagons.

Place an hexagon inside each of the three inner-most faces of as in Fig. 9 (left), an octagon inside each outer-most internal face of as in Fig. 9 (right) and a nonagon inside each other internal face of as in Fig. 10.
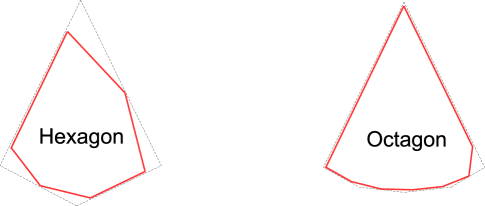

Since each face of has an even number of sides, the placement of the polygons described above may be done in such a way that for each internal edge of a side of the polygon lying on one side of is parallel (and closed enough) to while a vertex of the polygon lying on the other side of lies on as in Fig. 11.
Let be the set of polygons described above. The total number of sides among polygons in is
Each side among polygons in is relevant with respect to , therefore our bound on the number of sides in Lemma 1 is almost tight.
3 Main Results
In this section we present our main results.
Lemma 2.
Let be a collection of pairwise disjoint convex polygons in the plane. There is a side of a polygon such that the line supporting separates from a subcollection of with at least polygons.
Proof.
Let be a collection of pairwise disjoint convex polygons satisfying conditions 1), 2) and 3) in Lemma 1 and let be the (multi)set of lines supporting the sides of each polygon in . We include copies of a line if supports sides of polygons in . Therefore we can associate a unique polygon to each line such that a side of is supported by . For let be the closed halfplane determined by that does not contain .
Define a bipartite graph with a vertex for each polygon and a vertex for each line . Graph has an edge if polygon is contained in .
For each pair of polygons there is at least one side of one of them such that the line supporting separates from . Therefore graph has at least one edge for each pair with . This implies that there is a vertex whose degree in is at least .
This means that the line separates polygon from at least polygons in . By Property 2) in Lemma 1, line supports a side of polygon .
∎
Theorem 2.
In any collection of pairwise disjoint compact convex sets in the plane, there is a pair of sets and such that any line that separates from separates either or from a subcollection of with at least sets.
Proof.
Let be an integer and be a collection of pairwise disjoint compact convex sets in the plane and let be a triangle containing all sets in in its interior.
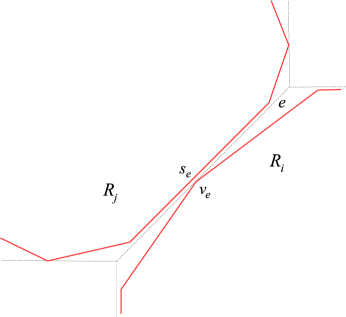
For any line let and be the number of sets in lying to the left and to the right of , respectively; for a horizontal line , and are the number of sets in lying above and bellow , respectively. For let be a line separating from for which is as small as posible.
Each line determines two closed halfplanes and containing and , respectively. For , let . Then For , is a convex polygon that contains set such that each side is supported by a line or by a side of .
Let . By Lemma 2, there is a side of a polygon such that the line supporting separates from a subcollection of with at least polygons.
Since no side of separates polygons in , is of the form . By the choice of each line that separates sets from separates either or from at least sets in . ∎
References
- [1] Herbert Edelsbrunner, Arch D. Robison and Xiao Jun Shen. Covering convex sets with non-overlapping polygons, Discrete Mathematics 81: 153 – 164, 1990.
- [2] László Fejes Tóth. Illumination of convex discs, Acta Mathematica Academiae Scientiarum Hungaricae 29(3 - 4): 355 – 360, 1997.
- [3] Rafael Hope and Meir Katchalski. Separating plane convex sets, Mathematica Scandinavica 66 (1): 44–46, 1990.
- [4] Eduardo Rivera-Campo and Jeno Töröcsik. On separation of plane convex sets, European Journal of Combinatorics 14: 113 – 116, 1993.
- [5] Helge Tverberg. A separation property of plane convex sets, Mathematica Scandinavica 45: 255–260, 1979.