Convex pentagons and concave octagons that can form
rotationally
symmetric tilings
Abstract
In this study, the properties of convex pentagons that can form rotationally symmetric edge-to-edge tilings are discussed. Because the rotationally symmetric tilings are formed by concave octagons that are generated by two convex pentagons connected through a line symmetry, they are considered to be equivalent to rotationally symmetric tilings with concave octagons. In addition, under certain circumstances, tiling-like patterns with a regular polygonal hole at the center can be formed using these convex pentagons.
1) The Interdisciplinary Institute of Science, Technology and Art
2) Japan Tessellation Design Association
E-mail: [email protected]
Keywords: pentagon, octagon, tiling, rotational symmetry, monohedral, spiral
1 Introduction
In this study, as shown in Figure 1(a), let us label the vertices (interior angles) of the convex pentagon , , , , and , and its edges , , , , and in a fixed manner. A convex pentagonal tile111 A tiling (or tessellation) of the plane is a collection of sets that are called tiles, which covers a plane without gaps and overlaps, except for the boundaries of the tiles. The term “tile” refers to a topological disk, whose boundary is a simple closed curve. If all the tiles in a tiling are of the same size and shape, then the tiling is monohedral [3, 14]. In this study, a polygon that admits a monohedral tiling is called a polygonal tile [10, 9, 11]. Note that, in monohedral tiling, it admits the use of reflected tiles. that satisfies the conditions “” belongs to the Type 1 family222 To date, fifteen families of convex pentagonal tiles, each of them referred to as a “Type,” are known [3, 10, 14]. For example, if the sum of three consecutive angles in a convex pentagonal tile is , the pentagonal tile belongs to the Type 1 family. Convex pentagonal tiles belonging to some families also exist. Known convex pentagonal tiles can form periodic tiling. In May 2017, Michaël Rao declared that the complete list of Types of convex pentagonal tiles had been obtained (i.e., they have only the known 15 families), but it does not seem to be fixed as of March 2020 [14]. [3, 9, 10, 14]. The tile is called “C11-T1A” in [13] and its geometric properties are shown. Because this convex pentagon has four equal-length edges, its interior can be divided into a triangle BDE and two isosceles triangles ABE and BCD as shown in Figure 1(b). Given the foregoing properties, the relational expression of the interior angle of each vertex of C11-T1A can be rewritten as follows:


| (1) |
where . From the relationship between the five interior angles, the vertex concentrations that are always valid in tilings are “.” If , then the edge length of can be expressed as follows:
As shown in Figure 2, C11-T1A can form the representative tiling of Type 1 or variations of Type 1 tilings (i.e., tilings whose vertices are formed only by the relations of and ). The edge of C11-T1A is the only edge of different length. As shown in Figure 1(c), an equilateral concave octagon formed by two convex pentagons, connected through a line symmetry whose axis is edge , is referred to as the Octa-unit. C11-T1A can form tilings that are not contained in the variations of Type 1 tilings, as shown in Figure 3, by using Octa-units. That is, C11-T1A can also form tilings by freely combining Octa-units with different directions in one direction [5, 13]
In this study, we introduce the convex pentagon C11-T1A that can generate countless numbers of rotationally symmetric tilings. Because the Octa-unit of C11-T1A is used in these rotationally symmetric tilings, it is considered similar to the concave octagons that can generate countless rotationally symmetric tilings.

2 Rotationally symmetric tilings
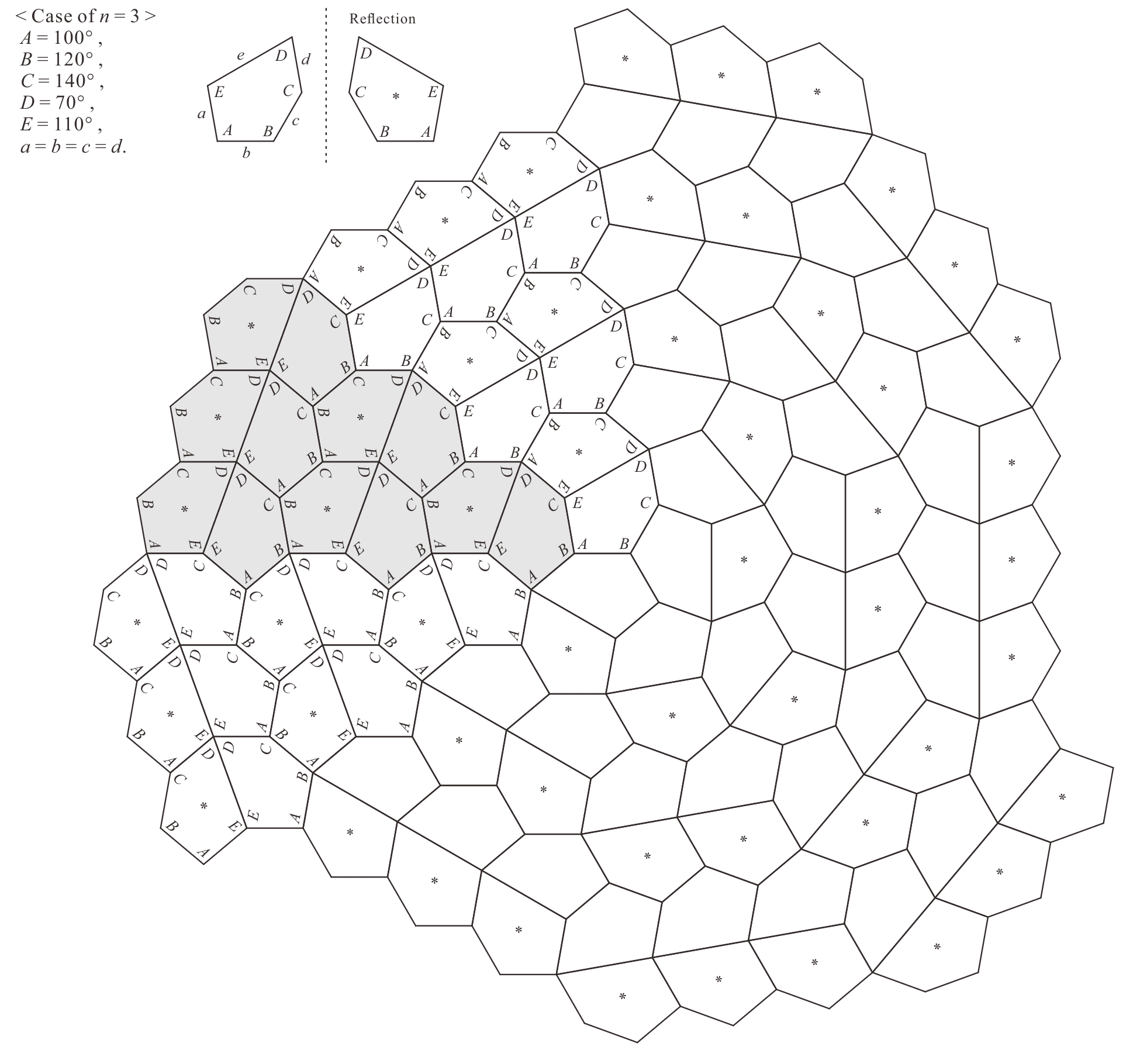
In [5], there are figures of four-fold, five-fold, six-fold, and ten-fold rotationally symmetric edge-to-edge333 A tiling by convex polygons is edge-to-edge if any two convex polygons in a tiling are either disjoint or share one vertex or an entire edge in common. Then other case is non-edge-to-edge [3, 9, 10]. tilings using convex pentagonal tiles (or tiles that can be regarded as concave octagons). In [5], there are multiple types of edge-to-edge tilings with six-fold rotational symmetry by an equilateral convex pentagon, including Hirschhorn and Hunt’s types [4]. The convex pentagons forming these rotationally symmetric edge-to-edge tilings corresponded to C11-T1A.
By using the relational expression of the interior angles of (1), the conditions of pentagonal tile C11-T1A that can form -fold rotationally symmetric edge-to-edge tilings are expressed in (2).
| (2) |
where is an integer greater than or equal to three, because .
Table 1 presents some of the relationships between the interior angles of convex pentagons satisfying (2) that can form the -fold rotationally symmetric edge-to-edge tilings. (For , tilings with convex pentagonal tiles are drawn. For further details, Figures 5–15.) Given that , the convex pentagonal tile that satisfies (2) is an equilateral convex pentagon, and can form several different six-fold rotationally symmetric edge-to-edge tilings [4, 5, 13, 14]. The tiling in Figure 8 is one of the six-fold rotationally symmetric edge-to-edge tilings by the equilateral convex pentagon that Hirschhorn and Hunt presented [4]. Note that the -fold rotationally symmetric edge-to-edge tilings by convex pentagonal tiles satisfying (2) have symmetry444 “” is based on the Schoenflies notation for symmetry in a two-dimensional point group [15, 16]. “” represents an -fold rotation axis without reflection. The notation for symmetry is based on that presented in [6]. because they have rotational symmetry, but no axis of reflection symmetry.
| Value of interior angle (degree) | Edge length of | Figure number | |||||
| A | B | C | D | E | |||
| 3 | 1.732 | 5 | |||||
| 4 | 1.414 | 6 | |||||
| 5 | 1.176 | 7 | |||||
| 6 | 1 | 8 | |||||
| 7 | 0.868 | 9 | |||||
| 8 | 0.765 | 10 | |||||
| 9 | 0.684 | 11 | |||||
| 10 | 0.618 | 12 | |||||
| 11 | 0.563 | 13 | |||||
| 12 | 0.518 | 14 | |||||
| 13 | 0.479 | 15 | |||||
| 14 | 0.445 | ||||||
| 15 | 0.416 | ||||||
| 16 | 0.390 | ||||||
| 17 | 0.367 | ||||||
| 18 | 0.347 | ||||||
| … | … | ||||||

Here, the formation of rotationally symmetric edge-to-edge tiling with convex pentagonal tiles is briefly explained. First, as shown in STEP 1 in Figure 4, create a unit connecting the Octa-units that are generated by convex pentagons satisfying (2) in one direction so that . The Octa-units can then be assembled in such a way as to increase the number of pieces from one to two to three, and so on, in order. Then, copy the two units in STEP 1. In STEP 2, first, rotate one of the two copied units by , with respect to the original (see STEP 2 of Figure 4, wherein the axis of has a rotation of with respect to the axis of ), and connect it to the original to get the following results: , , and , as expressed in STEP 2 of Figure 4. Next, rotate the remaining unit by , with respect to the original (see STEP 2 of Figure 4, wherein the axis of has a rotation of with respect to the axis of ), and connect it in the same way as the one previously made to make a unit like that in STEP 2 in Figure 4. Next, copy the unit in STEP 2. Subsequently, take the unit from STEP 2 and rotate it by the value of the interior angle of vertex . When the original unit and the rotated unit are arranged as shown in STEP 3 (Rotationally symmetric tiling) in Figure 4, parts in the -fold rotationally symmetric tiling can be formed. Then, by repeating this process as many times as necessary, an -fold rotationally symmetric edge-to-edge tiling with convex pentagonal tiles can be formed.
Klaassen [6] presented the convex pentagonal tiles that can generate countless rotationally symmetric edge-to-edge tilings; however, the pentagon tilings were non-edge-to-edge. On the other hand, it was shown that the convex pentagonal tiles satisfying (2) can generate countless rotationally symmetric edge-to-edge tilings. Although the corresponding theorem and proof are not presented, similar to how it was in [6], it will still be understood that countless rotationally symmetric tilings can be generated by the foregoing explanations and methods.
3 Rotationally symmetric tilings (tiling-like patterns) with a regular polygonal hole at the center
In [5], there are figures of rotationally symmetric tiling-like patterns with a hole in the center of a regular heptagon, 10-gon, 12-gon, or 18-gon formed using convex pentagons (or elements that can be regarded as concave octagons). The regular 18-gonal hole can be filled with convex pentagons, but the other holes cannot be filled with convex pentagons. Note that the tiling-like patterns are not considered tilings due to the presence of a gap, but are simply called tilings in this study. The convex pentagons forming these rotationally symmetric tilings with a regular -gonal hole corresponded to C11-T1A.
By using the relational expression of the interior angles of (1), the conditions of pentagonal tile C11-T1A that can form rotationally symmetric tilings with a regular -gonal hole are expressed in (3).
| (3) |
where is an integer greater than or equal to seven, because . Note that, because “” corresponds to one interior angle of a regular -gon, the value of “” in (3) is equal to the outer angle () of one vertex of a regular -gon.
Table 2 presents some of the relationships between the interior angles of convex pentagons satisfying (3) that can form the rotationally symmetric tilings with a regular -gonal hole at the center. (For , tilings with a regular -gonal hole at the center formed by convex pentagons are drawn. For further details, Figures 18–26.) If these elements are considered to be convex pentagons, the connection is edge-to-edge. These tilings with a regular -gonal hole with symmetry555 “” is based on the Schoenflies notation for symmetry in a two-dimensional point group [15, 16]. “” represents an -fold rotation axis with reflection symmetry axes. at the center have symmetry. If convex pentagons satisfying (3) have that is divisible by three, they are also convex pentagonal tiles that satisfy (2).
| Value of interior angle (degree) | Edge length of | of Table 1 | Figure number | |||||
| A | B | C | D | E | ||||
| 7 | 1.950 | 16 | ||||||
| 8 | 1.848 | 17 | ||||||
| 9 | 1.732 | 3 | 18 | |||||
| 10 | 1.618 | 19 | ||||||
| 11 | 1.511 | |||||||
| 12 | 1.414 | 4 | 20 | |||||
| 13 | 1.326 | |||||||
| 14 | 1.247 | 21 | ||||||
| 15 | 1.176 | 5 | 22 | |||||
| 16 | 1.111 | |||||||
| 17 | 1.053 | |||||||
| 18 | 1 | 6 | 23 | |||||
| 19 | 0.952 | |||||||
| 20 | 0.908 | |||||||
| 21 | 0.868 | 7 | 25 | |||||
| 22 | 0.831 | |||||||
| 23 | 0.797 | |||||||
| 24 | 0.765 | 8 | 26 | |||||
| 25 | 0.736 | |||||||
| 26 | 0.709 | |||||||
| 27 | 0.684 | 9 | 27 | |||||
| … | … | |||||||
Rotationally symmetric tilings with a regular -gonal hole at the center can be made in almost the same way as the -fold rotationally symmetric edge-to-edge tiling (i.e., the manner of creation follows the same steps up to STEP 2 of Figure 4). The part with three edges AB, at the center of the unit made in STEP 2 of Figure 4, corresponds to the contour of a regular -gon. Therefore, copy the unit in STEP 2, take the unit from STEP 2 and rotate it by the value of the interior angle of vertex . When the original unit and the rotated unit are arranged as shown in STEP 3 (Tiling with a regular -gonal hole) in Figure 4, parts of a regular -gon can be formed. Then, by repeating this process as many times as necessary, a rotationally symmetric tiling with a regular -gonal hole at the center can be formed.
As shown in Table 2 and Figure 23, the convex pentagonal tile that satisfies (3), where , is an equilateral convex pentagon. As such, the regular 18-gonal hole can be filled with equilateral convex pentagons. The pentagonal arrangement pattern in the regular 18-gon is unique; however, the regular 18-gon can be reversed; therefore, two patterns can be used in the hole (see Figure 23). The tiling in Figure 24 is one of the six-fold rotationally symmetric edge-to-edge tilings with equilateral convex pentagons that Hirschhorn and Hunt present in [4]. In addition, the tiling in Figure 23 is that of Hirschhorn [7]. In [5], there are figures of tilings corresponding to Figures 8, 23, and 24, with the one corresponding to Figure 24 labeled as Hirschhorn’s rosette. These tilings with a regular 18-gonal hole that is filled with equilateral convex pentagons have symmetry. In Pegg’s research [2], they stated there exists the tiling of Figure 8, using the equilateral convex pentagon, and that there are also other interesting tilings, such as that with the “crystal-like” structure. Note that in Pegg’s research [2], there are non-monohedral tilings created using convex and concave pentagons.
As described above, the tiling of in Table 2 (see Figure 19) is listed in Iliev’s research [5], however, the value of the interior angle of the convex pentagon was erroneous, as well as in Smith’s research [8]. It is shown that the convex pentagon of in Table 2 is the same as the convex pentagonal tile belonging to both the Type 1 and Type 2 families, and that it can form various tilings [1, 5, 8]. In [1] and [8], there are also tilings with a regular pentagonal hole at the center using this convex pentagon of in Table 2. Moreover, it is interesting to note that the ring-shaped layer forming the periphery can be reversed in [8].
4 Spiral tilings
Klaassen [6] also showed the viewpoint of rotationally symmetric tilings with convex pentagons as a spiral structure. A similar spiral structure can be found in the rotationally symmetric edge-to-edge tilings with convex pentagons of C11-T1A. Figure 28 pertains to the case where , which makes the spiral structure easier to understand. From this spiral structure, the difference between the rotationally symmetric tilings with convex pentagons in [6] and the rotationally symmetric edge-to-edge tilings with C11-T1A other than the edge-to-edge property will be determinable.
Here, let us pay attention to the convex pentagon of in Table 2. This convex pentagon has the property of . From this property, the convex pentagon of in Table 2 can form spiral tilings666 It is difficult to determine what the spiral tiling is. There are some discussions, such as those in [7]. The tiling shown in Figure 28 can be regarded as a spiral, however, it has a radial structure extending from the center. Thus, we feel that it is more straightforward to regard it as a rotationally symmetric tiling. On the other hand, because the tiling of Figure 29 does not have a radial structure extending from the center or singularity point, we feel that it is a spiral rather than a rotationally symmetric tiling. with two-fold rotational symmetry, as shown in Figure 29(a). This convex pentagonal tile belongs to both the Type 1 and Type 7 families [3, 10, 9, 11, 14].
After finding the tiling in Figure 29(a), we found that, in “(6) Central block ‘wraparound’ ” of [1], Bailey presented the spiral tilings with two-fold rotational symmetry by the convex pentagon corresponding to the case of in Table 2. The spiral tiling is the same as that in Figure 30(a). Furthermore, from [1], we found that it is possible to form tilings that keep the spiral structure and extend in one direction only, as shown in Figures 30(b), 30(c), and 30(d). Then, we determined that the convex pentagon of in Table 2 can also form tilings that keep the spiral structure and extend in one direction (see Figures 29(b), 29(c), and 29(d)).
The convex pentagon of in Table 2 has , and belongs to both the Type 1 and Type 2 families. Similar to the convex pentagons of in Table 2, the convex pentagon of in Table 2 can also form the spiral tiling with two-fold rotational symmetry (see Figure 31(a)) and tilings that keep the spiral structure and extend in one direction (see Figures 31(b), 31(c), and 31(d)). For all convex pentagons of in Table 2, it is also possible to remove one spiral structure and to extend the belts wherein the Octa-units are arranged (see Figure 32).
5 Conclusions
The existence of convex pentagonal tiles that can generate countless number of rotationally symmetric edge-to-edge tilings is not well-known. As mentioned above, Klaassen presented a case where tilings are not edge-to-edge. From [5], we determined that the convex pentagon called C11-T1A in [13] had this property. In [5], Iliev presented the tilings corresponding to in Table 1 and in Table 2. It may have been inferred by Iliev that there are countless rotationally symmetric tilings similar to those; however, there seems to be no clarification on the matter. In particular, there is no description of the concrete properties (tile conditions), such as the convex pentagon of C11-T1A, as shown in this study.
It was previously recognized that the convex pentagon belonging to both the Type 1 and Type 7 families (i.e., convex pentagon corresponding to in Table 2) can generate various albeit limited tilings. However, in reality, we noticed that it is possible to generate more tilings. Among them are other rotational symmetric tilings and spiral tilings. We will introduce them in a different article [12] .
Acknowledgments. The author would like to thank Yoshiaki ARAKI of Japan Tessellation Design Association, for information of Bailey’s site, etc. and comments.
References
- [1] D. Bailey, David Bailey’s World of Escher-like Tessellations >Pentagon Tilings, http://www.tess-elation.co.uk/pentagon-tilings (accessed on 24 February 2020).
- [2] Ed Pegg Jr, Chaos tiles, http://www.vicher.cz/puzzle/chaos/chaos.htm (accessed on 23 February 2020).
- [3] B. Grünbaum, G.C. Shephard, Tilings and Patterns. W. H. Freeman and Company, New York, 1987, pp.15–35 (Chapter 1), pp.471–518 (Chapter 9).
- [4] M. D. Hirschhorn, D. C. Hunt, Equilateral convex pentagons which tile the plane, Journal of Combinatorial Theory, Series A 39, 1–18
- [5] I. Iliev, Mosaics from parquet forming irregular convex pentagons. Alliance print, Sofia, 2018.
- [6] B. Klaassen, Rotationally symmetric tilings with convex pentagons and hexagons, Elemente der Mathematik, 71 (2016) 137–144. doi:10.4171/em/310. Available online: https://arxiv.org/abs/1509.06297 (accessed on 23 February 2020).
- [7] B. Klaassen, How to Define a Spiral Tiling?, Mathematics Magazine, 90 (2017) 26–38. doi 10.4169/math.mag.90.1.26.
- [8] D. Smith, ‘Tiled House’, https://hedraweb.wordpress.com/2019/02/20/tilting-house-pentagon-part-one/; ‘Tiling House’ motif, https://hedraweb.wordpress.com/2019/02/28/tilting-house-part-two/; ‘Tilting House’, https://hedraweb.wordpress.com/2019/03/22/1787/ (accessed on 28 March 2020).
- [9] T. Sugimoto, Convex pentagons for edge-to-edge tiling, I, Forma, 27 (2012) 93–103. https://forma.katachi-jp.com/abstract/2701/27010093.html (accessed on 4 March 2022).
- [10] —, Tiling Problem: Convex pentagons for edge-to-edge tiling and convex polygons for aperiodic tiling (2015). https://arxiv.org/abs/1508.01864 (accessed on 23 February 2020).
- [11] —, Convex pentagons for edge-to-edge tiling, III, Graphs and Combinatorics, 32 (2016) 785–799. doi:10.1007/s00373-015-1599-1.
- [12] —, Rotationally symmetric tilings with convex pentagons belonging to both the Type 1 and Type 7 families (2020). https://arxiv.org/abs/2005.13980 (accessed on 29 May 2020).
- [13] T. Sugimoto, T. Ogawa, Systematic Study of Convex Pentagonal Tilings, II: Tilings by Convex Pentagons with Four Equal-length Edges, Forma, 24 (2009) 93–109. Available online: https://forma.katachi-jp.com/abstract/2403/24030093.html (accessed on 4 March 2022).
- [14] Wikipedia contributors, Pentagonal tiling, Wikipedia, The Free Encyclopedia, https://en.wikipedia.org/wiki/Pentagonal_tiling (accessed on 31 March 2020).
- [15] —, Point group, Wikipedia, The Free Encyclopedia, https://en.wikipedia.org/wiki/Point_group (accessed on 23 February 2020).
- [16] —, Schoenflies notation, Wikipedia, The Free Encyclopedia, https://en.wikipedia.org/wiki/Schoenflies_notation (accessed on 23 February 2020).
- [17]