Current Address: ]Department of Electrical and Computer Engineering, University of Michigan, Ann Arbor, Michigan 48109, USA
Current Address: ]Department of Physics and James Franck Institute, University of Chicago, Chicago, Illinois 60637, USA
Controlled Creation and Decay of Singly-Quantized Vortices
in a Polar Magnetic Phase
Abstract
We experimentally and theoretically explore the creation and time evolution of vortex lines in the polar magnetic phase of a trapped spin-1 87Rb Bose–Einstein condensate. A process of phase-imprinting a nonsingular vortex, its decay into a pair of singular spinor vortices, and a rapid exchange of magnetic phases creates a pair of three-dimensional, singular singly-quantized vortex lines with core regions that are filled with atoms in the ferromagnetic phase. Atomic interactions guide the subsequent vortex dynamics, leading to core structures that suggest the decay of the singly-quantized vortices into half-quantum vortices.
Vortices in superfluids with internal degrees of freedom, such as those existing within spinor Bose–Einstein condensates (BECs) Kawaguchi and Ueda (2012); Stamper-Kurn and Ueda (2013) and superfluid liquid He-3 Volovik (2003); Vollhardt and Wölfle (1990), exhibit a much richer phenomenology than do simple line vortices in scalar superfluids. Notable examples abound, including vortices with fractional charges Leonhardt and Volovik (2000); Ruostekoski and Anglin (2003); Ji et al. (2008); Lovegrove et al. (2012); Seo et al. (2015); Autti et al. (2016); Kang et al. (2019), vortices with like charges that sum to zero Weiss et al. (2019), vortices with charges that do not commute Kobayashi et al. (2009); Borgh and Ruostekoski (2016); Mawson et al. (2015); Semenoff and Zhou (2007); Barnett et al. (2007); Borgh et al. (2017); Mawson et al. (2019), and nonsingular textures with angular momentum Mizushima et al. (2002); Martikainen et al. (2002); Leanhardt et al. (2003); Leslie et al. (2009); Choi et al. (2012); Lovegrove et al. (2014). These features, inter alia, hint at their highly counter-intuitive dynamics.
The symmetry properties of the superfluid order parameter determine its magnetic phases and topologically permissible vortex excitations Kawaguchi and Ueda (2012); sup . The ground state of a spin-1 system, for example, exhibits two phases: a polar phase, which minimizes the total spin and is characterized by a nematic axis and condensate phase ; and a ferromagnetic (FM) phase, which maximizes the total spin and is characterized by a vector triad. In turn, the ground-state phase of an atomic BEC at zero magnetic field is determined by the nature of the interatomic interactions, which are themselves polar (e.g., in 23Na) or FM (e.g., in 87Rb) Kawaguchi and Ueda (2012). Thus do interactions at the atomic scale influence both the type and destiny of vortices within the condensate.
In the polar phase, a singly-quantized vortex (SQV) with phase winding is unstable against splitting into a pair of half-quantum vortices (HQVs), each with phase winding. This unusual possibility was proposed and analyzed in Ref. Lovegrove et al. (2012) and subsequently observed experimentally within a 23Na BEC in an effectively two-dimensional trapping geometry Seo et al. (2015, 2016). The core of a vortex in superfluid 3He- has similarly been predicted Thuneberg (1986); Salomaa and Volovik (1986) and observed Kondo et al. (1991) to consist of two HQVs; and, more recently, HQVs have been observed in the 3He polar phase Autti et al. (2016).
In this Letter we describe the controlled creation and subsequent time-evolution of a pair of three-dimensional (3D) singular SQVs in the polar phase of a spin-1 87Rb BEC with FM interatomic interactions. In contrast to techniques that randomly nucleate vortices throughout the superfluid by, e.g., stirring Rosenbusch et al. (2002); Neely et al. (2010); Seo et al. (2015) or rapid cooling through the superfluid transition Tilley and Tilley (1990); Weiler et al. (2008); Freilich et al. (2010), our experiment makes use of a deliberately applied strong bending of a nonsingular spin texture to generate a single pair of vortices with polar cores at a specific location within the BEC Weiss et al. (2019). A sudden exchange of the polar and FM phases results in the desired pair of polar SQVs, where the topological interface Borgh and Ruostekoski (2012); Lovegrove et al. (2016) between the two magnetic phases within each vortex core is imaged directly. In a final step, a radio-frequency spinor rotation causes each SQV to evolve towards a pair of HQVs. We numerically model these experimental conditions and show how the FM interactions influence and complicate the decay process as compared with polar interactions.
The theoretical analysis uses the mean-field model for a spin-1 BEC, with Hamiltonian density Kawaguchi and Ueda (2012); Stamper-Kurn and Ueda (2013)
| (1) |
for the spinor wavefunction
| (2) |
expressed in a basis quantized along the axis. Here, is the vector of spin-1 matrices, for atomic mass and radial trap frequency , and is the atomic density. The constants and parameterize the spin-independent and spin-dependent interaction strengths, respectively, and and give the linear and quadratic Zeeman energy shifts due to an applied magnetic field .
The ground state of the system is determined by the sign of the interaction strength and, at fixed magnetization, the quadratic Zeeman term sup . In our experiment , specifying an easy-axis polar (EAP) ground-state phase Kawaguchi and Ueda (2012). We shall see that this introduces significant dynamics when is not aligned with the magnetic field.
The experiment begins with an FM 87Rb condensate of atoms in an optical trap with frequencies . The atoms are exposed to a magnetic field described by
| (3) |
where is the strength of an applied bias field along the axis and is the strength of a 3D quadrupole field produced by a pair of anti-Helmholtz coils. The condensate spin is initially aligned along the axis, represented by the spinor in the space-fixed basis we adopt for the remaining discussion.
We use a phase imprinting process to introduce the polar SQVs, initially following the vortex creation technique introduced in Ref. Weiss et al. (2019). A nonsingular vortex is first created by linearly ramping the magnetic bias field from G to G at G/s, with G/cm. The atomic spins incompletely follow the nonadiabatic reorientation of the magnetic field Nakahara et al. (2000); Pietilä and Möttönen (2009) as its zero passes through the condensate, resulting in the desired spin texture. Immediately afterwards we ramp the field to its minimum value G in 10 ms, eliminate the magnetic quadrupole contribution , and adiabatically reorient the field to 1 G along the axis. In the subsequent 100 ms, the tight bending of the magnetization causes the nonsingular vortex to decay into two singular vortices in the FM phase, each described in this basis by , taking to be the azimuthal angle around each vortex line.
In scalar superfluids a singular defect implies that the superfluid density at the singularity vanishes, but in spinor BECs it is energetically favorable to accommodate the singularity by filling the vortex core with atoms in a different magnetic phase when the spin-dependent interaction is weaker than the spin-independent one Ruostekoski and Anglin (2003); Lovegrove et al. (2012); Kobayashi et al. (2012). The vortex core regions in our experiment contain atoms in the nonrotating polar phase, described by , as shown in Fig. 1(b). These exhibit a coherent, stable topological interface between the two distinct magnetic phases Borgh and Ruostekoski (2012); Lovegrove et al. (2016), where the magnetic phase changes continuously within the vortex core. Analogous topological interfaces are universal across many areas of physics, ranging from superfluid liquid 3He Finne et al. (2006); Bradley et al. (2008) to early-universe cosmology and superstring theory Kibble (1976); Sarangi and Tye (2002), as well as to exotic superconductivity Bert et al. (2011).
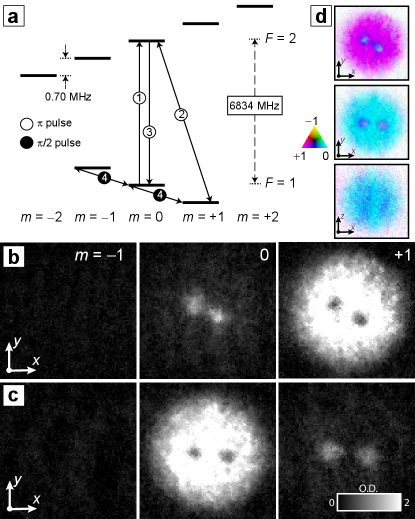
The next step in the SQV creation process is the rapid exchange of the polar and FM phases. For the texture described above this amounts to swapping the and spinor components with a sequence of three microwave pulses, as shown in Fig. 1(a). Afterwards, the topological interface between magnetic phases in the vortex core is reversed: along each singularity the atoms attain the pure FM phase, , while the surrounding circulating bulk superfluid is in the polar phase, . These features are clearly seen in Fig. 1(c). Creation of this novel vortex state using the magnetic phase exchange technique is one of the principal results of the present study.

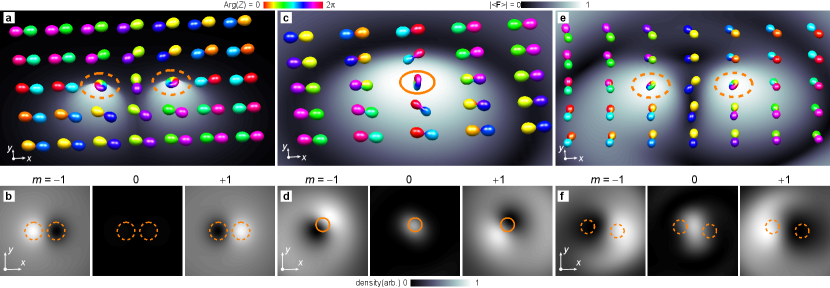
We model the two polar SQVs and their FM cores numerically in 3D [Fig. 2(a)]. Each vortex in the figure represents a polar SQV with a filled core. Analytically, the spinor representing both the vortex and its FM core can be constructed as Lovegrove et al. (2016)
| (4) |
where parameterizes the interpolation between the polar and FM phases as varies from in the bulk to on the vortex line. Here again denotes the azimuthal angle around the vortex line, whereas is the polar angle that determines the order-parameter orientation, varying from away from the vortex line to on the line singularity itself. The initial state is modeled numerically and shown in Fig. 2(a,b).
Although the spontaneous breaking of the defect core symmetry in the polar phase and the emergence of HQVs depend nontrivially on the relative interaction strength Ruostekoski and Anglin (2003); Shinn and Fischer (2018); Underwood et al. (2020), this dependence can easily be obscured by the density gradients in a harmonically trapped BEC. Of additional significance is the effect of the applied magnetic field, which can restore the vortex core isotropy at sufficiently high and suppress the decay into HQVs at sufficiently high Borgh et al. (2016); Underwood et al. (2020). We find empirically that an applied bias magnetic field of 1 G is sufficient to inhibit evolution of the experimental SQV state depicted in Fig. 1(c) towards HQVs.
To induce condensate dynamics, we therefore apply a -pulse within the manifold to rotate both the nematic director (in the polar phase) and the condensate spin (in the FM phase) into the plane. The spinor rotation can be understood by describing a single SQV as a vortex line in the component with core filled by atoms in the component. Under a spinor rotation about the axis, the spinor transforms as
| (5) |
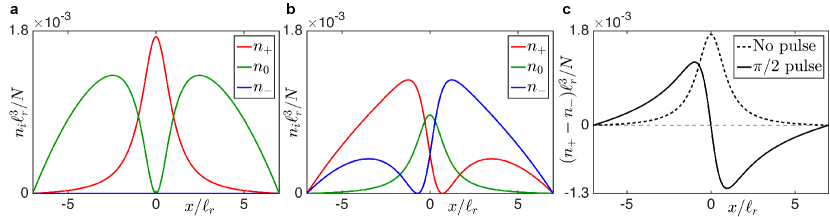
where approximates the vortex-core profile with size parameterized by . After the rotation, density maxima in the component appear at the locations of the vortex cores, each bracketed by symmetrically displaced density minima in the spinor components. These spatially offset phase singularities result from the sum of FM and polar terms of the initial spinor that transform differently within the vortex core Weiss et al. (2019); sup . We experimentally observe these principal features immediately after the pulse [Fig. 3(a)].
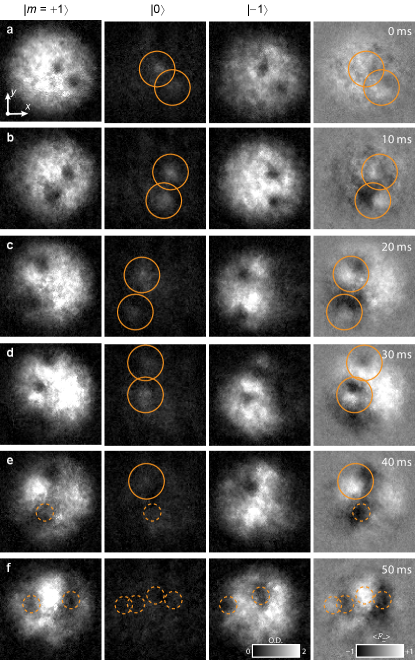
As the system evolves, the spatial separation between the phase singularities associated with both SQVs increase, and each phase singularity grows in size as it fills with fluid in the (or, for the other of the pair, ) spinor component (Fig. 3). These effects can be seen in the emergence of sharply defined proximate bright and dark regions in the total longitudinal magnetization density sup , shown in the rightmost column of Fig. 3, as well as directly from the locations of the density minima within the spinor components. The density of the spinor component also becomes more diffuse as the core region of each SQV grows.
We numerically simulate the dynamics using the coupled Gross–Pitaevskii equations derived from Eq. (1), also employing an algorithm to restore the conservation of longitudinal magnetization Lovegrove et al. (2014) in the presence of a small phenomenological dissipation. The resulting evolved state is shown in Fig. 2(e–f) where the pair of phase singularities associated with each SQV has formed a split pair of HQVs. In the simulation, the fully separated FM cores and the symmetry representation of the wavefunction shown in Fig. 2(e–f) permit straightforward identification of the HQVs. Once separated, the characteristic size of the filled regions is theoretically established by the spin healing length Lovegrove et al. (2012); Ruostekoski and Anglin (2003), which is much larger than the density healing length.
Connecting the experimentally obtained spinor component densities to the corresponding vortex states in the simulation requires some care, especially with respect to the presence of the spinor component. For the given magnetic field direction and the idealized case of a condensate with polar interactions in the easy-plane polar regime sup , an empty-core SQV splits into two spatially offset phase singularities in the spinor components and the component remains absent. These phase singularities are unambiguously HQVs, each surrounded by polar fluid where remains in the plane. For FM interactions in the EAP regime, however, the presence of the phase singularities in regions where the component is nonzero can indicate either the existence of nonzero transverse spin within the unsplit SQV core [Fig. 2(c–d)], or the rotation of out of the plane in a fully split pair of HQVs [Fig. 2(e–f)]. Only the disappearance of the spinor component in the experimental images, implying fully longitudinal spin domains with a director that remains in the plane, conclusively announces the presence of two HQV. This is approximately the situation in Fig. 3(e–f).
There are several effects that conspire to complicate the experimental interpretation of our results. First, the offset phase singularities of the two initial singular vortices may closely approach one another, making their disambiguation problematic. The approximate SQV locations may often be located by identifying density maxima in the spinor component, as shown in Fig. 3(a–d). The presence of a small and consistent but uncontrolled magnetic field gradient globally shifts the spinor components with respect to one another, creating less sharply defined regions of opposite magnetization on a size scale comparable to that of the condensate. This effect is most pronounced in Fig. 3(c,d), where the () spinor component is shifted to the right (left). Nevertheless, the vortices may often be located by identifying the density minima associated with the offset phase singularities in the spinor components, as suggested by the dashed circles in Fig. 3(e) and (f). The singularities can still be difficult to discern if they are near the edge of the condensate, if they are tilted with respect to the imaging axis, or if they exhibit longitudinal (Kelvin wave) excitations Bretin et al. (2003). One of the expected singularities in Fig. 3(e) likely cannot be cleanly identified as a result of one or more of these 3D effects.
We have implemented a controllable technique of rapid magnetic phase exchange to facilitate the controlled creation of a pair of singular SQVs with nonrotating FM cores in the polar magnetic phase of a spin-1 superfluid with FM interatomic interactions. Our experimental and theoretical analysis of the decay process in three dimensions suggests the emergence of HQVs. Similar techniques may be used to generate pairs of filled-core vortices in the magnetic phases of spin-2 condensates, where vortex collisions are predicted to possess a non-Abelian character Kobayashi et al. (2009); Borgh and Ruostekoski (2016); Semenoff and Zhou (2007); Mawson et al. (2019) and for which the topological interfaces may lead to exotic phenomena such as vortices with triangular cores Borgh and Ruostekoski (2016).
Acknowledgements.
We gratefully acknowledge experimental assistance and helpful conversations with T. Ollikainen. D.S.H. acknowledges financial support from the National Science Foundation (Grant No. PHY–1806318.) and J.R. from the UK EPSRC (Grant Nos. EP/P026133/1, EP/M013294/1).References
- Kawaguchi and Ueda (2012) Yuki Kawaguchi and Masahito Ueda, “Spinor Bose–Einstein condensates,” Phys. Rep. 520, 253–382 (2012).
- Stamper-Kurn and Ueda (2013) Dan M. Stamper-Kurn and Masahito Ueda, “Spinor Bose gases: Symmetries, magnetism, and quantum dynamics,” Rev. Mod. Phys. 85, 1191–1244 (2013).
- Volovik (2003) Grigory E. Volovik, The Universe in a Helium Droplet (Oxford University Press, 2003).
- Vollhardt and Wölfle (1990) Dieter Vollhardt and Peter Wölfle, The Superfluid Phases of Helium 3 (Taylor & Francis Ltd, London, UK, 1990).
- Leonhardt and Volovik (2000) U. Leonhardt and G. Volovik, “How to create an Alice string (half-quantum vortex) in a vector Bose–Einstein condensate,” JETP Lett. 72, 46–48 (2000).
- Ruostekoski and Anglin (2003) J. Ruostekoski and J. R. Anglin, “Monopole core instability and Alice rings in spinor Bose–Einstein condensates,” Phys. Rev. Lett. 91, 190402 (2003).
- Ji et al. (2008) An-Chun Ji, W. M. Liu, Jun Liang Song, and Fei Zhou, “Dynamical creation of fractionalized vortices and vortex lattices,” Phys. Rev. Lett. 101, 010402 (2008).
- Lovegrove et al. (2012) Justin Lovegrove, Magnus O. Borgh, and Janne Ruostekoski, “Energetically stable singular vortex cores in an atomic spin-1 Bose–Einstein condensate,” Phys. Rev. A 86, 013613 (2012).
- Seo et al. (2015) Sang Won Seo, Seji Kang, Woo Jin Kwon, and Yong-il Shin, “Half-quantum vortices in an antiferromagnetic spinor Bose–Einstein condensate,” Phys. Rev. Lett. 115, 015301 (2015).
- Autti et al. (2016) S. Autti, V. V. Dmitriev, J. T. Mäkinen, A. A. Soldatov, G. E. Volovik, A. N. Yudin, V. V. Zavjalov, and V. B. Eltsov, “Observation of half-quantum vortices in topological superfluid ,” Phys. Rev. Lett. 117, 255301 (2016).
- Kang et al. (2019) Seji Kang, Sang Won Seo, Hiromitsu Takeuchi, and Y. Shin, “Observation of wall-vortex composite defects in a spinor Bose–Einstein condensate,” Phys. Rev. Lett. 122, 095301 (2019).
- Weiss et al. (2019) L. S. Weiss, M. O. Borgh, A. Blinova, T. Ollikainen, M. Möttönen, J. Ruostekoski, and D. S. Hall, “Controlled creation of a singular spinor vortex by circumventing the Dirac belt trick,” Nat. Commun. 10, 4772 (2019).
- Kobayashi et al. (2009) Michikazu Kobayashi, Yuki Kawaguchi, Muneto Nitta, and Masahito Ueda, “Collision dynamics and rung formation of non-Abelian vortices,” Phys. Rev. Lett. 103, 115301 (2009).
- Borgh and Ruostekoski (2016) Magnus O. Borgh and Janne Ruostekoski, “Core structure and non-Abelian reconnection of defects in a biaxial nematic spin-2 Bose–Einstein condensate,” Phys. Rev. Lett. 117, 275302 (2016).
- Mawson et al. (2015) Thomas Mawson, Gary Ruben, and Tapio Simula, “Route to non-Abelian quantum turbulence in spinor Bose–Einstein condensates,” Phys. Rev. A 91, 063630 (2015).
- Semenoff and Zhou (2007) Gordon W. Semenoff and Fei Zhou, “Discrete symmetries and –quantum vortices in condensates of cold atoms,” Phys. Rev. Lett. 98, 100401 (2007).
- Barnett et al. (2007) Ryan Barnett, Ari Turner, and Eugene Demler, “Classifying vortices in Bose–Einstein condensates,” Phys. Rev. A 76, 013605 (2007).
- Borgh et al. (2017) Magnus O. Borgh, Justin Lovegrove, and Janne Ruostekoski, “Internal structure and stability of vortices in a dipolar spinor Bose–Einstein condensate,” Phys. Rev. A 95, 053601 (2017).
- Mawson et al. (2019) T. Mawson, T. C. Petersen, J. K. Slingerland, and T. P. Simula, “Braiding and fusion of non-abelian vortex anyons,” Phys. Rev. Lett. 123, 140404 (2019).
- Mizushima et al. (2002) T. Mizushima, K. Machida, and T. Kita, “Mermin–Ho vortex in ferromagnetic spinor Bose–Einstein condensates,” Phys. Rev. Lett. 89, 030401 (2002).
- Martikainen et al. (2002) J.-P. Martikainen, A. Collin, and K.-A. Suominen, “Coreless vortex ground state of the rotating spinor condensate,” Phys. Rev. A 66, 053604 (2002).
- Leanhardt et al. (2003) A. E. Leanhardt, Y. Shin, D. Kielpinski, D. E. Pritchard, and W. Ketterle, “Coreless vortex formation in a spinor Bose–Einstein condensate,” Phys. Rev. Lett. 90, 140403 (2003).
- Leslie et al. (2009) L. S. Leslie, A. Hansen, K. C. Wright, B. M. Deutsch, and N. P. Bigelow, “Creation and detection of skyrmions in a Bose–Einstein condensate,” Phys. Rev. Lett. 103, 250401 (2009).
- Choi et al. (2012) Jae-yoon Choi, Woo Jin Kwon, Moonjoo Lee, Hyunseok Jeong, Kyungwon An, and Yong-il Shin, “Imprinting skyrmion spin textures in Bose–Einstein condensates,” New J. Phys. 14, 053013 (2012).
- Lovegrove et al. (2014) Justin Lovegrove, Magnus O. Borgh, and Janne Ruostekoski, “Energetic stability of coreless vortices in spin-1 Bose–Einstein condensates with conserved magnetization,” Phys. Rev. Lett. 112, 075301 (2014).
- (26) See Supplemental Material for details, which includes Refs. Ho (1998); Ohmi and Machida (1998); Leonhardt and Volovik (2000); Zhou (2001, 2003); Lovegrove et al. (2012); Zhang et al. (2003); Murata et al. (2007); Sadler et al. (2006); Ruostekoski and Dutton (2007); Javanainen and Ruostekoski (2006); Lovegrove et al. (2014).
- Seo et al. (2016) Sang Won Seo, Woo Jin Kwon, Seji Kang, and Y. Shin, “Collisional dynamics of half-quantum vortices in a spinor Bose–Einstein condensate,” Phys. Rev. Lett. 116, 185301 (2016).
- Thuneberg (1986) E. V. Thuneberg, “Identification of vortices in superfluid 3He-,” Phys. Rev. Lett. 56, 359–362 (1986).
- Salomaa and Volovik (1986) M. M. Salomaa and G. E. Volovik, “Vortices with spontaneously broken axisymmetry in 3He-,” Phys. Rev. Lett. 56, 363–366 (1986).
- Kondo et al. (1991) Y. Kondo, J. S. Korhonen, M. Krusius, V. V. Dmitriev, Y. M. Mukharsky, E. B. Sonin, and G. E. Volovik, “Direct observation of the nonaxisymmetric vortex in superfluid 3He-,” Phys. Rev. Lett. 67, 81–84 (1991).
- Rosenbusch et al. (2002) P. Rosenbusch, V. Bretin, and J. Dalibard, “Dynamics of a single vortex line in a Bose–Einstein condensate,” Phys. Rev. Lett. 89, 200403 (2002).
- Neely et al. (2010) T. W. Neely, E. C. Samson, A. S. Bradley, M. J. Davis, and B. P. Anderson, “Observation of vortex dipoles in an oblate Bose–Einstein condensate,” Phys. Rev. Lett. 104, 160401 (2010).
- Tilley and Tilley (1990) David R. Tilley and John Tilley, Superfluidity and Superconductivity, 3rd ed. (IOP Publishing Ltd, Bristol, UK, 1990).
- Weiler et al. (2008) C. N. Weiler, T. W. Neely, D. R. Scherer, A. S. Bradley, M. J. Davis, and B. P. Anderson, “Spontaneous vortices in the formation of Bose–Einstein condensates,” Nature 455, 948–951 (2008).
- Freilich et al. (2010) D. V. Freilich, D. M. Bianchi, A. M. Kaufman, T. K. Langin, and D. S. Hall, “Real-time dynamics of single vortex lines and vortex dipoles in a Bose–Einstein condensate,” Science 329, 1182–1185 (2010).
- Borgh and Ruostekoski (2012) Magnus O. Borgh and Janne Ruostekoski, “Topological interface engineering and defect crossing in ultracold atomic gases,” Phys. Rev. Lett. 109, 015302 (2012).
- Lovegrove et al. (2016) Justin Lovegrove, Magnus O. Borgh, and Janne Ruostekoski, “Stability and internal structure of vortices in spin-1 Bose–Einstein condensates with conserved magnetization,” Phys. Rev. A 93, 033633 (2016).
- Nakahara et al. (2000) Mikio Nakahara, Tomoya Isoshima, Kazushige Machida, Shin ichiro Ogawa, and Tetsuo Ohmi, “A simple method to create a vortex in Bose–Einstein condensate of alkali atoms,” Physica B 284–288, 17–18 (2000).
- Pietilä and Möttönen (2009) Ville Pietilä and Mikko Möttönen, “Creation of Dirac monopoles in spinor Bose–Einstein condensates,” Phys. Rev. Lett. 103, 030401 (2009).
- Kobayashi et al. (2012) Shingo Kobayashi, Yuki Kawaguchi, Muneto Nitta, and Masahito Ueda, “Topological classification of vortex-core structures of spin-1 Bose–Einstein condensates,” Phys. Rev. A 86, 023612 (2012).
- Finne et al. (2006) A. P. Finne, V. B. Eltsov, R. Hänninen, N. B. Kopnin, J. Kopu, M. Krusius, M. Tsubota, and G. E. Volovik, “Dynamics of vortices and interfaces in superfluid 3He,” Rep. Prog. Phys. 69, 3157–3230 (2006).
- Bradley et al. (2008) D. I. Bradley, S. N. Fisher, A. M. Guenault, R. P. Haley, J. Kopu, H. Martin, G. R. Pickett, J. E. Roberts, and V. Tsepelin, “Relic topological defects from brane annihilation simulated in superfluid 3He,” Nat. Phys. 4, 46–49 (2008).
- Kibble (1976) T. W. B. Kibble, “Topology of cosmic domains and strings,” J. Phys. A Math. Gen. 9, 1387–1398 (1976).
- Sarangi and Tye (2002) Saswat Sarangi and S.-H. Henry Tye, “Cosmic string production towards the end of brane inflation,” Phys. Lett. B 536, 185–192 (2002).
- Bert et al. (2011) Julie A. Bert, Beena Kalisky, Christopher Bell, Minu Kim, Yasuyuki Hikita, Harold Y. Hwang, and Kathryn A. Moler, “Direct imaging of the coexistence of ferromagnetism and superconductivity at the LaAlO3/SrTiO3 interface,” Nat. Phys. 7, 767–771 (2011).
- Shinn and Fischer (2018) Seong-Ho Shinn and Uwe R. Fischer, “Mesoscopics of half-quantum vortex pair deconfinement in a trapped spin-one condensate,” Phys. Rev. A 98, 053602 (2018).
- Underwood et al. (2020) Andrew P. C. Underwood, D. Baillie, P. Blair Blakie, and H. Takeuchi, “Properties of a nematic spin vortex in an antiferromagnetic spin-1 Bose–Einstein condensate,” arXiv (2020), arXiv:2005.09203 .
- Borgh et al. (2016) Magnus O. Borgh, Muneto Nitta, and Janne Ruostekoski, “Stable core symmetries and confined textures for a vortex line in a spinor Bose–Einstein condensate,” Phys. Rev. Lett. 116, 085301 (2016).
- Bretin et al. (2003) V. Bretin, P. Rosenbusch, F. Chevy, G. V. Shlyapnikov, and J. Dalibard, “Quadrupole oscillation of a single-vortex Bose–Einstein condensate: Evidence for Kelvin modes,” Phys. Rev. Lett. 90, 100403 (2003).
- Ho (1998) Tin-Lun Ho, “Spinor Bose condensates in optical traps,” Phys. Rev. Lett. 81, 742–745 (1998).
- Ohmi and Machida (1998) Tetsuo Ohmi and Kazushige Machida, “Bose–Einstein condensation with internal degrees of freedom in alkali atom gases,” J. Phys. Soc. Jpn. 67, 1822–1825 (1998).
- Zhou (2001) Fei Zhou, “Spin correlation and discrete symmetry in spinor bose-einstein condensates,” Phys. Rev. Lett. 87, 080401 (2001).
- Zhou (2003) Fei Zhou, “Quantum spin nematic states in Bose–Einstein condensates,” Int. J. Mod. Phys. B 17, 2643–2698 (2003).
- Zhang et al. (2003) Wenxian Zhang, Su Yi, and Li You, “Mean field ground state of a spin-1 condensate in a magnetic field,” New J. Phys. 5, 77 (2003).
- Murata et al. (2007) Keiji Murata, Hiroki Saito, and Masahito Ueda, “Broken-axisymmetry phase of a spin-1 ferromagnetic Bose–Einstein condensate,” Phys. Rev. A 75, 013607 (2007).
- Sadler et al. (2006) L. E. Sadler, J. M. Higbie, S. R. Leslie, M. Vengalattore, and D. M. Stamper-Kurn, “Spontaneous symmetry breaking in a quenched ferromagnetic spinor Bose–Einstein condensate,” Nature 443, 312–315 (2006).
- Ruostekoski and Dutton (2007) J. Ruostekoski and Zachary Dutton, “Dynamical and energetic instabilities in multicomponent Bose–Einstein condensates in optical lattices,” Phys. Rev. A 76, 063607 (2007).
- Javanainen and Ruostekoski (2006) Juha Javanainen and Janne Ruostekoski, “Symbolic calculation in development of algorithms: split-step methods for the Gross–Pitaevskii equation,” J Phys A: Math Gen 39, L179–L184 (2006).
Supplemental Material for “Controlled Creation and Decay of Singly-Quantized Vortices in a Polar Magnetic Phase”
I Magnetic Phases
The two distinct ground-state phases in a spin-1 Bose–Einstein condensate at zero field are determined by the sign of the spin-dependent atomic interaction parameter in Eq. (1). For (e.g., for 87Rb) the system energy is maximized for , resulting in a ferromagnetic (FM) order-parameter space characterized by the group of 3D rotations, Ho (1998); Ohmi and Machida (1998). Contrariwise, for (e.g., for 23Na) the system energy is minimized for , resulting in a uniaxial nematic (polar) order-parameter space characterized by with local phase and nematic axis Leonhardt and Volovik (2000); Zhou (2001, 2003). Here, the two-element factor group appears due to the symmetry . It is this symmetry that permits vortices in the polar phase to carry half-integer circulation when runs between and around the vortex singularity and concurrently rotates by .
At stronger fields with fixed magnetization the quadratic Zeeman term becomes important for determining the ground state Zhang et al. (2003); Murata et al. (2007); Sadler et al. (2006); Ruostekoski and Dutton (2007), and within the polar phase itself there arise two relevant phases: the easy-axis polar (EAP), where is aligned with an applied magnetic field, and the easy-plane polar (EPP), where is perpendicular to the applied magnetic field. In our experiment , specifying an EAP ground-state phase.
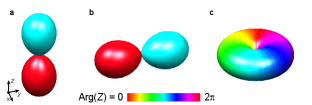
The order parameter symmetry in Fig. 2 is represented by the surface of , where expands the spinor in terms of the spherical harmonics , with local spherical coordinates , and gauge color given by . Simple examples of the polar and FM ground-state phases are shown in Fig. S-1.
II Vortex Lines in Three Dimensions
The Bose–Einstein condensate in our experiment is mildly oblate, as it is confined in a harmonic potential with trap frequencies . As a result, the vortices are lines in three dimensions rather than the points associated with highly oblate, quasi two-dimensional condensates. Several representative images of the expanded condensates, taken simultaneously from both the top and side, are shown in Fig. S-2.
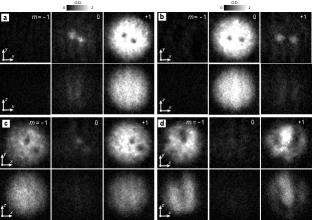
III Additional Numerical Simulations
We illustrate here some of the complications that arise in the interpretation of the experimental SQV evolution images with the help of Gross–Pitaevskii (GP) simulations of energy relaxation and dynamics of a single SQV. The GP equations are derived from Eq. (1) of the main text, in which the trap parameters are also defined. The simulations integrate the GP equations using the split-step method Javanainen and Ruostekoski (2006) and an algorithm to conserve the longitudinal magnetization Lovegrove et al. (2014).
Pure energy relaxation (i.e., propagation of the GP equations in imaginary time) for a single SQV in a 23Na BEC in the EPP regime provides the reference scenario [Fig. S-3(a)]. The vortex in this case is known to relax into a pair of HQVs Lovegrove et al. (2012). The HQVs are readily identified in the simulation by the order-parameter symmetry, also showing continuous deformation to the FM vortex core. The vector remains everywhere in the plane, yielding a completely depopulated spinor component and equal bulk densities in the components. The vortices appear in the form first proposed by Leonhardt and Volovik Leonhardt and Volovik (2000), as offset phase singularities in the populated components. In this case the HQVs can conversely be inferred directly from the component images where the spinor component vanishes, as this corresponds directly to the -component of .
As noted in the main text, however, the presence of the spinor component in the experimental images does not determine whether an SQV has split into two HQVs. By way of further numerical illustration we consider the time evolution of an SQV prepared initially in the EPP phase, but in a 87Rb BEC with (FM atom-atom interactions). Dissipation, included here phenomenologically by taking (where ) in the GP equations, causes the condensate to evolve towards the FM phase; on the other hand, the Zeeman energy favors rotating out of the plane. Both effects may lead to a nonzero density remaining in the component, which can correspond to either an unsplit SQV [Fig. S-3(b)] or two separated HQVs, where rotates out of the plane between the vortex lines [Fig. S-3(c)].
We further illustrate the experimental signatures by analytically modeling the effect of the -pulse applied to rotate the BEC from the EAP into the EPP phase immediately after initial preparation of the SQVs. We assume that the condensate away from the vortex core is exactly in these phases before and after the -pulse, respectively, which is a good approximation of the experimental situation. Figure S-4 corresponds directly to Eq. (5) in the main text, showing the spinor component density profiles for a single SQV before and after the -pulse. The spin rotation itself results in offset phase singularities in the components with non-zero at the vortex singularity between them, illustrating that the presence of the offset phase singularities alone does not imply splitting of the SQV. This effect is seen in the experiment in Fig. 3(a)–(d) in the main text. The pulse also rotates the condensate spin inside the vortex core resulting in offset, oppositely polarized peaks in the longitudinal magnetization density, presented as in Fig. S-4(c), that coincide with the phase singularities. These peaks thus appear before any splitting of the SQV has taken place. After the splitting the peaks locate the HQV cores, but are not in themselves complete evidence of the splitting.