Controllable transitions among phase-matching conditions in a single nonlinear crystal
Abstract
Entangled photon pairs are crucial resources for quantum information processing protocols. Via the process of spontaneous parametric down-conversion (SPDC), we can generate these photon pairs using bulk nonlinear crystals. Traditionally, the crystal is designed to satisfy specific type of phase-matching condition. Here, we report controllable transitions among different types of phase-matching in a single periodically poled potassium titanyl phosphate (PPKTP) crystal. By carefully selecting pump conditions, we can satisfy different phase-matching conditions. This allows us to observe first-order type-II, fifth-order type-I, third-order type-0, and fifth-order type-II SPDCs. The temperature-dependent spectra of our source were also analyzed in detail. Finally, we discussed the possibility of observing more than nine SPDCs in this crystal. Our work not only deepens the understanding of the physics behind phase-matching conditions, but also offers the potential for a highly versatile entangled biphoton source for quantum information research.
I Introduction
Quantum light sources, including single-photon sources and entangled photon sources, are fundamental resources for the study of quantum information processing Anwar et al. (2021); Zhang et al. (2022).One of the most widely used methods for preparing quantum light sources is spontaneous parametric down-conversion (SPDC) in a nonlinear optical crystal Christ et al. (2013); Zhang et al. (2021a).In an SPDC process, a pump photon interacts with a nonlinear crystal and is converted into a biphoton, which is a pair of correlated photons usually referred to as the signal and idler. The biphotons can be further engineered to prepare heralded single photon source or entangled photon source. The SPDC process can be engineered in different degrees of freedom, such as space, time, frequency, polarization, and phase Morrison et al. (2022); Zhu et al. (2023).
According to the polarization of the pump, signal and idler photons, the phase-matching conditions in nonlinear SPDC can be classified into three types: Type-0: HHH, or VVV; Type-I: HVV, or VHH;Type-II: HHV, or VHV.Here, “H” and “V” represent the horizontal and vertical polarizations respectively Dmitriev et al. (2013). In the type-0 and type-I cases, the signal and idler photons have the same polarization, resulting in broad spectral distributions and narrow temporal distributions. This feature of broad spectra is advantageous in quantum metrology Nielsen et al. (2023); Reisner et al. (2022), quantum optical coherence tomography Hayama et al. (2022), and quantum spectroscopy Tabakaev et al. (2021); Chen et al. (2021). Furthermore, the type-0 matching condition has the highest effective nonlinear coefficient among all three nonlinear phase-matching conditions Dmitriev et al. (2013). In the type-II cases, the signal and idler photons usually have much narrower spectra and have been widely used to perform quantum communication, computation, and measurement Yin et al. (2017a); Zhong et al. (2020); Lyons et al. (2018); Guo et al. (2023). Another important feature of the type-II matching condition is that the joint spectral distribution of biphotons can be engineered according to the group velocity differences Edamatsu et al. (2011). As a result, one can prepare photon pair sources with engineerable frequency correlation Graffitti et al. (2020); Morrison et al. (2022); Zhu et al. (2023).
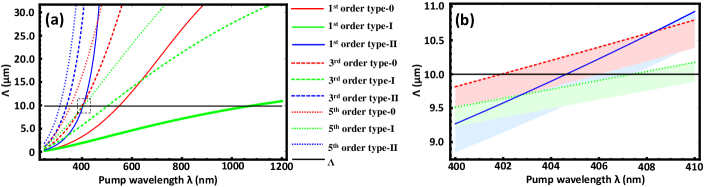
Traditionally, one crystal is usually designed to satisfy only one specific phase-matching condition for quantum information processing protocols. For different protocols, one may need different crystals supporting different phase-matching conditions. Previous works have demonstrated the possibility to realize two SPDC processes in a single PPKTP crystal. These studies were limited to only type-II and type-0 phase-matching conditions, and the detailed properties of such sources are unclear Lee et al. (2012); Steinlechner et al. (2014); Chen et al. (2009); Laudenbach et al. (2017). In this work, we demonstrate controllable transitions among all types of phase-matching in a single nonlinear crystal. Specifically, we find that a periodically poled potassium titanyl phosphate (PPKTP) with a poling period of 10 m can realize all three types of phase-matching conditions simultaneously at pump wavelengths around 405 nm. We observed first-order type-II (at 404.3 nm), fifth-order type-I (at 404.3 nm), third-order type-0 (at 408.8 nm), and fifth-order type-II (at 315 nm) phase-matching conditions. More importantly, the design principles, detailed spectra and tuning curves in our sources are revealed for future references. Our work may provide a versatile biphoton source for diverse tasks in quantum information technology.
| Poling order | Phase-matching | Polarization | Pump | Signal | Idler | ||
| Type-0 | 550.82 | 1101.65 | 1101.65 | ||||
| Type-I | 1070.91 | 2141.82 | 2141.82 | ||||
| Type-II | 404.63 | 809.27 | 809.27 | ||||
| Type-0 | 401.92 | 803.84 | 803.84 | 10 | |||
| Type-I | 505.21 | 1010.41 | 1010.41 | ||||
| Type-II | 338.73 | 677.45 | 677.45 | ||||
| Type-0 | 354.97 | 709.94 | 709.94 | ||||
| Type-I | 407.37 | 814.73 | 814.73 | ||||
| Type-II | 311.43 | 622.86 | 622.86 |
II Theory
In the process of an SPDC, the energy conservation law is satisfied and is given as
| (1) |
where is the angular frequency and the subscripts , , and denote the pump, signal, and idler, respectively. The momentum conservation law is also satisfied and can be expressed in the form of phase-matching function (PMF). For quasi-phase-matched (QPM) crystals, the PMF is given by
| (2) |
where is the wave vector, is the poling period, and is the poling order.
In a PPKTP crystal, the photons are usually designed to propagate along the x-direction but polarize in the y- and z-directions. Here, we assign y-direction to H polarization and z-direction to V polarization. Using the Sellmeier equations of KTP from Ref.Fan et al. (1987) for refractive index , Ref.Fradkin et al. (1999) for , and Ref.Emanueli and Arie (2003) for temperature-dependent dispersion, the PMF in Eq. 2 can be calculated.
In Fig. 1(a), we show the relation between pump wavelength and poling period with nine different combinations of poling order and phase-matching type. Tab. LABEL:Tab:1 shows the specific wavelength values of the cross points in Fig. 1(a). Notably, there are three SPDC processes near the wavelength of 405 nm. We inspect these three phase-matching conditions further in Fig. 1(b) by zooming in the wavelength range between 400 nm and 410 nm. We can confirm that the cross points are at the pump wavelengths of 401.9 nm (-order type-0), 404.6 nm (-order type-II), and 407.4 nm (-order type-I). This feature allows us to achieve a controllable transition among type-0, type-I, and type-II phase matching condition by tuning the pump wavelength in a small range between 401 nm and 408 nm. Moreover, we can adjust the cross points by tuning the temperature of the PPKTP crystal. Finally, we note that our calculation indicates the existence of another experimentally implementable SPDC process of -order type-II at 311.4 nm, as shown in Fig. 1 (a).
The effective nonlinear coefficient is an important parameter for QPM crystals, which could be different for phase-matching conditions of different types and orders. We define as the effective nonlinear coefficient of KTP and as the nonlinear coefficients of PPKTP at the position of . is a square-wave function Boyd (2020); Niu et al. (2023, 2021):
| (3) |
can also be expressed by Fourier series:
| (4) |
where , and can be expressed as
| (5) |
Intuitively speaking, is the spatial frequency of the grating structure of the PPKTP crystal, and is the coefficient of its eigenmode . The detailed derivation of and can be found in the Appendix.
III Experiment and results
| Poling period | 10 m | |||
| Pump wavelength | 404.3 nm | 404.3 nm | 408.8 nm | 315 nm |
| Phase-matching | Type-II | Type-I | Type-0 | Type-II |
| Polarization | HH+V | VH+H | VV+V | HH+V |
| Poling order | ||||
| Tuning range | 30 150 | 50 70 | 50 120 | 30 150 |
| Degenerate temperature | 126.8 | 57.2 | 58.4 | 62.8 |
| SC/CC (cps) | 1.3M/45k | 385k/15k | 5.4M/167k | N/A |
| Theoretical (pm/V) | ||||
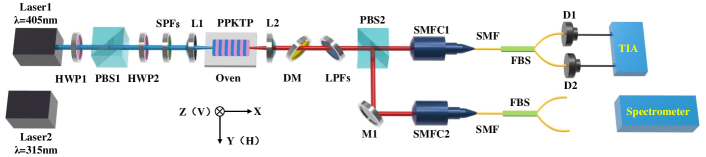
We experimentally verified the existence of these controllable transitions of phase-matching conditions using the experimental setup shown in Fig. 2. We have used two lasers as our pump. The first laser is a narrow-band laser (Kunteng QTechnics) with a tunable center wavelengths of 401-409 nm and a line width of 10 MHz. The second laser is a broadband laser Cai et al. (2022), which has a strong-power portion at 405 nm and a weak-power portion at around 315 nm. During our experiment, we control the pump power using a half-wave plate (HWP) and a polarizing beam splitter (PBS). By adding another HWP after the PBS, we can also control the polarization of the pump beam. Then the pump laser is filtered by a short-pass filter and then focused by a lens (L1, with a focal length of f = 50 mm) onto a temperature controlled 10-mm-long PPKTP crystal. Our PPKTP crystal has a poling period of 10 m, which is originally designed for a type-II phase-matched SPDC at 810 nm. The down-converted biphotons are collimated by the second lens (L2, f = 50 mm) and then filtered by a dichroic mirror and a long-pass filter. Then, these biphotons are separated by the PBS and 50:50 fiber beam splitter (FBS) which directs the photons to two avalanche photodiodes (APDs). Finally, we analyze the properties of these SPDC processes using a time-interval analyzer (Picoharp 300, PicoQuant) for single and coincidence counts. Moreover, the spectra of these biphotons are measured using a single-photon level spectrometer (SP2300, Princeton Instrument).
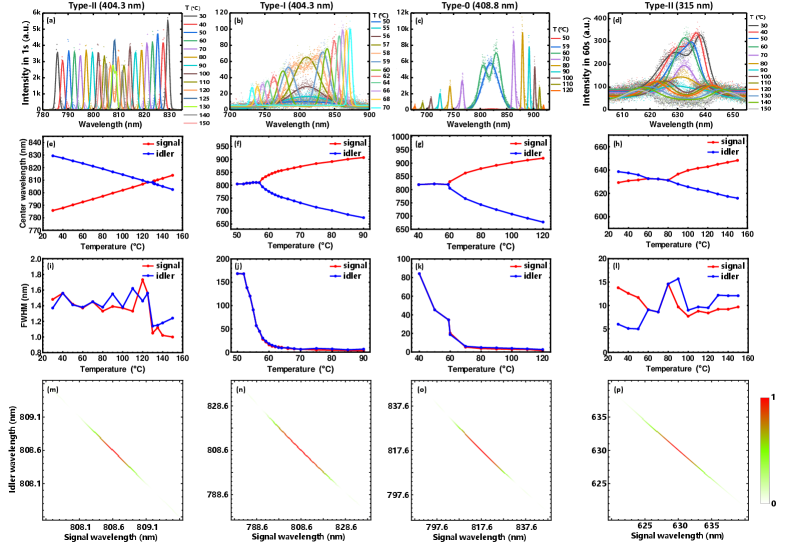
We report the measured single counts (SC) and coincidence counts (CC) in Tab. 1. We also plot the experimentally measured spectra in Fig. 3(a-d). For the -order type-II case, the pump wavelength is set at 404.3 nm, and the polarization is set to be horizontal. In this case, the signal and idler are separated by PBS and then coupled into single-mode fibers, which are connected to two APDs. At the spectral degeneracy temperature of 126.8 , SC and CC are measured to be 1.3 Mcps and 45 kcps, respectively. By adjusting the temperature of the crystal from 30 to 150 , we measured the spectra shown in Fig. 3(a). The center wavelength of the signal and idler photon, as a function of temperature, also known as the tuning curve, is shown in Fig. 3(e).
For the -order type-I case, we kept the pump wavelength at 404.3 nm, but we change the polarization of the pump to vertical. In this case, the signal and idler have the same horizontal polarization (H-polarized). These generated biphotons will transmit through the PBS, and we separate them using a 50:50 FBS to measure SC and CC. In particular, the measured SC and CC are 385 kcps and 15 kcps at the spectral degeneracy temperature of 57.2 . By adjusting the temperature from 50 to 90 , we measured the spectra shown in Fig. 3(b). The tuning curve is shown in Fig. 3(f), which is clearly different from Fig. 3(e).
For -order type-0 case, the pump wavelength is set to 408.8 nm, and the polarization is set to be vertical. The generated vertically-polarized biphotons are reflected by the PBS, collected and separated by another 50:50 FBS, and finally measured by two APDs. At the spectral degeneracy temperature of 58.4 , the SC and CC are 5.4 Mcps and 167 kcps, respectively. In this case, we tune the temperature of the PPKTP crystal from 50 to 120 , and we show the measured spectra in Fig. 3(c). The corresponding tuning curve is shown in Fig. 3(g).
In our final measurement, we use a broadband laser with a central wavelength of 315 nm to implement the -order type-II SPDC process. We note that in this case, the pump power is unknown due to the limitations of our devices. Nevertheless, in this case, the measured spectra and tuning curve are shown in Fig. 3(d) and (h). The measured temperature range is 30 to 150 and the spectral degeneracy temperature is measured to be 62.8 . The observed wavelength of 315 nm slightly deviates from the theoretically calculated value of 311.43 nm, which may indicate that the accuracy of the Sellmeier equation used in the calculations needs further improvement.
As a general observation, we note that the type-II SPDC has a much narrower FWHM than type-I and type-0 SPDC, as also indicated in Fig. 3(i-l).
IV Discussion
To gain a deeper understanding of the biphotons generated under different phase-matching condition, we calculated the joint spectral intensities (JSIs) Jin et al. (2013) under wavelength degenerate condition, as depicted in Fig. 3(m-p). Notably, the JSIs in panel (m-o) are distributed along the anti-diagonal direction. This is attributed to the narrow spectral width of the pump laser, causing the pump envelope function to predominantly shape the JSI. However, in panel (p), the JSI deviates from the anti-diagonal direction. This discrepancy arises from the broader spectral width of the pump laser, causing the phase-matching function to dominate the JSI.
In this experiment, we only observed four SPDC processes as listed in Tab. 1. In the future, it is possible to observe more than nine phase-matching conditions as long as the condition in Eq. 2 is satisfied. Our biphoton source allows for both broadband (type-0 and type-I) and narrowband (type-II) biphoton emission without changing the experimental setup or PPKTP crystal, which is convenient for operations in experiment. In the future, this biphoton source can be upgraded to a polarization-entangled photon source or a time-bin entangled photon source Zhang et al. (2021b); Shen et al. (2023).
One remarkable finding of this study is the observation of three phase-matching conditions matched within a very short pump wavelength range of 401-408 nm. This wavelength range, particularly around 405 nm, holds significant importance for entangled photon sources, being widely utilized not only in laboratory Fedrizzi et al. (2007); Liu et al. (2021); Hong et al. (2023) but also in satellite-based endeavors Yin et al. (2017b). The popularity of this wavelength range can be attributed to the maturity of blue-violet laser technology, which allows the production of high-power blue lasers at relatively affordable costs Jeong et al. (2016); Lohrmann et al. (2020); Cai et al. (2021); Yang et al. (2023); Wang et al. (2020); Zhang et al. (2020). The identification of three phase-matching conditions in this study holds the potential to advance the quantum applications of entangled photon sources utilizing blue lasers and PPKTP crystals.
V Conclusion
Entangled photon pairs are crucial for quantum information processing protocols. The possibility of realizing all three types of SPDC processes in a single PPKTP crystal could be beneficial for future research. Here, we experimentally observed four SPDC processes in a single PPKTP crystal with a poling period of 10 m. These processes include -order type-0, -order type-II, -order type-I, and -order type-II. We have also reported on the properties of these processes, including the coincidence count and thermally dependent spectra. Our scheme can provide a versatile biphoton source for future quantum protocols, as it allows for both broadband (type-0 and type-I) and narrowband (type-II) biphoton sources without changing the experimental setup or PPKTP crystal.
Appendix A: Calculation of for KTP
Here we derive the effective nonlinear coefficient of KTP . In the interaction of strong light with a nonlinear medium, the relationship between the dielectric polarization density and the electric field is nonlinear, and the induced by the medium can be expanded into a power series of . We only consider the second-order case Boyd (2020):
| (6) |
where is the permittivity of free space, is the second-order nonlinear optical susceptibility, and is the tensor product of the electrical field. When the Kleiman symmetry condition is established: . The nonlinear polarizations of the interacting waves in a PPKTP crystal can be given in the form:
| (7) |
where (=, , ) is the component of along the , , and axes; (; ), which is simplified from , represents the nonlinear susceptibility tensor of the KTP crystal. () is the electrical field of the fundamental wave along the , , and axes. For type-II SPDC, , and =. For type-I SPDC, , and =; For type-0 SPDC, , and =. Finally, for PPKTP, pm/V, pm/V, and pm/V Vanherzeele and Bierlein (1992).
Appendix B: Calculation of Fourier coefficient
Here we derive the Fourier coefficient (Eq. 5) in the main text. Considering is a square-wave function:
| (8) |
where denotes the nonlinear coefficient of the KTP and is the poling period of PPKTP.
For arbitrary periodic signals that satisfy the Dirichlet conditions Lanczos and Boyd (2016), they can be rewritten as Fourier series in exponential form:
| (9) |
where
| (10) |
Therefore, the Fourier coefficient of is calculated as follow:
| (11) | ||||
Now, we obtained the value of in Eq. 5 of the main text.
Additionally, can also be expressed in the form of square wave:
For ,
| (12) |
and for (L is the length of crystal),
| (13) |
We note that Eq. 5 can be intuitively understood as the Fourier transform of a square-wave function to a sinc function.
Acknowledgments
We thank Prof. Zhi-Yuan Zhou for helpful discussion. This work was supported by the National Natural Science Foundations of China (Grant Numbers 92365106, 12074299, and 11704290) and the Natural Science Foundation of Hubei Province (2022CFA039).
References
- Anwar et al. (2021) Ali Anwar, Chithrabhanu Perumangatt, Fabian Steinlechner, Thomas Jennewein, and Alexander Ling, “Entangled photon-pair sources based on three-wave mixing in bulk crystals,” Rev. Sci. Instrum. 92, 041101 (2021).
- Zhang et al. (2022) Kai Zhang, Shengshuai Liu, Yingxuan Chen, Xutong Wang, and Jietai Jing, “Optical quantum states based on hot atomic ensembles and their applications,” Photonics Insights 1, R06 (2022).
- Christ et al. (2013) Andreas Christ, Alessandro Fedrizzi, Hannes Hübel, Thomas Jennewein, and Christine Silberhorn, “Parametric down-conversion,” in Experimental Methods in the Physical Sciences (Elsevier, 2013) pp. 351–410.
- Zhang et al. (2021a) Chao Zhang, Yun-Feng Huang, Bi-Heng Liu, Chuan-Feng Li, and Guang-Can Guo, “Spontaneous parametric down-conversion sources for multiphoton experiments,” Adv. Quantum Technol. 4, 2000132 (2021a).
- Morrison et al. (2022) Christopher L. Morrison, Francesco Graffitti, Peter Barrow, Alexander Pickston, Joseph Ho, and Alessandro Fedrizzi, “Frequency-bin entanglement from domain-engineered down-conversion,” APL Photon. 7, 066102 (2022).
- Zhu et al. (2023) Jin-Long Zhu, Wen-Xin Zhu, Xiao-Tao Shi, Chen-Tao Zhang, Xiangying Hao, Zi-Xiang Yang, and Rui-Bo Jin, “Design of mid-infrared entangled photon sources using lithium niobate,” J. Opt. Soc. Am. B 40, A9 (2023).
- Dmitriev et al. (2013) Valentin G Dmitriev, Gagik G Gurzadyan, and David N Nikogosyan, Handbook of nonlinear optical crystals, Vol. 64 (Springer, 2013).
- Nielsen et al. (2023) Jens AH Nielsen, Jonas S Neergaard-Nielsen, Tobias Gehring, and Ulrik L Andersen, “Deterministic quantum phase estimation beyond n00n states,” Phys. Rev. Lett. 130, 123603 (2023).
- Reisner et al. (2022) Mattis Reisner, Florent Mazeas, Romain Dauliat, Baptiste Leconte, Djeylan Aktas, Rachel Cannon, Philippe Roy, Raphael Jamier, Gregory Sauder, Florian Kaiser, et al., “Quantum-limited determination of refractive index difference by means of entanglement,” npj Quantum Inf. 8, 58 (2022).
- Hayama et al. (2022) Kyohei Hayama, Bo Cao, Ryo Okamoto, Shun Suezawa, Masayuki Okano, and Shigeki Takeuchi, “High-depth-resolution imaging of dispersive samples using quantum optical coherence tomography,” Opt. Lett. 47, 4949–4952 (2022).
- Tabakaev et al. (2021) Dmitry Tabakaev, Matteo Montagnese, Geraldine Haack, Luigi Bonacina, J-P Wolf, Hugo Zbinden, and RT Thew, “Energy-time-entangled two-photon molecular absorption,” Phys. Rev. A 103, 033701 (2021).
- Chen et al. (2021) Yuanyuan Chen, Sebastian Ecker, Lixiang Chen, Fabian Steinlechner, Marcus Huber, and Rupert Ursin, “Temporal distinguishability in Hong-Ou-Mandel interference for harnessing high-dimensional frequency entanglement,” npj Quantum Inf. 7, 167 (2021).
- Yin et al. (2017a) Juan Yin, Yuan Cao, Yu-Huai Li, Sheng-Kai Liao, Liang Zhang, Ji-Gang Ren, Wen-Qi Cai, Wei-Yue Liu, Bo Li, Hui Dai, et al., “Satellite-based entanglement distribution over 1200 kilometers,” Science 356, 1140–1144 (2017a).
- Zhong et al. (2020) Han-Sen Zhong, Hui Wang, Yu-Hao Deng, Ming-Cheng Chen, Li-Chao Peng, Yi-Han Luo, Jian Qin, Dian Wu, Xing Ding, Yi Hu, Peng Hu, Xiao-Yan Yang, Wei-Jun Zhang, Hao Li, Yuxuan Li, Xiao Jiang, Lin Gan, Guangwen Yang, Lixing You, Zhen Wang, Li Li, Nai-Le Liu, Chao-Yang Lu, and Jian-Wei Pan, “Quantum computational advantage using photons,” Science 370, 1460–1463 (2020).
- Lyons et al. (2018) Ashley Lyons, George C Knee, Eliot Bolduc, Thomas Roger, Jonathan Leach, Erik M Gauger, and Daniele Faccio, “Attosecond-resolution Hong-Ou-Mandel interferometry,” Sci. Adv. 4, eaap9416 (2018).
- Guo et al. (2023) Yan Guo, Zi-Xiang Yang, Zi-Qi Zeng, Chunling Ding, Ryosuke Shimizu, and Rui-Bo Jin, “Comparison of multi-mode Hong-Ou-Mandel interference and multi-slit interference,” Opt. Express 31, 32849–32864 (2023).
- Edamatsu et al. (2011) Keiichi Edamatsu, Ryosuke Shimizu, Wakana Ueno, Rui-Bo Jin, Fumihiro Kaneda, Masahiro Yabuno, Hirofumi Suzuki, Shigehiro Nagano, Atsushi Syouji, and Koji Suizu, “Photon pair sources with controlled frequency correlation,” Prog. Inform. 8, 19–26 (2011).
- Graffitti et al. (2020) Francesco Graffitti, Peter Barrow, Alexander Pickston, Agata M. Brańczyk, and Alessandro Fedrizzi, “Direct generation of tailored pulse-mode entanglement,” Phys. Rev. Lett. 124, 053603 (2020).
- Lee et al. (2012) H. J. Lee, H. Kim, M. Cha, and H. S. Moon, “Simultaneous type-0 and type-II spontaneous parametric down-conversions in a single periodically poled KTiOPO4 crystal,” Appl. Phys. B 108, 585–589 (2012).
- Steinlechner et al. (2014) Fabian Steinlechner, Marta Gilaberte, Marc Jofre, Thomas Scheidl, Juan P. Torres, Valerio Pruneri, and Rupert Ursin, “Efficient heralding of polarization-entangled photons from type-0 and type-II spontaneous parametric downconversion in periodically poled KTiOPO4,” J. Opt. Soc. Am. B 31, 2068–2076 (2014).
- Chen et al. (2009) Jun Chen, Aaron J. Pearlman, Alexander Ling, Jingyun Fan, and Alan L. Migdall, “A versatile waveguide source of photon pairs for chip-scale quantum information processing,” Opt. Express 17, 6727 (2009).
- Laudenbach et al. (2017) Fabian Laudenbach, Sebastian Kalista, Michael Hentschel, Philip Walther, and Hannes Hübel, “A novel single-crystal single-pass source for polarisation- and colour-entangled photon pairs,” Sci. Rep. 7 (2017), 10.1038/s41598-017-07781-w.
- Fan et al. (1987) Tso Yee Fan, C. E. Huang, B. Q. Hu, R. C. Eckardt, Y. X. Fan, Robert L. Byer, and R. S. Feigelson, “Second harmonic generation and accurate index of refraction measurements in flux-grown KTiOPO4,” Appl. Optics 26, 2390 (1987).
- Fradkin et al. (1999) K. Fradkin, A. Arie, A. Skliar, and G. Rosenman, “Tunable midinfrared source by difference frequency generation in bulk periodically poled KTiOPO4,” Appl. Phys. Lett. 74, 914–916 (1999).
- Emanueli and Arie (2003) Shai Emanueli and Ady Arie, “Temperature-dependent dispersion equations for KTiOPO4 and KTiOAsO4,” Appl. Optics 42, 6661 (2003).
- Boyd (2020) Robert W Boyd, Nonlinear optics (Academic press, 2020).
- Niu et al. (2023) Sujian Niu, Zhiyuan Zhou, Jingxin Cheng, Zheng Ge, Chen Yang, and Baosen Shi, “Multi-color laser generation in periodically poled ktp crystal with single period,” Chin. Opt. Lett. 21, 021901 (2023).
- Niu et al. (2021) Su-Jian Niu, Chen Yang, Yan Li, Zheng Ge, Shi-Kai Liu, Zhi-Yuan Zhou, and Bao-Sen Shi, “Cavity-enhanced frequency doubling with a third-order quasi-phase-matched ppktp crystal,” J. Opt. Soc. Am. B 38, 2775–2779 (2021).
- Cai et al. (2022) Neng Cai, Wu-Hao Cai, Shun Wang, Fang Li, Ryosuke Shimizu, and Rui-Bo Jin, “Broadband-laser-diode pumped periodically poled potassium titanyl phosphate-sagnac polarization-entangled photon source,” J. Opt. Soc. Am. B 39, 77–82 (2022).
- Jin et al. (2013) Rui-Bo Jin, Ryosuke Shimizu, Kentaro Wakui, Hugo Benichi, and Masahide Sasaki, “Widely tunable single photon source with high purity at telecom wavelength,” Opt. Express 21, 10659–10666 (2013).
- Zhang et al. (2021b) Zichang Zhang, Chenzhi Yuan, Si Shen, Hao Yu, Ruiming Zhang, Heqing Wang, Hao Li, You Wang, Guangwei Deng, Zhiming Wang, Lixing You, Zhen Wang, Haizhi Song, Guangcan Guo, and Qiang Zhou, “High-performance quantum entanglement generation via cascaded second-order nonlinear processes,” npj Quantum Inf. 7 (2021b), 10.1038/s41534-021-00462-7.
- Shen et al. (2023) Si Shen, Chenzhi Yuan, Zichang Zhang, Hao Yu, Ruiming Zhang, Chuanrong Yang, Hao Li, Zhen Wang, You Wang, Guangwei Deng, Haizhi Song, Lixing You, Yunru Fan, Guangcan Guo, and Qiang Zhou, “Hertz-rate metropolitan quantum teleportation,” Light: Sci. Appl. 12 (2023), 10.1038/s41377-023-01158-7.
- Fedrizzi et al. (2007) Alessandro Fedrizzi, Thomas Herbst, Andreas Poppe, Thomas Jennewein, and Anton Zeilinger, “A wavelength-tunable fiber-coupled source of narrowband entangled photons,” Opt. Express 15, 15377–15386 (2007).
- Liu et al. (2021) Yi-Chen Liu, Dong-Jie Guo, Ran Yang, Chang-Wei Sun, Jia-Chen Duan, Yan-Xiao Gong, Zhenda Xie, and Shi-Ning Zhu, “Narrowband photonic quantum entanglement with counterpropagating domain engineering,” Photon. Res. 9, 1998–2005 (2021).
- Hong et al. (2023) Ling Hong, Yuning Zhang, Yuanyuan Chen, and Lixiang Chen, “Fast quantifier of high-dimensional frequency entanglement through hong–ou–mandel interference,” Adv. Quantum Technol. 6 (2023), 10.1002/qute.202300012.
- Yin et al. (2017b) Juan Yin, Yuan Cao, Yu-Huai Li, Sheng-Kai Liao, Liang Zhang, Ji-Gang Ren, Wen-Qi Cai, Wei-Yue Liu, Bo Li, Hui Dai, Guang-Bing Li, Qi-Ming Lu, Yun-Hong Gong, Yu Xu, Shuang-Lin Li, Feng-Zhi Li, Ya-Yun Yin, Zi-Qing Jiang, Ming Li, Jian-Jun Jia, Ge Ren, Dong He, Yi-Lin Zhou, Xiao-Xiang Zhang, Na Wang, Xiang Chang, Zhen-Cai Zhu, Nai-Le Liu, Yu-Ao Chen, Chao-Yang Lu, Rong Shu, Cheng-Zhi Peng, Jian-Yu Wang, and Jian-Wei Pan, “Satellite-based entanglement distribution over 1200 kilometers,” Science 356, 1140–1144 (2017b).
- Jeong et al. (2016) Youn-Chang Jeong, Kang-Hee Hong, and Yoon-Ho Kim, “Bright source of polarization-entangled photons using a PPKTP pumped by a broadband multi-mode diode laser,” Opt. Express 24, 1165 (2016).
- Lohrmann et al. (2020) Alexander Lohrmann, Chithrabhanu Perumangatt, Aitor Villar, and Alexander Ling, “Broadband pumped polarization entangled photon-pair source in a linear beam displacement interferometer,” Appl. Phys. Lett. 116 (2020), 10.1063/1.5124416.
- Cai et al. (2021) Neng Cai, Wu-Hao Cai, Shun Wang, Fang Li, Ryosuke Shimizu, and Rui-Bo Jin, “Broadband-laser-diode pumped periodically poled potassium titanyl phosphate-sagnac polarization-entangled photon source,” J. Opt. Soc. Am. B 39, 77 (2021).
- Yang et al. (2023) Zi-Xiang Yang, Zi-Qi Zeng, Ying Tian, Shun Wang, Ryosuke Shimizu, Hao-Yu Wu, Shilong Liu, and Rui-Bo Jin, “Spatial–spectral mapping to prepare frequency entangled qudits,” Opt. Lett. 48, 2361 (2023).
- Wang et al. (2020) Wei Wang, Kai Zhang, and Jietai Jing, “Large-Scale Quantum Network over 66 Orbital Angular Momentum Optical Modes,” Phys. Rev. Lett. 125, 140501 (2020).
- Zhang et al. (2020) Kai Zhang, Wei Wang, Shengshuai Liu, Xiaozhou Pan, Jinjian Du, Yanbo Lou, Sheng Yu, Shuchao Lv, Nicolas Treps, Claude Fabre, and Jietai Jing, “Reconfigurable hexapartite entanglement by spatially multiplexed four-wave mixing processes,” Phys. Rev. Lett. 124, 090501 (2020).
- Vanherzeele and Bierlein (1992) Herman Vanherzeele and John D. Bierlein, “Magnitude of the nonlinear-optical coefficients of KTiOPO4,” Opt. Lett. 17, 982 (1992).
- Lanczos and Boyd (2016) Cornelius Lanczos and John Boyd, Discourse on Fourier series (SIAM, 2016).