Controllable double optical bistability via photon and phonon interaction in a hybrid optomechanical system

The system under consideration is shown in Fig.1, which is consisted by two optical cavities coupled via two mechanical resonators respectively in addition to direct tunnel coupling[36, 37].

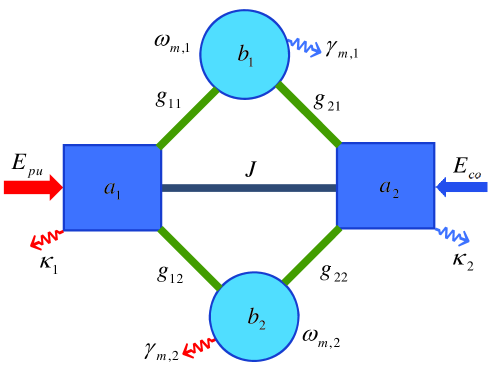
In order to investigate the optical response of the hybrid system, we assume that the two cavity modes are driven simultaneously by a strong pump field with frequency $\omega_{pu}$ and a weaker control field with frequency $\omega_{co}$, respectively. The Hamiltonian describing the system is given as

	$\displaystyle H$	$\displaystyle=\sum_{l=1}^{2}\hslash\left(\omega_{l}a_{l}^{\dagger}a_{l}+\omega_{m,l}b_{l}^{\dagger}b_{l}\right)-\sum_{k,l=1}^{2}\hslash g_{kl}a_{k}^{\dagger}a_{k}\left(b_{l}^{\dagger}+b_{l}\right)$
		$\displaystyle-\hslash J\left(a_{1}^{\dagger}a_{2}+a_{1}a_{2}^{\dagger}\right)+H_{dr},$		(1)

where $a_{l}^{\dagger}\left(a_{l}\right)$ and $b_{l}^{\dagger}\left(b_{l}\right)$ are the creation (annihilation) operator of the $l$th cavity mode and mechanical resonator, respectively. The $\omega_{l}$ and $\omega_{m,l}$ are the frequencies of the $l$th cavity mode and mechanical resonator mode. The $g_{kl}$ represents the coupling rate between the $k$th optical cavity and the $l$th mechanical oscillator. And $J$ is the photon tunneling amplitude through the two central mirror. The last term $H_{dr}$ describes the interaction between the driving fields and the optomechanical system: A strong pump field $E_{pu}$ of frequency $\omega_{pu}$ and a weak probe field of frequency $\omega_{pr}$ are simultaneously employed to drive the cavity mode $a_{1}$, and another strong control field $E_{co}$ of frequency $\omega_{co}$ is applied to drive the cavity $a_{2}$, i.e.,

$$H_{dr}=i\hslash\sqrt{\kappa_{e1}}E_{pu}e^{-i\omega_{pu}t}a_{1}^{\dagger}+i\hslash\sqrt{\kappa_{e2}}E_{co}e^{-i\omega_{co}t}a_{2}^{\dagger}+\text{H.c.},$$

(2)

where $E_{pu}$ and $E_{co}$ are the laser amplitude, i.e., $\left|E_{pu}\right|=\sqrt{\frac{2\kappa_{1}P_{pu}}{\hslash\omega_{pu}}}$ and $\left|E_{co}\right|=\sqrt{\frac{2\kappa_{2}P_{co}}{\hslash\omega_{co}}}$, with $P_{pu}$ the power of laser corresponding to pump field, $P_{co}$ the power of laser corresponding to control field, and $\kappa_{l}$ the cavity decay rate associated with the $l$th cavity mode $a_{l}$ ($l=1,2$).

In the rotating frame at the pump frequency $\omega_{pu}$, the Hamiltonian of the hybrid optomechanical system reads:

	$\displaystyle H^{\prime}$	$\displaystyle=\sum_{l=1}^{2}\hslash\left(\Delta_{l}a_{l}^{\dagger}a_{l}+\omega_{m,l}b_{l}^{\dagger}b_{l}\right)-\sum_{l,k=1}^{2}\hslash g_{lk}a_{l}^{\dagger}a_{l}\left(b_{k}^{\dagger}+b_{k}\right)$
		$\displaystyle-\hslash J\left(a_{1}^{\dagger}a_{2}+a_{1}a_{2}^{\dagger}\right)+H_{dr},$		(3)

where $\Delta_{1}=\omega_{1}-\omega_{pu}$, $\Delta_{2}=\omega_{2}-\omega_{co}$.

According to the Heisenberg-Langevin equations of motion[38], after introducing the corresponding damping and noise terms to the equations of motion associated with the Hamiltonian in Eq.(3), one can gets the following set of nonlinear equations which read as

	$\displaystyle\frac{da_{1}}{dt}$	$\displaystyle=-\left(i\Delta_{1}+\frac{\kappa_{1}}{2}\right)a_{1}+ig_{11}a_{1}X_{1}+ig_{12}a_{1}X_{2}+iJa_{2}$
		$\displaystyle+\sqrt{\kappa_{e1}}E_{pu}+\sqrt{2\kappa_{1}}a_{in,1},$
	$\displaystyle\frac{da_{2}}{dt}$	$\displaystyle=-\left(i\Delta_{2}+\frac{\kappa_{2}}{2}\right)a_{2}+ig_{21}a_{2}X_{1}+ig_{22}a_{2}X_{2}+iJa_{1}$
		$\displaystyle+\sqrt{\kappa_{e2}}E_{co}+\sqrt{2\kappa_{2}}a_{in,2},$
	$\displaystyle\frac{d^{2}X_{1}}{dt^{2}}$	$\displaystyle=-\gamma_{m,1}\frac{dX_{1}}{dt}-\left(\omega_{m,1}\right)^{2}X_{1}+2\omega_{m,1}g_{11}a_{1}^{\dagger}a_{1}$
		$\displaystyle+2\omega_{m,1}g_{21}a_{2}^{\dagger}a_{2}+\xi_{1},$
	$\displaystyle\frac{d^{2}X_{2}}{dt^{2}}$	$\displaystyle=-\gamma_{m,2}\frac{dX_{2}}{dt}-\left(\omega_{m,2}\right)^{2}X_{2}+2\omega_{m,2}g_{12}a_{1}^{\dagger}a_{1}$
		$\displaystyle+2\omega_{m,2}g_{22}a_{2}^{\dagger}a_{2}+\xi_{2},$		(4)

where $X_{l}=a_{l}^{\dagger}+a_{l}$ and $a_{in,1\text{ }}$and $a_{in,2\text{ }}$are the quantum vacuum fluctuations of the cavity mode $a_{1\text{ }}$and $a_{2\text{ }}$, which are fully characterized by the correlation $\left\langle a_{in,l}\left(t\right)a_{in,l}^{\dagger}\left(t^{\prime}\right)\right\rangle=\delta\left(t-t^{\prime}\right)$, $\left\langle a_{in,l}^{\dagger}\left(t\right)\right.$ $\ \left.a_{in,l}\left(t^{\prime}\right)\right\rangle=0$, $\xi_{l}$ is the Brownian stochastic force with zero mean value that obeys the correlation function $\left\langle\xi_{l}\left(t\right)\xi_{l}\left(t^{\prime}\right)\right\rangle=\frac{\gamma_{m,l}}{\omega_{m,l}}\int\frac{d\omega}{2\pi}\omega e^{-i\omega\left(t-t^{\prime}\right)}\left[\coth\left(\frac{\hslash\omega}{2k_{B}T_{l}}\right)+1\right]$ with $l=1,2$. Here $k_{B}$ is the Boltzmann constant and $T_{l}$ is the temperature of the reservoir of the $l$th mechanical resonator. The cavity modes decay at the rate $\kappa_{l}$ and are affected by the input vacuum noise operator $a_{in,l}$ with zero mean value, the mechanical mode is affected by a viscous force with damping rate $\gamma_{m,l}$ and by a Brownian stochastic force with zero mean value $\xi$[39]. To study the bistability of the presented system, we are interested in the steady-state solutions to the Eqs.(4). And the mean intracavity photon number $n_{p,l}=$ $\left|a_{l,s}\right|^{2}$ ($l=1,2$) can be determined by the coupled equations as following

	$\displaystyle n_{p,1}$	$\displaystyle=\frac{\kappa_{e1}\left(E_{pu}\right)^{2}+J^{2}n_{p,2}}{\left(\frac{\kappa_{1}}{2}\right)^{2}+\left(\Delta_{1}-g_{11}X_{1,s}-g_{12}X_{2,s}\right)^{2}},$
	$\displaystyle n_{p,2}$	$\displaystyle=\frac{\kappa_{e2}\left(E_{co}\right)^{2}+J^{2}n_{p,1}}{\left(\frac{\kappa_{2}}{2}\right)^{2}+\left(\Delta_{2}-g_{21}X_{1,s}-g_{22}X_{2,s}\right)^{2}},$		(5)

where $X_{1,s}$ and $X_{2,s}$ are the mechanical steady-state positions which are related to mean intracavity photon number:

	$\displaystyle X_{1,s}$	$\displaystyle=\frac{2}{\omega_{m,1}}\left(g_{11}n_{p,1}+g_{21}n_{p,2}\right),$
	$\displaystyle X_{2,s}$	$\displaystyle=\frac{2}{\omega_{m,2}}\left(g_{12}n_{p,1}+g_{22}n_{p,2}\right).$		(6)

Firstly, we investigate the optical bistability in the left cavity by adjusting the strengths of pump beam. The variations of the intracavity photon in the left cavity and right cavity, respectively, versus the left cavity-pump field detuning $\Delta_{1}$ for different pump strengths are shown in Fig.2(a) and Fig.2(b). As can be seen in Fig.2(a), the curve is a nearly Lorentzian peak when the strength of the left pump beam is lower; however, when the strength increases above a critical value, the system exhibits obvious bistable behavior, as shown in the curves for a range of values of the driving laser strength. Specifically, the initially nearly Lorentzian resonance curve becomes clear asymmetric in the pump beam strength $P_{pu}=0.10\mu$W and $P_{pu}=0.20\mu$W. In this case, the coupled cubic equation(5) for the mean intracavity photon number yield three real roots. The largest and smallest roots are stable, and the middle one is unstable, which is represented by the dashed lines in Fig.2(a). Furthermore, we can see that the larger cavity pump detuning is necessary to observe the optical bistable behavior with the increasing pump beam strength. The mean intracavity photon number $n_{p,2}$ in the right cavity as a function of the left cavity-pump beam detuning $\Delta_{1}$ is plotted in Fig.2(b). In this case, different from the behavior in the left cavity, the mean intracavity photon number all smaller than a certain value. When the strength of the pump beam is lower, the curve is a nearly Lorentzian dip. However, when the strength increases above a critical value, the system exhibits obvious bistable behavior for a range of values of the driving laser strength, as shown in the curves for $P_{pu}=0.10\mu$W and $0.20\mu$W, where the initially nearly Lorentzian curve becomes apparently asymmetric.

The optical bistability in the two cavities can be equivalently seen from the hysteresis loop for the mean intracavity photon number versus the pump power for a range of control power, as shown in Fig.3 and Fig.4. The solid and dashed curves are, respectively, corresponding to stable and unstable solutions. It is shown in Fig.3 that the mean intracavity photon number $n_{p,1}$ initially lies in the lower stable branch (corresponding to the smallest root). When the input pump power is gradually increased, the intracavity intensity in the left cavity initially scans the lower branch of the curve. When it arrives at the end of the lower branch, i.e., the first critical value, then it jumps to the upper stable branch. Therefore, increasing of input pump power shall leads to the increasing of intracavity photon number. After jumping to the upper branch, the intracavity intensity starts decreasing if the input pump power is decreased, but it still follows the upper stable branch. When the intracavity intensity reaches to the second critical point, it will jump down to the lower stable branch. Moreover, with the strengthening of control power, the pump power needed to observe the optical bistability is relatively lower.

The bistable behavior in the right cavity can be alternatively seen from the hysteresis loop for the mean intracavity photon number $n_{p,2}$ versus the pump power curve shown in Fig.4. Different from the case in the left cavity, as the power of control field is increased, it is interesting to notice that there emerges the double bistability in the right cavity. Specifically, the intracavity intensity in the right cavity $n_{p,2}$ initially scans the first lower branch of the curve when the input pump power is gradually increased. When it arrives at the end of the first lower branch, then it jumps to the first upper stable branch. After jumping to the upper branch, the intracavity intensity starts to increase if the input pump power is further increased; however, if the input pump power is further increased, then the intracavity intensity in the right cavity will jumps to the second upper stable branch. It is obvious that, with increasing control power, the second cavity switches from a bistable regime to a double bistable one. Physical concept behind this result can be expressed as the follows. A higher value of control power leads to enhanced nonlinearity in right cavity, and then the increased nonlinearity of the system shall leads to double bistable behavior in the cavity.

Bistability in the system also sensitively affected by the coupling rate $J$ between the two cavities, as depicted in Fig.5. In the weak coupling regime, the pump beam driving the left cavity cannot have enough impact on the photon numbers in the right cavity via the waveguide, thus the threshold value to observe bistability is relatively larger compared with the situation in stronger coupling regime. Thus, with the strengthening of coupling between the two cavities, the pump intensity needed to observe the optical bistability is relatively lower. It should be noted that the upper stable branches in the hysteresis loop of left cavity for different coupling intensities $J$ approach each other eventually in the larger pump beam intensity. The physical mechanism lies in the fact that the intracavity photon numbers are not only affected by the pump field but also affected by the control field through the tunnel coupling between the two cavities. Thus, the threshold of pump intensity to observe the optical bistability is relatively lower when there is stronger coupling. Additionally, the control field has little effect on photon number in the left cavity in times of stronger pump driving. Thus, it results in the phenomenon in which the upper stable branches in the hysteresis loop approach each other in larger pump beam intensity for different coupling intensities. Meanwhile, the pump intensity required to observe the optical bistability of the photon number in the right cavity will become lower with the increase of coupling intensity between the two cavities. This is similar to the case in the left cavity. The reason is that with the increasing of tunneling coupling between the two cavities, there are more photons from the left cavity tunneling to the right cavity. Then it is more likely to observe the bistable phenomenon in the right cavity, and thus the pump intensity required to observe the bistability is relatively lower. The photon number of the right cavity is affected by both the pump field and the control field. With the increase of coupling strength, the effect of pump field becomes stronger, which leads to a larger intracavity photon number in the upper stable branch in the hysteresis. As depicted in Fig.6, in the case of stronger control field comparing with that in Fig.5, with the increase of strengthening in coupling rate between the two cavities, it is more easier to observe the double bistability, for the threshold value of pump power to generate bistability is lower. The reason of observing optical bistability at lower pump power in the larger coupling intensity is a result of the enhanced interaction of control field through the tunnel effect.

If the right cavity is pumped on the red sideband, i.e., $\Delta_{2}$ $=$ $\omega_{m,2}$, then it can be seen from Fig.7 that the threshold value to observe the optical bistability in the left cavity is lower compared with that in blue sideband, i.e., $\Delta_{2}$ $=$ $-\omega_{m,2}$. However, the upper stable branches of the hysteresis loop in blue sideband is larger than that in red sideband. The mean intracavity photon number in right cavity $n_{p,2}$ under the condition of red sideband is manifestly smaller than the value obtained in blue sideband, as shown in Fig.8.

In this section, we will analyze the double bistability of mean intracavity photon number in the right cavity under different coupling rate between the left cavity and the first resonator. i.e., $g_{11}$. As shown in Fig.9, the variation of coupling rate will leads to the modulation of threshold value in the observation of bistability. Specifically, as the increase of coupling rate, the first critical value of pump power for observing the first bistable behavior is becoming lower; however, the second critical value of pump power for the emergence of bistability is becoming larger with the strengthening of coupling rate.

It is shown in Eq.(6) that the two steady-state positions of mechanical resonator, i.e., $X_{1,s}$ and $X_{2,s}$, are directly related to mean intracavity photon number $n_{p,1}$ and $n_{p,2}$. Thus it can be infer that the steady-state positions should exhibit similar bistable behavior to the mean intracavity photon number. According to the above analysis in the bistable property of intracavity photon number, it is found that the large photon number is necessary with the objective to realize the bistable phenomenon; however, it can be seen from Fig.10 that the double bistability can also be observed in relatively smaller photon number. For further illustration, in Fig.10, the two steady-state positions of mechanical resonator changing versus pump field driving strength $P_{pu}$ for different control beam strength are presented, respectively. Initially, the steady-state positions display bistability; however, when the control beam power is increased to $P_{co}=0.02$ $\mu$W, then the double optical bistability in the two steady-state positions of mechanical resonator can be observed. The increasing control field power will result in stronger nonlineary effect on photon number in both cavities, and then the radiation pressure on mechanical resonators is risen, therefore the double optical bistability can be taken place in the two steady-state positions of mechanical resonator.

Bistability in the mechanical resonator steady-state positions also sensitively affected by the coupling coefficient $J$ between two cavities, as depicted in Fig.11. Specifically, it can be straight forward to see that the two critical points to observe the double optical bistability become smaller as the strengthening of coupling coefficient between the two cavities.

As is shown in Fig.12(a), for a range of coupling rate $g_{11}$, the lower driving strength is needed to observe the first bistable behavior in steady-state position of the first mechanical resonator $X_{1,s}$ in the case of larger coupling strength $g_{11}$, while the second threshold value to observe the bistable phenomenon becomes larger in the case of larger coupling strength $g_{11}$. Similar features have taken place in the steady-state positions of the second mechanical resonator $X_{2,s}$, as shown in Fig.12(b), the steady-state position of the second mechanical resonator $X_{2,s}$ versus pump strength for several quantities in coupling strength $g_{11}$. Thus, the changing of coupling rate between the first mechanical resonator and the left cavity shall yields effective controllability over the behavior in the steady-state position of the second mechanical resonator.