Control of the magnon-polariton hybridization with a microwave pump
Abstract
Pump-induced magnon modes (PIMs) are recently discovered elementary excitations in ferrimagnets that offer significant tunability to spin dynamics. Here, we investigate the coupling between a PIM and cavity magnon polaritons (CMPs) by driving a cavity magnonic system away from equilibrium with a microwave pump. In our experiment, the Walker mode simultaneously couples with the PIM and cavity photons and thus combines two strongly coherent coupling processes in a single cavity structure. Such a PIM-CMP hybridization system acquires complementary properties from both the PIM and CMPs, allowing it to be freely manipulated by the magnetic field, the pump power and the pump frequency. These coherent manipulations exhibit unique behaviors beyond the intrinsic properties limited by the material nature and electromagnetic boundary conditions, thereby creating opportunities for extending the control of hybrid devices.
I Introduction
The last decade has seen the rapid development of the fruitful field of cavity magnonics Soykal and Flatté (2010); Huebl et al. (2013); Tabuchi et al. (2015); Goryachev et al. (2014a); Lachance-Quirion et al. (2019); Bhoi and Kim (2020); Cao et al. (2015); Boventer et al. (2018); Yu et al. (2019); Grigoryan et al. (2018); Rao et al. (2021); Li et al. (2022); Chelpanova et al. (2021). Because of its strong potential in quantum information processing and spintronics, this field of research has attracted increasing attention. A cavity magnonic system is typically composed of microwave cavities and bulk magnets Huebl et al. (2013); Tabuchi et al. (2015). Magnons, i.e., the engergy quanta of spin waves, in magnets can strongly interact with microwave photons in cavities, producing quasi-particles named “cavity magnon polaritons” (CMPs). These quasi-particles acquire complementary properties from cavity photons and magnons, and thus are highly tunable and have long coherenceZhang et al. (2015); Goryachev et al. (2014b); Yu et al. (2020), diverse non-linearitiesWang et al. (2018); Bi et al. (2021); Hyde et al. (2018), and excellent compatibilityHisatomi et al. (2016); Xu et al. (2021); Zhang et al. (2021). By exploiting these merits, numerous techniques and applications have been developed, such as long time memories Zhang et al. (2015); Shen et al. (2021), polaritonic logic gates Rao et al. (2019), magnon-phonon entanglement Li et al. (2018), spin current manipulation Bai et al. (2017), and information processing at the quantum limit Lachance-Quirion et al. (2020); Tabuchi et al. (2015, 2014). All these applications rely on an effective access to manipulate the photon-magnon coupling, which is usually implemented by delicately designing the microwave cavities.

A recent work has experimentally demonstrated that a ferrimagnet driven by a strong microwave can exhibit non-trivial properties, in particular the emergence of the pump-induced magnon mode (PIM) Rao et al. (2023). The formation of this peculiar magnon mode is attributed to the cooperative precession of unsaturated spins in the ferrimagnet under a microwave pump. The inherent nature of PIM allows it to be highly tunable by the microwave pump. Such a property is not possessed by any other magnon modes in magnets, including magnetostatic modes or Damon-Eshbach modes. If we incorporate a PIM into cavity magnonics, one straightforward consequence is that the cavity magnonic system will acquire an additional manipulation freedom inherited from the PIM and hence become tunable by the microwave pump. A similar technique that uses a strong microwave to manipulate a on-chip cavity magnonic device in the nonlinear regime has been demonstrated Li et al. (2019). Comparing to conventional cavity magnonic devices that highly depend on the design of microwave cavities, a tuning technique that merely needs to adjust the power or frequency of a microwave pump and can work in both the linear and nonlinear regimes is very useful. Moreover, the PIM can strongly couple to normal magnon modes in magnets via spin-spin interactions. This effect makes possible the hybridization of the PIM and CMP, and may hence produce new quasi-particles in cavity magnonics. Combined with the flexibility of PIM dynamics, such a quasiparticle would provide an ideal solution and significant impact on the high-dimensional tunability of the cavity magnonic system.
In this work, we introduce a PIM into cavity magnonics and investigate the strong interaction between the PIM and CMPs. The magnon mode commonly used to produce CMPs is the Walker modes Walker (1957); Dillon Jr (1957); Gloppe et al. (2019), i.e., a kind of magnetostatic modes in bulk magnets. Its effective spin number is constant determined by the saturated magnetization and volume of the bulk magnet, while its mode frequency is governed by the well-known Kittel formula that is a function of the effective magnetic field felt by a Walker mode. By contrast, the PIM differs in that its effective spin number and mode frequency are tunable via the pump. As a consequence, the PIM-CMP coupling strength follows a fourth root of the pump power (i.e., ). It can also be controlled via the detuning between the pump and the cavity mode because this detuning regulates the effective field intensity on the intra-cavity yttrium iron garnet (YIG) sphere. These results demonstrate the control of a cavity magnonic system with a microwave pump. This technique enriches the tunability of cavity magnonic systems and is useful for the magnon-based information processing. Attaining a better understanding of the nontrivial properties of the PIM-CMP interaction will be beneficial for the development of coherent/quantum information processing based on cavity magnonics.

II Experiment
Figure 1(a) shows the schematic picture of a simplest cavity magnonic device, which consists of a coplanar waveguide (CPW) cavity and a polished YIG sphere of diameter 1 mm. The CPW cavity is fabricated on a mm2 RO4350b board that contains a hydrocarbon ceramic laminate (0.76 mm) and two copper layers (0.035 mm). The fundamental mode of the CPW cavity is at GHz. Its external and intrinsic damping rates fitted from the transmission spectrum [Fig. 1(b)] are MHz and MHz, respectively. A strong microwave pump generated by a microwave generator is used to drive the system. It is a single-frequency signal at the frequency . A weak probe is emitted and collected by a vector network analyser, whose power is fixed at dBm throughout this work and whose frequency () is swept over a wide range for the transmission measurement. All measurements are performed at room temperature.
An external magnetic field parallel to the plane of the CPW is used to tune the Walker modes () in the YIG sphere. When a Walker mode, i.e. (2,2,0) mode in this work, matches the cavity mode (i.e., ), the strong photon-magnon coupling produces CMPs. The transmission spectrum [Fig. 1(c)] shows two resonance peaks with a Rabi gap, corresponding to two CMP eigenstates. We then turn on the pump and set its frequency to and its power to dBm. The strong pump drives the unsaturated spins in the YIG sphere via the cavity. The collective precession of these unsaturated spins forms a spin wave at the frequency , namely the PIM Rao et al. (2023). The PIM has much fewer spins than Walker modes, so it couples negligibly with the cavity mode. However, the PIM can strongly couple to the Walker mode via the spin-spin interaction, which is orders of magnitude stronger than the magnetic dipole-dipole interaction between a magnet and the rf-field. The PIM-CMP hybridization process is depicted in Fig. 1(a) as a three-mode coupling. The transmission spectrum in Fig. 1(d) shows three resonant peaks instead of the former Rabi splitting, representing the three eigenstates of the PIM-CMP hybridization.

The PIM-CMP hybridization arises from the strong coupling of three resonant modes. To quantitatively model this process, we construct a Hamiltonian model containing three modes and their coupling effects. We focus our research on the coupling effects in our system in the linear regime and thus disregard the self- and cross-Kerr effects Wu et al. (2021); Anderson and Suhl (1955). The Hamiltonian is
| (1) | |||||
where (), () and () represent the creation (annihilation) operators of the Walker mode, PIM and cavity photon mode, respectively. , and correspond to their complex frequencies, where MHz and MHz are the damping rates of the Walker mode and of the PIM, respectively. and are respectively the pump and probe intensities, which can be simply viewed as the voltage amplitudes of two microwave signals. They follow a square-root relation of microwave power, such as . MHz is the coupling strength between the cavity and the Walker mode, larger than the damping rates of all subsystems. is the coupling strength between the Walker mode and the PIM and has the form , where is a constant and is the effective spin number of the PIM Rao et al. (2023); Tabuchi et al. (2014). Because PIM is induced by the pump, its spin number should be equal to the magnon number excited by the pump, i.e., . is the coupling strength between the PIM and the cavity mode.
Under the two-tone driving, our system oscillates in a superposition of a steady oscillation driven by the strong pump and fluctuations perturbed by the weak probe. we assume that , and , where , and respectively represent the steady oscillating amplitudes of three modes at the frequency of . , and correspond to their fluctuations induced by the probe. These fluctuations can be derived from Eq. (1) (see Appendix A). By using the input-output relation of , we get the transmission spectrum of our device:
| (2) |
It can well reproduce the measured transmission spectra. This expression has three maxima, corresponding to the system’s eigenfrequencies. Turning off the pump, the PIM disappears, so that our system degrades to a normal cavity magnonic system with two CMP eigenfrequencies.
The Walker-PIM coupling strength can also be derived from Eq. (1) (see Appendix B). It is determined by a cubic equation with a form of
| (3) |
where and are the complex detunings of the Walker mode and the cavity mode with respect to the pump. If we set , the Walker-PIM coupling strength becomes
| (4) |
We now test the theoretical model from three aspects: the dependence of the PIM-CMP hybridization on the magnetic field , the pump power and the pump frequency . Figure 2(a) shows the transmission spectra of our device measured at different without the pump. When the Walker mode is tuned to get close to the cavity mode, a typical anticrossing occurs near 114 mT, indicating the strong photon-magnon coupling and hence the formation of CMPs. We then turn on the pump and set it at and dBm. A PIM at is excited by the pump, producing three hybridized modes from the transmission map [Fig. 2(b)]. The black dashed lines in Figs. 2(a) and 2(b) are eigenfrequencies of our system in the two cases. Transmission spectra measured at 111.7, 113.9 and 116.1 mT with the pump are plotted in Fig. 2(c), which can be well reproduced by using Eq. (2). fitted to these curves is MHz.
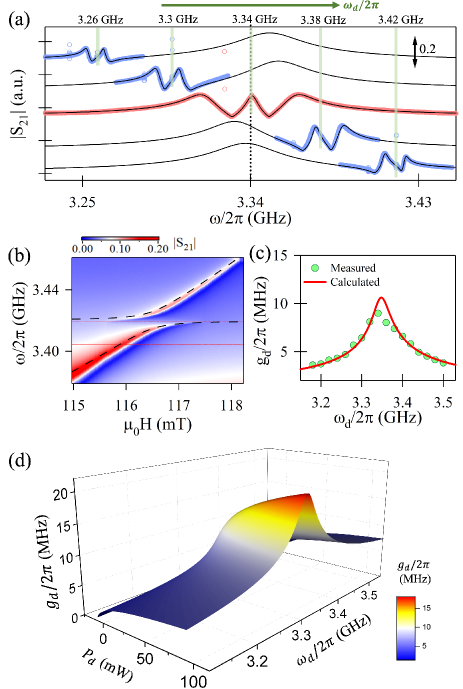
Unlike Walker modes, the PIM can be manipulated by the pump. Consequently, the PIM-CMP hybridization inherits this property, and becomes tunable by the pump power and frequency. We fix the Walker mode () and the pump frequency () to the cavity mode, i.e., and then tune the pump power and record the transmission spectrum at each power value. Figure 3(a) shows four typical spectra measured at -10, 0, 10 and 19 dBm. The PIM starts to appear at around dBm. Three hybridized modes then occur at and . Using Eq. (2) to fit each transmission spectra, we extract three hybridized modes’ frequencies and coupling strengths , and , which are plotted in Fig. 3(b) and (c). As the pump power increases, the gap between increases, whereas remains essentially constant at 24 MHz. Nevertheless, is approximately proportional to the fourth root of the pump power (). The physical origin is that the PIM’s spin number is equal to the magnons excited by the pump. In another word, the PIM’s spin number is altered by the pump power. Such a variation of can be well explained by Eq. (4), as shown by the red solid line in Fig. 3(c). During the calculation, is a constant , while is approximately set as . is almost zero, which indicates that the direct coupling effect between the PIM and the cavity photon mode is neglectable comparing to two other coupling processes. The physical reason is that the effective spin number of the PIM is much smaller than that of the Walker mode. The measured half coupling gaps at different pump powers, [i.e., ] are plotted in Fig. 3 (d) as purple circles. They can be fitted by , as shown by the red solid line in Fig. 3(d). At high powers, the experimental data (circles in Fig. 3(c) and 3(d)) gradually deviate from the fitting curves (red solid lines) due to the occurrence of nonlinearities that are not considered in this work. More discussion see Appendix C.
Another way to control the PIM-CMP hybridization is changing the pump detuning relative to the cavity mode (). The PIM strictly follows the pump frequency, making the anti-crossing of three hybridized modes controllable by the pump frequency. Moreover, the PIM-Walker coupling strength also exhibits a dependency on the pump detuning, because the pump field felt by the YIG sphere that determines the PIM’s spin number is regulated by the cavity, as well as its coupling with Walker modes. Figure 4(a) shows transmission spectra measured at different pump frequencies [see green lines in Fig. 4(a)]. Two resonance peaks appear with a coupling gap, when the CMP mode matches the pump frequency. [blue circles in Fig. 4(a)]. Specifically, we fix the pump frequency at GHz, and measure the transmission spectra at different , as shown in Fig. 4(b). The red color in the map indicates the upper branch of CMP modes. An anticrossing appears when the CMP mode approaches the pump at 3.42 GHz, because of the strong PIM-CMP coupling. Black dashed lines are eigenfrequencies calculated from the Hamiltonian (1), which are consistent with measurement results. The PIM-CMP coupling strength () is tunable by the pump detuning. It becomes larger, as the pump frequency approaches the cavity mode. fitted from Fig. 4(a) are plotted in Fig. 4(c). It reaches the maximum when the pump frequency matches the cavity mode, and decreases rapidly as the pump detuning increases. Using Eq. (3), we can calculate at different pump detuning, as shown by the red solid line in Fig. 4(c). Furthermore, we also calculate the variation of in a parameter space formed by the pump power and the pump frequency , as shown in Fig. 4(d). Increasing the pump power or decreasing the pump detuning can enhance the effective pump field applied to the YIG sphere. It increases the PIM’s spin number , and hence enhances the PIM-CMP coupling strength .
III Conclusion
We apply a strong microwave pump on a cavity magnonic system and observe the hybridization between a PIM and CMP modes. This hybrid system inherits intriguing properties from the PIM, allowing it to be controlled by the microwave pump, a feature that is absent in all previous cavity magnonic systems. By using either the pump power or the pump frequency, we can thus tune the PIM-CMP hybridization. In conventional cavity magnonic systems, photon-magnon coupling strength is determined by three parameters, i.e., the spin number of magnets, the mode volume of the cavity photon mode and the overlap coefficient between the cavity photon mode and the magnon mode. This fact causes that the photon-magnon coupling strength is a constant once a cavity magnonic device is fabricated. To adjust the photon-magnon coupling, we must redesign the device or add complicate mechanical structures to change the magnet position in the cavity. Now by utilizing the PIM-CMPs hybridization, we find a handy method that can in situ control the photon-magnon coupling by modulating the pump.Additionally, the parameters, such as the geometrical shape of magnets, the pump duration time and the material properties, are also promising to manipulate the PIM-CMPs hybridization. These methods help to enrich the toolbox for controlling cavity magnonic systems, which should benefit magnon-based signal processing in a broader perspective.
After years of study, CMP generated by the photon-magnon hybridization has become a well-developed technology, and our present work takes a step further. In addition to the formation of CMPs, coherent magnons excited by a pump are strongly coupled with CMPs. From the transmission spectra, we can clear see the anticrossing behaviour arsing from this PIM-CMP hybridization. Normally, anticrossing is an important experimental evidence for the formation of new elementary excitation. We thus conjecture that the PIM-CMP hybridization may generate new elementary excitation that is the combination of two magnons and one photon. This elementary offers a high-dimensional control to realize the photon-magnon entanglement for coherent/quantum information technologies. Our current results just uncover the tip of the iceberg of this elementary excitation and it is expected that more features of non-equilibrium cavity magnonic systems would be discovered.
Acknowledgements.
This work has been funded by National Natural Science Foundation of China under Grants Nos.12122413, 11974369, 11991063 and 12204306, STCSM Nos.21JC1406200 and 22JC1403300, the Youth Innovation Promotion Association No. 2020247 and Strategic priority research No. XDB43010200 of CAS, the National Key R&D Program of China (No. 2022YFA1404603, 2022YFA1604400), the SITP Independent Foundation, the Shanghai Pujiang Program (No. 22PJ1410700).Appendix A Dynamic equations of the PIM-CMP hybridization
From the Hamiltonian (Eq. (1)), we can derive the dynamic equations of the PIM-CMP hybridization, which are:
| (A.5) | |||||
Under the two-tone drive, the oscillation of our system can be viewed as a superposition of a steady oscillation and small fluctuations. The fluctuations are governed by three coupled equations
| (A.6) | |||||
from which we can obtain the fluctuation of the cavity mode, which is
| (A.7) |
Substituting Eq. (A.7) into the input-output relation of the cavity, i.e., , we can derive the transmission spectrum of our device, i.e., Eq. (2).
Appendix B Steady oscillation amplitude of the cavity mode
According to the experimental results shown in Fig. 3 (c), the direct coupling effect between the PIM and the cavity photon mode is neglectable, so that we assume . Then, the steady oscillation amplitudes of three modes derived from Eq. (A.5) follow
| (B.8) |
The PIM’s spin number is assumed to be the magnon number excited by the pump, i.e., , so that the PIM-Walker coupling strength is
| (B.9) | |||||
Substituting Eq. (B.9) into Eq. (B.8), we can derive a cubic equation of , i.e., Eq. (3).
Appendix C Distinguishing the coupling effect and interference, the coupling regime of

Because of the presence of the PIM, we can see three resonant peaks in the transmission spectra. Actually, there exist two different mechanisms that can produce this transmission. One is the coupling effect between the PIM and CMPs. The other is the interference effect, in which the PIM is an independent resonance that superposes on the transmission of the two CMP modes. In this case, there is no PIM-CMP coupling effect. Accordingly, we can write the expression of the transmission spectrum caused by the interference, which is
where the first term represents the transmission of two CMP modes, and the second term is a single resonance that represents the transmission spectrum of PIM. We use this expression to fit the measured transmission spectrum where the pump power is 10 dBm, but the fitting curve cannot reproduce the measured transmission spectrum well (see Fig.5(a) blue solid line). The red solid line is the fitting curve by using Eq.(2). The coefficient of determination for the red line is 0.998, while the coefficient of determination for the blue line is 0.976, KHz, MHz and MHz. refers to the damping of the magnet and cannot be so close to zero. From the comparison of these curve fitting results, we tend to believe that the PIM-CMP coupling effect does exist, rather than the interference.
In the main text, the PIM-CMP coupling effect locates in the regime of , but leaves the regime of unexplored. Increasing the pump power is a feasible method to reach the regime of , because is independent of the pump power. However, follows a forth root dependence on the pump power, i.e., . Therefore, we must use a very high power pump, which will ignite the complicate nonlinearities in magnetic materials. In addition to increasing the pump power, delicately adjusting the YIG position in the cavity can also reach the regime of . Accordingly, we slightly adjust the YIG position to lower the cavity-Walker mode coupling strength to MHz from the original 24 MHz. Then we turn on the pump. When the pump power is 10 dBm (i.e., 10 mW), the PIM-Walker mode coupling strength is MHz, still in the regime . When we increase the pump power to 20 dBm (100 mW), increases to 23.7 MHz, which is larger than the cavity-Walker mode coupling (). The measured results of these two coupling cases are respectively shown in Fig.5(b) with red and purple color, respectively. In the regime, besides those three resonant peaks, an additional resonant dip occurs near the pump frequency, as marked by a rectangle in Fig.5(b). This feature is beyond of our current theoretical model. We conjecture that it may arise from the strong nonlinearity of the Walker mode and the PIM in the .
References
- Soykal and Flatté (2010) Ö. O. Soykal and M. Flatté, Strong field interactions between a nanomagnet and a photonic cavity, Phys. Rev. Lett. 104, 077202 (2010).
- Huebl et al. (2013) H. Huebl, C. W. Zollitsch, J. Lotze, F. Hocke, M. Greifenstein, A. Marx, R. Gross, and S. T. Goennenwein, High cooperativity in coupled microwave resonator ferrimagnetic insulator hybrids, Phys. Rev. Lett. 111, 127003 (2013).
- Tabuchi et al. (2015) Y. Tabuchi, S. Ishino, A. Noguchi, T. Ishikawa, R. Yamazaki, K. Usami, and Y. Nakamura, Coherent coupling between a ferromagnetic magnon and a superconducting qubit, Science 349, 405 (2015).
- Goryachev et al. (2014a) M. Goryachev, W. G. Farr, D. L. Creedon, Y. Fan, M. Kostylev, and M. E. Tobar, High-cooperativity cavity qed with magnons at microwave frequencies, Phys. Rev. Appl. 2, 054002 (2014a).
- Lachance-Quirion et al. (2019) D. Lachance-Quirion, Y. Tabuchi, A. Gloppe, K. Usami, and Y. Nakamura, Hybrid quantum systems based on magnonics, Appl. Phys. Express 12, 070101 (2019).
- Bhoi and Kim (2020) B. Bhoi and S.-K. Kim, Roadmap for photon-magnon coupling and its applications, in Solid State Phys., Vol. 71 (Academic Press Inc Elsevier Science, San Diego, 2020) pp. 39–71.
- Cao et al. (2015) Y. Cao, P. Yan, H. Huebl, S. T. B. Goennenwein, and G. E. W. Bauer, Exchange magnon-polaritons in microwave cavities, Phys. Rev. B 91, 094423 (2015).
- Boventer et al. (2018) I. Boventer, M. Pfirrmann, J. Krause, Y. Schön, M. Kläui, and M. Weides, Complex temperature dependence of coupling and dissipation of cavity magnon polaritons from millikelvin to room temperature, Phys. Rev. B 97, 184420 (2018).
- Yu et al. (2019) W. Yu, J. Wang, H. Yuan, J. Xiao, et al., Prediction of attractive level crossing via a dissipative mode, Phys. Rev. Lett. 123, 227201 (2019).
- Grigoryan et al. (2018) V. L. Grigoryan, K. Shen, and K. Xia, Synchronized spin-photon coupling in a microwave cavity, Phys. Rev. B 98, 024406 (2018).
- Rao et al. (2021) J. Rao, P. Xu, Y. Gui, Y. Wang, Y. Yang, B. Yao, J. Dietrich, G. Bridges, X. Fan, D. Xue, et al., Interferometric control of magnon-induced nearly perfect absorption in cavity magnonics, Nat. Commun. 12, 1 (2021).
- Li et al. (2022) Y. Li, V. G. Yefremenko, M. Lisovenko, C. Trevillian, T. Polakovic, T. W. Cecil, P. S. Barry, J. Pearson, R. Divan, V. Tyberkevych, et al., Coherent coupling of two remote magnonic resonators mediated by superconducting circuits, Phys. Rev. Lett. 128, 047701 (2022).
- Chelpanova et al. (2021) O. Chelpanova, A. Lerose, S. Zhang, I. Carusotto, Y. Tserkovnyak, and J. Marino, Intertwining of lasing and superradiance under spintronic pumping, arXiv e-prints , arXiv (2021).
- Zhang et al. (2015) X. Zhang, C.-L. Zou, N. Zhu, F. Marquardt, L. Jiang, and H. X. Tang, Magnon dark modes and gradient memory, Nat. Commun. 6, 1 (2015).
- Goryachev et al. (2014b) M. Goryachev, W. G. Farr, D. L. Creedon, Y. Fan, M. Kostylev, and M. E. Tobar, High-Cooperativity Cavity QED with Magnons at Microwave Frequencies, Phys. Rev. Appl. 2, 054002 (2014b).
- Yu et al. (2020) W. Yu, T. Yu, and G. E. W. Bauer, Circulating cavity magnon polaritons, Phys. Rev. B 102, 064416 (2020).
- Wang et al. (2018) Y.-P. Wang, G.-Q. Zhang, D. Zhang, T.-F. Li, C.-M. Hu, and J. You, Bistability of Cavity Magnon Polaritons, Phys. Rev. Lett. 120, 057202 (2018).
- Bi et al. (2021) M. X. Bi, X. H. Yan, Y. Zhang, and Y. Xiao, Tristability of cavity magnon polaritons, Phys. Rev. B 103, 104411 (2021).
- Hyde et al. (2018) P. Hyde, B. M. Yao, Y. S. Gui, G.-Q. Zhang, J. Q. You, and C.-M. Hu, Direct measurement of foldover in cavity magnon-polariton systems, Phys. Rev. B 98, 174423 (2018).
- Hisatomi et al. (2016) R. Hisatomi, A. Osada, Y. Tabuchi, T. Ishikawa, A. Noguchi, R. Yamazaki, K. Usami, and Y. Nakamura, Bidirectional conversion between microwave and light via ferromagnetic magnons, Phys. Rev. B 93, 174427 (2016).
- Xu et al. (2021) A. Q. Xu, B. Zhao, B. M. Yao, and S. W. Wang, Controlling the radiative damping of an on-chip artificial magnon mode, J. Appl. Phys. 130, 105102 (2021).
- Zhang et al. (2021) Q. Zhang, J. Xue, Y. Sun, J. Guo, Y. Chen, Y. Tian, S. Yan, and L. Bai, Coupling of microwave photons to optical and acoustic magnon modes in the layered antiferromagnetic insulator , Phys. Rev. B 104, 094303 (2021).
- Shen et al. (2021) R.-C. Shen, Y.-P. Wang, J. Li, S.-Y. Zhu, G. Agarwal, and J. You, Long-time memory and ternary logic gate using a multistable cavity magnonic system, Phys. Rev. Lett. 127, 183202 (2021).
- Rao et al. (2019) J. Rao, S. Kaur, B. Yao, E. Edwards, Y. Zhao, X. Fan, D. Xue, T. J. Silva, Y. Gui, and C.-M. Hu, Analogue of dynamic hall effect in cavity magnon polariton system and coherently controlled logic device, Nat. Commun. 10, 1 (2019).
- Li et al. (2018) J. Li, S.-Y. Zhu, and G. Agarwal, Magnon-photon-phonon entanglement in cavity magnomechanics, Phys. Rev. Lett. 121, 203601 (2018).
- Bai et al. (2017) L. Bai, M. Harder, P. Hyde, Z. Zhang, C.-M. Hu, Y. Chen, and J. Q. Xiao, Cavity mediated manipulation of distant spin currents using a cavity-magnon-polariton, Phys. Rev. Lett. 118, 217201 (2017).
- Lachance-Quirion et al. (2020) D. Lachance-Quirion, S. P. Wolski, Y. Tabuchi, S. Kono, K. Usami, and Y. Nakamura, Entanglement-based single-shot detection of a single magnon with a superconducting qubit, Science 367, 425 (2020).
- Tabuchi et al. (2014) Y. Tabuchi, S. Ishino, T. Ishikawa, R. Yamazaki, K. Usami, and Y. Nakamura, Hybridizing ferromagnetic magnons and microwave photons in the quantum limit, Phys. Rev. Lett. 113, 083603 (2014).
- Rao et al. (2023) J. W. Rao, B. Yao, C. Y. Wang, C. Zhang, T. Yu, and W. Lu, Unveiling a pump-induced magnon mode via its strong interaction with walker modes, Phys. Rev. Lett. 130, 046705 (2023).
- Li et al. (2019) Y. Li, T. Polakovic, Y.-L. Wang, J. Xu, S. Lendinez, Z. Zhang, J. Ding, T. Khaire, H. Saglam, R. Divan, J. Pearson, W.-K. Kwok, Z. Xiao, V. Novosad, A. Hoffmann, and W. Zhang, Strong coupling between magnons and microwave photons in on-chip ferromagnet-superconductor thin-film devices, Phys. Rev. Lett. 123, 107701 (2019).
- Walker (1957) L. R. Walker, Magnetostatic modes in ferromagnetic resonance, Phys. Rev. 105, 390 (1957).
- Dillon Jr (1957) J. Dillon Jr, Ferrimagnetic resonance in yttrium iron garnet, Phys. Rev. 105, 759 (1957).
- Gloppe et al. (2019) A. Gloppe, R. Hisatomi, Y. Nakata, Y. Nakamura, and K. Usami, Resonant magnetic induction tomography of a magnetized sphere, Phys. Rev. Appl. 12, 014061 (2019).
- Wu et al. (2021) W.-J. Wu, D. Xu, J. Qian, J. Li, Y.-P. Wang, and J. You, Observation of magnon cross-kerr effect in cavity magnonics, arXiv preprint arXiv:2112.13807 (2021).
- Anderson and Suhl (1955) P. Anderson and H. Suhl, Instability in the motion of ferromagnets at high microwave power levels, Phys. Rev. 100, 1788 (1955).