Contrastive Instruction Tuning
Abstract
Instruction tuning has been used as a promising approach to improve the performance of large language models (LLMs) on unseen tasks. However, current LLMs exhibit limited robustness to unseen instructions, generating inconsistent outputs when the same instruction is phrased with slightly varied forms or language styles. This behavior indicates LLMs’ lack of robustness to textual variations and generalizability to unseen instructions, potentially leading to trustworthiness issues. Accordingly, we propose Contrastive Instruction Tuning (Coin), which maximizes the similarity between the hidden representations of semantically equivalent instruction-instance pairs while minimizing the similarity between semantically different ones. To facilitate this approach, we augment the existing FLAN collection by paraphrasing task instructions. Experiments on the PromptBench benchmark show that Coin consistently improves LLMs’ robustness to unseen instructions with variations across character, word, sentence, and semantic levels by an average of in accuracy.111Code is available at https://github.com/luka-group/CoIN.
1 Introduction
Instruction tuning has emerged to be an essential training paradigm of large language models (LLMs; Wei et al. 2022; Sanh et al. 2022; Mishra et al. 2022). By training models on various pairs of task instructions and instances, instruction tuning has been widely adopted in LLMs, such as TK-Instruct Wang et al. (2022), InstructGPT Ouyang et al. (2022), FLAN-T5 Wei et al. (2022), and Alpaca Taori et al. (2023), allowing them to follow various human instructions and fulfill user intents (Wang et al., 2022; Zhang et al., 2023).

Despite these advancements, current instruction-tuned LLMs are not robust to instruction variations. Their performance may vary significantly when one re-formulates an instruction with different forms or language styles (Zhu et al., 2023; Liu et al., 2023b). While optimal instructions for specific user intents may exist, there is no guarantee that user-crafted instructions will precisely match them. Indeed, user-crafted instructions often contain variations that can cause drop in LLMs’ performance, such as unintended minor mistakes (e.g., a typo; Wang et al. 2021, 2023a), different expression preferences (e.g., choice of synonyms or paraphrases; Gu et al. 2023; Zhu et al. 2023), inefficient descriptions Sun et al. (2023), and varying formats Liang et al. (2023). As shown in Figure 1, given different instructions of the same intent, an instruction-tuned LLM like Alpaca can generate entirely different responses, some of which can lead to wrong answers. LLMs’ current lack of robustness to instruction variations severely limits their real-world applications. However, prior instruction tuning methods mainly focus on aligning the desired output for a given instruction-input pair and do not explicitly address models’ robustness against variations in instructions Ouyang et al. (2022); Wei et al. (2022); Zhang et al. (2023); Longpre et al. (2023).
In this paper, we propose Contrastive Instruction Tuning (Coin), an instruction tuning method that leverages contrastive learning to align the hidden representations of instruction-instance pairs that are semantically equivalent but textually different and to differentiate those that are semantically distinct. Given the same input and output instance, we pair each instruction with its perturbed versions as positive samples. Observed that the hidden representations of data from different tasks already have low cosine similarity with each other Liu et al. (2023a), we use the same instruction paired with different instance input and output as hard negative samples (refer to Section 3.2 for more details). Intuitively, by recognizing that the same instruction with different formulations can have the same meaning, the model can generate more consistent answers given different instructions of the same intent and become more robust to variations in language expressions. At the same time, negative samples encourage the model to understand that an instruction can lead to different outcomes in different contexts, facilitating the model to distinguish inputs with different user intents.
We assess LLMs’ robustness on the PromptBench benchmark Zhu et al. (2023), which introduces variations to instructions of a diverse set of tasks at character, word, sentence, and semantic levels. Experiments on the benchmark show that Coin significantly improves task performance and reduces response variation of Alpaca on unseen instructions with variations at all four levels, achieving an average accuracy improvement of +2.5% compared with continual instruction tuning on the same dataset.
Our contributions are three-fold. First, we propose a contrastive instruction tuning method, Coin, to enhance LLMs’ robustness to semantic-invariant instruction variations. Second, experiments on PromptBench demonstrate the effectiveness of Coin in handling semantically equivalent instructions that differ at the character, word, sentence, and semantic levels. Third, to facilitate the proposed approach, we augmented the FLAN collection, a widely used instruction tuning dataset, with contrastive instructions. We will release the augmented dataset consisting of 52k entries and 104k instructions to support future work in this direction.
2 Related Work
In this section, we provide a brief summary of three highly related topics.
Instruction Tuning and Generalizability. Instruction tuning has emerged to be one of the pivotal techniques for enhancing the generalizability of LLMs (Sanh et al., 2022; Zhang et al., 2023; Ouyang et al., 2022). This capability is crucial for LLMs, as it determines models’ performance when encountering new data. The efficacy of instruction tuning has become more evident when the number of tasks scales up Xu et al. (2022). Consequently, many recent studies have been focusing on fine-tuning LLMs with a wide range of tasks. For instance, large-scale datasets that encompass numerous NLP tasks and multiple data sources have been curated for effectively enhancing LLMs’ zero-shot generalizability (Sanh et al., 2022; Wei et al., 2022; Niu et al., 2023; Kung et al., 2023; Wang et al., 2023b). Despite performance gained on unseen tasks, LLMs fine-tuned with large-scale instruction datasets remain vulnerable to how the same instruction is expressed differently (Wang et al., 2021; Zhu et al., 2023; Liu et al., 2023b; Sun et al., 2023; Liang et al., 2023). This limitation motivates us to enhance LLMs’ robustness to instruction variations in this work.
Robustness of Instruction-Tuned LLMs. With the increasing reliance on LLMs, recent works have focused on having a comprehensive understanding of the robustness of instruction-tuned language models. Zhu et al. (2023), Gu et al. (2023), and Wang et al. (2023a) add perturbations to instructions across multiple levels (character, word, sentence, etc.) and show that current LLMs are not robust to the introduced perturbations. LLMs’ performance can also be degraded when presented with unobserved, paraphrased versions of task instructions Sun et al. (2023). Furthermore, inconsistency in format and style in instruction expressions, such as placing instructions before, in between, or after the input instances, can decrease models’ performance Liang et al. (2023). While evaluating and analyzing LLMs’ robustness has garnered more attention, enhancing the models’ robustness, particularly against varied instructions of the same task, is an underexplored problem. Our work is dedicated to addressing this gap.
Contrastive Learning. Contrastive learning, a self-supervised technique that involves training a model to contrast between positive and negative pairs of data points, has rapidly evolved and been adapted in NLP tasks, such as sentence embedding Gao et al. (2022), summarization Liu et al. (2022), named entity recognition Layegh et al. (2023), and logical reasoning Bao et al. (2023). Within the context of instruction tuning, contrastive learning has been used with prefix-training to enhance the controllability towards desired attributes of LLMs Qian et al. (2022). However, the focus of the work remains on steering the generated outputs towards an attribute (such as being sentimentally positive) that is assumed to be known but is difficult to be specified given the diversity of tasks that LLMs may handle, and it does not explicitly tackle the challenge of LLMs’ robustness against variations in instruction expressions. Inspired by the observation that contrastive learning is suitable for aligning semantically related sentences Gao et al. (2022), we encourage LLMs to learn the semantic invariance of varied instructions for the same task and aim to address LLMs’ imperfect robustness at all four levels: character, word, sentence, and semantic.
3 Contrastive Instruction Tuning
In this section, we first provide a formal definition of contrastive instruction tuning (Section 3.1). Then, we introduce contrastive sample selection (Section 3.2) and the contrastive loss (Section 3.3) in our method Coin.
3.1 Overview
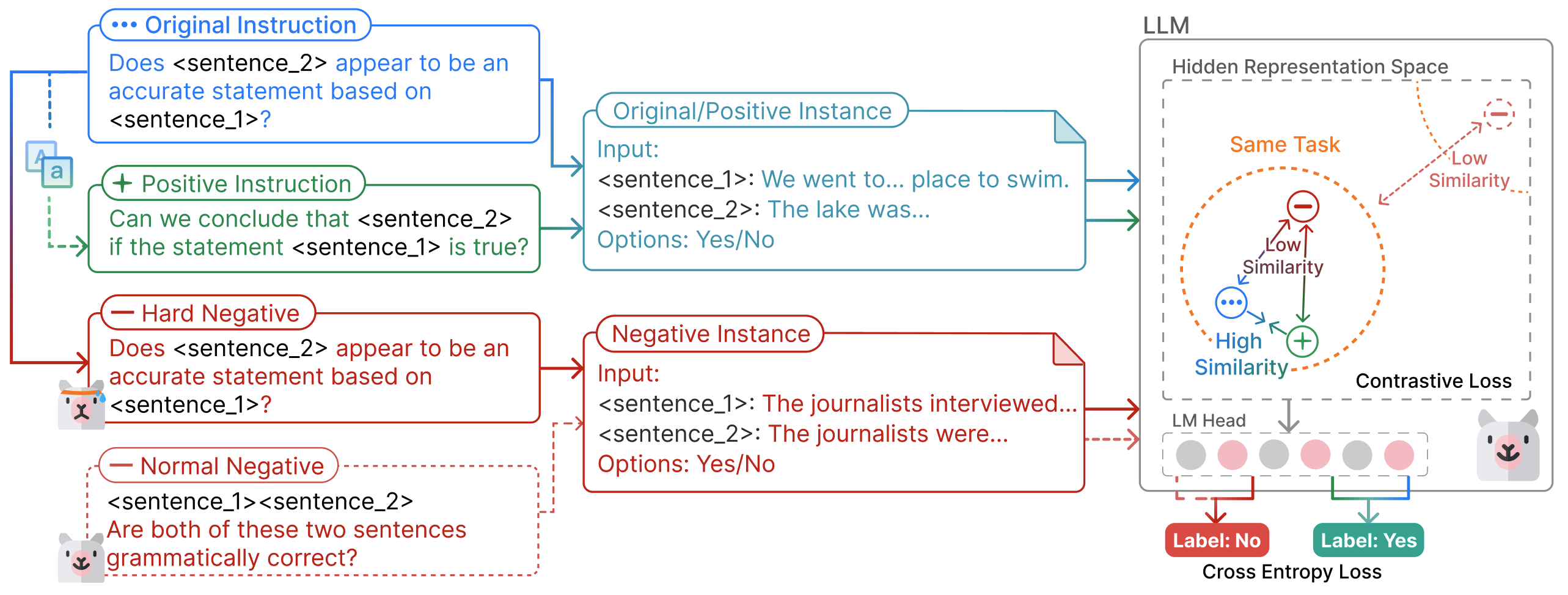
Assume that we have a (autoregressive) language model and a dataset , in which denotes the task instruction, is the instance input, and is the desired output. For each original entry, we create a semantically equivalent entry , where and . is constructed by adding textual perturbations to the original instruction while ensuring the underlying semantic meaning remains the same. Our goal is to learn a model such that its hidden representations of semantically equivalent instruction-instance pairs, denoted as and , are close to each other in ’s hidden representation space, thereby enhancing its robustness against instruction variations.
As explored by many previous studies, instruction-tuning with large-scale datasets mainly focuses on aligning the desired output for a given instruction-instance pair from various tasks (Sanh et al., 2022; Longpre et al., 2023; Wei et al., 2022). However, current LLMs exhibit a lack of robustness when facing the same instruction expressed in different forms (Sun et al., 2023; Zhu et al., 2023; Liang et al., 2023), causing LLMs to be unreliable when being deployed in the real world. To mitigate this limitation, our method Coin further leverages contrastive learning to maximize the similarity between hidden representations of semantically equivalent instruction-instance pairs. This approach enhances models’ robustness and consistency to variations in instruction expressions.
3.2 Contrastive Data Selection
Selecting effective positive and negative samples for each instruction is critical to contrastive learning. In Coin, we construct positive samples by varying the phrasing or template structure of original instructions, ensuring that the positive samples still share the same input and output with the original instance. This approach helps the model learn to align semantically similar instructions despite differences in phrasing.
For negative samples, we observe that the contrastive loss converges quickly when using instruction-input pairs of different tasks (i.e., normal negatives), leading to minor improvement in robustness. This observation is consistent with the findings in prior studies (Liu et al., 2023a): LLMs can distinguish between instructions of different tasks such that their hidden representations already have low cosine similarity. To collect hard negatives, we draw inspiration from near-OOD samples, which are data that come from the same task but with different classes Winkens et al. (2020); Fort et al. (2021); Liu et al. (2023a). Prior studies found that it is more difficult for models to detect near-OOD samples than samples from other tasks (far-OOD). This finding indicates that the hidden representations of near-OOD samples may not be distinguishable enough and thus can provide informative supervision signals for contrastive learning. Accordingly, we choose such a sample that shares the same instruction as the original instance () but is paired with different input () and output () as a negative sample. For example, if is "yes", then can be "no", ensuring the fundamental intent of the instruction-instance pair is different from the original one. Based on this approach, Coin encourages the model to align semantically equivalent instructions with different phrasings while contrasting inputs with different user intents.
3.3 Learning Objective
Our method Coin is illustrated in Figure 2. We construct the training batch such that each original sample is matched with a perturbed instruction and an identical instance as a positive sample. All other in-batch samples are hard negatives selected according to Section 3.2, i.e. share the same instruction but paired with different instances.
Let , , and indicate model ’s hidden representation of the original, positive, and negative instruction-instance pairs, respectively. Since each original pair may have multiple in-batch negatives, here we use to indicate the hidden representation of the negative samples. To align the hidden representation and , we optimize the model with the contrastive loss , which is defined as
where is the cosine similarity , and is a temperature hyperparameter. In Coin, we obtain the hidden representations by using the hidden state of the last token222We also experimented with other pooling methods such as max and average pooling but found that using the last token’s hidden state yielded better results. from the decoder of the language model.
To preserve the generation ability of the language model, we follow Liu et al. (2022) to include the standard cross entropy loss for each instruction pair, which can be defined as follows:
where is the length of the desired output for instruction-input pair . This loss is computed for all samples in the batch.
Combining the above two parts, the overall learning objective is
where detach() indicates that the loss value is detached from the computation graph and thus is treated only as a scalar. is the upper bound of the weight that is assigned to the contrastive loss. Based on empirical results, we found that setting too high, thereby significantly increasing the magnitude of the contrastive loss relative to the generation loss , adversely affects the models’ generation ability. To mitigate this issue, we scale the contrastive loss to the same magnitude as the generation loss while setting an upper bound to the weighting, ensuring a balanced influence between enhancing robustness and maintaining generative performance. For more details on the weighting choice of the contrastive loss, refer to 5.3.
4 Experiment
In this section, we evaluate Coin’s performance on enhancing LLMs’ robustness to instruction variations on PromptBench, specifically GLUE datasets with unseen333In this paper, “unseen instructions” refer to those whose textual expressions do not appear in the instruction-tuning dataset. Note that if the model exhibits inadequate robustness when handling unseen instructions for known tasks, its performance is likely to decrease further when confronted with unknown tasks. We consider the former as a rigorous evaluation setting without additional confounding factors. instructions perturbed at different levels. We first provide an overview of the experiment settings (Section 4.1, Section 4.2, and Section 4.3) and then present a detailed analysis of the experiment results Section 4.4.
4.1 Training Datasets
In this work, we conduct experiments on a widely used instruction tuning dataset: the FLAN Collection Wei et al. (2022). FLAN Collection Wei et al. (2022) is a large-scale data collection that encompasses a wide range of tasks, including natural language inference, common sense reasoning, sentiment analysis, paraphrase identification, etc. This data collection is created by transforming 62 publicly available text datasets into instructional formats. unique instruction templates are manually composed for each dataset. In this work, we choose 25 datasets with deterministic answers from the collection. To ensure each dataset has an equal chance of being sampled into the training set of Coin, we iterate through the training split of each dataset with a round-robin approach. For each entry, we create a positive sample by randomly selecting a predefined instruction template not used by the entry to paraphrase the instruction. Only paraphrasing is used for creating training data while various types of perturbations are included for evaluation (refer to Section 4.3). Avoiding assumptions about specific types of noise in instructions is crucial due to the high uncertainty LLMs face in real-world deployment. Hence, a robustness training method that can generalize to other types of perturbations is more desirable. We then select one entry from the remaining dataset as a negative sample, following the strategy in Section 3.2. Refer to Appendix A for more details of the processed dataset.
4.2 Implementation Details
We use Alpaca Taori et al. (2023), a model instruction-tuned from the LLaMA model Touvron et al. (2023) on the 52k Self-Instruct dataset, as the base model. When training models on the augmented FLAN collection, we use the same set of hyper-parameters, with the learning rate, batch size, and cut-off length set to , 64, and 256 respectively. Since we observe that the magnitude of the contrastive loss can be small during the later phase of training and following Gao et al. (2022), we set the temperature and to and . All experiments are run on 2 NVIDIA RTX A5000 GPUs.
4.3 Evaluation Setting
To evaluate models’ robustness against variations in expression of instructions, we adopt the PromptBench benchmark Zhu et al. (2023). Incorporating a diverse set of tasks, such as sentiment analysis, grammar correctness, duplicate sentence detection, and natural language inference, PromptBench introduces perturbation to task instructions at various levels: character, word, sentence, and semantic. Regarding the data used for evaluation, we sample 300 instruction-instance pairs from each GLUE task wherever the validation set exceeds this size.444Due to the extensive computational requirement of evaluating the models on the entire benchmark, we sample a subset of instructions and data from all possible instructions and datasets. For each dataset, PromptBench predefines instructions. We ensure that all selected and perturbed instructions for each dataset are not seen during the training time. Given that all instructions are unseen while GLUE tasks are seen during training time, this setting allows a more focused evaluation of LLMs’ robustness against variations in instructions without the confounding factor of task generalization.
Instruction Variations. Regarding instructions, we select six clean instructions predefined for each task. Then, we create perturbed versions of each instruction. Following PromptBench, we use DeepWordBug Gao et al. (2018) to introduce character-level perturbations for certain words, and use TextFooler Jin et al. (2020) to replace words with contextually similar words. At the sentence level, we implement the CheckList Ribeiro et al. (2020) and append randomly generated sequences, which all have a length of and consist of alphabets and digits, at the end of an instruction to distract LLMs. For the semantic-level perturbation, PromptBench defines instructions that paraphrase the original instruction for each task while following the linguistic behavior of six languages: Chinese, French, Arabic, Spanish, Japanese, and Korean. To keep the number of instructions the same as other types of perturbation, we randomly select one instruction from each language defined for each task, which are all different from the clean instructions. We also ensure that instructions used for evaluation differ from all instructions in the training dataset and thus are unseen by the model, preventing data contamination.
Metrics. For each type of perturbation, we report average accuracy and standard deviations of six instructions created for each GLUE dataset.
4.4 Results
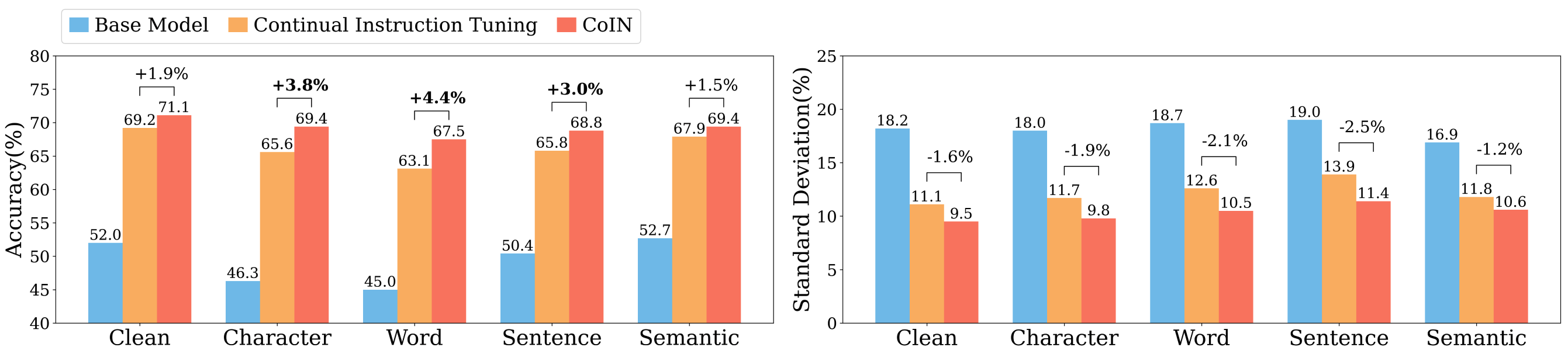
In Figure 3, we evaluate the base model, continual instruction tuning (i.e., base model fine-tuned on the same data as Coin with cross entropy loss only), and Coin on five groups of instructions across GLUE datasets. Except for the clean group, which includes the original instructions defined for each dataset, each group contains instructions with the same type of perturbation, including character, word, sentence, and semantic perturbations.
The base model exhibits low accuracy and large performance variance when given instructions with different perturbations or instructions within the same perturbation group. With only around accuracy on the clean instructions, the base model’s performance further decreases when the instructions are perturbed in all character, word, and sentence levels. The largest accuracy gap across different groups is , observed between the word and the semantic groups. For instructions within the same group, the base model exhibits a variance ranging from to . These observations demonstrate that the base model is sensitive to how instructions are formulated for different tasks.
Compared to the base model, the continually instruction-tuned model shows increases in accuracy, which is expected as the model is exposed to more data and trained with more steps. Nevertheless, the performance gap between different groups can still be as large as observed between the clean group and the group with word-level perturbation. This shows that the continually instruction-tuned model still lacks robustness to unseen instructions with variations across different levels.
Compared to continual instruction tuning, Coin further reduces performance variance and consistently improves accuracy for instructions within and across different groups without introducing any new data and training steps. As it can be seen from Figure 3, Coin achieves improvements in accuracy for all types of perturbation, up to for word-level perturbations where the continually instruction-tuned model exhibits its largest drop in performance. The largest performance gap is reduced to . The consistent improvement across all types of perturbations demonstrates the generalizability of Coin at enhancing models’ robustness against variations in instructions at different levels. Coin also decreases the performance variance on instructions from the five groups by , , , , and . This also shows that Coin can effectively help the model become less sensitive to specific instructions for each task and more consistent in its performance. For more detailed results, refer to Table 2.
5 Analyses
To provide a more comprehensive view of the impact of Coin on the model’s robustness to instruction variations, we further analyze the results of our method by examining the hidden representations of instruction variants (Section 5.1), task category (Section 5.2), and the weighting choice for the contrastive loss (Section 5.3).
5.1 Closer Representations of Instruction Variants
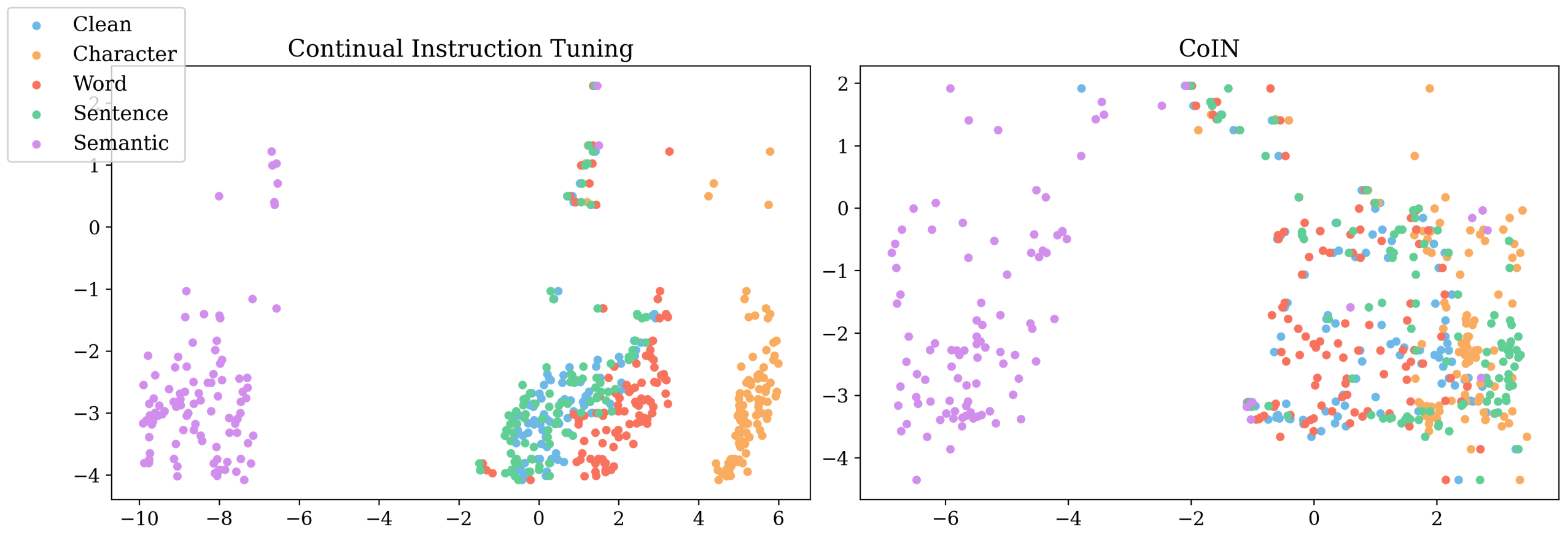
To understand the impact of Coin on the representations of instructions with variations at different levels, we visualize the hidden states of the last output tokens from the decoder’s last Transformer layer. Specifically, we select 300 data points from CoLA Warstadt et al. (2019), choose one of its instructions, add perturbations at different levels to the instruction, and obtain the hidden states from the model.
As observed in Figure 4, Coin’s hidden representations of inputs with instruction variations at different levels are much closer than those of the continually instruction-tuned model. In the embedding space of the continually instruction-tuned model, the representation of instructions with different perturbations, especially at character and word levels, are clustered almost into distinct groups. This may indicate that the model treats data points with the same instruction varied at different levels differently and thus is more sensitive to how the same instruction is formulated.
In contrast, the representations of data points with character, word, and sentence level variations are less distinguishable in Coin’s embedding space, with representations of instructions varied at the word level (red) having greater overlap with those of the clean group (blue). This observation can be associated with Coin’s varied improvement in performance across different perturbations. As shown in Figure 3, Coin achieves more evident improvement on instructions with word, character, and sentence level perturbations. It can be concluded from the two figures that when Coin effectively aligns the representations of perturbed instructions to those of the clean instructions, the model becomes more capable of capturing the original semantic meaning of the instructions. Thus, it becomes less sensitive to perturbations in instructions.
It can be observed that the representations of instructions with semantic level perturbation are located relatively far away from those of instructions with other types of perturbation. This is expected as paraphrasing introduces new structure and wording to the original instruction, which may lead to varied hidden representations. Nonetheless, Coin stabilizes the representation of the original and paraphrased instructions, demonstrating Coin can effectively align the representation of instruction variants with each other and thus enhance the model’s robustness to instruction variations.
5.2 Impact on Different Tasks
| (%) | Continual Instruction Tuning | Coin | ||||
| Task | Accuracy | Std | Accuracy | Std | Accuracy | Std |
| Sentiment Analysis | 89.0 | 4.1 | 90.4 | 3.1 | +1.4 | -1.1 |
| Natural Language Inference | 64.4 | 3.7 | 66.1 | 3.5 | +1.7 | -0.2 |
| Paraphrase Identification | 63.0 | 11.0 | 68.5 | 5.9 | +5.4 | -5.1 |
| Grammar Correctness | 62.0 | 9.2 | 68.4 | 3.9 | +6.3 | -5.3 |
We examine Coin’s influence on the model’s performance for different tasks. Based on the task category defined in the PromptBench benchmark, we split the GLUE datasets into four categories: (1) sentiment analysis, (2) natural language inference (NLI), (3) paraphrase identification, and (4) grammar correctness. Refer to Table 5 for specific datasets classified to each category.
As shown in Table 1, Coin achieves evident improvements in accuracy by +5.4% and +6.3% on paraphrase identification and grammar correctness tasks. Intuitively, these tasks can benefit more directly from Coin that aims to enhance the similarity of representations of semantically equivalent instruction-input pairs. For example, paraphrase identification can directly benefit from the model’s more refined ability to group textual inputs with similar semantic meanings, as Coin pushes representations of inputs with different meanings away from each other. Similarly, grammar correctness can also benefit from the contrastive loss, which may group hidden representations of grammatically correct inputs closer to each other and thus enable the model to become better at detecting inputs with invalid syntactic structures and grammatical rules.
On the other hand, Coin gains modest enhancement in accuracy on sentiment analysis and NLI tasks by +1.4% and +1.7% compared to the continual instruction-tuned model. For the sentiment analysis task, the continually instruction-tuned model has already achieved an accuracy of 89.0%. Obtaining further improvements can be challenging given that the model is already capable at distinguishing between sentences with different sentiments. Regarding NLI, the task requires a comprehensive understanding of the relationship between two sentences, which can depend on the model’s knowledge of various domains or reasoning ability to infer implicit meanings that are not directly stated. The complex relation between two sentences may not be explicitly captured by the hidden representations, meaning that Coin may not explicitly further enhance the model’s reasoning ability. However, Coin still obtains an improvement of +1.4% and +1.7% on the two tasks, demonstrating Coin’s effectiveness at enhancing the model’s ability to discern the nuanced inferential relation that underlies the overall semantic meaning of the instruction-input pairs.
| Model | Perturbation | CoLA | MNLI | MNLI-m | MNLI-mm | MRPC | QNLI | QQP | RTE | SST2 | WNLI | Average |
| Alpaca Baseline | Clean | 65.1 2.1 | 51.5 4.3 | 51.5 4.3 | 51.3 5.0 | 28.6 27.5 | 51.8 1.5 | 26.6 10.8 | 62.2 2.4 | 80.9 5.7 | 50.5 3.4 | 52.0 18.2 |
| Character | 61.8 4.6 | 47.2 6.4 | 47.2 6.4 | 49.3 4.5 | 27.4 24.1 | 42.7 6.9 | 15.6 10.9 | 55.5 5.6 | 66.7 15.6 | 49.3 3.5 | 46.3 18.0 | |
| Word | 61.7 2.0 | 49.6 3.8 | 49.6 3.8 | 49.2 4.7 | 43.3 21.8 | 24.8 17.4 | 14.7 8.1 | 57.5 4.9 | 46.4 25.8 | 53.1 2.7 | 45.0 18.7 | |
| Sentence | 64.8 1.8 | 51.2 3.6 | 51.2 3.6 | 52.9 2.2 | 15.3 10.7 | 50.2 3.2 | 22.6 6.8 | 61.5 3.3 | 82.3 4.1 | 52.1 2.0 | 50.4 19.0 | |
| Semantic | 65.4 1.9 | 52.1 1.2 | 52.1 1.2 | 51.6 1.8 | 37.9 25.6 | 52.1 3.7 | 25.8 10.0 | 59.2 4.4 | 82.1 3.3 | 48.6 4.4 | 52.7 16.9 | |
| Continual Instruction Tuning | Clean | 63.5 8.6 | 68.7 2.4 | 67.3 2.7 | 66.3 2.7 | 62.8 13.0 | 62.9 4.2 | 71.2 7.6 | 82.0 1.9 | 90.1 2.4 | 57.5 3.8 | 69.2 11.1 |
| Character | 64.9 3.1 | 64.9 2.1 | 64.1 2.3 | 63.4 1.9 | 62.1 11.9 | 54.7 3.6 | 61.9 11.8 | 75.7 4.8 | 90.5 2.0 | 54.0 5.1 | 65.6 11.7 | |
| Word | 58.9 12.6 | 64.8 4.1 | 65.4 3.8 | 64.3 3.5 | 56.4 10.5 | 46.8 6.7 | 62.5 8.2 | 73.8 3.5 | 84.2 12.6 | 54.0 2.1 | 63.1 12.6 | |
| Sentence | 58.6 15.2 | 66.4 1.9 | 65.3 1.4 | 65.1 3.7 | 55.9 16.8 | 53.2 8.6 | 66.6 8.1 | 80.3 3.0 | 90.4 1.2 | 55.9 4.3 | 65.8 13.9 | |
| Semantic | 64.3 6.6 | 67.0 2.9 | 67.1 2.5 | 66.0 3.1 | 61.4 14.3 | 56.4 9.9 | 69.6 8.1 | 80.0 4.4 | 89.6 2.5 | 58.0 4.6 | 67.9 11.8 | |
| Coin | Clean | 70.4 3.9 | 68.8 2.7 | 68.0 2.2 | 67.6 3.5 | 70.6 3.5 | 61.9 6.0 | 70.1 6.0 | 82.3 1.5 | 91.4 0.7 | 59.9 2.5 | 71.1 9.5 |
| Character | 66.9 3.0 | 68.2 2.0 | 67.5 1.3 | 66.6 4.0 | 72.4 2.5 | 58.7 4.2 | 64.7 8.0 | 78.5 3.1 | 91.1 2.1 | 58.9 2.6 | 69.4 9.8 | |
| Word | 66.5 4.5 | 67.4 1.7 | 67.7 3.0 | 66.1 2.3 | 71.9 5.4 | 49.9 7.5 | 63.9 6.0 | 75.6 3.5 | 85.6 11.6 | 60.1 3.8 | 67.5 10.5 | |
| Sentence | 68.4 7.2 | 67.7 3.5 | 68.2 2.6 | 66.3 3.6 | 63.3 9.6 | 55.4 9.5 | 66.8 6.1 | 79.8 3.5 | 92.3 0.6 | 59.6 2.8 | 68.8 11.4 | |
| Semantic | 69.7 1.2 | 66.3 1.8 | 67.0 0.5 | 64.3 2.6 | 72.6 5.8 | 56.1 10.0 | 68.5 6.3 | 78.5 4.5 | 91.6 0.6 | 59.2 2.0 | 69.4 10.6 |
5.3 Weighting of Contrastive Loss
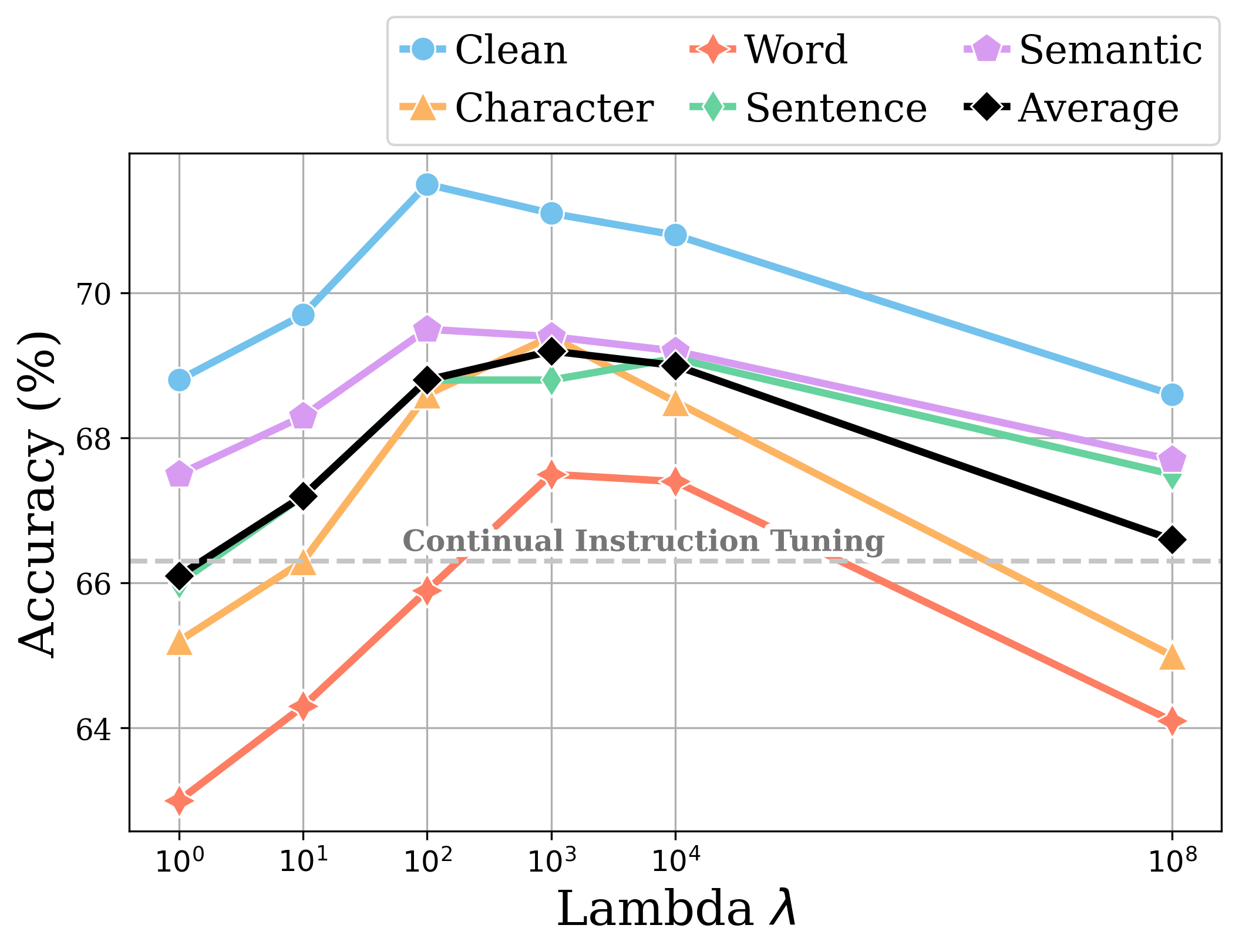
As the weight of the contrastive loss may affect the extent to which Coin align representations of instruction variants Liu et al. (2022), we examine how different values assigned to can affect Coin’s performance across different perturbation levels.
As shown in Figure 5, Coin achieves its best average performance when . When is small, contrastive loss does not have significant impact on the model due to its small magnitude. The resulting model has similar performance and sensitivity to instruction variations as the continual instruction-tuned model. As increases, Coin’s performance increases across different types of perturbations, indicating that the contrastive loss is guiding the model to align representations of instruction variations closer to each other and thus become more robust to the introduced perturbations.
However, when is too large, Coin’s performance decreases significantly, Therefore, based on the empirical results, we choose for higher accuracy and smaller standard deviation. Refer to Table 4 for detailed experiment results of models with different contrastive loss weighting.
6 Conclusion
In this paper, we proposed Coin that aligns hidden representations of semantically equivalent instruction-instance pairs. Evaluation results on PromptBench, with instructions that differ at character, word, sentence, and semantic levels, demonstrate Coin’s effectiveness of enhancing LLMs’ robustness to semantic-invariant instruction variations. Future work can apply contrastive instruction tuning to enhance the robustness of models and tasks in other modalities, and on other prompt components such as few-shot demonstrations and system prompts.
Limitation
We summarize the limitations of this work as follows: First, the current contrastive data selection method only considers paraphrasing for positive instruction augmentation. More semantic-invariant data augmentation methods could be explored. Second, the experiment scale could be enlarged to include more instruction tuning datasets, instruction-tuned models, and downstream tasks. This would provide additional evidence about Coin’s effectiveness. Third, while we use a rigorous evaluation setting to measure model robustness, evaluating the influence of Coin from other perspectives could enhance understanding of contrastive instruction tuning.
Acknowledgement
We appreciate the reviewers for their insightful comments and suggestions. Tianyi Yan was supported by the Center for Undergraduate Research in Viterbi Engineering (CURVE) Fellowship. Fei Wang was supported by the Amazon ML Fellowship. James Y. Huang was supported by a gift fund from the Amazon Center on Secure & Trusted ML. Muhao Chen was supported by the NSF Grant IIS 2105329, the NSF Grant ITE 2333736, the DARPA AIE Grant HR0011-24-9-0370, and an Amazon Research Award.
References
- Bao et al. (2023) Qiming Bao, Alex Yuxuan Peng, Zhenyun Deng, Wanjun Zhong, Gael Gendron, Timothy Pistotti, Neset Tan, Nathan Young, Yang Chen, Yonghua Zhu, Paul Denny, Michael Witbrock, and Jiamou Liu. 2023. Enhancing Logical Reasoning of Large Language Models through Logic-Driven Data Augmentation. ArXiv:2305.12599 [cs].
- Bar-Haim et al. (2006) Roy Bar-Haim, Ido Dagan, Bill Dolan, and Lisa Ferro. 2006. The second PASCAL recognising textual entailment challenge.
- Bentivogli et al. (2009) Luisa Bentivogli, Ido Dagan, Hoa Trang Dang, Danilo Giampiccolo, and Bernardo Magnini. 2009. The Fifth PASCAL Recognizing Textual Entailment Challenge.
- Cer et al. (2017) Daniel Cer, Mona Diab, Eneko Agirre, Iñigo Lopez-Gazpio, and Lucia Specia. 2017. SemEval-2017 Task 1: Semantic Textual Similarity Multilingual and Crosslingual Focused Evaluation. In Proceedings of the 11th International Workshop on Semantic Evaluation (SemEval-2017), pages 1–14, Vancouver, Canada. Association for Computational Linguistics.
- Clark et al. (2019) Christopher Clark, Kenton Lee, Ming-Wei Chang, Tom Kwiatkowski, Michael Collins, and Kristina Toutanova. 2019. BoolQ: Exploring the Surprising Difficulty of Natural Yes/No Questions. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers), pages 2924–2936, Minneapolis, Minnesota. Association for Computational Linguistics.
- Dagan et al. (2006) Ido Dagan, Oren Glickman, and Bernardo Magnini. 2006. The PASCAL Recognising Textual Entailment Challenge. In Machine Learning Challenges. Evaluating Predictive Uncertainty, Visual Object Classification, and Recognising Tectual Entailment, Lecture Notes in Computer Science, pages 177–190, Berlin, Heidelberg. Springer.
- Dolan and Brockett (2005) William B. Dolan and Chris Brockett. 2005. Automatically Constructing a Corpus of Sentential Paraphrases. In Proceedings of the Third International Workshop on Paraphrasing (IWP2005).
- Fort et al. (2021) Stanislav Fort, Jie Ren, and Balaji Lakshminarayanan. 2021. Exploring the Limits of Out-of-Distribution Detection. In Advances in Neural Information Processing Systems, volume 34, pages 7068–7081. Curran Associates, Inc.
- Gao et al. (2018) Ji Gao, Jack Lanchantin, Mary Lou Soffa, and Yanjun Qi. 2018. Black-box Generation of Adversarial Text Sequences to Evade Deep Learning Classifiers. ArXiv:1801.04354 [cs].
- Gao et al. (2022) Tianyu Gao, Xingcheng Yao, and Danqi Chen. 2022. SimCSE: Simple Contrastive Learning of Sentence Embeddings. ArXiv:2104.08821 [cs].
- Giampiccolo et al. (2007) Danilo Giampiccolo, Bernardo Magnini, Ido Dagan, and Bill Dolan. 2007. The Third PASCAL Recognizing Textual Entailment Challenge. In Proceedings of the ACL-PASCAL Workshop on Textual Entailment and Paraphrasing, pages 1–9, Prague. Association for Computational Linguistics.
- Go et al. (2009) Alec Go, Richa Bhayani, and Lei Huang. 2009. Twitter Sentiment Classification using Distant Supervision.
- Gu et al. (2023) Jiasheng Gu, Hongyu Zhao, Hanzi Xu, Liangyu Nie, Hongyuan Mei, and Wenpeng Yin. 2023. Robustness of Learning from Task Instructions. ArXiv:2212.03813 [cs].
- Hovy et al. (2001) Eduard Hovy, Laurie Gerber, Ulf Hermjakob, Chin-Yew Lin, and Deepak Ravichandran. 2001. Toward Semantics-Based Answer Pinpointing. In Proceedings of the First International Conference on Human Language Technology Research.
- Jin et al. (2020) Di Jin, Zhijing Jin, Joey Tianyi Zhou, and Peter Szolovits. 2020. Is BERT Really Robust? A Strong Baseline for Natural Language Attack on Text Classification and Entailment. ArXiv:1907.11932 [cs].
- Khashabi et al. (2018) Daniel Khashabi, Snigdha Chaturvedi, Michael Roth, Shyam Upadhyay, and Dan Roth. 2018. Looking Beyond the Surface: A Challenge Set for Reading Comprehension over Multiple Sentences. In Proceedings of the 2018 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long Papers), pages 252–262, New Orleans, Louisiana. Association for Computational Linguistics.
- Kung et al. (2023) Po-Nien Kung, Fan Yin, Di Wu, Kai-Wei Chang, and Nanyun Peng. 2023. Active Instruction Tuning: Improving Cross-Task Generalization by Training on Prompt Sensitive Tasks. ArXiv:2311.00288 [cs].
- Layegh et al. (2023) Amirhossein Layegh, Amir H. Payberah, Ahmet Soylu, Dumitru Roman, and Mihhail Matskin. 2023. ContrastNER: Contrastive-based Prompt Tuning for Few-shot NER. In 2023 IEEE 47th Annual Computers, Software, and Applications Conference (COMPSAC), pages 241–249. ArXiv:2305.17951 [cs].
- Levesque et al. (2012) Hector J. Levesque, Ernest Davis, and Leora Morgenstern. 2012. The Winograd schema challenge. In Proceedings of the Thirteenth International Conference on Principles of Knowledge Representation and Reasoning, KR’12, pages 552–561, Rome, Italy. AAAI Press.
- Li and Roth (2002) Xin Li and Dan Roth. 2002. Learning Question Classifiers. In COLING 2002: The 19th International Conference on Computational Linguistics.
- Liang et al. (2023) Shihao Liang, Kunlun Zhu, Runchu Tian, Yujia Qin, Huadong Wang, Xin Cong, Zhiyuan Liu, Xiaojiang Liu, and Maosong Sun. 2023. Exploring Format Consistency for Instruction Tuning. ArXiv:2307.15504 [cs].
- Liu et al. (2023a) Bo Liu, Liming Zhan, Zexin Lu, Yujie Feng, Lei Xue, and Xiao-Ming Wu. 2023a. How Good Are Large Language Models at Out-of-Distribution Detection? ArXiv:2308.10261 [cs].
- Liu et al. (2022) Yixin Liu, Pengfei Liu, Dragomir Radev, and Graham Neubig. 2022. BRIO: Bringing Order to Abstractive Summarization. ArXiv:2203.16804 [cs].
- Liu et al. (2023b) Yugeng Liu, Tianshuo Cong, Zhengyu Zhao, Michael Backes, Yun Shen, and Yang Zhang. 2023b. Robustness Over Time: Understanding Adversarial Examples’ Effectiveness on Longitudinal Versions of Large Language Models. ArXiv:2308.07847 [cs].
- Longpre et al. (2023) Shayne Longpre, Le Hou, Tu Vu, Albert Webson, Hyung Won Chung, Yi Tay, Denny Zhou, Quoc V. Le, Barret Zoph, Jason Wei, and Adam Roberts. 2023. The Flan Collection: Designing Data and Methods for Effective Instruction Tuning. ArXiv:2301.13688 [cs].
- Maas et al. (2011) Andrew L. Maas, Raymond E. Daly, Peter T. Pham, Dan Huang, Andrew Y. Ng, and Christopher Potts. 2011. Learning Word Vectors for Sentiment Analysis. In Proceedings of the 49th Annual Meeting of the Association for Computational Linguistics: Human Language Technologies, pages 142–150, Portland, Oregon, USA. Association for Computational Linguistics.
- Marneffe et al. (2019) Marie-Catherine de Marneffe, Mandy Simons, and Judith Tonhauser. 2019. The CommitmentBank: Investigating projection in naturally occurring discourse. Proceedings of Sinn und Bedeutung, 23(2):107–124. Number: 2.
- McInnes et al. (2020) Leland McInnes, John Healy, and James Melville. 2020. UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction. ArXiv:1802.03426 [cs, stat].
- Mishra et al. (2022) Swaroop Mishra, Daniel Khashabi, Chitta Baral, and Hannaneh Hajishirzi. 2022. Cross-Task Generalization via Natural Language Crowdsourcing Instructions. In Proceedings of the 60th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), pages 3470–3487, Dublin, Ireland. Association for Computational Linguistics.
- Nie et al. (2020) Yixin Nie, Adina Williams, Emily Dinan, Mohit Bansal, Jason Weston, and Douwe Kiela. 2020. Adversarial NLI: A New Benchmark for Natural Language Understanding. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, pages 4885–4901, Online. Association for Computational Linguistics.
- Niu et al. (2023) Yingjie Niu, Linyi Yang, Ruihai Dong, and Yue Zhang. 2023. Learning to Generalize for Cross-domain QA. ArXiv:2305.08208 [cs].
- Ouyang et al. (2022) Long Ouyang, Jeff Wu, Xu Jiang, Diogo Almeida, Carroll L. Wainwright, Pamela Mishkin, Chong Zhang, Sandhini Agarwal, Katarina Slama, Alex Ray, John Schulman, Jacob Hilton, Fraser Kelton, Luke Miller, Maddie Simens, Amanda Askell, Peter Welinder, Paul Christiano, Jan Leike, and Ryan Lowe. 2022. Training language models to follow instructions with human feedback. ArXiv:2203.02155 [cs].
- Pilehvar and Camacho-Collados (2019) Mohammad Taher Pilehvar and Jose Camacho-Collados. 2019. WiC: the Word-in-Context Dataset for Evaluating Context-Sensitive Meaning Representations. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers), pages 1267–1273, Minneapolis, Minnesota. Association for Computational Linguistics.
- Qian et al. (2022) Jing Qian, Li Dong, Yelong Shen, Furu Wei, and Weizhu Chen. 2022. Controllable Natural Language Generation with Contrastive Prefixes. In Findings of the Association for Computational Linguistics: ACL 2022, pages 2912–2924, Dublin, Ireland. Association for Computational Linguistics.
- Rajpurkar et al. (2018) Pranav Rajpurkar, Robin Jia, and Percy Liang. 2018. Know What You Don’t Know: Unanswerable Questions for SQuAD. In Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics (Volume 2: Short Papers), pages 784–789, Melbourne, Australia. Association for Computational Linguistics.
- Ribeiro et al. (2020) Marco Tulio Ribeiro, Tongshuang Wu, Carlos Guestrin, and Sameer Singh. 2020. Beyond Accuracy: Behavioral Testing of NLP Models with CheckList. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, pages 4902–4912, Online. Association for Computational Linguistics.
- Sanh et al. (2022) Victor Sanh, Albert Webson, Colin Raffel, Stephen H. Bach, Lintang Sutawika, Zaid Alyafeai, Antoine Chaffin, Arnaud Stiegler, Teven Le Scao, Arun Raja, Manan Dey, M. Saiful Bari, Canwen Xu, Urmish Thakker, Shanya Sharma Sharma, Eliza Szczechla, Taewoon Kim, Gunjan Chhablani, Nihal Nayak, Debajyoti Datta, Jonathan Chang, Mike Tian-Jian Jiang, Han Wang, Matteo Manica, Sheng Shen, Zheng Xin Yong, Harshit Pandey, Rachel Bawden, Thomas Wang, Trishala Neeraj, Jos Rozen, Abheesht Sharma, Andrea Santilli, Thibault Fevry, Jason Alan Fries, Ryan Teehan, Tali Bers, Stella Biderman, Leo Gao, Thomas Wolf, and Alexander M. Rush. 2022. Multitask Prompted Training Enables Zero-Shot Task Generalization. ArXiv:2110.08207 [cs].
- Schulman et al. (2017) John Schulman, Filip Wolski, Prafulla Dhariwal, Alec Radford, and Oleg Klimov. 2017. Proximal Policy Optimization Algorithms. ArXiv:1707.06347 [cs].
- Socher et al. (2013) Richard Socher, Alex Perelygin, Jean Wu, Jason Chuang, Christopher D. Manning, Andrew Ng, and Christopher Potts. 2013. Recursive Deep Models for Semantic Compositionality Over a Sentiment Treebank. In Proceedings of the 2013 Conference on Empirical Methods in Natural Language Processing, pages 1631–1642, Seattle, Washington, USA. Association for Computational Linguistics.
- Sun et al. (2023) Jiuding Sun, Chantal Shaib, and Byron C. Wallace. 2023. Evaluating the Zero-shot Robustness of Instruction-tuned Language Models. ArXiv:2306.11270 [cs].
- Taori et al. (2023) Rohan Taori, Ishaan Gulrajani, Tianyi Zhang, Dubois Yann, Xuechen Li, Carlos Guestrin, Percy Liang, and Tatsunori B. Hashimoto. 2023. Stanford Alpaca: An Instruction-following LLaMA Model. Original-date: 2023-03-10T23:33:09Z.
- Touvron et al. (2023) Hugo Touvron, Thibaut Lavril, Gautier Izacard, Xavier Martinet, Marie-Anne Lachaux, Timothée Lacroix, Baptiste Rozière, Naman Goyal, Eric Hambro, Faisal Azhar, Aurelien Rodriguez, Armand Joulin, Edouard Grave, and Guillaume Lample. 2023. LLaMA: Open and Efficient Foundation Language Models. ArXiv:2302.13971 [cs].
- Wang et al. (2018) Alex Wang, Amanpreet Singh, Julian Michael, Felix Hill, Omer Levy, and Samuel Bowman. 2018. GLUE: A Multi-Task Benchmark and Analysis Platform for Natural Language Understanding. In Proceedings of the 2018 EMNLP Workshop BlackboxNLP: Analyzing and Interpreting Neural Networks for NLP, pages 353–355, Brussels, Belgium. Association for Computational Linguistics.
- Wang et al. (2021) Boxin Wang, Chejian Xu, Shuohang Wang, Zhe Gan, Yu Cheng, Jianfeng Gao, Ahmed Hassan Awadallah, and Bo Li. 2021. Adversarial GLUE: A Multi-Task Benchmark for Robustness Evaluation of Language Models.
- Wang et al. (2023a) Jindong Wang, Xixu Hu, Wenxin Hou, Hao Chen, Runkai Zheng, Yidong Wang, Linyi Yang, Haojun Huang, Wei Ye, Xiubo Geng, Binxin Jiao, Yue Zhang, and Xing Xie. 2023a. On the Robustness of ChatGPT: An Adversarial and Out-of-distribution Perspective.
- Wang et al. (2023b) Yizhong Wang, Hamish Ivison, Pradeep Dasigi, Jack Hessel, Tushar Khot, Khyathi Raghavi Chandu, David Wadden, Kelsey MacMillan, Noah A Smith, Iz Beltagy, and Hannaneh Hajishirzi. 2023b. How far can camels go? exploring the state of instruction tuning on open resources. In Advances in Neural Information Processing Systems.
- Wang et al. (2022) Yizhong Wang, Swaroop Mishra, Pegah Alipoormolabashi, Yeganeh Kordi, Amirreza Mirzaei, Anjana Arunkumar, Arjun Ashok, Arut Selvan Dhanasekaran, Atharva Naik, David Stap, Eshaan Pathak, Giannis Karamanolakis, Haizhi Gary Lai, Ishan Purohit, Ishani Mondal, Jacob Anderson, Kirby Kuznia, Krima Doshi, Maitreya Patel, Kuntal Kumar Pal, Mehrad Moradshahi, Mihir Parmar, Mirali Purohit, Neeraj Varshney, Phani Rohitha Kaza, Pulkit Verma, Ravsehaj Singh Puri, Rushang Karia, Shailaja Keyur Sampat, Savan Doshi, Siddhartha Mishra, Sujan Reddy, Sumanta Patro, Tanay Dixit, Xudong Shen, Chitta Baral, Yejin Choi, Noah A. Smith, Hannaneh Hajishirzi, and Daniel Khashabi. 2022. Super-NaturalInstructions: Generalization via Declarative Instructions on 1600+ NLP Tasks. ArXiv:2204.07705 [cs].
- Warstadt et al. (2019) Alex Warstadt, Amanpreet Singh, and Samuel R. Bowman. 2019. Neural Network Acceptability Judgments. Transactions of the Association for Computational Linguistics, 7:625–641. Place: Cambridge, MA Publisher: MIT Press.
- Wei et al. (2022) Jason Wei, Maarten Bosma, Vincent Y. Zhao, Kelvin Guu, Adams Wei Yu, Brian Lester, Nan Du, Andrew M. Dai, and Quoc V. Le. 2022. Finetuned Language Models Are Zero-Shot Learners. ArXiv:2109.01652 [cs].
- Williams et al. (2018) Adina Williams, Nikita Nangia, and Samuel Bowman. 2018. A Broad-Coverage Challenge Corpus for Sentence Understanding through Inference. In Proceedings of the 2018 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long Papers), pages 1112–1122, New Orleans, Louisiana. Association for Computational Linguistics.
- Winkens et al. (2020) Jim Winkens, Rudy Bunel, Abhijit Guha Roy, Robert Stanforth, Vivek Natarajan, Joseph R. Ledsam, Patricia MacWilliams, Pushmeet Kohli, Alan Karthikesalingam, Simon Kohl, Taylan Cemgil, S. M. Ali Eslami, and Olaf Ronneberger. 2020. Contrastive Training for Improved Out-of-Distribution Detection. ArXiv:2007.05566 [cs, stat].
- Xu et al. (2022) Hanwei Xu, Yujun Chen, Yulun Du, Nan Shao, Yanggang Wang, Haiyu Li, and Zhilin Yang. 2022. ZeroPrompt: Scaling Prompt-Based Pretraining to 1,000 Tasks Improves Zero-Shot Generalization. ArXiv:2201.06910 [cs].
- Zhang et al. (2023) Shengyu Zhang, Linfeng Dong, Xiaoya Li, Sen Zhang, Xiaofei Sun, Shuhe Wang, Jiwei Li, Runyi Hu, Tianwei Zhang, Fei Wu, and Guoyin Wang. 2023. Instruction Tuning for Large Language Models: A Survey. ArXiv:2308.10792 [cs].
- Zhang et al. (2015) Xiang Zhang, Junbo Zhao, and Yann LeCun. 2015. Character-level Convolutional Networks for Text Classification. In Advances in Neural Information Processing Systems, volume 28. Curran Associates, Inc.
- Zhang et al. (2019) Yuan Zhang, Jason Baldridge, and Luheng He. 2019. PAWS: Paraphrase Adversaries from Word Scrambling. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers), pages 1298–1308, Minneapolis, Minnesota. Association for Computational Linguistics.
- Zhu et al. (2023) Kaijie Zhu, Jindong Wang, Jiaheng Zhou, Zichen Wang, Hao Chen, Yidong Wang, Linyi Yang, Wei Ye, Yue Zhang, Neil Zhenqiang Gong, and Xing Xie. 2023. PromptBench: Towards Evaluating the Robustness of Large Language Models on Adversarial Prompts. ArXiv:2306.04528 [cs].
Appendix A Datasets
| Task Category | Dataset | Count |
| Natural Language Inference(NLI) | ANLI(R1) | 2664 |
| ANLI(R2) | 2670 | |
| ANLI(R3) | 2658 | |
| CB | 232 | |
| MNLI-Matched | 2678 | |
| MNLI-Mismatched | 2678 | |
| QNLI | 2682 | |
| RTE | 2328 | |
| SNLI | 2682 | |
| WNLI | 920 | |
| Sentiment Analysis | IMDB | 354 |
| Sent140 | 2684 | |
| SST2 | 2682 | |
| Yelp | 834 | |
| Paraphrase Identification | MRPC | 2684 |
| QQP | 2684 | |
| PAWS Wiki | 2684 | |
| STS-B | 2682 | |
| Reading Comprehension | BoolQ | 1044 |
| MultiRC | 30 | |
| Coreference Resolution | WSC273 | 720 |
| Summarization | AG News | 2678 |
| Miscellaneous | TREC | 2682 |
| CoLA | 2684 | |
| WIC | 2684 | |
| Total | 52002 |
For the training dataset sampled from the FLAN collection released under Apache-2.0 license, we select 25 datasets with answer options, which can be classified into 7 categories:
-
1.
Natural Language Inference (NLI): how two sentences are related. The following datasets are used:
- 2.
- 3.
- 4.
-
5.
Coreference: find expressions that refer to the same entity in the input text. WSC273 dataset is used Levesque et al. (2012).
-
6.
Summarization: produce an abbreviated summary of the input text. For input with answer options, the model is asked to, for instance, choose the broader topic or the best summary among all choices provided. AG news dataaset is used Zhang et al. (2015).
-
7.
Miscellaneous:
Refer to Table 3 for number of entries filtered and selected out from each dataset following the rules described in section 4.1.
Appendix B Detailed Experiment Results
| Perturbation | CoLA | MNLI | MNLI-m | MNLI-mm | MRPC | QNLI | QQP | RTE | SST2 | WNLI | Average | |
| 1 | Clean | 66.4 6.0 | 67.7 2.6 | 67.8 2.6 | 65.8 1.4 | 63.6 15.2 | 62.3 5.5 | 66.4 12.1 | 81.7 2.9 | 90.1 1.7 | 56.6 3.9 | 68.8 11.6 |
| DeepWordBug | 65.0 3.4 | 65.2 1.7 | 64.6 1.8 | 63.3 2.0 | 63.3 11.3 | 54.7 3.5 | 57.6 11.2 | 75.3 3.6 | 90.3 1.8 | 52.8 4.2 | 65.2 11.8 | |
| TextFooler | 58.7 11.0 | 65.4 1.9 | 66.2 2.8 | 64.3 3.7 | 59.9 10.7 | 46.8 6.0 | 55.6 12.0 | 74.1 4.1 | 85.0 13.4 | 54.0 3.1 | 63.0 13.0 | |
| CheckList | 61.3 13.0 | 67.7 1.8 | 66.8 1.9 | 64.3 3.2 | 57.8 17.3 | 51.3 10.0 | 61.9 12.6 | 80.5 2.4 | 91.1 1.6 | 57.5 2.8 | 66.0 14.2 | |
| Semantic | 68.8 3.6 | 65.1 1.7 | 65.4 1.6 | 64.9 3.2 | 62.6 15.8 | 56.5 7.8 | 65.8 10.3 | 79.6 2.4 | 89.9 1.9 | 56.3 5.2 | 67.5 11.9 | |
| 10 | Clean | 69.6 3.2 | 65.8 2.1 | 65.4 2.7 | 64.6 2.2 | 71.7 8.1 | 62.5 5.2 | 68.7 9.5 | 81.7 2.9 | 90.0 2.4 | 56.8 3.0 | 69.7 10.4 |
| DeepWordBug | 66.3 2.5 | 64.8 1.8 | 64.9 1.5 | 61.3 1.6 | 70.4 6.6 | 55.4 4.0 | 57.4 7.2 | 76.5 3.6 | 89.4 2.6 | 56.8 4.7 | 66.3 10.7 | |
| TextFooler | 61.2 9.6 | 63.5 1.8 | 64.6 1.6 | 62.8 3.6 | 70.2 8.2 | 48.4 5.1 | 56.0 11.2 | 74.4 3.9 | 84.2 12.9 | 57.3 1.9 | 64.3 12.0 | |
| CheckList | 67.6 8.0 | 66.1 1.7 | 66.9 2.2 | 62.6 2.0 | 64.8 17.0 | 53.2 10.4 | 61.4 11.1 | 80.3 2.6 | 90.9 2.2 | 58.2 2.7 | 67.2 13.0 | |
| Semantic | 69.4 1.3 | 63.7 1.5 | 64.4 1.3 | 63.1 2.6 | 69.7 10.3 | 57.2 7.1 | 67.4 8.7 | 79.5 2.7 | 89.8 2.4 | 58.5 4.1 | 68.3 10.7 | |
| 100 | Clean | 69.3 3.2 | 68.9 1.7 | 69.1 1.9 | 66.8 3.1 | 73.6 3.8 | 62.3 5.9 | 70.1 7.8 | 82.4 1.6 | 90.6 1.1 | 62.0 3.2 | 71.5 9.2 |
| DeepWordBug | 66.5 3.8 | 68.4 1.8 | 68.7 1.6 | 65.5 2.9 | 73.5 2.7 | 55.2 4.3 | 61.9 8.4 | 77.3 3.6 | 91.1 2.1 | 57.5 2.5 | 68.6 10.6 | |
| TextFooler | 62.1 6.6 | 66.8 2.9 | 67.5 2.3 | 66.0 1.5 | 72.1 4.9 | 48.5 7.4 | 60.3 9.6 | 73.7 4.5 | 85.8 10.9 | 56.3 2.8 | 65.9 11.5 | |
| CheckList | 68.9 5.4 | 69.2 3.0 | 69.4 2.8 | 66.3 3.7 | 64.9 12.8 | 53.8 10.0 | 66.1 8.8 | 80.6 3.1 | 91.6 0.7 | 57.0 2.4 | 68.8 12.1 | |
| Semantic | 68.7 2.1 | 66.9 1.7 | 67.0 2.5 | 64.0 2.4 | 72.3 6.8 | 55.0 9.6 | 70.7 6.7 | 79.8 3.5 | 91.1 0.7 | 59.2 4.7 | 69.5 10.9 | |
| 1000 | Clean | 70.4 3.9 | 68.8 2.7 | 68.0 2.2 | 67.6 3.5 | 70.6 3.5 | 61.9 6.0 | 70.1 6.0 | 82.3 1.5 | 91.4 0.7 | 59.9 2.5 | 71.1 9.5 |
| DeepWordBug | 66.9 3.0 | 68.2 2.0 | 67.5 1.3 | 66.6 4.0 | 72.4 2.5 | 58.7 4.2 | 64.7 8.0 | 78.5 3.1 | 91.1 2.1 | 58.9 2.6 | 69.4 9.8 | |
| TextFooler | 66.5 4.5 | 67.4 1.7 | 67.7 3.0 | 66.1 2.3 | 71.9 5.4 | 49.9 7.5 | 63.9 6.0 | 75.6 3.5 | 85.6 11.6 | 60.1 3.8 | 67.5 10.5 | |
| CheckList | 68.4 7.2 | 67.7 3.5 | 68.2 2.6 | 66.3 3.6 | 63.3 9.6 | 55.4 9.5 | 66.8 6.1 | 79.8 3.5 | 92.3 0.6 | 59.6 2.8 | 68.8 11.4 | |
| Semantic | 69.7 1.2 | 66.3 1.8 | 67.0 0.5 | 64.3 2.6 | 72.6 5.8 | 56.1 10.0 | 68.5 6.3 | 78.5 4.5 | 91.6 0.6 | 59.2 2.0 | 69.4 10.6 | |
| 10000 | Clean | 69.6 5.5 | 67.9 2.4 | 68.6 2.1 | 67.4 1.7 | 69.0 8.5 | 63.9 6.0 | 72.9 5.9 | 81.1 2.2 | 91.3 0.9 | 56.8 4.7 | 70.8 10.1 |
| DeepWordBug | 66.4 3.7 | 67.2 2.7 | 67.4 2.0 | 66.9 3.5 | 64.3 8.0 | 59.8 4.4 | 65.9 9.0 | 77.2 2.4 | 90.7 2.7 | 58.5 2.7 | 68.5 10.0 | |
| TextFooler | 62.9 7.9 | 66.7 2.7 | 66.5 2.7 | 65.6 2.7 | 68.4 9.4 | 54.8 7.3 | 66.8 6.3 | 76.2 3.6 | 84.8 11.5 | 61.0 3.5 | 67.4 10.1 | |
| CheckList | 68.9 7.9 | 67.2 2.9 | 67.4 2.8 | 65.4 2.4 | 61.7 17.6 | 59.2 9.0 | 70.5 6.6 | 79.7 3.1 | 92.2 0.5 | 58.7 3.8 | 69.1 12.1 | |
| Semantic | 69.5 2.8 | 65.9 2.1 | 66.1 2.3 | 65.5 2.2 | 67.2 13.4 | 60.1 7.7 | 70.7 6.6 | 77.9 4.6 | 91.4 0.9 | 58.0 1.5 | 69.2 10.7 | |
| 100000000 | Clean | 70.4 3.0 | 66.2 2.1 | 66.1 1.9 | 65.7 1.7 | 55.0 10.3 | 61.2 7.3 | 70.9 4.9 | 83.3 1.1 | 90.6 1.5 | 56.6 3.7 | 68.6 11.5 |
| DeepWordBug | 64.4 4.5 | 63.4 3.0 | 63.2 2.7 | 64.1 2.0 | 46.2 4.3 | 60.3 5.8 | 64.6 6.0 | 80.3 2.4 | 86.7 6.3 | 56.3 4.0 | 65.0 11.6 | |
| TextFooler | 62.9 8.1 | 64.3 3.7 | 62.7 3.6 | 63.9 3.4 | 49.1 8.2 | 54.2 7.6 | 65.4 2.9 | 78.5 3.2 | 81.6 12.7 | 58.5 2.9 | 64.1 11.4 | |
| CheckList | 70.5 3.3 | 67.1 2.0 | 66.6 2.6 | 65.8 2.0 | 50.4 16.3 | 57.8 9.4 | 66.3 5.1 | 81.8 2.3 | 90.9 1.2 | 58.0 4.0 | 67.5 12.9 | |
| Semantic | 69.2 3.9 | 64.3 2.6 | 64.5 2.5 | 64.1 2.8 | 56.4 16.4 | 57.3 8.1 | 75.0 5.8 | 78.8 5.6 | 91.4 1.4 | 55.9 2.7 | 67.7 12.6 |
For the results of models trained with different contrastive loss weighting, refer to Table 4.
Appendix C GLUE Datasets Category
| Task Category | Datasets |
| Sentiment Analysis | SST-2 |
| Grammar Correctness | CoLA |
| Paraphrase Identification | QQP, MRPC |
| Natural Language Inference | MNLI, QNLI, RTE, WNLI |
Following the task category defined in PromptBench benchmark, we split the GLUE datasets into four categories as shown in Table 5.