Continuous generation of confined bubbles: viscous effect on the gravito-capillary pinch off
Abstract
We investigate continuous generation of bubbles from a bath of air in viscous liquid in a confined geometry. In our original setup, bubbles are spontaneously generated by virtue of buoyancy and a gate placed in the cell: the gate acts like an inverted funnel trapping air beneath it before continuously generating bubbles at the tip. The dynamics is characterized by the period of the bubble formation and the size of bubbles as a function of the amount of air under the gate. By analyzing the data obtained for various parameters, we successfully identified in a clear manner that the dynamics of the bubble formation is governed by dissipation in thin films whose thickness is determined by Derjaguin’s law balanced by a gravitational energy change due to buoyancy, after examining numerous possibilities of dissipation, demonstrating the potential of scaling analysis even in extremely complex cases. Furthermore, we uncover a novel type of pinch-off condition, which convincingly explains the size of the bubble created: in the present case viscosity plays a vital role beyond the conventional mechanism of Tate in which gravity competes with capillarity, revealing a general mechanism of pinching-off at low Reynolds number. Accordingly, the present study significantly and fundamentally advance our knowledge of bubble generation and bubble pinch-off in a clear manner with the results relevant for a wide variety of applications in many fields. In particular, the present study demonstrates a new avenue in microfluidics for understanding physical principles by scaling up the system, without losing the characters of the flow at low Reynolds numbers.
Drop and bubble formation at the end of a tube has been the subject of active investigations for a long time not only from fundamental but also from applicational interests in drop and bubbles DynamicsDroplets , which includes oil recovery HeleShawPetroleum2010 , soft electronics babatain2024droplets and energy harvesting xu2020droplet . As early as in 1864, Tate discussed a pendant drop at the tip of a tube starts falling when its weight surpasses the capillary force supporting the weight Tate , which remains a fundamental knowledge to measure surface tension vinet1993surface ; berry2015measurement . A technically more sophisticated modern version of Tate, the continuous generation of droplets becomes increasingly important in microfluidics umbanhowar2000monodisperse ; christopher2007microfluidic ; zhu2017passive due to recent demand for the manipulation of small amounts of liquids in various fields such as medicine, biochemistry, and pharmaceutical industries. However, basic physical principles governing the dynamics of the droplets formation at small scales and/or at low Reynolds numbers have yet to be elucidated. One of the difficulties in tacking with this problem in microfluidics is the smallness of the system. One possible strategy to cope with this difficulty might be to use highly viscous liquid on centimeter scales in confined space. By virtue of this strategy, we have unveiled a number of governing principles regarding drop and bubble dynamics in the form of scaling laws, focusing on viscous friction EriSoftMat2011 ; yahashi2016 ; murano2020rising ; tanaka2023viscous , coalescence EriOkumura2010 ; YokotaPNAS2011 ; koga2022inertial , breakup nakazato2018self ; nakazato2022air , and bursting murano2018bursting . In this study, we focus on the continuous formation of bubbles on centimeter scales in a confined geometry, which is much more directly relevant for microfluidics, to reveal physical principles governing the dynamics in the form of scaling laws. Using an original setup, we successfully obtained scaling laws through a clear data collapse with elucidating physical pictures behind the simple laws.
Salient features of the present study is as follows. (1) To provide an example of emergence of scaling laws from numerous possibility of viscous dissipations; in other words, we have obtained a remarkably simple physics from a seemingly very complex problem, demonstrating the power of scaling analysis at a high level not achieved previously. (2) To provide a condition of breakup in which viscous effect is crucial in addition to the conventional Tate’s mechanism of the balance of gravity and capillarity, revealing a novel and general mechanism of pinching-off. (3) To provide an example, in which physical principles relevant for microfluidics can be effectively elucidated by using a system on centimeter scales without losing the feature of the flow at low Reynolds numbers. The present results not only advance fundamental knowledge on drops and bubbles but also provide guiding principles relevant for numerous applications at low Reynolds numbers in various fields such as microfluidics and oil industry.
In this experiment, we fabricate a thin cell sometimes called a Hele-Shaw cell (of thickness to 2.0 mm, width 15 cm and height 20 cm) equipped with a gate (of width and angle to 60 deg.) and fill the cell with a viscous liquid (of kinematic viscosity to 50 cS), as in Fig. 1 (a). We inject air with a syringe through a brass tube (of inner radius 3.8 mm) at the bottom of the cell to observe a squashed chunk of air rising in the viscous liquid, which is trapped for a while under the gate with reducing its mass as a result of continuously generating bubbles, as in Fig. 1 (b). To characterize the dynamics, we measure the period of generation and the characteristic size () of the bubble seen from front as a function of the height of the air trapped under the gate [see the rightmost photo of Fig. 1 (b)].
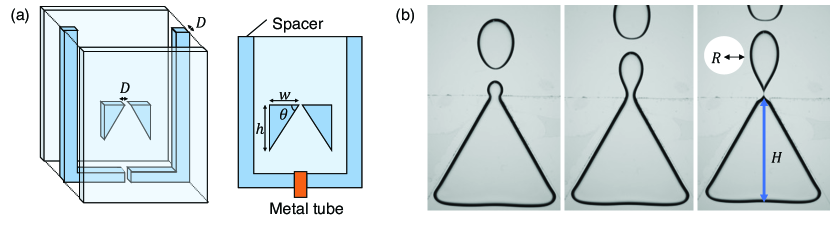
The density and surface tension of the viscous liquid [polydimethylsiloxane (PDMS)] are to kg/m3 and mN/m, respectively. To prevent cell deformation due to capillary adhesion, we use 5mm-thick acrylic plates for , 1.5 mm and 3 mm-thick acrylic plates for mm. In fact, the cell thickness is precisely determined using the laser distance sensor (ZS-HLD2, Omron) and the precise value is used in the analysis, although, for simplicity, is represented by approximate values (1.0, 1.5, or 3 mm) as above (differences are within 3%).
Since the bubble has a tear-drop shape (of area ) as seen in Fig.
1 (b), the characteristic size is defined through the relation
. The period of generation for a bubble is defined as the
time difference between the moment of pinch-off the bubble of our focus and
that of the previous bubble. Similarly, for a bubble of our focus is
defined as the height at the moment of pinch-off of the previous
bubble.
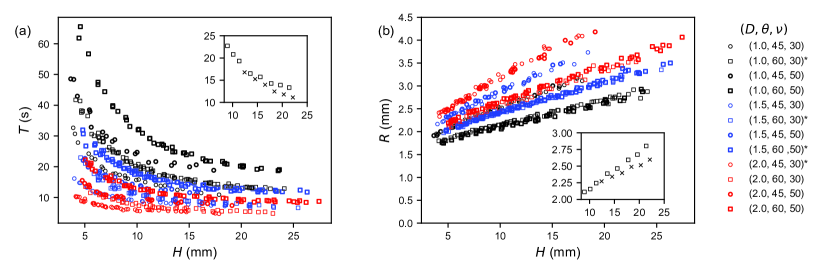
In Fig. 2 (a) and (b), we respectively show and as a function of . The data corresponding to the label with the * mark contain data obtained on different days with refabricating cells on each day (those without * are obtained within two hours using the same cell). We see the data sets with * for a parameter set are well on a master curve, which demonstrates a reasonably good reproducibility of the experiment.
The insets shows that and as a function of start bifurcating (or oscillating with ) as decreases, where we analyze only the data on the upper branch (we do not use the data represented by the cross mark in the following). The reason of the bifurcation or oscillation is as follows. Due to the continuous bubble generation from air trapped under the gate, the volume of air under the gate (and thus ) keep decreasing, and the period of generation of bubbles decreases with time (and thus with decrease in ). This implies that the distance between created bubbles becomes short with time. As a result, at certain point, the upwards flow caused by a bubble just created could start to affect the creation of the next bubble. If the th bubble drags the th bubble, which results in and in the lower branch (represented by the cross mark), then the th bubble is no longer affected by the th bubble. However, the th bubble does drag the th bubble. In this way, we observe the alternate bifurcation (or oscillation with ), where the th bubbles (with ) are of our focus because the creation of them is completed without the drag effect of the pervious bubble.
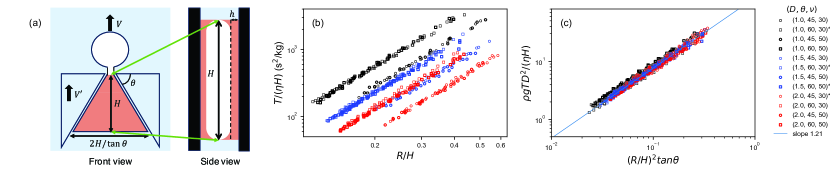
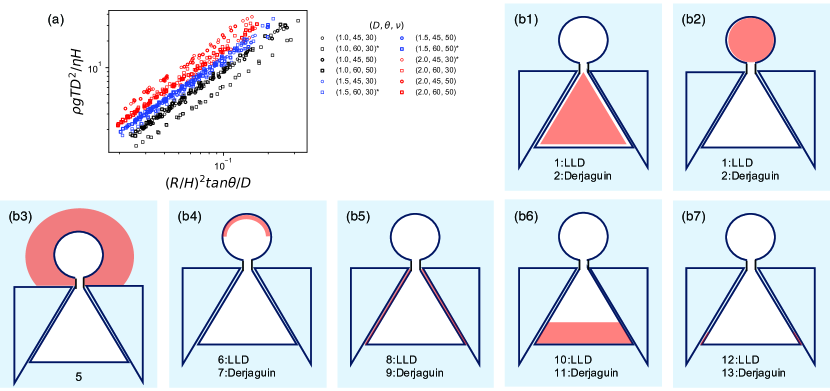
Figure 3 explains the relation between as a function of with the illustration in (a) summarizing the physical picture: the dynamics is determined by the balance between the gravitational energy change due to buoyancy and viscous dissipation in thin films whose thickness is determined by the theory not of Landau, Levich, and Derjaguin (LLD) LandauLevich ; Derjaguin1943 but of Derjaguin Derjaguin1943 ; derjaguin1993thickness . To justify this, we first confirm in (b) the relation
| (1) |
with , where the coefficient is dependent on and (Note that the former dependence is visible when the data of different colors with the same symbol are compared while the latter when those of different marks with the same colors). Then, we consider numerous possibilities of dissipation balanced with the energy change due to buoyancy, as explained in detail in Fig. 5 below. As a result, we remarkably find out that this form of scaling is possible only in the case of the dissipation in the thin film of thickness , which scales as multiplied per a volume per time. Here, characterizes the velocity inside the thin film, which should be smaller than and could be estimated by a volume conservation: . We balance this dissipation energy with the change in gravitational energy per time: with the assumption for the estimation of the volume of the bubble. If we further use the Derjaguin’s expression, with the capillary length and the capillary number , we obtain
| (2) |
This relation is convincing confirmed by a clear collapse of data shown in Fig. 3 (c) without any fitting parameters, although the agreement is not perfect: The slope of the straight line in (c) obtained by numerical fitting is , which is slightly larger than the expected value, unity. As discussed in Fig. 5 below, the theory of LLD fails to show a collapse of the data, which supports our present argument based on Derjaguin’s law.
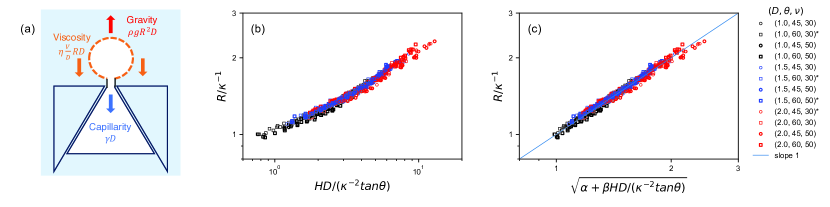
Figure 4 explains the relation between as a function of with the illustration in (a) summarizing a surprising physical picture: buoyancy opposed not only capillarity but also viscosity determines the condition of pinch-off, different from Tate’s law. If we consider a natural form of viscous stress acting on the circumference of the disk-shaped bubble whose area scales as (with the assumption ), we obtain a force balance
| (3) |
with dimensionless coefficients and . To remove from this equation, we use an equation for the bubble velocity and Eq. (2) for , we arrive at the following relation based on the unexpected pinch-off condition:
| (4) |
This equation reveals that the dimensionless quantity should be a function of a dimensionless quantity , which is convincingly confirmed in Fig. 4 (b) without any fitting parameters. We further use Eq. (4) to fit the data to obtain and by taking averages of numerical fitting for each parameter. An excellent agreement between this result of fitting and the data is shown in Fig. 4 (c).
Throughout the present study, we ignored the effect of inertia, which is justified as follows. We can estimate the upper bound for Reynolds number by once a relevant characteristic length scale is identified. Judging from Eqs. (2) and (4), it is natural to consider that would scale as , which is comparable with . Then, considering the range of parameters in the present study, we confirmed is less than 0.0005 (for mm), which means , as we assumed.
We remark that the use of Derjaguin’s law for the thickness of the thin film is supported not only by Fig. 3 but also by Fig. 4, since Eq. (4) is based on Eq. (2). In addition, as previously mentioned, we see in Fig. 5 (a) that the theory of LLD, which predicts and replaces Eq. (2) with the expression , fails to explain our results: we could not see a collapse of the data when is plotted as a function . In general, LLD is valid only for , while Derjaguin law is valid for larger values of CapilaryText ; maleki2011landau . In the present study, is in the range from 0.00661 to 0.146, with the average 0.045 and the standard deviation 0.03, to confirm , which supports the appropriateness of the use of Derjaguin’s law, beyond the agreement shown in Figs. 4 and 5.
We examine the validity of the assumption . Considering the range of parameters in the present study, we can confirm to be in the range from 0.12 to 0.19 with the average 0.16 and the standard deviation 0.01, to reasonably well confirm .
As announced previously, we considered various possibilities for dissipation as specified in Fig. 5 (b1) to (b7), where the dissipation in thin films suggested in red was considered except for (b3), by which the dissipation developed around the bubble characterized by is represented. For the film thickness we considered both cases of LLD and Derjaguin. In total, we considered 13 possibilities, as suggested in the illustration. As a result, we found that Case 3 to 7 fail to show the dependence on observed in experiment, while Case 8 to 13 could not be put into the form in Eq. (1). The remaining possibilities were then Case 1 and 2, which were the cases already examined in the text. See further details for Appendix.
As far as we know, there are no previous studies in which a governing dissipation is singled out from numerous possibilities to results in simple and clear scaling laws as in the present study. In this sense, our case is a remarkable example, in which a simple physics emerges from complexity.
In addition, the effect of viscosity on the Tate’s condition of pinch-off uncovered in the present study should be a general mechanism to be considered in many other cases in microfluidics or/and at low Reynolds numbers. Together with this, the present study provides a clear and fundamental physical understanding for the dynamics of continuous bubble formation relevant for numerous applications, advancing and impacting on the field, demonstrating a system on centimeter scales could be useful.
Acknowledgments
We thank Mana Iwasaki and Yuka Katsumata for contribution for initial stage of the present work. This work was supported by JSPS KAKENHI Grant Number JP19H01859 and JP24K00596.
References
- (1) A. Frohn and N. Roth. Dynamics of Droplets. Springer, Berlin, 2000.
- (2) Saeed Shad, Majid Salarieh, Brij Maini, and Ian D Gates. The velocity and shape of convected elongated liquid drops in narrow gaps. J. Petroleum Sci. Eng., 72(1):67–77, 2010.
- (3) Wedyan Babatain, Min Sung Kim, and Muhammad Mustafa Hussain. From droplets to devices: Recent advances in liquid metal droplet enabled electronics. Advanced Functional Materials, 34(31):2308116, 2024.
- (4) Wanghuai Xu, Huanxi Zheng, Yuan Liu, Xiaofeng Zhou, Chao Zhang, Yuxin Song, Xu Deng, Michael Leung, Zhengbao Yang, Ronald X Xu, et al. A droplet-based electricity generator with high instantaneous power density. Nature, 578(7795):392–396, 2020.
- (5) T. Tate. Xxx. on the magnitude of a drop of liquid formed under different circumstances. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 27(181):176–180, 1864.
- (6) B Vinet, JP Garandet, and L Cortella. Surface tension measurements of refractory liquid metals by the pendant drop method under ultrahigh vacuum conditions: Extension and comments on tate’s law. Journal of applied physics, 73(8):3830–3834, 1993.
- (7) Joseph D Berry, Michael J Neeson, Raymond R Dagastine, Derek YC Chan, and Rico F Tabor. Measurement of surface and interfacial tension using pendant drop tensiometry. Journal of colloid and interface science, 454:226–237, 2015.
- (8) PB Umbanhowar, V Prasad, and David A Weitz. Monodisperse emulsion generation via drop break off in a coflowing stream. Langmuir, 16(2):347–351, 2000.
- (9) Gordon F Christopher and Shelly L Anna. Microfluidic methods for generating continuous droplet streams. Journal of Physics D: Applied Physics, 40(19):R319, 2007.
- (10) Pingan Zhu and Liqiu Wang. Passive and active droplet generation with microfluidics: a review. Lab on a Chip, 17(1):34–75, 2017.
- (11) Ayako Eri and Ko Okumura. Viscous drag friction acting on a fluid drop confined in between two plates confined in between two plates. Soft Matter, 7:5648, 2011.
- (12) Misato Yahashi, Natsuki Kimoto, and Ko Okumura. Scaling crossover in thin-film drag dynamics of fluid drops in the hele-shaw cell. Sci. Rep., 6:31395, 2016.
- (13) Mayuko Murano and Ko Okumura. Rising bubble in a cell with a high aspect ratio cross-section filled with a viscous fluid and its connection to viscous fingering. Physical Review Research, 2(1):013188, 2020.
- (14) Nana Tanaka and Ko Okumura. Viscous friction acting on a solid disk falling in confined fluid: Lessons for the scaling analysis. Physical Review Research, 5(3):L032047, 2023.
- (15) Ayako Eri and Ko Okumura. Bursting of a thin film in a confined geometry: Rimless and constant-velocity dewetting. Phys. Rev. E, 82(3):030601(R), Sep 2010.
- (16) Maria Yokota and Ko Okumura. Dimensional crossover in the coalescence dynamics of viscous drops confined in between two plates. Proc. Nat. Acad. Sci. (U.S.A.), 108:6395–6398; In this issue, PNAS, 108 (2011) 6337., 2011.
- (17) Yukina Margaret Koga and Ko Okumura. Inertial coalescence of a liquid drop surrounded by viscous liquid. Journal of the Physical Society of Japan, 91(2):025001, 2022.
- (18) Hana Nakazato, Yuki Yamagishi, and Ko Okumura. Self-similar dynamics of air film entrained by a solid disk in confined space: A simple prototype of topological transitions. Physical Review Fluids, 3(5):054004, 2018.
- (19) Hana Nakazato and Ko Okumura. Air entrained into viscous liquid by a disk: Confinement induced suppression of breakup. Physical Review Research, 4(1):013150, 2022.
- (20) Mayuko Murano and Ko Okumura. Bursting dynamics of viscous film without circular symmetry: The effect of confinement. Physical Review Fluids, 3(3):031601, 2018.
- (21) L Landau and B Levich. Physicochim. Acta. Physicochim (URSS), 17:42, 1942.
- (22) B.V. Derhaguin. Doklady AN S.S.S.R., 11:39, 1943.
- (23) BVCR Derjaguin. On the thickness of the liquid film adhering to the walls of a vessel after emptying. Progress in Surface Science, 43(1-4):134–137, 1993.
- (24) P.-G. de Gennes, F. Brochard-Wyart, and David Quéré. Gouttes, Bulles, Perles et Ondes, 2nd. eds. Belin, Paris, 2005.
- (25) M Maleki, M Reyssat, F Restagno, D Quéré, and Christophe Clanet. Landau–levich menisci. Journal of colloid and interface science, 354(1):359–363, 2011.
Appendix
A1 Scaling for various possibilities of dissipation
Scaling laws for 13 possibilities of dissipation illustrated in Fig. 5 are summarized below:
| (A1.5) | ||||
| (A1.6) | ||||
| (A1.7) | ||||
| (A1.8) | ||||
| (A1.9) | ||||
| (A1.10) | ||||
| (A1.11) | ||||
| (A1.12) | ||||
| (A1.13) | ||||
| (A1.14) | ||||
| (A1.15) | ||||
| (A1.16) | ||||
| (A1.17) |