Context-tree weighting for real-valued time series:
Bayesian inference with hierarchical mixture models
Abstract
Real-valued time series are ubiquitous in the sciences and engineering. In this work, a general, hierarchical Bayesian modelling framework is developed for building mixture models for times series. This development is based, in part, on the use of context trees, and it includes a collection of effective algorithmic tools for learning and inference. A discrete context (or ‘state’) is extracted for each sample, consisting of a discretised version of some of the most recent observations preceding it. The set of all relevant contexts are represented as a discrete context tree. At the bottom level, a different real-valued time series model is associated with each context-state, i.e., with each leaf of the tree. This defines a very general framework that can be used in conjunction with any existing model class to build flexible and interpretable mixture models. Extending the idea of context-tree weighting leads to algorithms that allow for efficient, exact Bayesian inference in this setting. The utility of the general framework is illustrated in detail when autoregressive (AR) models are used at the bottom level, resulting in a nonlinear AR mixture model. The associated methods are found to outperform several state-of-the-art techniques on simulated and real-world experiments.
I Introduction
Modelling and inference of real-valued time series are critical tasks with important applications throughout the sciences and engineering. A wide range of approaches exist, including classical statistical methods [7, 15] as well as modern machine learning (ML) techniques, notably matrix factorisations [47, 10], Gaussian processes [34, 36, 11], and neural networks [5, 2, 48]. Despite their popularity, there has not been conclusive evidence that in general the latter outperform the former in the time series setting [24, 23, 1]. Motivated in part by the two well-known limitations of neural network models (see, e.g., [5]), namely, their lack of interpretability and their typically very large training data requirements, in this work we propose a general class of flexible hierarchical Bayesian models, which are both naturally interpretable and suitable for applications with limited training data. Also, we provide computationally efficient (linear complexity) algorithms for inference and prediction, offering another important practical advantage over ML methods [24].
The first step in the modelling design is the identification of meaningful discrete states. Importantly, these are observable rather than hidden, and given by the discretised values of some of the most recent samples. The second step is the assignment of a different time series model to each of these discrete context-based states. In technical terms, we define a hierarchical Bayesian model, which at the top level selects the set of relevant states (that can be viewed as providing an adaptive partition of the state space), and at the bottom level associates an arbitrary time series model to each state. These collections of states (equivalently, the corresponding state space partitions) are naturally represented as discrete context-trees [35, 17], which are shown to admit a natural interpretation and to enable capturing important aspects of the structure present in the data. We call the resulting model class, the Bayesian Context Trees State Space Model (BCT-SSM).
Although BCT-SSM is referred to as a ‘model’, it is in fact a general framework for building Bayesian mixture models for time series, that can be used in conjunction with any existing model class. The resulting model family is rich, and much more general than the class one starts with. For example, using any of the standard linear families (like the classical AR or ARIMA) leads to much more general models that can capture highly nonlinear trends in the data, and are easily interpretable.
It is demonstrated that employing this particular type of observable state process (as opposed to a conventional hidden state process), also facilitates very effective Bayesian inference. This is achieved by exploiting the structure of context-tree models and extending the ideas of context-tree weighting (CTW) [44] and the Bayesian Context Trees (BCT) framework of [17], which were previously used only in the restricted setting of discrete-valued time series. In this discrete setting, CTW has been used very widely for data compression [44, 43], and BCTs have been used for a range of statistical tasks, including model selection, prediction, entropy estimation, and change-point detection [32, 20, 30, 21, 29, 31]. Context-trees in data compression were also recently studied in [25, 27] and were employed in an optimisation setting in [37].
The resulting tools developed for real-valued data make the BCT-SSM a powerful Bayesian framework, which in fact allows for exact and computationally very efficient Bayesian inference. In particular, the evidence [22] can be computed exactly, with all models and parameters integrated out. Furthermore, the a posteriori most likely (MAP) partition (i.e., the MAP set of discrete states) can be identified, along with its exact posterior probability. It is also shown that these algorithms allow for efficient sequential updates, which are ideally suited for online forecasting, offering an important practical advantage over standard ML approaches.
To illustrate the application of the general framework, the case where AR models are used as a building block for the BCT-SSM is examined in detail. We refer to the resulting model class as the Bayesian context tree autoregressive (BCT-AR) model. The BCT-AR model is shown to be a flexible, nonlinear mixture of AR models which is found to outperform several state-of-the-art methods in experiments with both simulated and real-world data from standard applications of nonlinear time series from economics and finance, both in terms of forecasting accuracy and computational requirements.
Finally, we note that a number of earlier approaches employ discrete patterns in the analysis of real-valued time series [3, 4, 18, 6, 12, 14, 19, 28, 38]. These works illustrate the fact that useful and meaningful information can indeed be extracted from discrete contexts. However, in most cases the methods are either application- or task-specific, and typically resort to ad hoc considerations for performing inference. In contrast, in this work, discrete contexts are used in a natural manner by defining a hierarchical Bayesian modelling structure upon which principled Bayesian inference is performed.
II The Bayesian Context Trees State Space Model
II-A Discrete contexts
Consider a real-valued time series . The first key element of the present development is the use of an observable state for each , based on discretised versions of some of the samples preceding it. We refer to the string consisting of these discretised previous samples as the discrete context; it plays the role of a discrete-valued feature vector that can be used to identify useful nonlinear structure in the data. These contexts are extracted via simple quantisers , of the form,
| (1) |
where in this section the thresholds and the resulting quantiser are considered fixed. A systematic way to infer the thresholds from data is described in Section III-B.
This general framework can be used in conjunction with an arbitrary way of extracting discrete features, based on an arbitrary mapping to a discrete alphabet, not necessarily of the form in (1). However, the quantisation needs to be meaningful in order to lead to useful results. Quantisers as in (1) offer a generally reasonable choice although, depending on the application at hand, there are other useful approaches, e.g., quantising the percentage differences between samples.
II-B Context trees
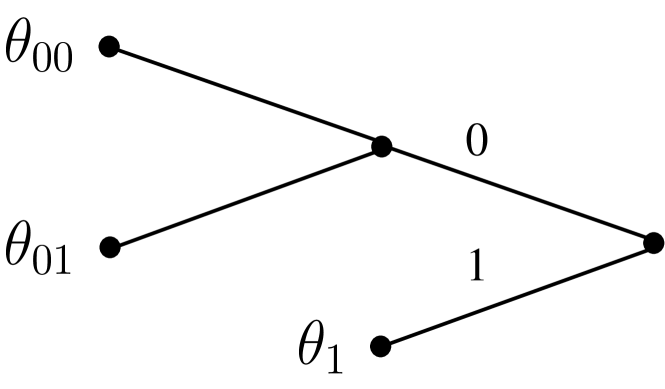
Given a quantiser as in (1), a maximum context length , and a proper -ary context tree , the context (or ‘state’) of each sample is obtained as follows. Let be the discretised string of length preceding ; the context of is the unique leaf of that is a suffix of . For example, for the context tree of Figure 1, if and then , whereas if then .
The leaves of the tree define the set of discrete states in the hierarchical model. So, for the example BCT-SSM of Figure 1, the set of states is . Equivalently, this process can be viewed as defining a partition of into three regions indexed by the contexts in
To complete the specification of the BCT-SSM, a different time series model is associated with each leaf of the context tree , giving a different conditional density for . At time , given the context determined by the past samples , the distribution of is determined by the model assigned to . Parametric models with parameters at each leaf are considered. Altogether, the BCT-SSM consists of an -ary quantiser , an -ary tree that defines the set of discrete states, and a collection of parameter vectors for the parametric models at its leaves.
Identifying with the collection of its leaves , and writing for the segment , the likelihood is,
where is the set of indices such that the context of is , and .
II-C Bayesian modelling and inference
For the top level we consider collections of states represented by context trees in the class of all proper -ary trees with depth no greater than , where is proper if any node in that is not a leaf has exactly children.
Prior structure. For the trees with maximum depth at the top level of the hierarchical model, we use the Bayesian Context Trees (BCT) prior of [17],
| (2) |
where is a hyperparameter, , is the number of leaves of , and is the number of leaves of at depth . This prior penalises larger trees by an exponential amount, a desirable property that discourages overfitting. The default value [17] is used. Given a tree model , an independent prior is placed on each , so that .
Typically, the main obstacle in performing Bayesian inference with a time series is the computation of the normalising constant (or evidence) of the posterior distriburion,
| (3) |
The power of the proposed Bayesian structure is that, although is enormously rich, consisting of doubly-exponentially many models in , it is actually possible to perform exact Bayesian inference efficiently. To that end, we introduce the Continuous Context Tree Weighting (CCTW) algorithm, and the Continuous Bayesian Context Tree (CBCT) algorithm, generalising the corresponding algorithms for discrete time series in [17]. It is shown that CCTW computes the normalising constant exactly (Theorem 1), and CBCT identifies the MAP tree model (Theorem 2). The main difference from the discrete case in [17], both in the algorithmic descriptions and in the proofs of the theorems (given in Appendix A), is that a new generalised form of estimated probabilities is introduced and used in place of their discrete versions. For a time series , these are,
| (4) |
Let be a time series, and let denote the corresponding quantised samples.
CCTW: Continuous context-tree weighting algorithm
-
1.
Build the tree , whose leaves are all the discrete contexts . Compute as given in (4) for each node of .
-
2.
Starting at the leaves and proceeding recursively towards the root compute:
where is the concatenation of context and symbol .
CBCT: Continuous Bayesian context tree algorithm
-
1.
Build the tree and compute for each node of , as in CCTW.
-
2.
Starting at the leaves and proceeding recursively towards the root compute:
-
3.
Starting at the root and proceeding recursively with its descendants, for each node: If the maximum is achieved by the first term, prune all its descendants from .
Theorem 1.
The weighted probability at the root is exactly the normalising constant of (3).
Theorem 2.
The tree produced by the CBCT algorithm is the MAP tree model, as long as .
Even in cases where the integrals in (4) are not tractable, the fact that they are in the form of standard marginal likelihoods makes it possible to compute them approximately using standard methods, e.g., [8, 9, 46]. The above algorithms can then be used with these approximations as a way of performing approximate inference for the BCT-SSM. However, this is not investigated further in this work. Instead, the general principle is illustrated via an interesting example where the estimated probabilities can be computed explicitly and the resulting mixture model is a flexible nonlinear model of practical interest. This is described in the next section, where AR models are associated to each leaf . We refer to the resulting model as the Bayesian context tree autoregressive (BCT-AR) model, which is just a particular instance of the general BCT-SSM.
III The BCT Autoregressive Model
Here we consider the BCT-SSM model class where an AR model of order is associated to each leaf of the tree ,
| (5) |
where , and .
The parameters of the model are the AR coefficients and the noise variance, so that . An inverse-gamma prior is used for the noise variance, and a Gaussian prior is placed on the AR coefficients, so that the joint prior on the parameters is , with,
where are the prior hyperparameters. This prior specification allows the exact computation of the estimated probabilities of (4), and gives closed-form posterior distributions for the AR coefficients and the noise variance. These are given in Lemmas 1 and 2, which are proven in Appendix B.
Lemma 1. For the AR model, the estimated probabilities as in (4) are given by,
| (6) |
| where | |||
| and | |||
with the sums defined as:
Lemma 2. Given a tree model , at each leaf , the posterior distributions of the AR coefficients and the noise variance are,
| (7) | ||||
| (8) |
where denotes a multivariate -distribution with degrees of freedom. Here, , and,
Corollary. The MAP estimators of and are given by,
III-A Computational complexity and sequential updates
For each symbol in a time series , exactly nodes of need to be updated, corresponding to its contexts of length . For each one of these nodes, only the quantities need to be updated, which can be done efficiently by just adding an extra term to each sum. Using these and Lemma 1, the estimated probabilities can be computed for all nodes of .
Hence, the complexity of both algorithms as a function of and is only : linear in the length of the time series and the maximum depth. Therefore, the present methods are computationally very efficient and scale well with large numbers of observations. [Taking into account and as well, it is easy to see that the complexity is .]
The above discussion also shows that, importantly, all algorithms can be updated sequentially. When observing a new sample , only nodes need to be updated, which requires operations, i.e., as a function of . In particular, this implies that sequential prediction can be performed very efficiently. Empirical running times in the forecasting experiments show that the present methods are much more efficient than essentially all the alternatives examined. In fact, the difference is quite large, especially when comparing with state-of-the-art ML models that require heavy training and do not allow for efficient sequential updates, usually giving empirical running times that are larger by several orders of magnitude; see also [24] for a relevant review comparing the computational requirements of ML versus statistical techniques.
III-B Choosing the quantiser and AR order
Finally, a principled Bayesian approach is introduced for the selection of the quantiser thresholds of (1) and the AR order . Viewed as extra parameters on an additional layer above everything else, uniform priors are placed on and , and Bayesian model selection [22] is performed to obtain their MAP values: The resulting posterior distribution is proportional to the evidence , which can be computed exactly using the CCTW algorithm (Theorem 1). So, in order to select appropriate values, suitable ranges of possible and are specified, and the values with the higher evidence are selected. For the AR order we take for an appropriate ( in our experiments), and for the we perform a grid search in a reasonable range (e.g., between the 10th and 90th percentiles of the data).
IV Experimental results
The performance of the BCT-AR model is evaluated on simulated and real-world data from standard applications of nonlinear time series in economics and finance. It is compared with the most successful previous approaches for these types of applications, considering both classical and modern ML methods. Useful resources include the R package forecast [16] and the Python library ‘GluonTS’ [2], containing implementations of state-of-the-art classical and ML methods, respectively. We briefly discuss the methods used, and refer to the packages’ documentation and for more details on the methods themselves and the training procedures carried out. Among classical statistical approaches, we compare with ARIMA and Exponential smoothing state space (ETS) models [15], with self-excited threshold autoregressive (SETAR) models [41], and with mixture autoregressive (MAR) models [45]. Among ML techniques, we compare with the Neural Network AR (NNAR) model [48], and with the most successful RNN-based approach, ‘deepAR’ [39].
IV-A Simulated data
First an experiment on simulated data is performed, illustrating that the present methods are consistent and effective with data generated by BCT-SSM models. The context tree used is the tree of Figure 1, the quantiser threshold is , and the AR order . The posterior distribution over trees, , is examined. On a time series consisting of only observations, the MAP tree identified by the CBCT algorithm is the empty tree corresponding to a single AR model, with posterior probability 99.9%. This means that the data do not provide sufficient evidence to support a more complex state space partition. With observations, the MAP tree is now the true underlying model, with posterior probability 57%. With observations, the posterior of the true model is 99.9%. So, the posterior indeed concentrates on the true model, indicating that the BCT-AR inferential framework can be very effective even with limited training data.
Forecasting. The performance of the BCT-AR model is evaluated on out-of-sample 1-step ahead forecasts, and compared with state-of-the-art approaches in four simulated and three real datasets. The first simulated dataset (sim_1) is generated by the BCT-AR model used above, and the second (sim_2) by a BCT-AR model with a ternary tree of depth 2. The third and fourth ones (sim_3 and sim_4) are generated from SETAR models of orders and , respectively. In each case, the training set consists of the first 50% of the observations; also, all models are updated at every time-step in the test set. For BCT-AR, the MAP tree with its MAP parameters is used at every time-step, which can be updated efficiently (Section III-A). From Table I, it is observed that the BCT-AR model outperforms the alternatives, and achieves the lowest mean-squared error (MSE) even on the two datasets generated from SETAR models. As discussed in Section III-A, the BCT-AR model also outperforms the alternatives in terms of empirical running times.
| BCT-AR | ARIMA | ETS | NNAR | deepAR | SETAR | MAR | |
|---|---|---|---|---|---|---|---|
| sim_1 | 0.131 | 0.150 | 0.178 | 0.143 | 0.148 | 0.141 | 0.151 |
| sim_2 | 0.035 | 0.050 | 0.054 | 0.048 | 0.061 | 0.050 | 0.064 |
| sim_3 | 0.216 | 0.267 | 0.293 | 0.252 | 0.273 | 0.243 | 0.283 |
| sim_4 | 0.891 | 1.556 | 1.614 | 1.287 | 1.573 | 0.951 | 1.543 |
| unemp | 0.034 | 0.040 | 0.042 | 0.036 | 0.036 | 0.038 | 0.037 |
| gnp | 0.324 | 0.364 | 0.378 | 0.393 | 0.473 | 0.394 | 0.384 |
| ibm | 78.02 | 82.90 | 77.52 | 78.90 | 75.71 | 81.07 | 77.02 |
IV-B US unemployment rate
An important application of SETAR models is in modelling the US unemployment rate [13, 26, 42]. As described in [42], the unemployment rate moves countercyclically with business cycles, and rises quickly but decays slowly, indicating nonlinear behaviour. Here, the quarterly US unemployment rate in the time period from 1948 to 2019 is examined (dataset unemp, 288 observations). Following [26], the difference series is considered, and a constant term is included in the AR model. For the quantiser alphabet size, is a natural choice, as will become apparent below. The threshold selected using the procedure of Section III-B is , and the MAP tree is the tree of Figure 1, with depth , leaves , and posterior probability 91.5%. The fitted BCT-AR model with its MAP parameters is,
with , and corresponding regions if , if , and if .
Interpretation. The MAP BCT-AR model finds significant structure in the data, providing a very natural interpretation. It identifies 3 meaningful states: First, jumps in the unemployment rate higher than 0.15 signify economic contractions (context 1). If there is no jump at the most recent time-point, the model looks further back to determine the state. Context 00 signifies a stable economy, as there are no jumps in the unemployment rate for two consecutive quarters. Finally, context 01 identifies an intermediate state: “stabilising just after a contraction”. An important feature identified by the BCT-AR model is that the volatility is different in each case: Higher in contractions (), smaller in stable economy regions (), and in-between for context 01 ().
Forecasting. In addition to its appealing interpretation, the BCT-AR model outperforms all benchmarks in forecasting, giving a 6% lower MSE than the second-best method (Table I).
IV-C US Gross National Product
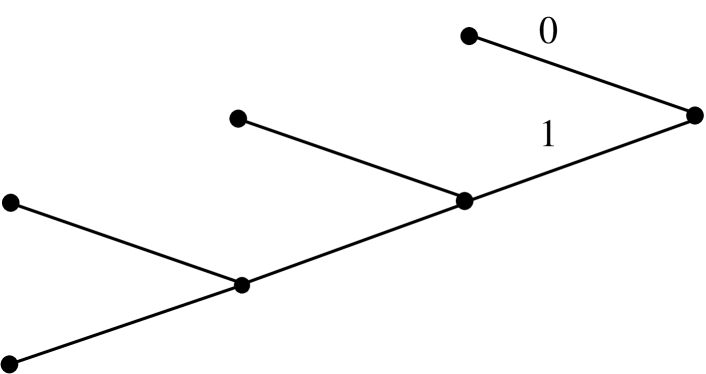
Another important example of a nonlinear time series is the US Gross National Product (GNP) [33, 13]. The quarterly US GNP in the time period from 1947 to 2019 is examined (291 observations, dataset gnp). Following [33], the difference in the logarithm of the series, , is considered. As above, is a natural choice for the quantiser size, helping to differentiate economic expansions from contractions – which govern the underlying dynamics. The MAP BCT-AR tree is shown in Figure 2: It has depth , its leaves are and its posterior probability is 42.6%.
Interpretation. Compared with the previous example, here the MAP BCT-AR model finds even richer structure in the data and identifies four meaningful states. First, as before, there is a single state corresponding to an economic contraction (which now corresponds to instead of , as the GNP obviously increases in expansions and decreases in contractions). And again, the model does not look further back whenever a contraction is detected. Here, the model also shows that the effect of a contraction is still present even after three quarters (), and that the exact ‘distance’ from a contraction is also important, with the dynamics changing depending on how much time has elapsed. Finally, the state corresponds to a flourishing, expanding economy, without a contraction in the recent past. An important feature captured by the BCT-AR model is again that the volatility is different in each case. More specifically, it is found that the volatility strictly decreases with the distance from the last contraction, starting with the maximum for and decreasing to for .
Forecasting. The BCT-AR model outperforms all benchmarks in forecasting, giving a 12% lower MSE than the second-best method, as presented in Table I.
IV-D The stock price of IBM
Finally, the daily IBM common stock closing price from May 17, 1961 to November 2, 1962 is examined (dataset ibm, 369 observations), taken from [7]. This is a well-studied dataset, with [7] fitting an ARIMA model, [40] fitting a SETAR model, and [45] fitting a MAR model to the data. Following previous approaches, the first-difference series, , is considered. The value is chosen for the alphabet size of the quantiser, with contexts naturally corresponding to the states {down, steady, up} for the stock price. Using the procedure of Section III-B to select the thresholds, the resulting quantiser regions are: if , if , and otherwise. The MAP tree is shown in Figure 3: It has depth , and its leaves are , hence identifying five states. Its posterior probability is 99.3%, suggesting that there is very strong evidence in the data supporting this exact structure, even with only 369 observations.
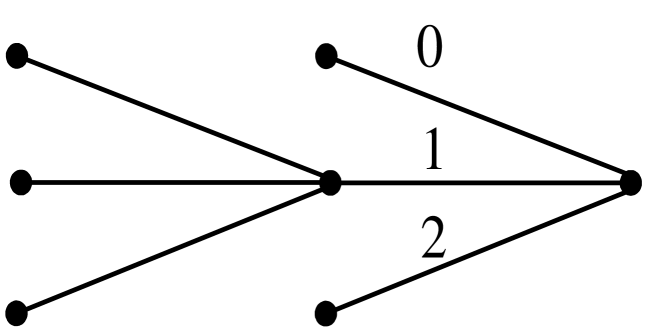
Interpretation. The BCT-AR model reveals important information about apparent structure in the data. Firstly, it admits a very simple and natural interpretation: In order to determine the AR model generating the next value, one needs to look back until there is a significant enough price change (corresponding to contexts 0, 2, 10, 12), or until the maximum depth of 2 (context 11) is reached. Another important feature captured by this model is the commonly observed asymmetric response in volatility due to positive and negative shocks, sometimes called the leverage effect [42, 7]. Even though there is no suggestion of that in the prior, the MAP parameter estimates show that negative shocks increase the volatility much more: Context 0 has the highest volatility (), with 10 being a close second (), showing that the effect of a past shock is still present. In all other cases the volatility is much smaller ().
Forecasting. As shown Table I, in this example deepAR performs marginally better in 1-step ahead forecasts, with BCT-AR, ETS and MAR also having comparable performance.
References
- [1] N.K. Ahmed, A.F. Atiya, N.E. Gayar, and H. El-Shishiny. An empirical comparison of machine learning models for time series forecasting. Econometric reviews, 29(5-6):594–621, 2010.
- [2] A. Alexandrov, K. Benidis, M. Bohlke-Schneider, V. Flunkert, J. Gasthaus, T. Januschowski, D.C. Maddix, S. Rangapuram, D. Salinas, J. Schulz, et al. GluonTS: Probabilistic time series models in python. arXiv preprint arXiv:1906.05264, 2019.
- [3] F.M. Alvarez, A. Troncoso, J.C. Riquelme, and J.S.A. Ruiz. Energy time series forecasting based on pattern sequence similarity. IEEE Transactions on Knowledge and Data Engineering, 23(8):1230–1243, 2010.
- [4] S. Alvisi, M. Franchini, and A. Marinelli. A short-term, pattern-based model for water-demand forecasting. Journal of Hydroinformatics, 9(1):39–50, 2007.
- [5] K. Benidis, S.S. Rangapuram, V. Flunkert, B. Wang, D. Maddix, C. Turkmen, J. Gasthaus, M. Bohlke-Schneider, D. Salinas, L. Stella, et al. Neural forecasting: Introduction and literature overview. arXiv preprint arXiv:2004.10240, 2020.
- [6] D.J. Berndt and J. Clifford. Using dynamic time warping to find patterns in time series. In KDD Workshop, volume 10, pages 359–370. Seattle, WA, USA, 1994.
- [7] G.E.P. Box, G.M. Jenkins, G.C. Reinsel, and G.M. Ljung. Time series analysis: forecasting and control. John Wiley & Sons, 2015.
- [8] S. Chib. Marginal likelihood from the Gibbs output. Journal of the american statistical association, 90(432):1313–1321, 1995.
- [9] S. Chib and I. Jeliazkov. Marginal likelihood from the Metropolis–Hastings output. Journal of the American statistical association, 96(453):270–281, 2001.
- [10] C. Faloutsos, J. Gasthaus, T. Januschowski, and Y. Wang. Forecasting big time series: old and new. Proceedings of the VLDB Endowment, 11(12):2102–2105, 2018.
- [11] R. Frigola. Bayesian time series learning with Gaussian processes. PhD thesis, University of Cambridge, 2015.
- [12] T.C. Fu, F.L. Chung, R. Luk, and C.M. Ng. Stock time series pattern matching: Template-based vs. rule-based approaches. Engineering Applications of Artificial Intelligence, 20(3):347–364, 2007.
- [13] B.E. Hansen. Threshold autoregression in economics. Statistics and its Interface, 4(2):123–127, 2011.
- [14] Q. Hu, P. Su, D. Yu, and J. Liu. Pattern-based wind speed prediction based on generalized principal component analysis. IEEE Transactions on Sustainable Energy, 5(3):866–874, 2014.
- [15] R. Hyndman, A.B. Koehler, J.K. Ord, and R.D. Snyder. Forecasting with exponential smoothing: the state space approach. Springer Science & Business Media, 2008.
- [16] R.J. Hyndman and Y. Khandakar. Automatic time series forecasting: the forecast package for R. Journal of Statistical Software, 26(3):1–22, 2008. https://CRAN.R-project.org/package=forecast.
- [17] I. Kontoyiannis, L. Mertzanis, A. Panotopoulou, I. Papageorgiou, and M. Skoularidou. Bayesian Context Trees: Modelling and exact inference for discrete time series. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 84(4):1287–1323, 2022.
- [18] S.S. Kozat, A.C. Singer, and G.C. Zeitler. Universal piecewise linear prediction via context trees. IEEE Transactions on Signal Processing, 55(7):3730–3745, 2007.
- [19] X. Liu, Z. Ni, D. Yuan, Y. Jiang, Z. Wu, J. Chen, and Y. Yang. A novel statistical time-series pattern based interval forecasting strategy for activity durations in workflow systems. Journal of Systems and Software, 84(3):354–376, 2011.
- [20] V. Lungu, I. Papageorgiou, and I. Kontoyiannis. Change-point detection and segmentation of discrete data using Bayesian Context Trees. arXiv preprint arXiv:2203.04341, 2021.
- [21] V. Lungu, I. Papageorgiou, and I. Kontoyiannis. Bayesian change-point detection via context-tree weighting. In 2022 IEEE Information Theory Workshop (ITW), pages 125–130. IEEE, 2022.
- [22] D.J.C. MacKay. Bayesian interpolation. Neural Computation, 4(3):415–447, 1992.
- [23] S. Makridakis, E. Spiliotis, and V. Assimakopoulos. The M4 Competition: Results, findings, conclusion and way forward. International Journal of Forecasting, 34(4):802–808, 2018.
- [24] S. Makridakis, E. Spiliotis, and V. Assimakopoulos. Statistical and machine learning forecasting methods: Concerns and ways forward. PloS one, 13(3):e0194889, 2018.
- [25] T. Matsushima and S. Hirasawa. Reducing the space complexity of a Bayes coding algorithm using an expanded context tree. In 2009 IEEE International Symposium on Information Theory, pages 719–723. IEEE, 2009.
- [26] A.L. Montgomery, V. Zarnowitz, R.S. Tsay, and G.C. Tiao. Forecasting the US unemployment rate. Journal of the American Statistical Association, 93(442):478–493, 1998.
- [27] Y. Nakahara, S. Saito, A. Kamatsuka, and T. Matsushima. Probability distribution on full rooted trees. Entropy, 24(3):328, 2022.
- [28] G. Ouyang, C. Dang, D.A. Richards, and X. Li. Ordinal pattern based similarity analysis for eeg recordings. Clinical Neurophysiology, 121(5):694–703, 2010.
- [29] I. Papageorgiou and I. Kontoyiannis. The posterior distribution of Bayesian Context-Tree models: Theory and applications. In 2022 IEEE International Symposium on Information Theory (ISIT), pages 702–707. IEEE, 2022.
- [30] I. Papageorgiou and I. Kontoyiannis. Posterior representations for Bayesian Context Trees: Sampling, estimation and convergence. Bayesian Analysis, to appear, arXiv preprint arXiv:2202.02239, 2022.
- [31] I. Papageorgiou and I. Kontoyiannis. Truly Bayesian entropy estimation. arXiv preprint arXiv:2212.06705, 2022.
- [32] I. Papageorgiou, I. Kontoyiannis, L. Mertzanis, A. Panotopoulou, and M. Skoularidou. Revisiting context-tree weighting for Bayesian inference. In 2021 IEEE International Symposium on Information Theory (ISIT), pages 2906–2911, 2021.
- [33] S.M. Potter. A nonlinear approach to US GNP. Journal of applied econometrics, 10(2):109–125, 1995.
- [34] C.E. Rasmussen and C.K.I. Williams. Gaussian processes for machine learning. MIT Press, 2006.
- [35] J. Rissanen. A universal data compression system. IEEE Transactions on Information Theory, 29(5):656–664, 1983.
- [36] S. Roberts, M. Osborne, M. Ebden, S. Reece, N. Gibson, and S. Aigrain. Gaussian processes for time-series modelling. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 371(1984):20110550, 2013.
- [37] J.J. Ryu, A. Bhatt, and Y.H. Kim. Parameter-free online linear optimization with side information via universal coin betting. In International Conference on Artificial Intelligence and Statistics, pages 6022–6044. PMLR, 2022.
- [38] E. Sabeti, P.X.K. Song, and A.O. Hero. Pattern-based analysis of time series: Estimation. In 2020 IEEE International Symposium on Information Theory (ISIT), pages 1236–1241, 2020.
- [39] D. Salinas, V. Flunkert, J. Gasthaus, and T. Januschowski. DeepAR: Probabilistic forecasting with autoregressive recurrent networks. International Journal of Forecasting, 36(3):1181–1191, 2020.
- [40] H. Tong. Non-linear time series: a dynamical system approach. Oxford University Press, 1990.
- [41] H. Tong and K.S. Lim. Threshold autoregression, limit cycles and cyclical data. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 42(3):245–268, 1980.
- [42] R.S. Tsay. Analysis of financial time series, volume 543. John Wiley & Sons, 2005.
- [43] F.M.J. Willems. The context-tree weighting method: extensions. IEEE Transactions on Information Theory, 44(2):792–798, 1998.
- [44] F.M.J. Willems, Y.M. Shtarkov, and T.J. Tjalkens. The context-tree weighting method: basic properties. IEEE Transactions on Information Theory, 41(3):653–664, 1995.
- [45] C. S. Wong and W. K. Li. On a mixture autoregressive model. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 62(1):95–115, 2000.
- [46] S.N. Wood. Fast stable restricted maximum likelihood and marginal likelihood estimation of semiparametric generalized linear models. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 73(1):3–36, 2011.
- [47] H.F. Yu, N. Rao, and I.S. Dhillon. Temporal regularized matrix factorization for high-dimensional time series prediction. Advances in neural information processing systems, 29, 2016.
- [48] G. Zhang, B.E. Patuwo, and M.Y. Hu. Forecasting with artificial neural networks: The state of the art. International journal of forecasting, 14(1):35–62, 1998.
A. Proofs of Theorems 1 and 2
The important observation here is that using the new, different form of the estimated probabilities in (4), it is still possible to factorise the marginal likelihoods for the general BCT-SSM as,
where the second equality follows from the likelihood of the general BCT-SSM, and the fact that we use independent priors on the parameters at the leaves, so that . Then, the proofs of Theorems 1 and 2 follow along the same lines as the proofs of the corresponding results for discrete time series in [17], with the main difference being that the new general version of the estimated probabilities of (4) need to be used in place of their discrete versions.
The -BCT algorithm of [17] can be generalised in a similar manner to the way the CTW and BCT algorithms were generalised. The resulting algorithm identifies the top- a posteriori most likely context trees. The proof of the theorem claiming this is similar to the proof of Theorem 3.3 of [17]. Again, the important difference, both in the algorithm description and in the proof, is that the estimated probabilities are used in place of their discrete counterparts .
B. Proofs of Lemmas 1 and 2
The proofs of these lemmas are mostly based on explicit computations. Recall that, for each context , the set consists of those indices such that the context of is . The important step in the following two proofs is the factorisation of the likelihood using the sets . In order to prove the lemmas for the AR model with parameters , we first consider an intermediate step in which the noise variance is assumed to be known and equal to .
B.1. Known noise variance
Here, an AR model with known variance is associated with every leaf of the context tree , so that,
| (9) |
In this setting, the parameters of the model are only the AR coefficients: . For these, a Gaussian prior is used,
| (10) |
where are hyperparameters.
Lemma B. The estimated probabilities for the known-variance case are given by,
| (11) |
where is the identity matrix and is given by:
| (12) |
Proof.
For the AR model of (9),
so that,
Expanding the sum in the exponent gives,
from which we obtain that,
by completing the square, where , , and,
| (13) |
So, multiplying with the prior,
where , and,
| (14) |
Therefore,
| (15) |
and hence,
Using standard matrix inversion properties, after some algebra the product can be rearranged to give exactly the required expression in (11). ∎
B.2. Proof of Lemma 1
Getting back to the original case as described in the main text, the noise variance is considered to be a parameter of the AR model, so that, . Here, the joint prior on the parameters is , where,
| (16) |
and where are hyperparameters. For , we just need to compute the integral:
| (17) |
The inner integral has exactly the form of the estimated probabilities from the previous section, where the noise variance was fixed. The only difference is that the prior of (16) now has covariance matrix instead of . So, using (11)-(12), with replaced by , we get,
with and as in Lemma 1. And using the inverse-gamma prior of (16),
| (18) |
with and . The integral in (18) has the form of an inverse-gamma density with parameters and . Its closed-form solution, as required, completes the proof of the lemma:
∎
B.3. Proof of Lemma 2
In order to derive the required expressions for the posterior distributions of and , for a leaf of model , first consider the joint posterior , given by,
where we used the fact that, in the product, only the terms involving indices are functions of . So,
Here, the first two terms can be computed from (15) of the previous section, where the noise variance was known. Again, the only difference is that we have to replace with because of the prior defined in (16). After some algebra,
with defined as in Lemma 2, and . Substituting the prior in the last expression,
| (19) |
From (19), it is easy to integrate out and get the posterior of ,
which is of the form of an inverse-gamma distribution with parameters and , proving the first part of the lemma.
However, as is a function of , integrating out requires more algebra. We have,
and substituting this in (19) gives that is proportional to,
which, as a function of , has the form of an inverse-gamma density, allowing to be integrated out. Denoting , and ,
So, as a function of , the posterior is,
which is exactly in the form of a multivariate -distribution, with being the dimension of , and with and exactly as given in Lemma 2, completing the proof. ∎