Context-sensitive neocortical neurons transform the effectiveness and efficiency of neural information processing
Abstract
Deep learning (DL) has big-data processing capabilities that are as good, or even better, than those of humans in many real-world domains, but at the cost of high energy requirements that may be unsustainable in some applications and of errors, that, though infrequent, can be large. We hypothesise that a fundamental weakness of DL lies in its intrinsic dependence on integrate-and-fire point neurons that maximise information transmission irrespective of whether it is relevant in the current context or not. This leads to unnecessary neural firing and to the feedforward transmission of conflicting messages, which makes learning difficult and processing energy inefficient. Here we show how to circumvent these limitations by mimicking the capabilities of context-sensitive neocortical neurons that receive input from diverse sources as a context to amplify and attenuate the transmission of relevant and irrelevant information, respectively. We demonstrate that a deep network composed of such local processors seeks to maximise agreement between the active neurons, thus restricting the transmission of conflicting information to higher levels and reducing the neural activity required to process large amounts of heterogeneous real-world data. As shown to be far more effective and efficient than current forms of DL, this two-point neuron study offers a possible step-change in transforming the cellular foundations of deep network architectures.
Introduction
For more than a century, theories of brain function have seen pyramidal cells as integrate-and-fire ‘point’ neurons that integrate all the incoming synaptic inputs in an identical way to compute a net level of cellular activation
[1, 2]. Modern DL models [3] and their hardware implementations (e.g. [4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16]), inspired by the point neuron, have demonstrated ground-breaking performance improvements in a range of real-world problems, including speech processing, image recognition, and object detection, yet their energy demand and complexity scale so rapidly that the technology often becomes economically, technically, and environmentally unsustainable [17, 18, 19, 20]. Attempts to solve energy issues in DL models have shown efficient computing [21, 22, 23, 24, 25, 26, 27, 28], though a biologically plausible solution which can achieve human-level computational efficiency remains an open question.
Recent neurobiological breakthroughs [29, 30, 31] have revealed
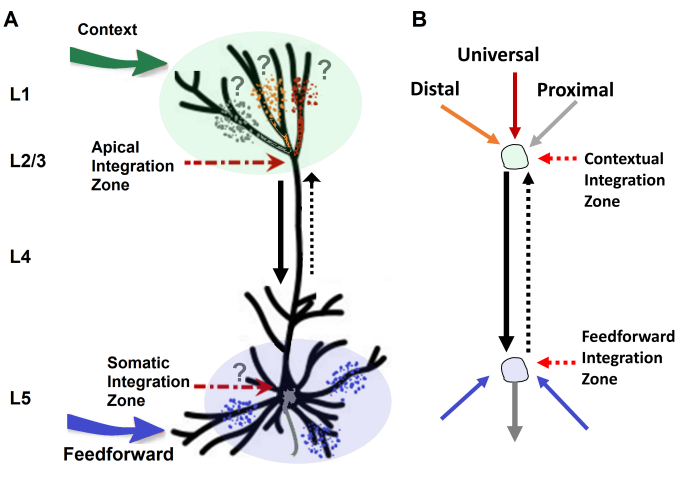
that two-point layer 5 pyramidal cells
(L5PCs) in the mammalian neocortex use their apical inputs as context to modulate the transmission of coherent feedforward (FF) inputs to their basal dendrites (Figure 1A) [29, 30, 32, 33, 31, 34, 35, 36, 37, 38, 39]. Such modulatory regulation via apical dendrites has been associated with the flexibility and reliability of neocortical dynamics [40, 41, 42]. For example, a rigorous dynamic systems perspective [43] suggests that neuromodulation selectively upregulates, and thus flexibly integrates, a subset of disparate cortical regions that would otherwise operate more independently. At a granular level, a recently reported dataset directly recorded from slices of rodent neocortex shows how L5PCs process information in a context-sensitive manner [44, 45, 46] e.g., the L5PC transmits unique information about the FF data without transmitting any unique information about the context. However, depending upon the strength of the FF input, the context adds synergy, which is the information requiring both the context and FF input. These studies test the relationship between context and FF inputs and convincingly validate the biological plausibility of the context-sensitive style of neural information
processing.
Despite rapidly growing neurobiological evidence suggesting that context-sensitive two-point neurons are fundamental for optimal learning and processing in the brain and could circumvent the computational limitations of DL, the computational potential of these neurons to process large-scale complex real-world data remained underestimated [47, 34, 48]. Therefore, these neurons have not been widely exploited by state-of-the-art DL models. Although a few machine learning studies such as [49, 50, 51] have been inspired by the discovery of two-point neurons, these methods focused predominantly on using apical inputs for credit assignment (learning). In contrast, the apical input from the feedback and lateral connections is multifaceted and far more diverse with far greater implications for ongoing learning and processing in the brain than realised [35]. Therefore, to fully benefit from the capabilities these neurons have to offer, it is critical to understand the kinds of information that arrive at the apical tuft and their influence on the cell’s response to the FF input (Figure 1B). Inspired by the latest fundamental
advances in cellular neurobiology [29, 30, 31, 32, 33, 40, 41, 42, 43, 36, 37, 38, 39, 44, 45, 46, 47, 52, 53, 54, 55, 56, 57, 58], here we address these issues and demonstrate that context-sensitive two-point neurons have information processing capabilities of the kind displayed by the neocortex and can circumvent the computational limitations of DL.
Results


Figure 2 illustrates a context-sensitive two-point neuron-inspired cooperative context-sensitive neural information processing mechanism applied to robustly deal with speech-in-noise (SIN) [61, 62, 63, 64, 65]. Specifically, Figure 2A depicts a single context-sensitive two-point auditory processor that receives input from diverse sources at the contextual integration zone and uses it as context to amplify and suppress the transmission of relevant and irrelevant FF speech signals received at the FF integration zone, respectively. For example, the processor uses information from distal visual processors as distal context (D), neighbouring auditory processors as proximal context (P), and cross-modal working memory (M) as universal context (U). The context-sensitive processor uses integrated context (C) via asynchronous modulatory transfer function (AMTF) (Figure 2B) to selectively amplify and suppress the FF transmission of the relevant and irrelevant auditory information, respectively.
The proposed AMTF uses C as a driving force to split the signal into relevant and irrelevant signals. In previously proposed AMTFs (Figure S1) [45, 46], the receptive field (R) drives the neural activity of the two-compartment L5PC. If R is strong, context is neither necessary nor sufficient for the neuron to transmit information about the R. If R is very weak (or does not exist), even a very strong context does not encourage amplification of neural activity. Here we show that context can overrule the strength of R and can conversely discourage or encourage amplification of neural activity if R is strong or weak, respectively. This new AMTF uses context as a ‘modulatory force’ to push the processor output to the positive side of the activation function (e.g., rectified linear unit (ReLU)) if R is important, otherwise to the negative side. This mechanism enhances cooperation and seeks to maximise agreement between the active processors. Nonetheless, the modulatory force that enables this move systematically could be generated in several different ways, linearly or non-linearly e.g., instead of ReLU, half-Gaussian filter could be used. The modulatory transfer function could be seen as a signalling module that signals ‘Yes’ with certain confidence if a match between data streams has been found regarding a specific sensory or cognitive feature.

Figure 3 depicts how individual local processors cooperate moment-by-moment via different contextual fields (P, D, and U) to conditionally segregate the coherent and conflicting FF signals [35, 52, 53, 54, 55]. Here, P defines the modulatory signal coming from the neighbouring cell of the same network or the cell’s output at time t-1, D defines the modulatory sensory signal coming from some other parts of the brain (in principle from anywhere in space-time), and U defines the outside environment and anticipated behavior or widely distributed general context (based on past learning and reasoning) [35]. For simplicity, U is linked to brief memory formation and retrieval which is universal in that its modulatory effect is broadcasted to all sensory modalities [59, 60].
The individual two-point processors at time t-1 use P and D to conditionally segregate the coherent and incoherent multisensory information streams and then recombine only the coherent multistream to extract synergistic FF components (brief memory). The extracted brief memory components are broadcasted and received by neighbouring processors at time t along with the current P and D. The integrated context (C) and integrated R are used by the AMTF to split the signal into coherent and incoherent signals. Here the brief working memory could be seen as if the selected relevant receptive fields (Rs) are temporarily preserved at time t-1, while attention at time t is engaged with the upcoming R e.g., holding a person’s address in mind while listening to instructions about how to get there. This is the ability of the network to retain information for a short period of time [38]. The formation of brief memory resonates well with the recent neurobiological study [57, 58], suggesting that working memory depends on recurrent amplification combined with divisive normalization. In general, U could explicitly be extended to the sources of inputs to include general information about the target domain acquired from prior experiences, emotional states, intentions, cognitive load, and semantic knowledge. Figure 4 depicts an example context-sensitive processors-driven deep convolutional neural net architecture.
The proposed basic context-sensitive neural information mechanism includes many of the anatomical and functional elements observed in slices of rodent neocortex. While our model is extremely simplified, it captures critical processing steps found, e.g., in [29, 30, 31, 44, 45, 46, 47] where the apical input amplifies and suppresses the transmission of FF input; in [52, 53, 54, 55] where the apical tuft incorporates input from both thalamic and different cortical sources to enable conditional segregation and recombination of multiple input streams; in the dataset [44, 45, 46, 47] recorded from slices of rodent neocortex that shows how inputs to the apical dendrites have distinct effects on the output that context sensitivity implies; in [59, 60] where the modulatory effect of brief memory formation and retrieval is broadcasted to all sensory modalities; and in [56, 57, 58] where apical amplification is described as recurrent drive and the recurrent weights are similar to the contextual fields specified by synapses of the apical dendrites. Furthermore, how such functional models can simulate key sequential phenomena of working memory, and in addition to being temporarily stored, information can be modified by complex sequential dynamics [58].
The proposed mechanism is compared against the point processors-driven variational autoencoder (VAE) and the vanilla version of our model (baseline). For a fair comparison, the baseline/ state-of-the-art convolutional deep model is integrated with the cross-channel communication (C3)/attention blocks [66, 67, 68, 69]. The baseline models implement C3 or cross-channel fusion through concatenation, addition, or multiplication using the ‘point’ processor [2]. Thus, each processor integrates all the incoming streams in an identical way i.e., simply summing up all the excitatory and inhibitory inputs with an assumption that they have the same chance of affecting the processor’s output [1]. The deep models reconstruct an ideal binary mask (IBM) [70] or clean short-time Fourier transform (STFT) of the audio signal given noisy audio and visuals [65, 71]. All deep models are trained with equal number of parameters using the benchmark AV Grid [72] and ChiME3 [73] corpora, with 4 different real-world noise types (cafe, street junction, public transport (BUS), pedestrian area) (see materials and methods for more details and Table S1). Comparative results demonstrate that a deep net composed of context-sensitive processors can process large amounts of AV information effectively using far fewer local processors at any time compared to point processors.


Context-sensitive processors guide audio signal processing towards the currently relevant information far more effectively and efficiently than current forms of DL: For AV speech denoising on Grid and ChiME3 datasets, we used a deep net comprising an input layer, two convolution layers, and an output layer. Audio and visual features of time instances were fed into the model, where k represents the time instance. See methods and supplementary material for detailed configurations and parameters. Training results demonstrate that a context-sensitive processors-driven deep net can reconstruct clean speech using far less number of processors compared to conventional point processors-driven deep net. Figure 5A depicts selective information processing results. It is to be observed that context-sensitive processors quickly evolve to become highly sensitive to a specific type of high-level information and ‘turn on’ only when the received signals are relevant in the current context. This allows the network to be selective as to what data is worth paying attention to and therefore processing that, instead of having to process everything. This reduction in neural activity is equivalent to a magnitude of energy efficiency during training if the synapses associated with the cells with zero activity are turned off in the hardware. Overall, in the network of 16 million parameters, the context-sensitive processors reduce their neural activity to 0.01 compared to the baseline, which converges to the neural activity of 0.45. Remarkably, context-sensitive processors achieve this low activity in just a few training updates. For a larger model comprising 40 million parameters, the context-sensitive processors reduce their activity to less than 0.008% i.e., 1250x less (per FF transmission) than the baseline (Figure S2). However, the reconstruction accuracy for both point and two-point processors drop. In this case, more tuning and optimisation are required to search for Pareto-optimal. When the context-sensitive processors were trained without memory, the network converged to the overall neural activity of 0.2 compared to 0.01 with memory (Figure S3). This suggests that selective information processing is highly dependent on the strength of context.
The effect of selective information processing is evident in mutual information (MI) estimation between high dimensional clean visual and noisy speech signals (Figure 5B). It is to be observed that the baseline models remain deficient in achieving high MI, regardless of the experimental setup, hyper-parameters, and loss function. In contrast, context-sensitive processors driven deep model converges quickly to the higher MI. We also remark that context-sensitive processors converge quickly to the true MI when the same network is used for multivariate Gaussian random variables [74] and compared against three popular point processors-driven MI neural estimation methods: f-divergence, KL-divergence, and density ratio [74] (Figure 5C).
Furthermore, context-sensitive processors are inherently robust against sudden damage. It is to be observed that when trained deep models
were tested for resilience with up to 35% randomly killed processors, context-sensitive processors degraded performance gracefully compared to point processors (Figure 5D). Despite using a few processors at any moment, context-sensitive processors-driven deep net enable faster learning at the early training stage (Figure 5E) with comparable prediction accuracy (Figure 5F).
Similar results achieved when deep models were used to reconstruct high dimensional short-time Fourier transform (STFTs) of the clean speech (Figures S4-S5). In this case, the quality of reconstruction with context-sensitive processors remained sensitive to fine-grained details and distinguished the relevant signal more easily and clearly. This had a significant impact on the reconstructed time-domain speech signal and its intelligibility (Figure S6) [65]. We conclude that context-sensitive processors-driven deep net can effectively process large amounts of heterogeneous real-world AV data using far fewer processors at any moment than point-processors-driven deep net.
Figure 6A reveals the selective amplification and suppression properties of context-sensitive processors compared to the point processors. It is to be observed that the baseline treats each input with equal importance and computes features regardless of the underlying nature of the signal. On the contrary, context-sensitive processors highlight relevant and irrelevant features. This analysis could also be seen as a Fourier analysis or time-frequency analysis explaining what matters when. We hypothesise that context-sensitive processors highlight which phonemes matters the most and discover the aspects of speech seen in the video or the structure (high-level features) at early layers. These results also show that context-sensitive processors have more processing ability to make important decisions at the cellular level. In general, these patterns are certainly providing important information as compared to the baseline. We found similar behaviour for visual features (Figure S7) and audio features in different signal-to-noise ratios (SNRs) (Figure S8). Furthermore, Figure 6B provides further insight by depicting how the data is statistically transformed through different deep layers. The autocorrelation and cross-correlation data from 32 processors are shown. It is to be observed that cross-correlation reduces significantly in the case for context-sensitive processors when data moves from one layer to the next i.e., more information passes on to the next block. In contrast, the baseline passes more redundant data to the next layer as high cross-correlation could be observed.
Discussion
Results support our hypothesis that the fundamental weakness of state-of-the-art deep learning is its dependence on a long-established simplified point processor that maximises the transmission of information regardless of its relevance to other processors or the long-term benefit of the whole network. In contrast, context-sensitive processors cooperate moment-by-moment and transmit information only when the received FF information is coherent to the overall activity of the network or relevant to the task at hand. This new style of cooperative context-sensitive neural information processing enables relevant feature extraction at very early stages in the network, leading to faster learning, reduced neural activity, and enhanced resilience.
Although point processors allow DL to learn the representation of information with multiple levels of abstraction, their processing is shallow [75]. Specifically, point processors encode the FF information based on repetition activity (learning) without any search for coherence. In contrast, our proposed cooperative context-sensitive neural information processing promotes deep information processing (DIP) [75] that allows individual processors to have more deeper and well-reasoned interaction with the received FF information. For example, the demonstration of relevant and irrelevant signals amplification and suppression, respectively, and the construction of high-level features at low-level layers show how low-level layers can make strategic decisions and restrict the transmission of conflicting information to the higher layers to avoid disorganization and achieve harmony.
It is worth mentioning that our work is not a model, but a demonstration that the cooperative context-sensitive style of computing has exceptional big data information processing capabilities. Our contribution to this rapidly growing field of research encourages machine learning experts to exploit context-sensitive processors in state-of-the-art DL models for applications where speed and the efficient use of energy are crucial. It also encourages neurobiologists to search for the essentials (fine-tunings) which were necessary to make this neurobiological mechanism work.
We learnt that cellular-level context-sensitivity plays an essential role in selective information processing, higher the context, the higher the efficient information processing. For example, when models were trained without memory (universal context), context-sensitive processors reduced the overall neural net activity but far less than processors with memory. We also found that memory components could be effectively formed through conditional segregation of relevant and irrelevant information streams and the recombination of relevant data streams. Therefore, the formation of different kinds of contexts arriving at the apical and their influence on the cell’s response to the FF input are crucial for context-sensitive neural information processing.
The proposed work also bridges the gap between Dendritic Integration Theory [53] and Global Neuronal Workspace Theory [59] e.g., the notion of universal context matches with the universal role of the NSP-thalamus whose modulatory effect is broadcasted to all sensory modalities activating other brain areas [60]. We suggest that in addition to the synergy between apical and basal information flow in L5PC [52], the synergy between different coherent information streams could be closely related to the L5PC processing. Whether this holds true or not, the role of universal context is of great importance since things are experienced differently in positive and negative frames of mind and with different intentions, attentions, hopes, and emotional states. We suggest that the universal context may be analogous to signals that regulate the balance between apical/internal/top-down/feedback and basal/external/sensory/FF inputs. Thus, switching the mode of apical function between amplification (or drive) and isolation. If so, the idea of the universal context may be relevant to a major physiological process that is only now being seen to be important [76, 54]. Finally, the notion of universal context leads us to think that the ‘self’ is an enduring part of the internal context. So, are ‘we’ the enduring internal context within which our experiences occur?
Our work supports the argument that the leaky integrate-and-fire conception of the neuron harms our progress in understanding brain function [34]. Therefore, the proposed work could help to better understand neurodevelopmental disorders such as autism and sensory overload when early brain layers fail to filter out irrelevant information and the brain becomes overwhelmed due to excessive contradictory messages transmitted to higher perceptual levels [77, 78], or epilepsy when the bursts of electrical activity in the brain cause seizures. Last but not least, the proposed work sheds light on human’s basic cooperative instinct that achieves harmony via organized cooperation between diverse neurons [79, 80, 81]. For example, the review evidence shows unequivocally that changes in brain state such as those from sleeping to waking or from low to high arousal depend on the neuromodulatory regulation of apical function in pyramidal cells [82]. It is shown how impairments of apical dendritic function have a key role in some common neurodevelopmental disorders, including autism spectrum disorders [83]. The apical dendritic mechanisms rooted in genetic foundations experience specific genetic mutations that impair these fundamental cellular mechanisms. A few convincing reviews [84, 52, 85, 76] also suggest that the thalamocortical loops with a key role in conscious experience depend on apical dendrites in L1.
Overall, to the best of our knowledge, this is the first time context-sensitive two-point L5PC mechanism has been applied to solve any challenging real-world problem, reflecting its potential to transform the capabilities of neurocomputational systems. We believe that the proposed cooperative context-sensitive style of information processing, supported by the latest and rapidly growing neurobiological discoveries on two-point cells, may be fundamental to the capabilities of the mammalian neocortex. The context sensitivity at the cellular level indeed has information processing abilities of the kind displayed by the mammalian neocortex.
Ongoing work involves using local context as a feedback error e.g., for credit assignment, as opposed to the way it is typically used for training standard deep learning algorithms [51, 49]. We aim to provide further insights into cooperative context-sensitive learning mechanism. Ongoing work also involves the demonstration of the proposed modulatory concept within unimodal streams to extend cooperative context-sensitive information processing well beyond multimodal applications. Although our results demonstrated how video modulates the transmission of auditory information and vice versa, the clean video available at each of the deep layers in our architecture may be guiding the discovery of structure shared by the audio and visual streams. Thus, ongoing work also includes analysis of the trivariate MI components transmitted by each of the deep layers in our architecture that we believe may provide a wholly new perspective on the multisensory processing and ‘merging of the senses’ in neocortex that has long been studied by many neurobiologists and psychologists. Furthermore, we will evaluate whether the proposed AV algorithm improves the transmit ion of prosodic audio information, such as tone of voice, dialect, and other audio information specific to the selected speech stream. The latter possibility is not equivalent to recognizing the phonemes in the speech and then using that to generate audio output. This issue may be crucial to identifying the distinctive capabilities of the proposed algorithms.
Materials and Methods
Context-sensitive processor:
For the sake of mathematical simplicity and generality across this section, we use Einstein tensor notation. We also reduce the discussion to vector spaces indexed by a single element as in machine learning we are only interested in numerable collections of vector spaces. Nonetheless, in some cases, it may be useful to include certain topological properties as different indices i.e. an image can be represented as . In addition, we restrict ourselves to the simple case of two channels and denote the analogue variable for the other channel with a bar and, in a huge abuse of notation, we denote every learnable variable with . Unlike previous works, our idea is to compute only the relevant information shared between channels while, at the same time, preventing local non-important information from each channel to overtake the computation. Thus, we consider a family of parametric functions composed almost entirely by transformations .
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
where is the collection of learnable parametric linear transformations of ; the operator denotes the hadamard product between and . Notice that this implicitly assumes that the vector space of both operands is of the same size, and is the activation function. In practice, we also consider another set of trainable variables which are added to the result of each transformation but including them in the previous equations may obscure the most relevant part of the computation. We can replace the operator with other operators to simulate a more complex relationship between R and C. We suspect that the exploration of better modulatory operators may play a major role in the near future. Intuitively, we enforce variables and to extract the core information that is currently held in the other parallel streams. Similarly, we enforce the term to act as a collective reservoir of important information extracted at a previous layer from both channels.
For MI estimation and speech denoising we used the following loss functions:
is a differentiable approximation for the number of firings (neural activity above zero).
We adjust the coefficients of the loss functions to make the secondary objectives significantly less important than the main goal; in particular, we set to a really small value in all experiments. Even for very small , we encounter that the gradient signal from the energy may be several orders of magnitude greater than the signal originated from the MI estimation.
MI estimation: Multimodal (MM) representation learning via MI maximization has proven to significantly improve both the classification and regression tasks [74, 86, 87]. However, MI maximization between high dimensional input variables in the presence of extreme noise is a serious challenge. Here we pose a problem of learning MM representation via estimating and maximizing the MI between high dimensional clean visual and noisy speech signals. For direct computation of the entropy or the Kullback–Leibler divergence, we uses Donsker-Varadhan representation. In other words, we transformed the mutual information estimation problem into an optimization problem [74].
Consider and two random multidimensional variables indexed by , with and and distributed as and , respectively.
The mutual information between these two variables, , is given by,
In general, direct computation of the entropy or the KL divergence is not feasible. Fortunately, it is possible to rewrite this expression using the Donsker-Varadhan representation. Thus,
| (8) |
where is a set of functions with finite expectations under and .
Hence, we have:
| (9) |
AV corpus: For AV speech processing, the Grid [72] and ChiME3 [73] corpora are used [65], including four different noise types; cafe, street junction, public transport (bus), and pedestrian area with the signal-to-noise ratio (SNRs) ranging from -12dB to 12dB with a step size of three. Grid and ChiME3 corpora are publicly available and open-source, thus, ethical approval is not needed. See Table S1 and Figure S9.
Deep multimodal supervised reconstruction: For this task, we used the mask estimation approach for speech enhancement presented in [70, 71].
A few possible configurations for context-sensitive deep information processing: (i) Feature map-wise modulation: scalar contextual fields (CFs). In this case, each feature map (FM) is averaged and multiplied by a single weight value (e.g., for P, for D, and for U) in the non-parametric modulation (NPM) layer. This configuration has an overhead of 32 parameter per CF. (ii) Feature map reduction: scalar CFs. In this case, 32 FMs are reduced, averaged, and multiplied by a single weight value. This configuration has an overhead of 1 parameter per CF (P, D, and U) (iii) Feature map-wise modulation: FM CFs In this case, each FM is passed through an integrated contextual block (C) that comprises a mixture of convolutional and Max pooling layers. This configuration has an overhead of 0.5K parameters per CF.
Simulation details: All deep models have a similar structure, layers, configuration, and total parameters. We used two convolutional layers, each with 32 filters, kernels of size 5 and stride 2. For each channel embedding, we used 128 units and for the global embedding, we used 256 units. Additional terms to the losses, like ELBO loss, were added to the loss function model-wise. All activation functions are ReLUs. All networks are initialized with a glorot uniform distribution. The Adam optimizer with a learning rate of and is used for all the experiments. Although we do not claim these configurations are optimal, we empirically observed models behaved well with this set of parameters.
Each element of the dataset is a tuple containing a noisy audio signal (ideal binary mask (IBM) [70], STFT), a snapshot of the lips of the speaker (image), and a clean audio signal. The SNR varies from +12dB to -12dB in steps of 3dB. The noisy audio was corrupted with several different noise sources. Although, more sophisticated approaches for denoising using neural networks exist, our goal is to measure the capabilities of the network using as few resources as possible (neural activity). For this experiment, we introduced a small change into the modulatory step, in which we also take the activity of neighbouring processors into account twice, once when we compute the context and again when we apply the modulation. This small change is equivalent to replacing the delta operator of equation 6.
As usual in machine learning, we take a split 80%-20% for training and testing; we leave a single sample out of training and testing splits to use as a proxy for the figures in this work.
Data is normalized across the whole dataset and presorted to break all order correlations.
The dataset is shuffled once more with a seed to add some variability between different runs and to ensure that different models encounter a similar landscape.
We use a mini-batch size of 256 for all the experiments. The average was taken from 5 different runs, using the same seeds for different models.
Auto-correlation and cross-correlation analysis: For this analysis, a semi-supervised AV speech processing with the shallow MCC and baseline model is analysed. In this experimental setup, logFB audio features of dimension 22 and DCT visual features of dimension 50 were used [64].
Resilience test: Random processors were killed (set to zero) with a probability P. To make the comparison as fair as possible, only processors from the convolutional layers were killed. Points were estimated from P=0 to 0.5 with steps of 0.025. We observed the whole testing dataset 50 times per point. The average/standard deviation was taken from the 5 runs of each model. It was observed that context-sensitive processors had significantly better resistance to processor damage. This is due to the fact that our model highlights the important features given the nature of the input, and does not look at the input processed features without any vis a vis importance or weight of the features. Empirically, we observed that the quality of the reconstruction drastically decreased when going above the 0.01 error.
Decoder details: The decoder’s initial layer is a fully connected layer followed by an (8,8,64) reshape.
We apply four transpose convolutional transformations with 64, 32, 16 and 1 filters respectively.
Kernel size is 3, the stride is 2 for all four convolutional steps.
Activation function is ReLU. Batch normalization is added prior to each ReLU to enhance even further learning speed. The decoder’s network is initialized with a glorot uniform distribution.
This simple decoder is enough to achieve an almost perfect reconstruction when provided with the clean input in just a matter of a few updates (data not shown).
Thus, the final quality of the reconstruction is entirely dependent on the quality of the features provided by the encoder.
Additional decoders required by the autoencoders have a similar structure.
Acknowledgments
This research was supported by the UK Engineering and Physical Sciences Research Council (EPSRC) Grant Ref. EP/T021063/1. We would like to acknowledge Professor Bill Phillips from the University of, Professor Peter König from the University of Osnabrück, Dr James Kay from the University of Glasgow, and Professor Newton Howard from Oxford Computational Neuroscience for their help and support in several different ways, including reviewing our work, appreciation, and encouragement.
Contributions
AA conceived and developed the original idea, wrote the manuscript, and analysed the results. AA, MF, MR, and KA performed the simulations.
Competing interests
AA has a provisional patent application for the algorithm described in this article. The other authors declare no competing interests.
Data availability The data that support the findings of this study are available on request.
References
- [1] M. Häusser, “Synaptic function: Dendritic democracy,” Current Biology, vol. 11, no. 1, pp. R10–R12, 2001.
- [2] A. Burkitt, “A review of the integrate-and-fire neuron model: I. homogeneous synaptic input,” Biological cybernetics, vol. 95, pp. 1–19, 08 2006.
- [3] Y. LeCun, Y. Bengio, and G. Hinton, “Deep learning,” nature, vol. 521, no. 7553, pp. 436–444, 2015.
- [4] M. Davies, N. Srinivasa, T.-H. Lin, G. Chinya, Y. Cao, S. H. Choday, G. Dimou, P. Joshi, N. Imam, S. Jain et al., “Loihi: A neuromorphic manycore processor with on-chip learning,” Ieee Micro, vol. 38, no. 1, pp. 82–99, 2018.
- [5] P. A. Merolla, J. V. Arthur, R. Alvarez-Icaza, A. S. Cassidy, J. Sawada, F. Akopyan, B. L. Jackson, N. Imam, C. Guo, Y. Nakamura et al., “A million spiking-neuron integrated circuit with a scalable communication network and interface,” Science, vol. 345, no. 6197, pp. 668–673, 2014.
- [6] S. B. Furber, F. Galluppi, S. Temple, and L. A. Plana, “The spinnaker project,” Proceedings of the IEEE, vol. 102, no. 5, pp. 652–665, 2014.
- [7] B. V. Benjamin, P. Gao, E. McQuinn, S. Choudhary, A. R. Chandrasekaran, J.-M. Bussat, R. Alvarez-Icaza, J. V. Arthur, P. A. Merolla, and K. Boahen, “Neurogrid: A mixed-analog-digital multichip system for large-scale neural simulations,” Proceedings of the IEEE, vol. 102, no. 5, pp. 699–716, 2014.
- [8] P. Lichtsteiner, C. Posch, and T. Delbruck, “A latency asynchronous temporal contrast vision sensor,” IEEE journal of solid-state circuits, vol. 43, no. 2, pp. 566–576, 2008.
- [9] S. Moradi, N. Qiao, F. Stefanini, and G. Indiveri, “A scalable multicore architecture with heterogeneous memory structures for dynamic neuromorphic asynchronous processors (dynaps),” IEEE transactions on biomedical circuits and systems, vol. 12, no. 1, pp. 106–122, 2017.
- [10] C. S. Thakur, J. L. Molin, G. Cauwenberghs, G. Indiveri, K. Kumar, N. Qiao, J. Schemmel, R. Wang, E. Chicca, J. Olson Hasler et al., “Large-scale neuromorphic spiking array processors: A quest to mimic the brain,” Frontiers in neuroscience, vol. 12, p. 891, 2018.
- [11] N. Qiao, H. Mostafa, F. Corradi, M. Osswald, F. Stefanini, D. Sumislawska, and G. Indiveri, “A reconfigurable on-line learning spiking neuromorphic processor comprising 256 neurons and 128k synapses,” Frontiers in neuroscience, vol. 9, p. 141, 2015.
- [12] A. Valentian, F. Rummens, E. Vianello, T. Mesquida, C. L.-M. de Boissac, O. Bichler, and C. Reita, “Fully integrated spiking neural network with analog neurons and rram synapses,” in 2019 IEEE International Electron Devices Meeting (IEDM). IEEE, 2019, pp. 14–3.
- [13] R. Wang, C. S. Thakur, G. Cohen, T. J. Hamilton, J. Tapson, and A. van Schaik, “Neuromorphic hardware architecture using the neural engineering framework for pattern recognition,” IEEE transactions on biomedical circuits and systems, vol. 11, no. 3, pp. 574–584, 2017.
- [14] J. Pei, L. Deng, S. Song, M. Zhao, Y. Zhang, S. Wu, G. Wang, Z. Zou, Z. Wu, W. He et al., “Towards artificial general intelligence with hybrid tianjic chip architecture,” Nature, vol. 572, no. 7767, pp. 106–111, 2019.
- [15] C. Frenkel, M. Lefebvre, J.-D. Legat, and D. Bol, “A 0.086-mm2 12.7-pj/sop 64k-synapse 256-neuron online-learning digital spiking neuromorphic processor in 28-nm cmos,” IEEE Transactions on Biomedical Circuits and Systems, vol. 13, no. 1, pp. 145–158, 2019.
- [16] G. K. Chen, R. Kumar, H. E. Sumbul, P. C. Knag, and R. K. Krishnamurthy, “A 4096-neuron 1m-synapse 3.8-pj/sop spiking neural network with on-chip stdp learning and sparse weights in 10-nm finfet cmos,” IEEE Journal of Solid-State Circuits, vol. 54, no. 4, pp. 992–1002, 2018.
- [17] A. Mehonic and A. J. Kenyon, “Brain-inspired computing needs a master plan,” Nature, vol. 604, no. 7905, pp. 255–260, 2022.
- [18] N. C. Thompson, K. Greenewald, K. Lee, and G. F. Manso, “The computational limits of deep learning,” ArXiv, vol. abs/2007.05558, 2020.
- [19] E. Strubell, A. Ganesh, and A. McCallum, “Energy and policy considerations for deep learning in nlp,” Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, pages 3645–3650, 2019.
- [20] ——, “Energy and policy considerations for modern deep learning research,” in Proceedings of the AAAI Conference on Artificial Intelligence, vol. 34, no. 09, 2020, pp. 13 693–13 696.
- [21] Y. Chen, D. Paiton, and B. Olshausen, “The sparse manifold transform,” Advances in neural information processing systems, vol. 31, 2018.
- [22] T. Hoefler, D. Alistarh, T. Ben-Nun, N. Dryden, and A. Peste, “Sparsity in deep learning: Pruning and growth for efficient inference and training in neural networks,” Journal of Machine Learning Research, vol. 22, no. 241, pp. 1–124, 2021.
- [23] A. Makhzani and B. J. Frey, “Winner-take-all autoencoders,” Advances in neural information processing systems, vol. 28, 2015.
- [24] M. Kurtz, J. Kopinsky, R. Gelashvili, A. Matveev, J. Carr, M. Goin, W. Leiserson, S. Moore, N. Shavit, and D. Alistarh, “Inducing and exploiting activation sparsity for fast inference on deep neural networks,” in International Conference on Machine Learning. PMLR, 2020, pp. 5533–5543.
- [25] D. C. Mocanu, E. Mocanu, P. Stone, P. H. Nguyen, M. Gibescu, and A. Liotta, “Scalable training of artificial neural networks with adaptive sparse connectivity inspired by network science,” Nature communications, vol. 9, no. 1, pp. 1–12, 2018.
- [26] S. Ahmad and L. Scheinkman, “How can we be so dense? the benefits of using highly sparse representations,” arXiv preprint arXiv:1903.11257, 2019.
- [27] S. Changpinyo, M. Sandler, and A. Zhmoginov, “The power of sparsity in convolutional neural networks,” arXiv preprint arXiv:1702.06257, 2017.
- [28] T. Gale, M. Zaharia, C. Young, and E. Elsen, “Sparse gpu kernels for deep learning,” in SC20: International Conference for High Performance Computing, Networking, Storage and Analysis. IEEE, 2020, pp. 1–14.
- [29] M. E. Larkum, J. J. Zhu, and B. Sakmann, “A new cellular mechanism for coupling inputs arriving at different cortical layers,” Nature, vol. 398, no. 6725, pp. 338–341, 1999.
- [30] M. Larkum, “A cellular mechanism for cortical associations: an organizing principle for the cerebral cortex,” Trends in neurosciences, vol. 36, no. 3, pp. 141–151, 2013.
- [31] W. A. Phillips, “Cognitive functions of intracellular mechanisms for contextual amplification,” Brain and Cognition, vol. 112, pp. 39–53, 2017.
- [32] G. Major, M. E. Larkum, and J. Schiller, “Active properties of neocortical pyramidal neuron dendrites,” Annual review of neuroscience, vol. 36, pp. 1–24, 2013.
- [33] S. Ramaswamy and H. Markram, “Anatomy and physiology of the thick-tufted layer 5 pyramidal neuron,” Frontiers in cellular neuroscience, vol. 9, p. 233, 2015.
- [34] M. E. Larkum, “Are dendrites conceptually useful?” Neuroscience, vol. 489, pp. 4–14, 2022.
- [35] A. Adeel, “Conscious multisensory integration: Introducing a universal contextual field in biological and deep artificial neural networks,” Frontiers in Computational Neuroscience, vol. 14, 05 2020.
- [36] K. P. Körding and P. König, “Learning with two sites of synaptic integration,” Network: Computation in neural systems, vol. 11, no. 1, pp. 25–39, 2000.
- [37] B. Schuman, S. Dellal, A. Prönneke, R. Machold, and B. Rudy, “Neocortical layer 1: An elegant solution to top-down and bottom-up integration,” Annual Review of Neuroscience, vol. 44, no. 1, pp. 221–252, 2021, pMID: 33730511.
- [38] P. Poirazi and A. Papoutsi, “Illuminating dendritic function with computational models,” Nature Reviews Neuroscience, vol. 21, pp. 1–19, 05 2020.
- [39] M. E. Larkum, L. S. Petro, R. N. Sachdev, and L. Muckli, “A perspective on cortical layering and layer-spanning neuronal elements,” Frontiers in neuroanatomy, vol. 12, p. 56, 2018.
- [40] J. M. Shine, P. G. Bissett, P. T. Bell, O. Koyejo, J. H. Balsters, K. J. Gorgolewski, C. A. Moodie, and R. A. Poldrack, “The dynamics of functional brain networks: integrated network states during cognitive task performance,” Neuron, vol. 92, no. 2, pp. 544–554, 2016.
- [41] J. M. Shine, M. Breakspear, P. T. Bell, K. A. Ehgoetz Martens, R. Shine, O. Koyejo, O. Sporns, and R. A. Poldrack, “Human cognition involves the dynamic integration of neural activity and neuromodulatory systems,” Nature neuroscience, vol. 22, no. 2, pp. 289–296, 2019.
- [42] J. M. Shine, “Neuromodulatory influences on integration and segregation in the brain,” Trends in cognitive sciences, vol. 23, no. 7, pp. 572–583, 2019.
- [43] J. M. Shine, E. J. Müller, B. Munn, J. Cabral, R. J. Moran, and M. Breakspear, “Computational models link cellular mechanisms of neuromodulation to large-scale neural dynamics,” Nature neuroscience, vol. 24, no. 6, pp. 765–776, 2021.
- [44] J. M. Schulz, J. W. Kay, J. Bischofberger, and M. E. Larkum, “Gaba b receptor-mediated regulation of dendro-somatic synergy in layer 5 pyramidal neurons,” Frontiers in cellular neuroscience, vol. 15, p. 718413, 2021.
- [45] J. W. Kay and W. A. Phillips, “Contextual modulation in mammalian neocortex is asymmetric,” Symmetry, vol. 12, no. 5, p. 815, 2020.
- [46] J. W. Kay, J. M. Schulz, and W. A. Phillips, “A comparison of partial information decompositions using data from real and simulated layer 5b pyramidal cells,” Entropy, vol. 24, no. 8, p. 1021, 2022.
- [47] A. Gidon, T. A. Zolnik, P. Fidzinski, F. Bolduan, A. Papoutsi, P. Poirazi, M. Holtkamp, I. Vida, and M. E. Larkum, “Dendritic action potentials and computation in human layer 2/3 cortical neurons,” Science, vol. 367, no. 6473, pp. 83–87, 2020.
- [48] S. G. Sarwat, T. Moraitis, C. D. Wright, and H. Bhaskaran, “Chalcogenide optomemristors for multi-factor neuromorphic computation,” Nature communications, vol. 13, no. 1, pp. 1–9, 2022.
- [49] A. Payeur, J. Guerguiev, F. Zenke, B. A. Richards, and R. Naud, “Burst-dependent synaptic plasticity can coordinate learning in hierarchical circuits,” Nature neuroscience, vol. 24, no. 7, pp. 1010–1019, 2021.
- [50] J. Sacramento, R. Ponte Costa, Y. Bengio, and W. Senn, “Dendritic cortical microcircuits approximate the backpropagation algorithm,” Advances in neural information processing systems, vol. 31, 2018.
- [51] J. Guerguiev, T. Lillicrap, and B. Richards, “Towards deep learning with segregated dendrites,” eLife, vol. 6, p. e22901, 12 2017.
- [52] J. Aru, M. Suzuki, and M. Larkum, “Cellular mechanisms of conscious processing,” Trends in Cognitive Sciences, vol. 25, 10 2021.
- [53] T. Bachmann, M. Suzuki, and J. Aru, “Dendritic integration theory: a thalamo-cortical theory of state and content of consciousness,” Philosophy and the Mind Sciences, vol. 1, no. II, 2020.
- [54] J. Shin, G. Doron, and M. Larkum, “Memories off the top of your head,” Science, vol. 374, pp. 538–539, 10 2021.
- [55] B. Schuman, S. Dellal, A. Prönneke, R. Machold, and B. Rudy, “Neocortical layer 1: An elegant solution to top-down and bottom-up integration,” Annual Review of Neuroscience, vol. 44, no. 1, pp. 221–252, 2021, pMID: 33730511.
- [56] D. J. Heeger, “Theory of cortical function,” Proceedings of the National Academy of Sciences, vol. 114, no. 8, pp. 1773–1782, 2017.
- [57] D. J. Heeger and W. E. Mackey, “Oscillatory recurrent gated neural integrator circuits (organics), a unifying theoretical framework for neural dynamics,” Proceedings of the National Academy of Sciences, vol. 116, no. 45, pp. 22 783–22 794, 2019.
- [58] D. J. Heeger and K. O. Zemlianova, “A recurrent circuit implements normalization, simulating the dynamics of v1 activity,” Proceedings of the National Academy of Sciences, vol. 117, no. 36, pp. 22 494–22 505, 2020.
- [59] B. Baars, “Global workspace theory of consciousness: Toward a cognitive neuroscience of human experience,” Progress in brain research, vol. 150, pp. 45–53, 02 2005.
- [60] A. Vasconcelos and J.-C. Cassel, “The nonspecific thalamus: A place in a wedding bed for making memories last?” Neuroscience & Biobehavioral Reviews, vol. 54, 11 2014.
- [61] H. McGurk and J. MacDonald, “Hearing lips and seeing voices,” Nature, vol. 264, no. 5588, pp. 746–748, 1976.
- [62] M. Middelweerd and R. Plomp, “The effect of speechreading on the speech-reception threshold of sentences in noise,” The Journal of the Acoustical Society of America, vol. 82, no. 6, pp. 2145–2147, 1987.
- [63] A. MacLeod and Q. Summerfield, “A procedure for measuring auditory and audiovisual speech-reception thresholds for sentences in noise: Rationale, evaluation, and recommendations for use,” British journal of audiology, vol. 24, no. 1, pp. 29–43, 1990.
- [64] A. Adeel, M. Gogate, A. Hussain, and W. Whitmer, “Lip-reading driven deep learning approach for speech enhancement,” IEEE Transactions on Emerging Topics in Computational Intelligence, vol. PP, pp. 1–10, 09 2019.
- [65] A. Adeel, M. Gogate, and A. Hussain, “Contextual deep learning-based audio-visual switching for speech enhancement in real-world environments,” Information Fusion, vol. 59, 08 2019.
- [66] J. Yang, Z. Ren, C. Gan, H. Zhu, and D. Parikh, “Cross-channel communication networks,” Advances in Neural Information Processing Systems, vol. 32, 2019.
- [67] C. Cangea, P. Veličković, and P. Lio, “Xflow: Cross-modal deep neural networks for audiovisual classification,” IEEE Transactions on Neural Networks and Learning Systems, vol. 31, no. 9, pp. 3711–3720, 2019.
- [68] W. Guo, J. Wang, and S. Wang, “Deep multimodal representation learning: A survey,” IEEE Access, vol. PP, pp. 1–1, 05 2019.
- [69] A. Bhatti, B. Behinaein, D. Rodenburg, P. Hungler, and A. Etemad, “Attentive cross-modal connections for deep multimodal wearable-based emotion recognition,” in 2021 9th International Conference on Affective Computing and Intelligent Interaction Workshops and Demos (ACIIW). IEEE, 2021, pp. 01–05.
- [70] M. Gogate, A. Adeel, R. Marxer, J. Barker, and A. Hussain, “Dnn driven speaker independent audio-visual mask estimation for speech separation,” in Interspeech 2018. ISCA, 2018, pp. 2723–2727.
- [71] M. Gogate, K. Dashtipour, A. Adeel, and A. Hussain, “Cochleanet: A robust language-independent audio-visual model for speech enhancement,” Information Fusion, vol. 63, 04 2020.
- [72] M. Cooke, J. Barker, S. Cunningham, and X. Shao, “An audio-visual corpus for speech perception and automatic speech recognition (l),” The Journal of the Acoustical Society of America, vol. 120, pp. 2421–4, 12 2006.
- [73] J. Barker, R. Marxer, E. Vincent, and S. Watanabe, “The third ‘chime’ speech separation and recognition challenge: Analysis and outcomes,” Computer Speech & Language, vol. 46, 10 2016.
- [74] M. I. Belghazi, A. Baratin, S. Rajeshwar, S. Ozair, Y. Bengio, A. Courville, and D. Hjelm, “Mutual information neural estimation,” in International conference on machine learning. PMLR, 2018, pp. 531–540.
- [75] F. I. Craik and R. S. Lockhart, “Levels of processing: A framework for memory research,” Journal of Verbal Learning and Verbal Behavior, vol. 11, no. 6, pp. 671–684, 1972.
- [76] T. Marvan, M. Polák, T. Bachmann, and W. A. Phillips, “Apical amplification—a cellular mechanism of conscious perception?” Neuroscience of consciousness, vol. 2021, no. 2, p. niab036, 2021.
- [77] T. Rinaldi, C. Perrodin, and H. Markram, “Hyper-connectivity and hyper-plasticity in the medial prefrontal cortex in the valproic acid animal model of autism,” Frontiers in neural circuits, vol. 2, p. 4, 2008.
- [78] K. Markram and H. Markram, “The intense world theory–a unifying theory of the neurobiology of autism,” Frontiers in human neuroscience, p. 224, 2010.
- [79] M. Ridley and F. B. d. Waal, “The origins of virtue,” Nature, vol. 383, no. 6603, pp. 785–785, 1996.
- [80] J. K. Rilling, D. A. Gutman, T. R. Zeh, G. Pagnoni, G. S. Berns, and C. D. Kilts, “A neural basis for social cooperation,” Neuron, vol. 35, no. 2, pp. 395–405, 2002.
- [81] A. Delle Fave, I. Brdar, M. P. Wissing, U. Araujo, A. Castro Solano, T. Freire, M. D. R. Hernández-Pozo, P. Jose, T. Martos, H. E. Nafstad et al., “Lay definitions of happiness across nations: The primacy of inner harmony and relational connectedness,” Frontiers in psychology, vol. 7, p. 30, 2016.
- [82] M. L. Tantirigama, T. Zolnik, B. Judkewitz, M. E. Larkum, and R. N. Sachdev, “Perspective on the multiple pathways to changing brain states,” Frontiers in Systems Neuroscience, vol. 14, p. 23, 2020.
- [83] A. D. Nelson and K. J. Bender, “Dendritic integration dysfunction in neurodevelopmental disorders,” Developmental Neuroscience, vol. 43, no. 3-4, pp. 201–221, 2021.
- [84] J. Aru, M. Suzuki, R. Rutiku, M. E. Larkum, and T. Bachmann, “Coupling the state and contents of consciousness,” Frontiers in Systems Neuroscience, vol. 13, p. 43, 2019.
- [85] G. M. Shepherd and N. Yamawaki, “Untangling the cortico-thalamo-cortical loop: cellular pieces of a knotty circuit puzzle,” Nature Reviews Neuroscience, vol. 22, no. 7, pp. 389–406, 2021.
- [86] P. Velickovic, W. Fedus, W. L. Hamilton, P. Liò, Y. Bengio, and R. D. Hjelm, “Deep graph infomax.” ICLR (Poster), vol. 2, no. 3, p. 4, 2019.
- [87] R. Liao, D. Moyer, M. Cha, K. Quigley, S. Berkowitz, S. Horng, P. Golland, and W. M. Wells, “Multimodal representation learning via maximization of local mutual information,” in International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer, 2021, pp. 273–283.
Supplementary Material








![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/c98940ed-34ce-4022-965b-08120732c260/x13.png)
