Constraints on the maximum mass of neutron stars with a quark core from GW170817 and NICER PSR J0030+0451 data
Abstract
We perform a Bayesian analysis of the maximum mass of neutron stars with a quark core, incorporating the observational data from tidal deformability of the GW170817 binary neutron star merger as detected by LIGO/Virgo and the mass and radius of PSR J0030+0451 as detected by NICER. The analysis is performed under the assumption that the hadron-quark phase transition is of first order, where the low-density hadronic matter described in a unified manner by the soft QMF or the stiff DD2 equation of state (EOS) transforms into a high-density phase of quark matter modeled by the generic “Constant-sound-speed” (CSS) parameterization. The mass distribution measured for the pulsar, MSP J0740+6620, is used as the lower limit on . We find the most probable values of the hybrid star maximum mass are () for QMF (DD2), with an absolute upper bound around , to the posterior credible level. Such results appear robust with respect to the uncertainties in the hadronic EOS. We also discuss astrophysical implications of this result, especially on the post-merger product of GW170817, short gamma-ray bursts, and other likely binary neutron star mergers.
1 Introduction
Recently, an increasing number of binary systems are found to have at least one compact object falling into the possible gap between neutron star (NS) and black hole (BH) masses (Özel et al., 2010), e.g. the compact remnants of two NS-NS merger events GW170817 (Abbott et al., 2017a) () and GW190425 () (Abbott et al., 2020a), as well as the secondary component in the binary merger event GW190814 () (Abbott et al., 2020b). There are also recent reports on the plausible lowest-mass black hole () (Thompson et al., 2019) and the possibly most massive NS so far in PSR J2215+5135 () (Linares et al., 2018).
The maximum mass of NSs, , has generated much interest due to its crucial importance on the formation of such systems (e.g., Liu et al., 2021; Safarzadeh & Loeb, 2020; Yang et al., 2020; Zevin et al., 2020) and their merger rates (e.g., Fishbach et al., 2020), the detectability of produced kilonova (e.g., Drozda et al., 2020), the mass distribution for NSs (e.g., Gupta et al., 2020), or discriminating between NSs and BHs through late inspiral to post-merger gravitational wave (GW) signal and electromagnetic (EM) counterparts (e.g., Hannam et al., 2013; Littenberg et al., 2015; Mandel et al., 2015; Yang et al., 2018), among many aspects. Currently, it is still challenging to discriminate between these two populations (e.g., Tsokaros et al., 2020). Despite many recent works specifically discussing on the nature of GW190814 (e.g., Dexheimer et al., 2021; Godzieba et al., 2021; Tews et al., 2021; Zhang & Li, 2020; Zhou et al., 2020; Miao et al., 2021) and the merger remnant of GW170817 (e.g., Margalit & Metzger, 2017; Rezzolla et al., 2018; Ruiz et al., 2018; Shibata et al., 2019; Ai et al., 2020; Bauswein et al., 2020), the conclusions have been diverse because of the unknown maximum mass and the uncertain equation of state (EOS) of NSs. While the Shapiro delay measurement of MSP J0740+6620 (Cromartie et al., 2020) with mass (68% confidence level) tightly constrained the lower bound on , its actual value is still a subject of debate. Theoretically, the EOS gives rise to a unique sequence of stellar configurations under hydrostatic equilibrium through the Tolman-Oppenheimer-Volkoff (TOV) equations, which naturally predicts a maximum mass for NSs. As NS cores possess densities possibly up to (where is the nuclear saturation density), a description of the high-density core matter in terms of only hadrons and leptons might be inadequate (Annala et al., 2020). In addition, Bayesian analyses of NS observational data can lead to different results depending on whether phase transition is taken into account or not in the prior assumption of the EOS (Al-Mamun et al., 2021; Lim et al., 2020). It is worth mentioning that the standard interpretation for the LIGO/Virgo and NICER data are usually based on the parameterization of the EOS using a piecewise polytrope model, which does not explicitly include phase transitions.
In this work we use Bayesian inference to infer in the context of a strong phase transition from hadronic matter into quark matter inside dense cores of NSs, by exploiting the binary tidal deformability () constraint from GW170817 by LIGO/Virgo (Abbott et al., 2017a) and the mass () and radius () measurements of PSR J0030+0451 by NICER (Miller et al., 2019; Riley et al., 2019). For the hadronic phase, we utilize two different EOSs with varying stiffness at higher densities (Fortin et al., 2016; Zhu et al., 2018) while maintaining consistency with low-density laboratory nuclear experiments. The main uncertainty arises from the quark phase EOS for which we treat using the generic parametrization based on sound velocity (Alford et al., 2013). The phase transition parameters are then constrained to be compatible with the LIGO/Virgo and NICER data.
This paper is organized as follows. In Section 2, we introduce the unified EOSs for the hadronic phase of NSs and the CSS parameterization for the hadron-quark transition, and the quark matter EOS. Section 3 presents the observational constraints employed and the Bayesian analysis method that we apply. Our results are presented in Section 4 and summarized in Section 5.
2 Neutron star equation of state
We describe a static hybrid NS for which gravity is balanced by the pressure
of the compressed dense matter encountered in its interior.
From the NS surface to its core, with increasing density
the following regions appear sequentially:
Outer crust: non-uniform Coulomb lattice of neutron-rich nuclei embedded in a degenerate electron gas (below the neutron drip density).
The properties of NS outer crust are well constrained and we use the standard EOS proposed by Baym et al. (1971);
Inner crust: non-uniform system composed of more
exotic neutron-rich nuclei, degenerate electrons, and superfluid neutrons/superconducting protons (below the nuclear saturation density);
Outer core: uniform dense nuclear matter in weak-interaction equilibrium (or equilibrium) with leptons.
We describe both
the inner crust and the outer core
using the unified EOSs with the same underlying nuclear interaction as explained in Sec. 2.1;
Inner core: uniform quark matter
EOS represented by the CSS parameterization as explained in Sec. 2.2.
2.1 Unified EOSs for nonuniform and uniform hadronic matter: QMF and DD2


The QMF (Zhu et al., 2018) and DD2 (Fortin et al., 2016) models are employed to represent fiducial soft and stiff hadronic matter, respectively. To avoid uncertainties due to the crust, we utilize unified EOSs with a consistent treatment of NS crusts and the crust-core transition properties along with their cores. For NSs without a quark core, the soft QMF EOS leads to a maximum mass and a typical radius , whereas for the stiff DD2 EOS and . Both EOSs are constructed within the widely used relativistic mean-field (RMF) approach, based on an effective Lagrangian with meson fields mediating strong interactions between quarks or hadrons. Compatibility with available experimental as well as observational constraints at sub-nuclear and higher densities is ensured (e.g., Drischler et al., 2020).
2.2 CSS parameterization for the hadron-quark phase transition ()
For high-density quark matter the “constant-speed-of-sound” (CSS) parameterization (Alford et al., 2013) is applied, and the EOS from the onset of the phase transition up to the maximum central density of a star is determined by three dimensionless parameters: the transition density , the transition strength , and the sound speed squared in quark matter (we work in units where ). The full EOS is
where and , and is essentially the finite discontinuity in the energy density at the phase boundary. In practice, our study is limited to first-order phase transitions with a sharp interface (Maxwell construction).
Since there exists a one-to-one correspondence between the underlying EOS and global properties of NSs such as (), predicted values for these quantities can therefore be characterized by the three CSS parameters () in the hybrid EOSs. In Fig. 1 we show four parameter sets as examples for the high-density quark matter together with the unified QMF and DD2 EOSs for the inner crust and the outer core. Before reporting our results, we first introduce the scheme of the Bayesian inference approach that allows direct and consistent utilization of the LIGO/Virgo and NICER observational data.
3 Observational constraints and Bayesian analysis
According to Bayes theorem, the posterior probability density function (PDF) of a set of parameters given a data is expressed as
| (3) |
Here , usually written in , is the likelihood function of a data given a set of parameters , and is the prior PDF of the parameters, which reflects our preliminary knowledge of the parameters. The denominator is the evidence for given data and can be treated as a normalization factor. We employ the Python Bilby (Ashton et al., 2019) package to sample the parameters and calculate the marginal likelihoods. For the sampler we choose the Pymultinest (Buchner, 2016) code which is based on a nested sampling algorithm. The credible intervals (regions) of one (two) parameter(s) can then be obtained by marginalizing over all other parameters.

3.1 Likelihoods and constraint
In the present analysis, the likelihood is defined as
| (4) |
where is the likelihood to encapsulate the mass measurement of a pulsar source. and are the likelihoods of the GW170817 data and the mass-radius measurement of PSR J0030+0451 by NICER, respectively. If we only focus on the GW (PSR) data, we will neglect the PSR (GW) data.
Lower bound on from MSP J0740+6620 (catalog ). The mass measurements of massive pulsars establish a firm lower bound on the NS maximum mass. Only the EOSs that support a larger than this lower bound can pass this constraint, while others will be rejected. Assuming the mass measurement is a Gaussian distribution N, the likelihood can be written as
| (5) |
where is the standard Gaussian cumulative distribution function. In the present analysis, we choose the highest mass measured through Shapiro delay, (68% confidence level) of MSP J0740+6620 (catalog ) (Cromartie et al., 2020), to place the constraint. We fit the mass distribution of this source by a Gaussian distribution with and .
GW170817. The first binary NS merger GW170817 detected by the LIGO/Virgo collaboration (Abbott et al., 2017a) provided significant insight into the matter EOS and the NS internal structure because of their effects on the gravitational waveform. Assuming that the noise in the LIGO/Virgo detectors is Gaussian and stationary, the functional form of likelihood is often expressed as
| (6) |
where , , and denote the power spectral density (PSD), the Fourier transform of the measured strain data, and the frequency domain waveform generated using the parameter set , respectively. In the present analysis we adopt a 128s strain data111https://www.gw-openscience.org/eventapi from GPS time 1187008682s to 1187008890s and the PSDs222https://doi.org/10.7935/KSX7-QQ51 of GW170817 (Abbott et al., 2019b) released by the LIGO/Virgo collaboration. We also take the waveform model IMRPhenomD_NRTidal (Dietrich et al., 2017) for illustrative purposes.
| Parameters | pulsar | +GW170817 | +NICER | +GW170817+NICER | |
|---|---|---|---|---|---|
| QMF | |||||
| DD2 | |||||
| QMF | |||||
| DD2 | |||||
| QMF | |||||
| DD2 | |||||
| QMF | |||||
| DD2 | |||||
| QMF | |||||
| DD2 | |||||
| QMF | |||||
| DD2 |
PSR J0030+0451 (catalog ). The recent simultaneous mass-radius measurements of PSR J0030+0451 from NICER, , (Miller et al., 2019) and , (Riley et al., 2019), to the credibility interval, provide an additional useful constraint on the NS EOS. Since results in Riley et al. (2019) and Miller et al. (2019) are consistent with each other, we select the best fit scenario within the ST+PST model of Riley et al. (2019). In this case, the likelihood of generating the mass-radius distribution of PSR J0030+0451 (catalog ) is expressed as
| (7) |
where the right-hand side is a Gaussian Kernel Density Estimation (KDE) of the posterior samples of the mass and radius given by Riley et al. (2019).
3.2 Parameters and priors
The parameters related to the hybrid star EOSs are within the CSS parameterization. Given that a normal NS reaches the maximum-mass configuration with its central density below / for the QMF/DD2 hadronic EOS, we choose a uniform distribution of for hybrid stars in the range of /, respectively. For the sound speed squared in quark matter , we vary its value from (the conformal limit in perturbative QCD matter) to (the causal limit), with a uniform distribution. We also assign a reasonably wide range for the energy density discontinuities as with a uniform distribution.
For GW170817, the GW parameters are chirp mass in the detector frame, mass ratio, tidal deformabilities, aligned spins, inclination angle, geocentric time, polarization of GW, orbital phase at coalescence, red-shift of the source, and its position in the sky, i.e., . We fix the location of the source to the position determined by EM observations (Abbott et al., 2017b; Levan et al., 2017) with , and . , , , and are chosen to distribute uniformly in the range , , , s, and . For the inclination angle , we assume a uniform prior distribution.333Both the GW data (Abbott et al., 2017a) and the EM data (Mooley et al., 2018) as well as structured jet modeling (Troja et al., 2020) can give some constraints on the viewing angle for GW170817. However, since the constrained viewing angle in these studies gives a very wide distribution, the uniform prior distribution can serve for the purpose of our study. The tidal deformabilities and are related to the component-star masses through the hybrid star EOS, i.e.,
| (8) |
where the component-star masses , can be obtained with
| (9) |
To improve the convergence rate of the nest sampler, we marginalize the likelihood over the orbital phase at coalescence.
The mass and radius entering the likelihood of PSR data are related to the hybrid star EOS via the central pressure of the star, , i.e.,
| (10) |
Therefore we only need one additional parameter to perform the analysis if we take account of the PSR data.


We carry out four main tests to investigate how each data set
(see details in Sec. 3.1) would affect the result, namely:
(i) pulsar: where we apply the minimum constraint from MSP J0740+6620 (catalog );
(ii) +GW170817: where we consider
both
the constraint in (i) and the GW data of GW170817;
(iii) +NICER: where we consider
both the constraint in (i) and the NICER measurement of PSR J0030+0451;
(iv) +GW170817+NICER: where we combine the data of PSR J0030+0451 and GW170817 all together with the maximum-mass constraint in (i).
4 Results and discussion
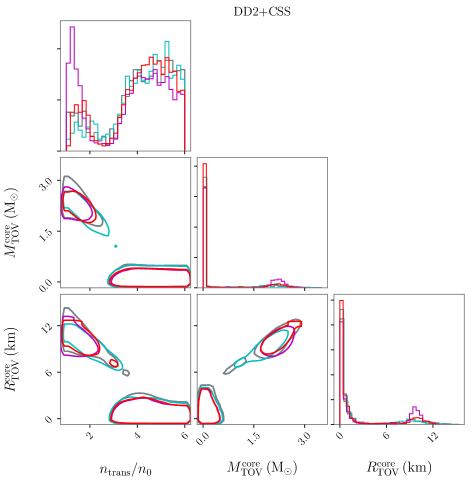
Our analysis first reveals that there are two scenarios for the maximum-mass hybrid stars: with a small () or large () quark core, corresponding to an early or late onset of the quark phase in the hybrid EOS, respectively. As detailed in Fig. 2, this conclusion is not subject to the hadronic EOS used or the choice of including or excluding any individual data. Since the small-core hybrid stars have a high threshold density for quark matter to appear which is close to the central density of the maximum-mass hybrid stars (see e.g. the dot-dashed curves in Fig. 1), only a small fraction of the NS is made of quark matter. This results in a limited or even negligible effect on the EOS and a similar maximum mass for hybrid stars compared to that of pure hadronic stars.
We further compute the Bayes Factor of the hybrid EOS with respect to the purely hadronic one to quantify this effect, and indeed find its value in general close to 1, e.g. for QMF (DD2) within the joint GW170817+NICER analysis. Consequently, in the following analysis we only focus on the large-core hybrid stars because it allows a much larger parameter space for the NS masses and radii compared to the small-core case (Miao et al., 2020). To do this, hereafter we reset the prior of to be in the range of / for the large-core case within QMF/DD2+CSS, while for the small-core case the range is /. In Appendix A, we report supplementarily detailed results for the small-core hybrid stars in the QMF hadronic case.
4.1 Hybrid star EOS and the maximum mass
Figure 3 illustrates the posterior distributions of the hybrid EOS, and the most probable values for the phase transition parameters and their confidence boundaries are summarized in Table 1, to columns. The columns of Table 1 list the corresponding results for three properties of maximum-mass hybrid stars (). In Fig. 4, we report in details the posterior PDFs of five stellar configuration parameters (). See also Appendix B for similar predictions for and hybrid stars.
It is commonly accepted that the inclusion of extra degrees of freedom (such as deconfined quarks discussed in the present work) tends to soften the NS matter EOS. However, as long as the high-density phase is sufficiently stiff i.e. with a large enough sound speed, through the introduction of a hadron-quark phase transition the parameter space for NS EOSs could be extended significantly (Miao et al., 2020) (see e.g. colored solid curves and pink shaded regions in Fig. 3), especially for soft hadronic EOSs such as QMF. In fact, the QMF hadronic EOS is quite soft due to the inclusion of the quark interaction for describing the inner structure of a nucleon in vacuum; see details in a recent review (Li et al., 2020). As a result, of hybrid NSs with a quark core is larger/smaller (thus the corresponding central density is relatively smaller/larger) than that of normal NSs based on the soft QMF/stiff DD2 hadronic EOS, falling in a relatively robust range of (90% confidence level). The probability distribution of quark matter for the maximum-mass star peaks within a sphere of with its mass fraction larger than , corresponding to the scenario of a big quark core.
From Table 1 one can see that the joint analysis of the GW170817 and NICER data prefers the hadron-quark phase transition taking place at not-too-high densities ( for QMF and for DD2, respectively). Such a low threshold is consistent with previous studies (Al-Mamun et al., 2021; Xie & Li, 2021), while the sound speed squared above the transition should be larger than () for QMF (DD2), indicating a rather stiff quark EOS generically. The current statistical analysis is also consistent with previous model calculations which confirm that to ensure a large mass for hybrid stars above two solar masses, the core sound speed needs to be necessarily large (Xia et al., 2019), even when the assumption of a first-order phase transition is relaxed (Drischler et al., 2020).
4.2 Astrophysical implications
We now turn to examine the nature and properties of several merger events based on our results of the hybrid star maximum mass. Even though there is a wide distribution of from our results, the peak value suggests that the possibility that the secondary component of GW190814 with a mass (Abbott et al., 2020b) could be a spinning supermassive NS is not ruled out, even if one takes into account the limitation of the intrinsic r-mode instability (Zhou et al., 2020). Within this scenario, however, the supramassive NS needs to carry a low dipolar magnetic field so that it has not been spun down yet at the time of merger. A more likely situation is that this secondary component is a black hole, since the typical spin-down timescale is quote short (Sarin et al., 2020). Considering the maximal spin observed in Galactic NSs, Abbott et al. (2019a) inferred that the 90% credible intervals for the component masses of the GW170817 event lie between and (with the most probable total mass around ), and Abbott et al. (2020a) reported the corresponding component masses ranging from to (with the most probable total mass around ) for the GW190425 event. Our results on the maximum mass of NSs (up to to the 90% confidence level) suggest that the remnant of GW170817 could be a massive rotating NS (Ai et al., 2020). In comparison, the GW190425 event may be more compatible with a BH remnant, especially given that it has no detection of a luminous counterpart, and the inferred total mass is above the most massive observed binary NS system (PSR J1913+1102). Further studies on the stellar evolution are warranted to clarify these important issues. See Appendix C for our results using the GW190425 data.


The scenario that GW170817 left behind a massive NS has implications in interpreting the EM counterparts of binary NS mergers. First, since GW170817 was associated with the short GRB 170817A, it suggests that the launch of a GRB jet does not require the formation of a black hole to begin with. The argument that the existence of a short GRB necessitates the formation of a black hole, and hence, a small (e.g. Margalit & Metzger, 2017; Rezzolla et al., 2018; Ruiz et al., 2018), is flawed. Rather, it suggests that there might exist an underlying long-lived engine that powers the late EM counterpart, including the kilonova (Li et al., 2018; Yu et al., 2018) and late X-ray emission (Piro et al., 2019; Troja et al., 2020). The 1.7 s delay between GRB 170817A and GW170817 was not due to the delay time to form a black hole, but rather due to the time delay for a promptly launched jet to reach the energy dissipation radius (Zhang et al., 2018; Zhang, 2019). The lack of significant energy injection in the GW170817/GRB 170817A remnant required that the dipolar magnetic field strength is below G (Ai et al., 2018, 2020). Alternatively, most of the spin energy of the post-merger massive NS could have been carried away via secular gravitational waves (Fan et al., 2013; Gao et al., 2016) or deconfined quarks (Drago et al., 2016; Li et al., 2016; Sarin et al., 2020). For a review on the post-merger remnant of binary NSs and GW170817 in particular, see Bernuzzi (2020); Sarin & Lasky (2020). The existence of a long-lived NS engine for short GRBs is consistent with the interpretation of the X-ray plateau commonly existing in short GRB afterglows (Rowlinson et al., 2010, 2013; Lü et al., 2015) and the X-ray transients CDF-S XT2 and XT1 (Xue et al., 2019; Sun et al., 2019), which pointed towards a in the range of (Lasky et al., 2014; Gao et al., 2016; Li et al., 2016; Radice et al., 2018). According to this picture, a large fraction of binary NS mergers will be accompanied by a bright X-ray emission component (Zhang, 2013). Future regular monitoring of X-ray counterparts from binary NS merger GW sources with e.g. Einstein Probe (Yuan et al., 2018), will test the scenario of a relatively large suggested here.


5 Conclusions
In conclusion, the uncertain maximum mass of NSs has been a crucial problem with ever increasing precision of the observations on NS binaries and pulsars. We explicitly include the hadron-quark phase transition in NS EOSs and perform a Bayesian analysis on of hybrid NSs with a quark core, using the available data from LIGO/Virgo and NICER. Two unified hadronic EOSs (the soft QMF and the stiff DD2) are applied in order to test the effect due to low-density hadronic matter and the model dependence of the results for . We determine the maximum mass that a hybrid star can reach to be (), to the 90% posterior credible level, for soft QMF (stiff DD2), which appears robust with respect to the uncertainties of the hadronic EOS. This result could have profound implications for the minimum black hole mass, as well as help identify the nature of a compact object with its mass falling into the possible mass gap. Further discussions along this line have also been provided.
There are several caveats in the present work. The major one is our assumption that the switching of a hadronic EOS (presently nucleonic EOS) to quark matter EOS is through a first-order phase transition. The transition may be of second order or even a smooth crossover. Nevertheless, our framework successfully describes all current laboratory nuclear experiments and astrophysical observations related to NSs. The general requirements adopted here (e.g., causality) should also apply to any alternative hadron-quark phase transition scenarios or other types of strangeness phase transitions (see discussions on hyperons, kaons in, e.g., Li et al., 2020). Therefore, our main conclusions remain valid and useful for identifying compact objects’ nature with its mass falling into the possible mass gap. Another assumption that should be taken with caution is about an early onset density () for the phase transition in the cores of NSs. We mainly discuss this big-core case because the alternative scenario with a late appearance of quarks at much higher densities () results in similar predictions for hybrid stars with respect to normal NSs, where is primarily determined by the nucleonic interaction instead of properties of the possible phase transitions. It is worth mentioning that for normal NSs some microscopic calculations including three-body nucleonic interactions (Wei et al., 2019) incidentally give rise to a value of close to that found for NSs with a quark core in the present work. At last, the prior dependence in the Bayesian analysis that can be strongly related to the form of the assumed EOS (for which we chose to use the CSS parameterization) has been a well-known restriction, and we plan to examine its effect in more detail in a separate study.
Appendix A Small-core hybrid stars resemble an NS
We demonstrate in Fig. 5 the properties of small-core hybrid stars along with the corresponding EOS parameters within QMF+CSS. For such small-core hybrid stars, a strong first-order transition of occurs at , to the 90% confidence level. Their maximum masses are very similar to their hadronic counterparts. In general a hadron-quark phase transition taking place above is hard to probe (e.g., Miao et al., 2020). There have been discussions in the literature on probing the sharp phase transition in hybrid stars through tidal deformation measurements, which could be effective when the size of the elastic hadronic region of a hybrid star is large enough (Pereira et al., 2020).
Appendix B Typical and massive hybrid stars
| Parameters | pulsar | +GW170817 | +NICER | +GW170817+NICER | |
|---|---|---|---|---|---|
| QMF | |||||
| DD2 | |||||
| QMF | |||||
| DD2 | |||||
| QMF | |||||
| DD2 | |||||
| QMF | |||||
| DD2 | |||||
| QMF | |||||
| DD2 | |||||
| QMF | |||||
| DD2 |




We supplementarily provide various properties of typical hybrid stars with masses and in Fig. 6 and Fig. 7, and the data of radius, tidal deformability, and central density are summarized in Table 2. The results (to the 90% confidence level) are collected as follows which are conditioned on the joint analysis priors ( pulsar+GW170817+NICER).
For hybrid stars, we find that the radius and tidal deformability are and for the QMF case and and for the DD2 case, corresponding to a central density of and , respectively. The probability distribution of the quark matter core in a hybrid star peaks within a sphere of . The corresponding mass fraction of quark matter is . For hybrid stars, it is found that and for the QMF case, and and for the DD2 case, corresponding to a central density of and , respectively. The probability distribution of quark matter core in a hybrid star peaks within a sphere of . The corresponding mass fraction of quark matter is increased to .
Appendix C Adding the GW190425 tidal deformability data


The recent reported GW190425’s component masses range from to ( for high spin priors) (Abbott et al., 2020a) are compatible with existing constraints on the NS maximum mass (), suggesting that the event system might be an NS binary. We therefore in this Appendix add the GW190425 event into the analysis and discuss its effects on the parameter space of the theoretical model and the hybrid star properties.
In Fig. 8 we present the posterior PDFs of the CSS parameters for different analyses as well as those of the hybrid star properties i.e., the maximum mass, the radius and tidal deformability of a star. The GW190425 results are found, in most cases, very similar to that based on the pulsar constraint, and the additional GW190425 data provides little improvement to the results (mainly due to the intrinsically much smaller tidal deformability and its low signal-to-noise ratio).
References
- Abbott et al. (2017a) Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2017, Phys. Rev. Lett., 119, 161101. doi:10.1103/PhysRevLett.119.161101
- Abbott et al. (2017b) Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2017, ApJ, 848, L12. doi:10.3847/2041-8213/aa91c9
- Abbott et al. (2019a) Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2019, Physical Review X, 9, 011001. doi:10.1103/PhysRevX.9.011001
- Abbott et al. (2019b) Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2019, Physical Review X, 9, 031040. doi:10.1103/PhysRevX.9.031040
- Abbott et al. (2020a) Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2020, ApJ, 892, L3. doi:10.3847/2041-8213/ab75f5
- Abbott et al. (2020b) Abbott, R., Abbott, T. D., Abraham, S., et al. 2020, ApJ, 896, L44. doi:10.3847/2041-8213/ab960f
- Ai et al. (2018) Ai, S., Gao, H., Dai, Z.-G., et al. 2018, ApJ, 860, 57. doi:10.3847/1538-4357/aac2b7
- Ai et al. (2020) Ai, S., Gao, H., & Zhang, B. 2020, ApJ, 893, 146. doi:10.3847/1538-4357/ab80bd
- Al-Mamun et al. (2021) Al-Mamun, M., Steiner, A. W., Nättilä, J., et al. 2021, Phys. Rev. Lett., 126, 061101. doi:10.1103/PhysRevLett.126.061101
- Alford et al. (2013) Alford, M. G., Han, S., & Prakash, M. 2013, Phys. Rev. D, 88, 083013. doi:10.1103/PhysRevD.88.083013
- Annala et al. (2020) Annala, E., Gorda, T., Kurkela, A., et al. 2020, Nature Physics, 16, 907. doi:10.1038/s41567-020-0914-9
- Ashton et al. (2019) Ashton, G., Hübner, M., Lasky, P. D., et al. 2019, Astrophysics Source Code Library. ascl:1901.011
- Bauswein et al. (2020) Bauswein, A., Blacker, S., Vijayan, V., et al. 2020, Phys. Rev. Lett., 125, 141103. doi:10.1103/PhysRevLett.125.141103
- Baym et al. (1971) Baym, G., Pethick, C., & Sutherland, P. 1971, ApJ, 170, 299. doi:10.1086/151216
- Buchner (2016) Buchner, J. 2016, Astrophysics Source Code Library. ascl:1606.005
- Cromartie et al. (2020) Cromartie, H. T., Fonseca, E., Ransom, S. M., et al. 2020, Nature Astronomy, 4, 72. doi:10.1038/s41550-019-0880-2
- Dexheimer et al. (2021) Dexheimer, V., Gomes, R. O., Klähn, T., et al. 2021, Phys. Rev. C, 103, 025808. doi:10.1103/PhysRevC.103.025808
- Dietrich et al. (2017) Dietrich, T., Bernuzzi, S., & Tichy, W. 2017, Phys. Rev. D, 96, 121501. doi:10.1103/PhysRevD.96.121501
- Drago et al. (2016) Drago, A., Lavagno, A., Metzger, B. D., et al. 2016, Phys. Rev. D, 93, 103001. doi:10.1103/PhysRevD.93.103001
- Drischler et al. (2020) Drischler, C., Furnstahl, R. J., Melendez, J. A., et al. 2020, Phys. Rev. Lett., 125, 202702. doi:10.1103/PhysRevLett.125.202702
- Drischler et al. (2020) Drischler, C., Han, S., Lattimer, J. M., et al. 2020, arXiv:2009.06441
- Drozda et al. (2020) Drozda, P., Belczynski, K., O’Shaughnessy, R., et al. 2020, arXiv:2009.06655
- Fan et al. (2013) Fan, Y.-Z., Wu, X.-F., & Wei, D.-M. 2013, Phys. Rev. D, 88, 067304. doi:10.1103/PhysRevD.88.067304
- Fishbach et al. (2020) Fishbach, M., Essick, R., & Holz, D. E. 2020, ApJ, 899, L8. doi:10.3847/2041-8213/aba7b6
- Fortin et al. (2016) Fortin, M., Providência, C., Raduta, A. R., et al. 2016, Phys. Rev. C, 94, 035804. doi:10.1103/PhysRevC.94.035804
- Gao et al. (2016) Gao, H., Zhang, B., & Lü, H.-J. 2016, Phys. Rev. D, 93, 044065. doi:10.1103/PhysRevD.93.044065
- Godzieba et al. (2021) Godzieba, D. A., Radice, D., & Bernuzzi, S. 2021, ApJ, 908, 122. doi:10.3847/1538-4357/abd4dd
- Gupta et al. (2020) Gupta, A., Gerosa, D., Arun, K. G., et al. 2020, Phys. Rev. D, 101, 103036. doi:10.1103/PhysRevD.101.103036
- Hannam et al. (2013) Hannam, M., Brown, D. A., Fairhurst, S., et al. 2013, ApJ, 766, L14. doi:10.1088/2041-8205/766/1/L14
- Lasky et al. (2014) Lasky, P. D., Haskell, B., Ravi, V., et al. 2014, Phys. Rev. D, 89, 047302. doi:10.1103/PhysRevD.89.047302
- Levan et al. (2017) Levan, A. J., Lyman, J. D., Tanvir, N. R., et al. 2017, ApJ, 848, L28. doi:10.3847/2041-8213/aa905f
- Li et al. (2016) Li, A., Zhang, B., Zhang, N.-B., et al. 2016, Phys. Rev. D, 94, 083010. doi:10.1103/PhysRevD.94.083010
- Li et al. (2020) Li, A., Zhu, Z.-Y., Zhou, E.-P., et al. 2020, Journal of High Energy Astrophysics, 28, 19. doi:10.1016/j.jheap.2020.07.001
- Li et al. (2018) Li, S.-Z., Liu, L.-D., Yu, Y.-W., et al. 2018, ApJ, 861, L12. doi:10.3847/2041-8213/aace61
- Lim et al. (2020) Lim, Y., Bhattacharya, A., Holt, J. W., et al. 2020, arXiv:2007.06526
- Linares et al. (2018) Linares, M., Shahbaz, T., & Casares, J. 2018, ApJ, 859, 54. doi:10.3847/1538-4357/aabde6
- Littenberg et al. (2015) Littenberg, T. B., Farr, B., Coughlin, S., et al. 2015, ApJ, 807, L24. doi:10.1088/2041-8205/807/2/L24
- Liu et al. (2021) Liu, T., Wei, Y.-F., Xue, L., et al. 2021, ApJ, 908, 106. doi:10.3847/1538-4357/abd24e
- Lü et al. (2015) Lü, H.-J., Zhang, B., Lei, W.-H., et al. 2015, ApJ, 805, 89. doi:10.1088/0004-637X/805/2/89
- Mandel et al. (2015) Mandel, I., Haster, C.-J., Dominik, M., et al. 2015, MNRAS, 450, L85. doi:10.1093/mnrasl/slv054
- Margalit & Metzger (2017) Margalit, B. & Metzger, B. D. 2017, ApJ, 850, L19. doi:10.3847/2041-8213/aa991c
- Miao et al. (2020) Miao, Z., Li, A., Zhu, Z., et al. 2020, ApJ, 904, 103. doi:10.3847/1538-4357/abbd41
- Miao et al. (2021) Miao, Z., Jiang, J., Tang, S., Li, A., Chen, L., Submitted
- Miller et al. (2019) Miller, M. C., Lamb, F. K., Dittmann, A. J., et al. 2019, ApJ, 887, L24. doi:10.3847/2041-8213/ab50c5
- Mooley et al. (2018) Mooley, K. P., Deller, A. T., Gottlieb, O., et al. 2018, Nature, 561, 355. doi:10.1038/s41586-018-0486-3
- Özel et al. (2010) Özel, F., Psaltis, D., Narayan, R., et al. 2010, ApJ, 725, 1918. doi:10.1088/0004-637X/725/2/1918
- Pereira et al. (2020) Pereira, J. P., Bejger, M., Andersson, N., et al. 2020, ApJ, 895, 28. doi:10.3847/1538-4357/ab8aca
- Piro et al. (2019) Piro, L., Troja, E., Zhang, B., et al. 2019, MNRAS, 483, 1912. doi:10.1093/mnras/sty3047
- Bernuzzi (2020) Bernuzzi, S. 2020, General Relativity and Gravitation, 52, 108. doi:10.1007/s10714-020-02752-5
- Radice et al. (2018) Radice, D., Perego, A., Bernuzzi, S., et al. 2018, MNRAS, 481, 3670. doi:10.1093/mnras/sty2531
- Rezzolla et al. (2018) Rezzolla, L., Most, E. R., & Weih, L. R. 2018, ApJ, 852, L25. doi:10.3847/2041-8213/aaa401
- Riley et al. (2019) Riley, T. E., Watts, A. L., Bogdanov, S., et al. 2019, ApJ, 887, L21. doi:10.3847/2041-8213/ab481c
- Rowlinson et al. (2013) Rowlinson, A., O’Brien, P. T., Metzger, B. D., et al. 2013, MNRAS, 430, 1061. doi:10.1093/mnras/sts683
- Rowlinson et al. (2010) Rowlinson, A., O’Brien, P. T., Tanvir, N. R., et al. 2010, MNRAS, 409, 531. doi:10.1111/j.1365-2966.2010.17354.x
- Ruiz et al. (2018) Ruiz, M., Shapiro, S. L., & Tsokaros, A. 2018, Phys. Rev. D, 97, 021501. doi:10.1103/PhysRevD.97.021501
- Safarzadeh & Loeb (2020) Safarzadeh, M. & Loeb, A. 2020, ApJ, 899, L15. doi:10.3847/2041-8213/aba9df
- Sarin & Lasky (2020) Sarin, N. & Lasky, P. D. 2020, arXiv:2012.08172
- Sarin et al. (2020) Sarin, N., Lasky, P. D., & Ashton, G. 2020, Phys. Rev. D, 101, 063021. doi:10.1103/PhysRevD.101.063021
- Shibata et al. (2019) Shibata, M., Zhou, E., Kiuchi, K., et al. 2019, Phys. Rev. D, 100, 023015. doi:10.1103/PhysRevD.100.023015
- Sun et al. (2019) Sun, H., Li, Y., Zhang, B.-B., et al. 2019, ApJ, 886, 129. doi:10.3847/1538-4357/ab4bc7
- Tews et al. (2021) Tews, I., Pang, P. T. H., Dietrich, T., et al. 2021, ApJ, 908, L1. doi:10.3847/2041-8213/abdaae
- Thompson et al. (2019) Thompson, T. A., Kochanek, C. S., Stanek, K. Z., et al. 2019, Science, 366, 637. doi:10.1126/science.aau4005
- Troja et al. (2020) Troja, E., van Eerten, H., Zhang, B., et al. 2020, MNRAS, 498, 5643. doi:10.1093/mnras/staa2626
- Tsokaros et al. (2020) Tsokaros, A., Ruiz, M., Shapiro, S. L., et al. 2020, Phys. Rev. Lett., 124, 071101. doi:10.1103/PhysRevLett.124.071101
- Wei et al. (2019) Wei, J.-B., Figura, A., Burgio, G. F., et al. 2019, Journal of Physics G Nuclear Physics, 46, 034001. doi:10.1088/1361-6471/aaf95c
- Xia et al. (2019) Xia, C., Zhu, Z., Zhou, X., et al. 2019, arXiv:1906.00826
- Xie & Li (2021) Xie, W.-J. & Li, B.-A. 2021, Phys. Rev. C, 103, 035802. doi:10.1103/PhysRevC.103.035802
- Xue et al. (2019) Xue, Y. Q., Zheng, X. C., Li, Y., et al. 2019, Nature, 568, 198. doi:10.1038/s41586-019-1079-5
- Yang et al. (2018) Yang, H., East, W. E., & Lehner, L. 2018, ApJ, 856, 110. doi:10.3847/1538-4357/aab2b0
- Yang et al. (2020) Yang, Y., Gayathri, V., Bartos, I., et al. 2020, ApJ, 901, L34. doi:10.3847/2041-8213/abb940
- Yu et al. (2018) Yu, Y.-W., Liu, L.-D., & Dai, Z.-G. 2018, ApJ, 861, 114. doi:10.3847/1538-4357/aac6e5
- Yuan et al. (2018) Yuan, W., Zhang, C., Chen, Y., et al. 2018, Scientia Sinica Physica, Mechanica & Astronomica, 48, 039502. doi:10.1360/SSPMA2017-00297
- Zevin et al. (2020) Zevin, M., Spera, M., Berry, C. P. L., et al. 2020, ApJ, 899, L1. doi:10.3847/2041-8213/aba74e
- Zhang (2013) Zhang, B. 2013, ApJ, 763, L22. doi:10.1088/2041-8205/763/1/L22
- Zhang (2019) Zhang, B. 2019, Frontiers of Physics, 14, 64402. doi:10.1007/s11467-019-0913-4
- Zhang et al. (2018) Zhang, B.-B., Zhang, B., Sun, H., et al. 2018, Nature Communications, 9, 447. doi:10.1038/s41467-018-02847-3
- Zhang & Li (2020) Zhang, N.-B. & Li, B.-A. 2020, ApJ, 902, 38. doi:10.3847/1538-4357/abb470
- Zhou et al. (2020) Zhou, X., Li, A., & Li, B.-A. 2020, arXiv:2011.11934
- Zhu et al. (2018) Zhu, Z.-Y., Zhou, E.-P., & Li, A. 2018, ApJ, 862, 98. doi:10.3847/1538-4357/aacc28