Constraints on neutrino non-standard interactions from COHERENT and PandaX-4T
Abstract
We investigate constraints on neutrino non-standard interactions (NSIs) in the effective field theory framework, using data from the first measurement of solar 8B neutrinos via coherent elastic neutrino-nucleus scattering (CENS) in the PandaX-4T experiment and the COHERENT experiment. In the PandaX-4T experiment, due to relatively large statistical uncertainties and measured CENS counts that significantly differ from the Standard Model predictions, its sensitivities to the neutrino NSIs are currently limited, compared to the COHERENT experiment. However, the PandaX-4T experiment is uniquely sensitive to the neutrino NSIs for the flavor due to oscillation feature of the solar 8B neutrinos. We also assess how the experimental central value, exposure, and systematic uncertainties will affect the constraints on neutrino NSIs from various CENS measurements in the future.
I Introduction
In the Standard Model (SM), neutrinos interact with ordinary matter through the exchange of and bosons. Neutrino non-standard interactions (NSIs) in the charged and neutral currents beyond the SM (BSM) were initially formulated by Lee-Yang Lee and Yang (1956) and Wolfenstein Wolfenstein (1978), respectively. While the detection of neutrinos in neutrino oscillation experiments only involves charged-current interactions, the coherent elastic neutrino-nucleus scattering (CENS) Freedman (1974) serves as a unique probe of the neutral-current neutrino NSIs, potentially arising from new mediators, such as boson Barranco et al. (2005).
Despite the coherent enhancement of the CENS cross section, this process is difficult to detect due to small deposited energy. It was first observed in the COHERENT experiment using the CsI[Na] scintillation detector Akimov et al. (2017) and later argon Akimov et al. (2021) and germanium Adamski et al. (2024) detectors with neutrinos produced from the spallation neutron source (SNS). These results as well as the follow-up detection with a larger exposure of CsI[Na] Akimov et al. (2022a) and other experimental efforts Aguilar-Arevalo et al. (2019); Bonet et al. (2021); Alekseev et al. (2022); Colaresi et al. (2022); Su et al. (2023); Augier et al. (2023); Ackermann et al. (2024); Yang et al. (2024); Cai et al. (2024); Xiao (2024) have motivated diverse phenomenological studies Coloma et al. (2017a); Liao and Marfatia (2017); Cadeddu et al. (2018); Ge and Shoemaker (2018); Aristizabal Sierra et al. (2018a); Ciuffoli et al. (2018); Farzan et al. (2018); Billard et al. (2018); Aristizabal Sierra et al. (2018b); Cadeddu and Dordei (2019); Altmannshofer et al. (2019); Miranda et al. (2019); Aristizabal Sierra et al. (2019); Papoulias (2020); Giunti (2020); Canas et al. (2020); Hoferichter et al. (2020); Skiba and Xia (2022); Cadeddu et al. (2021); Du et al. (2022); Dasgupta et al. (2021); Atzori Corona et al. (2022); De Romeri et al. (2023); Li et al. (2024), see also Refs. Lindner et al. (2017); Dent et al. (2017); Coloma et al. (2017b) for earlier studies and Ref. Abdullah et al. (2022) for a recent review.
On the other hand, with the tremendous progress in the sensitivity of dark matter (DM) direct detection, it is anticipated that the DM experiments can detect neutrinos from astrophysical sources. These neutrinos exhibit nuclear recoil signatures resembling those of DM, which pose as irreducible backgrounds in DM direct detection and are often referred to as the “neutrino frog” Billard et al. (2014); O’Hare (2021); Tang and Zhang (2023). This is not unexpected since the idea of detecting DM that scatters off nuclei Goodman and Witten (1985) was inspired by the proposal to detect MeV-range neutrinos via CENS Drukier and Stodolsky (1984).
Recently, the solar 8B neutrino was measured through CENS in the PandaX-4T Bo et al. (2024) and XENONnT Aprile et al. (2024) experiments with corresponding statistical significance of and , which signify the first step into the neutrino frog experimentally. Assuming the SM cross section of CENS, the signals are interpreted as the measurements of solar 8B neutrino flux of and , respectively, both of which are consistent with the standard solar model predictions Vinyoles et al. (2017); Bahcall et al. (1996, 2006) and the results from dedicated solar neutrino experiments Aharmim et al. (2013); Abe et al. (2011, 2016); Agostini et al. (2020).
In the SM, empirical nuclear form factors Helm (1956); Klein and Nystrand (1999) that parameterize the nuclear response are usually adopted to calculate the cross section of CENS. However, an improved treatment is necessary if neutrino NSIs are present, which is feasible in the effective field theory (EFT) approach Altmannshofer et al. (2019); Skiba and Xia (2022); Hoferichter et al. (2020)111For vector and axial-vector NSIs, one can also refine the CENS cross section by modifying the weak charge Barranco et al. (2005); Abdullah et al. (2022). , analogous to the situation of DM-nucleus scattering Cirigliano et al. (2012); Menendez et al. (2012); Klos et al. (2013); Vietze et al. (2015); Hoferichter et al. (2015); Fitzpatrick et al. (2013); Anand et al. (2014); Bishara et al. (2017a, b).
An end-to-end EFT framework Altmannshofer et al. (2019) was developed and utilized to describe the CENS process from the new physics scale to the nuclear scale, which takes advantages of the heavy baryon chiral perturbation theory (HBChPT) Jenkins and Manohar (1991) and multipole expansions for nuclear responses Walecka (1995)222Indeed, the multipole analysis was applied to neutrino-nucleus scattering processes in the SM weak charged currents slightly before the proposal of CENS O’ Connell et al. (1972). The effect of SM weak neutral currents in neutrino scattering off nuclei was later investigated in Ref. Donnelly and Peccei (1979). . Compared to the nuclear form factor approach, the EFTs enable controlled uncertainties in systematic power countings, which allows for potential theoretical improvements in nuclear shell-model calculations Hoferichter et al. (2020) and beyond Abdel Khaleq et al. (2024).
In this work, we will investigate the sensitivities to neutrino NSIs in the EFT framework, including matching between several EFTs. We consider relevant dimension-6 operators in the low-energy effective field (LEFT) and QCD chiral Lagrangian with external sources and heavy baryon expansion, and finally match to nuclear response function to obtain the most stringent constraints from the measurement conducted with the CsI[Na] detector in the COHERENT experiment Akimov et al. (2022a) and the first result of new physics using the measurement of solar 8B neutrinos by PandaX-4T Bo et al. (2024).
The remainder of the paper is organized as follows. In Sec. II, we discuss the neutrino NSIs from quark level to the nucleon level using the LEFT and HBChPT. In Sec. III, we derive the CENS cross section using the multipole expansions for nuclear responses. In Sec. IV, we evaluate the event rates of the CENS signals in the COHERENT and PandaX-4T experiments (considering the matter effects in the neutrino propagation by using package PEANUTS), and obtain the constraints on the Wilson coefficients for specific neutrino flavors, which are interpreted as lower bounds on the NSI energy scale using the analysis. Two-dimensional constraint on the NSI parameters is also obtained for the comparison of these two CENS experiments. We have an assessment of the sensitivities of future measurements of solar 8B neutrinos via CENS in DM detectors. We conclude in Sec. V. In the appendix, we provide details of the detector resolution and efficiency in COHERENT CsI measurement.
II Neutrino non-standard interactions
The neutral-current (NC) neutrino-quark interactions can be parameterized as Wolfenstein (1978); Scholberg (2006); Barranco et al. (2005); Davidson et al. (2003); Du et al. (2022)
| (1) |
where , denote the flavors of neutrinos, and , is the Fermi constant.
In the LEFT, the relevant effective Lagrangian is
| (2) |
where the dimension-6 operators are defined as Jenkins et al. (2018); Altmannshofer et al. (2019)
| (3) |
The correspondence between the coefficients and the Wilson coefficients and is
| (4) |
The SM contributions to the Wilson coefficients after integrating out the boson are Altmannshofer et al. (2019); Abdullah et al. (2022)
| (5) | ||||
| (6) |
where is the weak mixing angle with Workman et al. (2022). We consider contributions from neutrino NSIs, so that
| (7) |
The dimensionful Wilson coefficient can also be expressed as
| (8) |
where is dimensionless, and the energy scale is determined by the mass of mediator that is responsible for the neutrino NSIs333For light mediator, there is additional momentum dependence from its propagator..
To obtain the neutrino-nucleus cross section of CENS, we need to consider the matching in two steps Altmannshofer et al. (2019); Hoferichter et al. (2020): (1) from the quark level to the nucleon level; (2) from the nucleon level to the nucleus level. In the first step, the nucleons in the target are considered non-relativistic due to the small momentum exchange compared to the nucleon mass. The interaction Lagrangian for the neutrinos and non-relativistic nucleons is
| (9) |
where , and denotes the number of derivatives in the operator.
By using the HBChPT, the following neutrino-nucleon operators at leading order are obtained:
| (10) | ||||
| (11) |
where denotes the large component of the nucleon field, and is the nucleon velocity, the spin operator with . In the lab frame, , and with being the Pauli matrices. Denoting and ( and ) as the momenta of income and outcome neutrinos (nucleons), respectively, we can define the momentum transfer as .
From the quark-level interactions to the nucleon-level interactions, the matching conditions are expressed as444Note that we use the symbol to represent both the momentum transfer and the quark in the conventional manner.
| (12) |
where denote the momentum-dependent nucleon form factors describing the hadronization of quark currents. We use the values of evaluated at Bishara et al. (2017b), which are accurate enough for our purpose,
| (13) |
III Cross section of CENS
In the second step, the nuclear response to neutrino scattering needs to be considered at the nuclear level, which is described similarly to DM detection Fitzpatrick et al. (2013); Anand et al. (2014). In this framework, the many-body nuclear matrix elements are expanded using the multipole expansions Walecka (1995) in the harmonic oscillator basis, and can be calculated in the nuclear shell model Haxton and Lunardini (2008); Hoferichter et al. (2020).
To this end, we classify the Lagrangian terms according to charge operator () and nuclear spin operator () Altmannshofer et al. (2019):
| (14) |
where the Dirac structures are given by
| (15) |
and in Eq. (14) is the spatial three-vector components of .
The differential cross section in the rest frame of the target nucleus is Altmannshofer et al. (2019)555We have corrected a missing factor of in Eq.(3.23) of Ref. Altmannshofer et al. (2019), and have verified it by comparing the SM result with the calculation using the nuclear form factor Lindner et al. (2017); Abdullah et al. (2022).
| (16) |
where is the target nucleus mass, is the initial neutrino energy, is the nuclear recoil energy, and the spin-averaged amplitude square is expressed as
| (17) | |||
Here, is the spin of the target nucleus, denotes the nucleus response functions Fitzpatrick et al. (2013); Anand et al. (2014), and the kinematic factors are given by Altmannshofer et al. (2019)
| (18) | ||||
| (19) | ||||
| (20) | ||||
where are the isospin indices, , and . In the isospin basis, and .
IV Event rates and constraints
In the CENS experiments, neutrinos from the source will interact with detector target nuclei, causing nucleus recoils. The resulting signal can be translated into the event rate. In the following, we will investigate constraints on neutrino NSIs from the measurements by the COHERENT and PandaX-4T experiments.
IV.1 Constraints from COHERENT
We first consider the measurements of the CENS process in the COHERENT experiment using CsI[Na] Akimov et al. (2022a)666We do not consider the COHERENT measurement using Ar detector Akimov et al. (2021) since its sensitivity cannot compete with that CsI detector, even though the combination of these measurements can break degeneracy between different NSI parameter combinations De Romeri et al. (2023). . The differential event rate per target for neutrino flavor is expressed as Abdel Khaleq et al. (2024); Altmannshofer et al. (2019):
| (21) |
where is the differential cross section given in Eq. (16). The minimum initial neutrino energy is , where is the nucleus mass. The upper integration limit is given by the maximal energy of initial neutrinos produced in . For and , , while for , Atzori Corona et al. (2022); Aristizabal Sierra et al. (2018b), where and are the mass of the muon and pion, respectively.
The total neutrino fluxes are described by the Michel spectrum Coloma et al. (2017b); Liao and Marfatia (2017)
| (22) | ||||
| (23) | ||||
| (24) |
where is the Dirac -function, and the overall factor depends on the number of neutrinos that are produced for each proton on target (POT), the number of protons on target and the distance between the source and the detector . For the CsI[Na] detector in COHERENT experiment, , and Akimov et al. (2022a).
The time-integrated expected number of CENS events in the th bin of the number of photoelectrons (PEs) for the flavor is given by Aristizabal Sierra et al. (2018b); Papoulias (2020); Atzori Corona et al. (2022); De Romeri et al. (2023)
| (25) |
where we have taken into account the recoils of Cs and I with the fractions and , respectively. The number of target nuclei in the detector is , where kg is the detector active mass, is the molar mass of CsI, and denotes the Avogadro number. The detector energy resolution and efficiency as well as the average time efficiency are described in Appendix A.
In Fig. 1, we compare the expected number of CENS events in the SM as a function of , which is calculated using the nuclear response functions described in Sec. III, with the experimental data from COHERENT. The contributions from different neutrino fluxes are included.

To constrain the neutrino NSIs, we perform the binned analysis using the following least-squares function Fogli et al. (2002); Aristizabal Sierra et al. (2018b),
| (26) |
where and represent the measured number of CENS events, and the expected number of beam-related neutron (BRN) and neutrino-induced neutron (NIN) background events in the th bin of , respectively. The associated statistical uncertainty is . The expected number of CENS events is given by
| (27) |
which depends on the neutrino NSIs.
The relative systematic uncertainties from the quenching factor , neutrino flux and signal acceptance Akimov et al. (2022a); De Romeri et al. (2023), and the response functions are considered777It is noted that in the approach of nuclear form factor, the relative systematic uncertainty is about Papoulias (2020). Here, we assume that the uncertainties associated with the response functions are comparable. , which lead to the total uncertainty . Besides, with the uncertainties of BRN and NIN backgrounds are and , respectively.
The quantity is minimized over the systematic nuisance parameters and , so that we can derive the 90% confidence level (C.L.) bounds on the Wilson coefficients of neutrino NSIs by requiring . In Eq. (8), assuming and summing over the fluxes of and , we obtain the one-parameter-a-time lower bounds on for specific flavors, which are presented in Table 1.
| 390 | 395 | |
| 407 | 414 | |
| 44.7 | 68.4 | |
| 26.4 | 40.9 |
IV.2 Constraints from PandaX-4T
The recent measurements of solar 8B neutrinos in the CENS process Ma et al. (2023); Bo et al. (2024); Aprile et al. (2024) can also impose constraints on the neutrino NSIs. In this work, we consider the results of the PandaX-4T experiment using the liquid xenon Bo et al. (2024).
The differential event rate per target for neutrino flavor is expressed as
| (28) |
where the minimum neutrino energy with the mass of 131Xe, and the maximum energy is about 16 Bahcall et al. (1996).
The solar 8B neutrino is produced in the Sun, and then propagates to the Earth. The total flux of neutrino detected at the Earth is defined as
| (29) |
where and denote the exposure and detector active mass, respectively, and is the predicted solar 8B neutrino flux Vinyoles et al. (2017)888The predictions by the other groups based on the standard solar model can be found in Refs. Bahcall et al. (1996, 2006). . is the probability of solar neutrino to manifest as at the Earth averaged over the exposure.
Due to the neutrino oscillation, the flavor composition of solar neutrinos detected at the Earth differs from that produced in the Sun. In the analysis, we use the package PEANUTS Gonzalo and Lucente (2024) to compute with matter effects in the neutrino propagation being included, which are shown in Fig. 2 for different flavors of neutrinos.

The expected number of CENS events for the flavor is given by Li et al. (2024),
| (30) |
where is the detection efficiency, which depends on the nuclear recoil function. The number of target nuclei in the detector of the PandaX-4T experiment is with the molar mass .
Two datasets are collected by PandaX-4T, which differ in the energy threshold, as displayed in Table 2. Note that the numbers of signal events for the pair data and US2 data are obtained from the combined likelihood fit Bo et al. (2024). Given the smaller number of signal events in paired data, we only consider the US2 data. The exposure in Eq. (29) is thus given by .
| PandaX-4T data | paired | US2 |
|---|---|---|
| energy threshold | keV | keV |
| total exposure | tonneyear | tonneyear |
| event number | 3.5 | 75 |
In the analysis by the PandaX-4T Collaboration Bo et al. (2024), the signals are interpreted in terms of the measured solar 8B neutrino flux assuming the SM cross section of CENS, which is with the relative statistical uncertainty being . Therefore, for our purpose, instead of taking the number of signal events post the combined likelihood fit, we calculate the number of signal events for the US2 data using the signal efficiency from Figure 1 of Ref. Bo et al. (2024). We obtain the measured number of CENS events with the statistic uncertainty .
To constrain the neutrino NSIs, we perform the single-bin analysis Fogli et al. (2002),
| (31) |
Here, the expected number of CENS events is given by
| (32) |
which depends on the neutrino NSIs, and the SM prediction calculated using the solar 8B neutrino flux Vinyoles et al. (2017). The relative systematic uncertainties from the selection efficiency , signal modeling and solar 8B neutrino flux Bo et al. (2024); Vinyoles et al. (2017), and the response functions are considered, which lead to the total uncertainty .
Again, is minimized over the nuisance parameter to derive the 90% C.L. limits on the Wilson coefficients by requiring . In Eq. (8), assuming , we obtain the one-parameter-a-time lower bounds on for specific flavors, which are presented in Table 3.
| 287.46 | 289.61 | 286.70 | |
| 304.61 | 306.88 | 303.80 | |
| 14.70 | 14.81 | 14.60 | |
| 23.32 | 23.48 | 23.15 |
Owing to the neutrino oscillation, a significant portion of the solar neutrino fluxes reaching the Earth are composed of as depicted in Fig. 2. Therefore, the CENS measurement of PandaX-4T can give unique constraints on the neutrino NSIs for the flavor as shown in the last column of Table 3. For the and flavors, the measurement of COHERENT CsI provides more stringent constraints on the Wilson coefficients of NSIs than the constraints provided by PandaX-4T.
For comparison, we also obtain the two-dimensional constraint on the neutrino NSI parameters and , which are defined as Abdullah et al. (2022)
| (33) |
By requiring , we obtain the 90% C.L. allowed regions in Fig. 3. Note that our fitted result using the COHERENT CsI measurement agrees with Ref. De Romeri et al. (2023). It is shown that the constraints on and from the CENS measurement by PandaX-4T are weaker than those from COHERENT.
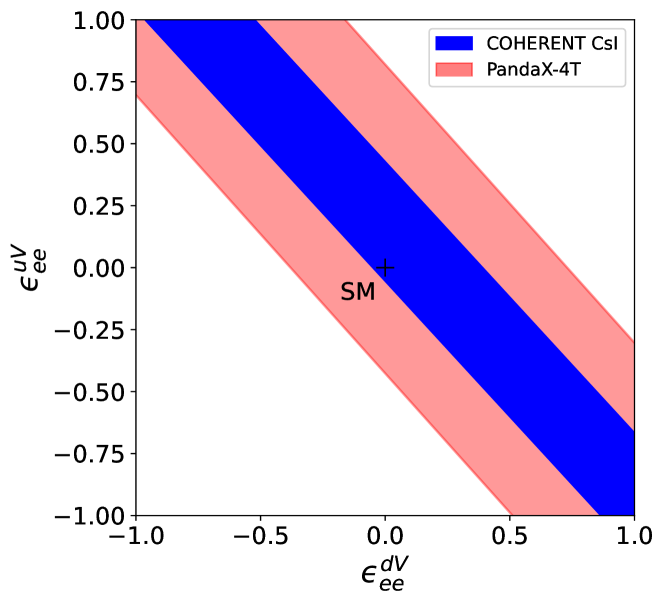
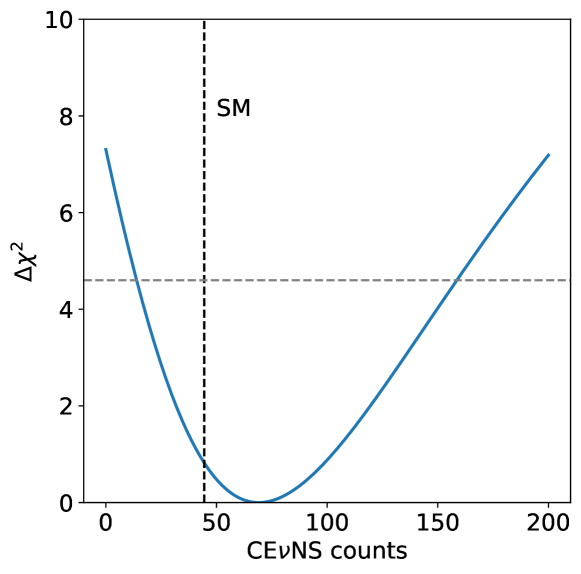

We find that the central value of experimentally measured CENS counts has a significant impact on the constraints on the NSI parameters999It is noted that the central value measured by XENONnT is slightly smaller than the SM prediction, whereas the associated statistical uncertainty is larger compared to PandaX-4T Aprile et al. (2024).. To understand it, we present the distribution as a function of the CENS counts in Fig. 4, using the US2 data from PandaX-4T. The upper limit of the CENS counts with determines the boundaries of the blue bands in Fig. 5. It is verified that with the central value unchanged, the sensitivity of PandaX-4T shows a mild improvement for times larger exposure.
We further assess the sensitivities of future solar 8B neutrino measurements via CENS in DM detectors, leveraging the current results from PandaX-4T as a reference. In Fig. 5, we show the projected constraints on the NSI parameters under the assumption of and . We consider two cases with the total systematic uncertainty being included or not. The resulting constraints are represented in lighter red and darker red bands with solid and dashed boundaries, respectively. One can observe that the anticipated constraint from PandaX-4T with the systematic uncertainties is weaker than that from COHERENT. If in the future the systematic uncertainties are well controlled, with the assumption that they are negligible, we could achieve a sensitivity comparable to that of the COHERENT CsI measurement.
V Conclusion
In this work, we have studied the constraints on the neutrino non-standard interactions (NSIs) using the latest CENS measurements in the COHERENT and PandaX-4T experiments. The cross section of CENS is calculated within an end-to-end effective field theory framework. In this approach, the dimension-6 operators in the low-energy EFT are matched to hadronic operators in the heavy baryon chiral perturbation theory, while the nuclear response of target nuclei is described using multipole expansions.
We have performed the analyses of the CENS events observed in the CsI[Na] detector of COHERENT and PandaX-4T, and have derived the one-parameter-a-time lower bounds on the NSI scale for specific neutrino flavors. We have found that the constraints for the and flavors from COHERENT are more stringent than those from PandaX-4T, while the latter provides unique sensitivities to the neutrino NSIs for the flavor due to the oscillation of solar 8B neutrinos propagating from the Sun to the Earth (considering the matter effects in the neutrino propagation by using package PEANUTS). Besides, we have compared the two-dimensional constraints on the NSI parameters for the flavor from COHERENT and PandaX-4T, and have obtained that the sensitivity of PandaX-4T is limited by the central value of measured CENS counts.
Moreover, we have assessed the measurements of the solar 8B neutrinos via CENS in dark matter detectors, leveraging the current results from PandaX-4T as a reference. Assuming that the central value of measured CENS counts aligns with the SM prediction, the sensitivity is significantly improved for the exposure of , and is comparable to that imposed by the COHERENT CsI measurement if the systematic uncertainties are further disregarded.
Note added: After this paper was finished, another paper Aristizabal Sierra et al. (2024) appeared, which has some overlap of our work. However, we use an end-to-end EFT framework to investigate the neutrino NSIs sensitivities, and we emphasize that it is important to include systematic uncertainties in the analysis.
Acknowledgements.
We would like to express our gratitude to Yu-Feng Li for the valuable help with the fitting of the COHERENT data. GL also thanks Xun-Jie Xu for useful correspondence regarding Ref. Lindner et al. (2017). FT thanks Ningqiang Song for the discussion on the solar neutrino and Bing-Long Zhang for the discussion on numerical calculations. This work is supported by the National Science Foundation of China under Grants No. 12347105, No. 12375099 and No. 12047503, and the National Key Research and Development Program of China Grant No. 2020YFC2201501, No. 2021YFA0718304. GL is also supported by the Guangdong Basic and Applied Basic Research Foundation (2024A1515012668), and SYSU startup funding.Appendix A Detector resolution and efficiency in COHERENT CsI measurement
In Eq. (IV.1), the number of PEs is Papoulias (2020); Akimov et al. (2022a)
| (34) |
where the true electron-equivalent recoil energy is related to the true nuclear recoil energy as
| (35) |
The quenching factor can be parameterized as Akimov et al. (2022b)
| (36) |
where the parameters , , and .
The detector energy resolution is modeled with the gamma function,
| (37) |
where and .
The reconstructed energy and time are uncorrelated, thus allowing us to deal with the energy and time efficiency independently Akimov et al. (2022a),
| (38) | ||||
| (39) |
where the parameters are , , , , and s, s Akimov et al. (2022a).
The efficiency has been implemented in the integration over in Eq. (IV.1). On the other hand, we consider the average time efficiency
| (40) |
where represents the -integrated expected number of the SM CENS events in the reconstructed time for each flavor of neutrino flux depicted in the right panel of Figure 1 in Ref. Akimov et al. (2022a). Due to variations in neutrino arrival times, the time efficiencies for different flavors are distinct, , and .
References
- Lee and Yang (1956) T. D. Lee and C.-N. Yang, Phys. Rev. 104, 254 (1956).
- Wolfenstein (1978) L. Wolfenstein, Phys. Rev. D 17, 2369 (1978).
- Freedman (1974) D. Z. Freedman, Phys. Rev. D 9, 1389 (1974).
- Barranco et al. (2005) J. Barranco, O. G. Miranda, and T. I. Rashba, JHEP 12, 021 (2005), arXiv:hep-ph/0508299 .
- Akimov et al. (2017) D. Akimov et al. (COHERENT), Science 357, 1123 (2017), arXiv:1708.01294 [nucl-ex] .
- Akimov et al. (2021) D. Akimov et al. (COHERENT), Phys. Rev. Lett. 126, 012002 (2021), arXiv:2003.10630 [nucl-ex] .
- Adamski et al. (2024) S. Adamski et al., (2024), arXiv:2406.13806 [hep-ex] .
- Akimov et al. (2022a) D. Akimov et al. (COHERENT), Phys. Rev. Lett. 129, 081801 (2022a), arXiv:2110.07730 [hep-ex] .
- Aguilar-Arevalo et al. (2019) A. Aguilar-Arevalo et al. (CONNIE), Phys. Rev. D 100, 092005 (2019), arXiv:1906.02200 [physics.ins-det] .
- Bonet et al. (2021) H. Bonet et al. (CONUS), Phys. Rev. Lett. 126, 041804 (2021), arXiv:2011.00210 [hep-ex] .
- Alekseev et al. (2022) I. Alekseev et al. (GeN), Phys. Rev. D 106, L051101 (2022), arXiv:2205.04305 [nucl-ex] .
- Colaresi et al. (2022) J. Colaresi, J. I. Collar, T. W. Hossbach, C. M. Lewis, and K. M. Yocum, Phys. Rev. Lett. 129, 211802 (2022), arXiv:2202.09672 [hep-ex] .
- Su et al. (2023) C. Su, Q. Liu, and T. Liang (CLOVERS, CENS@CSNS), Phys. Sci. Forum 8, 19 (2023), arXiv:2303.13423 [physics.ins-det] .
- Augier et al. (2023) C. Augier et al. (Ricochet), Nucl. Instrum. Meth. A 1057, 168765 (2023), arXiv:2304.14926 [physics.ins-det] .
- Ackermann et al. (2024) N. Ackermann et al., (2024), arXiv:2401.07684 [hep-ex] .
- Yang et al. (2024) L. T. Yang, Y. F. Liang, and Q. Yue, PoS TAUP2023, 296 (2024).
- Cai et al. (2024) C. Cai et al., (2024), arXiv:2405.05554 [hep-ex] .
- Xiao (2024) X. Xiao, “Cicenns: a 300-kg csi(na) detector for coherent elastic neutrino-nucleus scattering,” (2024).
- Coloma et al. (2017a) P. Coloma, M. C. Gonzalez-Garcia, M. Maltoni, and T. Schwetz, Phys. Rev. D 96, 115007 (2017a), arXiv:1708.02899 [hep-ph] .
- Liao and Marfatia (2017) J. Liao and D. Marfatia, Phys. Lett. B 775, 54 (2017), arXiv:1708.04255 [hep-ph] .
- Cadeddu et al. (2018) M. Cadeddu, C. Giunti, Y. F. Li, and Y. Y. Zhang, Phys. Rev. Lett. 120, 072501 (2018), arXiv:1710.02730 [hep-ph] .
- Ge and Shoemaker (2018) S.-F. Ge and I. M. Shoemaker, JHEP 11, 066 (2018), arXiv:1710.10889 [hep-ph] .
- Aristizabal Sierra et al. (2018a) D. Aristizabal Sierra, N. Rojas, and M. H. G. Tytgat, JHEP 03, 197 (2018a), arXiv:1712.09667 [hep-ph] .
- Ciuffoli et al. (2018) E. Ciuffoli, J. Evslin, Q. Fu, and J. Tang, Phys. Rev. D 97, 113003 (2018), arXiv:1801.02166 [physics.ins-det] .
- Farzan et al. (2018) Y. Farzan, M. Lindner, W. Rodejohann, and X.-J. Xu, JHEP 05, 066 (2018), arXiv:1802.05171 [hep-ph] .
- Billard et al. (2018) J. Billard, J. Johnston, and B. J. Kavanagh, JCAP 11, 016 (2018), arXiv:1805.01798 [hep-ph] .
- Aristizabal Sierra et al. (2018b) D. Aristizabal Sierra, V. De Romeri, and N. Rojas, Phys. Rev. D 98, 075018 (2018b), arXiv:1806.07424 [hep-ph] .
- Cadeddu and Dordei (2019) M. Cadeddu and F. Dordei, Phys. Rev. D 99, 033010 (2019), arXiv:1808.10202 [hep-ph] .
- Altmannshofer et al. (2019) W. Altmannshofer, M. Tammaro, and J. Zupan, JHEP 09, 083 (2019), [Erratum: JHEP 11, 113 (2021)], arXiv:1812.02778 [hep-ph] .
- Miranda et al. (2019) O. G. Miranda, G. Sanchez Garcia, and O. Sanders, Adv. High Energy Phys. 2019, 3902819 (2019), [Erratum: Adv.High Energy Phys. 2022, 9874517 (2022)], arXiv:1902.09036 [hep-ph] .
- Aristizabal Sierra et al. (2019) D. Aristizabal Sierra, V. De Romeri, and N. Rojas, JHEP 09, 069 (2019), arXiv:1906.01156 [hep-ph] .
- Papoulias (2020) D. K. Papoulias, Phys. Rev. D 102, 113004 (2020), arXiv:1907.11644 [hep-ph] .
- Giunti (2020) C. Giunti, Phys. Rev. D 101, 035039 (2020), arXiv:1909.00466 [hep-ph] .
- Canas et al. (2020) B. C. Canas, E. A. Garces, O. G. Miranda, A. Parada, and G. Sanchez Garcia, Phys. Rev. D 101, 035012 (2020), arXiv:1911.09831 [hep-ph] .
- Hoferichter et al. (2020) M. Hoferichter, J. Menéndez, and A. Schwenk, Phys. Rev. D 102, 074018 (2020), arXiv:2007.08529 [hep-ph] .
- Skiba and Xia (2022) W. Skiba and Q. Xia, JHEP 10, 102 (2022), arXiv:2007.15688 [hep-ph] .
- Cadeddu et al. (2021) M. Cadeddu, N. Cargioli, F. Dordei, C. Giunti, Y. F. Li, E. Picciau, and Y. Y. Zhang, JHEP 01, 116 (2021), arXiv:2008.05022 [hep-ph] .
- Du et al. (2022) Y. Du, H.-L. Li, J. Tang, S. Vihonen, and J.-H. Yu, Phys. Rev. D 105, 075022 (2022), arXiv:2106.15800 [hep-ph] .
- Dasgupta et al. (2021) A. Dasgupta, S. K. Kang, and J. E. Kim, JHEP 11, 120 (2021), arXiv:2108.12998 [hep-ph] .
- Atzori Corona et al. (2022) M. Atzori Corona, M. Cadeddu, N. Cargioli, F. Dordei, C. Giunti, Y. F. Li, C. A. Ternes, and Y. Y. Zhang, JHEP 09, 164 (2022), arXiv:2205.09484 [hep-ph] .
- De Romeri et al. (2023) V. De Romeri, O. G. Miranda, D. K. Papoulias, G. Sanchez Garcia, M. Tórtola, and J. W. F. Valle, JHEP 04, 035 (2023), arXiv:2211.11905 [hep-ph] .
- Li et al. (2024) Y.-Y. Li, Y.-F. Li, and S.-Y. Xia, (2024), arXiv:2406.07477 [hep-ph] .
- Lindner et al. (2017) M. Lindner, W. Rodejohann, and X.-J. Xu, JHEP 03, 097 (2017), arXiv:1612.04150 [hep-ph] .
- Dent et al. (2017) J. B. Dent, B. Dutta, S. Liao, J. L. Newstead, L. E. Strigari, and J. W. Walker, Phys. Rev. D 96, 095007 (2017), arXiv:1612.06350 [hep-ph] .
- Coloma et al. (2017b) P. Coloma, P. B. Denton, M. C. Gonzalez-Garcia, M. Maltoni, and T. Schwetz, JHEP 04, 116 (2017b), arXiv:1701.04828 [hep-ph] .
- Abdullah et al. (2022) M. Abdullah et al., (2022), arXiv:2203.07361 [hep-ph] .
- Billard et al. (2014) J. Billard, L. Strigari, and E. Figueroa-Feliciano, Phys. Rev. D 89, 023524 (2014), arXiv:1307.5458 [hep-ph] .
- O’Hare (2021) C. A. J. O’Hare, Phys. Rev. Lett. 127, 251802 (2021), arXiv:2109.03116 [hep-ph] .
- Tang and Zhang (2023) J. Tang and B.-L. Zhang, Phys. Rev. D 108, 062004 (2023), arXiv:2304.13665 [hep-ph] .
- Goodman and Witten (1985) M. W. Goodman and E. Witten, Phys. Rev. D 31, 3059 (1985).
- Drukier and Stodolsky (1984) A. Drukier and L. Stodolsky, Phys. Rev. D 30, 2295 (1984).
- Bo et al. (2024) Z. Bo et al. (PandaX), (2024), arXiv:2407.10892 [hep-ex] .
- Aprile et al. (2024) E. Aprile et al. (XENON), (2024), arXiv:2408.02877 [nucl-ex] .
- Vinyoles et al. (2017) N. Vinyoles, A. M. Serenelli, F. L. Villante, S. Basu, J. Bergström, M. C. Gonzalez-Garcia, M. Maltoni, C. Peña Garay, and N. Song, Astrophys. J. 835, 202 (2017), arXiv:1611.09867 [astro-ph.SR] .
- Bahcall et al. (1996) J. N. Bahcall, E. Lisi, D. E. Alburger, L. De Braeckeleer, S. J. Freedman, and J. Napolitano, Phys. Rev. C 54, 411 (1996), arXiv:nucl-th/9601044 .
- Bahcall et al. (2006) J. N. Bahcall, A. M. Serenelli, and S. Basu, Astrophys. J. Suppl. 165, 400 (2006), arXiv:astro-ph/0511337 .
- Aharmim et al. (2013) B. Aharmim et al. (SNO), Phys. Rev. C 88, 025501 (2013), arXiv:1109.0763 [nucl-ex] .
- Abe et al. (2011) S. Abe et al. (KamLAND), Phys. Rev. C 84, 035804 (2011), arXiv:1106.0861 [hep-ex] .
- Abe et al. (2016) K. Abe et al. (Super-Kamiokande), Phys. Rev. D 94, 052010 (2016), arXiv:1606.07538 [hep-ex] .
- Agostini et al. (2020) M. Agostini et al. (Borexino), Phys. Rev. D 101, 062001 (2020), arXiv:1709.00756 [hep-ex] .
- Helm (1956) R. H. Helm, Phys. Rev. 104, 1466 (1956).
- Klein and Nystrand (1999) S. Klein and J. Nystrand, Phys. Rev. C 60, 014903 (1999), arXiv:hep-ph/9902259 .
- Cirigliano et al. (2012) V. Cirigliano, M. L. Graesser, and G. Ovanesyan, JHEP 10, 025 (2012), arXiv:1205.2695 [hep-ph] .
- Menendez et al. (2012) J. Menendez, D. Gazit, and A. Schwenk, Phys. Rev. D 86, 103511 (2012), arXiv:1208.1094 [astro-ph.CO] .
- Klos et al. (2013) P. Klos, J. Menéndez, D. Gazit, and A. Schwenk, Phys. Rev. D 88, 083516 (2013), [Erratum: Phys.Rev.D 89, 029901 (2014)], arXiv:1304.7684 [nucl-th] .
- Vietze et al. (2015) L. Vietze, P. Klos, J. Menéndez, W. C. Haxton, and A. Schwenk, Phys. Rev. D 91, 043520 (2015), arXiv:1412.6091 [nucl-th] .
- Hoferichter et al. (2015) M. Hoferichter, P. Klos, and A. Schwenk, Phys. Lett. B 746, 410 (2015), arXiv:1503.04811 [hep-ph] .
- Fitzpatrick et al. (2013) A. L. Fitzpatrick, W. Haxton, E. Katz, N. Lubbers, and Y. Xu, JCAP 02, 004 (2013), arXiv:1203.3542 [hep-ph] .
- Anand et al. (2014) N. Anand, A. L. Fitzpatrick, and W. C. Haxton, Phys. Rev. C 89, 065501 (2014), arXiv:1308.6288 [hep-ph] .
- Bishara et al. (2017a) F. Bishara, J. Brod, B. Grinstein, and J. Zupan, JCAP 02, 009 (2017a), arXiv:1611.00368 [hep-ph] .
- Bishara et al. (2017b) F. Bishara, J. Brod, B. Grinstein, and J. Zupan, JHEP 11, 059 (2017b), arXiv:1707.06998 [hep-ph] .
- Jenkins and Manohar (1991) E. E. Jenkins and A. V. Manohar, Phys. Lett. B 255, 558 (1991).
- Walecka (1995) J. D. Walecka, Theoretical nuclear and subnuclear physics, Vol. 16 (1995).
- O’ Connell et al. (1972) J. S. O’ Connell, T. W. Donnelly, and J. D. Walecka, Phys. Rev. C 6, 719 (1972).
- Donnelly and Peccei (1979) T. W. Donnelly and R. D. Peccei, Phys. Rept. 50, 1 (1979).
- Abdel Khaleq et al. (2024) R. Abdel Khaleq, J. L. Newstead, C. Simenel, and A. E. Stuchbery, (2024), arXiv:2405.20060 [hep-ph] .
- Scholberg (2006) K. Scholberg, Phys. Rev. D 73, 033005 (2006), arXiv:hep-ex/0511042 .
- Davidson et al. (2003) S. Davidson, C. Pena-Garay, N. Rius, and A. Santamaria, JHEP 03, 011 (2003), arXiv:hep-ph/0302093 .
- Jenkins et al. (2018) E. E. Jenkins, A. V. Manohar, and P. Stoffer, JHEP 03, 016 (2018), [Erratum: JHEP 12, 043 (2023)], arXiv:1709.04486 [hep-ph] .
- Workman et al. (2022) R. L. Workman et al. (Particle Data Group), PTEP 2022, 083C01 (2022).
- Haxton and Lunardini (2008) W. Haxton and C. Lunardini, Comput. Phys. Commun. 179, 345 (2008), arXiv:0706.2210 [nucl-th] .
- Akimov et al. (2018) D. Akimov et al. (COHERENT), (2018), 10.5281/zenodo.1228631, arXiv:1804.09459 [nucl-ex] .
- Fogli et al. (2002) G. L. Fogli, E. Lisi, A. Marrone, D. Montanino, and A. Palazzo, Phys. Rev. D 66, 053010 (2002), arXiv:hep-ph/0206162 .
- Ma et al. (2023) W. Ma et al. (PandaX), Phys. Rev. Lett. 130, 021802 (2023), arXiv:2207.04883 [hep-ex] .
- Gonzalo and Lucente (2024) T. E. Gonzalo and M. Lucente, Eur. Phys. J. C 84, 119 (2024), arXiv:2303.15527 [hep-ph] .
- Aristizabal Sierra et al. (2024) D. Aristizabal Sierra, N. Mishra, and L. Strigari, (2024), arXiv:2409.02003 [hep-ph] .
- Akimov et al. (2022b) D. Akimov et al. (COHERENT), JINST 17, P10034 (2022b), arXiv:2111.02477 [physics.ins-det] .