Constraining dark boson decay using neutron stars111Invited Review Article for a Special Edition on Neutron decay anomalies for UNIVERSE.
Abstract
Inspired by the well known anomaly in the lifetime of the neutron, we investigate its consequences inside neutron stars. We first assess the viability of the neutron decay hypothesis suggested by Fornal and Grinstein within neutron stars, in terms of the equation of state and compatibility with observed properties. This is followed by an investigation of the constraint information on neutron star cooling can place on the decay rate of the dark boson into standard model particles, in the context of various BSM ideas.
I Introduction
Neutrons are a fundamental constituent of our universe. It has been over almost a century since they were discovered but their lifetime Wietfeldt and Greene (2011) still presents a challenging problem to solve. In particular, current experiments appear to show a difference in the neutron lifetime when measured with different methods. In the bottle method Serebrov et al. (2018); Pattie et al. (2018); Tan (2019); Steyerl et al. (2012) the neutrons are trapped and the number counted after a fixed time, with no specific determination of the decay mode. In contrast, using beam method Yue et al. (2013); Otono (2017); Olive (2016) one actually observes the protons produced in decay. Of course, the lifetime of the neutron should be the same, regardless of the method of measurement. However, the lifetime of the neutron shows a discrepancy. Using the bottle method, Ref. Gonzalez et al. (2021) found the lifetime of the neutron to be 877.75 s, which is very close to the lifetime measured in Ref. Pattie et al. (2018) and Ref. Serebrov et al. (2018). On the other hand, using the beam method the lifetime measured has been measured to be 887.7 s Pattie et al. (2018).
A resolution of this discrepancy in the lifetime of the neutrons could potentially lead to new physics. A solution along those lines was recently proposed by Fornal and Grinstein Fornal and Grinstein (2018); Grinstein et al. (2019); Fornal and Grinstein (2020), who proposed an extra decay channel of the neutron into dark matter. Based on the difference in lifetimes, they suggested that roughly 1% of the time neutrons decay into dark matter, wile for the remaining 99% of the time they undergo decay. In the beam method the dark matter would go undetected and uncounted, while in the bottle method the effect of dark matter is automatically included.
According to the hypothesis of Fornal and Grinstein the dark decay mode of the neutron is
| (1) |
where is the dark fermion and the dark boson. This hypothesis has attracted the interest of many physicists. For example, experimental studies showed very quickly that the particle could not be a photon Tang et al. (2018); Serebrov et al. (2008). The hypothesis was also very rapidly subject to tests using the properties the neutron stars, which indicated that the dark fermions, , has to experience a strong vector repulsion in order to be consistent with the observations Motta et al. (2018a, b); Baym et al. (2018); McKeen et al. (2018). A recent study Husain et al. (2022) suggested that there might be an observable signal of this decay if one could observe the neutron star right after its birth. An interesting discussion about the neutron decay can be found in Ivanov et al. (2018).
An alternative to the Fornal and Grinstein hypothesis was proposed by Strumia in Ref. Strumia (2021), where the author suggested that the neutrons might decay into three identical dark fermions, ,
| (2) |
with each of them having baryon number 1/3 and mass = (mass of neutron)/3. An advantage of this proposal was that, to be consistent with the constraint on the maximum mass of neutron stars, the dark fermions, , are not required to be self-interacting. Our recent study in Ref. Husain and Thomas (2022) on the Strumia hypothesis agrees with this claim and indicated that one could find observable signals of neutron decay similar to those found within the Fornal and Grinstein hypothesis.
Within the Fornal and Grinstein hypothesis, shown in Eq. (1), the mass of the decay products must be in the range 937.9 MeV ¡ ¡ 938.7 MeV for the known stable nuclei to remain stable Fornal and Grinstein (2018); Grinstein et al. (2019). To date, most of the studies on the hypothesis using neutron stars, have considered the as an extremely light particle which escapes the neutron star immediately and treating the as almost degenerate with the neutron. There is a possibility that if boson has a mass close to the difference of the masses of the neutron and the , for example of order 1 MeV, then it may remain trapped inside the neutron star.
Here, the focus is on trapped bosons and their effects on neutron star heating. This leads to a strong constraint on the lifetime of the , which is then compared with limits from other studies of dark matter candidates. The manuscript is divided into sections as follows. Section II covers the necessary model for the equation of state of nuclear matter inside the neutron star and explains the change associated with neutron decay into and . This is followed by section III, where the consequence of trapping the boson are explored. In section IV the decay modes of the boson have been studied in detail. Finally, section V presents a summary of our findings.
II Neutron stars
Neutron stars are comparatively small objects that come into existence when an ordinary star of mass 8 M⊙ - 15 M⊙ dies. Neutrons are not surprisingly the dominant component of a neutron star and if neutrons decay into and then this decay must also take place inside the neutron star. Therefore, the neutron stars must contain fermions and in the circumstances explained earlier also bosons, and their presence inside neutron stars must change their properties Mukhopadhyay et al. (2017); Bertone and Fairbairn (2008); Kouvaris (2008); Ciarcelluti and Sandin (2011); Sandin and Ciarcelluti (2009); Leung et al. (2011); Ellis et al. (2018); Bell et al. (2020); Husain and Thomas (2021); Mielke and Schunck (2000); Blinnikov and Khlopov (1983); McKeen et al. (2018); Horowitz and Reddy (2019); Bertoni et al. (2013); Berryman et al. (2022); McKeen et al. (2021); de Lavallaz and Fairbairn (2010); Busoni (2021); Sen and Guha (2021); Guha and Sen (2021). There are some strong constraints on the properties of neutron stars imposed by observations that a realistic neutron star model must follow. For example, Ref. Abbott et al. (2018) showed that a neutron star of mass 1.4 M⊙ should have a radius 10 - 14 km. PSR J1614-2230 Demorest et al. (2010) and PSR J0348+0432 Antoniadis et al. (2013) have masses 1.928 and 2.01 M⊙, respectively, so the neutron star model must predict maximum mass of neutron stars at least 2 M⊙ 222Note that recent observations of pulsars PSR J0030+0451Riley et al. (2019), and PSR J0740+6620 Riley et al. (2021) constrain their masses and radii to be 1.34 M⊙ and 12.71 km and 2.072 M⊙ and 12.39 km respectively. See also Miller et al. (2019, 2021). . The tidal deformability should be consistent with the discovery Abbott et al. (2017, 2019) of gravitational wave detection by LIGO and VIRGO observatories. Therefore neutrons stars can be very helpful in testing the Fornal and Grinstein hypothesis.
Neutron star interiors covers a wide range of densities right from the surface to the core Lawley et al. (2006); Whittenbury et al. (2014, 2016); Bodmer (1971); Witten (1984); Bombaci et al. (2004); Ren and Zhang (2020); Terazawa (1989); Bednarek et al. (2012); Vidaña (2015); Oertel et al. (2016); Akmal et al. (1998); Balberg and Gal (1997); Glendenning (1985); Kaplan and Nelson (1986); Glendenning et al. (1997); Glendenning and Moszkowski (1991); Glendenning (1997); Haensel and Zdunik (2017); Shuryak (1980); Weber et al. (2007); Spinella and Weber (2019); Weber (2016); Terazawa (2001); Husain and Thomas (2021); Lattimer and Prakash (2001); Zhao and Lattimer (2020); Drischler et al. (2021); Cierniak and Blaschke (2021); Shahrbaf et al. (2022); Nishizaki et al. (2002); Yamamoto et al. (2017, 2022); Motta and Thomas (2022), with the cores containing the most dense matter in the universe. To model the neutron star, one needs to adopt a suitable equation of state for the nuclear matter. At the core of a neutron star the density could be as high as 6 times the density of normal matter. Therefore, one needs to chose a model capable of describing the physics at such high densities. In this study quark meson coupling (QMC) model Guichon (1988); Guichon et al. (1996); Stone et al. (2016); Rikovska Stone et al. (2007) is adopted to model the neutron star matter. A brief description of the QMC model is presented below.
II.1 Quark Meson Coupling model
The quark meson coupling model was initially proposed by Guichon Guichon (1988) and further developed by Guichon, Thomas and collaborators Guichon et al. (1996); Saito et al. (2007). In this model the nucleons are treated as a collection of 3 quarks confined in an MIT bag DeGrand et al. (1975). The internal structure of the nucleon is treated with great importance, unlike other models where nucleons are considered as a point like objects. In the QMC model the interaction between baryons is generated by the exchange of mesons, which couple self-consistently to the confined quarks. The strong scalar mean field in particular drives significant changes in the structure of the bound baryons.
The equation of state based on the QMC model has shown been shown to lead to an acceptable description of neutron star properties Rikovska Stone et al. (2007); Motta and Thomas (2022); Husain and Thomas (2022). The effective mass of the nucleon in-medium may be expressed in terms of the scalar polarisability, ’’, the mass of the free nucleon, , and the coupling constant of the field to the nucleon in free space, , as
| (3) |
The details of QMC model can be found in Refs. Guichon (1988); Guichon et al. (1996, 2018). For simplicity, in this study it is assumed that neutron stars do not contain hyperons or strange matter at the higher energy densities, a nucleon only equation of state is used Husain et al. (2022).
II.2 Formalism including neutron decay
According to the hypothesis given in Eq. (1), the neutron stars must contain and . As mentioned above there is no a priori constraint on the mass of the , within the small window allowed. We have chosen to study the case = 1 MeV, = 937.7 MeV in this work, where is the mass of boson and the mass of the fermion. In this case the velocity of the boson is sufficiently low that it will be trapped inside the neutron star.
Inside the neutron star the bosons must condense, according the Bose-Einstein condensation theory Husain et al. (2022); Motta et al. (2019). But the total contribution of the will be far too small to make any significant changes in the existing mass, radius, and tidal deformability constraints, even after condensation. In fact, we will see in later sections that the contribution of the bosons to the total mass is only about 1/106 M⊙. Although this is small, nevertheless amount of mass may contribute to the heating of the neutron star if the bosons decay into standard model particles. Therefore the focus of this study is on the boson decay into standard model particles inside neutron stars.
The equations are solved using Hartree-Fock approximation. The full Hartree-Fock terms can be found in Husain et al. (2022); Motta et al. (2019); Krein et al. (1999). Although the bosons will be in the lowest possible quantum state, the dark fermions will constitute a gas of fermions. The dark fermions are assumed to be self-interacting, in order to survive against the observational constraints on the neutron star properties. The self-interaction of the dark fermions is assumed to be similar to the neutron- interaction.
The presence of and inside the neutron stars changes their composition. Therefore, the chemical equilibrium equations are Motta et al. (2018b, a)
| (4) |
where represents the chemical potential of the different associated particles, and , and stand for the number of neutrons, protons, electrons. The dark fermions, dark bosons and nuclear matter particles are assumed to not interact with each other. Therefore, the neutron star contains two non-interacting fluids. However, because the contribution of the dark matter compared to nuclear matter is very small, using the two-fluid TOV equation is not necessary. Therefore for ease of the calculation one fluid TOV is used.
II.3 Tolman Oppenheimer Volkoff (TOV) equations
To calculate the properties of the neutron star the equation of state is combined with the structural equations derived using the Einstein’s equations of general relativity. Therefore, the TOV equations Tolman (1934); Oppenheimer and Volkoff (1939); Ciarcelluti and Sandin (2011); Sandin and Ciarcelluti (2009) given as
| (5) |
| (6) |
are integrated from the centre of the neutron star towards the surface, using the boundary conditions that at the surface the pressure and energy density should be zero. Here, is the total pressure, and is the total energy density, including the energy density of nuclear matter and dark matter. The tidal deformability is calculated by using the method explained in Ref. Hinderer (2008); Hinderer et al. (2010).
III Results
In this section the consequences of the neutron decay on the properties of the neutron stars are given. The vector interaction of dark fermions is increased until it follows the constraint Motta et al. (2018b); Grinstein et al. (2019); Baym et al. (2018); Cline and Cornell (2018); Berryman et al. (2022); Strumia (2021); Rajendran and Ramani (2021); Tang et al. (2018); Berezhiani et al. (2021) on the properties of the neutron stars.
As shown in Fig. (1), the mass of the neutron star is reduced after the neutron decay. In fact, the maximum mass of the neutron star falls below 2 M⊙ after the neutron decay Motta et al. (2018a); Baym et al. (2018); McKeen et al. (2018) if the dark fermions are considered to be non-self-interacting. However, neutron stars of mass above 2 M⊙ Özel and Freire (2016); Demorest et al. (2010); Antoniadis et al. (2013) have been observed. Therefore, in order to survive, a neutron star model must predict neutron stars of maximum mass of at least 2 M⊙. Fig. (1) indicates that the dark fermions must have self-repulsion with a strength parameter of order 26 fm2 to be consistent with the observations. Moreover, there is a significant reduction in the radius of the neutron stars after the decay, which suggest that neutron stars should spin up during the decay.
Figure (2) shows the tidal deformability against the radius of the neutron star. The analysis of the gravitational waves Abbott et al. (2017, 2019); Bramante et al. (2018) indicated that a neutron star of mass 1.4 M⊙ must have tidal deformability in the range 70 - 580, with 90% confidence level. Fig. (2) shows that dark fermions with a vector self-repulsion of strength 26 fm2 satisfy the constraint on mass and tidal deformability.
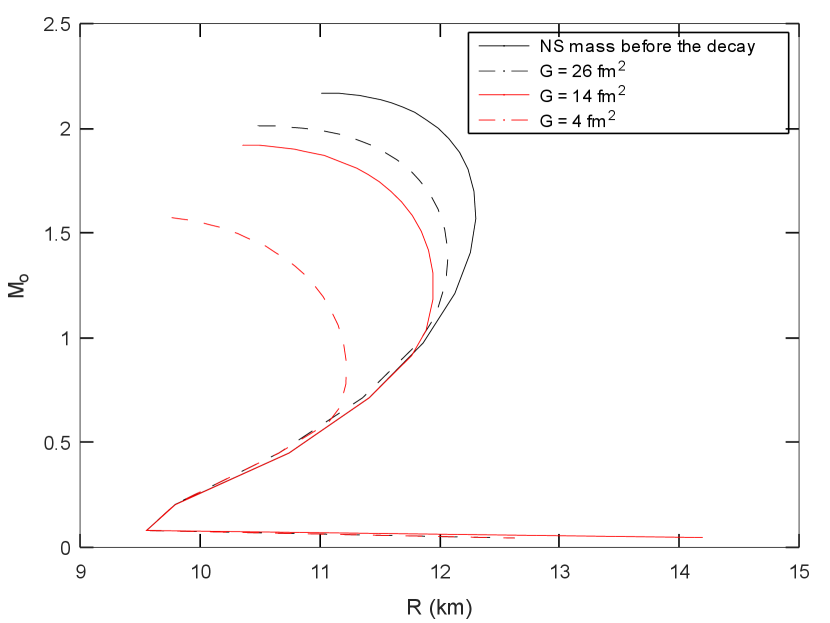
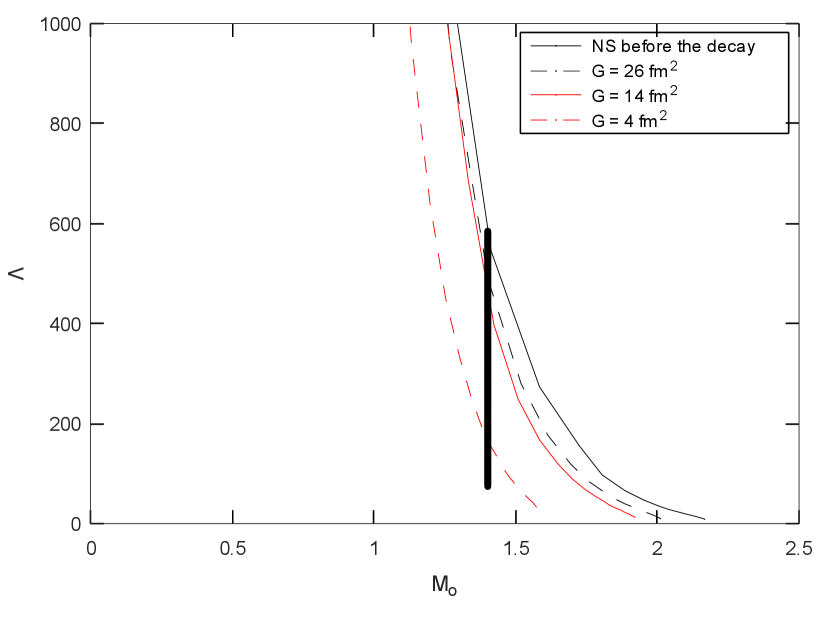
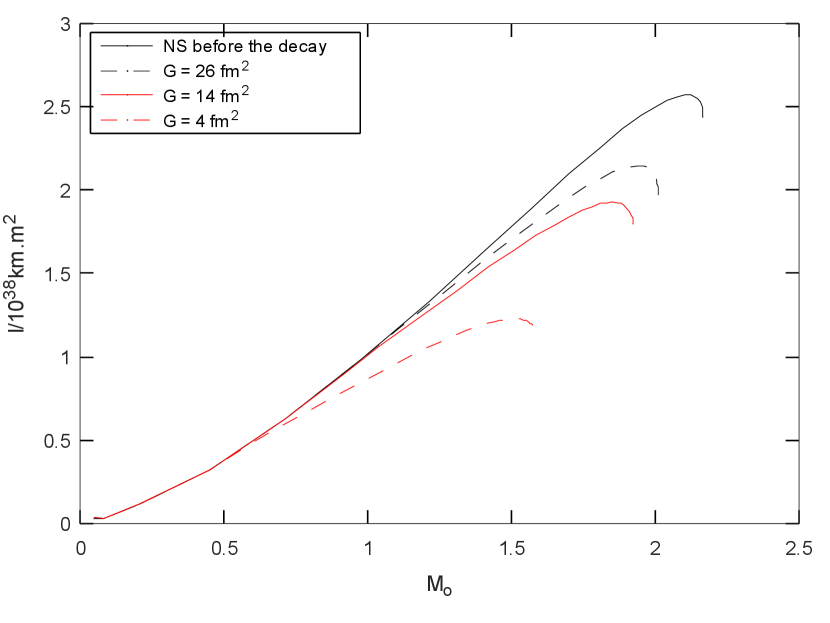
Figure 3 shows the moment of inertia against the mass of the neutron star. The moment of inertia is reduced after the neutron decay. When the dark fermion vector-interaction is lowered the difference in moment of inertia increases. Thus we are only interested in the case when the dark fermions, , have a vector interaction strength 26 fm2. Figure 3 indicates that the moment of inertia of heavier neutron stars is significantly reduced even when 26fm2, which should result in spinning up of the neutron star. That in turn may provide a signal of the neutron’s exotic decay.
Most studies indicate that neutron stars cool down very quickly by the standard Urca process. After approximately a million years the neutron stars have a luminosity of order 1031.5 erg/s. Therefore, if the boson decays into photons it will contribute to the heating of the neutron star and after a million years it must not contribute a luminosity 1031.5 erg/s. Based on the luminosity after 1 million years, we find that the lifetime () of the bosons must be greater than 1.85 1011 years. With such a long lifetime the luminosity stays essentially constant.
In the next section the consequences of boson decay into standard model particles are explored.
IV Decay modes of bosons
The decay products of the neutron, the and are BSM particles (particles beyond the Standard Model) that can originate from some UV complete theory or be considered within some low energy effective theory. While remaining agnostic about their origin we can comment on the constraints on them from a variety of sources. The massive fermion, , is an ideal candidate for dark matter and can form the bulk or all of the observed relic density today. We leave a detailed discussion on the details of this mechanism for a later expanded work. The other product of the decay, the boson, can originate from a BSM source. On general grounds and experimental considerations the possibility that the boson is a photon has been ruled out. Here we consider some simple possibilites for the bosons to couple SM particles, and constraints on the basis of findings in the previous sections.
IV.1 Scalars and Pseudoscalars
In the last few years light scalar and pseudo-scalar particles have emerged as leading new physics candidates that can be constrained from a variety of sources. While the primary motivation is derived from axions, simplified models with light scalars or pseudo-scalars have triggered a lot of attention. Here we assess their viability given our findings above.
The first bosonic candidate is a scalar coupled to the electromagnetic field strength,
| (7) |
where is the scalar field, the electromagnetic field strength, and the Dirac spinor for the leptons. The overall normalization is model dependent, while is the mass of the lepton. The linear couplings can be generated by from the scalar coupling to Higgs, as . A quadratic coupling can also be generated if carries a symmtery,
| (8) |
In both cases the dots indicate any other couplings that may be induced.
Couplings to the neutron can be obtained by integrating out, for example, heavy fermions yielding dimension 6 operators, such that the effective neutron coupling can be written as,
| (9) |
The linear (and quadratic) couplings induce a shift in the electromagnetic couplings that can be constrained from a variety of sources. A summary of these can be found in Ref. Antypas et al. (2022).
The next possibility is that of a pseudoscalar that couples like an axion (like particle) to photons, and derivatively to electrons
| (10) |
For axion-like particles in Eq. 10, the effective ALP coupling to leptons generates a coupling,
| (11) |
where the dots indicate terms proportional to . The decay widths to charged fermions are given by,
| (12) |
Analogous to scalars the effective ALP coupling to neutrons can be written as,
| (13) |
A comprehensive account of UV complete models and their phenomenological consequences is left for future work. In principle, since the bosons in our case are heavy, the most general Lagrangian will contain interaction terms involving not only photons and leptons, but hadrons as well.
The decay widths for pseudoscalars to diphotons are given by,
| (14) |
The lifetime is
| (15) |
where is the conversion factor from to seconds. From the estimates derived above, for a boson mass of 1 MeV, a lifetime of years, and if this is only decay channel relevant, the effective coupling, . Note that a lifetime of years is about seconds. The lifetime of the universe is about seconds and therefore this boson is cosmologically stable and should add to the total relic density of the universe. The exact amount of dark matter density depends on the co-efficient , as well as the decay constant . Typically in axion like models, like the ones considered here, we can obtain a significant fraction of the dark matter with a (1) misallignement angle.
There are however significant constraints of models of this class. For scalars and pseudoscalars, one of the strongest constraints at this mass originates from the consideration that photons produced during ALP decays when the Universe is transparent should not exceed the total extragalactic background light (EBL) Cadamuro and Redondo (2012). For pseudoscalar ALPs, this limits lifetimes to seconds, such that the effective ALP coupling is restricted . Furthermore X-rays produced from ALP decays in galaxies must not exceed the known backgrounds. This limits seconds leading to an effective coupling Cadamuro and Redondo (2012).
IV.2 Spin-1
While the decay to a photon has been ruled out, a possible solution is that the spin-1 boson can be a dark (kinetically) mixed photon. The massless part of the most general theory of two Abelian gauge bosons can be written as,
| (16) |
The masses of these can be obtained via a Stuckelberg mechanism, or via a spontaneously broken gauge symmetry
| (17) |
Consider a hypercharge mixing with the usual photon,
| (18) |
Then, the effective Lagrangian becomes,
| (19) |
where and are the dark sector current and the dark photon coupling to the dark sector. Once the boson is integrated out we can see that the coupling of the dark photon to SM fermions is proportional to , i.e., millicharged dark photons which are constrained from various sources. The effective coupling to neutrons can be written as,
| (20) |
Below the two electron threshold, the constraints on dark photons originate from stellar cooling bounds and from the Xenon-1T experiments Caputo et al. (2021); Aprile et al. (2022). The constraints on the kinetic mixing parameter is for .
If the dark photon is extremely light, if produced non-thermally like a condensate, like the axion with a misallignement mechanism. In this case the mass is generated by the Stuckelberg mechanism, and the generation of the relic follows like the usual axion.
Additionally, in most relevant models, the dark photon is accompanied to dark fermions. Here dark photon can account for the relic density through a freeze-in mechanism within the dark sector or through feeble couplings to SM.
V Conclusion
In this work, we explored the consequences of neutron decays into a dark sector inside neutron stars. Working on the hypothesis that , we analyzed the feasibility of this decay by studying the effect of the corresponding equation of state on the properties of the neutron star, including its mass, radius and tidal deformability. We then focused on the possibility that the remains trapped inside the star leading to heating. We concluded that if the has a mass of around 1 MeV, based upon observations of luminosity of stars as a function of age, the must have a lifetime greater than years. Finally we studied the consequences and of a coupled to standard model particles within simplified ALP like models. An expanded work with cosmological consequences, as well as a study of UV completions, is left for future work.
Acknowledgements.
This study has been supported by a University of Adelaide International Scholarship (WH) and by the Australian Research Council through the ARC Centre for Dark Matter Particle Physics (CE200100008).References
- Wietfeldt and Greene (2011) Wietfeldt, F.E.; Greene, G.L. Colloquium: The neutron lifetime. Rev. Mod. Phys. 2011, 83, 1173–1192. https://doi.org/10.1103/RevModPhys.83.1173.
- Serebrov et al. (2018) Serebrov, A.P.; et al. Neutron lifetime measurements with a large gravitational trap for ultracold neutrons. Phys. Rev. C 2018, 97, 055503, [arXiv:nucl-ex/1712.05663]. https://doi.org/10.1103/PhysRevC.97.055503.
- Pattie et al. (2018) Pattie, Jr., R.W.; et al. Measurement of the neutron lifetime using a magneto-gravitational trap and in situ detection. Science 2018, 360, 627–632, [arXiv:nucl-ex/1707.01817]. https://doi.org/10.1126/science.aan8895.
- Tan (2019) Tan, W. Neutron oscillations for solving neutron lifetime and dark matter puzzles. Physics Letters B 2019, 797, 134921. https://doi.org/https://doi.org/10.1016/j.physletb.2019.134921.
- Steyerl et al. (2012) Steyerl, A.; Pendlebury, J.M.; Kaufman, C.; Malik, S.S.; Desai, A.M. Quasielastic scattering in the interaction of ultracold neutrons with a liquid wall and application in a reanalysis of the Mambo I neutron-lifetime experiment. Phys. Rev. C 2012, 85, 065503. https://doi.org/10.1103/PhysRevC.85.065503.
- Yue et al. (2013) Yue, A.T.; Dewey, M.S.; Gilliam, D.M.; Greene, G.L.; Laptev, A.B.; Nico, J.S.; Snow, W.M.; Wietfeldt, F.E. Improved Determination of the Neutron Lifetime. Phys. Rev. Lett. 2013, 111, 222501. https://doi.org/10.1103/PhysRevLett.111.222501.
- Otono (2017) Otono, H. LiNA – Lifetime of neutron apparatus with time projection chamber and solenoid coil. Nucl. Instrum. Meth. A 2017, 845, 278–280, [arXiv:physics.ins-det/1603.06572]. https://doi.org/10.1016/j.nima.2016.05.042.
- Olive (2016) Olive, K. Review of Particle Physics. Chinese Physics C 2016, 40, 100001. https://doi.org/10.1088/1674-1137/40/10/100001.
- Gonzalez et al. (2021) Gonzalez, F.M.; et al. Improved Neutron Lifetime Measurement with UCN. Phys. Rev. Lett. 2021, 127, 162501, [arXiv:nucl-ex/2106.10375]. https://doi.org/10.1103/PhysRevLett.127.162501.
- Pattie et al. (2018) Pattie, R.W.; Callahan, N.B.; Cude-Woods, C.; Adamek, E.R.; Broussard, L.J.; Clayton, S.M.; Currie, S.A.; Dees, E.B.; Ding, X.; Engel, E.M.; et al. Measurement of the neutron lifetime using a magneto-gravitational trap and in situ detection. Science 2018, 360, 627–632, [https://www.science.org/doi/pdf/10.1126/science.aan8895]. https://doi.org/10.1126/science.aan8895.
- Serebrov et al. (2018) Serebrov, A.P.; Kolomensky, E.A.; Fomin, A.K.; Krasnoshchekova, I.A.; Vassiljev, A.V.; Prudnikov, D.M.; Shoka, I.V.; Chechkin, A.V.; Chaikovskiy, M.E.; Varlamov, V.E.; et al. Neutron lifetime measurements with a large gravitational trap for ultracold neutrons. Phys. Rev. C 2018, 97, 055503. https://doi.org/10.1103/PhysRevC.97.055503.
- Fornal and Grinstein (2018) Fornal, B.; Grinstein, B. Dark Matter Interpretation of the Neutron Decay Anomaly. Phys. Rev. Lett. 2018, 120, 191801, [arXiv:hep-ph/1801.01124]. [Erratum: Phys.Rev.Lett. 124, 219901 (2020)], https://doi.org/10.1103/PhysRevLett.120.191801.
- Grinstein et al. (2019) Grinstein, B.; Kouvaris, C.; Nielsen, N.G. Neutron Star Stability in Light of the Neutron Decay Anomaly. Phys. Rev. Lett. 2019, 123, 091601, [arXiv:hep-ph/1811.06546]. https://doi.org/10.1103/PhysRevLett.123.091601.
- Fornal and Grinstein (2020) Fornal, B.; Grinstein, B. Neutron’s dark secret. Mod. Phys. Lett. A 2020, 35, 2030019, [arXiv:hep-ph/2007.13931]. https://doi.org/10.1142/S0217732320300190.
- Tang et al. (2018) Tang, Z.; et al. Search for the Neutron Decay n X+ where X is a dark matter particle. Phys. Rev. Lett. 2018, 121, 022505, [arXiv:nucl-ex/1802.01595]. https://doi.org/10.1103/PhysRevLett.121.022505.
- Serebrov et al. (2008) Serebrov, A.P.; et al. Experimental search for neutron: Mirror neutron oscillations using storage of ultracold neutrons. Phys. Lett. B 2008, 663, 181–185, [arXiv:nucl-ex/0706.3600]. https://doi.org/10.1016/j.physletb.2008.04.014.
- Motta et al. (2018a) Motta, T.F.; Guichon, P.A.M.; Thomas, A.W. Implications of Neutron Star Properties for the Existence of Light Dark Matter. J. Phys. G 2018, 45, 05LT01, [arXiv:nucl-th/1802.08427]. https://doi.org/10.1088/1361-6471/aab689.
- Motta et al. (2018b) Motta, T.F.; Guichon, P.A.M.; Thomas, A.W. Neutron to Dark Matter Decay in Neutron Stars. Int. J. Mod. Phys. A 2018, 33, 1844020, [arXiv:nucl-th/1806.00903]. https://doi.org/10.1142/S0217751X18440207.
- Baym et al. (2018) Baym, G.; Beck, D.H.; Geltenbort, P.; Shelton, J. Testing Dark Decays of Baryons in Neutron Stars. Phys. Rev. Lett. 2018, 121, 061801. https://doi.org/10.1103/PhysRevLett.121.061801.
- McKeen et al. (2018) McKeen, D.; Nelson, A.E.; Reddy, S.; Zhou, D. Neutron Stars Exclude Light Dark Baryons. Physical Review Letters 2018, 121. https://doi.org/10.1103/physrevlett.121.061802.
- Husain et al. (2022) Husain, W.; Motta, T.F.; Thomas, A.W. Consequences of neutron decay inside neutron stars. JCAP 2022, 10, 028, [arXiv:hep-ph/2203.02758]. https://doi.org/10.1088/1475-7516/2022/10/028.
- Ivanov et al. (2018) Ivanov, A.N.; Höllwieser, R.; Troitskaya, N.I.; Wellenzohn, M.; Berdnikov, Y.A. Neutron Dark Matter Decays 2018. [arXiv:hep-ph/1806.10107].
- Strumia (2021) Strumia, A. Dark Matter interpretation of the neutron decay anomaly 2021. [arXiv:hep-ph/2112.09111].
- Husain and Thomas (2022) Husain, W.; Thomas, A.W. Novel neutron decay mode inside neutron stars 2022. [arXiv:hep-ph/2206.11262].
- Mukhopadhyay et al. (2017) Mukhopadhyay, S.; Atta, D.; Imam, K.; Basu, D.N.; Samanta, C. Compact bifluid hybrid stars: hadronic matter mixed with self-interacting fermionic asymmetric dark matter. The European Physical Journal C 2017, 77. https://doi.org/10.1140/epjc/s10052-017-5006-3.
- Bertone and Fairbairn (2008) Bertone, G.; Fairbairn, M. Compact stars as dark matter probes. Phys. Rev. D 2008, 77, 043515. https://doi.org/10.1103/PhysRevD.77.043515.
- Kouvaris (2008) Kouvaris, C. WIMP annihilation and cooling of neutron stars. Phys. Rev. D 2008, 77, 023006. https://doi.org/10.1103/PhysRevD.77.023006.
- Ciarcelluti and Sandin (2011) Ciarcelluti, P.; Sandin, F. Have neutron stars a dark matter core? Physics Letters B 2011, 695, 19–21. https://doi.org/https://doi.org/10.1016/j.physletb.2010.11.021.
- Sandin and Ciarcelluti (2009) Sandin, F.; Ciarcelluti, P. Effects of mirror dark matter on neutron stars. Astroparticle Physics 2009, 32, 278–284. https://doi.org/10.1016/j.astropartphys.2009.09.005.
- Leung et al. (2011) Leung, S.C.; Chu, M.C.; Lin, L.M. Dark-matter admixed neutron stars. Phys. Rev. D 2011, 84, 107301, [arXiv:astro-ph.CO/1111.1787]. https://doi.org/10.1103/PhysRevD.84.107301.
- Ellis et al. (2018) Ellis, J.; Hütsi, G.; Kannike, K.; Marzola, L.; Raidal, M.; Vaskonen, V. Dark matter effects on neutron star properties. Physical Review D 2018, 97. https://doi.org/10.1103/physrevd.97.123007.
- Bell et al. (2020) Bell, N.F.; Busoni, G.; Motta, T.F.; Robles, S.; Thomas, A.W.; Virgato, M. Nucleon Structure and Strong Interactions in Dark Matter Capture in Neutron Stars, 2020, [arXiv:hep-ph/2012.08918].
- Husain and Thomas (2021) Husain, W.; Thomas, A.W. Possible nature of dark matter. Journal of Cosmology and Astroparticle Physics 2021, 2021, 086. https://doi.org/10.1088/1475-7516/2021/10/086.
- Mielke and Schunck (2000) Mielke, E.W.; Schunck, F.E. Boson stars: alternatives to primordial black holes? Nuclear Physics B 2000, 1, 185–203, [arXiv:gr-qc/gr-qc/0001061]. https://doi.org/10.1016/S0550-3213(99)00492-7.
- Blinnikov and Khlopov (1983) Blinnikov, S.I.; Khlopov, M. Possible astronomical effects of mirror particles. Sov. Astron. 1983, 27, 371–375.
- Horowitz and Reddy (2019) Horowitz, C.; Reddy, S. Gravitational Waves from Compact Dark Objects in Neutron Stars. Physical Review Letters 2019, 122. https://doi.org/10.1103/physrevlett.122.071102.
- Bertoni et al. (2013) Bertoni, B.; Nelson, A.E.; Reddy, S. Dark matter thermalization in neutron stars. Physical Review D 2013, 88. https://doi.org/10.1103/physrevd.88.123505.
- Berryman et al. (2022) Berryman, J.M.; Gardner, S.; Zakeri, M. Neutron Stars with Baryon Number Violation, Probing Dark Sectors, 2022, [arXiv:hep-ph/2201.02637].
- McKeen et al. (2021) McKeen, D.; Pospelov, M.; Raj, N. Neutron Star Internal Heating Constraints on Mirror Matter. Phys. Rev. Lett. 2021, 127, 061805, [arXiv:hep-ph/2105.09951]. https://doi.org/10.1103/PhysRevLett.127.061805.
- de Lavallaz and Fairbairn (2010) de Lavallaz, A.; Fairbairn, M. Neutron Stars as Dark Matter Probes. Phys. Rev. D 2010, 81, 123521, [arXiv:astro-ph.GA/1004.0629]. https://doi.org/10.1103/PhysRevD.81.123521.
- Busoni (2021) Busoni, G. Capture of Dark Matter in Neutron Stars 2021. [arXiv:hep-ph/2201.00048].
- Sen and Guha (2021) Sen, D.; Guha, A. Implications of feebly interacting dark sector on neutron star properties and constraints from GW170817. Mon. Not. Roy. Astron. Soc. 2021, 504, 3, [arXiv:hep-ph/2104.06141]. https://doi.org/10.1093/mnras/stab1056.
- Guha and Sen (2021) Guha, A.; Sen, D. Feeble DM-SM interaction via new scalar and vector mediators in rotating neutron stars. JCAP 2021, 09, 027, [arXiv:hep-ph/2106.10353]. https://doi.org/10.1088/1475-7516/2021/09/027.
- Abbott et al. (2018) Abbott, B.P.; et al. GW170817: Measurements of neutron star radii and equation of state. Phys. Rev. Lett. 2018, 121, 161101, [arXiv:gr-qc/1805.11581]. https://doi.org/10.1103/PhysRevLett.121.161101.
- Demorest et al. (2010) Demorest, P.B.; Pennucci, T.; Ransom, S.M.; Roberts, M.S.E.; Hessels, J.W.T. A two-solar-mass neutron star measured using Shapiro delay. nat 2010, 467, 1081–1083, [arXiv:astro-ph.HE/1010.5788]. https://doi.org/10.1038/nature09466.
- Antoniadis et al. (2013) Antoniadis, J.; Freire, P.C.C.; Wex, N.; Tauris, T.M.; Lynch, R.S.; van Kerkwijk, M.H.; Kramer, M.; Bassa, C.; Dhillon, V.S.; Driebe, T.; et al. A Massive Pulsar in a Compact Relativistic Binary. Science 2013, 340, 448, [arXiv:astro-ph.HE/1304.6875]. https://doi.org/10.1126/science.1233232.
- Riley et al. (2019) Riley, T.E.; et al. A View of PSR J0030+0451: Millisecond Pulsar Parameter Estimation. Astrophys. J. Lett. 2019, 887, L21, [arXiv:astro-ph.HE/1912.05702]. https://doi.org/10.3847/2041-8213/ab481c.
- Riley et al. (2021) Riley, T.E.; et al. A NICER View of the Massive Pulsar PSR J0740+6620 Informed by Radio Timing and XMM-Newton Spectroscopy. Astrophys. J. Lett. 2021, 918, L27, [arXiv:astro-ph.HE/2105.06980]. https://doi.org/10.3847/2041-8213/ac0a81.
- Miller et al. (2019) Miller, M.C.; et al. PSR J0030+0451 Mass and Radius from Data and Implications for the Properties of Neutron Star Matter. Astrophys. J. Lett. 2019, 887, L24, [arXiv:astro-ph.HE/1912.05705]. https://doi.org/10.3847/2041-8213/ab50c5.
- Miller et al. (2021) Miller, M.C.; et al. The Radius of PSR J0740+6620 from NICER and XMM-Newton Data. Astrophys. J. Lett. 2021, 918, L28, [arXiv:astro-ph.HE/2105.06979]. https://doi.org/10.3847/2041-8213/ac089b.
- Abbott et al. (2017) Abbott, B.; Abbott, R.; Abbott, T.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.; Adya, V.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Physical Review Letters 2017, 119. https://doi.org/10.1103/physrevlett.119.161101.
- Abbott et al. (2019) Abbott, B.; Abbott, R.; Abbott, T.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.; Adya, V.; Affeldt, C.; et al. GWTC-1: A Gravitational-Wave Transient Catalog of Compact Binary Mergers Observed by LIGO and Virgo during the First and Second Observing Runs. Physical Review X 2019, 9. https://doi.org/10.1103/physrevx.9.031040.
- Lawley et al. (2006) Lawley, S.; Bentz, W.; Thomas, A.W. Nucleons, nuclear matter and quark matter: A Unified NJL approach. J. Phys. G 2006, 32, 667–680, [nucl-th/0602014]. https://doi.org/10.1088/0954-3899/32/5/006.
- Whittenbury et al. (2014) Whittenbury, D.L.; Carroll, J.D.; Thomas, A.W.; Tsushima, K.; Stone, J.R. Quark-Meson Coupling Model, Nuclear Matter Constraints and Neutron Star Properties. Phys. Rev. C 2014, 89, 065801, [arXiv:nucl-th/1307.4166]. https://doi.org/10.1103/PhysRevC.89.065801.
- Whittenbury et al. (2016) Whittenbury, D.L.; Matevosyan, H.H.; Thomas, A.W. Hybrid stars using the quark-meson coupling and proper-time Nambu–Jona-Lasinio models. Phys. Rev. C 2016, 93, 035807, [arXiv:nucl-th/1511.08561]. https://doi.org/10.1103/PhysRevC.93.035807.
- Bodmer (1971) Bodmer, A.R. Collapsed Nuclei. Phys. Rev. D 1971, 4, 1601–1606. https://doi.org/10.1103/PhysRevD.4.1601.
- Witten (1984) Witten, E. Cosmic separation of phases. Phys. Rev. D 1984, 30, 272–285. https://doi.org/10.1103/PhysRevD.30.272.
- Bombaci et al. (2004) Bombaci, I.; Parenti, I.; Vidana, I. Quark Deconfinement and Implications for the Radius and the Limiting Mass of Compact Stars. The Astrophysical Journal 2004, 614, 314–325. https://doi.org/10.1086/423658.
- Ren and Zhang (2020) Ren, J.; Zhang, C. Quantum nucleation of up-down quark matter and astrophysical implications. Phys. Rev. D 2020, 102, 083003. https://doi.org/10.1103/PhysRevD.102.083003.
- Terazawa (1989) Terazawa, H. Super-Hypernuclei in the Quark-Shell Model. Journal of the Physical Society of Japan 1989, 58, 3555–3563, [https://doi.org/10.1143/JPSJ.58.3555]. https://doi.org/10.1143/JPSJ.58.3555.
- Bednarek et al. (2012) Bednarek, I.; Haensel, P.; Zdunik, J.L.; Bejger, M.; Mańka, R. Hyperons in neutron-star cores and a 2M pulsar. Astronomy & Astrophysics 2012, 543, A157. https://doi.org/10.1051/0004-6361/201118560.
- Vidaña (2015) Vidaña, I. Hyperons and neutron stars. AIP Conference Proceedings 2015, 1645, 79–85, [https://aip.scitation.org/doi/pdf/10.1063/1.4909561]. https://doi.org/10.1063/1.4909561.
- Oertel et al. (2016) Oertel, M.; Gulminelli, F.; Providência, C.; Raduta, A.R. Hyperons in neutron stars and supernova cores. The European Physical Journal A 2016, 52. https://doi.org/10.1140/epja/i2016-16050-1.
- Akmal et al. (1998) Akmal, A.; Pandharipande, V.R.; Ravenhall, D.G. Equation of state of nucleon matter and neutron star structure. Phys. Rev. C 1998, 58, 1804–1828. https://doi.org/10.1103/PhysRevC.58.1804.
- Balberg and Gal (1997) Balberg, S.; Gal, A. An effective equation of state for dense matter with strangeness. Nuclear Physics A 1997, 625, 435–472. https://doi.org/https://doi.org/10.1016/S0375-9474(97)81465-0.
- Glendenning (1985) Glendenning, N.K. Neutron stars are giant hypernuclei ? apj 1985, 293, 470–493. https://doi.org/10.1086/163253.
- Kaplan and Nelson (1986) Kaplan, D.; Nelson, A. Strange goings on in dense nucleonic matter. Physics Letters B 1986, 175, 57–63. https://doi.org/https://doi.org/10.1016/0370-2693(86)90331-X.
- Glendenning et al. (1997) Glendenning, N.K.; Pei, S.; Weber, F. Signal of Quark Deconfinement in the Timing Structure of Pulsar Spin-Down. Phys. Rev. Lett. 1997, 79, 1603–1606. https://doi.org/10.1103/PhysRevLett.79.1603.
- Glendenning and Moszkowski (1991) Glendenning, N.K.; Moszkowski, S.A. Reconciliation of neutron-star masses and binding of the in hypernuclei. Phys. Rev. Lett. 1991, 67, 2414–2417. https://doi.org/10.1103/PhysRevLett.67.2414.
- Glendenning (1997) Glendenning, N.K., Quark Stars. In Compact Stars: Nuclear Physics, Particle Physics and General Relativity; Springer US: New York, NY, 1997; pp. 289–302. https://doi.org/10.1007/978-1-4684-0491-3_8.
- Haensel and Zdunik (2017) Haensel, P.; Zdunik, J.L., Nuclear Matter in Neutron Stars. In Handbook of Supernovae; Alsabti, A.W.; Murdin, P., Eds.; Springer International Publishing: Cham, 2017; pp. 1331–1351. https://doi.org/10.1007/978-3-319-21846-5_68.
- Shuryak (1980) Shuryak, E.V. Quantum chromodynamics and the theory of superdense matter. physrep 1980, 61, 71–158. https://doi.org/10.1016/0370-1573(80)90105-2.
- Weber et al. (2007) Weber, F.; Negreiros, R.; Rosenfield, P. Neutron Star Interiors and the Equation of State of Superdense Matter, 2007, [arXiv:astro-ph/0705.2708].
- Spinella and Weber (2019) Spinella, W.M.; Weber, F. Hyperonic neutron star matter in light of GW170817. Astronomische Nachrichten 2019, 340, 145–150. https://doi.org/10.1002/asna.201913579.
- Weber (2016) Weber, F., Strange Quark Matter Inside Neutron Stars. In Handbook of Supernovae; Alsabti, A.W.; Murdin, P., Eds.; Springer International Publishing: Cham, 2016; pp. 1–24. https://doi.org/10.1007/978-3-319-20794-0_71-1.
- Terazawa (2001) Terazawa, H. A new trend in high-energy physics: Current topics in nuclear and particle physics. In Proceedings of the International Conference on New Trends in High-Energy Physics: Experiment, Phenomenology, Theory, 2001, pp. 246–255.
- Husain and Thomas (2021) Husain, W.; Thomas, A.W. Hybrid stars with hyperons and strange quark matter. PROCEEDINGS OF THE 14TH ASIA-PACIFIC PHYSICS CONFERENCE 2021. https://doi.org/10.1063/5.0036994.
- Lattimer and Prakash (2001) Lattimer, J.M.; Prakash, M. Neutron Star Structure and the Equation of State. The Astrophysical Journal 2001, 550, 426–442. https://doi.org/10.1086/319702.
- Zhao and Lattimer (2020) Zhao, T.; Lattimer, J.M. Quarkyonic matter equation of state in beta-equilibrium. Physical Review D 2020, 102. https://doi.org/10.1103/physrevd.102.023021.
- Drischler et al. (2021) Drischler, C.; Han, S.; Lattimer, J.M.; Prakash, M.; Reddy, S.; Zhao, T. Limiting masses and radii of neutron stars and their implications. Physical Review C 2021, 103. https://doi.org/10.1103/physrevc.103.045808.
- Cierniak and Blaschke (2021) Cierniak, M.; Blaschke, D. Hybrid neutron stars in the mass-radius diagram. Astron. Nachr. 2021, 342, 819–825, [arXiv:nucl-th/2106.06986]. https://doi.org/10.1002/asna.202114000.
- Shahrbaf et al. (2022) Shahrbaf, M.; Blaschke, D.; Typel, S.; Farrar, G.R.; Alvarez-Castillo, D.E. Sexaquark dilemma in neutron stars and its solution by quark deconfinement 2022. [arXiv:nucl-th/2202.00652].
- Nishizaki et al. (2002) Nishizaki, S.; Yamamoto, Y.; Takatsuka, T. Hyperon-Mixed Neutron Star Matter and Neutron Stars*). Progress of Theoretical Physics 2002, 108, 703–718, [https://academic.oup.com/ptp/article-pdf/108/4/703/5414579/108-4-703.pdf]. https://doi.org/10.1143/PTP.108.703.
- Yamamoto et al. (2017) Yamamoto, Y.; Togashi, H.; Tamagawa, T.; Furumoto, T.; Yasutake, N.; Rijken, T.A. Neutron-star radii based on realistic nuclear interactions. Physical Review C 2017, 96. https://doi.org/10.1103/physrevc.96.065804.
- Yamamoto et al. (2022) Yamamoto, Y.; Yasutake, N.; Rijken, T.A. Quark-quark interaction and quark matter in neutron stars. Physical Review C 2022, 105. https://doi.org/10.1103/physrevc.105.015804.
- Motta and Thomas (2022) Motta, T.F.; Thomas, A.W. The role of baryon structure in neutron stars. Mod. Phys. Lett. A 2022, 37, 2230001, [arXiv:nucl-th/2201.11549]. https://doi.org/10.1142/S0217732322300014.
- Guichon (1988) Guichon, P.A.M. A Possible Quark Mechanism for the Saturation of Nuclear Matter. Phys. Lett. B 1988, 200, 235–240. https://doi.org/10.1016/0370-2693(88)90762-9.
- Guichon et al. (1996) Guichon, P.A.M.; Saito, K.; Rodionov, E.N.; Thomas, A.W. The Role of nucleon structure in finite nuclei. Nucl. Phys. A 1996, 601, 349–379, [nucl-th/9509034]. https://doi.org/10.1016/0375-9474(96)00033-4.
- Stone et al. (2016) Stone, J.R.; Guichon, P.A.M.; Reinhard, P.G.; Thomas, A.W. Finite Nuclei in the Quark-Meson Coupling Model. Phys. Rev. Lett. 2016, 116, 092501, [arXiv:nucl-th/1601.08131]. https://doi.org/10.1103/PhysRevLett.116.092501.
- Rikovska Stone et al. (2007) Rikovska Stone, J.; Guichon, P.; Matevosyan, H.; Thomas, A. Cold uniform matter and neutron stars in the quark–meson-coupling model. Nuclear Physics A 2007, 792, 341–369. https://doi.org/https://doi.org/10.1016/j.nuclphysa.2007.05.011.
- Saito et al. (2007) Saito, K.; Tsushima, K.; Thomas, A.W. Nucleon and hadron structure changes in the nuclear medium and impact on observables. Prog. Part. Nucl. Phys. 2007, 58, 1–167, [hep-ph/0506314]. https://doi.org/10.1016/j.ppnp.2005.07.003.
- DeGrand et al. (1975) DeGrand, T.A.; Jaffe, R.L.; Johnson, K.; Kiskis, J.E. Masses and Other Parameters of the Light Hadrons. Phys. Rev. D 1975, 12, 2060. https://doi.org/10.1103/PhysRevD.12.2060.
- Guichon et al. (2018) Guichon, P.A.M.; Stone, J.R.; Thomas, A.W. Quark–Meson-Coupling (QMC) model for finite nuclei, nuclear matter and beyond. Prog. Part. Nucl. Phys. 2018, 100, 262–297, [arXiv:nucl-th/1802.08368]. https://doi.org/10.1016/j.ppnp.2018.01.008.
- Motta et al. (2019) Motta, T.F.; Kalaitzis, A.M.; Antić, S.; Guichon, P.A.M.; Stone, J.R.; Thomas, A.W. Isovector Effects in Neutron Stars, Radii and the GW170817 Constraint. Astrophys. J. 2019, 878, 159, [arXiv:nucl-th/1904.03794]. https://doi.org/10.3847/1538-4357/ab218e.
- Krein et al. (1999) Krein, G.; Thomas, A.W.; Tsushima, K. Fock terms in the quark meson coupling model. Nucl. Phys. A 1999, 650, 313–325, [nucl-th/9810023]. https://doi.org/10.1016/S0375-9474(99)00117-7.
- Tolman (1934) Tolman, R.C. Effect of Inhomogeneity on Cosmological Models. Proceedings of the National Academy of Sciences 1934, 20, 169–176, [https://www.pnas.org/content/20/3/169.full.pdf]. https://doi.org/10.1073/pnas.20.3.169.
- Oppenheimer and Volkoff (1939) Oppenheimer, J.R.; Volkoff, G.M. On Massive Neutron Cores. Phys. Rev. 1939, 55, 374–381. https://doi.org/10.1103/PhysRev.55.374.
- Hinderer (2008) Hinderer, T. Tidal Love Numbers of Neutron Stars. The Astrophysical Journal 2008, 677, 1216–1220. https://doi.org/10.1086/533487.
- Hinderer et al. (2010) Hinderer, T.; Lackey, B.D.; Lang, R.N.; Read, J.S. Tidal deformability of neutron stars with realistic equations of state and their gravitational wave signatures in binary inspiral. Physical Review D 2010, 81. https://doi.org/10.1103/physrevd.81.123016.
- Cline and Cornell (2018) Cline, J.M.; Cornell, J.M. Dark decay of the neutron. JHEP 2018, 07, 081, [arXiv:hep-ph/1803.04961]. https://doi.org/10.1007/JHEP07(2018)081.
- Berryman et al. (2022) Berryman, J.M.; Gardner, S.; Zakeri, M. Neutron Stars with Baryon Number Violation, Probing Dark Sectors 2022. [arXiv:hep-ph/2201.02637].
- Rajendran and Ramani (2021) Rajendran, S.; Ramani, H. Composite solution to the neutron lifetime anomaly. Physical Review D 2021, 103. https://doi.org/10.1103/physrevd.103.035014.
- Tang et al. (2018) Tang, Z.; Blatnik, M.; Broussard, L.; Choi, J.; Clayton, S.; Cude-Woods, C.; Currie, S.; Fellers, D.; Fries, E.; Geltenbort, P.; et al. Search for the Neutron Decay n , Where is a Dark Matter Particle. Physical Review Letters 2018, 121. https://doi.org/10.1103/physrevlett.121.022505.
- Berezhiani et al. (2021) Berezhiani, Z.; Biondi, R.; Mannarelli, M.; Tonelli, F. Neutron-mirror neutron mixing and neutron stars. The European Physical Journal C 2021, 81. https://doi.org/10.1140/epjc/s10052-021-09806-1.
- McKeen et al. (2018) McKeen, D.; Nelson, A.E.; Reddy, S.; Zhou, D. Neutron stars exclude light dark baryons. Phys. Rev. Lett. 2018, 121, 061802, [arXiv:hep-ph/1802.08244]. https://doi.org/10.1103/PhysRevLett.121.061802.
- Özel and Freire (2016) Özel, F.; Freire, P. Masses, Radii, and the Equation of State of Neutron Stars. Ann. Rev. Astron. Astrophys. 2016, 54, 401–440, [arXiv:astro-ph.HE/1603.02698]. https://doi.org/10.1146/annurev-astro-081915-023322.
- Bramante et al. (2018) Bramante, J.; Linden, T.; Tsai, Y.D. Searching for dark matter with neutron star mergers and quiet kilonovae. Phys. Rev. D 2018, 97, 055016. https://doi.org/10.1103/PhysRevD.97.055016.
- Antypas et al. (2022) Antypas, D.; et al. New Horizons: Scalar and Vector Ultralight Dark Matter 2022. [arXiv:hep-ex/2203.14915].
- Cadamuro and Redondo (2012) Cadamuro, D.; Redondo, J. Cosmological bounds on pseudo Nambu-Goldstone bosons. JCAP 2012, 02, 032, [arXiv:hep-ph/1110.2895]. https://doi.org/10.1088/1475-7516/2012/02/032.
- Caputo et al. (2021) Caputo, A.; O’Hare, C.A.J.; Millar, A.J.; Vitagliano, E. Dark photon limits: a cookbook 2021. [arXiv:hep-ph/2105.04565].
- Aprile et al. (2022) Aprile, E.; Abe, K.; Agostini, F.; Ahmed Maouloud, S.; Alfonsi, M.; Althueser, L.; Angelino, E.; Angevaare, J.R.; Antochi, V.C.; Antón Martin, D.; et al. Emission of single and few electrons in XENON1T and limits on light dark matter. Phys. Rev. D 2022, 106, 022001. https://doi.org/10.1103/PhysRevD.106.022001.